浙江省杭州市学军中学等五校2020届高三下学期联考技术答案
2020届浙江省杭州市学军中学高三下学期高考模拟数学试题

2020届浙江省杭州市学军中学高三下学期高考模拟数学试题考生注意:1.全卷满分150分.考试用时120分钟.2.答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填在试题卷和答题纸规定的位置上.3.所有答案必须写在答题卷上,写在试卷上的答案一律无效.4.考试结束后,只需上交答题卷. 参考公式:若事件A ,B 互斥,则()()()P A B P A P B +=+ 若事件A ,B 相互独立,则()()()P AB P A P B =若事件A 在一次试验中发生的概率是p ,则n 次独立重复试验中事件A 恰好发生k 次的概率()()() 1 0,1,2,,n kk kn n P k C p p k n -=-=台体的体积公式:()1213V S S h =+,其中1S ,2S 分别表示台体的上、下底而积,h 表示台体的高柱体的体积公式: VSh =,其中S 表示柱体的底面积,h 表示柱体的高 锥体的体积公式:13V Sh =,其中S 表示锥体的底面积,h 表示锥体的高球的表面积公式:24S R π=,球的体积公式:343V R π=,其中R 表示球的半径选择题部分(共40分)一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{}1,2,4A =,{}0,2,4B =,则A B =( )A. {}2,4B. {}0,1,2,4C. {}0,1,2,2,4D. {}04x x ≤≤【答案】B 【解析】 【分析】根据并集的定义计算,【详解】∵{}1,2,4A =,{}0,2,4B =,∴{0,1,2,4}A B ⋃=.故选:B .【点睛】本题考查集合的并集运算,属于简单题.2. 双曲线22149x y -=的实轴长为( )A. 2B. 3C. 4D. 6【答案】C 【解析】 【分析】根据双曲线标准方程知实轴长为2a ,可知双曲线22149x y -=的实轴长【详解】由双曲线标准方程22221x y a b-=中,实轴长为2a 可知:在双曲线22149x y -=中,实轴长为4故选:C【点睛】本题考查了双曲线的几何性质,利用标准方程及实轴定义求实轴长.3. 已知圆()22:11C x y -+=,直线l 过点()0,1且倾斜角为θ,则“0θ=”是“直线l 与圆C 相切”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A 【解析】 【分析】求出直线与圆相切时的θ值,然后判断.【详解】圆C 是以(1,0)为圆心,1为半径的圆,因此过点(0,1)的切线有两条,方程是1y =和0x =,倾斜角为0θ=或2πθ=.∴“0θ=”是“直线l 与圆C 相切”的充分不必要条件. 故选:A .【点睛】本题考查充分必要条件的判断,充分必要条件的判断方法有两种,一种是根据充分必要条件的定义判断,另一种是根据充分必要条件与集合包含之间的关系判断.4. 若复数312a ii++(a R∈,i为虚数单位)是纯虚数,则实数a的值为()A. -6B. 6C. 4D. 3【答案】A【解析】【分析】把已知复数利用复数代数形式的乘除运算化简,然后由实部等于0且虚部不等于0求得a的值.【详解】∵()()()()()()31263231212125a i i a a ia ii i i+-++-+==++-为纯虚数,∴a+6=0且3−2a≠0,解得:a=−6.故选:A.【点睛】本题考查复数代数形式的乘除运算及复数概念的应用,纯虚数为实部等于0且虚部不等于0,得出结果后一定要做验证,属于基础题.5. 已知函数1()ln1f xx x=--,则()y f x=的图象大致为().A. B.C. D.【答案】B【解析】【分析】根据特殊值的函数值排除,,A C D,从而选B.【详解】因为1111ln1f eee e⎛⎫==>⎪⎝⎭--,所以选项A错;因为11()0ln12f ee e e==>---,所以选项C错;因为()222211()ln 13f ef e ee e ==<---,所以选项D 错, 故选:B .【点睛】本题考查了由函数解析式选择函数图象,考查了特值排除法,属于基础题. 6. 设l ,m 是条不同的直线,α是一个平面,以下命题正确的是( ) A. 若//l α,//m α,则//l m B. 若//l α,m l ⊥,则m α⊥ C. 若l α⊥,m l ⊥,则//m α D. 若l α⊥,m α⊥,则//l m【答案】D 【解析】 【分析】逐项进行分析,在选项A 中,l 与m 相交、平行或异面;在选项B 中,m 与α相交、平行或m ⊂α;在选项C 中,m∥α或m ⊂α;在选项D 中,由线面垂直的性质定理得l∥m. 【详解】由l ,m 是条不同的直线,α是一个平面,知:在选项A 中,若l∥α,m∥α,则l 与m 相交、平行或异面,故A 错误; 在选项B 中,若l∥α,m⊥l,则m 与α相交、平行或m ⊂α,故B 错误; 在选项C 中,若l⊥α,m⊥l,则m∥α或m ⊂α,故C 错误;在选项D 中,若l⊥α,m⊥α,则由线面垂直的性质定理得l∥m,故D 正确. 故选D .【点睛】本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查空间想象能力,是基础题.7. 《周髀算经》有这样一个问题:从冬至日起,依次小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种十二个节气日影长减等寸,冬至、立春、春分日影之和为三丈一尺五寸,前九个节气日影之和为八丈五尺五寸,问芒种日影长为( ) A. 一尺五寸 B. 二尺五寸C. 三尺五寸D. 四尺五寸【答案】B 【解析】 【分析】从冬至日起各节气日影长设为{}n a ,可得{}n a 为等差数列,根据已知结合前n 项和公式和等差中项关系,求出通项公式,即可求解.【详解】由题知各节气日影长依次成等差数列,设为{}n a ,n S 是其前n 项和,则()19959985.52a a S a +===,所以59.5a =,由题知1474331.5a a a a ++==, 所以410.5a =,所以公差541d a a =-=-, 所以1257 2.5a a d =+=,故芒种日影长为二尺五寸. 故选:B .【点睛】本题考查等差数列应用问题,考查等差数列的前n 项和与通项公式的基本量运算,属于中档题. 8. 设a ,b ,c 为平面向量,2a b a b ==⋅=,若()()20c a c b ⋅--=,则c b ⋅的最大值是( )A.B.52+ C.174D.94【答案】B 【解析】 【分析】先求出a 与b 的夹角,在直角坐标系中用坐标表示a 、b 且设(,)c OC x y ==,有c b ⋅= 2x ,结合()()20c a c b ⋅--=用坐标表示数量积,可得到方程,根据方程有解求x 范围即可求得c b ⋅的最大值.【详解】∵2a b a b ==⋅=,若a 与b 的夹角为θ知1cos 2θ=, ∴3πθ=,建立直角坐标系, 令(2,0),(1,3)b OB a OA ====,设(,)c OC x y == ,而c b ⋅= 2x ,故求它的最大值即是求x 的最大值,故2(21,2c a x y -=--,(2,)c b x y -=-,又()()20c a c b ⋅--=即(2)()c a c b -⊥-∴(21)(2)(20x x y y --+=,即22(21)(2)0y x x -+--= , 方程有解:38(21)(2)0x x ∆=---≥,解得:5544x -+≤≤.∴c b ⋅的最大值为52. 故选:B【点睛】本题考查了应用坐标表示向量的数量积求最值,根据数量积的坐标公式,结合一元二次方程有解求参数范围,进而求最大值9. 定义在R 上的奇函数()f x 满足()()2f x f x +=-,且当[]0,1x ∈时,()2cos xf x x =-,则下列结论正确的是( ) A. ()20202019201832f f f ⎛⎫⎛⎫<<⎪ ⎪⎝⎭⎝⎭B. ()20202019201832f f f ⎛⎫⎛⎫<<⎪ ⎪⎝⎭⎝⎭C. ()20192020201823f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭D. ()20192020201823f f f ⎛⎫⎛⎫<<⎪ ⎪⎝⎭⎝⎭【答案】C 【解析】 【分析】根据f (x )是奇函数,以及f (x+2)=f (-x )即可得出f (x+4)=f (x ),即得出f (x )的周期为4,从而可得出f (2018)=f (0),2019122f f ⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭,20207312f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭然后可根据f (x )在[0,1]上的解析式可判断f (x )在[0,1]上单调递增,从而可得出结果.【详解】∵f(x )是奇函数;∴f(x+2)=f (-x )=-f (x );∴f(x+4)=-f (x+2)=f (x ); ∴f (x )的周期为4;∴f (2018)=f (2+4×504)=f (2)=f (0),2019122f f ⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭,20207 312f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭∵x∈[0,1]时,f (x )=2x -cosx 单调递增;∴f(0)<12f ⎛⎫⎪⎝⎭<712f ⎛⎫ ⎪⎝⎭∴()20192020201823f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭,故选C.【点睛】本题考查奇函数,周期函数的定义,指数函数和余弦函数的单调性,以及增函数的定义,属于中档题.10. 设等差数列{}n a 的前n 项和为n S ,并满足:对任意*n ∈N ,都有2020n n S S +≥,则下列命题不一定...成立的是( ) A. 20202021S S ≤ B. 20212022S S ≤ C. 10101011a a ≤ D. 10111012a a ≤【答案】C 【解析】【分析】设等差数列{}n a 的公差为d ,对d 分为0d =、0d >、0d <三种情况讨论,在0d =时验证即可;在0d >时,取2d =,可设()2n S n tn t R =+∈,根据2020n n S S +≥恒成立求得实数t 的取值范围,逐一验证各选项即可;同理可判断出0d <时各选项的正误.【详解】设等差数列{}n a 的公差为d ,则()2111222n n n d d d S na n a n -⎛⎫=+=+- ⎪⎝⎭. ①当0d =时,则1n a a =,1n S na =,则2020n n S S +≥对任意的*n ∈N 恒成立, A 、B 、C 、D 四个选项都成立; ②当0d >时,不妨取2d =,记12d t a =-,则2n S n tn =+, 由2020n n S S +≥可得2220200n n S S +-≥,即()()202020200n n n n S S S S ++-+≥,则()()222404020202020240402020220200n tnn tn t ++++++≥,令24040202020200n t ++=,可得22020t n =--;令22240402020220200n n tn t ++++=,可得2101010101010t n n ⎛⎫=-++ ⎪+⎝⎭.()()2222101010101010101010102202010100101010101010n n n n n n n +-⎛⎫-++---=+-=> ⎪+++⎝⎭, 则210101010220201010n n n ⎛⎫-++>-- ⎪+⎝⎭,解关于t 的不等式()()222404020202020240402020220200n tnn tn t ++++++≥,可得22020t n ≤--或2101010101010t n n ⎛⎫≥-++ ⎪+⎝⎭,所以()min 22020t n ≤--或2max 101010101010t n n ⎡⎤⎛⎫≥-++⎢⎥ ⎪+⎝⎭⎣⎦.由于数列{}22020n --单调递减,该数列没有最小项;由双勾函数单调性可知,函数21010y x x=+在区间[1010,+∞)上单调递增,所以,数列2101010101010n n ⎧⎫⎛⎫⎪⎪-++⎨⎬ ⎪+⎪⎪⎝⎭⎩⎭单调递减,该数列的最大项为2101010111011--,2101010111011t ≥--. 对于A 选项,2202020202020S t =+,2202120212021S t =+,则()()()()22222021202020212020202120204041404120202021S S S S S S t t -=-+=+++,22101010104041404110113030010111011t +≥--=->,2222240411010404120202021202020214041101101011t ⨯++≥+-⨯->,则()()()()222220212020202120202021202040414041202020210S S S S S S t t -=-+=+++>,所以,20212020S S >,A 选项成立; 对于B 选项,2202220222022S t =+,则()()()()22222022202120222021202220214043404320212022S S S S S S t t -=-+=+++,22101010104043404310113032010111011t +≥--=->,2222240431010404320212022202120224043101101011t ⨯++≥+-⨯->,则()()()()222220222021202220212022202140434043202120220S S S S S S t t -=-+=+++>,所以,20222021S S >,B 选项成立; 当1n =时,111a S t ==+;当2n ≥时,()()()2211121n n n a S S n tn n t n n t -⎡⎤=-=+--+-=+-⎣⎦. 11a t =+满足21n a n t =+-,()21n a n t n N *∴=+-∈.对于C 选项,10102019a t =+,10112021a t =+,()()()2222101110102021201942020a a t t t -=+-+=+,222101010101010100910112020101110090101110111011⎛⎫-⨯----=-=> ⎪⎝⎭, 当21010101120201011t --<<-时,()2210111010420200a a t -=+<,所以,C 选项不一定成立; 对于D 选项,10122023a t =+,()()()2222210121011101020232021420224202210111011aat t t ⎛⎫-=+-+=+≥-- ⎪⎝⎭()222410111010101041011010111011-⎛⎫=-=> ⎪⎝⎭, 所以,10121011a a >, D 选项成立;③当0d <时,由②同理可知,C 选项不一定成立. 故选:C.【点睛】本题考查数列不等式的验证,考查等差数列前n 项和的性质,考查推理能力与计算能力,属于难题.非选择题部分(共110分)二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.11. 已知随机变量X 服从二项分布(),B n p ,若E(X)=3,()2D X =,则p =________,()1P X ==________.【答案】 (1). 13 (2). 2562187【解析】 【分析】首先根据已知条件得到()312np np p =⎧⎨-=⎩,解不等式组即可得到13p =,再计算()1P X =即可.【详解】因为随机变量X 服从二项分布(),B n p ,若E(X)=3,()2D X =,所以()312np np p =⎧⎨-=⎩,解得139p n ⎧=⎪⎨⎪=⎩,即随机变量X 服从二项分布19,3B ⎛⎫ ⎪⎝⎭.()819122561332187⎛⎫==⨯⨯=⎪⎝⎭P X C .故答案为:1 3,2562187【点睛】本题主要考查二项分布的均值和方差,同时考查n次独立重复试验,属于简单题.12. 已知实数x,y满足约束条件2020220x yx yx y+-≥⎧⎪--≤⎨⎪--≥⎩,则2z x y=+的最小值为________;1yx+的取值范围是________.【答案】(1). 2(2).1,22⎡⎫⎪⎢⎣⎭【解析】【分析】首先根据题意画出可行域,再根据目标函数的几何意义结合图形即可得到答案.【详解】不等式组表示的可行域如图所示,由目标函数2z x y=+得到122zy x=-+,z的几何意义表示直线122zy x=-+的y轴截距的2倍.所以当直线122zy x=-+过()2,0A时,z取得最小值,min2z=.令()111--+==-yyzx x,1z的几何意义表示:可行域内的点(),x y与()0,1B-构成的斜率.由图知:()1min 12==BA z k ,12<z ,故11,22⎡⎫∈⎪⎢⎣⎭z . 故答案为:(1)2;(2)1,22⎡⎫⎪⎢⎣⎭【点睛】本题主要考查线性规划问题,同时考查了数形结合的思想,属于中档题. 13. 若将函数()7=f x x 表示为()()()()201277111f x a a x a x a x =+-+-++-,其中0a ,1a ,2a ,,7a 为实数,则3a =________,0246a a a a +++=________. 【答案】 (1). 35 (2). 64 【解析】 【分析】首先将()f x 转化为()()711=+-⎡⎤⎣⎦f x x ,再利用二项式定理得展开式即可得到3a 的值;分别令2x =和0x =,再把两个式子相加除以2即可得到答案.【详解】因为()()()()()7207717211111==+-=⎡⎤⎣-+-+-⎦++a a f x a x a x x x x ,所以33735==a C .令2x =得:()7012722++==++a a a a f ①, 令0x =得:()012700-+=--=a a a a f ②,①+②得到()7024622+++=a a a a ,所以024664+++=a a a a .故答案为:35;64【点睛】本题主要考查二项式定理,同时考查学生分析问题的能力,属于简单题.14. 己知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,且cos 3sin a C a C b c =+,则A =________;又若2b =,a x =,△ABC 有两解,则实数x 的取值范围是________.【答案】 (1). 3π(2). 32x <<【解析】 【分析】由cos 3sin a C a C b c +=+结合正弦定理化简得到1sin()62A π-=,由(0,)A π∈即可得到A 的大小;同样由正弦定理及2b =,a x =,(1)的结论可得3sin B =,2(0,)3B π∈且△ABC 有两解,即可知3sin (,1)B ∈,可求x 的范围. 【详解】cos 3sin a C a C b c +=+知,sin cos 3sin sin sin sin A C A C B C +=+,而()B A C π=-+,∴sin cos 3sin sin sin()sin sin cos cos sin sin A C A C A C C A C A C C +=++=++, 即13sin cos 1sin()62A A A π=+⇒-=,又(0,)A π∈, ∴3A π=,由2b =,a x =sin sin 3x c c A C =⇒=, 而cos 3sin a C a C b c +=+有:23333cos sin sin()3x C C C π===++,即3sin B =, 2(0,)3B π∈且△ABC 有两解,知:3sin (,1)B ∈, ∴(3,2)x ∈, 故答案:(1)3π;(2)32x <<. 【点睛】本题考查了正弦定理,运用了两角和差的正弦公式,三角形内角和为π,化简求值和参数范围.15. 已知抛物线24y x =,过点()1,2A 作直线l 交抛物线于另一点B ,点Q 是线段AB 的中点,过点Q 作与y 轴垂直的直线1l ,交抛物线于点C ,若点P 满足QC CP =,则OP 的最小值是__________.【答案】2【解析】 【分析】由24y x =,可设2,4b B b ⎛⎫⎪⎝⎭,由题意逐步表示出点,,Q C P 的坐标,于是可以表示出||OP 并求得其最小值.【详解】由24y x =,可设2,4b B b ⎛⎫⎪⎝⎭.因为()1,2A ,Q 是AB 的中点,所以242,82b b Q ⎛⎫++ ⎪⎝⎭. 所以直线1l 的方程为22b y +=.代入24y x =,可得()222,162b b C ⎛⎫++ ⎪ ⎪⎝⎭. 因为QC CP =,所以点C 为PQ 的中点,可得2,22b b P +⎛⎫⎪⎝⎭. 所以()()2222211||14422b b OP b +=+=++.所以当1b =-时,2||OP 取得最小值12,即||OP 的最小值为2.故答案为2. 【点睛】本题考查抛物线的基本问题,设出坐标表示出目标函数,利用函数求最值.16. 将5个不同的小球全部放入编号为1,2,3,4的四个盒子中,若每个盒子中所放的球的个数不大于其编号数,则共有_________种不同的放法. 【答案】535 【解析】 【分析】根据每个盒子中所放的球的个数不大于其编号数,将每个盒子能放入的球个数列举出来,由总球数为5,以可能的球数组合列举分组,结合组合数求出它们所有不同放法. 【详解】四个盒子放球的个数如下 1号盒子:{0,1} 2号盒子:{0,1,2}3号盒子:{0,1,2,3} 4号盒子:{0,1,2,3,4}结合由5个不同的小球全部放入盒子中,不同组合下放法 5 = 1 + 4:153C 种 5 = 2 + 3:254C 种 5 = 1 + 1 + 3:31526C C 种 5 = 1 + 2 + 2:22536C C 种 5 = 1 + 1 + 1 + 2:2115323C C C 种∴5个相同的小球放入四个盒子方式共有535种. 故答案为:535.【点睛】本题考查了组合数,对问题分类、分组,应用组合数的计算17. 已知三棱锥A BCD -的所有顶点都在球O 的球面上,AD ⊥平面ABC ,90BAC ∠=︒,2AD =,若球O 的表面积为29π,则三棱锥A BCD -的侧面积的最大值为__________.【答案】254【解析】 【分析】根据球的性质可知球心O 必在过BC 中点E 且平行于AD 的直线上,根据勾股定理可确定112AF DF OE AD ====;根据球的表面积公式可确定半径2R =,勾股定理可得到222225AB AC x y +=+=;将三棱锥侧面积表示为12S x y xy =++,利用基本不等式可求得最大值.【详解】取BC 中点E ,90BAC ∠= E ∴为ABC ∆的外接圆圆心,过E 作AD 的平行线,由球的性质可知,球心O 必在此平行线上, 作//OF AE ,交AD 于F ,如图所示:OA OE =2222OD OF DF AD DF =+=+OA OD = 112AF DF OE AD ∴==== 球O 的表面积为29π ∴球O 的半径29294R ==设AB x =,AC y =由222229142x y R OC CE OE +==+=+=得2225x y += 又12ABD S AB AD x ∆=⋅=,12ACD S AC AD y ∆=⋅=,1122ABC S AB AC xy ∆=⋅= ∴三棱锥A BCD -侧面积12S x y xy =++由222x y xy +≥得:252xy ≤(当且仅当522x y ==时取等号) 又()2222222550x y x y xy x y +=++≤++=(当且仅当522x y ==时取等号) 25524S ∴≤(当且仅当52x y == 故答案为:25524【点睛】本题考查空间多面体的外接球的相关问题的求解,涉及到利用基本不等式求解最值的问题,关键是能够根据球的性质确定球心位置,从而利用勾股定理得到变量所满足的等量关系,从而结合基本不等式求得结果.三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.18. 设函数()3cos 2cos 262x x x a f ππ⎛⎫=+--+ ⎛⎫⎪⎝⎪⎭⎭⎝的最小值是1-. (1)求a 的值及()f x 的对称中心;(2)将函数()f x 图象的横坐标压缩为原来的一半(纵坐标不变),再向右平移12π个单位,得到()g x 的图象,若()12g x ≥-,求x 的取值范围. 【答案】(1)0a =,对称中心是,026k ππ⎛⎫- ⎪⎝⎭()k Z ∈;(2)7,224224ππππ⎡⎤-+⎢⎥⎣⎦k k ()k Z ∈. 【解析】 【分析】(1)首先利用三角函数恒等变换化简得到()sin 23π⎛⎫=++ ⎪⎝⎭f x x a ,根据()f x 的最小值得到0a =,再求()f x 的对称中心即可.(2)首先根据三角函数的平移变换得到()sin 4g x x =,再解不等式1sin 42≥-x 即可. 【详解】(1)()3cos 2cos 262x x x a f ππ⎛⎫=+--+ ⎛⎫⎪⎝⎪⎭⎭⎝.112sin 2sin 22sin 2sin 2223x x x a x x a x a π⎛⎫=-++=++=++ ⎪⎝⎭ 因为()min 11=-+=-f x a ,所以0a =,即()sin 23f x x π⎛⎫=+ ⎪⎝⎭. 令23x k ππ+=,解得62πk πx =-+()k Z ∈.所以()sin 23f x x π⎛⎫=+⎪⎝⎭的对称中心是,026k ππ⎛⎫-⎪⎝⎭()k Z ∈; (2)()sin 4sin 4123ππ⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦g x x x , 因为()12g x ≥-,即1sin 42≥-x , 所以724266k x k ππππ-≤≤+()k Z ∈,解得:7224224ππππ-≤≤+k k x ()k Z ∈, ∴x 的取值范围是7,224224ππππ⎡⎤-+⎢⎥⎣⎦k k ()k Z ∈. 【点睛】第一问考查三角函数的恒等变换,同时考查正弦函数的对称性,第二问考查正弦函数图象变换,同时考查三角不等式,属于中档题.19. 如图,在直三棱柱111ABC A B C -中,11112A B A C ==,123CC =, 120BAC ∠=︒,点O 为线段11B C 的中点,点P 为线段1CC 上一动点(异于点1C C 、),点Q 为线段BC 上一动点,且QP OP ⊥.(Ⅰ)求证:平面1A PQ ⊥平面1A OP ;(Ⅱ)若//BO PQ ,求直线OP 与平面1A PQ 所成角的正弦值. 【答案】(Ⅰ)证明见解析;219. 【解析】 【分析】(Ⅰ)要证平面1A PQ ⊥平面1A OP ,转证QP ⊥平面1A OP ,即证1QP AO QP OP ⊥⊥,; (Ⅱ)建立如图空间直角坐标系O xyz -,求出平面1A PQ 的法向量,代入公式可得结果. 【详解】(I )证明:因为11112A B A C ==,O 为线段11B C 的中点,所以111AO B C ⊥, 在直三棱柱111ABC A B C -中,易知1CC ⊥平面111A B C ,11AO CC ∴⊥,而1111CC B C C ⋂=; 1A O ∴⊥平面11CBB C ,1QP A O ∴⊥;又因为QP OP ⊥,A 1O ∩OP=O ; 所以QP ⊥平面1A OP ,又QP ⊂平面1A OP ;所以平面1A PQ ⊥平面1A OP ; (II )由(I )可建立如图空间直角坐标系O xyz -,因为120BAC ︒∠=所以113OB OC =,则()()()110,0,0,3,0,0,3,0O C B -,(()10,3,23,1,0,0B A --, 设()(3,,0,,23P a Q b ,所以()(0,3,23,0,3,23QP b a OB =--=-,因为QP OP ⊥,//BO PQ , 所以0,//QP OP OB QP ⋅=,()(()(33230233323b a a b a ⎧-=⎪∴⎨-=--⎪⎩, 解得:3324a b ==(P 异于点1,C C ) ,13333331,3,,0,,,0,3,A P QP OP ⎛⎫⎛⎫⎛∴==-= ⎪ ⎪ ⎪ ⎪ ⎝⎭⎝⎭⎝⎭设平面1A QP 的法向量为(),,n x y z = ,则100n A P n QP ⎧⋅=⎨⋅=⎩即33033330x z y z ⎧++=⎪⎪= ,可取 ()53,4,2n =- , 设直线OP 与平面1A QP 所成角为θ ,则433219sin 15954n OP n OPθ⋅+===⋅ ,直线OP 与平面1A QP. 【点睛】本题考查了面面垂直的判定,空间向量的应用,线面角的计算,考查空间想象能力与计算能力,属于中档题.20. 已知数列{}n a 满足12a =,210a =,212n n n a a a ++=+,n *∈N . (1)证明:数列{}1n n a a ++是等比数列; (2)求数列{}n a 的通项公式; (3)证明:1211134n a a a +++<. 【答案】(1)证明见解析;(2)()1221nn n a +=+⋅-;(3)证明见解析. 【解析】 【分析】 (1)由212n n n a a a ++=+,得2112n n n na a a a ++++=+,即可得到本题答案;(2)由1132n n n a a +++=⋅,得11122222n n n na a ++⎛⎫-=-⋅- ⎪⎝⎭,即可得到本题答案;(3)当1n =时,满足题意;若n 是偶数,由12123111111111n nn a a a a a a a a +⎛⎫⎛⎫+++<+++++ ⎪ ⎪⎝⎭⎝⎭,可得1211134n a a a ++⋯+<;当n 是奇数,且3n ≥时,由1211231111111111n n n n a a a a a a a a a --⎛⎫⎛⎫++++=+++++ ⎪ ⎪⎝⎭⎝⎭,可得1211134n a a a ++⋯+<,综上,即可得到本题答案.【详解】(1)因为212n n n a a a ++=+,所以()2112n n n n a a a a ++++=+, 因为12120a a +=≠,所以2112n n n na a a a ++++=+,所以数列{}1n n a a ++是等比数列;(2)因为1132n n n a a +++=⋅,所以1113222n nn na a +++⋅=, 所以11122222n n n n a a ++⎛⎫-=-⋅- ⎪⎝⎭,又因为12a =,所以1212a -=-,所以22n n a ⎧⎫-⎨⎬⎩⎭是以1-为首项, 12-为公比的等比数列,所以11222n n n a -⎛⎫-=-- ⎪⎝⎭,所以()1221nn n a +=+⋅-;(3)①当1n =时,11324n a =<; ②若n 是偶数,则1213211113122222242142n n n n n nn n a a +++⋅+=+=<⋅+-⋅+-, 所以当n 是偶数时,121211111111n n n a a a a a a a ++++<++++ 123111111nn a a a a a +⎛⎫⎛⎫=+++++ ⎪ ⎪⎝⎭⎝⎭ 241311124222n⎡⎤⎛⎫⎛⎫⎛⎫<+⋅+++⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦11334124414<+⋅=-; ③当n 是奇数,且3n ≥时,121211111111n n na a a a a a a -+++=++++ 123111111n n a a a a a -⎛⎫⎛⎫=+++++ ⎪ ⎪⎝⎭⎝⎭2411311124222n -⎡⎤⎛⎫⎛⎫⎛⎫<+⋅+++⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦11334124414<+⋅=-;综上所述,当n *∈N 时,1211134n a a a +++<. 【点睛】本题主要考查利用构造法证明等比数列并求通项公式,以及数列与不等式的综合问题.21. 椭圆M :22221(0)x y a b a b+=>>的焦距为23,点(0,2)P 关于直线y x =-的对称点在椭圆M 上.(1)求椭圆M 的方程;(2)如图,椭圆M 的上、下顶点分别为A ,B ,过点P 的直线l 与椭圆M 相交于两个不同的点C ,D . ①求OC OD ⋅的取值范围;②当AD 与BC 相交于点Q 时,试问:点Q 的纵坐标是否是定值?若是,求出该定值;若不是,说明理由.【答案】(1)2214x y +=(2)①13[1,)4OC OD ⋅∈-②12【解析】 【详解】 【分析】试题分析:(1)求椭圆标准方程,一般利用待定系数法,联立方程组求解:因为点(0,2)P 关于直线y x =-的对称点为(2,0)-,所以2a =.又223c =3c =,21b =(2)①直线与椭圆位置关系问题,一般联立方程组,借助于韦达定理进行求解:设直线l 的方程为2,y kx =+代入222,{1,4y kx x y =++=消去y 整理得22(14)16120k x kx +++=,因为1212OC OD x x y y ⋅=+,由1212221612,1414k x x x x k k +=-=++得217114OC OD k ⋅=-++再由>0∆,可得243k >,13[1,)4OC OD ⋅∈-②求定值问题,一般以算代证:先分别表示直线AD :2211y y x x -=+,BC :1111y y x x +=-,解得121221233kx x x x y x x ++=-,再将1212221612,1414k x x x x k k +=-=++代入化简得12y = 试题解析:(1)因为点(0,2)P 关于直线y x=-的对称点为(2,0)-,且(2,0)-在椭圆M 上,所以2a =.又2c =c =222431b a c =-=-=.所以椭圆M 的方程为2214x y +=. (2)①当直线l 的斜率不存在时,(0,1),(0,1)C D -,所以OC OD ⋅=-1.当直线l 的斜率存在时,设直线l 的方程为11222,(,),(,)y kx C x y D x y =+,222,{1,4y kx x y =++=消去y 整理得22(14)16120k x kx +++=,由>0∆,可得243k >,且1212221612,1414k x x x x k k +=-=++,所以1212OC OD x x y y ⋅=+ 21212217(1)2()4114k x x k x x k =++++=-++,所以1314OC OD -<⋅<,综上13[1,)4OC OD ⋅∈-.②由题意得,直线AD :2211y y x x -=+,直线BC :1111y y x x +=-,联立方程组,消去x 得121221233kx x x x y x x ++=-,又121243()kx x x x =-+,解得12y =,故点Q 的纵坐标为定值12.考点:直线与椭圆位置关系.22. 已知实数1a ≥-,设()()ln ,0f x x a x x =+>.(1)若1a =-,有两个不同实数1x ,2x 满足()()12f x f x ''=,求证:122x x +>;(2)若存在实数214c e e<<,使得()f x c =有四个不同的实数根,求a 的取值范围. 【答案】(1)证明见解析;(2)210a e<<.【解析】 【分析】(1)首先求出函数的导函数,依题意可得121212ln 20x x x x x x +-+=,先证121x x ≥.再利用基本不等式即可得证;(2)原题即()f x c =±共有四个不同的实数根,对a 分类讨论,分别利用导数研究函数的单调性与最值,即可求出参数的取值范围;【详解】解:(1)()1ln 1f x x x'=+-. 因为()f x '在0x >上单调递增,故()()120f x f x ''+=,即121212ln 20x x x x x x +-+= 先证明:121x x ≥.因为()10f '=,故不妨11x >,201x <<. 设2211x x '=>. 由基本不等式知:()()222212220f x f x x x ⎛⎫'''+=-+<-= ⎪⎝⎭.因为()f x '在0x >上单调递增且()()120f x f x ''+=, 所以12x x '>即121x x ≥.因为12x x ≠,由基本不等式得:122x x +>>.(2)原题即()f x c =±共有四个不同的实数根. 因为()ln 1af x x x'=++. ①10a -≤≤,因为()f x '在0x >上单调递增, 且当0x →时()f x '→-∞,当x →+∞时()f x '→+∞,故存在唯一实数00x >, 使得()00f x '=,即()00ln 1a x x =-+.因此()f x 在()00,x 上单调递减,在()0,x +∞上单调递增. 由10a -≤≤可知011x e≤≤. 把()00ln 1a x x =-+代入得:()f x 的极小值()()2000ln f x x x =-.令()()2ln h x x x =-,()ln (ln 2)h x x x '=-+.当210,x e ⎛⎫∈ ⎪⎝⎭时,()0h x '<;当21,1x e ⎛⎫∈⎪⎝⎭时,()0h x '>. 因此()h x 在210,e ⎛⎫ ⎪⎝⎭上单调递减,在21,1e ⎛⎫ ⎪⎝⎭上单调递增. 故()01,0f x e⎡⎤∈-⎢⎥⎣⎦,所以()f x c =上至多有两个不同的实数根,()f x c =-上至多有一个的实数根,故不合题意. ②0a >,当0x →时()f x '→+∞, 当x →+∞时()f x '→+∞,()2x af x x-''=. 当()0,x a ∈时,()0f x ''<;当(),x a ∈+∞时,()0f x ''>,()2ln f a a '=+. 因此()f x '在()0,a 上单调递减,在(),a +∞上单调递增. (i )若21a e ≥,则()0f x '≥(当且仅当21a x e==时取等), 故()f x 在0x >上单调递增.因此()f x c =±上至多有两个不同的实数根,故不合题意. (ii )若210a e<<,则()0f a '<, 故存在()10,x a ∈和21,x a e ⎛⎫∈ ⎪⎝⎭,使得()()120f x f x ''==. 因此()f x 在()10,x 和()2,x +∞上单调递增,在()12,x x 上单调递减. 因为当0x →时()f x →-∞,当x →+∞时()f x '→+∞,且()()2111ln 0f x x x =-≤,故()f x c =上有且仅有一个实数根.由①的()h x 可知:()124,0f x e ⎛⎫∈-⎪⎝⎭,()2241,f x ee ⎛⎫∈-- ⎪⎝⎭. 故存在()()()21,c f x f x -∈, 使得214c e e<<.此时()f x c =-上恰有三个不同的实数根. 此时()f x c =±共有四个不同的实数根. 综上:210a e <<满足条件. 【点睛】本题考查利用导数研究函数的单调性与最值,以及函数的零点问题,考查分类讨论思想,属于难题.。
浙江省杭州市学军中学等五校2020届高三下学期联考数学试题答案

|
Hale Waihona Puke BM||BN
|
2
yM
2
yN
=4+
2( y1 1) x1 2
+
2( y2 1) x2 2
=4+ 2[2kx1x2 (2k 2)(x1 x2 ) 8] =4+ 4kx1x2 2(2k 2)(x1 x2 ) 16
x1x2 2(x1 x2 ) 4
x1x2 2(x1 x2 ) 4
∴ an1 2an n2 3n可化为an1 (n 1)2 (n 1) 2(an n2 n) ………(5 分)
又 a1 12 1 0 ……………………………………………………………………(6 分)
故存在 1, 1 使得数列 an n 2 n 是等比数列 ……………(7 分)
⑵证明:由⑴得 an n2 n (a1 12 1) 2n1 ∴ an 2n1 n 2 n ,
故
bn
an
1 n
2 n1
1 n2
……………………………………………… (8 分)
∵
bn
1 n2
4 4n2
4 4n2 1
2 2n 1
2 2n 1
………………………… (9 分)
∴ n 2时,
2
2
因为 x 0 时 f '(x) , x 时 f '(x) . f '(1 ) 1 ln 2 0 2
所以
f
'(x)
0
有两个不同的实数根
x
x0 ,
x
1(其中
x0
(0,
1 ) ). 2
x (0, x0 ) (1,) 时 f '(x) 0 ,即 f (x) 单调递减;
浙江省高三“五校联考”考试参考答案

2020学年第一学期浙江省高三“五校联考”考试参考答案1-10.CBCADCDBBA11.{|1}x x ≠,{|12}x x << 12.43π,1213.2y x =±,8314.54e -,(27,12](11,)---+∞ 15.43 16.1217.335[,]41218.解:1cos 2()sin (sin )22-=+=x f x x x x x 1sin(2)62π=-+x (3)分由3222262πππππ+≤-≤+k x k ,∈k Z 得536ππππ+≤≤+k x k ,∈k Z ∴()f x 的单调递减区间为5[,]36k k k Z ππππ++∈ ……………6分 (2)∵13()sin(2)622π=-+=f A A ,则sin(2)16π-=A , ∵0π<<A ,∴112666πππ-<-<A , 262ππ-=A ,解得3π=A . ……………8分 法一: ∵2=a ,3π=A ,由余弦定理得,2222cos3a b c bc π=+-,即224b c bc +-= ……10分∴2()43b c bc +-=,则22()43()2b c b c ++-≤ …………12分 又∵2b c +>,∴24b c <+≤ …………13分 ∴△ABC 周长的范围是(6,8] …………14分法二:由正弦定理得2sin sin sin a b cR A B C====∴sin )b c B C +=+ …………10分∵23sin sin sin sin()sin )3226B C B B B B B ππ+=+-=+=+ ………12分 又∵2(0,)3B π∈,∴1sin()(,1]62B π+∈,∴(4,6]b c +∈ …………13分∴△ABC 周长的范围是(6,8] …………14分 19.(1)BC ABAM PB PA ABCD BC PA BC PAB AM BC AM PBC BC ABCD AB PA A PB BC B AM PAB PC PBC ⊥⊥⎫⎫⎫⎫⊥⎫⎪⎪⎪⎪⇒⊥⇒⊥⇒⊥⇒⊥⎬⎬⎬⎬⎬⊂⎭⎪⎪⎪⎪==⊂⊂⎭⎭⎭⎭面面面面面面 =PC AMPC AN PC AMN AM AN A ⇒⊥⎫⎪⊥⇒⊥⎬⎪⎭面 ………7分(2)方法一:作DE AC E ⊥于,EF PC F ⊥于,连DF ,PA ABCD ⊥面,PAC ABCD ∴⊥面面,DE PAC ∴⊥面,DDE PC ∴⊥,EF PC ⊥,EF DE E =,PC DEF ∴⊥面,DF PC ∴⊥,DFE ∴∠是二面角D PC A --的平面角,………11分2PA AD ==,AB =AC ∴=,30PCA ∴∠=︒DE ∴=,CE =,EF =tan DE DFE EF ∴∠== DFE ∴∠是二面角D PC A --. ………15分方法二:建立坐标系(以AD 为x 轴,以AB 为y 轴,以AP 为z 轴).(0,0,0),(0,(2,(2,0,0),(0,0,2)A B C D P (0,22,0),(2,22,2),(0,0,2)DC PC AP ==-=平面DPC 的法向量1(1,0,1)n =,平面APC 的法向量2(2,1,0)n =-设二面角D PC A --的平面角为α,12cos |cos ,|n n α=<>=tan α= 20. (1)证明:1222a a +-=,23210a a +=,两式作差得112c =…………3分对任意*n N ∈,21212231n n n a a ---++=①,2221231n n n a a ++=+② …………2分②-①,得21212134n n n a a -+-⨯-=,即2134n n c -⨯=,于是14n nc c +=.所以{}n c 是等比数列. …………7分 (2)证明当*n N ∈且2n ≥时,2113153752123()()()()n n n a a a a a a a a a a =+-+-+-+⋅⋅⋅-+---22131(19)92922129n n --=+++++⋅⋅⋅=⋅+ …………10分由(1)得112339321922n n n a --⋅++=-⋅+,所以2194n n a -= …………12分12123(19)4n n n a a --+=-,得2391()48n n S n -=- …………15分21.解:(1)由已知c e a ==,2b =,222a b c =+得2b a ==,故椭圆C 的22142x y +=;……………………5分(2)设()()()112200,,,,,A x y B x y M x y ,则由2224x y y kx m⎧+=⎨=+⎩得()222214240k x mkx m +++-= 2121222424,2121mk m x x x x k k -⇒+=-=++,点O 到直线l的距离d =1122S d AB =⋅⋅=()222242221m k m k ++-=≤=+S 22242m k m =+-即2221m k =+,① ……………10分此时21200022221,221x x mk k k x y kx m m k m m m+==-=-=+=-+=+,法一:即00001,22x m m k x y y ==-=-代入①式整理得()22000102x y y +=≠,即点M 的轨迹为椭圆()221:102x C y y +=≠ ………13分且点N 恰为椭圆1C 的左焦点,则MN的范围为)1 ……………15分法二:MN ==由①得kMN m===- ………13分 设k t m =代入2221m k =+得22221m m t =+,即22(12)1t m -=,221012m t =>-∴22t -<<,即22k m -<<∴)1MN ∈……………15分22、解答:(Ⅰ)当2a =时,()2sin sin 2f x x x =+,于是()2cos 2cos22(1cos )(2cos 1)f x x x x x '=+=+- …………3分于是()0f x '>,解得(0,)3x π∈;()0f x '<,解得(,)3x ππ∈即(0,)3x π∈函数()f x 单调递增,(,)3x ππ∈函数()f x 单调递减 …………6分(Ⅱ)当1a =时,()sin sin 2cos f x x x bx x =+≥对任意2(0,)3x π∈恒成立首先考察(0,)2x π∈时,易得0b >∵()sin sin 2sin (12cos )cos f x x x x x bx x =+=+≥∴2(,)23x ππ∈时,()0cos f x bx x ≥≥,显然成立 …………9分于是只考察()sin sin 2cos f x x x bx x =+≥对任意(0,)2x π∈恒成立由()14242f b ππ=+≥⋅,于是18b +≤138+>,所以3b ≤…11分 下证:()sin sin 23cos f x x x x x =+≥对任意(0,)2x π∈恒成立考察函数()tan 2sin 3g x x x x =+-,(0,)2x π∈32222212cos 3cos 1(cos 1)(2cos 1)()2cos 30cos cos cos x x x x g x x x x x-+-+'=+-==> 于是()g x 在(0,)2x π∈上单调递增,则()(0)0g x g >=即tan 2sin 30x x x +->,则sin sin 23cos x x x x +≥ 综上可知,max 3b = ………15分。
2020届浙江省杭州学军中学高三教学质量监测卷化学试题(解析版)

浙江省杭州学军中学2020届高三教学质量监测卷可能用到的相对原子质量:H 1 C 12 N 14 O 16 S 32 Cl 35.5 K 39 Ti 48 Fe 56 I 127 Ag-108一、选择题:本大题包括7小题,每小题6分。
在每小题给出的四个选项中,只有一项符合题目要求。
1.下列生活用品中主要由合成纤维制造的是()A. 尼龙绳B. 宣纸C. 羊绒衫D. 棉衬衣『答案』A『详解』合成纤维是化学纤维的一种,是用合成高分子化合物做原料而制得的化学纤维的统称。
它以小分子的有机化合物为原料,经加聚反应或缩聚反应合成的线型有机高分子化合物,如聚丙烯腈、聚酯、聚酰胺等。
A、尼龙绳的主要成分是聚酯类合成纤维,故A正确;B、宣纸的的主要成分是纤维素,故B错误;C、羊绒衫的主要成分是蛋白质,故C错误;D、棉衬衫的主要成分是纤维素,故D错误。
『点睛』掌握常见物质的组成以及合成纤维的含义是解答本题的关键,题目难度不大,注意羊绒衫和棉衬衣的区别。
2.下列有关化学用语表示正确的是()PA. 质量数为31的磷原子:3115B. 氟原子的结构示意图:C. CaCl2的电子式:D. 明矾的化学式:Al2(SO4)3『答案』A『详解』A.磷原子的质子数是15,质量数是31,故A正确;B.氟原子是9号元素,核外电子数为9,所以原子结构示意图:,故B错误;C.离子化合物中阴、阳离子间隔排列,其电子式中离子分开写,不能合并,CaCl2的电子式:,故C错误;KAl SO12H O,故D错误;D.明矾是十二水合硫酸铝钾,即()422故答案选A。
3. 乌洛托品在合成、医药、染料等工业中有广泛用途,其结构式如图所示。
将甲醛水溶液与氨水混合蒸发可制得乌洛托品。
若原料完全反应生成乌洛托品,则甲醛与氨的物质的量之比为()A. 1∶1B. 2∶3C. 3∶2D. 2∶1 『答案』C『详解』试题分析:根据结构简式以及元素守恒,1mol乌洛托品有4molN,因此需要4molNH3·H2O,6molC需要6mol甲醛的水溶液,因此两者的比值为6:4=3:2,故选项B 正确。
2020学年浙江省高三下学期3月联考通用试题参考答案

第二部分通用技术(共50分)一、选择题(本大题共13小题,每小题2分,共26分。
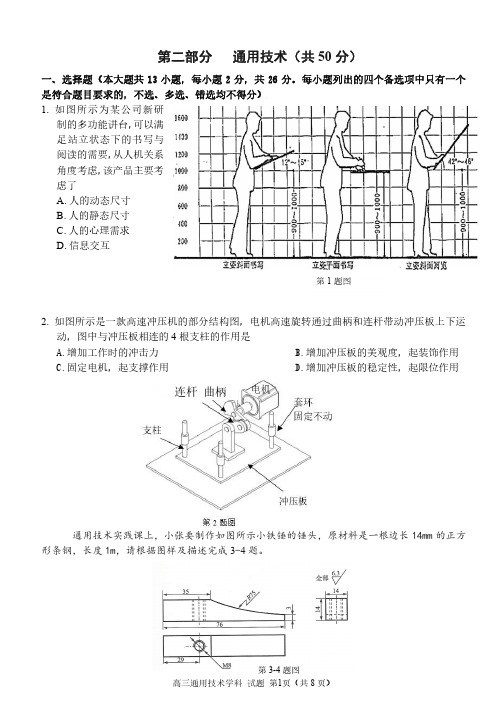
每小题给出的四个选项中,只有一个是符合题目要求的,不选、多选、错选均不得分)1.如图所示,为一款多功能插座面板,下列设计中没有涉及人机关系的是()A.边缘圆角设计B.通电后亮起红色提示灯C.有双孔和三孔插座D.配有绝缘开关按钮2如图所示是某电动汽车品牌研发的电动自行车,下列评价中不恰当的是()A.使用环保材料制作,体现了经济原则B.将电池放置在结构的中下部,提高了结构的稳定性C.知名品牌提高了产品价值,体现了设计的实用原则D.整车加装360°安全探测防护系统,体现了设计的创新原则3.制作如图所示的手工木质相框,使用厚度为30mm的木条,以下最合理的连接方式是()A. B. C. D.通用技术课上,小明设计了如图所示的零件。
请根据题图完成第4,5题。
4.图中漏标的尺寸共有()A. 1处B. 2处C. 3处D. 4处5.用厚度为5mm的钢板制作该零件,下列说法中不合理的是()A.在钻孔时,需要戴防护眼镜,不能戴防护手套B.加工流程可以为:划线→冲眼→锯割→钻孔→锉削C.此次加工中需要用到丝锥D.用半圆锉加工该零件内孔的各段圆弧6.如图所示,是一款体育训练比赛所用的可升降跨栏架,底座带配重砣,用ABS树脂材料制作横杆结合结构稳定性与设计的关系,下列说法错误的是()A.用ABS树脂材料替换常用的金属材料制作横杄,是为了保证强度的前提下,降低结构的重心,提高栏架的稳定性B.栏架设计成L形,跨栏的右侧(起跑方向)设有支撑面,且配有重砣,是为了提高栏架的稳定性,以减少非运动员触碰而造成的栏架翻倒的情况,以满足比赛需求C.栏架设计成L形,跨栏的左侧(终点方向)没有设置支撑面,是为了降低栏架的稳定性,从而提高栏架在运动员触碰时,快速倒下,以保护运动员D.重心位置的左右移动,影响了栏架的稳定性,但横杆高度的升降,不会影响栏架的稳定性7.如图所示是某城市的污水处理流程图。
2020年杭州市学军中学高三英语下学期期末考试试卷及答案解析

2020年杭州市学军中学高三英语下学期期末考试试卷及答案解析第一部分阅读(共两节,满分40分)第一节(共15小题;每小题2分,满分30分)阅读下列短文,从每题所给的A、B、C、D四个选项中选出最佳选项ASwimming Holes in AmericaIn America, these secret swimming holes are hidden and hard to reach but well worth the adventure.Cummins FallsLooking for the best place to escape the summer heat in the heartland of America? For more than 100 years, Cummins Falls, a scenic,75-foot waterfall located in Jackson County, TN, has been a treasure for Tennessee natives. But now, the secret is out! Although it’s a bit tough to get to, once in the park, the mountains and river provide unmatched beauty on your way to taking a swim in Tennessee's eighth-largest waterfall.Sliding RockA popular place to cool off during those hot North Carolina summers, Sliding Rock waterfall is located in the Pisgah National Forest in Transylvania County. A flattened rock about 60 feet lies in a nearly 7-foot-deep pool at the bottom, making this natural waterslide a great place to visit with people of all ages.Mooney FallsIt is the tallest water feature in the Grand Canyon, rising 190 feet above the surface. Named after an explorer in the 1800s, Mooney Falls is accessible only by crawling(爬)through 2 underground passages and then climbing down a sheer cliff(峭壁)face with just a couple of chains to hold on to. Although it is tough to get to, the view and the cool alone make it worth the trip.Lihue EstateA private swimming hole at the old Lihue Sugar Farm on Kauai, HI, was changed into an inner-tube water ride by Kauai Backcountry Adventures in 2003 and opened to adults. The waters for this 2.5-mile journey, which come from near the top of Mount Waialeale—one of the wettest spots in the world—are channeled through ditches(沟渠)that were hand-dug by farm workers over a century ago.1. Which hole may be the favourable destination for families?A. Lihue Estate.B. Sliding Rock.C. Mooney Falls.D. Cummins Falls.2. What can we learn about Mooney Falls from the text?A. It wasfound by an explorer.B. It was hand-dug in the 1800s.C. It is dangerous to arrive there.D. It is the tallest fall in the world.3. What is special about Lihue Estate?A. It is man-made.B. It is a private area.C. Its water is from underground.D. It lies on the top of Mount WaialealeBWhat about your emotions? How do they help you to understand what you are reading?In Jane Yolan'sOwl Moon,a girl explores with her father on a snowy night. She longs for this special night.And she's amazed when she sees an owl.Have you felt longing before? Amazement? Well, if you have, it helps you have a sense of agreement. When we can put ourselves inside a story we can understand it better. Our brain tells us,"Oh, this girl's experience is a bit like mine."And boom! We can relate to her.But this skill is not born in us.So young kids have to learn it.Pictures and images help young readers to understand and recognize feelings.Readers feel joy when seeing the smiling faces of friends.They feel fear when turning the page to find a scary monster. They are just pictures,but the feelings are real. This skill, to understand the thinking and feeling of others, is what researchers call "theory of mind".For example, think about the faces of people and animals in stories. The Big Bad Wolf's scary teeth. The 'o' shape of a surprised character's mouth. Or big, wide eyes like the girl inOwl Moon.By noticing the faces,readers can start to figure out what it feels like to be that character.And that helps to figure out how people feel and think in real life.But most young readers don't go into deep,scary woods.And some may not go to the beach or play basketball.In the bookYo!Yes?two kids meet and play ball. The kids start the story on opposite pages.But as the story goes on,they get closer until they are together.Some young readers might not play basketball, but they can read the clues on the page to figure out how the kids are feeling.And some readers might not like the game,but they can feel excited for the characters because of how the characters look and move.4. What can we learn from the second paragraph?A.Owl Moontalks about the exploration of the Moon.B. The feeling of"amazement"is a sense of agreement.C. Readers are blessed with the ability to interpret others.D. Readers with similar experience understand the story better.5. Which of the following might help readers develop"theory of mind"?A. True feelings.B. Smiling faces.C. Picture books.D. Reading skills.6. Young readers can go deeper into a story by________.A. tracking the plotB. developing new skillsC. sharing similar hobbiesD. analyzing the background7. What is the text mainly about?A. How thinking influences reading.B. How readers improve reading skills.C. How emotions help enhance reading.D. How kids figure out the clues of stories.COn World Oceans Day, which falls on June 8, the US National Geographic Society announced it would recognize the Southern Ocean in Antarctica, bringing the global total to five.Unlike the Arctic, Atlantic, Indian and PacificOceans—which are defined by the continents that bound them—the Southern Ocean is instead characterized by the Antarctic Circumpolar Current(南极洋流). According to the National Geographic, the Southern Ocean includes most of the waters surrounding Antarcticaout to 60 degrees south latitude(纬度)."Encircled by the powerfully swift ACC, it is the only ocean to touch three others and to completely embrace a continent rather than being embraced by them," Sylvia Earle, a marine biologist and oceanographer, told the Daily Mail.Those familiar with the Southern Ocean know it's unlike any other. "Anyone who has been there will struggle to explain what's so charming about it, but they'll all agree that the glaciers are bluer, the air colder, the mountains more awful and the landscapes morecaptivatingthan anywhere else you can go," Seth Sykora-Bodie, a marine scientist at the National Oceanic and Atmospheric Administration, told National Geographic.National Geographic hopes their revised maps will bring public awareness to the region, thereby encouraging Southern Ocean conservation—but its significance is beyond that."We think it's really important from an educational standpoint, as well as from a map-labeling standpoint, to bring attention to the Southern Ocean as a fifth ocean," Alex Tait, National Geographic Society geographer, told The Post. "So when students learn about parts of the ocean world, they learn it's an interconnected ocean, and they learn there are these regions called oceans that are really important, and there's a distinct one in the icy waters around Antarctica."8. Why is the Southern Ocean different from other oceans?A. It has never been explored before.B. It surrounds the Antarctic all around.C. It is enclosed by the fast-flowing ACC.D. It has ecologically distinct environment.9. What does the underlined word "captivating" in paragraph 4 probably mean?A. Strange.B. Unusual.C. Attractive.D. Informal.10. What does the National Geographic think of the Southern Ocean?A. It will be instructive for students.B. It will promote tourism development.C. It will encourage public to treasure water.D. It will draw scientists to study in the Antarctic.11. What is the best title for the text?A. World Oceans DayB. Revised Antarctic MapsC. Adding a New OceanD. New Discovery under the SeaDWhat will people die of 100 years from now? If you think that is a simple question,you have not been paying attention to the revolution that is taking place in bio-technology(生物技术). With the help of new medicine,the human body will last a very long time. Death will come mainly from accidents,murder and war. Today’s leading killers,such as heart disease,cancer,and aging itself,will become distant memories.In discussion of technological changes,the Internet gets most of the attention these days. But the change in medicine can be the real technological event of our times. How long can humans live? Human brains were known to decide the final death. Cells(细胞)are the basic units of all living things,and until recently,scientists were sure that the life of cells could not go much beyond 120 years because the basic materials of cells,such as those of brain cells,would not last forever. But the upper limits will be broken by new medicine. Sometime between 2050 and 2100,medicine will have advanced to the point at which every 10 years or so,people will beable to take medicine to repair their organs(器官). The medicine,made up of the basic building materials of life,will build new brain cells,heart cells,and so on-in much the same way our bodies make new skin cells to take the place of old ones.It is exciting to imagine that the advance in technology may be changing the most basic condition of humanexistence,but many technical problems still must be cleared up on the way to this wonderful future.12. According to the passage,human death is now mainly caused by ________.A. diseases and agingB. accidents and warC. accidents and agingD. heart disease and war13. In the author’s opinion,today’s most important advance in technology lies in(在于)________.A. the InternetB. medicineC. brain cellsD. human organs14. Humans may live longer in the future because ________.A. heart disease will be far away from usB. human brains can decide the final deathC. the basic materials of cells will last foreverD. human organs can be repaired by new medicine15. How long can humans live in the future according to the passage?A. Over 100 years.B. More than 120 years.C. About 150 years.D. The passage doesn’t tell us.第二节(共5小题;每小题2分,满分10分)阅读下面短文,从短文后的选项中选出可以填入空白处的最佳选项。
2020届浙江省杭州市学军中学高三下学期高考模拟数学试题(解析版)

C.若 , ,则 D.若 , ,则
【答案】D
【解析】逐项进行分析,在A中,l与m相交、平行或异面;在B中,m与α相交、平行或m⊂α;在C中,m∥α或m⊂α;在D中,由线面垂直的性质定理得l∥m.
【详解】
由l,m是条不同的直线,α是一个平面,知:
在A中,若l∥α,m∥α,则l与m相交、平行或异面,故A错误;
2020届浙江省杭州市学军中学高三下学期高考模拟数学试题
一、单选题
1.已知集合 , ,则 ()
A. B. C. D.
【答案】B
【解析】根据并集的定义计算
【详解】
∵ , ,∴ .
故选:B.
【点睛】
本题考查集合的并集运算,属于简单题.
2.双曲线 的实轴长为()
A.2B.3C.4D.6
【答案】C
【解析】根据双曲线标准方程知实轴长为2a,可知双曲线 的实轴长
【详解】
由双曲线标准方程 中,实轴长为2a可知:
在双曲线 中,实轴长为4
故选:C
【点睛】
本题考查了双曲线的几何性质,利用标准方程及实轴定义求实轴长
3.已知圆 ,直线l过点 且倾斜角为 ,则“ ”是“直线l与圆C相切”的()
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
【答案】A
故选:B
【点睛】
本题考查了应用坐标表示向量的数量积求最值,根据数量积的坐标公式,结合一元二次方程有解求参数范围,进而求最大值
9.定义在 上的奇函数 满足 ,且当 时, ,则下列结论正确的是( )
A. B.
C. D.
【答案】C
【解析】根据f(x)是奇函数,以及f(x+2)=f(-x)即可得出f(x+4)=f(x),即得出f(x)的周期为4,从而可得出f(2018)=f(0), , 然后可根据f(x)在[0,1]上的解析式可判断f(x)在[0,1]上单调递增,从而可得出结果.
浙江省名校协作体2020届高三下学期联考通用技术试题含答案
第二部分 通用技术(共50分)一、选择题(本大题共13小题,每小题2分,共26分。
每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分) 1. 如图所示为某公司新研制的多功能讲台,可以满足站立状态下的书写与阅读的需要,从人机关系角度考虑,该产品主要考虑了A .人的动态尺寸B .人的静态尺寸C .人的心理需求D .信息交互2. 如图所示是一款高速冲压机的部分结构图,电机高速旋转通过曲柄和连杆带动冲压板上下运动,图中与冲压板相连的4根支柱的作用是 A.增加工作时的冲击力 B.增加冲压板的美观度,起装饰作用 C.固定电机,起支撑作用 D.增加冲压板的稳定性,起限位作用通用技术实践课上,小张要制作如图所示小铁锤的锤头,原材料是一根边长14mm 的正方形条钢,长度1m,请根据图样及描述完成3-4题。
第3-4题图连杆 曲柄第1题图3. 加工该锤头时,下列加工工艺及其工具选择中不需要...或者不合理...的是 A .划线:划针和钢直尺 B .锯割:台虎钳和钢锯C .钻孔:麻花钻和平口钳D .攻丝:丝锥和手钳4. 小张在加工过程中,进行了以下操作,其中操作正确的是A .下料时将条钢夹持在台虎钳上,锯下一段长度为76mm 的方钢B .加工圆弧面时,先锯割出大致形状然后用圆锉锉削出圆弧面C .钻孔时用平口钳夹持钻直径为8mm 的圆孔D .在攻丝时添加了润滑油5. 如图所示的尺寸标注中,漏标的尺寸共有 A .1处 B .2处 C.3处 D .4处6. 如图所示的省力剪刀,在力F 的作用下可以剪断细钢丝,在这个过程中下列关于各个构件及细钢丝的受力分析中,合理的是A .手柄1受压、构件DC 受压B .手柄2受弯曲、构件DC 受拉 C .构件BA 受弯曲、钢丝受压D .构件BA 受拉、钢丝受剪切7. 如图所示是高校开学后校园和宿舍区安全管理流程图。
下列关于该流程分析中不正确...的是 A .学生进校需在校门处测体温并评估B .家长不能进宿舍C .无关人员在校园内要做好防护D.学生在宿舍内有发热症状的马上引导就诊并按相关工作流程处理第7题图第5题图第6题图手柄 1 手柄2如图所示为涡轮发动机中采用的离心式调速器的工作原理图。
