第4章 作业参考答案
第四章 作业参考答案

第四章作业参考答案4. 用推广的Euclid算法求67 mod 119的逆元解:初始化:(1,0,119), (0,1,67)1:Q=119/67=1,(0,1,67) , (1,-1,52)2:Q=67/52=1,(1,-1,52), (-1,2,15)3:Q=52/15=3,(-1,2,15), (4,-7,7)4:Q=15/7=2,(4,-7,7), (-9,16,1)所以67-1 mod 119=1610.设通信双方使用RSA加密体制,接收方的公开钥是(e,n)=(5,35),接收到的密文是C =10,求明文M。
解:由n=35,易知35=5×7,进而ϕ(n)=ϕ(35)=24,由RSA加密体制可知,ed≡1 mod ϕ(n),即5d≡1 mod 24,所以d=5∴M=C d mod n=105 mod 35=511. 已知c d mod n的运行时间是O(log3n),用中国剩余定理改进RSA的解密运算。
如果不考虑中国剩余定理的计算代价,证明改进后的解密运算速度是原解密运算速度的4倍。
证明:RSA的两个大素因子p,q的长度近似相等,约为模数n的比特长度log n的一半,即(log n)/2,而在中国剩余定理中要计算模p和模q两个模指数运算,与c d mod n的运行时间规律相似,每一个模指数运算的运行时间仍然是其模长的三次幂,即O[((log n)/2)3]= O(log3n)/8,这样在不考虑中国剩余定理计算代价的情况下,总的运行时间为两个模指数的运行时间之和,即O(log3n)/8+O(log3n)/8=O(log3n)/4,得证。
12. 设RSA加密体制的公开钥是(e,n)=(77,221)。
(1) 用重复平方法加密明文160,得中间结果为1602(mod 221)=185,1604(mod 221)=191,1608(mod 221)=16,16016(mod 221)=35,16032(mod 221)=120,16064(mod 221)=35,16072(mod 221)=118,16076(mod 221)=217,16077(mod 221)=23,若敌手得到以上中间结果就很容易分解n,问敌手如何分解n解:由以上中间结果得16016(mod 221)=35=16064(mod 221),此即16064-16016=0 (mod 221)即(16032-1608) (16032+1608)=0 (mod 221)(120-16)(120+16)=0 (mod 221)104×136=0 (mod 221)由gcd(104,221)=13及gcd(136,221)=17,可知221的分解为221=13×17(2) 求解密密钥dd=e-1mod ϕ(221)=77-1 mod 12×16由扩展Eucild算法可得d=5。
第4章课后习题及答案

返 回
第 4 章 供 电 与 用 电
练习题解答
4.1.1 某三相同步发电机,三相绕组联结成星形时的线电压为 10.5kV,若将它联结成三角形,则线电压是多少?若联结成星形 时,L2相绕组的首末端接反了,则三个线电压的有效值U12 , U23 和U31各是多少? · · · · U31= U3 -U1 · -U2 解: 星形联结时UlY = 10.5kV U3 · U 3 UlY 10.5 = kV = 6.06kV ∴UpY = · · U 1=U23 √ 3 √3 · ·-U =U 三角形联结时相电压不变, 2 3 · UlY = UpY =6.06kV L2首末端接反的相量图如图所示:
· · · 0 0 0 IL2 = I2 - I1 ( 8 . 8 30 8 . 8 0 ) A 4 . 56 105 A · · · 0 0 0 IL3 = I3 - I2 ( 8 . 8 30 8 . 8 30 ) A 8 . 8 90 A
XL= Z sin = 77.1×0.6 Ω = 46.3 Ω
返 回 上一题 下一题
第 4 章 供 电 与 用 电
4.3.2 某三相负载,额定相电压为220V,每相负载的电阻为4Ω,感 抗为3Ω,接于线电压为380V的对称三相电源上,试问该负载应
采用什么联结方式?负载的有功功率、无功功率和视在功率?
· I
l2
· I
l3
· I
2
· I
3
-jXC
解: 负载为不对称三相负载
· · 0 U U 220 120 2 23 · 0 I2 = Z = -jX = 8 . 8 30 A -j25 2 C
返 回 上一题 下一题
习题参考答案(第4章)
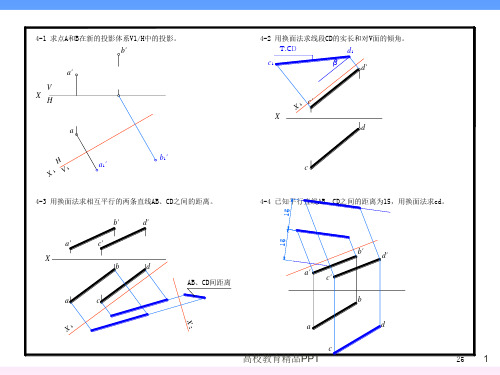
a' V XH
a
4-2 用换面法求线段CD的实长和对V面的倾角。
T.CD
d1
c1 d'
X 1 c' X
d
H X1 V1
a1'
b1'
c
4-3 用换面法求相互平行的两条直线AB、CD之间的距离。
b'
d'
a'
c'
X
b
d
a
c
AB、CD间距离
4-4 已知平行直线AB、CD之间的距离为15,用换面法求cd。
15
15
a' c'
b'
d'
b
X2
பைடு நூலகம்X1
a
d
c
高校教育精品PPT
25 1
4-5 已知直线AB与CD垂直相交,用换面法求c'd'。 b'
a'
c a
b d
4-6 用换面法求点到直线BC距离,并求垂足。
a'
c'
b'
c a
A到BC距离 b
O2
4-7 已知点A到直线BC的距离为15,求a。 a1
R15
b1
c1
O1
a b
c a'1
c'1 c2
a2
b1' b2
高校教育精品PPT
27 3
4-11 已知直线AB与 CDE的距离为10,用换面法求ab。
c' e'
b'
a' X
物理光学第4章习题答案

• 因此,这个衍射屏具有类似透镜的性质。
• (2)对于因子exp(iar2 ):a= - k/2f1,
• 得f1 = - k/2a= -π/aλ< 0,发散;
• 对于因子 exp(-iar2): a= k/2f2,
• 得f2 = k/2a=π/aλ> 0,汇聚;
• 对于因子1/2,1/2=1/2*e0, • 可得 f3 = ∞。
•
=∫±L (A/2i)*( ei2πu0x – e -i2πu0x )
•
*exp(-i2πux)dx
•
=∫±L (A/2i)*[ ei2π(u0-u)x – e -i2π(u0+u)x ] dx
•
=(A/4 π) *[(1/u-u0) *ei2π(u0-u)x - (1/u+u0)
*ei2π(u0+u)x ] |±L
S
D
2
sin
cos
2
而
cos l'v
D
故
S
D
2
c
os1
l ' v
v
2
2
D D D
光瞳的面积为:
SD
2
D 2
2
因此得到沿v轴的光学传递函数为:
可见沿v轴的截止频率为:
vm a x
D
l'
(2)再来计算沿u轴的光学传递函数。 在ξ轴上分开λl’u的两个光瞳的重叠面积,如下图所示:
最后得到强度分布
I (x) (x) 2
=cos2
2
u0
x
1 2
(1
cos
4
u0 x)
可见,像面上的强度分布仍是一正弦式分布,但空间频率为物分布的2倍。
第4章 习题及答案
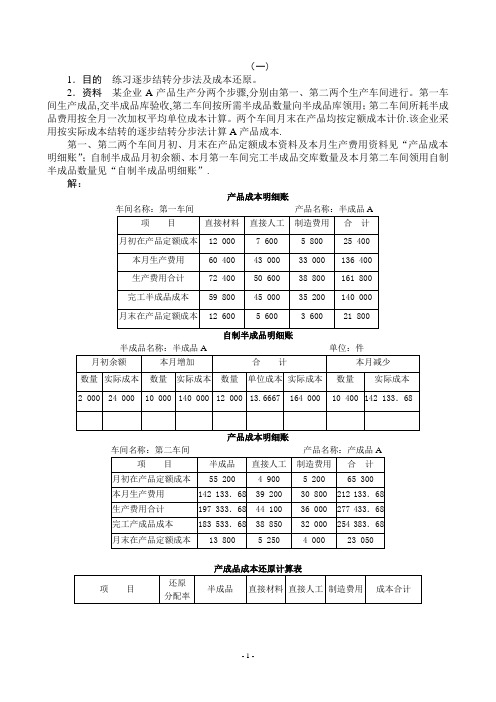
(一)1.目的练习逐步结转分步法及成本还原。
2.资料某企业A产品生产分两个步骤,分别由第一、第二两个生产车间进行。
第一车间生产成品,交半成品库验收,第二车间按所需半成品数量向半成品库领用;第二车间所耗半成品费用按全月一次加权平均单位成本计算。
两个车间月末在产品均按定额成本计价.该企业采用按实际成本结转的逐步结转分步法计算A产品成本.第一、第二两个车间月初、月末在产品定额成本资料及本月生产费用资料见“产品成本明细账”;自制半成品月初余额、本月第一车间完工半成品交库数量及本月第二车间领用自制半成品数量见“自制半成品明细账”.解:产品成本明细账车间名称:第一车间产品名称:半成品A自制半成品明细账半成品名称:半成品A 单位:件产品成本明细账产成品成本还原计算表(二)1.目的练习产品成本计算的综合结转分步法.2.资料某企业生产甲产品,分三个生产步骤进行生产。
该企业设有第一、第二、第三三个基本生产车间,甲产品由这三个车间顺序加工而成。
成本计算采用综合结转法。
原材料在第一车间开始加工时一次投入,半成品不通过中间仓库收发,上一步骤完工后全部交由下一步骤继续加工。
月末在产品按约当产量法计算,各车间月末在产品完工程度均为50%。
该企业本年5月份有关成本计算资料如表1、表2所示。
表1产量记录表2月初在产品成本和本月发生费用表3产品成本计算单135070÷(88+16)=1298。
75 24960÷(88+16×50%)=260 19200÷(88+16×50%)=200表4产品成本计算单173890÷(8050%)=326。
6表5产品成本计算单244450÷(96+4)=2444.5 34300÷(96+4×50%)=350 23520÷(96+4×50%)=240表6(三)1.目的练习产品成本计算的平行结转分步法.2.资料某厂设有三个基本生产车间,第一车间生产甲半成品,交第二车间继续加工,第二车间生产乙半成品,交第三车间生产丙产成品。
第4章 习题答案

50������-2 = 0
������������������������ = -0.5 +
������������
解得 L=10(已舍去负值)
且
������2������������������ ������������2
=
-100������-3<0
所以,当劳动投入量 L=10 时,劳动的
第四章 生产论 3. 已知生产函数 Q=f(L,K)=2KL-0.5L2 -0.5K2, 假定厂商目前处于短期生产,且 K =10。
(1)写出在短期生产中该厂商关于劳动的 总产量 TPL 函数、劳动的平均产量 APL 函数 和劳动的边际产量 MPL 函数。
(2)分别计算当劳动的总产量 TPL、劳动 的平均产量 APL 和劳动的边际产量 MPL 各自 达到最大值时的厂商的劳动投入量。
有 MP=0,于是,有 35+16L-3L2=0。
解得������ = − 5
3
和
L=7。������
=
-
5 3
不合
理,舍去,故取 L=7。
由此可得,生产要素 L 投入量的合理区 间为[4,7]。因此,企业对生产要素 L 的使用 量为 6 是处于短期生产的合理区间的。
11. 已知生产函数 Q=AL1/3K2/3。 判断:(1)在长期生产中,该生产函数的规模 报酬属于哪一种类型?
50 劳动的平均产量函数:
APL=
TPL =20-0.5L- 50
������
������
劳动的边际产量函数:
MPL=
������������������������ ������������
=20-L
(2)关于总产量的最大值:
电力系统暂态分析(第四章习题答案)

=
1 3
1 1 1
a a2
1
a2 a 1
za 0
0
0
zb 0
0 0 zc
1 a2
a
1
a a2
1 1 1
1 =3
za + zb + zc Z2 Z1
Z1 za + zb + zc
Z2
Z2 Z1 za + zb + zc
其中: Z1 = za + a2zb + azc; Z2 = za + azb + a2zc
解:对应于三个网络的零序等效网络如下所示。
(1)图 a 中,在 k 点短路时,由于外接负载 L 不 接地,零序电流不能流通。且零序电压加在变压器 T2 的 Y 侧,零序电流也无法流通。零序电抗 x0 。 (2)图 b 中,在 k 点短路时,因为 xm0 ,所以, 零 序 等 效 电 路 如 图 7 - 10 所 示 。 零 序 电 抗 x 0 xT1(0) xL1(0) 。 (3)图 c 中,在 k 点短路时,因为 xm0 所以零 序电流在短路点右侧没有通路。零序电抗 x 0 xT1(0) xL1(0) 。 4-9 如图所示电力系统, 试作出 k 点发生单相接地故
33 13 (6 + 6 ) − j(6 + 6 )
=
33
13
6 − 6 + j(− 6 + 6 )
1 j3
②各序分量解藕单独作用分别求解序电流
正序电流:
I1
=
E1 j2
=
(−
1 12
−
3 12)
−
3 j(12
+
(完整版)固定收益证券(姚长辉)第四章作业参考答案

第四章 持续期与凸性1、有效持续期为105.5100//102.5 5.37%1effective P P D P y y -+-+--===-所以有效持续期为5.37%。
2、根据1的结果,D=5.37%△P=D*1%=5.37%P’=102.5*(1+5.37%)=1086债券价格为108元3、(不会)参考答案:因为是浮动利率债券,所以比率持续期接近0.5。
4、5.49%*98.63*2=10.79债券价格的变化为10.795、设N 3为持有3年期零息债券的数目,N 20为持有20年期债券数目投资者权益在初始状态下的金额持续期为3*200-185*9=-1065为了让资产组合与负债在持续期上匹配,并且要保证权益价值,因此建立下面的策略100N 3+100N 20=200003N3+20N20-185*9=0N3=137.35, N20=62.65即投资者应当持有3年期零息债券数量为137.35个单位,价值13735,持有20年期零息债券数量为62.65个单位,价值为6265。
6.已知,一年期零息债券的到期收益率为5.02%时,价值为51.60,到期收益率为4.98%时,价值为51.98。
∵Ω=Δ金额/P D e=(P-P’\y+– y-)/P在到期收益率为5%时,Ω= D e,(5%为中点)∴Δ金额=P-P’\y+– y-代入,得Δ金额=(51.98-51.6)/(5.02%-4.98%)=950∴Δ金额=950*1%=9.57已知,一年期零息债券的到期收益率为5.02%时,价值为51.60,到期收益率为5.06%时,价值为51.40。
同理,得Δ金额=51.60-51.4/5.06%-5.02%=500∴Δ金额=500*1%=58.当到期收益率为5.02时Г=D1-D2/Δ=9.5-5/0.04%=112.5%=⨯+⨯-⨯=-9、D15.4210100025.761525039.9846130030118.605 3D=90355.8又14%V 770.051000645.04250573.211300186137=⨯+⨯-⨯=所以解得11%17%V 186********.8=95781.2V 186********.8=267192.8=-=+资产负债表资产净值与利率的关系图如下:0.411000 1.04250 2.9013003100Γ=⨯+⨯-⨯=-119310091395022∆=⨯Γ=⨯=14%11%17%V 770.051000645.04250573.211300186137V 95781.21395081831.2V 267192.813950253242.8=⨯+⨯-⨯='=-='=-=资产负债表资产净值与利率的关系图如下:10、1)79.20151.110001.1200073=+2)设两年期零息债券投资x ,十年期投资y 比例,则有:372000/1.1 2.92821000/1.1x y ==所以根据x+y=1,得到x=74.4%;y=25.6%3)利率突然上升,组合亏损11、(1)、一年期的即期收益率为1r =10016%94.3-=两年期的即期收益率2r ()212109.59.5105.40311r r +=++ 解得27%r =三年期的即期收益率为()33310017.5%1+r r =-=(2)、()()()201,210016%110017%f ⨯++=⨯+解得01,28.01%f =()()()()301,202,310016%1110017.5%f f ⨯+++=⨯+解得02,38.51%f =(3)、99.56(4)、()()239%9%9%10016%17%17.5%FV FV FV FV +=+++++解得FV=90.35()29%9%93.6916%17%FV FV FV P ⨯⨯+=+=++()29%9%93.6911FV FV FV P r r ⨯⨯+=+=++解得7%r ≈(5)、()()()()2323771077710716%117%17.5%11y y y ++=++++++++()()2377107231111% 2.611M y y y y +⨯+⨯+++Ω=⨯=+(6)2.61%(7)因为凸性的存在,在市场利率下降时,债券价格会上升,但上升的幅度比单单通过持续期估计的价格上升幅度来得大;而如果市场利率上升,债券价格下降的幅度,要小于单单通过持续期估计的价格下降的幅度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对于 r (s) 和 n (s) , 尽管开环传递函数和闭环 极点相同而闭环零点不同, 但是却具有相同的根轨迹。
习题4-6 分离点方程:
2 1 1 d d a d 1
(a 3) a 2 10a 9 解得 d 4 由d的表达式可确定: 当a=10时,有两个分离点: d1, 2 2.5,4 当a=9时,有一个分离点: d1, 2 3 d1, 2 2.75 j0.66 不是分离点。 当a=8时,
根轨迹方程
K ( s 1) 1 s ( s 2)
分离点 dห้องสมุดไป่ตู้,2 1 3 该系统的根轨迹必须按零度根轨迹的绘制法则进行绘制。
K1 (s 2) C ( s) r ( s) 习题4-12 R(s) s( s 5)(s 5) K1 (s 2) C ( s) (s 2 ( ) s 5)(s 5) n ( s) N ( s) s( s 5)(s 5) K 1 ( s 2) 闭环特征方程 D(s) s(s 5)(s 5) K1 (s 2) 0 K1 ( s 2) 等效开环传递函数 Gk ( s) G1 ( s)G2 ( s) s( s 5)(s 5)
第4章 作业参考答案
Root Locus
2.5
习题4-3
Imaginary Axis
2 1.5 1 0.5 0 -0.5 -1 -1.5 -2 -2.5 -7 -6 -5 -4 -3
Real Axis
(1) 分离点: d=-4.24
-2
-1
0
1
(2) 分离点:
K * (s 4 8s3 36s 2 18s 80)
d1, 2 1.5 j0.866 不是分离点。 当a=3时,
a=10
a=9
a=8
a=3
习题4-8 开环传递函数
1 G (s) s(s 1 a)
Imaginary Axis
Root Locus
1
0.5
特征方程
s ( s 1 a) 1 0
0
等效开环传递函数 分离点 d 1
2 j 6 ( K1 100)
-2+j4
j
由
dK * 0 ds
-4
0
解得 s1、2= 2,s3、4= 2±j 6
K1
j 10 ( K1 260)
习题4-5 (1) K1>0时,根轨迹中的两个分 支始终位于s 右半平面,系统 不稳定;
(2) 增加一个零点z = 1之后,根 轨迹左移,根轨迹中的三个 分支始终位于s 左半平面,系 统稳定。
a
1 (0.5 j 0.866) 1 (0.5 j 0.866) 1 0
1
习题4-9(1)
习题4-9(2)
1.58
习题4-9(3)
3.5
习题4-10 将开环传递函数写成标准形式
K (1 s) K ( s 1) G( s) s( s 2) s( s 2)
as Geq (s) 2 s s 1
-0.5
-1
-1.5
-1
Real Axis
-0.5
0
(1) Kv=1,essv=1,=0.5,ts=3.5/n=7(s) (2) 当a=0时,欠阻尼,系统的阶跃响应为衰减振荡过 程;当a=2时,过阻尼,系统的阶跃响应为单调上升过程。
(3) 临界阻尼时
