理论力学18
理论力学试题含答案
精选文档理论力学试题及答案一、是非题(每题2分。
正确用√,错误用×,填入括号内。
)1、作用在一个物体上有三个力,当这三个力的作用线汇交于一点时,则此力系必定均衡。
2、力关于一点的矩不因力沿其作用线挪动而改变。
()3、在自然坐标系中,假如速度υ=常数,则加快度α=0。
()4、虚位移是偶想的,极细小的位移,它与时间,主动力以及运动的初始条件没关。
5、设一质点的质量为m,其速度与x轴的夹角为α,则其动量在x轴上的投影为mvx=mvcosa。
二、选择题(每题3分。
请将答案的序号填入划线内。
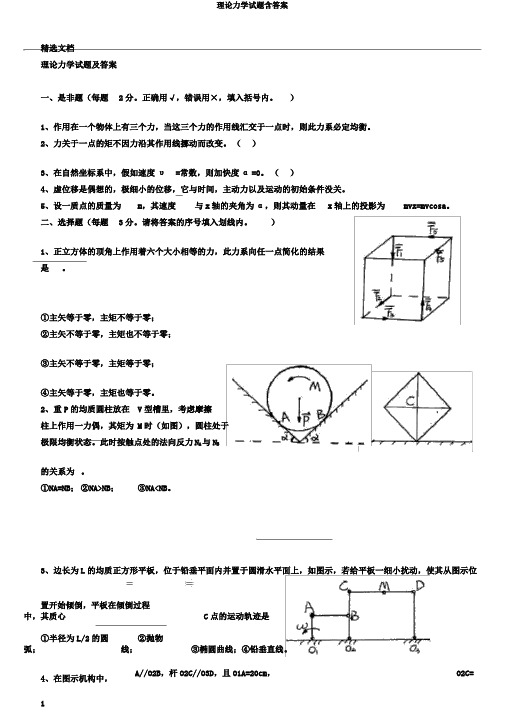
)1、正立方体的顶角上作用着六个大小相等的力,此力系向任一点简化的结果是。
①主矢等于零,主矩不等于零;②主矢不等于零,主矩也不等于零;③主矢不等于零,主矩等于零;④主矢等于零,主矩也等于零。
2、重P的均质圆柱放在V型槽里,考虑摩擦柱上作用一力偶,其矩为 M时(如图),圆柱处于极限均衡状态。
此时按触点处的法向反力N A与N B的关系为。
①N A=NB;②N A>NB;③N A<NB。
3、边长为L的均质正方形平板,位于铅垂平面内并置于圆滑水平面上,如图示,若给平板一细小扰动,使其从图示位置开始倾倒,平板在倾倒过程中,其质心C点的运动轨迹是。
①半径为L/2的圆弧;②抛物线;③椭圆曲线;④铅垂直线。
4、在图示机构中,A//O2B,杆O2C//O3D,且O1A=20cm,O2C=杆O140cm,CM=MD=30cm,若杆AO1以角速度ω=3rad/s匀速转动,则D点的速度的大小为cm/s,M点的加快度的大小为cm/s2。
①60;②120;③150;④360。
.精选文档5、曲柄OA以匀角速度转动,当系统运动到图示地点(OA//O1B。
AB |OA)时,有V A V B,A B,ωAB 0,AB 0。
①等于;②不等于。
三、填空题(每题5分。
请将简要答案填入划线内。
)1、已知A重100kN,B重25kN,A物与地面间摩擦系数为0.2。
理论力学复习试题和答案(哈工大版)

C :作用于质点系的约束反力主矢恒等于零; D:作用于质点系的主动力主矢恒等于零;
..
..
6、 若作用在 A 点的两个大小不等的力 F 1 和 F 2,沿同一直
反。则其合力可以表示为
③
。
① F 1- F 2; ② F 2- F 1; ③ F 1+ F 2;
7、 作用在一个刚体上的两个力 F A、 F B,满足 F A=- F B 的条件,则该二力可能是②
( √) (× )
14、 已知质点的质量和作用于质点的力,质点的运动规律就完全确定。
(× )
15、 质点系中各质点都处于静止时,质点系的动量为零。于是可知如果质点
系的动量为零,则质点系中各质点必都静止。
(×)
16、 作 用 在 一 个 物 体 上 有 三 个 力 , 当 这 三 个 力 的 作 用 线 汇 交 于 一 点 时 , 则 此 力 系 必 然 平 衡 。
..
..
..
..
2、图示平面结构,自重不计。 求支座 A 的约束反力。
B 处为铰链联接。已知: P = 100 kN , M = 200 kN · m, L1 = 2m , L2 = 3m 。试
3、 一 水平 简支梁 结 构, 约 束和载 荷如 图 所示 , 求支座
q A
D
M B
E
P C
A和
B 的约束反力。
一、 是非题
1、 力 有 两 种 作 用 效 果 , 即 力 可 以 使 物 体 的 运 动 状 态 发 生 变 化 , 也 可 以 使 物 体 发 生 变 形 。
( √)
2、 在理论力学中只研究力的外效应。
( √)
3、 两端用光滑铰链连接的构件是二力构件。
理论力学(哈工大)考试选填判断简答重点内容

1、二力杆:只在两个力作用下平衡的构件。
2、静力学公理:1)平行(力的平行四边形法则):作用于物体上同一点的两个力,可以合成为一个合力,合力也作用于该点,合力的大小和方向,由这两个力构成的平行四边形的对角线确定。
刚体或者变形体都适用。
2)平衡(二力平衡公理):作用于刚体上的两个力,使刚体处于平衡的必要和充分条件是这两个力的大小相等,方向相反,且在同一直线上。
只适用于刚体。
3)加减(加减平衡力系公理):在作用于刚体上的任意力系中,加上或减去任意的平衡力系,并不改变原力系对刚体的作用。
只适用于刚体。
(1)可传(力的可传性原理):作用于刚体上某点的力,可以沿着它的作用线移动到刚体上的任意一点,并不改变该力对刚体的作用。
(2)三交汇(三力平衡交汇定理):作用于刚体上三个相互平衡的力,其中两个力的作用线汇交于一点,则此三力必在平面上,且第三个力的作用线也通过该汇交点。
4)相互(作用与反作用定律):作用力和反作用力总是同时存在,大小相等、方向相反,沿同一直线,分别作用在两个相互作用的物体上。
对刚体或变形体都适用。
5)刚化(刚化原理):变形体在某一力系作用下处于平衡,若将此变形体刚化为刚体,则平衡状态保持不变。
3、自由体和非自由体:运动不受限制的物体称为自由体;运动受到限制的物体称为非自由体。
4、两力相等和两个力等效不是一回事,力相等(大小、方向、作用点),力等效(根据力的可传递性原理,作用点可不一样,教材第7页;一个合力可以与力系等效,但合力不等于力系)。
平衡力系:物体处于平衡状态时,作用于物体上的力系。
等效力系:如果作用于物体上的力系可以用另一个力系代替,二不改变物体的原有状态。
5、约束反力,存在于相互接触之处,与约束所能限制的位移方向相反。
光滑铰链约束特点:构件只能绕销钉的轴线转动,而不能相对移动。
6、各种约束的约束特点:柔性约束:方向沿着绳索中心线而背离物体。
光滑面约束:约束反力作用在接触点,沿接触面的公法线指向被约束物体。
陈世民理论力学简明教程(第二版)课后答案

第零章 数学准备一 泰勒展开式 1 二项式的展开()()()()()m23m m-1m m-1m-2f x 1x 1mx+x x 23=+=+++!!2 一般函数的展开()()()()()()()()230000000f x f x f x f x f x x-x x-x x-x 123!''''''=++++!!特别:00x =时, ()()()()()23f 0f 0f 0f x f 0123!x x x ''''''=++++!!3 二元函数的展开(x=y=0处)()()00f f f x y f 0x+y x y ⎛⎫∂∂=++ ⎪∂∂⎝⎭,22222000221f f f x 2xy+y 2x x y y ⎛⎫∂∂∂++ ⎪ ⎪∂∂∂∂⎝⎭!评注:以上方法多用于近似处理与平衡态处的非线性问题向线>性问题的转化。
在理论力问题的简单处理中,一般只需近似到三阶以内。
二 常微分方程1 一阶非齐次常微分方程: ()()x x y+P y=Q通解:()()()P x dx P x dx y e c Q x e dx -⎛⎫⎰⎰=+ ⎪⎝⎭⎰注:()()(),P x dxP x dx Q x e dx ⎰±⎰⎰积分时不带任意常数,()x Q 可为常数。
2 一个特殊二阶微分方程2y A y B =-+ 通解:()02B y=K cos Ax+Aθ+注:0,K θ为由初始条件决定的常量 3 ,4 二阶非齐次常微分方程 ()x y ay by f ++=通解:*y y y =+;y 为对应齐次方程的特解,*y 为非齐次方程的一个特解。
非齐次方程的一个特解 (1) 对应齐次方程0y ay by ++=设x y e λ=得特征方程2a b 0λλ++=。
解出特解为1λ,2λ。
*若12R λλ≠∈则1x 1y e λ=,2x 2y e λ=;12x x 12y c e c e λλ=+*若12R λλ=∈则1x 1y e λ=,1x 2y xe λ=; 1x 12y e (c xc )λ=+*若12i λαβ=±则x 1y e cos x αβ=,x 2y e sin x αβ=;x 12y e (c cos x c sin x)αββ=+(2) "(3) 若()2000x f a x b x c =++为二次多项式*b 0≠时,可设*2y Ax Bx C =++ *b 0≠时,可设*32y Ax Bx Cx D =+++注:以上1c ,2c ,A,B,C,D 均为常数,由初始条件决定。
理论力学第18讲(运动学习题课)

x
定系-固连于机座。 因为
O'
OO ut , OM y a sin( kt ),
所以,笔尖 M 的相对运动方程:
x OO ut , y OM a sin( kt ).
kx y a sin u
消去时间t 得笔尖在纸带上所描绘出的轨迹:
牵连运动-直线平动 。
23
例题
3. 速度分析
A M 绝对速度va: va=v1 ,方向已知。
v2
B
v1
30
牵连速度ve: ve=v2 ,方向水平向左 。 相对速度vr:大小和方向未知。
ve
60
应用速度合成定理
M β
va ve v r
vr
24
va
例题
va ve v r
A M v2 B 由几何关系
2
例题
例 题 1
振动仪中纪录振动的笔尖 M 沿铅直固定轴 Oy 作间谐振动
y=asin(kt+α)。纸带以水平匀速u向左运动,求笔尖在纸带上所描 绘出的轨迹。
y'
y u
x'
M
O
M
y'
x'
x
O'
O
3
例题
y' x' M
O
y
u
M O
解:
动点-笔尖M 。
动系-O´x´ y´,固连于工件上。
x'
y'
v1
x' x
v2
相对运动-沿AB的直线运动。
20
例题
O φ
y
3. 速度分析。 绝对速度va: va =v2,大小待求,方向沿OB。 牵连速度ve: ve = v1 ,方向沿轴Ox正向。
理论力学练习

一、是非题1、作用在一个物体上有三个力,当这三个力的作用线汇交于一点时,则此力系必然平衡。
2、力对于一点的矩不因力沿其作用线移动而改变。
( ) 3。
力偶没有合力,力偶平衡只能由力偶来平衡。
4、利用速度合成定理分析动点的运动时,动点的牵连速度是指某瞬时动系上与动点重合点的速度。
5、平面运动的刚体瞬时平动时,刚体上各点的速度和加速度都相同. ( ) 6。
当刚体平动时,刚体内各点的轨迹形状都相同。
( ) 7。
作用在刚体上的力是滑动矢量,力的三要素为大小、方向和作用线。
( )8、动量矩定理建立了质点和质点系相对于某固定点(固定轴)的动量矩的改变与外力对同一点(轴)之矩两者之间的关系.9.作用于质点系的外力主矢恒等于零,则质点系动量守恒。
( ) 10、作用于质点系上的所有内力做功的总和一定等于零. ( )11、作用在一个物体上有三个力,当这三个力的作用线汇交于一点时,则此力系必然平衡. 12。
作用在刚体上的力是滑动矢量,力的三要素为大小、方向和作用线。
( ) 13。
力对点的矩矢在通过该点的任意轴上的投影等于这力对于该轴的矩. ( ) 14. 在有摩擦的情况下,全约束力与法向约束力之间的夹角称为摩擦角。
( )15.平面运动刚体瞬时平动时,刚体上各点的速度和加速度都相同。
( )16.在非惯性参考系中,牵连惯性力F Ie 与一般力的不同之处在于,只有受力体,而没有施力体.17.动参考系给动点直接影响的是该动系上与动点相重合一点,这点称为瞬时重合点或动点牵连点。
18。
质点系中各质点都处于静止时,质点系的动量为零。
可知如果质点系的动量为零,则质点系中各质点必都静止。
19。
力与其作用时间的乘积称为力的冲量,冲量表示力在其作用时间内对物体作用累积效应度量。
20。
绝对运动、相对运动都是指点的运动,可能是直线运动或者是曲线运动。
选择题1.杆AB 的正确受力图为 。
A 。
B. C. D 。
2.空间任意力系向某一定点O 简化,若主矢0≠'R ,主矩00≠M ,则此力系简化的最后结果 . A 。
高教出版社理论力学习题部分答案

静力学1-3 试画出图示各结构中构件AB 的受力图F AxF A yF B(a)(a)F AF BF BF DF D F BxF ByF BxF CF BF CF By1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a1-5bF AxF A y F DF ByF A F BxF B F AF Ax F A y F DxF Dy WT EF CxF C yWF AxF A yF BxF B yF CxF C yF DxF DyF Bx F ByT EN’F BF DF A N F AF BF D1-8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示: 由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F 对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =F ABF BC F CD 60o F 130o F 2 F BC45o F 2F BC F ABB45oy xF CD C60o F 130o F BC x y450302-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
《理论力学》习题集含答案

理论力学习题集答案
理论力学教研室
目录
目录 (1)
第一章:静力学的基本概念 (2)
第二章:平面基本力系 (6)
第三章:平面任意力系 (10)
第五章:空间基本力系 (24)
第六章:空间任意力系 (25)
第七章:重心 (32)
第八章:点的运动 (34)
第九章:刚体的基本运动 (36)
第十章:点的复合运动 (38)
第十一章:刚体的平面运动 (52)
第十二章:刚体的转动合成 (66)
第十四章:质点动力学基础 (70)
第十五章:质点的振动 (75)
第十七章:动能定理 (82)
第十八章:动量定理 (94)
第十九章:动量矩定理 (100)
第二十章:碰撞理论 (115)
第二十一章:达朗伯原理 (118)
第二十二章:虚位移原理 (125)
第一章:静力学的基本概念
第二章:平面基本力系
第三章:平面任意力系
第五章:空间基本力系
第六章:空间任意力系
第七章:重心
第八章:点的运动
第九章:刚体的基本运动
第十章:点的复合运动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M
i 1
n
O
(I )
e i
在一定的时间间隔内,质点系动量矩的改变等于 同一时间间隔内,作用在质点系上所有外力冲量矩 的主矩。
2013年8月4日 理论力学CAI
30
碰撞时刚体定轴转动运动微分方程的积分形式
J O 2 J O 1 M O ( I e )
碰撞时刚体平面运动微分方程的积分形式
15 I 2 16 m
2013年8月4日 理论力学CAI
48
碰撞的动能定理
1 T T0 v i v i 0 I i 2
2013年8月4日 理论力学CAI
12
(3) 局部变形的刚体碰撞过程分为两个阶段
u2
n
I1
tm
t1
F dt
u1
V2 V1
变形阶段的碰撞冲量;
F
I2
t2
tm
F dt 恢复阶段的碰撞冲量。
t1
I1 I2 tm t2
t
13
2013年8月4日 理论力学CAI
(5) 恢复因数-碰撞的恢复阶段 的冲量与变形阶段的冲量之比,用 e 表示:
4 1 3 2I mL AB mL 3 3 2mL
2013年8月4日 理论力学CAI
AB
3 2I 8m L
47
1 1 1 2 2 2 2 T J A AB J C BD m v B vC B 2 12 2
1 2 1 1 2 1 L2 2 2 2 2 mL AB mL2 BD mL AB m BD 6 24 2 2 4
mvC 0 Icos I Ox 0 Isin I Oy J O 0 Ihcos
33
O1 y
得到
2013年8月4日 理论力学CAI
Iy
mvC 0 Icos I Ox 0 Isin I Oy
Ix O
d
x
vC
J O 0 Ihcos
O1 y
0
JO h md
2013年8月4日 理论力学CAI
35
Iy Ix O
d
JO 0, h md
x
vC h
撞击中心位于刚体质心与转轴 轴心的连线或连线的延长线上; 撞击中心到转轴的垂直距离为
JO h md
I
C
O1
y
2013年8月4日 理论力学CAI
主动力的碰撞冲量通过撞击中 心、并且垂直于刚体质心与转轴 轴心的连线或连线的延长线,则 在转轴轴承处不会引起碰撞约束 力。
19
2013年8月4日 理论力学CAI
20
对心碰撞:碰撞时两物体质心的连线与接触点公法线重合 否则称为偏心碰撞。 对心正碰撞:碰撞时两质心的速度也都沿两质心连线方向,
则称为对心正碰撞(正碰撞),否则称为对心斜碰撞(斜碰
撞)。
2013年8月4日 理论力学CAI
21
2013年8月4日 理论力学CAI
研究碰撞现象,就是为了掌握其规律,以利用其有利
的一面,而避免其危害。
203年8月4日 理论力学CAI
5
2013年8月4日 理论力学CAI
6
2013年8月4日 理论力学CAI
7
2013年8月4日 理论力学CAI
8
2013年8月4日 理论力学CAI
9
2013年8月4日 理论力学CAI
m2 15000 (1 e 2 ) ( 1 0.6 2 ) 0.6 60% m1 m2 1000 15000
若将锻件加热,可使e减小。当达到一定温度时,可使锤 不回跳,此时可近似认为e =0,于是汽锤效率
2013年8月4日 理论力学CAI
m2 0.94 94% m1 m2
I
C
h
O1
I Ox=mvC Icos I Oy Isin Ihcos JO
y
2013年8月4日 理论力学CAI
34
I Ox=mvC Icos
Iy Ix O
d
I Oy Isin
x
vC h
Ihcos JO
vC d
I
C
为使轴承的碰撞约束力等于零, 必须使IOx和IOy同时等于零。
h2 e= h1
v A
2 gh2
2013年8月4日 理论力学CAI
17
恢复因数的取值范围
0 < e <1
部分弹性碰撞: 变形不能完全恢复;
e 1
完全弹性碰撞:无能量损耗,
碰撞后变形完全恢复;
e 0
完全塑性碰撞: 能量完全损耗, 变形完全不能恢复。
2013年8月4日 理论力学CAI
18
2013年8月4日 理论力学CAI
2013年8月4日 理论力学CAI 15
2013年8月4日 理论力学CAI
16
例 对于球A与固定平面的正碰撞情形
I 2 v v A e= = B I1 v A v B v =v B=0 B
hh2 2
A A
I2 v , e= =- A I1 vA
vA v'A
B
h1
v A 2 gh1 ,
e m xC 2 m xC 1 I x
m yC 2 m yC 1 I e y
J C 2 J C 1 M C ( I e )
2013年8月4日 理论力学CAI 31
Iy Ix O x
vC h
具有质量对称平面的刚体绕垂 直于对称平面的固定轴转动。 当刚体受到位于对称平面内的 碰撞冲量作用时,刚体的转动角 速度将发生变化,同时在转动轴 的轴承支承处将产生相应的碰撞 约束力。 刚体上,能够使碰撞约束力等于零 的主动力的碰撞冲量作用点,称为撞 击中心,或打击中心。
第十八章
碰 撞
在前面讨论的问题中,物体在力的作用下,运动速度都 是连续地、逐渐地改变的。本章研究另一种力学现象——物
体运动速度突然发生有限的改变。
碰撞:运动着的物体在突然受到冲击(包括突然受到约
束或解除约束)时,其运动速度发生急剧的变化,这种现象
称为碰撞。
2013年8月4日 理论力学CAI 1
18.1 碰撞的特征和基本假定
22
2013年8月4日 理论力学CAI
23
2013年8月4日 理论力学CAI
24
2013年8月4日 理论力学CAI
25
m1m2 T T1 T2 ( 1 e 2 )( v1 v2 )2 2( m1 m2 )
塑性碰撞 e = 0 , v2= 0
m1m 2 T1 2 T= vA = m1 2m1 m 2 1 m2
I
C
O1
y
2013年8月4日 理论力学CAI
32
Iy
Ix O I C
vC h
应用平面运动微分方程的积分 形式 mx mx I e
C2 C1 x e my C 2 my C1 I y
x
定轴转动微分方程的积分形式
J O 2 J O 1 M O ( I e )
2013年8月4日 理论力学CAI
45
解:系统对A:
v B L AB
vC
B
L BD 2
1 J A AB J C AB m Lv B LvC I 2 L 2 B
1 2 1 1 2 2 2 mL AB mL BD mL AB mL BD I 2 L 3 12 4
28
18.2
研究碰撞的矢量力学方法
1. 碰撞时的动量定理
p2 p1 m vc
Ie
m v c0
i 1
I
n
i
在一定的时间间隔内,质点系动量的改变等于 同一时间间隔内,作用在质点系上所有外力冲量 的主矢。
2013年8月4日 理论力学CAI 29
2. 碰撞时的冲量矩定理
L O 2 L O1
=1/1000s , 碰撞后榔头以v2=1.5m/s的速度回跳。求榔头打击铁块
的力的平均值。
以榔头为研究对象,根据动量定理
mv 2 mv1 I 的投影形式得
10 ( 1.5 6 ) I ; I 7.65 N s g
塑料
碰撞力的变化大致情况如图所示。 平均打击力 F * I / 7650 N ,是榔头重的765倍。
碰撞结束时:
3g 2 e1 e 2a
2013年8月4日 理论力学CAI 38
对0取动量矩
J 0 2 J 0 ( 1 ) I l
JO 4ma 2 ( 1 e ) 3 g I ( 1 2 ) l 3l 2a
2013年8月4日 理论力学CAI
39
水平方向取动量定理:
36
例 均质杆质量m,长2a,可绕O轴转动, 杆由水平无初速落下,撞到一固定物块。 设恢复系数为e,求碰撞后杆的角速度, 碰撞时轴承的碰撞冲量及撞击中心的位置。
2013年8月4日 理论力学CAI
37
解:碰撞开始时,由动能定理:
1 1 1 2 2 mga J O 1 0 m( 2a )2 1 2 2 3 求得: 3g 1 2a
m ( a 2 a1 ) I Ox I I Oy 0
4a 2 I Ox m ( 1 a 2 )( a) 3l I Oy 0
撞击中心位置:
( 令 I Ox 0 , 得到)
2013年8月4日 理论力学CAI
