理论力学期末试卷1(带答案)
本科理论力学期末考试卷及答案3套
诚信应考,考试作弊将带来严重后果!本科生期末测试1《 理论力学 I 》2020-2021(1)注意事项:1. 开考前请将密封线内各项信息填写清楚; 2. 所有答案请直接答在试卷上; 3.考试形式:(闭)卷;4. 本试卷共 ( 六 )大题,满分100分,考试时间120分钟。
题 号 一二 三 四 五 六 总分 得 分一、 判断题 (正确打“√”,错误打“×”,将答案填在下表中,每小题1分,共10分) 题号 1 2 3 4 5 6 7 8 9 10 答案 XXX√√XX√√√1. 力在两个坐标轴上的投影与力沿这两个坐标轴方向进行分解得到的分力的意义是相同的。
2. 力偶无合力的意思是说力偶的合力为零。
3. 质点系惯性力系的主矢与简化中心的选择有关,而惯性力系的主矩与简化中心的选择无关。
4. 平面力系向某点简化之主矢为零,主矩不为零。
则此力系可合成为一个合力偶,且此力系向任一点简化之主矩与简化中心的位置无关。
5. 某瞬时刚体上各点的速度矢量都相等,而各点的加速度矢量不相等,因此该刚体不是作平动。
6. 两齿轮啮合传动时,传动比等于主动轮与从动轮的转速比,若主动轮转速增大,则传动比也随之增大。
7. 若刚体内各点均作圆周运动,则此刚体的运动必是定轴转动。
8. 不管质点做什么样的运动,也不管质点系内各质点的速度为何,只要知道质点系的质量,质点系质心的速度,即可求得质点系的动量。
9. 质点系的内力不能改变质点系的动量与动量矩。
10. 刚体受到一群力作用,不论各力作用点如何,此刚体质心的加速度都一样。
姓名 学号学院 专业班级 座位号( 密 封 线 内 不 答 题 ) ……………………………密………………………………………………封………………………………………线……………………………………得分oyxFF'c 二、 单项选择题(8小题,每题2分,共16分,将答案填在下表中。
)题号 1 2 3 4 5 6 7 8 答案 ADAADBBC1. 二力平衡条件的使用范围是( )A . 刚体 B. 刚体系统 C. 变形体 D. 任何物体或物体系统 2. 不经计算,可直接判定出图示桁架中零力杆的根数为( )。
大学期末考试理论力学试卷(含答案详解)

一、选择题(每题2分,共20分)1.若平面力系对一点A 的主矩等于零,则此力系( )。
A .不可能合成为一个力 B .不可能合成为一个力偶C .一定平衡D .可能合成为一个力偶,也可能平衡2.刚体在四个力的作用下处于平衡,若其中三个力的作用线汇交于一点,则第四个力的作用线( )。
A .一定通过汇交点B .不一定通过汇交点C .一定不通过汇交点3.将平面力系向平面内任意两点简化,所得主矢相等,主矩也相等,且主矩不为零,则该力系简化的最后结果为( )。
A .一个力 B .一个力偶 C .平衡4.图1中,已知P =60kN ,F =20kN静摩擦系数f s =0.5,动摩擦系数f d =0.4,则物体所受 摩擦力的大小为( )。
A .25kN B .20kN C .17.3kN5.一点做曲线运动,开始时的速度s m v /100=,恒定切向加速度2/4s m a =τ,则2s 末该点的速度大小为( )。
A .2m/sB .18m/sC .12m/sD .无法确定6.圆轮绕某固定轴O 转动,某瞬时轮缘上一点的速度v 和加速度a 如图2所示,试问哪些情况下是不可能的?( ) A .(a )、(b )运动是不可能的 B .(a )、(c )运动是不可能的 C .(b )、(c )运动是不可能的 D .均不可能7.如图3所示平行四边形机构,在图示瞬时,杆O 1A以角速度ω转动,滑块M 相对AB 杆运动,若取M 动点,动系固联在AB 上,则该瞬时动点M 的牵连速度与杆AB 间的夹角为( )。
A .00 B .300 C .600图28.平面机构如图4所示,选小环M 为动点,动系固联 在曲柄OCD 杆上,则动点M 的科氏加速度的方向( )。
A .垂直于CD B .垂直于AB C .垂直于OM D .垂直于纸面9.如图5所示,两物块A 、B ,质量分别为A m 和B m 初始静止。
如A 沿斜面下滑的相对速度为r v ,设B 向左运动的速度为v ,根据动量守恒定律理有(A .v m v mB r A =θcos B.v m v m B r A=C.v m v v m B r A =+)cos (θD. v m v v m B r A =-)cos (θ10.已知刚体质心C 到相互平行的z '、z 轴之间的距离分别为a 、b ,刚体的质量为m ,对z 轴的转动惯量为z J ,则'z J 的计算公式为( )。
理论力学-理论力学期末考试(答案题解)
理论力学课程期末考试(答案题解)
一、1、(1) 研究全系统,由 M O (F ) 0 计算;(2)三种方法:平面运动刚
体运动微分方程;(3)静力学平衡方程和虚位移原理。
2、两个自由度,理想约束,完整约束,定常约束
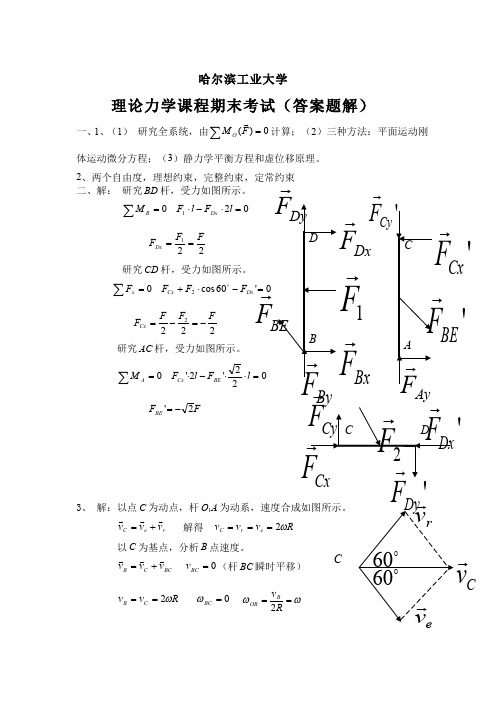
二、解: 研究 BD 杆,受力如图所示。
F F ' M B 0 F1 l FDx 2l 0
mvC2
力所作的功为 W
M
2
由动能定理有
2
M
11 12
mvC2
解得 vC
6M 11m
C
1 R
6M 11m
BC
1 2R
6M 11m
以 C 为基点,分析 B 点加速度,加速度合成图如图所示。
aBt
a
n B
aC
aBt C
aBnC
向 aBt 方向投影,有
3 2
R
FC
R
3 2
mR 2
C
3mR 2
解得
M 10mR 2
S
所以 O1A
M 10mR 2
C
2
M 5mR 2
BC 0
OB
M 10mR 2
分析圆盘,建立相对质心 C 的动量矩定理,有
FE
R
mR 2 2
C
5、 解:分析 BC 杆,瞬心为 B。
解得
FCx '2l FBE '
2 2
l
0
理论力学期末考试试题(卷)(试题(库)带答案解析)

理论力学 期末考试试题1-1、自重为P=100kN 的T 字形钢架ABD,置于铅垂面,载荷如图所示。
其中转矩M=20kN.m ,拉力F=400kN,分布力q=20kN/m,长度l=1m 。
试求固定端A 的约束力。
解:取T 型刚架为受力对象,画受力图.1-2 如图所示,飞机机翼上安装一台发动机,作用在机翼OA 上的气动力按梯形分布:1q =60kN/m ,2q =40kN/m ,机翼重1p =45kN ,发动机重2p =20kN ,发动机螺旋桨的反作用力偶矩M=18kN.m 。
求机翼处于平衡状态时,机翼根部固定端O 所受的力。
解:1-3图示构件由直角弯杆EBD以及直杆AB组成,不计各杆自重,已知q=10kN/m,F=50kN,M=6kN.m,各尺寸如图。
求固定端A处及支座C的约束力。
1-4 已知:如图所示结构,a, M=Fa, 12F F F ==, 求:A ,D 处约束力.解:1-5、平面桁架受力如图所示。
ABC 为等边三角形,且AD=DB 。
求杆CD 的力。
1-6、如图所示的平面桁架,A 端采用铰链约束,B 端采用滚动支座约束,各杆件长度为1m 。
在节点E 和G 上分别作用载荷E F =10kN ,G F =7 kN 。
试计算杆1、2和3的力。
解:2-1 图示空间力系由6根桁架构成。
在节点A上作用力F,此力在矩形ABDC平面,且与铅直线成45º角。
ΔEAK=ΔFBM。
等腰三角形EAK,FBM和NDB在顶点A,B和D处均为直角,又EC=CK=FD=DM。
若F=10kN,求各杆的力。
2-2 杆系由铰链连接,位于正方形的边和对角线上,如图所示。
在节点D沿对角线LD方向作用力F。
在节点C沿CH边铅直向下作用力F。
如铰链B,L和H是固定的,杆重不D计,求各杆的力。
2-3 重为1P =980 N ,半径为r =100mm 的滚子A 与重为2P =490 N 的板B 由通过定滑轮C 的柔绳相连。
已知板与斜面的静滑动摩擦因数s f =0.1。
理论力学1 期末考试试题及参考答案

理论力学复习题1一、是非题(正确用√,错误用×)1:作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
( )2:作用在一个物体上有三个力,当这三个力的作用线汇交于一点时,则此力系必然平衡。
( ) 3:刚体的运动形式为平动,若刚体上任一点的运动已知,则其它各点的运动随之确定。
( )4: 瞬时速度中心点的速度等于零,加速度一般情况下不等于零。
( )5:一个质点只要运动,就一定受到力的作用,而且运动的方向就是它受力的方向。
( )二、选择题(单选题)1. 一重W 的物体置于倾角为α的斜面上,若摩擦系数为f ,且tg α<f ,若增加物体重量,则物体会 () 。
A: 静止不动; B: 向下滑动; C: 运动与否取决于平衡条件。
2. 一动点作平面曲线运动,若其速率不变,则其速度矢量与加速度矢量( ) 。
A :平行;B :夹角随时间变化;C :垂直;D :不能确定3. 牵连运动是指( )A.动系相对于静系的运动B.牵连点相对于动系的运动C.静系相对于动系的运动D.牵连点相对于静系的运动4. 图示均质杆OA 质量为m 、长度为l ,则该杆对O 轴转动惯量为( )A .12m lB .12m 2lC .3mlD .3m 2l5.质点系动量守恒的条件是( )。
A :作用于质点系的内力主矢恒等于零;B :作用于质点系的外力主矢恒等于零;C :作用于质点系的约束反力主矢恒等于零;D :作用于质点系的主动力主矢恒等于零;三、已知图示结构中的F 、a ,试求结构A 、B 的约束反力。
理论力学期末试卷1(带答案)

一.选择题(每题3分,共15分。
请将答案的序号填入划线内。
)1.空间同向平行力系1F 、2F 、3F 和4F ,如图所示。
该力系向O 点简化,主矢为'R F,主矩为OM ,则 (B )(A) 主矢主矩均不为零,且'R F 平行于O M(B) 主矢主矩均不为零,且'RF 垂直于O M(C) 主矢不为零,而主矩为零 (D) 主矢为零,而主矩不为零2.已知点M 的运动方程为ct b s +=,其中b 、c 均为常数,则( C )。
(A) 点M 的轨迹必为直线 (B) 点M 必作匀速直线运动 (C) 点M 必作匀速运动 (D) 点M 的加速度必定等于零3.如图所示若尖劈两侧与槽之间的摩擦角均为m ϕ,则欲使尖劈被打入后不致自动滑出,θ角应为( C )(A) θ≤m ϕ (B) θ≥m ϕ(C) θ≤2m ϕ (D) θ≥2m ϕ4.若质点的动能保持不变,则( D )。
(A) 该质点的动量必守恒 (B)(C) 该质点必作变速运动 (D) 5.直管AB 以匀角速度ω绕过点O 且垂直于管子轴线的定轴转动,小球M 在管内相对于管子以匀速度r v 运动,在如图所示瞬时,小球M 正好经过轴O 点,则在此瞬时小球M 的绝对速度a v 和绝对加速度a a 大小是( D )。
(A)a v =,a a = (B) a rv v =,0a a =(C) 0a v =,2a r a v ω= (D) a r v v =,2a ra v ω=二.填空题(每空2分,共30分。
请将答案填入划线内。
)1.平面汇交力系平衡的几何条件是 各力构成的力多边形自行封闭 ;平面汇交力系平衡的解析条件是0x F =∑、0y F =∑。
2.空间力偶的三个要素是 力偶矩的大小 、 力偶作用面的方位 和 力偶的转向 。
3.如图所示,均质长方体的高度30h cm =,宽度20b cm =,重量600G N =,放在粗糙水平面上,它与水平面的静摩擦系数0.4s f =。
理论力学期末试卷-模拟试卷01(带答案)
《理论力学》期末考试卷模拟试卷01一.判断题(认为正确的请在每题括号内打√,否则打×;每小题3分,共15分)(√)1.几何约束必定是完整约束,但完整约束未必是几何约束。
(×)2.刚体做偏心定轴匀速转动时,惯性力为零。
(×)3.当圆轮沿固定面做纯滚动时,滑动摩擦力和动滑动摩擦力均做功。
(√)4.质点系动量对时间的导数等于作用在质点系上所有外力的矢量和。
(√)5.平面运动随基点平动的运动规律与基点的选择有关,而绕基点转动的规律与基点选取无关。
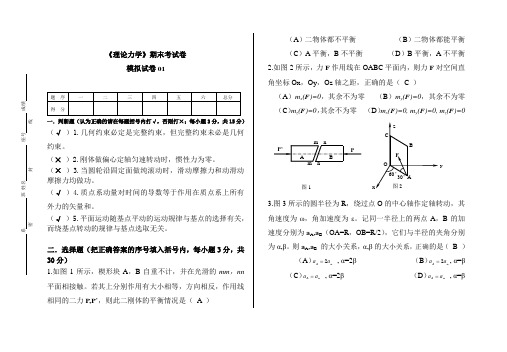
二.选择题(把正确答案的序号填入括号内,每小题3分,共30分)1.如图1所示,楔形块A,B自重不计,并在光滑的mm,nn 平面相接触。
若其上分别作用有大小相等,方向相反,作用线相同的二力P,P’,则此二刚体的平衡情况是( A )(A)二物体都不平衡(B)二物体都能平衡(C)A平衡,B不平衡(D)B平衡,A不平衡2.如图2所示,力F作用线在OABC平面内,则力F对空间直角坐标Ox,Oy,Oz轴之距,正确的是( C )(A)m x(F)=0,其余不为零(B)m y(F)=0,其余不为零(C)m z(F)=0,其余不为零(D)m x(F)=0, m y(F)=0, m z(F)=03.图3所示的圆半径为R,绕过点O的中心轴作定轴转动,其角速度为ω,角加速度为ε。
记同一半径上的两点A,B的加速度分别为a A,a B(OA=R,OB=R/2),它们与半径的夹角分别为α,β。
则a A,a B的大小关系,α,β的大小关系,正确的是(B )(A)BAaa2=, α=2β(B)BAaa2=, α=β(C)BAaa=, α=2β(D)BAaa=, α=βy图14.直管AB 以匀角速度ω绕过点O 且垂直于管子轴线的定轴转动,小球M 在管子内相对于管子以匀速度v r 运动。
在图4所示瞬时,小球M 正好经过轴O 点,则在此瞬时小球M 的绝对速度v ,绝对加速度a 是(D )(A )v=0,a =0 (B )v=v r, a =0 (C )v=0,r v a ω2=,← (D )v=v r , r v a ω2=,← 5. 图5所示匀质圆盘质量为m ,半径为R ,可绕轮缘上垂直于盘面的轴转动,转动角速度为ω,则圆盘在图示瞬时的动量是( B ) (A )K=0 (B )K=mR ω,↓ (C )K=2mR ω ,↓ (D )K=mR ω2 ,←6. 条件同前题(5),则圆盘的动能是(D )(A )2221ωmR T = (B )2241ωmR T =(C )22ωmR T = (D )2243ωmR T =7. 匀质半圆盘质量为m ,半径为R ,绕过圆心O 并垂直于盘面的定轴转动(图6),其角速度为ω,则半圆盘对点O 的动量矩的大小L 0 是( C )。
完整版理论力学期末考试试题题库带答案

理论力学期末测试试题1-1、自重为P=100kN的T字形钢架ABD,置于铅垂面内,载荷如下列图.其中转矩M=20kN.m ,拉力F=400kN,分布力q=20kN/m,长度l=1m.试求固定端A的约束力.解:取T型刚架为受力对象,画受力图其中耳一;q •次-3(ikN工已二“产看十骂—F£m6<r = 0工弓=0 ^-?-Fcos600 = 0一.一^ A必-W-Fi/十外必60F + F疝g= 0i^ = 3164kN 为二SOQkNMi= - IlSSkNm1-2如下列图,飞机机翼上安装一台发动机,作用在机翼OA上的气动力按梯形分布:解:q i=60kN/m, q2 =40kN/m ,机翼重P i=45kN ,发动机重P2 =20kN ,发动机螺旋桨的反作用力偶矩M=18kN.m .求机翼处于平衡状态时,机翼根部固定端.所受的力.幅研究机翼.把梯形教荷分解为一三角形载荷与一轮修救荷,其合力分利为Fja = y(^)- q2) , 9 = 90 kN,F k2= 9 * = 36° kN分别作用在矩赛.点3m与4.5 m处,如下列图,由= 口,F山=01Y = 0, F% - K - P# 1 中k=0SM0(F1 = Q t Mo - 3.6P| — 4.2尸工一M + 3F RI + 4.$F R1 = 0解得For = 0T F Q,=- 3S5 k\, M0 二-1 626 kN * m1-3图示构件由直角弯杆EBD以及直杆AB组成,不计各杆自重,q=10kN/m , F=50kN , M=6kN.m ,各尺寸如图.求固定端A处及支座C的约束力.6 m 1 i m } I m !M 先研究构架EBD如图(b),由WX= 0, F小-F sin30' = 0E Y = 0.F HJ + F3 - F mfi30 = 02A什⑺=0T F2 T - M + 2F = 0 解得= 25 kN. = 87.3 kN. F/ =-44 kN 再研究AB梁如图(a).由解:XX = 04 -如* 6 sinJO* * F旭一Fn, = 0XV - 0,为-1 6 (xx3tf . F* 二UEM八F) - 0, - 2 * -j * & * fl coeJO -白产皿"0懈得F〞 = 40 kN. F A I= 113 3 kN. M A= 575,S kN - m it愿也可先研究EBD,求得F*之后.再研究整体,求a处反力।这样祈减少平街方程数■但计算鼠并未明髭减少,1-4:如下列图结构, a, M=Fa, F1 F2 F,求:A, D处约束力.以上修为明究时聚.受力如下列图.广%-0 加-:'=. T工… 4・%七.二工9口 : 0 A<P -I %'二昌1'二小l nF吗一:F /=F1-5、平面桁架受力如下列图. ABC为等边三角形,且AD=DB .求杆CD的内力.H 翌体受力如图Q).由工M A(F)=0,方,/\ *F\B"4B - F - 1■心・sinbU- - Q 6蹲得Fw 一§F⑸.反将桁架微升.研究右边局部,如图化)所 \ __________________示,由人汽J^*Wf)= g Fft* ■ DB * sinfiO f+ F.nc , flH - F , £)P - sinGO,= 0 %⑻解樗Ffp = -|F/再研究节点匚,如图(cl由尔工K =①(Ftr- F在加曲,=0 代〞的EV = 0, -(F CF +F C¥)m&S0,- F QJ = Q *3 57ffl解得Fm =一与F t) 866F(压)本剧晟筒单的解法是.菖先断定QE杆为零杆,再觎取&BDF来研兆,只由一个方覆LM a(f> =.,即可健出R* ,读者不妨一试.1-6、如下列图的平面桁架,A端采用钱链约束,B端采用滚动支座约束, 各杆件长度为1m.在节点E和G上分别作用载荷F E=10kN, F G=7 kN.试计算杆1、2和3的内力.解:取圣体.求支庄为束力.工…小口口小0%+品一3%A取= 9kN / = SLN用盘面法,取疗架上边局部,s城■ g一月1 y〔峪3.“ 一/.」二9▽5=.&+鸟/疝16.“ 一鸟二0 E氏=0 F{\H 十巴83600 —.^ = l04kN(aj ^=l.l?kN 但弓।牛iilkNlji】2-1图示空间力系由6根桁架构成.在节点A上作用力F,此力在矩形ABDC平面内,且与铅直线成45o角.A EAK= A FBM.等腰三角形EAK , FBM和NDB在顶点A, B和D处均为直角,又EC=CK=FD=DM .假设F=10kN ,求各杆的内力.解节点受力分别如图所开:,对节点八,由工X —0, F1 sin45 - % sin45 = 0+ F sin45' = 0£Y " F3= 0, —F] C3s45 —F± COH45-F cos45 - 0解得Fi = F:= -5kN〔压〕, F3=一7.07 kN〔压〕再对节点B,由SX ~ 0, F$ stn45* - F< sin45, ; 0EV = 0. Fi sin45 - F3 = 0三2 士0, 一居a>s45 - F? crt?45" - F6 co^45' = 0 解得F4 = 5 kN〔拉〕,R=5卜^1〔拉〕,5& =- 10 kN〔压〕2-2杆系由钱链连接, 位于正方形的边和对角线上,如下列图.在节点D沿对角线LD方向作用力F D.在节点C沿CH边铅直向下作用力F.如钱链B, L和H是固定的,杆重不计, 求各杆的内力.求解TY = 0,SZ = 0,求二 0,F| 4M5* + Fj + F. sn45 = 0 厕 4,30 图解得 Fi = F D (1C),F $ =F J =二 Ji F 虱电然后研究节点c ,由SX = 0, - Fj - F*W cut45' - 0v3 £Y = ar -Fj - Fi — sin45 = 0心SZ = 0h - F, - F - F4言=0得 Fj = 7年户口,匕=-/5匹口. Fs M- (F + \2F D )2-3 重为R=980 N,半径为r =100mm 的滚子A 与重为P 2 = 490 N 的板B 由通过定滑轮 C 的柔绳相连.板与斜面的静滑动摩擦因数f s =0.1 o 滚子A 与板B 间的滚阻系数为8C 为光滑的.求各杆的内力. 先研究节点D,由- F)cts?45 + F 口 au45 - 0=0.5mm,斜面倾角a =30o,柔绳与斜面平行,柔绳与滑轮自重不计,钱链 拉动板B 且平行于斜面的力 F 的大小.〔l i 设闻拄口有向下漆动慧等.取国校DFsu 话出—凡-H-3=0EFf =❶ /一 Fcosfl = 0一% /Vine 7- co*?i 算豉圄杜.有向匕浪动越势.虢S ]社“ 三H 』二UJ£ 一%】R l J 'O U _EF F - 0 及-Fai%一.又Mn>« =的&- /J(siii 口 \ — u.凶 81J JI ,13.jp."系怩平衍叶F4五河n 日一)co* 6}工A4 尸I 五m n 8一 3 cow R'\-3/c - 0 1氏-A& =0 工尸j 二.尸M -FCQ博.二.只浪不滑3t.应点 门“用=¥斗型8那么上之£ y K 同理一圆柱.有向上填动趋势时得二二三 K 间柱匀速蛇淳时. f一 R2-4两个均质杆AB 和BC 分别重P i 和P 2 ,其端点A 和C 用球较固定在水平面, 另一端B 由 球镀链相连接,靠在光滑的铅直墙上,墙面与 AC 平行,如下列图.如 AB 与水平线的交角 为45o, / BAC=90.,求A 和C 的支座约束力以及墙上点B 所受的压力.解先研究AB 杆,受力如图(b),由। n 投阅柱.有向下滚动越舜O题4.27-SMjF)三0, 一几,QA = 0 得1 0 再取AB、CD两杆为一体来研究,受力如图(月海茉:由EM AC(F)= 0t(P[ + Pj) <WG45_F N* AB 热in45 —0XX = 0,九十 % = 0工My(F)= 0, Fc - AC - pj • AC = 0 LNZ 〞开工+如一2】一丹=0(F) —0, -(F AT+ FQ • OA - Fc y *- AC= 0工M塞2 K = 0, % + % + Fn = 0解得Fx = y(Pi + Pj)»Fer =.产值=2^P:t町=Pi +yp2>F o= 0,%=-2(P[ + 尸口3-1:如下列图平面机构中,曲柄OA=r,以匀角速度°转动.套筒A沿BC杆滑动.BC=DE ,且BD=CE=l.求图示位置时,杆BD的角速度和角加速度.解:].动点:滑块T 动系:贰广杆绝对运动:国周运动〔.点〕相对运动:直线运动〔£「二)j|iij V V V&加速度4_ 3/十&*)疝13伊_ J5诏r(/+r)耳cos30Q ST?收属/(/ + r)cz w= 1—1=----- 不 ------w BD 3 户3-2 图示钱链四边形机构中, O i A = O2B =100mm ,又QO2 = AB,杆O〔A以等角速度=2rad/s绕轴01转动.杆AB上有一套筒C,此套筒与杆CD相较接.机构的各部件都在同一铅直面内.求当①二60o时杆CD的速度和加速度.〔15分〕解取CD杆上的点C为动点,AB杆为动系,时动点作速度分析和加速度分析,如图S〕、〔b〕所示,图中式中口月=〔八一4 •田二0一2 ir〕/s5 - 0iA • J = 0*4 m/s2 解出杆CD的速度.加速度为G =-UA coep = 0. I mA&3 = since;= 0,3464 m/s2«1aAM1Al1V!4-1:如下列图凸轮机构中,凸轮以匀角速度3绕水平.轴转动,带动直杆AB沿铅直线上、下运动,且O, A, B共线.凸轮上与点A接触的点为A',图示瞬时凸轮轮缘线上' '点A的曲率半径为 A ,点A的法线与OA夹角为e , OA=l.求该瞬时AB的速度及加速度.〔15 分〕绝对运动: 相对运动: 奉连道处:2.速度大小 方向 1, 二、Ja 】iH=「WkmH I丫3,加速度 比=凡."'+ %r 门 大小9炉『『、;"2 方向 / /4-2:如下列图,在外啮合行星齿轮机构中,系杆以匀角速度 定,行星轮半径为r,在大轮上只滚不滑.设 A 和B 是行星轮缘 上的两点,点 A 在O 1O 的延长线上,而点 B 在垂直于o 1o 的半径上.求:点 A 和B 的加速度.解:2.选基点为〔〕亓*二后.*疗;口 +疗;. 大小0 *忒0 1时 方向“ J JJi7A ~ a ? +^C?I .轮I 作平面运动,瞬心为「沿"轴投勉乙8々4 * ■献i 1+ .1绕O i 转动.大齿轮固S 二「" 直线运动 曲线运动 定购林动 功系:凸轮. C 凸轮外边瘴〕〔.轴〕大小,方向?% ="g =仃口+ "什=fuclaii——=闺.㈢11 -4-3: 动.摇杆OC铅直,〔科氏加速度〕如下列图平面机构, AB长为1,滑块A可沿摇杆OC的长槽滑OC以匀角速度3绕轴O转动,滑块B以匀速v 1沿水平导轨滑动.图示瞬时AB与水平线OB夹角为300.求:此瞬时AB杆的角速度及角加速度.〔20分〕* *沿】:方向投彩大小方句V4B COS30J LD F福:速度分析1-杆.〞作平面运动,族点为瓦V A = V S - y AP2.动点:滑块.心动系:〞抨沿£方向强彩以一=1■沿吃方向表恁% ; gin 30" -4?os 对15-1如下列图均质圆盘,质量为m 、半径为R,沿地面纯滚动,角加速为3.求圆盘对图中A,C 和P 三点的动量矩. 平行轴定理:4二=一十/嫉 一或点P 为睡心 3hL ? = ^^R-\ L e =mP 2it 〕\ 1相?\"= -15-2 〔动量矩定理〕:如下列图均质圆环半径为 r,质量为m,其上焊接刚杆 OA,杆加生度介册 0f Ai = = 3VJtv 2AB点「为眉心上匚二J屯+ 1师;-G长为r,质量也为m.用手扶住圆环使其在OA水平位置静止.设圆环与地面间为纯滚动.独汰庵一方「.斗管力加玛所示建丸平为走动微分方程2f -月—+Y2由朱加R先K熹法瑞拽彩到水平强错乱两个才向20 r3"悟105-3 11-23 〔动量矩定理〕均质圆柱体的质量为m,半径为r,放在倾角为60o的斜面上, 一细绳绕在圆柱体上,其一端固定在A点,此绳和A点相连局部与斜面平行,如下列图.如圆柱体与斜面间的东摩擦因数为f=1/3,求圆柱体的加速度.〔15〕(15)解:解IW柱受力与运动分析如图.平而运动徽分方程为nta〔;= mg sin60* 一尸一Fj,.=F\ —fiig CQt^ff』社- 〔F=—广〕『式中F = /Fv» ac - fQ解得口c=O.355q5-4 11-28 〔动量矩定理〕均质圆柱体A和B的质量均为m,半径均为r, 一细绳缠在绕固定轴.转动的圆柱A上,绳的另一端绕在圆柱B上,直线绳段铅垂,如下列图.不计摩擦.求:〔1〕圆柱体B下落时质心的加速度;〔2〕假设在圆柱体A上作用一逆时针转向力偶矩M,试问在什么条彳^下圆柱体B的质心加速度将向上.〔15分〕解:解“〕两轮的受力与运动分析分别如用w.1 2 ET™r=近]对E轮,有以轮与直樊和切点为基点,明轮心B的加速度〃工,M t s4解得5g〔2〕再分别对两卷作受力与运动分析如图〔b〕对内轮,有fflaa =ntg -Ppj~2 tfrr~afj —rFj2依然存运动学关系dj}二皿用+的日J但Q.i中也B〕令< 0,可解得31柱体B的质心加速度向上的条件:M〉217UJT6-1:轮O的半径为R1 ,质量为ml,质量分布在轮缘上;均质轮C的半径为R2 , 质量为m2 ,与斜面纯滚动,初始静止.斜面倾角为.,轮.受到常力偶M驱动. 求: 轮心C走过路程s时的速度和加速度.〔15分〕韩:轮C1月轮0扶同作为一个质点系九一a『w 一阁7j = o石—,血人"吊斗!岫甘&岫对网」言必二% =9 1V :3/聚TH得J弘口日=-^―〔+3JJL〕旭〕中二二¥ =:羡居迎日一式G〕是函数关系式.两端计『求导,得-〔Jffij + 访看网收=M -Kin H - 鸟2 例U 尸―- :〔加1+.%啊〕局6-2均质杆 OB=AB=l,质量均为 m,在铅垂面内运动,AB 杆上作用一不变的力偶矩M,系统初始静止,不计摩擦.求当端点 A 运动到与端点 .重合时的速度. 〔15分〕解:由于A 京不离并地面,那么,EAO= /BOA.牝=可=H嫌同:是否可以利用求寻求此蜓时的商和速段? 〔H 与行没 有必然联系,角度不是时间的函数.〕6-3:重物m,以v 匀速下降,钢索刚度系数为 k .求轮D 突然卡住时,钢索的最大张 力.〔15分〕1J 上口『9-"将『〔1-E 穹 2/ V itt由「二心〞;有6-4均质杆 AB 的质量m=4kg,长l=600mm,均匀圆盘B 的质量为6kg,半径为r=600mm, 作纯滚动.弹簧刚度为 k=2N/mm,不计套筒A 及弹簧的质量.连杆在与水平面成 30o 角时无 初速释放.求〔1〕当AB 杆达水平位置而接触弹簧时,圆盘与连杆的角速度;〔2〕弹簧的最大压缩量 max o 〔 15分〕彝:卡住前E 二些 s* kF - kS SJ - mg - 2.45kN卡隹后取点物平街位苜1为更力加弹性力的 搴势T ; 一"解U〕该系统初始静tL.动能为杆达水平位置时.B 点是33杆的速度瞬心,网盅的角速度3H = 0,设杆的角速度为那么业,山幼能近理,得\ * ;配%品-0 = mg * ~ 5in341,解得连杆的角速度号〞:4;殳巴丝⑵AB杆达水平位置接触赢亚,统的动能为“,弹簧达到最大压缩量bz.的瞬时,系魂再次鄢止.动能丁;:= 0.由72 - 7】二五得0 _ [■闻]品=-J 6ra«二+ mJ片0 W *■解得1AM= 87.1 mm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三明学院
《理论力学》期末考试卷1答案
(考试时间:120分钟)
使用班级:学生数:任课教师:考试类型闭卷
一.判断题(认为正确的请在每题括号内打√,否则打×;每小题3分,共15分)(√)1.几何约束必定是完整约束,但完整约束未必是几何约束。
(×)2.刚体做偏心定轴匀速转动时,惯性力为零。
(×)3.当圆轮沿固定面做纯滚动时,滑动摩擦力和动滑动摩擦力均做功。
(√)4.质点系动量对时间的导数等于作用在质点系上所有外力的矢量和。
(√)5.平面运动随基点平动的运动规律与基点的选择有关,而绕基点转动的规律与基点选取无关。
二.选择题(把正确答案的序号填入括号内,每小题3分,共30分)
1.如图1所示,楔形块A,B自重不计,并在光滑的mm,nn平面相接触。
若其上分别作用有大小相等,方向相反,作用线相同的二力P,P’,则此二刚体的平衡情况是(A )(A)二物体都不平衡(B)二物体都能平衡
(C)A平衡,B不平衡(D)B平衡,A不平衡
2.如图2所示,力F作用线在OABC平面内,则力F对空间直角坐标Ox,Oy,Oz轴之距,正确的是(C )
(A)m x(F)=0,其余不为零(B)m y(F)=0,其余不为零
(C)m z(F)=0,其余不为零(D)m x(F)=0, m y(F)=0, m z(F)=0
3.图3所示的圆半径为R,绕过点O的中心轴作定轴转动,其角速度为ω,角加速度为ε。
记同
一半径上的两点A,B的加速度分别为a A,a B(OA=R,OB=R/2),它们与半径的夹角分别为α,β。
则a A,a B的大小关系,α,β的大小关系,正确的是(B )
(A)
B
A
a
a2
=, α=2β(B)
B
A
a
a2
=, α=β
(C)
B
A
a
a=, α=2β(D)
B
A
a
a=, α=β
4.直管AB以匀角速度ω绕过点O且垂直于管子轴线的定轴转动,小球M在管子内相对于管子以匀速度v r运动。
在图4所示瞬时,小球M正好经过轴O点,则在此瞬时小球M的绝对速度v,绝对加速度a 是(D )
(A)v=0,a=0
(B)v=v r,
a=0
(C)v=0,
r
v
aω
2
=,←
(D)v=v r ,
r
v
aω
2
=
,←
5. 图5所示匀质圆盘质量为m,半径为R,可绕轮缘上垂直于盘面的轴转动,转动角速度为ω,则
图
5
图4
图3
y
图1
圆盘在图示瞬时的动量是( B )
(A )K=0 (B )K=mR ω,↓ (C )K=2mR ω ,↓ (D )K=mR ω2 ,←
6. 条件同前题(5),则圆盘的动能是(D )
(A )2221ωmR T = (B )2
24
1ωmR T =
(C )22ωmR T = (D )2
24
3ωmR T =
7. 匀质半圆盘质量为m ,半径为R ,绕过圆心O 并垂直于盘面的定轴转动(图6),其角速度为ω,则半圆盘对点O 的动量矩的大小L 0 是( C )。
(质心C 位置:OC=
π
34R
) (A )201
3L mR ω=
(B )20L mR ω= (C )2
012L mR ω= (D )204()3R L m ωπ
=
8.匀质细杆质量为m ,长为l ,绕过杆端A 并垂直于杆的定轴转动(图7)。
若在图示瞬时,转动的角速度为零,角加速度为ε ,则杆的惯性力简化为( A ) (A )作用于图面内的一个力偶L Q 和作用于A 的一个力R Q : ε231ml L Q =
,εml R Q 2
1
=; (B )其它同(A ),但其中ε212
1
ml L Q =
(C )仅为作用于杆质心的一个力:εml R Q 2
1
=
(D )仅为作用于图面内的一个力偶:ε2
3
ml L Q =
9. 两个相同的定滑轮如下图示,开始时都处于静止,问下面描述正确的是(A ) (A ),A B A B ωωεε>> (B ),A B A B ωωεε<< (C ),A B A B ωωεε== (D ),A B A B ωωεε<>
(A) (B)
10. 矩形板ABCD 以匀角速度ω 绕固定轴 z 转动,点M 1和点M 2分别沿板的对角线BD 和边线CD 运动,在图示位置时相对于板的速度分别为v 1和v 2 ,下列说法中正确的是(D ) (A )M 1点科氏加速度大小为12sin v ωα,方向垂直纸面向外
M 2点科氏加速度大小为22v ω,方向垂直向上
(B )M 1点科氏加速度大小为12sin v ωα,方向垂直纸面向里
M 2点科氏加速度大小为22v ω,方向垂直向上
(C )M 1点科氏加速度大小为12sin v ωα,方向垂直纸面向外
M 2点科氏加速度为0
(D )M 1点科氏加速度大小为12sin v ωα,方向垂直纸面向里
M 2点科氏加速度为0
三.已知:曲柄连杆机构OA =AB =l ,曲柄OA 以匀ω 转动。
求:当ϕ =45º时, 滑块B
的速度及AB 杆的角速度.(10分) 解:研究AB ,已知 的方向,因此可确定出P 点为速度瞬心
四.一根直杆和一个圆盘焊接组成的系统,它们的质量均为8 kg ,可绕O 点转动,当OA 处于水平位置时, 系统具有角速度ω =4rad/s 。
求该瞬时轴承O 的反力。
(15分)
A
ε
B
图7
R C O ω
图6
,A B v v ,//2()A AB A B AB v l AP l v AP l l v BP l ωωωωωω==∴====⋅=←O
O
A
D
B
C
解:选系统为研究对象。
受力分析如图示。
由定轴转动微分方程
根据质心运动微分方程,得
五.质量为M 长为l 的均质杆AC 和BC 由理想铰链C 连接,A 端用理想铰链固定于水平
面上 , B 端置于光滑水平面上在铅垂平面内运动如图示,设开始时,θ =60o ,速度为零,求当 θ=30o
时两杆的角速度. (15分)
解:系统机械能守恒, 当 θ=30o
时BC 杠的瞬心I 如图所示AC ' = C 'I = l ωAC = ωBC = ω T 1
= 0 T 2 =
T AC + T BC
由:T 1+V 1 = T 2+V
六.如图所示, 均质杆AB 的质量m =40 kg, 长l =4 m, A 点以铰链连接于小车上。
不
计摩擦, 当小车以加速度a =15 m/s 向左运动时, 请用达朗伯原理求解D 处和铰A 处的约束力。
(15分)
解:以杆为研究对象, 受力如图,虚加惯性力F g R =-ma ,则由质点系的达朗伯原理
A
Ay
F x
c1y c2y 20.598 89.80.2589.80.7
15.78 rad/s εε⨯⋅=⨯⨯+⨯⨯= 0.250.7O I mg mg ε=⋅+⋅222110.70.5932O
I ml mR m m =++⨯≈12C x C x x ma ma F --=12C y C y y ma ma F mg mg --=--2212 ()8 (40.25 40.7 )121.6 N x C x C x F m a a ∴=-+=-⨯+⨯=-289.88 ( 15.780.25 15.780.7 ) 36.87 N y F =⨯⨯-⨯+⨯=0011
2sin 60sin 602
V Mgl Mgl =⨯=222111236AC AC
T Ml Ml ωω2⎛⎫== ⎪⎝⎭
(
)2
202
2115
sin 6021212
BC BC
T Ml M l Ml ωω2⎡⎤=+=
⎢⎥⎣⎦
22
712T Ml ω2=02sin 30V Mgl =g ()0
cos30sin 300
222
A D R M l l l
mg F F ∑=--=F (cos30sin 30)D F m g a =-g 0sin300x Ax R D F F F F ∑=++=0cos300y Ay D F F F mg ∑=+-=617.9357.8239.47Ax Ay D F N F N F N
=-==。
