江苏师大附校简介
2023-2024学年江苏省南京师大附中高一(上)期末语文试卷

2023-2024学年江苏省南京师大附中高一(上)期末语文试卷一、课本与读本阅读1.(2分)语文学习小组计划梳理必修上课本中的重要作家及其作品,初稿中需要修正的一条是()A.荀子是战国末期儒家学派代表人物之一。
《荀子》一书大部分为荀子自著,其余为其弟子记录的荀子言论和思想观点。
B.韩愈字退之,中唐政治家、散文家、诗人,与柳宗元发起了“古文运动”。
他自称“郡望昌黎”,作品集名为《韩昌黎集》。
C.苏轼字子瞻,北宋政治家、文学家,与父亲苏洵和弟弟苏辙并称“三苏”。
他精通诗、词、文,词集名为《稼轩长短句》。
D.姚鼐字姬传,清代散文家,桐城派代表人物之一。
他提出“义理、考据、辞章”三者不可偏废,有《惜抱轩诗文集》传世。
2.(2分)学习文言文,要特别留心古今含义不同以及古代常用而现代不常用的词。
下列对文言实词解释有误的一项是()A.闻道有先后,术业有专攻.攻:学习、研究B.壬戌之秋,七月既望.望:农历每月十五日C.酾.酒临江,横槊赋诗酾:劝客饮酒D.泰山之阳.,汶水西流阳:山的南面3.(2分)成语从历史中走来,带有许多古汉语的印记。
将熟悉的成语与正在学习的文言名篇结合起来,是一件饶有趣味之事。
下面是小李在课本旁批注的成语()A.小学而.大遗(华而.不实)B.耳得之而.为声(侃侃而.谈)C.君子博学而.日参省乎己(犯而.不校)D.青,取之于蓝,而.青于蓝(背道而.驰)4.(2分)小李对家乡的文化现象很感兴趣,他细致梳理南京地名,从中归纳出若干条命名规则,按照他的思路将这些地名按命名规则来分类,正确的一组是()①幕府山:传晋元帝过江,王导设幕府(参谋部)于此②栖霞山:此山每到秋天,“丹枫似火,漫山凝霞”③迈皋桥:传桥南原有卖奶糕的小店,桥以店名。
④彩霞街:原为集市,每天上街做买卖的大多是穿草鞋的农民,故名。
⑤乌衣巷:三国孙吴曾在此驻军,穿黑色军衣,称乌衣营⑥珍珠泉:泉出于巨石间,似串串珍珠,故名。
A.①②/③④/⑤⑥B.①③/②④/⑤⑥C.①④/②⑤/③⑥D.①⑤/②⑥/③④5.(2分)阅读写景抒情散文,要关注作品中的自然景物描写和人生思考,体会作者观察、欣赏和表现自然景物的角度()A.《故都的秋》善于从寻常景物中发现诗意。
学校名称江苏如皋师范学校附属小学

类号学校名称江苏省如皋师范学校附属小学所在设区市南通市姓名朱爱华申报学科语文现聘专业技术职务正高级填表日期2018年10月27日江苏省专业技术人员职称(职业资格)工作领导小组办公室监制1.本表供中小学(幼儿园)教师申报中小学正高级教师任职资格使用,评审表一式3份。
审批盖章后,本人人事档案、县(市、区)、设区市教育局各存1份。
2.本表第一至十项的内容由本人填写,学校审核;其余内容由学校有关职能部门填写。
3.按表中各栏目要求填写,要求真实、全面地反映申报人员水平、能力和实绩。
某些栏目填写不下,可另加附页,并装订入内。
4.本表用钢笔、签字笔填写,或用计算机打印。
5.本表一律A4大小,正反打印,不得放大或缩小。
本人郑重声明:本人在表中所填写的内容及所提供的参评材料是真实准确的,如有不实之处,本人愿承担相关责任。
声明人(签字):日期:2018年10月27日一、基本情况注:学术团体任职、社会兼职、荣誉称号、专业获奖需提供相应佐证材料。
二、学习、工作经历(一)学习经历(从初中毕业后填起)(二)工作经历注:专职教科研训人员,需明确填写在中小学幼儿园一线从事教学工作的时间段。
三、近五年参加继续教育情况单位组织人事部门对第一至三项填写内容的审核意见:审核人签字:2018年10 月27日四、任现职以来教学工作情况1.任现职超过5年的,填写近5年的教学工作情况。
按学年逐年填写;2.教科研训人员填写听课情况,“双肩挑”人员除填授课课时外还需填听课情况。
五、任现职以来承担班主任及其他教育教学管理工作情况(包括担任少先队大队辅导员、教研组长、年级组长、校级中层及以上管理干部等情况)六、任现职以来担任指导青年教师、名师工作室培育站领衔人、师范教育课程兼职教师、硕士生指导教师等专业示范情况七、任现职(201108)以来开设研究课、示范课、专题讲座等情况注:任现职超过5年的,填写近5年的开设研究课、示范课、专题讲座等情况,需提供佐证材料,教师和教科研训人员分别限填15份、25份。
徐州市区普通高中及3+4试点学校招生计划
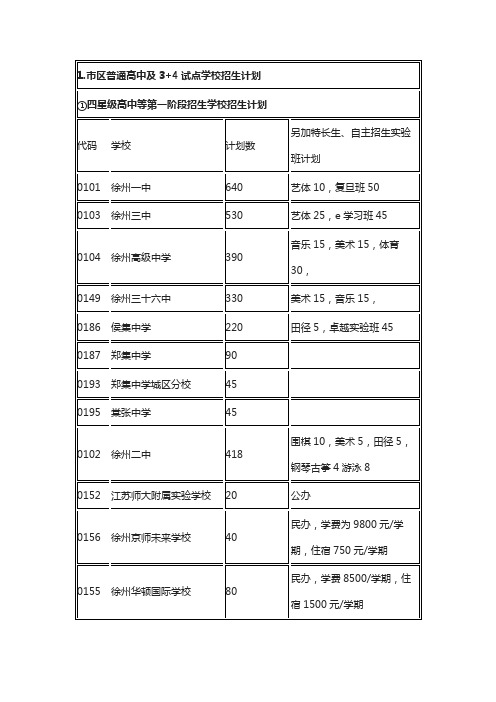
①四星级高中等第一阶段招生学校招生计划
代码
学校
计划数
另加特长生、自主招生实验班计划
0101
徐州一中
640
艺体10,复旦班50
0103
徐州三中
530
艺体25,e学习班45
0104
徐州高级中学
390
音乐15,美术15,体育30,
0149
徐州三十六中
330
美术15,音乐15,
1152
江苏师大附属实验学校(贾汪)国际班
20
国际班20,单独编班,完成国家规定课程达到高中毕业标准方可申领教育局统一的高中毕业证。每年收取国际课程费用5万元
合计
3495
245
注:各校最终招生计划数以市教育局批文为准。各民办学校及国际班的收费标准以物价局批文为准。
0186
侯集中学
220
田径5,卓越实验班45
0187
郑集中学
90
0193
郑集中学城区分校
45
0195
棠张中学
45
0102
徐州二中
418
围棋10,美术5,田径5,钢琴古筝4游泳8
0152
江苏师大附属实验学校
20
公办
0156
徐州京师未来学校
40
民办,学费为9800元/学期,住宿750元/学期
0155
徐州华顿国际学校
国示范
7201
14
会计
会计学
7202
14
物流服务与管理
物流管理
7203
14
软件与信息服务
软件工程
江苏省丰县中等专业学校国示范ຫໍສະໝຸດ 徐州工程学院7301
2024-2025学年江苏省南京师范大学附属中学树人学校八年级上学期第一次月考数学及答案

2024-2025学年江苏省南京师大附中树人学校八年级(上)第一次月考数学试卷一、选择题1. 下列图形中,不是轴对称图形的是( )A. B.C D.2. 如图,ABC DEF ≌△△,若100A ∠=°,47F ∠=°,则E ∠的度数为( )A. 100°B. 53°C. 47°D. 33°3. 如图,ABC DEF ≌△△,点D ,E 在直线AB 上,4BE =,1AE =,则DE 的长为( )A. 5B. 4C. 3D. 24. 等腰三角形一边为4,一边为3,则此三角形的周长是( )A. 10cmB. 11cmC. 6cm 或8cmD. 10cm 或11cm5. A 、B 、C 三名同学玩“抢凳子”游戏.他们所站的位围成一个ABC ,在他们中间放一个木凳,谁先抢到凳子谁获胜,为保证游戏公平,则凳子应放的最适当的位置是在ABC 的( )A. 三边垂直平分线的交点B. 三边中线的交点C. 三个内角角平分线的交点D. 三边高的交点 6. 如图1,已知三角形纸片ABC ,AB AC =,50A ∠=°,将其折叠,如图2所示,使点A 与点B重.的合,折痕为ED ,点E ,D 分别在AB ,AC 上,那么DBC ∠的度数为( )A. 10°B. 15°C. 20°D. 30°7. 如图,已知ABC 的周长是36cm ,ABC ∠和ACB ∠的角平分线交于点O ,OD BC ⊥于点D ,若3cm OD =,则ABC 的面积是( )A. 248cmB. 254cmC. 260cmD. 266cm8. 如图,点P 为定角AOB ∠的平分线上的一个定点,且MPN ∠与AOB ∠互补,若MPN ∠在绕点P 旋转的过程中,其两边分别与OA OB ,交于点M N ,,则一下结论:①PM PN =恒成立;②OM ON +的值不变;③四边形PMON MN 的长不变;其中正确的个数为( )个A. 1B. 2C. 3D. 4二、填空题9. 如图,已知AD BC =,要使ABC CDA △△≌,还要添加的一个条件可以是______.(只需填上一个正确的条件).10. 如图,在ABC 中,点D 、E 、F 分别是BC AB AC ,,上的点,若B C BF CD ∠=∠=,,54BD CE EDF =∠=°,,则A ∠=________.11. 如图,把一个长方形纸条ABCD 沿EF 折叠,若154∠=°,则FGE ∠=_______.12. 如图,在3×3的方格中,每个小方格的边长均为1,则1∠与2∠的数量关系是________.13. 如图所示.A ,B ,C ,D 是四个村庄,B ,D ,C 在一条东西走向公路的沿线上,1km BD =,1km DC =,村庄A 与C ,A 与D间也有公路相连,且公路AD 是南北走向,3km AC =,只有A ,B 之间由于间隔了一个小湖,所以无直接相连的公路.现决定在湖面上造一座斜拉桥,测得 1.2km AE =,0.7km BF =,则建造的斜拉桥长至少有____________km .14. 如图,在ABC 中,4AB =, 5.5AC =,ABC ∠和ACB ∠的平分线交于点E ,过点E 作MN BC ∥分别交AB 、AC 于点M 、N ,则AMN 的周长为_________.15. 如图,ABC 的面积为212cm ,AP 垂直B ∠的平分线BP 于点P ,则PBC △的面积为__________2cm .16. 如图,射线OA OB ,上分别截取11OA OB =,连接11A B ,在11B A 、1B B 上分别截取1212B A B B =,连接22A B ,…按此规律作下去,若11A B O α∠=,则20232023A B O ∠=______.17. 如图,7cm AB =,60CAB DBA ∠=∠=°,5cm AC =,点P 在线段AB 上以2cm/s 的速度由点A 向点B 运动,同时点Q 在射线BD 上运动,当点P 运动结束时,点Q 随之结束运动,当点P Q ,运动到某处时有ACP △与BPQ 全等,则Q 的运动速度是 ________________cm/s .18. 如图,在ABC 中,BA BC =,BD 平分ABC ∠,交AC 于点D ,点M N 、分别为BD BC 、上动点,若4BC =,ABC 的面积为6,则CM MN +的最小值为_______.在的三、解答题19. 如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A 、B 、C 在小正方形的顶点上.(1)在图中画出与ABC 关于直线l 成轴对称的A B C ′′′ .(2)ABC 的面积为__________.(3)在直线l 上找一点P (在答题纸上图中标出),使PB PC +的长最短.20. 如图,已知B 、E 、C 、F 在同一条直线上,AB DE =,AC DF =,BE CF =,AC 与DE 交于点G .(1)求证:ABC DEF ≌△△;(2)若50B ∠=°,60ACB ∠=°,求EGC ∠的度数.21. 麒麟某数学兴趣小组的同学用数学知识测一池塘的长度,他们所绘如图,点B ,F ,C (点F ,C 之间不能直接测量,为池塘的长度),点A ,D 在l 的异侧,且AB DE ∥,A D ∠=∠,测得AB DE =.(1)求证:ABC DEF ≌△△;(2)若100m 30m BE BF ==,,求池塘FC 的长. 22. 如图,四边形ABCD 中,BC CD =,AC DE =,90B DCE ∠=∠=°,AC 与DE 相交于点F .(1)求证:ABC ECD ∆≅∆(2)判断线段AC 与DE 的位置关系,并说明理由.23. 如图,在ABC 中,DM EN 、分别垂直平分AC 和BC ,交AB 于M N 、两点,DM 与EN 相交于点F .(1)若CMN 的周长为15cm ,求AB 的长;(2)若70MFN ∠=°,求MCN ∠的度数.24. 如图,已知ABC ,点P 为BAC ∠的平分线上一点,PE AB ⊥,PF AC ⊥,垂足分别为E 、F(1)求证∶ PE PF =(2)若BE CF =,求证:点P 在BC 的垂直平分线上.25. 如图,已知ABC (AC AB BC <<),请用无刻度的直尺和圆规,完成下列作图(不写作法,保留作图痕迹);(1)如图1,在AB 边上寻找一点M ,使AMC ACB ∠=∠;(2)如图2,在BC 边上寻找一点N ,使得NA NB BC +=.26. 如图甲,已知在ABC 中,90ACB ∠=°,AC BC =,直线MN 经过点C ,且AD MN ⊥于D ,BE MN ⊥于E .(1)说明ADC CEB △≌△.(2)说明AD BE DE +=.(3)已知条件不变,将直线MN 绕点C 旋转到图乙位置时,若3DE =、 5.5AD =,则BE=_____.27. 阅读理解:【概念学习】定义①:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“形似三角形”.定义②:从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“形似三角形”,我们把这条线段叫做这个三角形的“巧妙分割线”.【概念理解】(1)如图1,在ABC 中,36A ∠=°,AB AC =,CD 平分ACB ∠,则CBD △与ABC ______(填“是”或“不是”)互为“形似三角形”.的(2)如图2,在ABC 中,CD 平分ACB ∠,36A ∠=°,48B ∠=°,求证:CD 为ABC 的“巧妙分割线”;【概念应用】(3)在ABC 中,45A ∠=°,CD 是ABC 的巧妙分割线,直接写出ACB ∠的度数.28. 在ABC 中,,8AB AC BC ==,点M 从点B 出发沿射线BA 移动,同时点N 从点C 出发沿线段AC 的延长线移动,点M ,N 移动的速度相同,MN 与BC 相交于点D .(1)如图1,过点M 作//ME AC ,交BC 于点E ;①图中与BBBB 相等的线段________、_________;②求证:DME DNC ≌;(2)如图2,若60A ∠=°,当点M 移动到AABB 的中点时,求CCCC 的长度;(3)如图3,过点M 作MF BC ⊥于点F ,在点M 从点B 向点A (点M 不与点A ,B 重合)移动的过程中,线段BF 与CCCC 的和是否保持不变?若保持不变,请直接写出BF 与CCCC 的长度和;若改变,请说明理由.2024-2025学年江苏省南京师大附中树人学校八年级(上)第一次月考数学试卷一、选择题1. 下列图形中,不是轴对称图形的是( )A. B.C. D.【答案】C【解析】【分析】根据轴对称图形的概念逐项分析判断即可,轴对称图形的概念:平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形.【详解】解:选项A 、B 、D 均能找到这样的一条直线,使直线两旁的部分能够完全重合的图形,所以是轴对称图形;选项C 故选:C .【点睛】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合. 2. 如图,ABC DEF ≌△△,若100A ∠=°,47F ∠=°,则E ∠的度数为( )A. 100°B. 53°C. 47°D. 33°【答案】D【解析】 【分析】首先根据全等三角形的性质得到100D A ∠=∠=°,然后利用三角形内角和定理求解即可.【详解】解:∵ABC DEF ≌△△,100A ∠=°,∴100D A ∠=∠=°,在DEF 中,47F ∠=°,∴18033E D E ∠=°−∠−∠=°,故选:D .【点睛】此题考查了全等三角形的性质,三角形内角和定理,解题的关键是熟练掌握以上知识点. 3. 如图,ABC DEF ≌△△,点D ,E 在直线AB 上,4BE =,1AE =,则DE 的长为( )A. 5B. 4C. 3D. 2【答案】A【解析】 【分析】由ABC DEF ≌△△,可得DE AB =,由点D ,E 在直线AB 上,可得DE AB AE BE ==+,计算求解即可.【详解】解:∵ABC DEF ≌△△,∴DE AB =,∵点D ,E 在直线AB 上,∴5DE AB AE BE ==+=,故选:A .【点睛】本题考查了全等三角形的性质.解题的关键在于明确线段之间的数量关系.4. 等腰三角形的一边为4,一边为3,则此三角形的周长是( )A. 10cmB. 11cmC. 6cm 或8cmD. 10cm 或11cm 【答案】D【解析】【分析】分边4是底边和腰长两种情况讨论,再根据三角形的任意两边之和大于第三边判断是否能组成三角形,然后求解即可.【详解】解:若4是底边,则三角形的三边分别为4、3、3,能组成三角形,周长43310=++=,若4是腰,则三角形的三边分别为4、4、3,能组成三角形,周长44311=++=,综上所述,此三角形的周长是10或11.故选:D .【点睛】本题考查了等腰三角形的性质,三角形的三边关系,难点在于分情况讨论并判断是否能组成三角形.5. A 、B 、C 三名同学玩“抢凳子”游戏.他们所站的位围成一个ABC ,在他们中间放一个木凳,谁先抢到凳子谁获胜,为保证游戏公平,则凳子应放的最适当的位置是在ABC 的( )A. 三边垂直平分线的交点B. 三边中线的交点C. 三个内角角平分线的交点D. 三边高的交点【答案】A【解析】【分析】为使游戏公平,要使凳子到三个人的距离相等,于是利用线段垂直平分线上的点到线段两端的距离相等可知,要放在三边中垂线的交点上.【详解】解:利用线段垂直平分线的性质得:要放在三边垂直平分线的交点上.故选:A .【点睛】本题主要考查了线段垂直平分线的性质的应用;利用所学的数学知识解决实际问题是一种能力,要注意培养.想到要使凳子到三个人的距离相等是正确解答本题的关键.6. 如图1,已知三角形纸片ABC ,AB AC =,50A ∠=°,将其折叠,如图2所示,使点A 与点B 重合,折痕为ED ,点E ,D 分别在AB ,AC 上,那么DBC ∠的度数为( )A. 10°B. 15°C. 20°D. 30°【答案】B【解析】 【分析】本题考查了等腰三角形的性质,折叠的性质,根据50A ∠=°,AB AC =可求得180652A ABC °−∠∠==°,结合折叠的性质,得到50ABD A ∠=∠=°根据15DBC ABC ABD ∠=∠−∠=°,选择即可.【详解】.∵50A ∠=°,AB AC =,∴180652A ABC °−∠∠==°, 折叠的性质,得到50ABD A ∠=∠=°, ∴15DBC ABC ABD ∠=∠−∠=°,故选B .7. 如图,已知ABC 的周长是36cm ,ABC ∠和ACB ∠的角平分线交于点O ,OD BC ⊥于点D ,若3cm OD =,则ABC 的面积是( )A. 248cmB. 254cmC. 260cmD. 266cm【答案】B【解析】 【分析】过点O 作OE ⊥AB 于点E ,OF ⊥AC 于点F ,根据角平分线的性质定理可得OD =OE =OF =3cm ,再由ABC ABO CBO CAO S S S S =++ ,即可求解.【详解】解∶如图,过点O 作OE ⊥AB 于点E ,OF ⊥AC 于点F ,∵ABC ∠和ACB ∠的角平分线交于点O ,OD BC ⊥,∴OD =OE ,OD =OF ,∴OD =OE =OF =3cm ,∵ABC 的周长是36cm ,∴AB +BC +AC =36cm ,∵ABC ABO CBO CAO S S S S =++ ,∴()21111136354cm 22222ABC S AB OE CB OD CA OF AB BC AC OD =⋅+⋅+⋅=++⋅=××= . 故选:B 【点睛】本题主要考查了角平分线的性质,熟练掌握角平分线上点到角两边的距离是解题的关键. 8. 如图,点P 为定角AOB ∠的平分线上的一个定点,且MPN ∠与AOB ∠互补,若MPN ∠在绕点P 旋转的过程中,其两边分别与OA OB ,交于点M N ,,则一下结论:①PM PN =恒成立;②OM ON +的值不变;③四边形PMON 的面积不变;④MN 的长不变;其中正确的个数为( )个A. 1B. 2C. 3D. 4【答案】C【解析】 【分析】根据角平分线的性质,作PE OA PF OB ⊥⊥,,可得PE PF OE OF MPE NPF == ,,≌,由此可判定①②③,连接EF ,根据三角形三边关系可判定④,由此即可求解.【详解】解:∵点P 在AOB ∠∴AOP BOP ∠=∠,如图所示,过点P 作PE OA ⊥于点E ,作PF OB ⊥于点B ,∴90PEO PFO ∠=∠=°,PE PF =,OE OF =,∴在四边形PEOF 中,180EOF EPF ∠+∠=°,∵180AOB MPN ∠+∠=°,∴MPN EPF ∠=∠,即MPE EON EON NOF ∠+∠=∠+∠,∴MPE NPF ∠=∠,∴()MPE NPF SAS ≌,∴PM PN =,故①正确;由①正确可得,ME NF =,∴22OM ON OE EM OF NF OE OF +=++−==,故②正确;由MPE NPF ≌可得MPE NPF S S = ,∴MPE EPO OPN EPO OPN NPF PMON PEOF S S S S S S S S ++=++== 四边形四边形,∴四边形PMON 的面积是定值,故③正确;如图所示,连接EF ,由上述结论可得,PM PN PE PF ==,,MPN EPF ∠=∠,PM PE >,PN PF >,∴MN CD ≠,即MN 的长度发生变化,故④错误;综上所述,正确的有①②③,共3个,故选:C .【点睛】本题考查了角平分线的性质,全等三角形的判定和性质,旋转的性质,四边形面积的计算方法等知识,掌握添加合理的辅助线,构造三角形全等是解题的关键.二、填空题9. 如图,已知AD BC =,要使ABC CDA △△≌,还要添加的一个条件可以是______.(只需填上一个正确的条件).【答案】AB CD =(答案不唯一)【解析】【分析】本题考查了全等三角形的判定,根据全等三角形的判定定理即可求解,掌握全等三角形的判定定理是解题的关键.【详解】解:ABC 与CDA 中,∵AB CD BC AD AC CA = = =,在∴()SSS ABC CDA △≌△,∴添加的一个条件可以是AB CD =,故答案为:AB CD =.10. 如图,在ABC 中,点D 、E 、F 分别是BC AB AC ,,上的点,若B C BF CD ∠=∠=,,54BD CE EDF =∠=°,,则A ∠=________.【答案】72°##72度【解析】【分析】由“SAS ”可证≌BDF CED ,可得BFD CDE ∠=∠,由外角的性质可得54B EDF ∠=∠=°,可求解.【详解】解:在BDF 和CED △中,===BF CD B C BD CE∠∠ ,∴()SAS BDF CED ≌ ,∴BFD CDE ∠=∠,∵FDC B BFD FDE EDC ∠=∠+∠=∠+∠,∴54B EDF ∠=∠=°,∴54C ∠=°∴180180545472A B C ∠=°−∠−∠=°−°−°=°,故答案为:72°.【点睛】本题考查了全等三角形的判定和性质,三角形内角和定理,掌握全等三角形的判定是本题的关键.11. 如图,把一个长方形纸条ABCD 沿EF 折叠,若154∠=°,则FGE ∠=_______.【答案】72°##72度【解析】【分析】先证明154DEF ∠=∠=°,AEG FGE ∠=∠,由折叠可得54DEF GEF ∠=∠=°,利用平角的含义可得18025472AEG ∠=°−×°=°,从而可得答案.【详解】解:∵154∠=°,AD BC ∥,∴154DEF ∠=∠=°,AEG FGE ∠=∠, 由折叠可得:54DEF GEF ∠=∠=°,∴18025472AEG ∠=°−×°=°,∴72FGE ∠=°.故答案为:72°【点睛】本题考查的是平行线的性质,轴对称的性质,熟记轴对称的性质与平行线的性质求解角度的大小是解本题的关键.12. 如图,在3×3的方格中,每个小方格的边长均为1,则1∠与2∠的数量关系是________.【答案】1290∠+∠=° 【解析】【分析】证明ABC DEF ≌△△得出2DEF ∠=∠,根据190DEF ∠+∠=°即可得出1290∠+∠=°. 【详解】解:根据网格特点可知,90ACB DFE ∠=∠=°,EF BC =,AC DF =,∴ABC DEF ≌△△,∴2DEF ∠=∠,∵190DEF ∠+∠=°,∴1290∠+∠=°.故答案为:1290∠+∠=°. 【点睛】本题主要考查了三角形全等的判定和性质,解题的关键是熟练掌握三角形全等的判定方法.13. 如图所示.A ,B ,C ,D 是四个村庄,B ,D ,C 在一条东西走向公路的沿线上,1km BD =,1km DC =,村庄A 与C ,A 与D间也有公路相连,且公路AD 是南北走向,3km AC =,只有A ,B 之间由于间隔了一个小湖,所以无直接相连的公路.现决定在湖面上造一座斜拉桥,测得 1.2km AE =,0.7km BF =,则建造的斜拉桥长至少有____________km .【答案】1.1【解析】【分析】根据全等三角形的判定得出(SAS)ADB ADC ≌ ,进而得出3km AB AC ==,这样可以得出斜拉桥长度.【详解】解:由题意知:BD CD =,90BDA CDA ∠∠==°,∵在ADB 和ADC 中, DB DC ADB ADC AD AD = ∠=∠ =, ∴(SAS)ADB ADC ≌ ,∴3km AB AC ==,故斜拉桥至少有3 1.20.7 1.1km −−=,故答案为1.1.【点睛】此题主要考查了全等三角形的判定及其性质,根据已知得出(SAS)ADB ADC ≌ 是解题的关键. 14. 如图,在ABC 中,4AB =, 5.5AC =,ABC ∠和ACB ∠的平分线交于点E ,过点E 作MN BC ∥分别交AB 、AC 于点M 、N ,则AMN 的周长为_________.【答案】9.5【解析】【分析】根据角平分线定义、平行线的性质和可得ME MB NE NC ==,,进而求解. 【详解】解∶BE 平分ABC ∠,,ABE EBC ∴∠=∠MN BC ∥,MEB EBC ∴∠=∠,MEB ABE ∴∠=∠,MB ME ∴=同理可得∶NE NC =,9.5AMN C AM AN MN AM AN ME EN AM AN MB NC AB AC ∴=++=+++=+++=+= 故答案为∶9.5【点睛】本题考查等腰三角形的判定及性质,解题关键是掌握角平分线的定义,掌握平行线的性质. 15. 如图,ABC 的面积为212cm ,AP 垂直B ∠的平分线BP 于点P ,则PBC △的面积为__________2cm .【答案】6【解析】【分析】延长AP 交BC 于点D ,根据角平分线和垂线的定义,易证()ASA APB DPB ≌,得到12ABP DBP ABD S S S == ,AP DP =,进而得到12ACP DCP ACD S S S == ,即可求出PBC △的面积. 【详解】解:如图,延长AP 交BC 于点D ,BP 平分ABC ∠,ABP DBP ∴∠=∠,AP BP ⊥ ,90APB DPB ∴∠=∠=°,在APB △和DPB 中,ABP DBP BP BPAPB DPB ∠=∠ = ∠=∠, ()ASA APB DPB ∴ ≌,12ABP DBP ABD S S S ∴== ,AP DP =, ACP ∴△和DCP 等底同高,12ACP DCP ACD S S S ∴== , ()1122DPB DCP ABD ACD ABC PBC S S S S S S ∴=+=+= , ABC 的面积为212cm ,21126cm 2PBC S ∴=×= , 故答案为:6.【点睛】本题考查了角平分线的定义,全等三角形的判定和性质,三角形面积公式等知识,作辅助线构造全等三角形是解题关键.16. 如图,在射线OA OB ,上分别截取11OA OB =,连接11A B ,在11B A 、1B B 上分别截取1212B A B B =,连接22A B ,…按此规律作下去,若11A B O α∠=,则20232023A B O ∠=______.【答案】20222α【解析】 【分析】根据等腰三角形两底角相等用α表示出22A B O ∠,依此类推即可得到结论.【详解】解:1212B A B B = ,11A B O α∠=, 2212A B O α∴∠=, 同理332111222A B O αα∠=×=, 44312A B O α∠=, 112n n n A B O α−∴∠=, 2023202320222A B O α∴∠=, 故答案为:20222α. 【点睛】本题考查了等腰三角形两底角相等的性质,图形的变化规律,依次求出相邻的两个角的差,得到分母成2的指数次幂变化,分子不变的规律是解题的关键.17. 如图,7cm AB =,60CAB DBA ∠=∠=°,5cm AC =,点P 在线段AB 上以2cm/s 的速度由点A 向点B 运动,同时点Q 在射线BD 上运动,当点P 运动结束时,点Q 随之结束运动,当点P Q ,运动到某处时有ACP △与BPQ 全等,则Q 的运动速度是 ________________cm/s .【答案】2或207【解析】【分析】本题考查了全等三角形的性质,由ACP △与BPQ 全等,分两种情况:AC BP =①,AP BQ =,AC BQ =②,AP BP =,建立方程组求得答案即可,熟练掌握知识点的应用及分情况分析是解题的关键.【详解】解:设它们运动的时间为s t ,点Q 的运动速度为cm /s x ,则2AP tcm =,()72cm PBt =−,cm BQ xt =,①若ACP BPQ △≌△,则AC PB =,AP BQ =,可得:572t =−,2t xt =,解得:2x =,1t =;②若ACP BQP △≌△,则AC BQ =,AP PB =,可得:5xt =,272t t =−, 解得:207x =,74t =; 综上:Q 的运动速度为2cm /s 或20cm /s 7, 故答案为:2或207. 18. 如图,在ABC 中,BA BC =,BD 平分ABC ∠,交AC 于点D ,点M N 、分别为BD BC 、上的动点,若4BC =,ABC 的面积为6,则CM MN +的最小值为_______.【答案】3【解析】【分析】本题考查了等腰三角形的性质,线段垂直平分线的性质,两点之间线段最短,垂线段最短,根据等腰三角形的性质可知,BBBB 垂直平分AC ,根据垂直平分线的性质得出CM AM =,由此可得CM MN AM MN +=+,又由“两点之间线段最短”和“垂线段最短”可得当A M N 、、三点共线且AN BC ⊥时AM MN +最短,根据三角形的面积公式可求出AN 的长,即CM MN +的最小值,熟练掌握知识点的应用是解题的关键.【详解】解:如图,连接AM ,∵在ABC 中,BA BC =,BD 平分ABC ∠,∴BD AC ⊥,AD CD =,∴BD 垂直平分AC ,∴CM AM =,∴CM MN AM MN +=+,如图,当A M N 、、三点共线且AN BC ⊥时, CM MN AM MN AN +=+=,此时AN 最小,即CM MN +的值最小,∵162ABC S BC AN =×= , ∴1462AN ××=, 解得3AN =,∴CM MN +的最小值为3,故答案为:3.三、解答题19. 如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A 、B 、C 在小正方形的顶点上.(1)在图中画出与ABC 关于直线l 成轴对称的A B C ′′′ .(2)ABC 的面积为__________.(3)在直线l 上找一点P (在答题纸上图中标出),使PB PC +的长最短.【答案】(1)图见解析(2)72(3)图见解析【解析】【分析】本题主要考查了轴对称作图,三角形面积计算,轴对称的性质,解题的关键是熟练掌握轴对称的性质.(1)先作出点B 、C 关于直线l 对称的点B ′、C ′,然后再顺次连接即可;(2)利用割补法求值三角形的面积即可;(3)连接BC ′,交l 于P ,点P 即为所求.【小问1详解】解:如图所示,A B C ′′′ 即为所求. 【小问2详解】解:111372412131481222222×−××−××−××=−−−=. 故答案为:72. 【小问3详解】解:连接BC ′,交l 于P ,点P 即为所求.连接PC ,根据轴对称可知:PC PC ′=,∴PB PC PB PC ′+=+,∵两点之间线段最短,∴当B 、P 、C ′在同一直线上时,BP PC ′+最小,即PB PC +最小.20. 如图,已知B 、E 、C 、F 在同一条直线上,AB DE =,AC DF =,BE CF =,AC 与DE 交于点G .(1)求证:ABC DEF ≌△△(2)若50B ∠=°,60ACB ∠=°,求EGC ∠的度数.【答案】(1)见解析 (2)70°【解析】【分析】本题考查了全等三角形的判定与性质,三角形内角和定理,熟练掌握以上知识点并灵活运用是解此题的关键.(1)由BE CF =得出BC EF =,再利用SSS 证明ABC DEF ≌△△即可;(2)由全等三角形的性质得出50DEF B ∠=∠=°,再由三角形内角和定理计算即可得出答案. 【小问1详解】证明:∵BE CF =,∴BE CE CF CE +=+,即BC EF =,在ABC 和DEF 中,AB DE AC DF BC EF = = =,∴()SSS ABC DEF ≌;【小问2详解】解:如图:,∵ABC DEF ≌△△,∴50DEF B ∠=∠=°, ∴180180506070EGC GEC GCE ∠=°−∠−∠=°−°−°=°.21. 麒麟某数学兴趣小组的同学用数学知识测一池塘的长度,他们所绘如图,点B ,F ,C (点F ,C 之间不能直接测量,为池塘的长度),点A ,D 在l 的异侧,且AB DE ∥,A D ∠=∠,测得AB DE =.(1)求证:ABC DEF ≌△△;(2)若100m 30m BE BF ==,,求池塘FC 的长. 【答案】(1)见解析 (2)FC 的长是40m【解析】【分析】(1)利用“ASA ”即可求证;(2)利用全等三角形的性质即可求解.【小问1详解】证明:∵AB DE ∥,∴ABC DEF ∠=∠,在ABC 与DEF 中,ABC DEF AB DEA D ∠=∠ = ∠=∠∴(ASA)ABC DEF ≌ ;【小问2详解】解:∵ABC DEF ≌△△∴BC EF =∴BF FC EC FC +=+,∴BF EC =,∵100m30m BE BF ==, ∴100303040FC =−−=m .答:FC 的长是40m【点睛】本题考查了全等三角形的判定与性质.熟记相关定理内容是解题关键.22 如图,四边形ABCD 中,BC CD =,AC DE =,90B DCE ∠=∠=°,AC 与DE 相交于点F .(1)求证:ABC ECD ∆≅∆(2)判断线段AC 与DE 的位置关系,并说明理由.【答案】(1)见解析 (2)AC DE ⊥,理由见解析【解析】【分析】(1)根据HL 即可证明ABC ECD △△≌.(2)根据ABC ECD △△≌得到BCA CDE ∠=∠,结合90B DCE ∠=∠=°得到90DFC ∠=°,即可得结论.【小问1详解】解:在Rt ABC △和Rt ECD △中AC DE AB EC== , ∴ABC ECD △△≌..【小问2详解】解:AC DE ⊥.理由如下:∵ABC ECD △△≌,∴BCA CDE ∠=∠,∵90B DCE ∠=∠=°,∴90BCA ACD ∠+∠=°,∴90CDE ACD ∠+∠=°,∴180()90DFCCDE ACD ∠=°−∠+∠=°, ∴AC DE ⊥.【点睛】本题考查全等三角形的判定与性质,常用的判定方法有:SSS 、SAS 、ASA 、AAS 、HL 等,熟练掌握全等三角形的判定定理是解题的关键.23. 如图,在ABC 中,DM EN 、分别垂直平分AC 和BC ,交AB 于M N 、两点,DM 与EN 相交于点F .(1)若CMN 的周长为15cm ,求AB 的长;(2)若70MFN ∠=°,求MCN ∠的度数.【答案】(1)15cm AB =(2)40°【解析】【分析】此题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,等边对等角的性质,三角形的内角和定理,解题的关键是熟练掌握以上知识的应用及整体思想的应用.(1)根据线段垂直平分线上的点到线段两端点的距离相等可得AM CM =,BN CN =,然后求出CMN 的周长AB =;(2)根据三角形的内角和定理列式求出 MNF NMF ∠+∠,再求出A B ∠∠+,根据等边对等角可得A ACM ∠=∠,B BCN ∠=∠,然后利用三角形的内角和定理列式计算即可得解.【小问1详解】解:∵DM 、EN 分别垂直平分AC 和BC ,∴AM CM =,BN CN =,∴CMN 的周长CM MN CN AM MN BN AB =++=++=,∵CMN 的周长为15cm ,∴15cm AB =;【小问2详解】解:∵70MFN ∠=°,∴18070110MNF NMF ∠+∠=°−°=°,∵AMD NMF ∠=∠, BNE MNF ∠=∠,∴110AMD BNE MNF NMF ∠+∠=∠+∠=°,∴909018011070A B AMD BNE ∠+∠=°−∠+°−∠=°−°=°,∵AM CM =,BN CN =,∴A ACM ∠=∠,B BCN ∠=∠,∴()180218027040MCN A B ∠=°−∠+∠=°−×°=°. 24. 如图,已知ABC ,点P 为BAC ∠的平分线上一点,PE AB ⊥,PF AC ⊥,垂足分别为E 、F(1)求证∶ PE PF =(2)若BE CF =,求证:点P 在BC 的垂直平分线上.【答案】(1)见解析 (2)见解析【解析】【分析】(1)通过证明APE APF ≌△△,即可求证;(2)连接PB 、PC ,通过证明BPE CPF △≌△,得到BP CP =,即可求证.【小问1详解】证明:∵点P 为BAC ∠的平分线上一点∴BAP FAP ∠=∠∵PE AB ⊥,PF AF ⊥∴90PEA PFA ∠=∠=°在APE 和APF 中BAP FAP PEA PFA AP AP ∠=∠ ∠=∠ =∴()AAS APE APF ≌∴PE PF =【小问2详解】证明:连接PB 、PC ,如下图:由(1)可得:90BEP CFP ∠=∠=°又∵PE PF =,BE CF =∴()SAS BPE CPF ≌∴BP CP =∴点P 在BC 的垂直平分线上【点睛】此题考查了全等三角形的判定与性质,垂直平分线的判定,解题的关键是熟练掌握全等三角形的判定方法与性质.25. 如图,已知ABC (AC AB BC <<),请用无刻度的直尺和圆规,完成下列作图(不写作法,保留作图痕迹);(1)如图1,在AB 边上寻找一点M ,使AMC ACB ∠=∠;(2)如图2,BC 边上寻找一点N ,使得NA NB BC +=.在【答案】(1)见解析;(2)见解析【解析】【分析】(1)利用作一个角等于已知角的方法作图即可;(2)作AC 的垂直平分线,交BC 于点N 即可.【详解】解:(1);(2).【点睛】此题考查作图问题,关键是根据作一个角等于已知角和线段垂直平分线的作法解答. 26. 如图甲,已知在ABC 中,90ACB ∠=°,AC BC =,直线MN 经过点C ,且AD MN ⊥于D ,BE MN ⊥于E .(1)说明ADC CEB △≌△.(2)说明AD BE DE +=.(3)已知条件不变,将直线MN 绕点C 旋转到图乙的位置时,若3DE =、 5.5AD =,则BE=_____. 【答案】(1)见解析 (2)见解析(3)2【解析】【分析】本题考查了全等三角形判定与性质,垂线的定义,直角三角形的性质,熟练掌握以上知识点并灵活运用是解此题的关键.(1)由垂线的定义得出90ADC CEB ∠=∠=°,再由同角的余角相等得出BCE =∠∠CAD ,最后利用AAS 证明ADC CEB △≌△即可;(2)由全等三角形的性质可得=AD CE ,BE CD =,即可得证;(3)由垂线的定义得出90ADC CEB ∠=∠=°,再由同角的余角相等得出BCE =∠∠CAD ,最后利用AAS 证明ADC CEB △≌△,得出 5.5CE AD ==,BE CD =,即可得解.【小问1详解】证明:∵AD MN ⊥于D ,BE MN ⊥于E .∴90ADC CEB ∠=∠=°,∴90DAC ACD ∠+∠=°,∵90ACB ∠=°,∴90BCE ACD ∠+∠=°,∴BCE =∠∠CAD ,∵AC BC =,∴()AAS ADC CEB ≌;【小问2详解】证明:∵ADC CEB △≌△,∴=AD CE ,BE CD =,∴AD BE CE CD DE +=+=;【小问3详解】证明:∵AD MN ⊥于D ,BE MN ⊥于E .∴90ADC CEB ∠=∠=°,∴90DAC ACD ∠+∠=°,∵90ACB ∠=°,∴90BCE ACD ∠+∠=°,∴BCE =∠∠CAD ,∵AC BC =,∴()AAS ADC CEB ≌,∴ 5.5CE AD ==,BE CD =,的∴ 5.532BE CD CE DE ==−=−=,故答案为:2.27. 阅读理解:【概念学习】定义①:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“形似三角形”.定义②:从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“形似三角形”,我们把这条线段叫做这个三角形的“巧妙分割线”.【概念理解】(1)如图1,在ABC 中,36A ∠=°,AB AC =,CD 平分ACB ∠,则CBD △与ABC ______(填“是”或“不是”)互为“形似三角形”.(2)如图2,在ABC 中,CD ACB ∠,36A ∠=°,48B ∠=°,求证:CD 为ABC 的“巧妙分割线”;【概念应用】(3)在ABC 中,45A ∠=°,CD 是ABC 的巧妙分割线,直接写出ACB ∠的度数.【答案】(1)是;(2)证明见解析;(3)90°或105°或112.5°【解析】【分析】(1)由题意推出36BCD ∠=°,72ABC ∠=°,72BDC ∠=°,从而得出结论; (2)根据题意,通过计算得出BCD △是等腰三角形,36A A ∠=∠=°,48ACD B ∠=∠=°,96ADC ACB ∠=∠=°,从而得出结论;(3)根据题意,分为当ACD 是等腰三角形和BCD △是等腰三角形两类,当ACD 是等腰三角形时,再分为:AC AD =,AD CD =,AC CD =三种情形讨论;同样当BCD △是等腰三角形时,也分为三种情形讨论,分别计算出ACB ∠的度数即可.【详解】解:(1)∵在ABC 中,36A ∠=°,AB AC =, ∴180722A ABC ACB °−∠∠=∠==°, ∵CD 平分ACB ∠, ∴1362BCD ACB ∠=∠=°, ∴18072BDC BCD B =°−−=°∠∠∠,∴BCD A B B BDC ACB ===∠∠,∠∠,∠∠,∴CBD △与是互为“形似三角形”,故答案为:是;(2)∵在ABC 中,36A ∠=°,48B ∠=°,∴18096ACB A B =°−−=°∠∠∠,∵CD 平分ACB ∠, ∴1482ACD BCD ACB ===°∠∠∠, ∴18096ADC A ACD B BCD =°−−°=∠∠∠,∠∠,∴A A ACD B ADC ACB DC DB ====∠∠,∠∠,∠∠,,∴ACD 与ABC 是互为“形似三角形”,且BCD △是等腰三角形,∴CD 为ABC 的“巧妙分割线”;(3)(Ⅰ)当ACD 是等腰三角形,另一个三角形与原三角形是“形似三角形”时,①如图1所示:当AD CD =时,则45ACD A ∠=∠=°,90BDC A ACD ∴∠=∠+∠=°,此时,C ABC BD 、△△是“形似三角形”,可知45BCD A ∠=∠=°,∴9045B BCD A =°−=°=∠∠∠,∴90ACB ∠=°;②如图2所示:当AC AD =时,则1804567.52ACD ADC °−°∠=∠==°, 此时,C ABC BD 、△△是“形似三角形”,可知45BCD A ∠=∠=°,4567.5112.5ACB ∴∠=°+°=°;③当AC CD =时,这种情况不存在;(Ⅱ)当BCD △是等腰三角形,另一个三角形与原三角形是“形似三角形”时,①如图3所示:当CD DB =时,45B BCD ∠=∠=°,同理可知90ACB ∠=°;②如图4所示:当BC BD =时,BDC BCD ∠=∠,此时,ABC ACD 、是“形似三角形”,可知ACD B ∠=∠,45BCD BDC ACD A ACD ∴∠=∠=∠+∠=∠+°,在BCD △中,由三角形内角和可知2180B BDC ∠+∠=°,得()245180ACD ACD ∠+∠+°=°, 30ACD ∴∠=°,45230105ACB ACD BCD ∴∠=∠+∠=°+×°=°;③当CD CB =时,这种情况不存在;综上所述:ACB ∠的度数为90°或105°或112.5°.【点睛】本题主要考查了等腰三角形的性质与判定,角平分线的定义,三角形内角和定理和三角形外角的性质,解决问题的关键是利用分类讨论的思想求解.28. 在ABC 中,,8AB AC BC ==,点M 从点B 出发沿射线BA 移动,同时点N 从点C 出发沿线段AC 的延长线移动,点M ,N 移动的速度相同,MN 与BC 相交于点D .(1)如图1,过点M 作//ME AC ,交BC 于点E ;①图中与BBBB 相等的线段________、_________;②求证:DME DNC ≌;(2)如图2,若60A ∠=°,当点M 移动到AABB 的中点时,求CCBB 的长度;(3)如图3,过点M 作MF BC ⊥于点F ,在点M 从点B 向点A (点M 不与点A ,B 重合)移动的过程中,线段BF 与CCBB BF 与CCBB 的长度和;若改变,请说明理由.【答案】(1)①CN 、EM ; ②见解析;(2)CCBB 的长度为2;(3)保持不变;BF +CD =4.【解析】【分析】(1)①根据移动过程分析和等腰三角形的性质即可解答;②由平行的性质、等腰三角形的性质进行等边和等角转换,最后运用AAS 即可证明结论;(2)由(1)的结论和等边三角形的性质,通过等量转换即可得解;(3)首先过点M 作ME //AC ,由等腰三角形的性质以及全等三角形的性质,即可求得BF 与CD 的长度保持不变.【详解】(1) ①∵点M 、N 同时移动且移动的速度相同,∴BM =CN ,∵AB =AC ,∴∠B =∠ACB又∵ME//AC,∴∠N=∠DME,∠ACB=∠MEB,∴∠MEB=∠B,∴BM=ME,故答案是:CN、EM;②∵BM=ME,BM=CN∴ME=CN,∵MN与BC相交于点D,∴∠MDE=∠NDC,在△DME和△DNC中∠MDE=∠NDC,∠DME=∠N,ME=NC ∴△DME≌△DNC(AAS);(2) 如图:过点M作ME//AC,交BC于点E ∵∠A=60°,AB=AC,∴△ABC是等边三角形,∴∠B=∠ACB=60°∵ME//C,∴∠BEM=∠ACB=60°,∴△BEM是等边三角形,∴BE=BM.∵M是AB的中点,∴1122 BE BM AB BC ===∴BE=CE=4.由(1)可证△DME≌△DNC ∴DE=CD,∴CD=12CE=2,∴CD的长度为2;.。
苏州2024年民办初中学校具体详细排名有哪几所学校

苏州2024年民办初中学校具体详细排名_有哪几所学校苏州2024年民办初中学校具体详细排名根据下表可知,2024苏州民办初中学校排名第一的是苏州立达中学;排名第二的是苏州平江中学;排名第三的是苏州星海实验中学。
具体详细排名信息如下:苏州民办初中学校排名一览表排名学校1苏州立达中学2苏州平江中学3苏州星海实验中学4苏州外国语学校5苏州市第四中学校6江苏省外国语学校7市外国语初级中学8外国语学校(初中部)苏州市第四中学校现有师生1500人,学校现有30个高、初中教学班。
学校依托苏州市教育改革、教育整体水平领先于全国的优势,在办学模式上进行了一定开拓,和苏州工业园区职业技术学院、省重点中学:苏州市十中联合办学,开办了高中实验班,强化了计算机教学与英语教学。
注:以上苏州民办初中排名数据****于网络,不代表本站观点!仅供参考。
民办初中是否还值得上(2024苏州学生参考)我们从师资、生源和升学率,几个大家最关心的角度分析一下:1、师资方面:民办初中有编制的老师撤回公办后,师资都是社保招聘的合同制的,从师资角度来看,和公办学校相比,并没有什么优势,稳定性还要差一些。
2、生源方面:从摇号开始,民办学校入学就是全凭运气,没办法选择生源,所以结果就是入学的学生水平是参差不齐的。
3、升学率方面,市重点高中的入学,从自主招生时代进入了名额分配时代,无论在哪个初中,都有同等百分比的学生通过名额分配到校进入市重点。
民办学校的优势不限学籍,优中择优由于公办初中学生水平参差不齐,而每位家长都希望孩子能“择良木而栖”,且优质公办初中的派位又存在随机性,很容易事与愿违。
因此为了追求优质学位,家长们把目光投向了自主招生的民办学校。
且民办学校只看成绩,不限条件,孩子们就可以凭借自己的实力去获得优质学位了。
管理严格,硬件条件好由于有民办学校自负盈亏,学校必须通过升学成绩来打造学校声誉、知名度等维持招生量,所以学校对于校风管理会非常严格,同时还就学校硬件设施等建设,提高家长对学校的印象分。
江苏省徐州市贾汪区师大附校历年考试真题

江苏省徐州市贾汪区师大附校历年考试真题1. The managers discussed the plan that they would like to see ______ the next year. [单选题] *A. carry outB. carrying outC. carried out(正确答案)D. to carry out2. -There's a hole in your bag.-I know, I'm going to have it __________. [单选题] *A. repairB. repairingC. repaired(正确答案)D. to be repaired3. Though he had often made his little sister _______, today he was made _____ by his little sister. [单选题] *A. cry; to cry(正确答案)B. crying; cryingC. cry; cryD. to cry; cry4. They would not allow him ______ across the enemy line. [单选题] *A. to risk going(正确答案)B. risking to goC. for risk to goD. risk going5. I found the door ________ when I got home. [单选题] *A. openedB. closeC. unlockingD. open(正确答案)6. The boy wanted to ride his bicycle in the street, but his mother told him _________. [单选题] *A. not to(正确答案)B. not to doC. not doD. do not to7. I couldn't do my homework with all that noise __________. [单选题] *A. going on(正确答案)B. goes onC. went onD. to go on8. I advised _________ at once. [单选题] *A. him to startingB. him to start(正确答案)C. to startingD. to start9. When I put my hand on his chest, I could feel his heart still ________. [单选题] *A. beatB. to be beatingC. beating(正确答案)D. was beating10. You had better get a doctor _________ your bad tooth. [单选题] *A. pull outB. to pull out(正确答案)C. pulled outD. pulling out11. He managed to make himself _______with his _______English. [单选题] *A. understand; breakingB. understand; brokenC. understood; breakingD. understood; broken(正确答案)12. The doctor asked him not to leave his wound(伤口) ______. [单选题] *A. exposeC. to exposeD. exposing13. They are going to have the service man _______ an electric fan in the office tomorrow. [单选题] *A. install(正确答案)B. to installC. to be installedD. installed14. —Did you have any difficulty in today's homework?—No. in fact I found ___________________. [单选题] *A. it very easy to do(正确答案)B. it very easy doneC. very easy for doingD. very easy to do it15. His remarks left me _________ about his real purpose. [单选题] *A. wonderedB. wonderC. to wonderD. wondering(正确答案)16. When I caught him__________ me, I stopped buying things there and started dealing with another shop. [单选题] *B. cheatC. to cheatD. to be cheating17. I feel _______unwise to give a child whatever he or she wants. [单选题] *A. thatB. it(正确答案)C. howD. what18. He found them ________ at a table __________. [单选题] *A. sat; to play chessB. sitting; play chessC. seated; playing chess(正确答案)D. seat; play the chess19. John rushed out in a hurry, __________ the door _________. [单选题] *A. leaving; unlocked(正确答案)B. leaving; unlockingC. left; unlockedD. to leave; unlocking20. _________everything _______, she left the supermarket with satisfaction. [单选题] *A. As; buyingB. For; to buyC. With; bought(正确答案)D. Because; to buy21. _______ the room, the nurse found the tape recorder(磁带录音机) ________. [单选题] *A. Entering; stealingB. Entering, gone(正确答案)C. To have entered; being stolenD. Having entered; to be stolen22. How about the two of us _________ a walk down the garden? [单选题] *A. to takeB. takeC. taking(正确答案)D. to be taking23. If you go to Xi an, you'll find the palaces there more magnificent than commonly ________. [单选题] *A. supposingB. to supposeC. supposed(正确答案)D. suppose (假定,认为)Questions 24-26 refer to the following notice.24. ______________ there has been a new statue(雕塑) at the entrance of the teaching building? [单选题] *(A) Have you noticed that(正确答案)(B) Do you noticing that(C) Have you noticing that(D) Noticed that25. Now we want to collect the ideas on naming it! We suggest everyone should__________ 1 to 2 names and then hand in(提交) tomorrow. [单选题] *(A) thinking about(B) think about(正确答案)(C) to think about(D) thought about26. The name must be novel and meaningful. In addition, we need every student to add your reasons __________ you want to name it. [单选题] *(A) who(B) what(C) why(正确答案)(D) thatQuestions 27-30 refer to the following notice.Dear Jason,27. I am writing to apologize for not going hiking with you this weekend. My cousin and his family just came to __________ my family and ask to go out together at the same time. [单选题] *(A) look(B) watch(C) see(D) visit(正确答案)28. ________________________________ since I saw him and he will leave next Monday. [单选题] *(A) It has been a long time(正确答案)(B) Has it been a long time(C) Long time it been has(D) Has been it a long time29. I really value this chance to _____________ him. So shall we postpone(推迟) our plan to next weekend? [单选题] *(A) stay with(正确答案)(B) stay up(C) stay on(D) stay off30. I am willing to lend my new series of comic books(漫画书) to you ________ you don't need to borrow from bookstores with the limitation of due time. Sorry again! [单选题] *(A) in order to(B) so as to(C) so that(正确答案)(D) that toYours, Lily。
江苏师范大学概况

江苏师范大学概况江苏师范大学位于苏、鲁、豫、皖四省交界的淮海经济区中心城市——徐州,是江苏省人民政府和教育部共建高校,是区域引领性示范高校。
是全国首批硕士学位授予单位,是全国首批有资格接收外国留学生的高校。
学校现有泉山、云龙、奎园、贾汪4个校区,占地2047亩。
学校设有3个试点学部、22个专业学院以及中俄学院、教师教育学院、继续教育学院、国际学院和独立学院科文学院。
现有86个本科专业,26个一级学科硕士点,1个一级学科博士点,1个博士后科研流动站,覆盖十一个学科门类。
有教育硕士、体育硕士、汉语国际教育硕士、艺术硕士、翻译硕士、工程硕士、法律硕士、公共管理硕士等8个专业硕士学位授权点,并具有以同等学力申请硕士学位授予权和硕士研究生推免权。
现有在校普通全日制学生28300人。
学校相继与美国、英国、日本、韩国、澳大利亚、俄罗斯、白俄罗斯、乌兹别克斯坦和巴基斯坦等国的44所高校建立了校际友好合作关系,先后接收26个国家和地区的留学生来校学习。
学校在美国和澳大利亚建立了孔子学院,与美国、澳大利亚、日本、俄罗斯和白俄罗斯等国高校开展合作办学和学分互认项目,与哈佛大学、香港大学等世界著名高校合作开展师资和管理人员培训项目。
建校以来,学校已向社会输送了十八万名毕业生,一大批取得突出成就的江苏师范大学校友活跃在海内外政治、经济、文化、科技和教育等各个领域。
学校积极实施人才强校战略,师资队伍建设取得显著成效。
在现有的1425名专任教师中,有教授215人(其中博士生导师45人)、副教授465人,具有博士学位者554人。
目前我校有长江学者特聘教授1人、讲座教授1人,江苏特聘教授5人;双聘院士量级人才9人,长江学者、国家“杰青”量级人才46人;专任教师中有4人获得“全国先进工作者”“全国五一劳动奖章”“全国模范教师”“全国优秀教师”等荣誉,3人入选“江苏省高校教学名师”,32人享受国务院颁发的政府特殊津贴,4人入选教育部“新世纪优秀人才”支持计划,9人获得“江苏省有突出贡献的中青年专家”称号,5人为省“双创计划”引进人才,11人为省“六大人才高峰”培养对象,91人入选省“333高层次人才培养工程”,128人入选省“青蓝工程”;有省“青蓝工程”优秀学科梯队3个、科技创新团队3个,江苏省“创新团队计划”引进团队4个,江苏省高校优秀科技创新团队3个,江苏高校哲学社会科学优秀创新团队1个。
江苏第二师范学院附属小学

江苏第二师范学院附属小学江苏第二师范学院附属小学是位于江苏省南京市秦淮区的一所优质小学。
学校创办于1999年,是江苏省教育厅直属全日制小学,也是南京市秦淮区的重点小学之一。
学校占地面积约6000平方米,建筑面积约3000平方米,拥有现代化的教学设施和优美的环境。
作为一所附属小学,江苏第二师范学院附属小学秉承了师范学院的办学理念,注重培养学生的综合素质和创新精神。
学校以优质的教学资源和师资力量为基础,致力于为学生提供全面发展的教育。
学校设有幼儿园部、小学部和特教部,共有幼儿园班、小学部24个教学班和特教部特教班,师生比例合理,保证了每个学生都能得到充分的关注和指导。
在教育教学方面,江苏第二师范学院附属小学注重培养学生的学习能力、思维能力和创新能力。
学校强调素质教育,倡导个性化发展,注重培养学生的创造性思维和实践能力。
学校提供丰富多样的学科课程,如语文、数学、英语、科学、美术、音乐等,以及多种兴趣班和课外活动,满足学生的学习需求和兴趣发展。
学校还定期组织各类竞赛、科技创新活动和社会实践,提高学生的综合素质。
江苏第二师范学院附属小学注重优秀传统文化的传承和培养学生的社会责任感。
学校开设了国学课程,让学生了解中国传统文化的精髓,培养品德修养和文化素养。
学校还重视社会实践和志愿服务,组织学生参加各类志愿活动,增强他们的社会责任感和团队合作精神。
学校注重师资队伍建设,拥有一支高素质、专业化的教师队伍。
学校致力于教师的专业发展和能力提升,定期组织各类教研活动和培训,促进教师的教学创新和教育教学方法的不断改进。
学校还建立了良好的家校合作关系,加强与家长的沟通与交流,共同关注学生的发展和成长。
在学校管理方面,江苏第二师范学院附属小学依据现代管理理念,建立了科学高效的管理体系。
学校注重规范教学秩序和校园文化建设,强化班级管理和学生管理,营造一个和谐、安全、积极的学习氛围。
学校还加强校园安全管理,保障学生的人身安全和财产安全。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏师范大学附属实验学校
江苏师范大学附属实验学校位于徐州市贾汪区大洞山风景区西麓,是江苏师范大学与贾汪区合作办学的结晶。
学校毗邻江苏师范大学贾汪校区,占地334亩,设有幼儿园、小学、初中、高中和国际项目部。
江苏师范大学和贾汪区人民政府本着相互依托、共同发展的原则助力学校向更高平台迈进。
贾汪区人民政府负责学校的硬件投入,江苏师范大学负责学校的管理运营,为江苏师范大学附属实验学校的腾飞插上了双翅,为学校未来的持续发展提供了保障。
学校拥有现代化的教室、学科实验室、多功能创新实验室、活动室、图书馆、体育运动场、宿舍、食堂等校舍建筑及辅助用房约10万平方米。
学校精心打造贾汪文化、师大文化、汉文化、中华文化相结合的,凸显人文关怀、彰显教育内涵、显现学校核心价值的“贯穿古今、融汇中西”的校园文化。
学校于2013年正式招生,目前有在校生5000余人,教职工407人,其中硕士45人。
教师群体年富力强,是一支稳步成长中的教师队伍,共有近700余人次在国家、省、市、县教师专业技能比赛中获奖。
学校还聘请了中国教育学会高中教育专业委员会副理事长、中国教育国际交流协会中外合作办学专业委员会中外合作办学质量认证委员会委员、原苏州中学校长倪振民先生担任名誉校长和学校总督学;江苏师范大学教师教育学院副院长,硕士生导师,美国纽约Chapel Field Christian Schools名誉校长,美国纽约州立大学宾汉姆顿大学名誉教授,原镇江外国语学校、镇江国际学校主管校长,省物理奥林匹克竞赛高级教练员,教育部课程改革调研专家组成员,江苏省高考命题库专家组成员周慰曾任我校首任校长。
江苏师范大学教育科学学院(教师教育学院)硕士生导师,江苏师范大学高等教育研究中心研究员(教授),南京师范大学在读博士朱景坤先生担任学校党总支书记、校长。
学校依托江苏师范大学的资源优势,探索“十五年一贯制”创新人才培养模式,得到顾明远、谈松华、朱永新等知名教育家以及中国教育学会、教育部基教司等单位领导的高度评价。
学校在“守正出新、坚志勇为”的江苏师范大学精神引领下,以探索“十五年一贯制”创新人才培养为使命,秉承“创新的教育,成就卓越的你”这一办学宗旨,树立培养学生“开阔的国际视野、活跃的创新思维、鲜明的个性特长、自主的交往能力、独立的人格魅力、博雅的素养品质”的育人目标,坚持“以爱的流淌滋润学生健康成长、以活动平台提升学生综合素养、以创新教育引领学生全面发展、以国际视野开拓学生多元未来”的育人途径,按照“小班化、精品化、现代化、国际化”的办学模式,致力于提升学生的自主能力,“千方百计唤醒学生自主学习的意识”,“千方百计培养学生自主学习的习惯”,“千方百计提升学生自主学习的能力”,打造“互动、愉悦、高效”课堂,努力培养具有中国灵魂、国际胸怀的世界公民。
学校在德育工作中始终围绕“赏识、励志、规范、诚信、阳光、快乐”的关键词,搭建“社团、学生会、团委”等工作平台,通过“全员导师制、个性化成长策划”等工作渠道,构建“学校、家庭、社区”三位一体的工作体系。
经常开展“读书节”、“书画作品展”、“远足社会实践”、“模拟交易市场”、“与名家对话”等学生活动,为学生的自由发展提供了充分空间。
学校在2014年江苏省汉字听写大会比赛中,荣获徐州大市第一名,代表徐州市参加比赛并荣获江苏省第二名;在美国斯坦福大学主办的“美国大联盟杯数学竞赛”初赛中荣获一等奖29人、复赛获得跨国竞赛资格的6人;在第五届淮海经济区机器人大赛中获得一项冠军,两项亚军,总计获奖16人次;第十五届“全国中小学信息技术创新与实践活动”(NOC)决赛中“FEG智能无人车”比赛中获得了该项赛事的初中组全国二等奖,在“物联创新设计”赛事项目上,我校同学携带自主设计的“智能房车”和“智能导盲犬”物联创新作品,获得了初中组个人赛全国二等奖;学校足球队聘请原国家足球队队长、亚洲足球先生范志毅为名誉教练。
学校在教学过程中,依托“教学云技术”的数字化校园平台,让虚拟课堂和现实课堂相互交汇、相得益彰,通过对学生的个性、心理、兴趣、学习优势等方面的科学测试,全方位地了解学生;通过“思维导图、全脑快学”的学习模式,有针对性地组织教学活动。
学校开设了二十余门旨在“培养积极心态、倡导爱心奉献、担当社会责任、提升科学素养、开发领导能力”的系列校本课程。
倡导“以赏识取代训斥、以励志取代说教、以过程取代结果、以多元取代单一、以互评取代他评”的评价机制。
江苏师范大学以信息化与智慧教育、卓越教师培养(“两翼”)为重要支撑,聚焦“十五年一贯制”创新人才培养(“一体”),力求推动我国基础教育人才培养模式的革命,以附属实验学校为平台,建成全国“十五年一贯制”创新人才培养的示范基地,成为全国基础教育“十五年一贯制”创新人才培养试点学校建设标准的研发与推广中心,教育学科日前成功获批江苏省优势学科。
作为江苏师范大学教育实践基地,附属实验学校围绕基础教育人才培养模式改革,在学制贯通、学生个性化发展、课程体系重组、课程运作机制等方面开展理论研究。
通过“专家学科引领、教师专业发展、学生成才成长”一体化运行机制,以智慧教育理论与方法为引领,以教育信息化平台建设为基础,以数据分析和数据管理为重要手段,开展“十五年一贯制”创新人才培养的实验探索。
集高校资源优势,与全国百所顶尖高中校联动,试点CAP课程。
与清华、北大、南大、中科大、北师大、中科院,美国斯坦福大学、南加州大学、加州大学伯克利分校等知名院校的专家互动,开阔国际视野,规划人生生涯,开拓多元未来。
学校在未来的发展道路上将坚定不移地探索十五年一贯制创新人才的培养模式,瞄准未来以“全球脑”为核心的知识传承和创新机制,努力通过国际化引领,现代化保障,办成一所富有创新人才培养特色的、徐州一流、省内知名的品牌学校。
