理工控制工程习题精讲
控制工程 作业问题及习题答案PPT29页

56、极端的法规,就是极端的不公。 ——西 塞罗 57、法律一旦成为人们的需要,人们 就不再 配享受 自由了 。—— 毕达哥 拉斯 58、法律规定的惩罚不是为了私人的 利益, 而是为 了公共 的利益 ;一部 分靠有 害的强 制,一 部分靠 榜样的 效力。 ——格 老秀斯 59、假如没有法律他们会更快乐的话 ,那么 法律作 为一件 无用之 物自己 就会消 灭。—— —西塞 罗
1、最灵繁的人也看不见自己的背脊。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事,无字句处读书。——周恩来 5、阅读使人充实,会谈使人敏捷,写作使人精确。——培根
控制工程第一章习题解答

工作原理:电压U2——大门实际位置;电压U1——开门(关门)开关的指令状 态确定的电压大小。 △u=U1-U2 当大门在打开位置时,电压U2 =U上: 若合上开门开关,U1=U上,△u=0,大门不动作;如合上关门开关, U1=U下,△u<0,大门逐渐关闭,直至完全关闭,使△u=0。 当大门在关闭位置,U2=U下:
B)水箱是控制对象,水箱的水位是被控量,水位的给定值h’由浮球拉杆的长度给定。杠 杆平衡时,进水阀位于某一开度,水位保持在给定值。当有扰动(水的使用流出量和给水 压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),到一定程度后, 在浮球拉杆的带动下,电磁阀开关被闭合(断开),进水阀门完全打开(关闭),开始进 水(断水),水位升高(降低),浮球也随之升高(降低),直至达到给定的水位高度。 随后水位进一步发生升高(降低),到一定程度后,电磁阀又发生一次打开(闭合)。此 系统是离散控制系统。
若合上开门开关,U1=U上,△u>0,大门执行开门指令,直至完全打开,
使△u=0;如合上关门开关,U1=U下,△u=0,大水箱的水位是被控量,水位的给定值h’由浮球顶杆 的长度给定,杠杆平衡时,进水阀位于某一开度,水位保持在给定值。当有 扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮 球位置也随着降低(升高),通过杠杆机构是进水阀的开度增大(减小), 进入水箱的水流量增加(减小),水位升高(降低),浮球也随之升高(降 低),进水阀开度增大(减小)量减小,直至达到新的水位平衡。此为连续 控制系统。
控制工程习题讲解一

则可绘出方框图如
F(s) +
+ +
—
—
1
—
m 1s 2
k
C1s
1 m 2s2
C2s
Y1 ( s )
+
— Y2 (s)
5
控制工程基础
F(s) +
—
— —
++
1 m 1s 2
k
C1s
1 m 2s2
Y1 ( s )
+
— Y2(s)
C2s
F(s) +
++
—
6
习题讲解
1 m1s 2 k
C1s
1 m 2s2
2
控制工程基础
习题讲解
例2 如图所示机械系统。f表示输入力,y2表示输出 位移,求系统微分方程模型、绘出系统方框图及化
简求出传递函数模型。
解:
C2
分别对m1,m2进行受力 分析,列写其动力学方程有
k
m1 C 1 y1 (t)
m2
f (t)
y2 (t)
3
控制工程基础
习题讲解
fC2y 2C 1(y 2y 1)m 2y2 C 1(y 1y 2)k1ym 1y1
++
—
1 m 2s2
Y2 (s)
C2s
F (s)
m 1 s 2 C 1 s k
Y2 (s)
m 1 m 2 s 4 [ m 2 C 1 m 1 C 1 m 1 C 2 ] s 3 ( m 2 k C 1 C 2 ) s 2 k ( C 1 C 2 ) s
8
控制工程基础
习题讲解
例3 用方框图等效化简求系统的闭环传递函数。
习题讲解
15
+
— Y2(s)
北理工843控制工程考研习题整理(2)
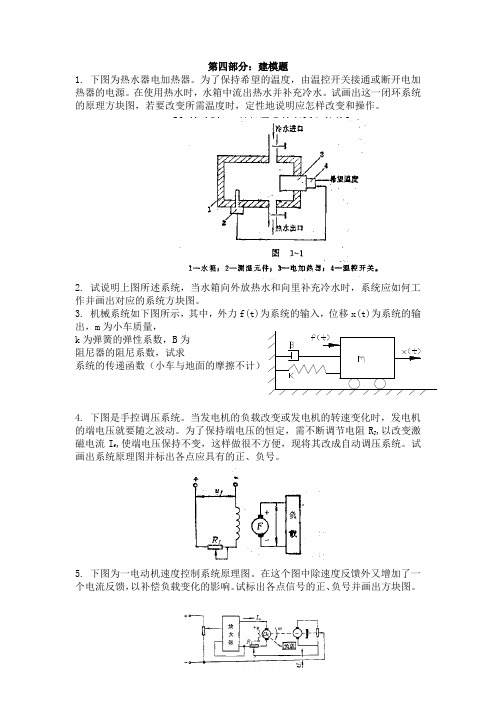
8. 已知单位负反馈系统的开环传递函数为 G( S )
K 试 (0.1S 1)(0.5S 1)( S 1)
求当K为多少时,闭环系统稳定。 9. 设单位反馈系统的开环传递函数为 G(s)=(as+1)/s2,试确定使相位裕量γ =+450 时的 a 值(a>0) 。 第六部分:结构图简化题 1.用等效变换规则化简如下动态结构图:
4. 下图是手控调压系统。当发电机的负载改变或发电机的转速变化时,发电机 的端电压就要随之波动。为了保持端电压的恒定,需不断调节电阻 RJ,以改变激 磁电流 If,使端电压保持不变,这样做很不方便,现将其改成自动调压系统。试 画出系统原理图并标出各点应具有的正、负号。
5. 下图为一电动机速度控制系统原理图。在这个图中除速度反馈外又增加了一 个电流反馈, 以补偿负载变化的影响。 试标出各点信号的正、 负号并画出方块图。
25. 试列写 右图所示机 械系统的运 动方程。
26. 列写图 2-13 所示系统的输出电压 u2 与输入为电动机转速间的微分方程;Ks 是隔离放大器。 (其中 C>>C1; C1>>C2)
27. 下图所示电路,起始处于稳太,在 t=0 时刻开关断开。试求电感 L 两端电压 对 t 的函数关系,并画出大致图形和用初值定理和终值定理演算。
6.今测得最小相位系统渐近对数幅频特性曲线如下图所示,试求其传递函数 G(S) 的表达式。
L() 20dB
7. 下图(a)与(b)均为自动调压系统。现在假设空载时(a)与(b)的发电 机的端电压相同均为 110 伏。试问带上负载后(a)与(b)哪个能保持 110 伏电 压不变,哪个电压要低于 110 伏,其道理何在?
控制工程基础习题PPT课件

精选PPT课件
22
1:判断下列系统在原点处的稳定性
1 x 2 1 1 3 x, 2x 1 1 1 1 x
精选PPT课件
23
第五章作业
• 4-1、4-4(2) • 4-5(1)、4-11(2) • 4-15
精选PPT课件
24
4-1 设单位反馈控制系统的开环传递函数为:
第一章作业
作业:p14,1-1,1-5 补充:1
精选PPT课件
1
1-1下图是液位自动控制系统原理示意图。在任意情 况下,希望液面高度c维持不变,试说明系统工作 原理并画出系统方块图。
精选PPT课件
2
1-5下图是电炉温度控制系统原理示意图。试分析系统保 持电炉温度恒定的工作过程,指出系统的被控对象、被 控量以及各部件的作用,最后画出系统方块图。
G(s) K * s 1
试用解析法绘出 K * 从零变到无穷时的闭环根轨迹图, 并判断下列点是否在根轨迹上:
(-2+j0),(0+j1),(-3+j2)
4-4设单位反馈控制系统开环传递函数如下,试概略绘 出相应的闭环根轨迹图(要求确定分离点坐标d)
(2) G(S) K(s1) s(2s1)
精选PPT课件
精选PPT课件
11
1、系统动态特性由下列微分方程描述,列写其 相应的状态空间表达式。
y 5 y 7 y 3 y u 2 u
2、已知系统的传递函数:列写其相应的状态空
间表达式。
G(s)
10(s1)
s(s1)(s3)
3、写如下传递函数的状态空间表达式的约当标
准型:
G(s)s2
5 6s5
精选PPT课件
控制工程基础部分习题解
(2、3、4)缺 2-22 以后缺
ya
n.
co
m
北京理工大学考研论坛
第三章
3-1 解:
3-2
ww
w.
bi
3-3 解:
tk
ao
- 21 -
ya
n.
co
m
北京理工大学考研论坛
3-4 解:
ww
w.Βιβλιοθήκη bitkao
- 22 -
tk
ao
ya
-2-
n.
1-5 解: (a) :对于图(a)所示的系统,水箱中输出流量和输入流量决定了水箱的水位变化,水 位的高低决定了浮球的位置,流量通过杠杆机械对应阀门的开启大小,阀门的大小决定输入 流量补偿输出流量,最终水位保持一定值。其职能方块图如下图所示:
co
(4): f (t ) = L−1 (
e−s ) = e t −1 ⋅1(t − 1) S −1
-4-
tk
− s 6
π π 6 Se 6Se = L[6 cos 3(t − ) ⋅1(t − )] = 2 = 2 2 4 4 S +3 S +9
ao
4 )]
− S 4
ww
2 5 9e + + 2 2 s + 20 ( s + 20) s +9
2-2 解:
(1): f (t ) = L−1 (
−1 2 + ) = ( −e − 2t + 2e −3t ) ⋅1(t ) S +2 S +3
1 (2): f (t ) = sin 2t ⋅1(t ) 2 1 (3): f (t ) = e t (cos 2t + sin 2t ) ⋅1(t ) 2
习题解析控制工程

60°
45°
(3)
0
[s]
Re
2024/9/30
n=2s-1
20
Im
[s]
3.13
0
Re
0<<1
Im [s]
0
Re
-1<<0
2024/9/30
Im
[s]
0
Re
=1
Im [s]
0
Re
=-1
21
3.14
Gs
s2
9 s
9
s2
2
32 1
3s
32
6
n 31 /
0.167
s
M p 58.8%
t p 1.06s
xo t 10 t 0.1 0.1e10t
单位阶跃响应: (上式旳一阶导数)
xou t 10 1 e10t
单位脉冲响应:
(上式旳二阶导数或xou(t)旳一阶导数)
xoi t 100e10t
2024/9/30
8
系统旳闭环传递函数为:
3.8
GB
s
1
K 0G s K1Gs
15
3.11 内部局部闭环传递函数:
GB1s
s
2 n
2n
K
f n2
整个系统旳闭环传递函数:
GB
s
1
1 s
GB1s
1 s
GB1
s
s2
2 n
2 n
K
f
2 n
s
2 n
2024/9/30
16
GB s s2
n2
2 n
K
f
2 n
s
控制工程基础习题解答教学提纲PPT文档共86页

控制工程基础习题解答教学提纲
36、如果我们国家的法律中只有某种 神灵, 而不是 殚精竭 虑将神 灵揉进 宪法, 总体上 来说, 法律就 会更好 。—— 马克·吐 温 37、纲纪废弃之日,便是暴政兴起之 时。— —威·皮 物特
38、若是没有公众舆论的支持,法律 是丝毫 没有力 量的。 ——菲 力普斯 39、一个判例造出另一个判例,它们 迅速累 聚,进 而变成 法律。 ——朱 尼厄斯
40、人类法律,事物有规律,这是不 容忽视 的。— —爱献 生
66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做,明天再早也 是耽误 了。——裴斯 洛齐 68、决定一个人的一生,以及整个命运 的,只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
武汉汽车工业大学 控制系统考试 <内部> 一、填空在典型闭环控制系统中,系统的控制部分由以下给定环节、测量环节、比较环节、放大及运算环节和执行环节组成。
5.按系统响应产生的原因分为 零状态 响应和零输入 响应。
1.对控制系统的基本要求一般可以归纳为稳定性、快速性 和准确性。
2. 就系统及其输入、输出三者之间的动态关系而言,当系统已定、并且输入已知时,求出系统的输出(响应),并通过输出来研究系统本身的有关问题,是_系统分析___。
3. 当系统已定,确定输入,且确定的输入应使得输出尽可能符合给定的最佳要求,此即为最优控制问题。
4. 当输入已知,确定系统,且确定的系统应使得输出尽可能符合给定的最佳要求,此即为最优设计问题。
5. 按系统有无反馈,通常可将控制系统分为 开环控制系统 和 闭环控制系统 。
6. 在控制工程基础课程中描述系统的数学模型有微分方程 、传递函数等。
7. 稳态误差反应稳态响应偏离系统希望值的程度,它用来衡量系统控制精度的程度。
8.评价二阶控制系统对单位阶跃输入的瞬态时域性能指标有p t 、p M 和s t 等。
其中,p M 反映了系统的相对稳定性。
9. 一阶系统11Ts +的单位阶跃响应的表达是/1t T e --。
是指 在系统中增加一些环节,用以改善系统性能 ,按校正环节的频率特性12.已知开环系统为当输入为单位阶跃函数时,系统的稳态由图可知系统稳定偏差为 0 _,当输入为单位速度输入时,稳态偏差为_0.5__,单位加速度输入时,稳态偏差为无穷大。
二.判断正误(×)1.控制系统的被控变量简称控制量。
(√)2.闭环系统稳定,则其开环系统未必是稳定的。
(×)3.由系统初始状态引起的响应,称为零状态响应。
(×)4.控制系统的谐振峰值就是系统的最大超调量.(√)5.稳定的系统不一定是非最小相位系统。
(×)6.Nyquist判据既能反映绝对稳定性,也能反映相对稳定性,但不能用于延迟系统.1. 传递函数只适用与线性定常系统。
(√)2.稳态误差不仅取决于系统自身的结构参数,而且与输入信号的类型有关。
(√)3.系统的稳定性不仅与系统自身结构有关,而且与初始条件、外作用的幅值有关。
(×)4.系统的开环增益越大,系统的稳态误差越小。
(√)5.频率响应是线性定常系统对正弦输入的稳态响应。
(√)三、简答题:微分方程:在时域中描述系统(或元件)动态特性的数学模型。
传递函数:在外界输入作用前,输入、输出的初始条件为零时,线性定常系统、环节或元件的输出的拉普拉斯变换与输入的拉普拉斯变换之比。
前向通道传递函数反馈回路传递函数什么是时间响应?答:机械工程系统在外加作用(输入)激励下,其输出量随时间变化的函数关系称之为系统的时间响应,通过对时间响应的分析可揭示系统本身的动态特性。
4-2 时间响应有哪两部分组成?各部分的定义是什么?答:任一系统的时间响应都是由瞬态响应和稳态响应两部分组成。
瞬态响应:系统受到外加作用激励后,从初始状态到最终状态的响应过程称为瞬态响应。
稳态响应: 时间趋于无穷大时,系统的输出状态称为稳态响应。
瞬态响应反映了系统动态性能,而稳态响应偏离系统希望值的程度可用来衡量系统的精确程度。
试述开环控制系统的主要优缺点。
答:优点:开环控制系统无反馈回路,结构简单,成本较低。
缺点:控制精度低,容易受到外界干扰,输出一旦出现误差无法补偿。
6-1 什么是频率特性?答:当不断改变输入的正弦波频率(由0变化到无穷大)时,该幅值比和相位差的变化情况即称为系统的频率特性。
7-1 系统稳定性的定义是什么?答:一个控制系统在实际应用中,当受到扰动作用时,就要偏离原来的平衡状态,产生初始偏差。
所谓控制系统的稳定性,就是指当扰动消失之后,系统从初始偏差恢复到原平衡状态的能力。
7-2 一个系统稳定的充分和必要条件是什么?答:系统特征方程的全部根都具有实部。
或者说,闭环传递函数的全部极点均在[s]平面的左半部。
8-3 系统在何种情况下采用相位超前校正、相位滞后校正和相位滞后-超前校正。
解答:01为了既能提高系统的响应速度,又能保证系统的其他特性不变坏,需要采用相位超前校正;02为了减小稳态误差而又不影响稳定性和响应的快速性,只要加大低频段的增益就可以时,需要采用相位滞后校正;03需要同时改善系统的瞬态响应和稳态精度时,用相位滞后-超前校正四、计算题1.已知系统微分方程为传递函数为2.某线性定常系统,在单位阶跃输入作用下,其输出为试求系统的传递函数。
()()()()22153323656i Y s s s s Y s s s G s X s s s =-+++++==++3. 4-9 设单位反馈系统的开环传递函数为()212ss s G +=求这个系统的单位脉冲响应和单位阶跃响应。
4-6 设单位反馈控制系统的开环传递函数为()()11+=s s s G()()()()()2683y t y t y t x t x t ++=+325ydt 7y y y r +++=⎰()()()32325Y s s G s R s s s s ==+++()()()231268Y s s G s X s s s +==++()32153t t y t e e --=-+试求系统的上升时间、峰值时间、最大过调量和调整时间。
()()()22111r 0011211 0.51cos t 2.42 t 3.63 16.3 R n n nd p d p G s s s s s M eeξωωξωπξωπω---=++=⎧=⎧⎪⇒⎨⎨==⎪⎩⎩-===========解:()()336 =0.050.5 t 448 =0.020.5ns n s s ξωξω⎧==∆⎪⎪=⎨⎪==∆⎪⎩4-7 设有一闭环系统的传递函数为()()2222nn n s s s R s C ωξωω++=为了使系统对阶跃输入的响应有约5%的过调量和2秒的调整时间,试求ξ和n ω值应为等于多大。
()005 0.690.0242222.90.690.0532p s nn s nM e t s t ξξωωξξω=====∆======∆===解:若则若()33 2.17220.69n s ωξ===⨯则6-2 已知系统的单位阶跃响应为()491 1.80.8tt C t e e --=-+,t≥0;试求系统幅频特性和相频特性。
解:()()()()()()()()()()()()491 1.80.81 1.80.8491 1.80.8491364949t t C t e e C s s s s C s s s s C s s R s s R s ss s A arctgarctgφφωωωϕω--=-+=-+++-+++=⇒===++==--6-6 已知系统传递函数方框图如图(题6-6)所示,现作用于系统输入信号()t t x i 2sin =,试求系统的稳态输出。
系统的传递函数如下:(1)()();1,15=+=s H s s G (2)()();1,5==s H s s G(3)()()2,15=+=s H s s G 。
解: (1)[]5()6()()arctan6()sin 2()(2)sin 2(2)2 ()2arctan 6 0.79sin(218.4)B G s s A s r t tc t A t c t t t ωϕωϕ=+==-=∴=+⎡⎤=-⎢⎥⎣⎦=-(2)5()5()()arctan52()2arctan 5 0.93sin(221.8)B G s s A c t t t ωωϕω=+==-⎡⎤=-⎢⎥⎣⎦=-(3)图(题6-6)10()11(()arctan112()arctan)110.89sin(210.3)B G s s A c t t t ωωϕω=+=-=-=-6-7 试绘制具有下列传递函数的各系统的Nyquist 图:(2) ();01.011ss G -=(3) ();101.01-=s s G (2) 1()10.01B G s s=-()360arctan 0.01ϕωω=-+(3)1G(s)0.01s 1=-试画出极坐标图(1)1G (s )0.21150.2T s ω=+==(2) 2()3G s = (3)()10G s s =7-8 判别图(题7-7)(a),(b )所示系统的稳定性。
解(a)()()()232320.110.190.20.10.190.20.1B s G s s s s D s s s s +=+++=+++3s 1 0.2 2s 0.19 0.1 1s -0.33图(题7-80s 0.1由劳斯表可以看出第一列数字不全大于零,所以系统不稳定。
(b )()()()3232101************B s G s s s s D s s s s +=+++=+++3s 1 10 2s 21 10 1s 9.52 0s 10由劳斯表可以看出第一列数字全大于零,所以该系统稳定。
7-9 画出下列各开环传递函数的乃奎斯特图,并判别系统是否稳定。
(1)()())1.01)(1(100s s s H s G ++=0,0,N P N P ===∴系统稳定(2)()())31)(21)(1(10s s s s H s G +++=奈氏轨迹穿过()1,0j -点,所以系统临界稳定。
(3)()())2.01)(1.01(102s s s s H s G ++=2,0,N P N P=-=≠∴系统不稳定8-4 已知两系统的开环传递函数幅频特性如图(题8-4)所示,试问在系统(a )中加入何种的串联环节可以达到系统(b )。
题(图8-4)(a)的传递函数为: ()1(1)511(1)(1)1.5100a s K S G S S S +=++20ca ω=1001.5=a 可求出K (b)的传递函数: ()1(1)1011(1)(1)3200b s K S G S S S +=++ 40ca ω= 4003∴=b 可求出K。
