宁波市高三五校适应性考试 (2)
浙江省宁波市2024年新高考选考适应性考试

浙江省宁波市2024年新高考选考适应性考试一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题如图所示,真空中有三个点电荷分别固定于直角三角形中的A、C、N三点处,C、N两点的点电荷的电荷量均为+q,A点的点电荷的电荷量Q未知,已知∠C=90°,∠B=30°,AC=a,N为AB的中点,MN垂直于AB,M点的电场强度为0,静电力常量为k。
下列说法错误的是()A.A点的点电荷的电荷量为B.B点的电场强度大小为C.C、N两点的点电荷受到的静电力不相同D.将N点的点电荷移到B点后,N点的电势高于M点的电势第(2)题2022年11月1日,梦天实验舱成功对接天宫空间站,至此我国空间站一期建设基本完成。
如图为梦天实验舱正在接近天宫空间站的对接情景,假设对接后组合体的轨道近似看成圆形,已知组合体运行周期为T,其轨道半径与地球半径的比值为n,引力常量为G。
下列说法正确的是( )A.图示时刻天宫空间站的运行速度大于7.9km/sB.图示时刻天宫空间站的加速度大于C.组合体的运行速度为D.地球的平均密度为第(3)题以下物理量为矢量,且单位是国际单位制基本单位的是()A.电流、AB.位移、mC.功、JD.磁感应强度、T第(4)题好多同学在寝室熄灯后使用台灯继续学习至深夜,某同学使用如图所示的一款充电宝和一款台灯来照明,部分参数如下表所示,已知深夜学习需要6W以上的照明功率,则以下说法不正确的是( )充电宝部分参数如下:产品名称快充移动电源聚合物电池容量品牌输出输入产品颜色黑色/白色产品重量若干克产品尺寸台灯部分参数如下:产品名称米格台灯灯珠144颗额定电压最大电流内置电池容量其他功能亮度从开始连续调节A.充电宝输出功率可达B.台灯的最大功率为C.打开台灯后每颗灯珠的功率都为D.仅用这款台灯和这款充电宝充满一次电的情况下使用,不能保证周日至周五每晚小时的学习时间第(5)题如图,在光滑绝缘的水平桌面上,有一方向垂直桌面的匀强磁场B,现有两条柔软的轻质通电金属直导线P和Q,恰好平行且静止在桌面上,则下列情况可能正确的是( )A.P和Q中电流大小相等、方向相同,磁场方向垂直桌面向上B.P和Q中电流大小不等、方向相同,磁场方向垂直桌面向下C.P和Q中电流大小不等、方向相反,磁场方向垂直桌面向上D.P和Q中电流大小相等、方向相反,磁场方向垂直桌面向下第(6)题潘多拉是电影《阿凡达》虚构的一个天体,其属于阿尔法半人马星系,即阿尔法半人马星系B-4号行星,大小与地球相差无几(半径与地球半径近似相等),若把电影中的虚构视为真实的,地球人登上该星球后发现:自己在该星球上体重只有在地球上体重的n倍(),由此可以判断( )A.潘多拉星球上的重力加速度是地球表面重力加速度的倍B.潘多拉星球的质量是地球质量的n倍C.若在潘多拉星球上发射卫星,最小发射速度是地球第一宇宙速度的n倍D.若在潘多拉星球上发射卫星,第二宇宙速度是11.2km/s第(7)题已知光速c=3.0×108m/s,引力常量G=6.67×10-11 N·m2/kg2,普朗克常量h=6.63×10-34J·s,用这三个物理量表示普朗克长度(量子力学中最小可测长度),其表达式可能是( )A.B.C.D.第(8)题水流从高处落下,对水轮机做了2×108 J的功,这句话的正确理解为( )A.水流在对水轮机做功前,,具有2×108 J的重力势能B.水流在对水轮机做功时,具有2×108 J的动能C.水流在对水轮机做功后,具有2×108 J的能量D.水流在对水轮机做功的过程中,能量减少了2×108 J二、多项选择题(本题包含4小题,每小题4分,共16分。
2024届浙江省宁波市高三下学期高考选考适应性考试(二模)物理试题
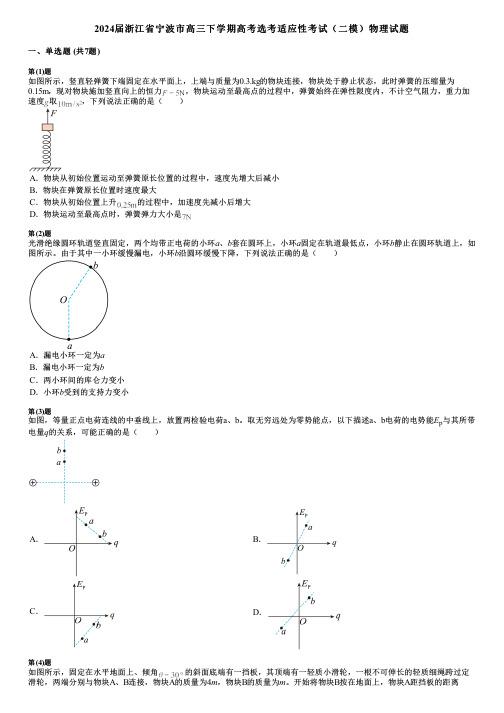
2024届浙江省宁波市高三下学期高考选考适应性考试(二模)物理试题一、单选题 (共7题)第(1)题如图所示,竖直轻弹簧下端固定在水平面上,上端与质量为0.3.kg的物块连接,物块处于静止状态,此时弹簧的压缩量为0.15m,现对物块施加竖直向上的恒力,物块运动至最高点的过程中,弹簧始终在弹性限度内,不计空气阻力,重力加速度取,下列说法正确的是( )A.物块从初始位置运动至弹簧原长位置的过程中,速度先增大后减小B.物块在弹簧原长位置时速度最大C.物块从初始位置上升的过程中,加速度先减小后增大D.物块运动至最高点时,弹簧弹力大小是第(2)题光滑绝缘圆环轨道竖直固定,两个均带正电荷的小环a、b套在圆环上,小环a固定在轨道最低点,小环b静止在圆环轨道上,如图所示。
由于其中一小环缓慢漏电,小环b沿圆环缓慢下降,下列说法正确的是( )A.漏电小环一定为aB.漏电小环一定为bC.两小环间的库仑力变小D.小环b受到的支持力变小第(3)题如图,等量正点电荷连线的中垂线上,放置两检验电荷a、b。
取无穷远处为零势能点,以下描述a、b电荷的电势能E p与其所带电量q的关系,可能正确的是( )A.B.C.D.第(4)题如图所示,固定在水平地面上、倾角的斜面底端有一挡板,其顶端有一轻质小滑轮,一根不可伸长的轻质细绳跨过定滑轮,两端分别与物块A、B连接,物块A的质量为4m,物块B的质量为m。
开始将物块B按在地面上,物块A距挡板的距离为d,突然放手后物块A开始下滑,与挡板碰撞后速度立刻变为0。
不计一切摩擦,则物块B上升的最大高度为( )A.B.C.D.第(5)题水平固定的平行光滑金属导轨间存在垂直导轨平面向下的匀强磁场,轨道左端接一电压恒定的直流电源。
将两根由同种材料制成的均质金属棒1、2从导轨同一位置先后由静止释放,两金属棒沿导轨运动的时间分别为、,离开导轨时的速度大小分别为、,通过两金属棒某截面的电荷量分别为、,两金属棒产生的热量分别为、。
2024届浙江省宁波市高三下学期高考选考适应性考试(二模)物理试题

2024届浙江省宁波市高三下学期高考选考适应性考试(二模)物理试题学校:_______ 班级:__________姓名:_______ 考号:__________(满分:100分时间:75分钟)总分栏题号一二三四五六七总分得分评卷人得分一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题用一种单色光照射某金属,产生光电子的最大初动能为E k,单位时间内发射光电子数量为n,若增大该入射光的强度,则( )A.E k增加,n增加B.E k增加,n不变C.E k不变,n不变D.E k不变,n增加第(2)题某学习小组设计了改变电容器极板间电压的电路,电压表可视为理想电表,下列电路中,电容器极板间电压变化范围较大的是( )A.B.C.D.第(3)题一个理想的自耦变压器左端通过定值电阻和电流表接交变电源,电源电压随时间变化的关系为,右端接入如图所示电路,、为定值电阻,为滑动变阻器,电压表和电流表均为理想交流电表。
,,的最大电阻也为,不计导线的电阻。
下列说法正确的是( )A.该自耦变压器属于升压变压器B.滑动变阻器的触头向上滑动时,电压表的示数减小C.当自耦变压器的可动端逆时针转动时,电流表的示数增大D.滑动变阻器的触头调至最上端,当电流表示数、电压表示数时,变压器原、副线圈的匝数比为第(4)题两端封闭、粗细均匀的玻璃管内,一段水银柱将内部的理想气体分隔成A、B两段,当玻璃管竖直静止时,A、B两段的长度相等,如图甲所示;仅将玻璃管旋转,再次平衡时,A、B两段的长度之比为1:2,如图乙所示。
下列说法正确的是()A.图甲中A、B两段气体的压强的比值为B.图甲中A、B两段气体的压强的比值为C.图乙中A、B两段气体的压强的比值为D.图乙中A、B两段气体的压强的比值为第(5)题理论认为,大质量恒星塌缩成黑洞的过程,受核反应的影响。
下列说法正确的是( )A.Y是粒子,射线穿透能力比射线强B.Y是粒子,射线电离能力比射线强C.Y是粒子,射线穿透能力比射线强D.Y是粒子,射线电离能力比射线强第(6)题如图所示,、、是竖直面内三根固定的光滑细杆,、、、位于同一圆周上,点为圆周的最高点,点为最低点。
2024届浙江省宁波市高三下学期高考选考适应性考试(二模)物理试题

2024届浙江省宁波市高三下学期高考选考适应性考试(二模)物理试题一、单项选择题:本题共8小题,每小题3分,共24分,在每小题给出的答案中,只有一个符合题目要求。
(共8题)第(1)题如图所示,两个不带电的导体A和B,用一对绝缘柱支持使它们彼此接触。
把用丝绸摩擦过的玻璃棒C置于A附近,贴在A、B下部的金属箔都张开,则( )A.此时A带正电,B带负电B.此时A电势低,B电势高C.移去C,贴在A、B下部的金属箔都闭合D.先把A和B分开,然后移去C,贴在A、B下部的金属箔都闭合第(2)题荡秋千深受孩子们的喜爱,如图为某同学荡秋千的场景,忽略空气阻力,该同学荡秋千时从由最低点O向最高点A摆的过程中( )A.重力做负功,重力势能减小B.重力的瞬时功率先增大后减小C.该同学受重力、绳子的拉力和向心力三个力作用D.该同学感觉到脚承受的力在增大第(3)题一列简谐横波在0时刻的波动图如图甲所示,传播方向上有平衡位置相距为10m的两个质点P、Q(图中未画出),质点P的振动图像如图乙所示,下列说法正确的是()A.该波的波长为5m B.该波的波速为2m/sC.6s时质点P沿y轴负方向振动D.6s时质点Q沿y轴负方向振动第(4)题医学治疗中常用放射性核素产生射线,而是由半衰期相对较长的衰变产生的。
对于质量为的,经过时间t后剩余的质量为m,其图线如图所示。
从图中可以得到的半衰期为( )A.B.C.D.第(5)题如图所示,质量为m的物体悬挂在轻质支架上,斜梁OB与竖直方向的夹角为θ,设横梁OA和斜梁OB作用于O点的弹力大小分别为F1和F2,以下结果正确的是( )A.B.C.D.第(6)题四川一大学生为备战2023年成都大运会跳高项目,在进行摸高跳训练时,为监测腿部肌肉力量的变化,某次运动员站在接有压力传感器的水平训练台上完成下蹲、起跳和回落动作,甲图中的小黑点表示人的重心,乙图是训练台所受压力随时间变化的图像,图中ab、bc、cd可视为直线。
浙江省宁波市五校高三5月适应性考试语文试题(Word版,含答案)

浙江省宁波市五校高三适应性考试语文一、语言文字运用(共24分,其中选择题每小题3分)1.下列词语中,加点字的注音全都正确的一项是()A.痤(cuó)疮嫉(jí)妒天台(tái)山硕果累累(léi)B.捧哏(gén)下载(zài)一会(huǐ)儿荦荦(luò)大端C.仍(réng)然侧(zhāi)歪压轴(zhòu)戏书声琅琅(lǎng)D.熬( āo)菜因为(wéi)刽(guì)子手忧心忡忡(chōng)2.下列各句中,没有错别字的一项是()A.“五一”假期接近尾声,很多人的“假日综合症”也逐渐呈现。
“放假比上班还累”!许多人感觉困倦、头昏,无精打采,严重的甚至身心乏力,精神不集中,并有头疼、疲劳、胃口不佳、失眠、瞌睡等种种不适。
B.艺术家罗恩·米勒通过翻译美国宇航局的“卡西尼”号和“信使”号等探测器获得的数据,带领我们进行一次太空之旅,一睹有待探险家前去探秘的最令人震惊的八大太阳系奇幻景观。
这些自然奇观的美丽程度,让地球上所有风景都暗淡无光。
C.汪国真的诗用明白畅晓的方式呈现了青年人的生活,更主要的是,传递了一种超然、豁达、飘逸、恬淡的人生态度。
这种人生态度,正是他的诗歌倍受年青读者欢迎的原因。
D.扪心自问,现今足坛的一线球员,你能叫出几个的名来?过往的世界杯真那么完美?如果放下矜持,不骗自己,相信你我都会坦承,我们能记住的精彩,无非是一些零星片断。
3.下列各句中,加点的词语运用正确的一项是()A.事实证明,只有以文化天下,为每一个人塑造更加富有弹性的心灵空间,社会才有可能在新的经济层面上建立新的人际关系。
B.技术是艺术生产的组成部分,艺术创作与传播从未离开技术的支持,而且,技术也从未扮演过艺术的主人,《史记》《红楼梦》等之所以成为经典,是因为其思想光芒与艺术魅力。
C.近一个多月来,股市节节上涨,投资者其喜洋洋,市场人气热得发烫。
宁波市高三五校适应性考试 (2).docx

2015年宁波市高三五校适应性考试数学(理科)说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。
注意:本卷考试时间120分钟,请考生将所有题目都做在答题卷上。
参考公式:球的表面积公式 柱体的体积公式S =4πR 2V =Sh 球的体积公式 其中S 表示柱体的底面积,h 表示柱体的高 V =34πR 3 台体的体积公式 其中R 表示球的半径 V =31h (S 1+21S S +S 2)锥体的体积公式 其中S 1, S 2分别表示台体的上、下底面积, V =31Sh h 表示台体的高 其中S 表示锥体的底面积,h 表示锥体的高选择题部分(40分)一、选择题(本大题共8小题,每小题5分,共40分.在每个小题给出的四个选项中只有一项是符合题目要求的)1. 已知命题“:p 0>∃x ,x x <ln ”,则p ⌝为( )A.0≤∃x ,ln x x ≥B.0>∀x ,ln x x ≥C.0≤∃x ,x x <lnD.0>∀x ,x x <ln2.已知互不相等的正数q p d c b a ,,,,,满足d b c a ,,,成等差数列,q b p a ,,,成等比数列,则( ) A.q d p c ><,B.q d p c >>,C.q d p c <>,D.q d p c <<,3. 已知直线b a ,,平面βα,,且α⊥a ,β⊂b ,则“b a ⊥”是“βα//”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件4.函数1211111(),(),,(),,()()n n f x f x f x x x f x x f x +===++L L 则函数2015()f x 是( ) A.奇函数但不是偶函数B.偶函数但不是奇函数C.既是奇函数又是偶函数D.既不是奇函数又不是偶函数5.已知不存在整数x 使不等式2(4)(4)0ax a x ---<成立,则实数a 的取值范围为( )A.(0,)+∞B. (0,2]C.[1,2]D.[1,4]6.已知某几何体的三视图(单位:cm ),如图所示,则此几何体的外接球的体积为( ) A. 392cm πB.336cm π侧视图正视图C.3643cm πD.39cm π7.已知过双曲线2222:1(0,0)x y C a b a b-=>>的中心的直线交双曲线于点,A B ,在双曲线C 上任取与点,A B 不重合的点P ,记直线,,PA PB AB 的斜率分别为12,,k k k ,若12k k k >恒成立,则离心率e 的取值范围为()A.1e <<B.1e <≤C. e >D.e ≥8. 设,x y 满足约束条件04312x y x x y ≥⎧⎪≥⎨⎪+≤⎩,则231x y x +++取值范围是()A .[1,5]B .[2,6]C .[3,11]D .[3,10]非选择题部分(110分)二、填空题(本大题共7小题,9~12小题每题6分,其它小题每题4分,共36分) 9. 已知直线012:1=-+y ax l ,直线03:2=-+by x l ,且1l 的倾斜角为4π,则a = ;若21l l ⊥,则b = ;若21//l l ,则两直线间的距离为 .10.太阳光的入射角(光线与地面所成的角)为6π,要使长为m 的木棒在地面上的影子最长,则木棒与地面所成的角应为 ,其最大影长为 . 11. 已知α为第二象限角,且1tan 41tan 3αα+=-,则tan()28απ+= ,sin()12πα+= .12.设函数2|1|1,0(),0x x f x x x x +-<⎧=⎨-+≥⎩,则((2))f f = ,函数(())y f f x =的零点个数为 .13.已知实数,x y 满足log 2log log 4a x x x a y ++=,其中常数1a >,当y 取最大值2时,对应的x 的值为 .14.已知抛物线24y x =过焦点F 的弦AB ,过弦AB 的中点作准线l 的垂线,垂足为M ,则MA MB⋅u u u r u u u r的值为 .15.已知函数()sin,2f x x π=任意的,t R ∈记函数()f x 在区间[],1t t +上的最大值为(),M t 最小值为()m t ,则函数()()()h t M t m t =-的值域为 .三、解答题(共5小题,共74分.解答时应写出必要的文字说明、证明过程或演算步骤) 16. (本小题满分15分)ABC ∆中,内角C B A ,,的对边分别为c b a ,,,且1)cos(32cos ++=C B A .(Ⅰ)求角A 的大小;(Ⅱ)若81cos cos -=C B ,且ABC ∆的面积为32,求a . 17. (本小题满分15分)如图,四边形ABCD 为平行四边形,5AB =,4,3AD BD ==,将BCD ∆沿着BD 翻折到平面1BC D 处(不与平面ABCD 重合),,E F 分别为对边1,AB C D 的中点,(Ⅰ)求证:EF BD ⊥;(Ⅱ)若异面直线1,EF BC 所成的角为30o,求二面角1C AB D --的平面角的正切值.18.(本小题满分15分)如图,已知椭圆2222:1(0)x y C a b a b +=>>的离心率12e =,右焦点为F ,右顶点为A ,P 为直线54x a =上的任意一点,且()2PF PA AF +⋅=u u u r u u u r u u u r . (Ⅰ)求椭圆C 的方程;(Ⅱ)若过点P 所作椭圆C 的切线l 与坐标轴不平行,切点为Q ,且交y 轴于点T ,试确定x 轴上是否存在定点M ,使得sin 2|cos |OTQ TQM ∠=∠.若存在,请求出点M 的坐标;若不存在,说明理由. 19. (本小题满分15分) 已知数列{}n a 满足2233312(1)4n n n a a a ++++=L ,n *∈N .(Ⅰ)求数列{}n a 的通项公式; (Ⅱ)证明:对任意的n N *∈,都有12331212342222nn a a a a na a a a a a a a ++++<----L . 20. (本小题满分14分)已知二次函数()2f x x bx c =++,其中常数,b c R ∈.(Ⅰ)若任意的[1,1]x ∈-,()0,(2)0f x f x ≥+≤,试求实数c 的取值范围; (Ⅱ)若对任意的[]12,1,1x x ∈-,有()()124f x f x -≤,试求实数b 的取值范围.(第18题图)第17题图CAB2015年五校高三适应性考试数学(理科)试题参考答案二、填空题:16. (Ⅰ)由1)cos(32cos ++=C B A 得,02cos 3cos 22=-+A A ,……………2分 即0)2)(cos 1cos 2(=+-A A ,所以,21cos =A 或2cos -=A (舍去) ……………4分 因为A 为三角形内角,所以3π=A .…………………6分(Ⅱ)由(Ⅰ)知21)cos(cos =+-=C B A , 则21sin sin cos cos -=-B A C B ; 由81cos cos -=C B ,得83sin sin =B A ,………………………9分 由正弦定理,有C cB b A a sin sin sin ==,即3sin 2B a b =,3sin 2C a c =,……………12分 由三角形的面积公式,得22833sin sin sin 21a C B a A bc S ===,即32832=a , 解得4=a .………………………15分17. 解法一:(Ⅰ)连结1CC ,并取1CC 的中点M ,连结,FM BM . 因为F 分别为1C D 的中点,所以,//FM DC 且12FM DC =; 因为四边形ABCD 为平行四边形,所以,//DC AB =;又E 分别为AB 的中点,所以,//FM EB =,即四边形FMBE 为平行四边形;………………………3分所以,//EF MB .因为5AB =,4,3AD BD ==,即222AD BD AB +=; 所以,BD AD ⊥,BD BC ⊥,1BD BC ⊥; 所以,BD ⊥平面1BCC .又因为BM ⊂平面1BCC ,所以BD BM ⊥,BD EF ⊥.………………………6分 (Ⅱ)取BC 的中点N ,过N 作线段AB 的垂线交AB 的延长线于点H .由(1)知,异面直线1,EF BC 所成的角为1C BM ∠ ,故130C BM ∠=o;因为1BC BC =,M 为1CC 的中点,所以, 160C BC ∠=o,即1C BC ∆为正三角形.所以1C N BC ⊥.………………………9分由(Ⅰ)知,异面直线1,EF BC 所成的角为1C BM ∠ ,故130C BM ∠=o;因为1BC BC =,M 为1CC 的中点,所以, 160C BC ∠=o,即1C BC ∆为正三角形.所以1C N BC ⊥.又BD ⊥平面1BCC ,所以,平面ABCD ⊥平面1BCC ;因为平面ABCD I 平面1BCC BC =,所以1C N ⊥平面ABCD ,1C N AB ⊥; 所以, 1C HN ∠为二面角1C AB D --的平面角. ………………………12分在1Rt C NH ∆中,12C N BC ==16sin 25BD NH NB NBH BC AB =⋅∠=⋅=,所以,11tan C N C HN NH ∠==,即二面角1C AB D --.………………………15分解法二:(Ⅰ)因为5AB =,4,3AD BD ==,即222AD BD AB +=; 所以,BD AD ⊥,BD BC ⊥,1BD BC ⊥; 所以,BD ⊥平面1BCC .………………………2分 以B 为原点,直线,BC BD 分别为x 轴、y 轴建立如图所示的空间直角坐标系. ………………………3分 则(4,0,0),(0,3,0),(4,3,0)C D A - ,设1(0,)CBC θπ∠=∈ ,则1(4cos ,0,4sin )C θθ,所以,中点33(2,,0),(2cos ,,2sin )22E F θθ-,所以,(2cos 2,0,2sin )EF θθ=+u u u r ,(0,3,0)BD =u u u r,所以,0EF BD ⋅=u u u r u u u r,即BD EF ⊥.………………………6分(Ⅱ) 因为异面直线1,EF BC 所成的角为30o,所以,11||||||cos 6EF BC EF BC π⋅=⋅⋅u u u r u u u u r u u u r u u u u r ,即88cos θ+=1cos 2θ=,3πθ=.即1C .…………8分设平面1C AB 的一个法向量(,,)m x y z =r,则100m AB m BC ⎧⋅=⎪⎨⋅=⎪⎩u u u r r u u u u r r,即43020x y x -=⎧⎪⎨+=⎪⎩,取4y =,则3,x z ==,即(3,4,m =r . ………………………11分又平面ABD 的一个法向量(0,0,1)n =r,………………………12分所以cos ,||||14m n m n m n ⋅===-r rr r r r,tan ,m n =r r 因为二面角1C AB D --为锐二面角,所以二面角1C AB D --的平面角的正切值为|tan ,|m n =r r .………………………15分18. (Ⅰ) 由题意,知右顶点(,0)A a ,设5(,)4P a m ,右焦点(,0)F c ,则2a c =,由()2PF PA AF +⋅=u u u r u u u r u u u r,得(23)()4c a c a --=,………………………2分 解得2,1a c ==,所以2223b a c =-=………………………4分EA所以椭圆C 的方程为22143x y +=. ………………………5分(注:取P 为特殊点求值,只能得4分)(Ⅱ)设切点0000(,),0Q x y x y ≠,切线方程为00()y y k x x -=-,与椭圆方程联立,得2220000(34)8()4()120k x k y kx x y kx ++-+--=有相等实根,所以,2220000[8()]4(34)[4()12]0k y kx k y kx ∆=--+--=,解得,034x k y =-, 又22003412x y +=,所以,切线方程为0034120x x y y +-=.………………………8分(注:用隐函数求导得切线方程同样得分)则切线与y 轴的交点03(0,)T y ,且原点O到切线的距离d =所以sin ||dOTQ OT ∠==.………………………11分若x 轴上存在定点(,0)M m 使sin 2|cos |OTQ TQM ∠=∠,由220000000033(,)(,),(,)4y x QT x x QM m x y y y -=-=-=--u u u r u u u ur 得,|||cos |||||QT QM TQM QT QM ⋅∠==⋅u u u r u u u u u ru u u r u u u u r 13分=对任意的0||(0,2)x ∈恒成立,化简,得21m =,1m =±.所以,x 轴上存在定点(1,0)M ±即椭圆C 的两焦点使sin 2|cos |OTQ TQM ∠=∠.………………………15分19. (Ⅰ)因为2233312(1)4n n n a a a ++++=L ,当1n =时,311a =,即11a =.………………………2分当2n ≥时,22333121(1)4n n n a a a --+++=L ,作差,得222233(1)(1)44n n n n n a n +-=-=, n a n =,………………………4分且11a =也满足此式;………………………5分(不检验,此步不得分) 所以,{}n a 的通项公式为n a n =.………………………6分(Ⅱ)由(Ⅰ)得22n n a nn a nna =--,因为12(1)2(21)2210n n n n n n n +-+=-+->-≥->, 所以,02n na na a >-,………………………8分又122(2)02(2)2n n n a n n n a n n n n n a ---=≤--,即122n n a n n a n a -≤-.………………………11分所以,123312112131112312322222222n n a a a a n n a a a a n a a a a ----++++≤++++----L L ,记11213111232222n nS ----=++++L , 由错位相减法,得211111122222n n n n S --=++++-L ,即22242n n S +⎛⎫=-< ⎪⎝⎭.………………………14分所以12331212342222n n a a a a na a a a a a a a ++++<----L .………………………15分20.(Ⅰ)因为11x -≤≤,则123x ≤+≤,由已知,有对任意的11x -≤≤,()0f x ≥恒成立,任意的13x ≤≤,()0f x ≤恒成立,故()10f ≥且(1)0f ≤,所以,(1)0f =,即1为函数()y f x =的一个零点.………………………2分因此可设()(1)()f x x x c =--.所以,任意的13x ≤≤,()0f x ≤恒成立,则[1,3][1,]c ⊆,………………………5分 即c 的取值范围为3c ≥………………………7分(Ⅱ)函数2()f x x bx c =++对12,[1,1]x x ∀∈-,有4|)()(|21≤-x f x f 恒成立, 即max min ()()4f x f x -≤,………………………8分记max min ()()f x f x M -=,则4M ≤. 当||12b->即||2b >时, |(1)(1)||2|4M f f b =--=>,与4M ≤矛盾; ………………………10分当||12b -≤即22b -≤≤时,max{(1),(1)}()2b M f f f =---2(1)(1)|(1)(1)|()(1)4222b f f f f bf +-+--=--=+≤,即22b -≤≤.………………………13分综上,c 的取值范围为22b -≤≤.………………………14分。
宁波市五校高三适应性考试题化学

2012年宁波市高三五校适应性考试化学测试本试题卷分选择题和非选择题两部分.全卷共12页,选择题部分1页至6页,非选择题部分6页至12页.满分300分,考试时间150分钟。
请考生按规定用笔将所有试题的答案涂、写在答题纸上.选择题部分(共120分)注意事项:1.答题前,考生务必将将自己的座位号、姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸相应的位置上。
2.每小题选出答案后,用2B铅笔把答题纸上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
不能答在试题卷上。
选择题部分共20小题,每小题6分,共120分。
可能用到的相对原子质量:H:1 C:12 O:16一、选择题(本题共17小题。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)7.下列叙述正确的是A.海水中蕴含的元素有80多种,其中Mg、Br、I在海水中的总储量分别约为1。
8×1015t、1×1014t、8×1010t。
由于海水中镁的储量很大,工业上常以海水为原料提取镁,因此,镁元素被成为“海洋元素"B.明胶是胶原的水解产物,和三聚氰胺(,俗称“蛋白精")一样都是蛋白质,但明胶可用于食品工业的添加剂,而三聚氰胺不可用于食品加工2NH3(g),增大氮气C.对于可逆反应N2(g)+3H2(g)催化剂高温高压浓度可增加活化分子百分数,从而使反应速率增大D.氨基酸是人体必需的营养物质,其晶体主要以内盐形式存在,不同的氨基酸从溶液中析出晶体的pH各不相同,利用这一差异,可以通过控制溶液的pH分离氨基酸8.下列有关实验的说法不正确的是A.在右图装置的稀硫酸中加入适量重铬酸钾或高锰酸钾晶体,可以使灯泡亮度增大,持续时间变长B. 金属材料电镀时,通常以待镀金属制品为阴极,以镀层金属为阳极,用含有镀层金属离子的溶液作电解质溶液C.用0.1mol/L的酸性KMnO4溶液配成的溶液滴定一定质量的草酸晶体(H2C2O4·nH2O)以测定其n值,若终点仰视读数,则n值偏大D.用移液管取液后,将移液管垂直放入稍倾斜的容器中,并使管尖与容器内壁接触,松开食指使溶液全部流出,数秒后,取出移液管9.已知X、Y、Z、W、R是原子序数依次增大的短周期主族元素,X是周期表中原子半径最小的元素,Y元素的最高正价与最低负价绝对值相等,Z的核电荷数是Y的2倍,W最外层电子数是最内层电子3倍.下列说法正确的是A.原子半径:R>W〉ZB.氢化物的热稳定性:W>RC.W与X、W与Z形成的化学键类型完全相同D.最高价氧化物对应的水化物酸性:W>Y10.有关下列化学用语正确的是A.盐酸和氢氧化钠溶液中和反应的热化学反应方程式:HCl (aq)+NaOH(aq)=NaCl (aq)+ H 2O(aq) △H=-57。
浙江省宁波市五校(奉化中学、宁波中学、北仑中学等)2020届高三适应性考试英语试题 含答案

浙江省宁波市2020届五校高三适应性考试英语试题1. 本试卷分第I 卷(选择题)和第 II 卷(非选择题)。
满分为 150 分,考试时间为 120 分钟。
2. 请用黑色签字笔将学校、班级、姓名、考号分别填写在答题卷和机读卡的相应位置上。
第Ⅰ卷(共 95 分)第一部分:听力(共两节,满分 30 分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节:(共 5 小题;每小题 1.5 分,满分 7.5 分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. How much did the man’s sister pay for her skirt?A. Sixty dollars.B. Fifty-six dollars.C. Twenty-eight dollars.2. Why did Paul take part in neither of Helen’s last two family parties?A. Because he doesn’t like her any more.B. Because Helen’s parents like him no more.C. Becaus e Helen doesn’t like him any more.3. What is the likely reason for their failure to make ends meet?A. They haven’t had their wages raised but the price keeps rising.B. They haven’t been promoted for a long time.C. They haven’t spent their money in a sm art way.4. What do we learn about the woman from the conversation?1A. She is black and blue all over.B. She has to see a doctor.C. She got hurt in an accident yesterday.5. What does the man think of the meals?A. Terrible.B. Satisfactory.C. Not delicious.第二节:(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年宁波市高三五校适应性考试数学(理科)说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。
注意:本卷考试时间120分钟,请考生将所有题目都做在答题卷上。
参考公式:球的表面积公式 柱体的体积公式S =4πR 2V =Sh 球的体积公式 其中S 表示柱体的底面积,h 表示柱体的高 V =34πR 3 台体的体积公式 其中R 表示球的半径 V =31h (S 1+21S S +S 2)锥体的体积公式 其中S 1,S 2分别表示台体的上、下底面积, V =31Sh h 表示台体的高 其中S 表示锥体的底面积,h 表示锥体的高选择题部分(40分)一、选择题(本大题共8小题,每小题5分,共40分.在每个小题给出的四个选项中只有一项是符合题目要求的)1.已知命题“:p 0>∃x ,x x <ln ”,则p ⌝为( )A.0≤∃x ,ln x x ≥B.0>∀x ,ln x x ≥C.0≤∃x ,x x <lnD.0>∀x ,x x <ln2.已知互不相等的正数q p d c b a ,,,,,满足d b c a ,,,成等差数列,q b p a ,,,成等比数列,则( ) A.q d p c ><,B.q d p c >>,C.q d p c <>,D.q d p c <<,3.已知直线b a ,,平面βα,,且α⊥a ,β⊂b ,则“b a ⊥”是“βα//”的( ) A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件4.函数1211111(),(),,(),,()()n n f x f x f x x x f x x f x +===++L L 则函数2015()f x 是( ) A.奇函数但不是偶函数B.偶函数但不是奇函数C.既是奇函数又是偶函数D.既不是奇函数又不是偶函数5.已知不存在整数x 使不等式2(4)(4)0ax a x ---<成立,则实数a 的取值范围为( )A.(0,)+∞B.(0,2]C.[1,2]D.[1,4]6.已知某几何体的三视图(单位:cm ),如图所示,则此几何体的外接球的体积为( )A.392cm πB.336cm π C.3643cm πD.39cm π7.已知过双曲线2222:1(0,0)x y C a b a b-=>>的中心的直线交双曲线于点,A B ,在双曲线C 上任取与点,A B 不重合的点P ,记直线,,PA PB AB 的斜率分别为12,,k k k ,若12k k k >恒成立,则离心率e 的取值范围为( )A.1e <<B.1e <≤C.e >D.e ≥8.设,x y 满足约束条件04312x y x x y ≥⎧⎪≥⎨⎪+≤⎩,则231x y x +++取值范围是()A .[1,5]B .[2,6]C .[3,11]D .[3,10]非选择题部分(110分)二、填空题(本大题共7小题,9~12小题每题6分,其它小题每题4分,共36分) 9.已知直线012:1=-+y ax l ,直线03:2=-+by x l ,且1l 的倾斜角为4π,则a = ;若21l l ⊥,则b = ;若21//l l ,则两直线间的距离为 .10.太阳光的入射角(光线与地面所成的角)为6π,要使长为m 的木棒在地面上的影子最长,则木棒与地面所成的角应为 ,其最大影长为.(第6题图)俯视图侧视图11.已知α为第二象限角,且1tan 41tan 3αα+=-,则tan()28απ+= ,sin()12πα+= .12.设函数2|1|1,0(),0x x f x x x x +-<⎧=⎨-+≥⎩,则((2))f f = ,函数(())y f f x =的零点个数为 .13.已知实数,x y 满足log 2log log 4a x x x a y ++=,其中常数1a >,当y 取最大值2时,对应的x 的值为 .14.已知抛物线24y x =过焦点F 的弦AB ,过弦AB 的中点作准线l 的垂线,垂足为M ,则MA MB⋅u u u r u u u r的值为 .15.已知函数()sin,2f x x π=任意的,t R ∈记函数()f x 在区间[],1t t +上的最大值为(),M t 最小值为()m t ,则函数()()()h t M t m t =-的值域为 .三、解答题(共5小题,共74分.解答时应写出必要的文字说明、证明过程或演算步骤) 16.(本小题满分15分)ABC ∆中,内角C B A ,,的对边分别为c b a ,,,且1)cos(32cos ++=C B A .(Ⅰ)求角A 的大小;(Ⅱ)若81cos cos -=C B ,且ABC ∆的面积为32,求a .17.(本小题满分15分)如图,四边形ABCD 为平行四边形,5AB =,4,3AD BD ==,将BCD ∆沿着BD 翻折到平面1BC D 处(不与平面ABCD 重合),,E F 分别为对边1,AB C D 的中点,(Ⅰ)求证:EF BD ⊥;(Ⅱ)若异面直线1,EF BC 所成的角为30o,求二面角1C AB D --的平面角的正切值.第17题图CA18.(本小题满分15分)如图,已知椭圆2222:1(0)x y C a b a b +=>>的离心率12e =,右焦点为F ,右顶点为A ,P 为直线54x a =上的任意一点,且()2PF PA AF +⋅=u u u r u u u r u u u r . (Ⅰ)求椭圆C 的方程;(Ⅱ)若过点P 所作椭圆C 的切线l 与坐标轴不平行,切点为Q ,且交y 轴于点T ,试确定x 轴上是否存在定点M ,使得sin 2|cos |OTQ TQM ∠=∠.若存在,请求出点M 的坐标;若不存在,说明理由.19.(本小题满分15分)已知数列{}n a 满足2233312(1)4n n n a a a ++++=L ,n *∈N .(Ⅰ)求数列{}n a 的通项公式; (Ⅱ)证明:对任意的n N *∈,都有12331212342222n n a a a a na a a a a a a a ++++<----L .20.(本小题满分14分)已知二次函数()2f x x bx c =++,其中常数,b c R ∈.(Ⅰ)若任意的[1,1]x ∈-,()0,(2)0f x f x ≥+≤,试求实数c 的取值范围; (Ⅱ)若对任意的[]12,1,1x x ∈-,有()()124f x f x -≤,试求实数b 的取值范围.(第18题图)2015年五校高三适应性考试数学(理科)试题参考答案一、选择题:16.(Ⅰ)由1)cos(32cos ++=C B A 得,02cos 3cos 22=-+A A ,……………2分 即0)2)(cos 1cos 2(=+-A A ,所以,21cos =A 或2cos -=A (舍去)……………4分 因为A 为三角形内角,所以3π=A .…………………6分(Ⅱ)由(Ⅰ)知21)cos(cos =+-=C B A , 则21sin sin cos cos -=-B A C B ; 由81cos cos -=C B ,得83sin sin =B A ,………………………9分 由正弦定理,有C cB b A a sin sin sin ==,即3sin 2B a b =,3sin 2C a c =,……………12分 由三角形的面积公式,得22833sin sin sin 21a C B a A bc S ===,即32832=a , 解得4=a .………………………15分17.解法一:(Ⅰ)连结1CC ,并取1CC 的中点M ,连结,FM BM . 因为F 分别为1C D 的中点,所以,//FM DC 且12FM DC =; 因为四边形ABCD 为平行四边形,所以,//DC AB =;又E 分别为AB 的中点,所以,//FM EB =,即四边形FMBE 为平行四边形;………………………3分所以,//EF MB .因为5AB =,4,3AD BD ==,即222AD BD AB +=; 所以,BD AD ⊥,BD BC ⊥,1BD BC ⊥; 所以,BD ⊥平面1BCC .又因为BM ⊂平面1BCC ,所以BD BM ⊥,BD EF ⊥.………………………6分 (Ⅱ)取BC 的中点N ,过N 作线段AB 的垂线交AB 的延长线于点H .由(1)知,异面直线1,EF BC 所成的角为1C BM ∠,故130C BM ∠=o;因为1BC BC =,M 为1CC 的中点,所以,160C BC ∠=o,即1C BC ∆为正三角形.所以1C N BC ⊥.………………………9分由(Ⅰ)知,异面直线1,EF BC 所成的角为1C BM ∠,故130C BM ∠=o;因为1BC BC =,M 为1CC 的中点,所以,160C BC ∠=o,即1C BC ∆为正三角形.所以1C N BC ⊥.又BD ⊥平面1BCC ,所以,平面ABCD ⊥平面1BCC ;因为平面ABCD I 平面1BCC BC =,所以1C N ⊥平面ABCD ,1C N AB ⊥; 所以,1C HN ∠为二面角1C AB D --的平面角.………………………12分在1Rt C NH ∆中,1C N ==16sin 25BD NH NB NBH BC AB =⋅∠=⋅=,所以,11tan 3C N C HN NH ∠==,即二面角1C AB D --的平面角的正切值为3.………………………15分解法二:(Ⅰ)因为5AB =,4,3AD BD ==,即222AD BD AB +=; 所以,BD AD ⊥,BD BC ⊥,1BD BC ⊥; 所以,BD ⊥平面1BCC .………………………2分 以B 为原点,直线,BC BD 分别为x 轴、y 轴建立如图所示的空间直角坐标系.………………………3分 则(4,0,0),(0,3,0),(4,3,0)C D A -,设1(0,)CBC θπ∠=∈,则1(4cos ,0,4sin )C θθ,所以,中点33(2,,0),(2cos ,,2sin )22E F θθ-,所以,(2cos 2,0,2sin )EF θθ=+u u u r ,(0,3,0)BD =u u u r,所以,0EF BD ⋅=u u u r u u u r,即BD EF ⊥.………………………6分(Ⅱ)因为异面直线1,EF BC 所成的角为30o,所以,11||||||cos 6EF BC EF BC π⋅=⋅⋅u u u r u u u u r u u u r u u u u r,即88cos θ+=1cos 2θ=,3πθ=.即1C .…………8分 设平面1C AB 的一个法向量(,,)m x y z =r,则100m AB m BC ⎧⋅=⎪⎨⋅=⎪⎩u u u r r u u u u r r,即43020x y x -=⎧⎪⎨+=⎪⎩,取4y =,则3,x z ==,即(3,4,m =r . ………………………11分又平面ABD 的一个法向量(0,0,1)n =r,………………………12分所以cos ,||||m n m n m n ⋅===r rr r r r,tan ,3m n =-r r , 因为二面角1C AB D --为锐二面角,所以二面角1C AB D --的平面角的正切值为|tan ,|3m n =r r .………………………15分18.(Ⅰ)由题意,知右顶点(,0)A a ,设5(,)4P a m ,右焦点(,0)F c ,则2a c =,由()2PF PA AF +⋅=u u u r u u u r u u u r,得(23)()4c a c a --=,………………………2分EA解得2,1a c ==,所以2223b a c =-=………………………4分所以椭圆C 的方程为22143x y +=. ………………………5分(注:取P 为特殊点求值,只能得4分)(Ⅱ)设切点0000(,),0Q x y x y ≠,切线方程为00()y y k x x -=-,与椭圆方程联立,得2220000(34)8()4()120k x k y kx x y kx ++-+--=有相等实根,所以,2220000[8()]4(34)[4()12]0k y kx k y kx ∆=--+--=,解得,034x k y =-, 又22003412x y +=,所以,切线方程为0034120x x y y +-=.………………………8分(注:用隐函数求导得切线方程同样得分)则切线与y 轴的交点03(0,)T y ,且原点O到切线的距离d =所以sin ||dOTQ OT ∠==.………………………11分若x 轴上存在定点(,0)M m 使sin 2|cos |OTQ TQM ∠=∠,由220000000033(,)(,),(,)4y x QT x x QM m x y y y -=-=-=--u u u r u u u ur 得,|||cos |||||QT QM TQM QT QM ⋅∠==⋅u u u r u u u u u ru u u r u u u u r 13分=对任意的0||(0,2)x ∈恒成立,化简,得21m =,1m =±.所以,x 轴上存在定点(1,0)M ±即椭圆C 的两焦点使sin 2|cos |OTQ TQM ∠=∠.………………………15分19.(Ⅰ)因为2233312(1)4n n n a a a ++++=L ,当1n =时,311a =,即11a =. ………………………2分当2n ≥时,22333121(1)4n n n a a a --+++=L ,作差,得222233(1)(1)44n n n n n a n +-=-=, n a n =,………………………4分且11a =也满足此式;………………………5分(不检验,此步不得分) 所以,{}n a 的通项公式为n a n =.………………………6分(Ⅱ)由(Ⅰ)得22n n a nn a nna =--,因为12(1)2(21)2210n n n n n n n +-+=-+->-≥->, 所以,02nna na a >-,………………………8分又122(2)02(2)2n n n a n n n a n n n n n a ---=≤--,即122n n a n n a n a -≤-.………………………11分所以,123312112131112312322222222n n a a a a n na a a a n a a a a ----++++≤++++----L L , 记11213111232222n nS ----=++++L , 由错位相减法,得211111122222n n n n S --=++++-L ,即22242n n S +⎛⎫=-< ⎪⎝⎭.………………………14分所以12331212342222n n a a a a na a a a a a a a ++++<----L .………………………15分20.(Ⅰ)因为11x -≤≤,则123x ≤+≤,由已知,有对任意的11x -≤≤,()0f x ≥恒成立,任意的13x ≤≤,()0f x ≤恒成立,故()10f ≥且(1)0f ≤,所以,(1)0f =,即1为函数()y f x =的一个零点.………………………2分因此可设()(1)()f x x x c =--.所以,任意的13x ≤≤,()0f x ≤恒成立,则[1,3][1,]c ⊆,………………………5分-------------------------------------------------------------------奋斗没有终点任何时候都是一个起点-----------------------------------------------------信达 即c 的取值范围为3c ≥………………………7分 (Ⅱ)函数2()f x x bx c =++对12,[1,1]x x ∀∈-,有4|)()(|21≤-x f x f 恒成立,即max min ()()4f x f x -≤,………………………8分记max min ()()f x f x M -=,则4M ≤. 当||12b ->即||2b >时,|(1)(1)||2|4M f f b =--=>,与4M ≤矛盾; ………………………10分 当||12b -≤即22b -≤≤时,max{(1),(1)}()2b M f f f =--- 2(1)(1)|(1)(1)|()(1)4222b f f f f b f +-+--=--=+≤,即22b -≤≤. ………………………13分 综上,c 的取值范围为22b -≤≤. ………………………14分。
