2018年秋九年级数学上册 1.2 二次函数的图象(第3课时)同步测试 (新版)浙教版
【初中数学】2018秋季学期最新人教版初中数学九年级上册精品习题:《二次函数的图象和性质》同步测试3

(8)当x取何值时,函数y有最值?其最值是多少?
(9)当y取何值时,-4<x<0;
(10)求函数图象与两坐标轴交点所围成的三角形面积.
综合、运用、诊断
一、填空题
13.已知抛物线y=ax2+bx+c(a≠0).
(1)若抛物线的顶点是原点,则____________;
24.二次函数y=mx2+2mx-(3-m)的图象如下图所示,那么m的取值范围是( )
A.m>0B.m>3
C.m<0D.0<m<3
25.在同一坐标系内,函数y=kx2和y=kx-2(k≠0)的图象大致如图( )
26.函数(ab<0)的图象在下列四个示意图中,可能正确的是( )
三、解答题
27.已知抛物线y=x2-3kx+2k+4.
(9)-8≤y<10;
(10)S△=12.
13.(1)b=c=0;(2)c=0;(3)b=0;(4)b2-4ac=0.
14.原. 15.2,y=2x2-3x. 16.4.
17.-1. 18.1. 19.一、二、三.
20.C. 21.B. 22.D. 23.B. 24.C. 25.B. 26.C.
27.(1)k=0;(2)k=-2.
——教学资料参考参考范本——
【初中数学】2018秋季学期最新人教版初中数学九年级上册精品习题:《二次函数的图象和性质》同步测试3
______年______月______日
____________________部门
课堂学习检测
一、填空题
1.把二次函数y=ax2+bx+c(a≠0)配方成y=a(x-h)2+k形式为______,顶点坐标是______,对称轴是直线______.当x=______时,y最值=______;当a<0时,x______时,y随x增大而减小;x______时,y随x增大而增大.
九年级数学上册1.2_1.3二次函数的图象及其性质同步练习(新版)浙教版【含解析】

1.2-1.3 二次函数的图象及其性质一、选择题(共10小题;共50分)1. 抛物线y=x2−4x−7的顶点坐标是 ( )A. (2,−11)B. (−2,7)C. (2,11)D. (2,−3)2. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是 ( )A. c>−1B. b>0C. 2a+b≠0D. 9a2+c>3b3. 在平面直角坐标系中,将抛物线y=x2−x−6向上(下)或向左(右)平移m个单位,使平移后的抛物线恰好经过原点,则∣m∣的最小值为 ( )A. 1B. 2C. 3D. 64. 将抛物线C:y=x2+3x−10,将抛物线C平移到Cʹ.若两条抛物线C,Cʹ关于直线x=1对称,则下列平移方法中正确的是 ( )个单位A. 将抛物线C向右平移52B. 将抛物线C向右平移3个单位C. 将抛物线C向右平移5个单位D. 将抛物线C向右平移6个单位5. 把抛物线y=x2+bx+c的图象先向右平移3个单位,再向下平移3个单位,所得图象的函数解析式为y=(x−1)2−4,则b,c的值为( )A. b=2,c=−3B. b=4,c=3C. b=−6,c=8D. b=4,c=−76. 已知两点A(−5,y1),B(3,y2)均在抛物线y=ax2+bx+c(a≠0)上,点C(x0,y0)是该抛物线的顶点,若y1>y2≥y0,则x0的取值范围是 ( )A. x0>−5B. x0>−1C. −5<x0<−1D. −2<x0<37. 已知二次函数y=x2+3x−10的图象为抛物线C,将抛物线C平移得到新的二次函数图象Cʹ.如果两个二次函数的图象C、Cʹ关于直线x=1对称,则下列平移方法中,正确的是 ( )个单位 B. 将抛物线C向右平移3个单位A. 将抛物线C向右平移52C. 将抛物线C向右平移5个单位D. 将抛物线C向右平移6个单位8. 下列关于二次函数y=ax2−2ax+1(a>1)的图象与x轴交点的判断,正确的是 ( )A. 没有交点B. 只有一个交点,且它位于y轴右侧C. 有两个交点,且它们均位于y轴左侧D. 有两个交点,且它们均位于y轴右侧9. 根据下表中的二次函数y=ax2+bx+c的自变量x与函数y的对应值,可判断该二次函数的图象与x轴 ( )A. 只有一个交点B. 有两个交点,且它们分别在y轴两侧C. 有两个交点,且它们均在y轴同侧D. 无交点10. 如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.如果抛物线经过图中的三个格点,那么以这三个格点为顶点的三角形称为该抛物线的"内接格点三角形".设对称轴平行于y轴的抛物线与网格对角线OM的两个交点为A,B,其顶点为C,如果△ABC是该抛物线的内接格点三角形,AB=3√2,且点A,B,C的横坐标x A,x B,x C满足x A<x C<x B,那么符合上述条件的抛物线条数是 ( )A. 7B. 8C. 14D. 16二、填空题(共10小题;共50分)11. 将抛物线y=3(x−4)2+2向右平移1个单位长度,再向下平移3个单位长度,平移后抛物线的解析式是.12. 二次函数y=x2+2x−5的对称轴是,顶点坐标是.13. 把抛物线y=x2先向右平移2个单位,再向上平移3个单位,平移后抛物线的表达式是.14. 关于x的一元二次方程ax2−3x−1=0的两个不相等的实数根都在−1和0之间(不包括−1和0),则a的取值范围是.15. 统计学规定:某次测量得到n个结果x1,x2,⋯,x n.当函数y=(x−x1)2+(x−x2)2+⋯+(x−x n)2取最小值时,对应x的值称为这次测量的“最佳近似值”.若某次测量得到5个结果9.8,10.1,10.5,10.3,9.8.则这次测量的“最佳近似值”为.16. 如图,一段抛物线:y=−x(x−2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180∘得到C2,交x轴于A2;将C2绕A2旋转180∘得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m=.17. 抛物线y=2x2−4x+3绕坐标原点旋转180∘所得的抛物线的解析式是.18. 已知点A(4,y1),B(√2,y2),C(−2,y3)都在二次函数y=(x−2)2−1的图象上,则y1,y2,y3的大小关系是.,0),有下列结论:19. 如图,抛物线y=ax2+bx+c的对称轴是x=−1,且过点(12① abc>0;② a−2b+4c=0;③ 25a−10b+4c=0;④ 3b+2c>0;⑤ a−b≥m(am−b).其中所有正确的结论.(填写正确结论的序号)20. 如图所示,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3,⋯,A n.将抛物线y=x2沿直线l:y=x向上平移,得一系列抛物线,且满足下列条件:①抛物线的顶点M1,M2,M3,⋯,M n都在直线l:y=x上;②抛物线依次经过点A1,A2,A3,⋯,A n,则顶点M2014的坐标为.三、解答题(共5小题;共65分)21. 已知抛物线C:y=−x2+bx+c经过A(−3,0)和B(0,3)两点.将这条抛物线的顶点记为M,它的对称轴于x轴的交点记为N.Ⅰ求抛物线C的表达式;Ⅱ求点M的坐标;Ⅲ将抛物线C平移到Cʹ,抛物线Cʹ的顶点记为Mʹ,它的对称轴于x轴的交点记为Nʹ.如果以点M、N、Mʹ、Nʹ为顶点的四边形是面积为16的平行四边形,那么应将抛物线C 怎样平移?为什么?22. 设函数y=(x−1)[(k−1)x+(k−3)](k是常数).Ⅰ当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k取0时函数的图象;Ⅱ根据图象,写出你发现的一条结论;Ⅲ将函数y2的图象向左平移4个单位,再向下平移2个单位,得到函数y3的图象,求函数y3的最小值.23. 如图,抛物线y1=−x2+2向右平移1个单位得到抛物线y2,回答下列问题:Ⅰ抛物线y2的顶点坐标;Ⅱ阴影部分的面积S = ;Ⅲ若再将抛物线y2绕原点O旋转180∘得到抛物线y3,求抛物线y3的解析式.24. 已知二次函数y=x2+2x+m的图象C1与x轴有且只有一个公共点.Ⅰ求C1的顶点坐标;Ⅱ将C1向下平移若干个单位后,得抛物线C2,如果C2与x轴的一个交点为A(−3,0),求C2的函数关系式,并求C2与x轴的另一个交点坐标;Ⅲ若P(n,y1),Q(2,y2)是C1上的两点,且y1>y2.直接写出实数n的取值范围.25. 已知抛物线C1:y=ax2+bx+c(x≤4)经过原点和点A(4,0),顶点为点C,将抛物线C1绕点A旋转180∘得到抛物线C2,顶点为点D,与x轴的另一个交点为点B.Ⅰ直接写出点B的坐标;Ⅱ求C,D两点的坐标(用含a的代数式表示);Ⅲ当四边形OCBD为矩形时,求a的值.答案第一部分1. A2. D3. B4. C5. B6. B7. C8. D9. B10. C第二部分11. y =3(x −5)2−1 或 y =3x 2−30x +74(写出任何一种形式均可)12. 直线 x =−1;(−1,−6)13. y =(x −2)2+314. −94<a <−2 15. 10.116. −117. −2x 2−4x −318. y 3>y 1>y 219. ①③⑤20. (4027,4027)第三部分21. (1) ∵ 抛物线 y =−x 2+bx +c 经过 A (−3,0) 和 B (0,3) 两点,∴ {−9−3b +c =0,c =3,解得 {b =−2,c =3.故此抛物线的解析式为:y =−x 2−2x +3.(2) ∵ 由(1)知抛物线的解析式:y =−x 2−2x +3,∴ 当 x =−b 2a =−−22×(−1)=−1 时,y =4,∴ M (−1,4).(3) 由题意得,以点 M 、 N 、 Mʹ 、 Nʹ 为顶点的平行四边形的边 MN 的对边只能是 MʹNʹ, ∴ MN ∥MʹNʹ,且 MN =MʹNʹ.∴ MN ⋅MʹNʹ=16,∴ NNʹ=4.(i)当M、N、Mʹ、Nʹ为顶点的平行四边形是四边形MNNʹMʹ时,将抛物线C向左或向右平移4个单位可得符合条件的抛物线Cʹ;(ii)当M、N、Mʹ、Nʹ为顶点的平行四边形是四边形MNMʹNʹ时,将抛物线C先向左或向右平移4个单位,在向下平移8个单位,可得符合条件的抛物线Cʹ.∴上述的四种平移,均可得到符合条件的抛物线Cʹ.22. (1)作图如图.(2)函数y=(x−1)[(k−1)x+(k−3)](k是常数)的图象都经过点(1,0).(答案不唯一)(3)∵y2=(x−1)2,∴将函数y2的图象向左平移4个单位,再向下平移2个单位,得到函数y3为y3=(x+3)2−2.∴当x=−3时,函数y3的最小值为−2.23. (1)(1,2)(2)2(3)抛物线y1=−x2+2向右平移1个单位得到y2=−(x−1)2+2=−x2+2x+1,再关于原点旋转180∘得到y3=x2+2x−1.24. (1)y=x2+2x+m=(x+1)2+m−1,对称轴为x=−1.∵与x轴有且只有一个公共点,∴顶点的纵坐标为0.∴C1的顶点坐标为(−1,0).(2)设C2的函数关系式为y=(x+1)2+k.把A(−3,0)代入上式得(−3+1)2+k=0,解得k=−4,∴C2的函数关系式为y=(x+1)2−4.∵抛物线的对称轴为x=−1,与x轴的一个交点为A(−3,0),由对称性可知,它与x轴的另一个交点坐标为(1,0).(3)n>2或n<−4.25. (1)点B的坐标为(8,0).(2)C1:y=ax(x−4)=a(x−2)2−4a,得C(2,−4a).C2:y=−a(x−4)(x−8)=−a(x−6)2+4a,得D(6,4a).(3)由抛物线的对称性得CO=CA.当四边形OCBD为矩形时,AO=AC,所以CO=CA=OA,即△OAC是等边三角形.所以∣y C∣=√32OA=2√3,即4a=±2√3,a=±√32.。
2018-2019学年最新人教版九年级数学上册:二次函数同步测试及解析-精品试题

22.1.1二次函数预习要点:1.一般地,形如的函数,叫做二次函数.其中, 是自变量, 分别是函数解析式的二次项系数、一次项系数和常数项.2.(2016春•衡阳县期中)下面的函数是二次函数的是( )A .y=3x+1B .y=x 2+2xC .y =x 2D .y =2x3.函数y=ax 2+bx+c (a ,b ,c 是常数)是二次函数的条件是( )A .a ≠0,b ≠0,c ≠0B .a <0,b ≠0,c ≠0C .a >0,b ≠0,c ≠0D .a ≠04.长方形的周长为24cm ,其中一边为xcm (其中x >0),面积为ycm 2,则这样的长方形中y 与x 的关系可以写为( )A .y=x 2B .y=12−x 2C .y=(12−x )xD .y=2(12−x )5.某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映,如果调整商品售价,每降价1元,每星期可多卖出20件.设每件商品降价x 元后,每星期售出商品的总销售额为y 元,则y 与x 的关系式为( )A .y=60(300+20x )B .y=(60−x )(300+20x )C .y=300(60−20x )D .y=(60−x )(300−20x )6.如果函数y=(a−1)x2是二次函数,那么a的取值范围是.7.(2016•银川校级一模)当m= 时,函数y=(m+1)x m2+1是二次函数.8.某企业今年第一月新产品的研发资金为100万元,以后每月新产品的研发资金与上月相比增长率都是x,则该厂今年第三月新产品的研发资金y(元)关于x的函数关系式为y= .同步小题12道一.选择题1.(2016•松江区一模)下列函数中,属于二次函数的是()A.y=2x+1 B.y=(x−1)2−x2C.y=2x2−7 D.y=−1 x22.已知二次函数y=1−3x+5x2,则其二次项系数a,一次项系数b,常数项c分别是()A.a=1,b=−3,c=5 B.a=1,b=3,c=5C.a=5,b=3,c=1 D.a=5,b=−3,c=13.若y=mx2+nx−p(其中m,n,p是常数)为二次函数,则()A.m,n,p均不为0 B.m≠0,且n≠0C.m≠0 D.m≠0,或p≠04.已知y=(m−2)x|m|+2是y关于x的二次函数,那么m的值为()A.−2 B.2 C.±2 D.05.已知矩形的周长为36m,矩形绕着它的一条边旋转形成一个圆柱,设矩形的一条边长为xm,圆柱的侧面积为ym2,则y与x的函数关系式为()A.y=−2πx2+18πx B.y=2πx2−18πxC.y=−2πx2+36πx D.y=2πx2−36πx6.n个球队进行单循环比赛(参加比赛的任何一只球队都与其他所有的球队各赛一场),总的比赛场数为y,则有()A.y=2n B.y=n2C.y=n(n−1)D.y=12n(n−1)二.填空题7.(2016•普陀区一模)在函数①y=ax2+bx+c,②y=(x−1)2−x2,③y=5x2−5x2,④y=−x2+2中,y关于x的二次函数是.(填写序号)8.已知y=(m+2)x m2−2是二次函数,则m= .9.如图,一农户要建一个矩形猪舍,猪舍的一边利用住房墙,另外三边用25m长的建筑材料围成,为方便进出,在CD边上留一个1m宽的门,若设AB为y(m),BC为x(m),则y与x之间的函数关系式为.10.某种产品原来的售价为150元,经过两次降价后售价为y元,如果两次降价的平均降价率为x,则y与x的函数关系是.三.解答题11.已知函数y=(m2−m)x2+(m−1)x+m+1.(1)若这个函数是一次函数,求m的值;(2)若这个函数是二次函数,则m的值应怎样?12.某商品每件成本40元,以单价55元试销,每天可售出100件.根据市场预测,定价每减少1元,销售量可增加10件.求每天销售该商品获利金额y(元)与定价x(元)之间的函数关系.答案:预习要点:1.y=ax2+bx+c(a,b,c是常数,a≠0)xa,b,c2.【分析】根据二次函数的定义:一般地,形如y=ax2+bx+c(a、b、c是常数,a≠0)的函数,判断各选项即可.【解答】解:A、y=3x+1,二次项系数为0,故本选项错误;B、y=x2+2x,符合二次函数的定义,故本选项正确;C、y=x2,二次项系数为0,故本选项错误;D、y=2x,是反比例函数,故本选项错误.故选B3.【解答】解:根据二次函数定义中对常数a,b,c的要求,只要a≠0,b,c可以是任意实数.故选D4.【分析】先得到长方形的另一边长,那么面积=一边长×另一边长.【解答】解:∵长方形的周长为24cm,其中一边为x(其中x>0),∴长方形的另一边长为12−x,∴y=(12−x)x.故选C5.【分析】根据降价x元,则售价为(60−x)元,销售量为(300+20x)件,由题意可得等量关系:总销售额为y=销量×售价,根据等量关系列出函数解析式即可.6.【分析】根据二次函数的定义列出不等式求解即可.【解答】解:由y=(a−1)x2是二次函数,得a−1≠0.解得a≠1,即a>1或a<1,答案:a>1或a<1.7.【分析】根据二次函数的定义列式计算即可得解.【解答】解:根据题意得:m2+1=2且m+1≠0,解得m=±1且m≠−1,所以m=1.答案:1.8.【分析】由一月份新产品的研发资金为100万元,根据题意可以得到2月份研发资金为100(1+x)万元,而三月份在2月份的基础上又增长了x,那么三月份的研发资金也可以用x表示出来,由此即可确定函数关系式.【解答】解:∵一月份新产品的研发资金为100万元,2月份起,每月新产品的研发资金与上月相比增长率都是x,∴2月份研发资金为100(1+x),∴三月份的研发资金为y=100(1+x)×(1+x)=100(1+x)2.答案:100(1+x)2.同步小题12道1.【分析】根据一次函数、反比例函数、二次函数的定义判断各选项即可得出答案.【解答】解:A、是一次函数,故本选项错误;B、整理后是一次函数,故本选项错误;C、y=2x2−7是二次函数,故本选项正确;D、y与x2是反比例函数关系,故本选项错误.故选:C2.【解答】解:∵函数y=1−3x+5x2是二次函数,∴a=5,b=−3,c=1.故选D3.【解答】解:根据题意得当m ≠0时,y=mx 2+nx −p (其中m ,n ,p 是常数)为二次函数. 故选C4.【分析】根据形如y=ax 2+bx+c (a ≠0)是二次函数,可得答案.【解答】解:由y=(m −2)x |m|+2是y 关于x 的二次函数,得|m|=2且m −2≠0.解得m=−2.故选A .5.【分析】先根据矩形周长求出矩形另一边长,根据圆柱体侧面积=底面周长×高,列出函数关系式即可.【解答】解:根据题意,矩形的一条边长为xcm ,则另一边长为:(36−2x )÷2=18−x (cm ),则圆柱体的侧面积y=2πx (18−x )=−2πx 2+36πx .故选C6.【分析】根据n 支球队举行比赛,若每个球队与其他队比赛(n −1)场,则两队之间比赛两场,由于是单循环比赛,则共比赛12 n (n −1),由此得出函数关系式即可. 【解答】解:n 支球队举行单循环比赛,比赛的总场数为:y=12n (n −1). 故选:D7.【分析】根据形如y=ax 2+bx+c (a ≠0)是二次函数,可得答案.【解答】解:①a=0时y=ax 2+bx+c 是一次函数,②y=(x −1)2−x 2是一次函数;③y=5x 2−5x 2 不是整式,不是二次函数;④y=−x 2+2是二次函数.答案:④8.【分析】根据二次函数的定义得出m+2≠0,m 2−2=2,求出即可.【解答】解:∵y =(m+2)x m2−2是二次函数,∴m+2≠0,m 2−2=2,解得:m=2, 答案:2.9.【分析】设AB 为y (m ),BC 为x (m ),根据AB+BC+CD −1=25列出方程即可.【解答】解:设AB 为y (m ),BC 为x (m ),根据题意得y+x+y −1=25,整理得y=13−12 x .答案:y=13−12 x .10.【分析】原来的售价为150元,第一次降价后的价格是150×(1−x )元,第二次降价是在第一次降价后的价格的基础上降价的为:150×(1−x )×(1−x )=150(1−x )2元,则函数解析式即可求得.【解答】解:设两次降价的平均降价率为x ,根据题意可得:y 与x 之间的函数关系为:y=150(1−x )2.答案:y=150(1−x )2.11.解:(1)根据一次函数的定义,得:m 2−m=0解得m=0或m=1又∵m−1≠0即m≠1;∴当m=0时,这个函数是一次函数;(2)根据二次函数的定义,得:m2−m≠0解得m1≠0,m2≠1∴当m1≠0,m2≠1时,这个函数是二次函数.12.【分析】首先根据题意得出当定价为x元时,每件降价(55−x)元,此时销售量为[100+10(55−x)]件,根据利润=销售量×(单价−成本),列出函数关系式即可.解:由题意得,商品每件定价x元时,每件降价(55−x)元,销售量为[100+10(55−x)]件,则y=[100+10(55−x)](x−40)=−10x2+1050x−26000,即每天销售该商品获利金额y(元)与定价x(元)之间的函数关系式为y=−10x2+1050x−26000.。
浙教版九年级上1.2二次函数的图象(3)同步练习含答案

1.2 二次函数的图象(三)1.抛物线y =2x 2-5x +6的对称轴是(A ) A. 直线x =54 B. 直线x =52C. 直线x =-54D. 直线x =-522.将二次函数y =x 2-2x +3化为y =(x -m )2+k 的形式,结果为(D ) A. y =(x +1)2+4 B. y =(x +1)2+2 C. y =(x -1)2+4 D. y =(x -1)2+23.二次函数y =-2x 2+4x -9的图象的最高点的纵坐标是(B ) A. 7 B. -7 C. 9 D. -94.已知二次函数y =ax 2+bx +c(a ≠0)的图象如图所示,则下列结论中正确的是(C )(第4题)A. a >0B. c <0C. x =3是方程ax 2+bx +c =0的一个根D. ab c>05.二次函数y =ax 2+bx +c(a ,b ,c 为常数且a ≠0)的图象如图所示,则一次函数y=ax +b 与反比例函数y =cx 的图象可能是(C )(第5题)6.已知抛物线y =ax 2+x +2经过点(-1,0). (1)求a 的值,并写出这条抛物线的顶点坐标.(2)若点P (t ,t )在抛物线上,则点P 叫做抛物线上的不动点,求出这个抛物线上所有不动点的坐标.【解】 (1)把点(-1,0)的坐标代入y =ax 2+x +2中,得a =-1.∴此抛物线的函数表达式为y =-x 2+x +2=-⎝⎛⎭⎫x -122+94,其顶点坐标是⎝⎛⎭⎫12,94.(2)把点P (t ,t )的坐标代入y =-x 2+x +2中, 得t =-t 2+t +2,解得t 1=2,t 2=- 2.∴此抛物线上的不动点有两个,即点P 1(2,2),P 2(-2,-2).7.在平面直角坐标系中,把一条抛物线先向上平移3个单位,然后绕原点旋转180°得到抛物线y =x 2+5x +6,则原抛物线的函数表达式是(A )A. y =-⎝⎛⎭⎫x -522-114B. y =-⎝⎛⎭⎫x +522- 114C. y =-⎝⎛⎭⎫x -522-14D. y =-⎝⎛⎭⎫x +522+14【解】 用倒推法做.∵y =x 2+5x +6=⎝⎛⎭⎫x +522-14,∴它的顶点坐标为⎝⎛⎭⎫-52,-14.把该抛物线绕原点旋转180°,顶点坐标变为⎝⎛⎭⎫52,14,且开口向下,函数表达式变为y =-⎝⎛⎭⎫x -522+14.再把它向下平移3个单位,得到y =-⎝⎛⎭⎫x -522-114.8.如图,二次函数y =ax 2+bx +c (a >0)的图象的顶点为D ,其图象与x 轴的交点A ,B 的横坐标分别为-1和3,则下列结论正确的是(D )(第8题)A. 2a -b =0B. a +b +c >0C. 3a -c =0D. 当a =12时,△ABD 是等腰直角三角形【解】 ∵抛物线与x 轴的交点A ,B 的横坐标分别为-1,3,∴抛物线的对称轴为直线x =1,即-b2a =1,∴2a +b =0,故A 错误.当x =1时,y <0,即a +b +c <0,故B 错误. ∵点A 的坐标为(-1,0),∴a -b +c =0. 又∵b =-2a ,∴a +2a +c =0, 即3a +c =0,故C 错误. ∵当a =12时,b =-1,c =-32, ∴抛物线的函数表达式为y =12x 2-x -32.把x =1代入,得y =12-1-32=-2,∴点D 的坐标为(1,-2).设对称轴x =1与x 轴的交点为E ,如解图,(第8题解)则AE =2,BE =2,DE =2,∴△ADE 和△BDE 都是等腰直角三角形, ∴∠DAE =∠DBE =45°,∴△ABD 是等腰直角三角形,故D 正确.9.如图,二次函数y =ax 2+bx 的图象经过点A (2,4),B (6,0). (1)求a ,b 的值.(2)若C 是该二次函数图象上A ,B 两点之间的一动点,横坐标为x (2<x <6),请写出四边形OACB 的面积S 最新点C 的横坐标x 的函数表达式,并求S 的最大值.(第9题)【解】 (1)将点A (2,4),B (6,0)的坐标分别代入y =ax 2+bx , 得⎩⎨⎧4a +2b =4,36a +6b =0,解得⎩⎪⎨⎪⎧a =-12,b =3.(2)如解图,过点A 作x 轴的垂线,垂足为D (2,0),过点C 作CE ⊥AD ,CF ⊥x 轴,垂足分别为E ,F ,连结AC ,BC ,C D.(第9题解)则S △OAD =12OD ·AD =12×2×4=4, S △ACD =12AD ·CE =12×4×(x -2)=2x -4,S △BCD =12BD ·CF =12×(6-2)×⎝⎛⎭⎫-12x 2+3x =-x 2+6x , ∴S =S △OAD +S △ACD +S △BCD =4+2x -4-x 2+6x =-x 2+8x , ∴S 最新x 的函数表达式为S =-x 2+8x (2<x <6). ∵S =-x 2+8x =-(x -4)2+16,∴当x =4时,四边形OACB 的面积S 有最大值,最大值为16.10.如图,已知抛物线y =ax 2+bx +c(a ≠0)的对称轴为直线x =-1,且抛物线经过A (1,0),C (0,3)两点,与x 轴交于点B.(1)若直线y =mx +n 经过B ,C 两点,求直线BC 和抛物线的函数表达式. (2)在抛物线的对称轴直线x =-1上找一点M ,使点M 到点A 的距离与到点C 的距离之和最小,求出点M 的坐标.(3)设P 为抛物线的对称轴x =-1上的一个动点,求使△BPC 为直角三角形的点P 的坐标.(第10题)【解】(1)由题意,得⎩⎪⎨⎪⎧-b2a =-1,a +b +c =0,c =3,解得⎩⎨⎧a =-1,b =-2,c =3.∴抛物线的函数表达式为y =-x 2-2x +3.∵抛物线的对称轴为直线x =-1,且抛物线经过点A (1,0),∴点B (-3,0). 把点B (-3,0),C (0,3)的坐标分别代入y =mx +n ,得⎩⎨⎧-3m +n =0,n =3,解得⎩⎨⎧m =1,n =3.∴直线BC 的函数表达式为y =x +3.(第10题解)(2)∵点A 与点B 最新直线x =-1对称,∴直线BC 与对称轴x =-1的交点就是使MA +MC 的值最小的点M .把x =-1代入y =x +3,得y =2, ∴点M (-1,2).(3)如解图,设点P (-1,t ).∵点B (-3,0),C (0,3),∴BC 2=18,PB 2=(-1+3)2+t 2=4+t 2,PC 2=(-1)2+(t -3)2=t 2-6t +10 ①若点B 为直角顶点,则BC 2+PB 2=PC 2,即18+4+t 2=t 2-6t +10,解得t =-2.②若点C 为直角顶点,则BC 2+PC 2=PB 2,即18+t 2-6t +10=4+t 2,解得t =4. ③若点P 为直角顶点,则PB 2+PC 2=BC 2,即4+t 2+t 2-6t +10=18,解得t 1=3+172,t 2=3-172.综上所述,点P 的坐标为(-1,-2)或(-1,4)或⎝ ⎛⎭⎪⎫-1, 3+172 或⎝ ⎛⎭⎪⎫-1, 3-172.。
九年级数学:二次函数图像和性质同步检测(有答案)
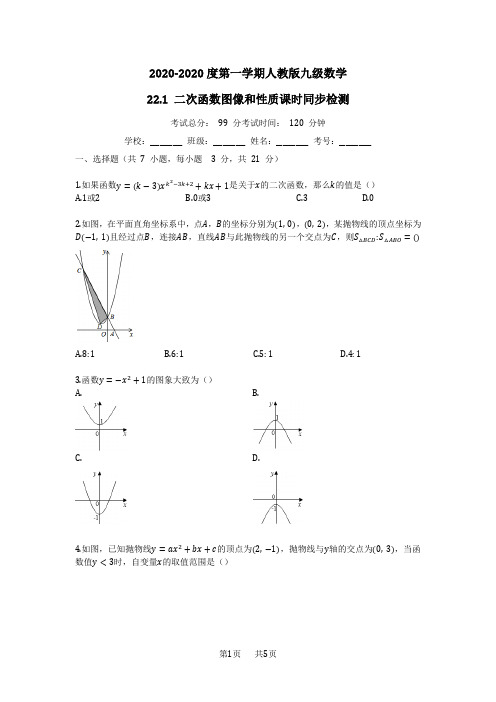
2020-2020度第一学期人教版九级数学22.1 二次函数图像和性质课时同步检测考试总分: 99 分考试时间: 120 分钟学校:__________ 班级:__________ 姓名:__________ 考号:__________一、选择题(共 7 小题,每小题 3 分,共 21 分)1.如果函数y =(k −3)x k 2−3k+2+kx +1是关于x 的二次函数,那么k 的值是()A.1或2B.0或3C.3D.02.如图,在平面直角坐标系中,点A ,B 的坐标分别为(1, 0),(0, 2),某抛物线的顶点坐标为D(−1, 1)且经过点B ,连接AB ,直线AB 与此抛物线的另一个交点为C ,则S △BCD :S △ABO =()A.8:1B.6:1C.5:1D.4:13.函数y =−x 2+1的图象大致为()A. B.C. D.4.如图,已知抛物线y =ax 2+bx +c 的顶点为(2, −1),抛物线与y 轴的交点为(0, 3),当函数值y <3时,自变量x 的取值范围是()A.0<x<2B.0<x<3C.0<x<4D.1<x<35.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列四个结论:①ac<0;②a+b+c>0;③4a−2b+c<0;④4ac−b2>0.其中正确的结论有()A.1B.2C.3D.46.已知二次函数y=ax2+bx+c的图象如图所示,则下列6个代数式:ab,ac,a+b+c,a−b+c,2a+b,2a−b中,其值为正的式子的个数是()A.2个B.3个C.4个D.5个7.若A(−3, y1)、B(0, y2)、C(2, y3)为二次函数y=(x+1)2+1的图象上的三点,则y1、y2、y3的大小关系是()A.y1<y2<y3B.y2<y1<y3C.y3<y1<y2D.y1<y3<y2二、填空题(共6 小题,每小题 3 分,共18 分)8.二次函数y=(x−1)2+2,当x=________时,y有最小值.9.已知抛物线的顶点坐标为(−1, −2),且通过点(1, 10),则该抛物线的解析式为________.10.将二次函数y=2x2−4x+7配方成y=a(x+m)2+k的形式为________.11.若二次函数y=ax2(a≠0),图象过点P(2, −8),则函数表达式为________.12.已知y=(k+2)x k2+k−4是二次函数,且当x>0时,y随x增大而增大,则k=________.2二次函数y=ax三、解答题(共5 小题,每小题12 分,共60 分)14.已知抛物线y=3x2−6x+10,求它的对称轴和顶点坐标.15.已知函数y=ax2+bx+c中a<0,b>0,c<0,△<0,画出函数的大致图象.16.已知四个互不相等的实数x1,x2,x3,x4,其中x1<x2,x3<x4.(1)请列举x1,x2,x3,x4从小到大排列的所有可能情况;(2)已知a为实数,函数y=x2−4x+a与x轴交于(x1, 0),(x2, 0)两点,函数y=x2+ax−4与x轴交于(x3, 0),(x4, 0)两点.若这四个交点从左到右依次标为A,B,C,D,且AB=BC= CD,求a的值.17.已知抛物线y=x2+bx+c的对称轴为x=−1,且经过点(−4, 5).(1)求抛物线的解析式;(2)抛物线y有无最小值,若有,求出最小值.若无,请说明理由;(3)当−2<x<3时,求y的取值范围.18.已知抛物线y=ax2+bx+c与y轴交于点(0, 3a),对称轴为x=1.(1)试用含a的代数式表示b、c.(2)当抛物线与直线y=x−1交于点(2, 1)时,求此抛物线的解析式.(3)求当b(c+6)取得最大值时的抛物线的顶点坐标.答案1.D2.B3.B4.C5.B6.A7.B8.19.y=3(x+1)2−210.y=2(x−1)2+511.y=−2x212.213.1−814.解:∵y=3x2−6x+10=3(x2−2x)+10=3(x−1)2+7,∴对称轴为直线x=1,顶点坐标为(1, 7).15.解:∵a<0,∴抛物线开口方向向下.∵a<0,b>0,则ab<0,∴该抛物线的对称轴在y轴的左侧.∵c<0,∴该抛物线与y轴交于负半轴.∵△<0,∴该抛物线与x轴没有交点,故其图象如图所示:.16.解:(1)x1<x2<x3<x4,x1<x3<x2<x4,x1<x3<x4<x2,x3<x4<x1<x2,x3<x1<x4<x2,x3<x1<x2<x4;(2)上述6种情况中第3,6种情况不可能出现.否则,两个函数的对称轴相同,则a=−4,从而x1=x3,x2=x4,这与题意不符,在其他4种情况中,都有|x2−x1|=|x4−x3|,因此有√16−4a=√a2+16,即a=0或−4(舍去),经检验a=0满足题意.17.解:(1)∵由抛物线的对称轴为x=−1,∴x=−b2×1=−1,得b=2∵抛物线y=x2+2x+c经过点(−4, 5)∴5=(−4)2+2×(−4)+c解得c=−3∴抛物线的解析式为y=x2+2x−3;(2)∵a=1>0∴抛物线y=x2+2x−3有最小值,最小值为y=(−1)2+2×(−1)−3=−4;(3)∵y=x2+2x−3,当y=0时,x2+2x−3=0,(x−1)(x+3)=0,x1=1,x2=−3,∵对称轴为x=−1,最小值为y=−4,∴−2<x<3时,−4≤y<12.18.解:(1)∵抛物线与y轴交于点(0, 3a)∴c=3a∵对称轴为=1,∴x=−b2a=1∴b=−2a;(2)∵抛物线与直线y=x−1交于点(2, 1),∴(2, 1)在抛物线上,∴1=a×22+2(−2a)+3a∴a=13∴b=−2a=−23c=3a=1∴抛物线为y=13x2−23x+1;(3)∵b(c+6)=−2a(3a+6)=−6a2−12a=−6(a+1)2+6当a=−1时,b(c+6)的最大值为6;∴抛物线y=−x2+2x−3=−(x−1)2−2故抛物线的顶点坐标为(1, −2).。
浙教版数学九年级上册同步测试:1.2 二次函数的图象

浙教版九年级数学上册同步测试:1.2 二次函数的图象一、选择题1.在平面直角坐标系中,下列函数的图象经过原点的是()A.y=﹣x+3 B.y= C.y=2x D.y=﹣2x2+x﹣72.下列函数中,图象经过原点的是()A.y=3x B.y=1﹣2x C.y= D.y=x2﹣13.若二次函数y=ax2的图象经过点P(﹣2,4),则该图象必经过点()A.(2,4) B.(﹣2,﹣4) C.(﹣4,2)D.(4,﹣2)4.二次函数y=﹣x2+bx+c的图象如图所示:若点A(x1,y1),B(x2,y2)在此函数图象上,x1<x2<1,y1与y2的大小关系是()A.y1≤y2B.y1<y2C.y1≥y2D.y1>y25.在平面直角坐标系中,下列函数的图象经过原点的是()A.y= B.y=﹣2x﹣3 C.y=2x2+1 D.y=5x6.二次函数y=ax2+bx﹣1(a≠0)的图象经过点(1,1),则a+b+1的值是()A.﹣3 B.﹣1 C.2 D.37.已知二次函数y=a(x﹣2)2+c,当x=x1时,函数值为y1;当x=x2时,函数值为y2,若|x1﹣2|>|x2﹣2|,则下列表达式正确的是()A.y1+y2>0 B.y1﹣y2>0 C.a(y1﹣y2)>0 D.a(y1+y2)>08.如果一种变换是将抛物线向右平移2个单位或向上平移1个单位,我们把这种变换称为抛物线的简单变换.已知抛物线经过两次简单变换后的一条抛物线是y=x2+1,则原抛物线的解析式不可能的是()A.y=x2﹣1 B.y=x2+6x+5 C.y=x2+4x+4 D.y=x2+8x+179.要将抛物线y=x2+2x+3平移后得到抛物线y=x2,下列平移方法正确的是()A.向左平移1个单位,再向上平移2个单位B.向左平移1个单位,再向下平移2个单位C.向右平移1个单位,再向上平移2个单位D.向右平移1个单位,再向下平移2个单位10.将抛物线y=x2向右平移2个单位,再向上平移3个单位后,抛物线的解析式为()A.y=(x+2)2+3 B.y=(x﹣2)2+3 C.y=(x+2)2﹣3 D.y=(x﹣2)2﹣311.已知点(x1,y1),(x2,y2)均在抛物线y=x2﹣1上,下列说法中正确的是()A.若y1=y2,则x1=x2B.若x1=﹣x2,则y1=﹣y2C.若0<x1<x2,则y1>y2D.若x1<x2<0,则y1>y212.二次函数y=ax2+bx﹣1(a≠0)的图象经过点(1,1),则代数式1﹣a﹣b的值为()A.﹣3 B.﹣1 C.2 D.513.对于实数a、b,定义一种运算“⊗”为:a⊗b=a2+ab﹣2,有下列命题:①1⊗3=2;②方程x⊗1=0的根为:x1=﹣2,x2=1;③不等式组的解集为:﹣1<x<4;④点(,)在函数y=x⊗(﹣1)的图象上.其中正确的是()A.①②③④B.①③C.①②③ D.③④14.已知二次函数y=﹣x2+3x﹣,当自变量x取m对应的函数值大于0,设自变量分别取m﹣3,m+3时对应的函数值为y1,y2,则()A.y1>0,y2>0 B.y1>0,y2<0 C.y1<0,y2>0 D.y1<0,y2<015.已知两点A(﹣5,y1),B(3,y2)均在抛物线y=ax2+bx+c(a≠0)上,点C(x0,y0)是该抛物线的顶点.若y1>y2≥y0,则x0的取值范围是()A.x0>﹣5 B.x0>﹣1 C.﹣5<x0<﹣1 D.﹣2<x0<316.已知点A(a﹣2b,2﹣4ab)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点坐标为()A.(﹣3,7)B.(﹣1,7)C.(﹣4,10)D.(0,10)17.二次函数y=ax2+bx+c(a≠0)的图象如图所示,若M=a+b﹣c,N=4a﹣2b+c,P=2a﹣b.则M,N,P中,值小于0的数有()A.3个B.2个C.1个D.0个18.如图,抛物线y=ax2+bx+c(a≠0)过点(1,0)和点(0,﹣2),且顶点在第三象限,设P=a ﹣b+c,则P的取值范围是()A.﹣4<P<0 B.﹣4<P<﹣2 C.﹣2<P<0 D.﹣1<P<0二、填空题19.当x=m和x=n(m≠n)时,二次函数y=x2﹣2x+3的函数值相等,当x=m+n时,函数y=x2﹣2x+3的值为.20.已知点A(4,y1),B(,y2),C(﹣2,y3)都在二次函数y=(x﹣2)2﹣1的图象上,则y1、y2、y3的大小关系是.21.如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+2上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为.22.在直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:若y′=,则称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(1,2),点(﹣1,3)的“可控变点”为点(﹣1,﹣3).(1)若点(﹣1,﹣2)是一次函数y=x+3图象上点M的“可控变点”,则点M的坐标为.(2)若点P在函数y=﹣x2+16(﹣5≤x≤a)的图象上,其“可控变点”Q的纵坐标y′的取值范围是﹣16<y′≤16,则实数a的取值范围是.23.抛物线y=ax2+bx+2经过点(﹣2,3),则3b﹣6a=.24.设抛物线y=ax2+bx+c(a≠0)过A(0,2),B(4,3),C三点,其中点C在直线x=2上,且点C到抛物线的对称轴的距离等于1,则抛物线的函数解析式为.25.已知当x1=a,x2=b,x3=c时,二次函数y=x2+mx对应的函数值分别为y1,y2,y3,若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3,则实数m的取值范围是.26.如图,在平面直角坐标系中,抛物线y=ax2+3与y轴交于点A,过点A与x轴平行的直线交抛物线y=于点B、C,则BC的长为.答案一、选择题1.C;2.A;3.A;4.B;5.D;6.D;7.C;8.B;9.D;10.B;11.D;12.B;13.C;14.D;15.B;16.D;17.A;18.A;二、填空题19.3;20.y3>y1>y2;21.1;22.(-1,2);0≤a<4;23.;24.y=x2-x+2或y=-x2+x+2;25.m>-;26.6;初中数学试卷灿若寒星制作。
九年级数学上册《二次函数的图像与性质》同步练习3 含答案

22.1《二次函数的图像与性质》同步练习3带答案一.选择题1.把二次函数2x y =的图象向右平移3个单位长度,得到新的图象的函数表达式是( )A. 32+=x yB. 32-=x yC. 2)3(+=x yD. 2)3(-=x y2.抛物线2)3(2--=x y 的顶点坐标和对称轴分别是( )A.3),0,3(-=-x 直线B. 3),0,3(=x 直线C. 3),3,0(-=-x 直线D. 3),3,0(-=x 直线3.已知二次函数2)1(3+=x y 的图象上有三点 ),2(),,2(),,1(321y C y B y A - ,则321,,y y y 的大小关系为( )A.321y y y >>B. 312y y y >>C. 213y y y >>D. 123y y y >>4.把抛物线2)1(6+=x y 的图象平移后得到抛物线26x y =的图象,则平移的方法可以是( )A.沿y 轴向上平移1个单位长度B.沿y 轴向下平移1个单位长度C.沿x 轴向左平移1个单位长度D.沿x 轴向右平移1个单位长度5.若二次函数12+-=mx x y 的图象的顶点在x 轴上,则m 的值是( )A. 2B. 2-C.0D. 2±6.对称轴是直线2-=x 的抛物线是( )A.22+-=x yB.22+=x yC.2)2(21+=x y D.2)2(3-=x y 7.对于函数2)2(3-=x y ,下列说法正确的是( )A. 当0>x 时,y 随x 的增大而减小B. 当0<x 时,y 随x 的增大而增大C. 当2>x 时,y 随x 的增大而增大D. 当2->x 时,y 随x 的增大而减小8.二次函数132+=x y 和2)1(3-=x y ,以下说法:①它们的图象都是开口向上;②它们的对称轴都是y 轴,顶点坐标都是原点(0,0);③当0>x 时,它们的函数值y 都是随着x 的增大而增大;④它们的开口的大小是一样的. 其中正确的说法有( ) A.1个 B.2个 C.3个 D.4个 二.填空题1.抛物线2)1(3--=x y 的开口向 ,对称轴是 ,顶点坐标是 。
【初中数学】2018秋季学期最新人教版初中数学九年级上册精品习题:《二次函数的图象和性质》同步测试1

20.(1)m=4,y=x2;(2)m=-1,y=-4x2.
21.(1)a=-1,b=-1;(2)
(3)S△OBC=.
22.(1); (2)B(-2,1);(3)S△OAB=2;
(4)设C点的坐标为则则得或
∴C点的坐标为
(3)函数______的图象关于y轴对称;函数______的图象关于原点对称.
(4)函数______有最大值为______;函数______有最小值为______.
12.已知函数y=ax2+bx+c(a,b,c是常数).
(1)若它是二次函数,则系数应满足条件______.
(2)若它是一次函数,则系数应满足条件______.
(3)求△OBC的面积.
22.已知抛物线y=ax2经过点A(2,1).
(1)求这个函数的解析式;
(2)写出抛物线上点A关于y轴的对称点B的坐标;
(3)求△OAB的面积;
(4)抛物线上是否存在点C,使△ABC的面积等于△OAB面积的一半,若存在,求出C点的坐标;若不存在,请说明理由.
参考答案
1.y=ax2+bx+c(a≠0),x,常数,a.
(3)a=______,b=______,c=______.
(4)a=______,b=______,c=______.
7.抛物线y=ax2,|a|越大则抛物线的开口就______,|a|越小则抛物线的开口就______.
8.二次函数y=ax2的图象大致如下,请将图中抛物线字母的序号填入括号内.
(1)y=2x2如图( );
5.当a<0时,在抛物线y=ax2的对称轴的左侧,y随x的增大而______,而在对称轴的右侧,y随x的增大而______;函数y当x=______时的值最______.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.2 二次函数的图象(第3课时)
1.二次函数y =ax 2
+bx +c (a ≠0)的图象:是一条抛物线,它的对称轴是____________,顶点坐标是____________,当a >0时,开口________,顶点是抛物线的最________点;当a <0时,开口________,顶点是抛物线的最________点.
2.利用抛物线图象判定a 、b 、c 符号:开口方向决定a 的正负;对称轴在y 轴的左侧,则a 、b 同号,对称轴在y 轴的右侧,则a 、b 异号;与y 轴交点纵坐标即为c .
3.会建立直角坐标系解决实际问题.
A 组 基础训练
1.抛物线y =12x 2-3x +5
2
的对称轴是( )
A .直线x =3
B .直线x =-3
C .直线x =6
D .直线x =-6 2.将二次函数y =-x 2
-4x +2化为y =a (x +m )2
+k 的形式,则( ) A .a =-1,m =-2,k =6 B .a =-1,m =2,k =6 C .a =1,m =-2,k =-6 D .a =-1,m =2,k =-6
3.二次函数y =ax 2
+bx +c 的图象如图所示,则下列结论正确的是( )
第3题图
A .a >0,b <0, c >0
B .a <0,b <0, c >0
C .a <0,b >0, c <0
D .a <0,b >0, c >0
4.(宁波中考)抛物线y =x 2-2x +m 2
+2(m 是常数)的顶点在( )
A .第一象限
B .第二象限
C .第三象限
D .第四象限 5.抛物线y =x 2
-2x -8的对称轴为直线________,顶点坐标为________. 6.抛物线y =-2x 2+bx +c 的对称轴为直线x =1,则b =________.
7.已知抛物线y =-2x 2
+bx +c 的顶点坐标为(-3,2),则b =________,c =________. 8.如图的一座拱桥,当水面宽AB 为12m 时,桥洞顶部离水面4m ,已知桥洞的拱形是抛物线,以水平方向为x 轴,建立平面直角坐标系,若选取点A 为坐标原点时的抛物线解析式是y =-19
(x -6)2
+4,则选取点B 为坐标原点时的抛物线解析式是________________.
第8题图
9.求出下列抛物线的顶点坐标和对称轴. (1)y =-2(x -1)2
-4; (2)y =-2x 2
+23x ; (3)y =-12x 2
+2x -3.
10.如图,四边形ABCD 是平行四边形,过点A ,C ,D 作抛物线y =ax 2
+bx +c (a≠0),与x 轴的另一交点为E ,连结EC ,点A ,B ,D 的坐标分别为(-2,0),(3,0),(0,4).求抛物线的解析式.
第10题图
B组自主提高
11.如图,在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为( )
11.已知抛物线y=x2+(m-2)x-2m,当m=________时,顶点在y轴上;当m=________时,顶点在x轴上;当m=________时,抛物线经过原点;无论m取何值,抛物线必经过定点________.
13.如图1是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.若把拱桥的截面图放在平面直角坐标系中(如图2).
第13题图
(1)求抛物线的解析式;
(2)求两盏景观灯之间的水平距离.
C 组 综合运用
12.如图,在平面直角坐标系中,O 是坐标原点,点A 的坐标是(-2,4),过点A 作AB⊥y 轴,垂足为B ,连结OA.
(1)求△OAB 的面积;
(2)若抛物线y =-x 2
-2x +c 经过点A. ①求c 的值;
②将抛物线向下平移m 个单位,使平移后得到的抛物线顶点落在△OAB 的内部(不包括△OAB 的边界),求m 的取值范围(直接写出答案即可).
第14题图
1.2 二次函数的图象(第3课时)
【课堂笔记】
1.直线x =-b 2a ⎝ ⎛⎭
⎪⎫
-b 2a ,4ac -b 2
4a 向上 低 向下 高
【课时训练】 1-4.ABDA
5. x =1 (1,-9)
6. 4
7. -12 -16
8. y =-19
(x +6)2
+4
9. (1)顶点(1,-4),对称轴:直线x =1; (2)顶点⎝
⎛⎭
⎪⎫
32,32,对称轴:直线x =32; (3)顶点(2,-1),对称轴:直线x =2.
10. 由已知得C(5,4).把A(-2,0),D(0,4),C(5,4)代入抛物线y =ax 2
+bx +c ,
得⎩⎪⎨⎪⎧4=25a +5b +c ,0=4a -2b +c ,4=c.
解得
⎩
⎪⎨⎪⎧a =-27,
b =107,
c =4.
所以抛物线的解析式为y =-27x 2+10
7x +4. 11. B
12. 2 -2 0 (2,0)
13. (1)抛物线的顶点坐标为(5,5),与y 轴交点坐标是(0,1),设抛物线的解析式是y
=a(x -5)2+5,把(0,1)代入y =a(x -5)2+5得a =-425,∴y =-425(x -5)2
+5(0≤x≤10);
(2)由已知得两景观灯的纵坐标都是4,∴4=-425(x -5)2+5,∴425(x -5)2
=1,∴x 1=152
,
x 2=52,∴两景观灯间的距离为152-5
2
=5米.
14. (1)∵点A 的坐标是(-2,4),AB ⊥y 轴,∴AB =2,OB =4,∴S △OAB =12AB ·OB =1
2
×
2×4=4;
第14题图
(2)①把点A 的坐标(-2,4)代入y =-x 2-2x +c ,得-(-2)2
-2×(-2)+c =4,∴c
=4; ②∵y=-x 2-2x +4=-(x +1)2
+5,∴抛物线顶点D 的坐标是(-1,5).∵OA 的中点F 的坐标是(-1,2),AB 的中点E 的坐标是(-1,4),∴m 的取值范围为1<m<3.。
