分数小数的列式计算
常见分数小数及百分数互化 常用平方数立方数及各种计算方法
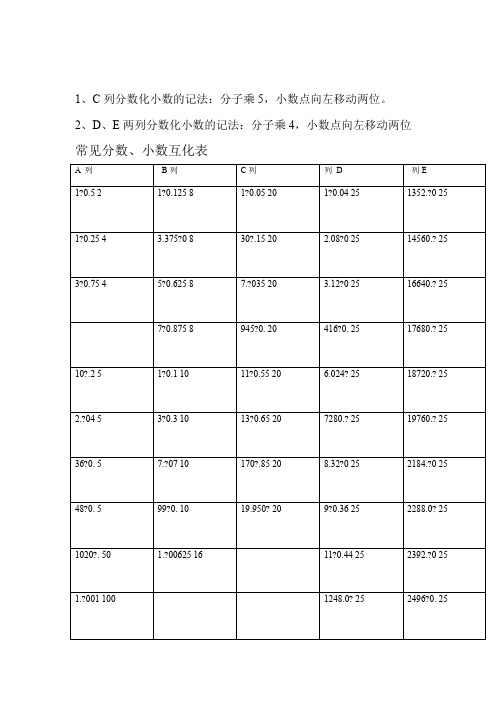
1、C列分数化小数的记法:分子乘5,小数点向左移动两位。
2、D、E两列分数化小数的记法:分子乘4,小数点向左移动两位常见分数、小数互化表1 / 12常见的分数、小数及百分数的互化常用平方数2 / 12常见立方数减错位相加/ ;9= A×10-A×9型速算技巧:A×A10-743=7430-743=6687 ×743×9=743例:;÷10A×9.9= A×10+AA×9.9型速算技巧:10=7430-74.3=7355.7 ÷×10-743例:743×9.9=74310+A;11= A型速算技巧:A××A×1110+743=7430+743=8173 11=743×例:743×100+A;×101= A×AA×101型速算技巧:100+743=75043 101=743×例:743×的速算技巧:25、125除以乘/5、;5=10A÷2×5型速算技巧:A×A2=43697.25 ÷÷2=87394.58739.45×5=8739.45×10例:2;A÷5=0.1A×5A÷型速算技巧:2=7.3686 ×2=3.6843×0.1×例:36.843÷5=36.843;÷4A×25型速算技巧:×25=100AA4=180850 4=723400÷25=7234×100÷7234例:×4;25=0.01A25÷型速算技巧:A÷×A4=148.564=37.140.0125=37143714例:÷×××3 / 12A×125型速算技巧:A×5=1000A÷8;例:8736×125=8736×1000÷8=8736000÷8=1092000A÷125型速算技巧:A÷1255=0.001A×8;例:4115÷125=4115×0.001×8=4.115×8=32.92减半相加:A×1.5型速算技巧:A×1.5=A+A÷2;例:3406×1.5=3406+3406÷2=3406+1703=5109“首数相同尾数互补”型两数乘积速算技巧:×(头+1);积的尾=尾×尾头=积的头例:23×27=首数均为2,尾数3与7的和是10,互补所以乘积的首数为2×(2+1)=6,尾数为3×7=21,即23×27=621本方法适合11~99 所有平方的计算。
五年级数学上册列式计算

五年级数学上册列式计算一、加法与减法运算在五年级数学上册中,学生将进一步巩固加法和减法的基本运算。
这包括整数、小数和分数的加法与减法。
例如:1.计算 32 + 17 =2.计算 5.6 -3.2 =3. 计算 1/2 + 2/5 =二、乘法与除法运算在掌握了基本的加法和减法后,学生将学习乘法和除法。
乘法部分会涉及到简单的乘法表,而除法则更注重于平均分配的概念。
例如:1.计算 6 × 8 =2.计算 15 ÷ 3 =3. 计算 6/7 × 21/8 =三、分数与小数运算分数和小数的运算是一个重要的概念,它要求学生将两者进行转换,并理解其背后的数学意义。
例如:1. 计算 2/3 + 3/4 = (将分数转换为小数进行运算)2. 将 0.8 转换为分数形式 =3. 计算 1.5 × 7/3 = (小数与分数的混合运算)四、综合运算(加、减、乘、除混合)综合运算要求学生能够按照正确的顺序(先乘除后加减)进行混合运算。
例如:1.计算 (10 + 5) × 2 - 4 =2. 计算 (7/8) × (4/9) + (1/2) = (分数和小数的混合运算)3. (4 × (15 - 9)) + (3 × 6) = (综合的加减乘除运算)五、分数与小数的互化学生需要掌握将分数和小数互化的技能,这有助于他们更清晰地理解两者的关系。
例如:1.将分数 3/8 转换为小数 =2.将小数 0.75 转换为分数 =3. 将分数 7/12 转换为最简形式 =六、应用题列式计算应用题是帮助学生理解数学概念在实际问题中的应用的关键题型。
例如:1. 一个果园里有400棵苹果树,其中1/4是红富士品种。
红富士品种的苹果树有多少棵?2. 小明有6本书,其中3本是故事书,3本是科普书。
他从书架上随机取出一本书,取到故事书的概率是多少?3. 一个长方形的长是6cm,宽是4cm。
分数乘法(小数乘分数、分数综合计算

分数乘法三:小数乘分数一、小数乘分数:1、把下面的小数化成分数,分数化成小数。
1.2 0.4 3.5 1.25 85 54 41 2512、小数乘分数:例题:甲数是3.6,乙数是甲数的45,乙数是多少? 列式:思考:这个算式和我们前面学习的分数乘法有什么不同?该如何进行计算?方法1、可以把小数化成分数:3.6=1036,3.6×45 = 1036×45 = 29 方法2、可以把分数化成小数:45= 1.25, 3.6×1.25 =4.5 小结:这两种方法都适用,主要还是要根据题目的事情情况来选择运用哪种方法。
二、练习巩固: 1、计算。
1.2×532.5×53 1.4×65 2.4×652、列式计算。
(1)2.4的 52是多少?(2)1.2的 43是多少?(3)甲数占乙数的 87,已知乙数是5.6,甲数是多少?(4)16.4吨的 41是多少吨?3、解决问题。
(1)一列火车每小时行87.9千米,从甲站到乙站行了31小时,甲乙两站间的铁路长多少千米?(2)一面墙的面积是27.8平方米,已经刷完了整面墙的 21。
已经刷完的面积是多少平方米?(3)一包茶叶重10.5克,用去 53,用去多少克?(4)一水果店,上午卖出苹果28.4千克,下午卖出的是上午的 43,下午卖出多少千克?(5)一根钢管长8.7米,用去一部分,还剩下全长的 31,还剩下多少米?分数乘法四:分数乘法混合运算积与因数的关系:一个数(0除外)乘大于1的数,积大于这个数。
a ×b=c,当b >1时,c>a 。
一个数(0除外)乘小于1的数,积小于这个数。
a ×b=c,当b <1时,c<a (b ≠0)。
一个数(0除外)乘等于1的数,积等于这个数。
a ×b=c,当b =1时,c=a 。
注意:在进行因数与积的大小比较时,要注意因数为0时的特殊情况。
分数化小数表

分数化小数表一、介绍分数化小数是将分数表示成小数形式的一种方式。
在数学中,分数是指两个整数之间的比值,通常由一个分子和一个分母组成。
而小数是指不完全是整数的数,可以用有限或无限的十进制表示。
在实际问题中,我们常常需要把分数转化为小数,以便更方便地进行计算和比较。
本文将介绍如何将分数转化为小数,并给出一份分数化小数表。
二、分数化小数的方法将分数化小数的方法主要有两种:长除法和分数除法。
1.长除法法长除法是将分数除以一个整数,得到一个小数的过程。
具体步骤如下:(1)将分子写在除号上面,分母写在除号下面,画一条横线。
(2)从左往右,将分子的第一位数与分母进行相除,得到商和余数。
(3)将商写在横线上方,将余数写在横线下方。
(4)将余数乘以10,得到一个新的被除数。
(5)将新的被除数与分母进行相除,得到新的商和余数。
(6)继续按照上述步骤进行操作,直到出现重复的余数或者得到指定位数的小数为止。
2.分数除法法分数除法是将分数除以一个小数,得到一个无限循环小数的过程。
具体步骤如下:(1)将分子写在除号上面,分母写在除号下面,画一条横线。
(2)判断分母是否能整除10,如果不能,则在分母的末尾加上一个0,得到新的分母。
(3)将新的分母与分子进行相乘,并将结果写在横线上方。
(4)将新的被除数写在横线下方,得到一个新的被除数。
(5)重复上述步骤,直到出现相同的被除数为止。
出现相同的被除数时,将出现重复的商,说明小数是无限循环的。
三、分数化小数表下面是一个分数化小数表,将常见的分数表示成小数形式。
1/2 = 0.51/3 ≈ 0.33331/4 = 0.251/5 = 0.21/6 ≈ 0.16661/7 ≈ 0.1428571/8 = 0.1251/9 ≈ 0.11111/10 = 0.12/3 ≈ 0.66662/5 = 0.42/8 = 0.253/4 = 0.753/5 = 0.63/8 ≈ 0.3754/5 = 0.84/7 = 0.5714285/6 ≈ 0.83335/8 = 0.6256/7 ≈ 0.8571427/8 = 0.875四、总结分数化小数是将分数转化为小数的一种方法,能够使我们更方便地进行计算和比较。
常见的分数、小数及百分数的互化,常用平方数、立方数及各种计算方法

1、C 列分数化小数的记法:分子乘 5,小数点向左挪动两位。
2、D 、E 两列分数化小数的记法:分子乘4,小数点向左挪动两位常有分数、小数互化表A 列B 列C 列D 列E 列11 1 1 0.0413 20.50.1250.050.52820252513 3 2 14 0.250.3750.150.080.564820252535 7 3 16 0.75 0.625 0.35 0.12 0.6448 20 25 2579 4 17 0.875 0.45 0.16 0.68820252511 11 6 18 0.20.10.550.240.7251020252523 13 7 19 0.4 0.3 0.65 0.28 0.765 10 20 25 2537 17 8 21 0.6 0.7 0.85 0.32 0.8451020252549 19 9 22 0.80.90.950.360.8851020252511 11 23 0.02 0.0625 0.44 0.9250 1625 251 12 24 0.01 0.48 0.961002525常有的分数、小数及百分数的互化除法除不尽(按四舍五入计算)除法比分数小数百分除法比分数小数百分1÷ 21:21/250%1÷ 31:31/333% 1÷ 41:41/425%2÷ 32:32/367% 1÷ 51:51/520%1÷ 61:61/617% 2÷ 52:52/540%5÷ 65:65/683% 3÷ 53:53/560%1÷ 71:71/714% 4÷ 54:54/580%2÷ 72:72/729% 1÷ 81:81/8%3÷ 73:73/743% 3÷ 83:83/8%4÷ 74:74/757% 5÷ 85:85/8%5÷ 75:75/771% 7÷ 87:87/8%6÷ 76:76/786% 1÷ 101:101/1010%1÷ 91:91/911% 3÷ 103:103/1030%2÷ 92:92/922% 7÷ 107:107/1070%4÷ 94:94/944% 9÷ 109:109/1090%5÷ 95:95/956% 3÷ 23:23/2150%7÷ 97:97/978% 5÷ 45:45/4125%8÷ 98:98/989% 7÷ 57:57/5140%4÷ 34:34/3133%备注除尽是指除数(前项、分子)除以除数(后项、分母)得商不出现循环(或无穷循环)小数;除不尽与除尽相反,是无穷循环小数。
六年级分数、小数四则混合运算

六年级分数、小数四则混合运算分数、小数四则运算是小学数学中的一项重要内容,它对于培养同学们的计算能力起着十分重要的作用,对于培养同学们的计算能力起着十分重要的作用,要想掌握要想掌握好分数、小数的四则混合运算,一要牢记分数、小数的基本运算法则,二要掌握分数与小数的互化。
运算法则,二要掌握分数与小数的互化。
分析与解 当题目中出现分数的个数大于出现的小数的个数时,可考虑将小数化为分数进行运算可考虑将小数化为分数进行运算..注意分数作为除数时,分子与分母的位置要互换后作乘数。
分子与分母的位置要互换后作乘数。
分析与解 此题目属于形式较复杂型题目此题目属于形式较复杂型题目..与例1不同的是,分数与小数在题目中出现的个数基本相同分数与小数在题目中出现的个数基本相同..因此在计算时先不要急于进行分数与小数的互换,而要考虑寻找题目的特点,争取用简便方法计算。
点,争取用简便方法计算。
=(10+1010+10)×1+0×6.04)×1+0×6.04)×1+0×6.04 =20+0 =20分析与解 当题目出现括号时,告诉我们要注意运算的先后顺序顺序..同时还要注意乘法分配律的应用。
同时还要注意乘法分配律的应用。
=48+1 =49分析与解 因为题目中有分数、小数还有百分数,因此要考虑它们之间的互化虑它们之间的互化..对于这道题目而言,将分数和百分数都化为小数比较容易计化为小数比较容易计=23.3×1.25+14×5+1.25×28.7=23.3×1.25+14×5+1.25×28.7 =1.25=1.25((23.3+28.723.3+28.7))+70 =1.25×52+70=1.25×52+70 =65+70 =135例5 某小学五年级四班为希望工程捐款,五(某小学五年级四班为希望工程捐款,五(11)班捐款150.25元,五(元,五(22)班比五()班比五(11)班多捐了)班多捐了 15.45 15.45元,五(元,五(33)班捐款是五(班捐款是五(22)元?元?分析与解 这是一道应用题,要根据题目中所给的条件列出算式,计算时还会遇到分数小数的四则混合运算,所以计算时不但要细心,还要尽量使用简便算法。
常见分数、小数及百分数互化-常用平方数、立方数及各种计算方法
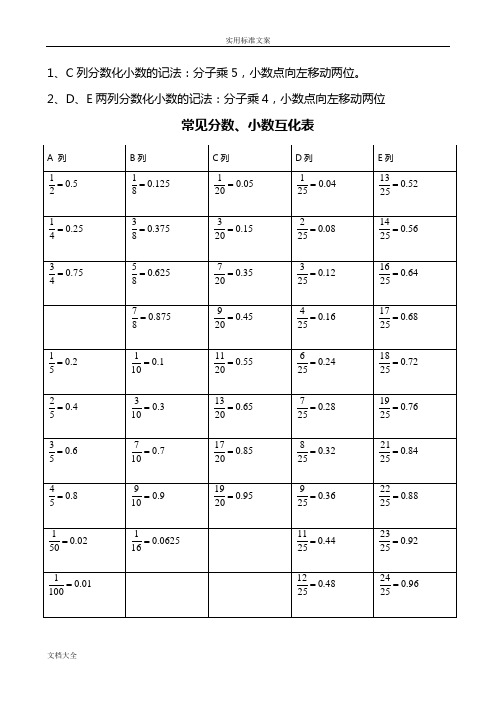
1、C列分数化小数的记法:分子乘5,小数点向左移动两位。
2、D、E两列分数化小数的记法:分子乘4,小数点向左移动两位常见分数、小数互化表常见的分数、小数及百分数的互化常用平方数常见立方数常见特殊数的乘积错位相加/减A×9型速算技巧:A×9= A×10-A;例:743×9=743×10-743=7430-743=6687A×9.9型速算技巧:A×9.9= A×10+A÷10;例:743×9.9=743×10-743÷10=7430-74.3=7355.7A×11型速算技巧:A×11= A×10+A;例:743×11=743×10+743=7430+743=8173A×101型速算技巧:A×101= A×100+A;例:743×101=743×100+743=75043乘/除以5、25、125的速算技巧:A×5型速算技巧:A×5=10A÷2;例:8739.45×5=8739.45×10÷2=87394.5÷2=43697.25A÷5型速算技巧:A÷5=0.1A×2;例:36.843÷5=36.843×0.1×2=3.6843×2=7.3686A×25型速算技巧:A×25=100A÷4;例:7234×25=7234×100÷4=723400÷4=180850A÷25型速算技巧:A÷25=0.01A×4;例:3714÷25=3714×0.01×4=37.14×4=148.56A×125型速算技巧:A×5=1000A÷8;例:8736×125=8736×1000÷8=8736000÷8=1092000A÷125型速算技巧:A÷1255=0.001A×8;例:4115÷125=4115×0.001×8=4.115×8=32.92减半相加:A×1.5型速算技巧:A×1.5=A+A÷2;例:3406×1.5=3406+3406÷2=3406+1703=5109“首数相同尾数互补”型两数乘积速算技巧:积的头=头×(头+1);积的尾=尾×尾例:23×27=首数均为2,尾数3与7的和是10,互补所以乘积的首数为2×(2+1)=6,尾数为3×7=21,即23×27=621本方法适合11~99 所有平方的计算。
分数乘以小数

复习巩固
1.将下列小数化为分数,分数化为小数。
3 4
12 5
0.48
1.5
= 0.75 = 2.4
= 12 25
=
3 2
复习巩固
2.判断下列是否合理。
3 4
×
5
=
3 20
应该是整数乘以分数的分子
7 4
×
5 7
=
35 28
没有约分
新知探索 (教材第8页例5)
5
松鼠的尾巴长度约占身体长度的
新知探索
(2)松鼠乐乐的尾巴有多长?
松鼠的尾巴长度约占身体的长度的
3 4
。
平均分成 4 份, 我身体长2.4dm。
取其中的 3 份。
乐乐
新知探索
画一画!
2.4dm 尾?巴
乐乐身体长度 自己试着 计算一下。
列式:
2.4 3 4
(dm)
2.4 3
4
=
0.6
2.4
3 41
=1.8(dm)
这样约分计算更简便。
新知探索
分数乘小数的三种计算方法: (1)分数化成小数; (2)小数化成分数; (3)分数的分母与小数约分后再计算。
课堂练习 (教材第8页“做一做”)
1.
1.2×
3 5
=
18 25
1.4×
5 6
=
7 6
2.5×
3 5
=
3 2
2.4×56 = 2
课堂练习
2.美国人均淡水资源约为1.38万立方米,我
3 2.1×
4
=
_1_.5_7__5(dm)
1.转化成小数乘小数:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
列式计算加强训练
1 、从3
8的倒数里减去
1
4的
2
3,差是多少?
2、2
3与
1
4的差等于一个数的
5
6,这个数是多少?
3、甲数是5的1
5,乙数的
1
5是5,两数相差多少?
4、一个数的3
比180的
1
多24,求这个数。
5、从30里减去48的1
2,所得的差去除3,商是多少?
6、一个数比4.5的1.6倍小0.72,求这个数。
7、一个数的7倍比13多7.4,求这个数。
(列方程)
8、用2除10
7的商,减去7的倒数,差是多少?
9、甲数的3
4等于乙数的
3
5,如果乙数是15,甲数是多少?
10、0.8与0.4的差,乘除1.25的商,积是多少?
11、3.4与5.6的和除以它们的差,商是多少?
12、 2除1.6的商加上5.4乘以5
的积,和是多少?
13、4
5的倒数除
5
3与
1
3的和,商是多少?
14、一个数的3倍加上5除以5
8的商,和是32.6,求这个数。
(方程解答)
15、某数的1
5比4.5的1.6倍少3.2,求这个数?。
