04-积分和微分运算电路例题
6.3.16.3基本运算电路积分微分运算电路学习资料
感谢观看
2. 微分电路
如果将积分电路中R和C的位置互换 便构成基本微分电路。它是积分的逆 运算。
根据虚断原则，有 iR iC
而
ic
C
dui dt
iR
uO R
uo
Hale Waihona Puke iR RRCdui dt
2. 微分电路
当输入电压us为阶跃信号时，输出 电压仍为一个有限值，随着C的充 电。uo将逐渐地衰减，最后趋近于 零。
1. 积分电路
根据“虚短” vN vP 0
根据“虚断”，得 iI 0
因此
i2
i1
vS R
电容器被充电，其充电电流为 i2 设电容器C的初始电压为零，则
1
vI vO C
1 i2dt C
vS dt R
1
vO RC vSdt
（积分运算）
1. 积分电路
当vS为阶跃电压时，有
vO
1 RC
vSdt
VS t RC
VS t
vO与 t 成线性关系
若输入为阶跃信号，则积分 电路表现为与输入成线性关 系增长直到C充电结束，使 运放进入饱和状态。充电时 间τ=RC。
ui
0
t
uo
0τ
t
若输入为方波信号，则积分
ui
电路表现为充电与放电交替
0
t
进行的状态（理想），对外
uo
表现为三角波。
0
t
积分电路与微分电路实验报告
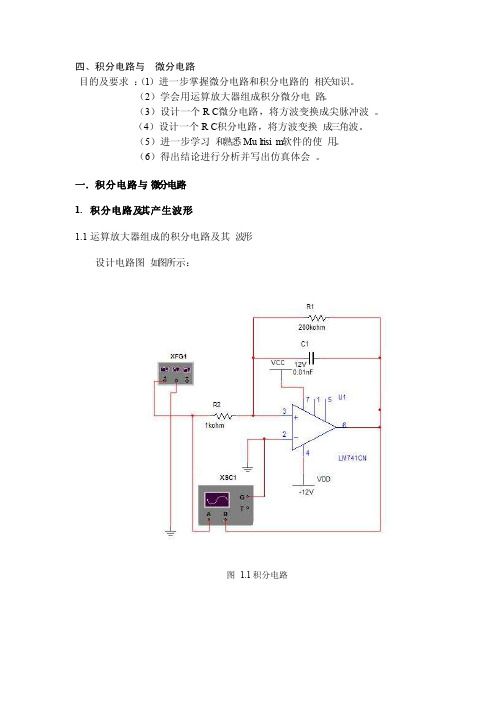
四、积分电路与微分电路目的及要求：（1）进一步掌握微分电路和积分电路的相关知识。
（2）学会用运算放大器组成积分微分电路。
（3）设计一个RC微分电路，将方波变换成尖脉冲波。
（4）设计一个RC积分电路，将方波变换成三角波。
（5）进一步学习和熟悉Mul tisim软件的使用。
（6）得出结论进行分析并写出仿真体会。
一．积分电路与微分电路1.积分电路及其产生波形1.1运算放大器组成的积分电路及其波形设计电路图如图所示：图 1.1积分电路其工作原理为：积分电路主要用于产生三角波，输出电压对时间的变化率与输入阶跃电压的负值成正比，与积分时间常数成反比，即01in U Ut R C∆=-∆ 式中，1R C 积分时间常数，in U 为输入阶跃电压。
反馈电阻的f R 主要作用是防止运算放大器LM741饱和。
C 为加速电容，当输入电压为方波时，输入端的高01U 电平等于正电源cc V +，低电平等于负电源电压d d V -，比较器的时0U U +-==，比较器翻转，输入从高电01U 平跳到低电平d d V -。
输出的是一个上升速度与下降速度相等的三角波形。
图1.2积分电路产生的波形1.2微分电路及其产生波形2. 运算放大器组成的微分电路及其波形设计的微分电路图：图2.1微分电路其工作原理为：将积分电路中的电阻与电容对换位子，并选用比较小的时间常数R C ，便得到了微分电路。
微分电路中，输出电压与输入电压对时间的变化率的负值成正比，与微分时间常数成反比，所以0inf U U R C t∆=-∆in R 的主要作用是防止运放L M 741产生自激振荡。
0/v R C d V d t =-，输出电压正比与输入电压对时间的微商，符号表示相位相反，当输入电压为方波时，当时输出电t o =压为一个有限制。
大学微积分中的积分计算题
大学微积分中的积分计算题微积分是数学的重要分支之一，是描述变化与积累的工具。
在大学微积分学习过程中，积分计算题是其中的重要部分。
通过解答这些积分计算题，可以加深对积分的理解，并培养解决实际问题的数学思维能力。
本文将以解析法为主，介绍常见的积分计算题的求解方法。
1. 不定积分计算题不定积分是求解函数原函数的过程，即反求导。
下面通过实际例题来展示不定积分的求解方法。
例题1：计算∫(6x^2 + 4x - 5)dx解析：根据不定积分的线性性质，我们可以将原函数分别对每一项进行积分。
∫(6x^2 + 4x - 5)dx = ∫6x^2dx + ∫4xdx - ∫5dx积分得到：2x^3 + 2x^2 - 5x + C其中，C为常数。
2. 定积分计算题定积分是求解函数在给定区间上的积分结果。
它可以表示曲线下的面积、物理中的质量、功等。
下面通过实际例题来展示定积分的求解方法。
例题2：计算∫[0, 2] (4x^2 - 2x)dx解析：根据定积分的性质，我们可以通过积分区间上限和下限的差值，对每一项进行积分。
∫[0, 2] (4x^2 - 2x)dx = [∫4x^2dx - ∫2xdx] |[0, 2]积分得到：[(4/3)x^3 - x^2] |[0, 2]代入上限和下限：[(4/3)(2)^3 - (2)^2] - [(4/3)(0)^3 - (0)^2]化简得：8/3 - 4/3 = 4/33. 部分积分法计算题部分积分法也称为莱布尼茨公式，用于解决乘积函数的积分问题。
下面通过实际例题来展示部分积分法的求解方法。
例题3：计算∫xsin(x)dx解析：根据部分积分公式∫u(x)v'(x)dx = u(x)v(x) - ∫v(x)u'(x)dx，我们可以将积分项拆分。
选取 u(x) = x，v'(x) = sin(x)则 u'(x) = 1，v(x) = -cos(x)应用部分积分公式进行求解：∫xsin(x)dx = -xcos(x) - ∫(-cos(x))dx化简得：-xcos(x) + sin(x) + C其中，C为常数。
电路分析四之积分微分电路
微分与积分电路1、电路的作用，与滤波器的区别和相同点。
2、微分和积分电路电压变化过程分析，画出电压变化波形图。
3、计算：时间常数，电压变化方程，电阻和电容参数的选择。
积分电路和微分电路的特点：积分电路、微分电路可以分别产生尖脉冲和三角波形的响应 1:积分电路可以使输入方波转换成三角波或者斜波微分电路可以使使输入方波转换成尖脉冲波2:积分电路电阻串联在主电路中，电容在干路中微分则相反3：积分电路的时间常数t要大于或者等于10倍输入脉冲宽度 微分电路的时间常数t要小于或者等于1/10倍的输入脉冲宽度 4：积分电路输入和输出成积分关系微分电路输入和输出成微分关系积分电路：1.延迟、定时、时钟2.低通滤波3.改变相角（减）微分电路：1.提取脉冲前沿2.高通滤波3.改变相角（加）微分图像（在单位阶跃响应的前提下）微分电路可把矩形波转换为尖脉冲波，此电路的输出波形只反映输入波形的突变部分，即只有输入波形发生突变的瞬间才有输出。
而对恒定部分则没有输出。
输出的尖脉冲波形的宽度与RC有关（即电路的时间常数），RC越小，尖脉冲波形越尖，反之则宽。
积分图像（在单位阶跃响应的前提下）积分电路是使输出信号与输入信号的时间积分值成比例的电路RC电路的分类（1）RC 串联电路电路的特点：由于有电容存在不能流过直流电流，电阻和电容都对电流存在阻碍作用，其总阻抗由电阻和容抗确定，总阻抗随频率变化而变化。
RC 串联有一个转折频率： f0=1/2πR1C1当输入信号频率大于 f0 时，整个 RC 串联电路总的阻抗基本不变了，其大小等于 R1。
（2）RC 并联电路RC 并联电路既可通过直流又可通过交流信号。
它和 RC 串联电路有着同样的转折频率：f0=1/2πR1C1。
当输入信号频率小于f0时，信号相对电路为直流，电路的总阻抗等于 R1;当输入信号频率大于f0 时 C1 的容抗相对很小，总阻抗为电阻阻值并上电容容抗。
当频率高到一定程度后总阻抗为 0。
积分与微分运算电路
控制系统中， PD调节器在调节过程中起加速作用，即使系统有较 快的响应速度和工作稳定性。
三相积电分源与的微相分线运电算压电关路系
比例积分微分运算电路 — PID调节器
+ uI –
电工技术与电子技术
R2 CD R2
CI
R1
–
+
+
+uO源自R2–PID 调节器是一种常见的控制电路，调节器的任务是将一定物理 量 (被调节参数X ) 调节到预先给定的理论值( 或称而定支W )，并克服 干扰的影响保持这一值。
uO
+ UO(sat)
O
–UO(sat) 输出电压随
线性积分时间 uI = –UI < 0
线性积分时间
积分饱和 t
uI = UI > 0
时间线性变化
三相积电分源与的微相分线运电算压电关路系
积分电路仿真
电工技术与电子技术
积分电路是一种应用广泛的电子电路。该电路除能实现对信号
的积分运算外，还用于精确的时间控制和信号发生电路及模拟量与 数字量的转换中。
三相积电分源与的微相分线运电算压电关路系
电工技术与电子技术
积分与微分运算电路
1. 积分运算电路
iF
uC +
–CF
+ i1 R1
–
+
+
uI
+
uO
–
R2
–
R2 =R1
2. 分析：
1
uO R1CF uIdt
当电容CF的初始电压为 uC(t0) 时
1 t
uO
R1CF
t0 uIdt uC
积分与微分运算电路
积分、微分、比例运算电路
模拟电路课程设计报告题目：积分、微分、比例运算电路一、设计任务与要求①设计一个可以同时实现积分、微分和比例功能的运算电路。
②用开关控制也可单独实现积分、微分或比例功能③用桥式整流电容滤波集成稳压块电路设计电路所需的正负直流电源（±12V）。
二、方案设计与论证用桥式整流电容滤波集成稳压块电路设计电路所需的正负直流电源（±12V），为运算电路提供偏置电源。
此电路设计要求同时实现比例、积分、微分运算等功能。
即在一个电路中利用开关或其它方法实现这三个功能。
方案一：用三个Ua741分别实现积分、微分和比例功能，在另外加一个Ua741构成比例求和运算电路，由于要单独实现这三个功能，因此在积分、微分和比例运算电路中再加入三个开关控制三个电路的导通与截止，从而达到实验要求。
缺点：开关线路太多，易产生接触电阻，增大误差。
此运算电路结构复杂，所需元器件多，制作难度大，成本较高。
并且由于用同一个信号源且所用频率不一样，因此难以调节。
流程图如下：图1方案二:用一个Ua741和四个开关一起实现积分、微分和比例功能，并且能够单独实现积分、微分或比例功能。
优点：电路简单，所需成本较低。
电路图如下：积分运算电路 微分运算电路 比例运算电路 比例求和运算电路图2三、单元电路设计与参数计算1、桥式整流电容滤波集成稳压块电路设计电路所需的正负直流电源（±12V ）。
其流程图为：图3直流电源电路图如下：电源变压器整流电路滤波电路稳压电路V1220 Vrms 50 Hz0¡ã U11_AMP T17.321D21N4007D31N4007D41N4007C13.3mF C23.3mF C3220nFC4220nF C5470nFC6470nF C7220uFC8220uFU2LM7812CTLINE VREGCOMMONVOLTAGEU3LM7912CTLINEVREGCOMMON VOLTAGE D51N4007D61N4007LED2LED1R11k¦¸R21k¦¸2345D11N40071516671417图4原理分析： (1)电源变压器：由于要产生±12V 的电压，所以在选择变压器时变压后副边电压应大于24V,由现有的器材可选变压后副边电压为30V 的变压器。
积分微分电路
积分微分电路
积分微分电路是一种常见的电路类型，它能够对输入信号进行积分或微分运算，从而对信号进行处理。
积分电路主要由电容器和电阻器组成，当输入信号经过该电路时，电容器会对信号进行积分运算，输出信号会随着时间的增加而不断增加。
微分电路则主要由电阻器和电容器组成，当输入信号经过该电路时，电容器会对信号进行微分运算，输出信号会随着时间的增加而越来越小。
积分微分电路广泛应用于信号处理、滤波、放大等领域，是电子工程中不可或缺的一部分。
- 1 -。
积分电路和微分电路的应用
积分电路和微分电路的应用积分电路和微分电路是电子工程中非常重要且广泛应用的两种电路。
积分电路可用于对输入信号进行积分运算，而微分电路则可以对输入信号进行微分运算。
这两种电路在不同领域中有着各自独特的应用。
一、积分电路的应用积分电路主要用于对信号进行时间积分运算，即对输入信号进行时间的累加。
其中最常见的应用就是在音频系统中，通过积分电路可以实现音频信号的频率分析和信号调制。
首先，积分电路可以对输入信号的幅度进行积分运算，从而得到输入信号的功率谱密度。
这对于音频系统来说尤为重要，因为它可以帮助我们了解音频信号的频谱分布情况，进而对音频信号进行合理的调整。
比如，在音乐录音室中，通过积分电路可以实时监测出音频信号在不同频段上的能量分布情况，从而调整音频设备的参数，使得音频产生的效果更加符合设计要求。
此外，积分电路还可以用于信号调制。
在通信系统中，调制是对输入信号进行编码和解码的过程，而积分电路可以用于信号的调制解调。
例如，在遥控器中，通过积分电路可以将输入信号进行编码，然后通过无线电波传输到接收端进行解码。
这种调制技术的应用，在遥控器、无线电和移动通信等领域得到广泛应用。
二、微分电路的应用微分电路则是对信号进行微分运算，可以对输入信号的变化率进行测量。
这种测量技术在很多领域中都有着重要的应用。
一个常见的应用就是在汽车领域中的刹车系统中。
刹车系统通过微分电路可以实时测量车轮的转速变化率，并将其与事先设定的规范进行比较，从而控制刹车力度。
这样可以实现自动刹车系统，在紧急情况下及时减速，保障行车安全。
此外，微分电路还被广泛应用于医疗设备中。
例如，在心电图仪中，通过微分电路可以实时检测心脏电信号的变化率，从而判断病人的心脏状况。
这对于医生来说非常重要，能够帮助他们及时发现心脏病变化，采取相应的治疗措施。
微分电路还可以应用于加速度计和陀螺仪等传感器中。
通过微分电路可以实时测量物体的加速度和角速度的变化率，从而判断物体的运动状态。
积分微分运算电路
3.直流反馈和交流反馈：反馈环路内直流信号可以 流通，则产生直流反馈；反馈环路内交流信号可以
流通，则产生交流反馈；若反馈环路内直流信 号和交流信号均可以流通，则既有直流反馈 又有交流。
11.2.2 交流负反馈的类型
Rf1
Rf2
解：这是两级运算电路，
u第o1一第 路电级二(，路1 为级其 ，同为输其R R 相反f出1 输比1 )相电出u例i比压1 电运 例为压算(运为1电算1u)i1 0 uR.Ro215+1 -AV 1 RuR01 f32R3u例R4i211-+-3A图25Vu0
平衡电阻：R2= R1 // Rf = 5k , R4= R3 // Rf2 ≈16.7K
注意：因要求静态时u+、 u– 对地电阻相同，
所以:R2 = R1 // Rf 称为平衡电阻 结论：
(1) Auf为负值，即 uo与 ui 极性相反。因为 ui 加在 反相输入端。
(2) Auf 的精度只与外部电阻 R1、RF 有关，与运放
本身参数无关。
11.3 信号的运算电路
(3) | Auf | 可大于 1，也可等于 1 或小于 1 。
11.2.4 负反馈组态的判定
1）输出端是电压反馈还是电流反馈的判定：
如图11-9a、b所示：
至输入端
（+） -
电压反馈
A
+
Rf
RL
至输入端
-
A
+
Rf
a ）
a）电图压11反-9馈反馈b组）态电判流定反馈）
b
RL
（-） 电流反馈
信号运算电路
（一）利用加法运算电路实现减法运算 ——将代表被减数的信号反相后，与代表减数的信
号相加，从而实现减法。
UoRR3f U2RR2f U1
优点：输入端没有共模 信号，允许U1、U2的共 模电压范围较大。
缺点：输入阻抗低。
3
第一节 加减运算电路
（二）用单一运算放大器实现减法运算
当 Rf/R 1R P/R 2
11
第三节 微分积分运算电路 一、积分运算电路
2、多重积分运算电路
I3 C U2 C I5
U 1 2 I s 2 C I1 2 sI3 C I3 R I1 I3 (1 2 sR ) C
R U1 R
I4 R/2 ∞
U 2 s I3 C I4 2 R I3 2 I5 R I5 I3 ( 1 s2 R )
-
Ui I1
I3
I2 2C
+ +N
Uo
U i (I1 I3 )R 2 I3 R (1 sR ) C U o(sI3C sI5C )2 sI3 C (1s1R)C
CC R/2 R/2
Uo s2RU2iC2
R 2R R
Ui C
C
+
∞ + N
Uo
4R
U o(t)R2 1 C 2 U i(t)d ()2 t
实际电路中，S1和S2一般由场效应管构成。
10
第三节 微分积分运算电路 一、积分运算电路
（二）具有特殊性能的积分电路 1、增量积分电路（比例积分电路）
R2 C
Ui
I1
R1 Ui
I1
∞
-
+ +N
Uo
实验6 积分与微分电路
实验6 积分与微分电路1. 实验目的学习使用运放组成积分和微分电路。
2. 实验仪器双踪示波器、信号发生器、交流毫伏表、数字万用表。
3. 预习内容1） 阅读OP07的“数据手册”，了解OP07的性能。
2） 复习关于积分和微分电路的理论知识。
3) 阅读本次实验的教材。
4. 实验内容1） 积分电路如图5.1。
在理想条件下，dt)t (dV C R )t (V o i -= ，当C 两端的初始电压为零时，则dt )t (V RC1)t (V to i o ⎰-= 因此而得名为积分电路。
（1） 取运放直流偏置为V 12±，输 入幅值V i =-1V 的阶跃电压，测量输出饱和电 压和有效积分时间。
若输入为幅值V i =-1V 阶跃电压时，输出为dt V RC1)t (V to i o ⎰-=t RC V i -=， (1) 这时输出电压将随时间增长而线性上升。
通常运放存在输入直流失调电压，图6.1 所示电路运放直流开路，运放以开环放大倍数放大输入直流失调电压，往往使运放输出限幅，即输出电压接近直流电源电压，输出饱和，运放不能正常工作。
在OP07的 “数据手册”中，其输入直流失调电压的典型值为30μV ；开环增益约为112dB ，即4×105。
据此可以估算，当V i =0V 时，V o =30μV ×4×105=12V 。
电路实际输出接近直流偏置电压，已无法正常工作。
建议用以下方法。
按图6.1接好电路后，将直流信号源输出端与此同时V i 相接，调整直流信号源，使其输出为-1V ，将输出V o 接示波器输入，用示波器可观察到积分电路输出饱和。
保持电路状态，关闭直流偏置电源，示波器X 轴扫描速度置0.2sec/div ，Y 轴输入电压灵敏度置2V/div ，将扫描线移至示波器屏的下方。
等待至电容上的电荷放尽。
当扫描光点在示波器屏的左下方时，即时打开直流偏置电源，示波器屏上积分电路的输出为线性上升的直线，大约1秒后，积分电路输出由线性上升的直线变为水平直线，即积分电路已饱和，立即按下示波器的“stop ”键。
微分运算电路
微分运算电路
微分电路的改进 为了消除高频干扰，实际的微分电路如图所示，输入端串 入的电阻R1和并联在RF两端的电容CF可以有效地消除高频 干扰的影响，电阻R1和电容CF的数值应满足以下关系式：
RF CF R1C
模拟电子技术
器两端电压之间的关系。电容器的电容量C等于电容上的电
荷q除以电容两端的电压降u：
Cq
q Cu
u
上式两边
式中ic为流过电容器的电流。上式说明， 流过电容器的电流等于电容量C和电容两 端电压降的微分。
下面分析微分运算电路输入、输出电压之间的关系。
微分运算电路
公式推导 根据理想运放的虚短路性质，流入反相输入端的电流为零，
因此流过电容C的电流等于流过电阻RF的电流，即
C d( u1 u ) u u0
dt
RF
左边是流过电容C的电流，它等于电
容量和电容两端电压降的导数。
流入反相端的电流为零，因此流经
电阻R2的电流等于零：
0 u 0 R2
根据理想运放的短路性质，同相端电压
与反相端电压相等，得： u u
两个输入端对地电压 匹配的要求为
由上述3个式子求得：
u0
RF C
du1 dt
RF R2
微分运算电路 高频干扰对微分电路的影响 假设输入电压为三角波，则微分后输出电压为方波，相应 的波形如图所示。
假如输入端有高频干扰，尽管干扰的电压幅度不大，也会在 输出端产生很大的干扰输出。原因是输出电压正比于输入信 号对时间的导数，而不是输入信号的幅度。干扰信号幅度虽 小，但变化迅速，其时间导数就很大，因此在输出端所产生 的干扰就很大。图（b）画出了输入电压上升沿存在一微小 的高频方波产生较大输出电压干扰的示意图。
实验九 积分与微分电路【范本模板】
实验九积分与微分电路学院：信息科学与技术学院专业:电子信息工程姓名：刘晓旭学号：2011117147一．实验目的1．掌握集成运算放大器的特点、性能及使用方法。
2．掌握比例求和电路、微积分电路的测试和分析方法。
3．掌握各电路的工作原理和理论计算方法。
二．实验仪器1．数字万用表2．直流稳压电源3．双踪示波器4．信号发生器5．交流毫伏表。
三．预习要求1.分析图7—8 实验电路，若输入正弦波，u o 与u i 的相位差是多少？当输入信号为100Hz、有效值为2V时，u o =？2.图7—8 电路中，若输入方波，u o 与u i 的相位差?当输入信号为160Hz幅值为1V时，输出u o =?3.拟定实验步骤，做好记录表格。
四．实验原理集成运放可以构成积分及微分运算电路，如下图所示:微积分电路的运算关系为：五．实验内容：1。
积分电路按照上图连接积分电路，检查无误后接通+12，-12V直流电源。
（1）取U i=-1v，用示波器观察波形u0，并测量运放输出电压的正向饱和电压值.（2）取U i=1V,测量运放的负向饱和电压值。
（3）将电路中的积分电容改为改为0。
1uF，u i分别输入1KHz幅值为2v的方波和正弦信号,观察u i和u o的大小及相位关系，并记录波形，计算电路的有效积分时间。
（4）改变电路的输入信号的频率，观察u i和u o的相位,幅值关系.2.微分电路实验电路如上图所示。
（1）输入正弦波信号，f=500Hz，有效值为1v，用示波器观察u i和u o的波形并测量输出电压值.（2）改变正弦波频率(20Hz—40Hz），观察u i和u o的相位，幅值变化情况并记录。
（3）输入方波，f=200Hz，U=5V，用示波器观察u0波形,并重复上述实验。
（4）输入三角波，f=200Hz，U=2V，用示波器观察u0波形，并重复上述实验3。
积分—微分电路实验电路如图所示（1）输入f=200Hz,u=6V的方波信号，用示波器观察u i和u o的波形并记录.（2）将f改为500Hz，重复上述实验。
微分和积分电路原理
微分和积分电路原理
微分电路原理
微分电路是一种能够实现电信号的微分运算的电路。
微分运算可以理解为对输入信号的斜率进行测量或计算。
微分电路的核心部件是电容器和电阻器。
当输入信号经过电阻器到达电容器时，电容器将对信号进行积分操作。
通过将输出信号与输入信号相减，可以得到信号的微分部分。
微分电路的数学模型可以表示为：
Vout = -RC(dVin/dt)
其中，Vout为输出电压，Vin为输入电压，R为电阻值，C为电容值，dt为时间微元。
通过适当选择电容和电阻的数值，可以调节微分电路的工作频率范围。
积分电路原理
积分电路是一种能够对输入信号进行积分运算的电路。
积分运算可以理解为对输入信号的面积进行测量或计算。
积分电路的核心部件是电容器和电阻器。
当输入信号经过电阻器到达电容器时，电容器将对信号进行积分操作。
通过将输出信号与输入信号相加，可以得到信号的积分部分。
积分电路的数学模型可以表示为：
Vout = -1/(RC) ∫(Vin dt)
其中，Vout为输出电压，Vin为输入电压，R为电阻值，C为电容值，∫为积分运算符，dt为时间微元。
通过适当选择电容和电阻的数值，可以调节积分电路的工作频率范围。
电路微分与积分电路
微分电路与积分电路分析积分与微分电路 (ZT)转贴电子资料2010-11-23 10:51:25 阅读166 评论1字号：大中小订阅积分与微分电路积分电路与微分电路是噪讯对策上的基本，同时也是具备对照特性的模拟电路。
事实上积分电路与微分电路还细分成数种电路，分别是执行真积分/微分的完全积分/微分电路，以及具有与积分/微分不同特性的不完全积分/微分电路。
除此之外积分/微分电路又分成主动与被动电路，被动型电路无法实现完全积分/微分，因此被动型电路全部都是不完全电路。
积分/微分电路必需发挥频率特性，为了使电路具备频率特性使用具备频率特性的电子组件，例如电容器与电感器等等。
被动电路不完全积分/微分电路图1是被动型不完全积分电路，如图所示组合具备相同特性的电路与，就可以制作上述两种电路。
图1与图2分别是使用电容器与电感器的电路，使用电容器的电路制作成本比较低，外形尺寸比较低小，容易取得接近理想性的组件，若无特殊理由建议读者使用电容器的构成的电路。
此外本文所有内容原则上全部以电容器的构成的电路为范例作说明。
图1与图2的两电路只要更换串联与并联的组件，同时取代电容器与电感器，就可以制作特性相同的电路。
不完全积分电路与微分电路一词，表示应该有所谓的完全积分电路与微分电路存在，然而完全积分电路与微分电路却无法以被动型电路制作，必需以主动型电路制作。
不完全积分电路与微分电路具有历史性的含义，主要原因是过去无法获得增幅器的时代，无法以主动型电路制作真的积分/微分电路，不得已使用不完全积分/微分电路。
由于不完全积分/微分电路本身具备与真的积分/微分电路相异特性，因此至今还具有应用价值而不是单纯的代用品。
不完全积分/微分电路又称为积分/微分电路，它的特性与真积分/微分电路相异，单纯的积分/微分电路极易与真积分/微分电路产生混淆，因此本讲座将它区分成:*完全积分电路/微分电路*不完全积分电路/微分电路不完全积分电路的应用不完全积分电路属于低通滤波器的一种，它与1次滤波器都是同一类型的电路，不完全积分电路经常被当成噪讯滤波器使用，广泛应用在模拟电路、数字电路等领域。
积分微分知识点及习题和答案(仅供参考)
仅供参考积分和微分积分一般分为不定积分、定积分和微积分三种1、不定积分设F(x) 是函数f(x) 的一个原函数,我们把函数f(x) 的所有原函数F(x)+C （C 为任意常数）叫做函数f(x) 的不定积分. 记作∫f(x)dx其. 中∫叫做积分号, f(x) 叫做被积函数, x 叫做积量,f(x)dx 叫做被积式,C 叫做积分常数,求已知函数的不定积分的过程叫做对这个函数进行积分.由定义可知：求函数f(x) 的不定积分,就是要求出f(x) 的所有的原函数,由原函数的性质可知,只要求出函数f(x) 的一个原函数,再加上任意的常数C,就得到函数f(x) 的不定积分.也可以表述成,积分是微分的逆运算,即知道了导函数,求原函数.2、定积分众所周知,微积分的两大部分是微分与积分.微分实际上是求一函数的导数,而积分是已知一函数的导数,求这一函数.所以,微分与积分互为逆运算.实际上,积分还可以分为两部分.第一种,是单纯的积分,也就是已知导数求原函数,而若F(x) 的导数是f(x), 那么F(x)+C （C 是常数）的导数也是f(x), 也就是说,把f(x) 积分,不一定能得到F(x), 因为F(x)+C 的导数也是f(x),C 是无穷无尽的常数,所以f(x) 积分的结果有无数个, 是不确定的,我们一律用F(x)+C 代替,这就称为不定积分.而相对于不定积分,就是定积分.所谓定积分,其形式为∫f(x) dx 上(限 a 写在∫上面,下限 b 写在∫下面).之所以称其为定积分, 是因为它积分后得出的值是确定的,是一个数,而不是一个函数.定积分的正式名称是黎曼积分,详见黎曼积分.用自己的话来说,就是把直角坐标系上的函数的图象用平行于y 轴的直线把其分割成无数个矩形,然后把某个区间[a,b] 上的矩形累加起来,所得到的就是这个函数的图象在区间[a,b] 的面积.实际上,定积分的上下限就是区间的两个端点a、b.我们可以看到,定积分的本质是把图象无限细分,再累加起来,而积分的本质是求一个函数的原函数.它们看起来没有任何的联系,那么为什么定积分写成积分的形式呢?定积分与积分看起来风马牛不相及,但是由于一个数学上重要的理论的支撑,使得它们有了本质的密切关系.把一个图形无限细分再累加,这似乎是不可能的事情,但是由于这个理论, 可以转化为计算积分.这个重要理论就是大名鼎鼎的牛顿-莱布尼兹公式,它的内容是：若F'(x)=f(x) 那么∫f(x) dx(上限 a 下限b)=F(a)-F(b)牛顿-莱布尼兹公式用文字表述,就是说一个定积分式的值,就是上限在原函数的值与下限在原函数的值的差.正因为这个理论,揭示了积分与黎曼积分本质的联系,可见其在微积分学以至更高等的数学上的重要地位,因此,牛顿-莱布尼兹公式也被称作微积分基本定理.3、微积分积分是微分的逆运算,即知道了函数的导函数,反求原函数.在应用上,积分作用不仅如此, 它被大量应用于求和,通俗的说是求曲边三角形的面积,这巧妙的求解方法是积分特殊的性质决定的。
(整理)微分与积分电路
微分与积分电路一、微分电路输出信号与输入信号的微分成正比的电路，称为微分电路。
原理：从图一得：Uo=Ric=RC(duc/dt),因Ui=Uc+Uo,当，t=to时，Uc=0,所以Uo=Uio随后C充电，因RC≤Tk,充电很快，可以认为Uc≈Ui，则有：Uo=RC(duc/dt)=RC(dui/dt)式一这就是输出Uo正比于输入Ui的微分（dui/dt)RC电路的微分条件：RC≤Tk图一、微分电路二、积分电路输出信号与输入信号的积分成正比的电路，称为积分电路。
原理：从图2得，Uo=Uc=(1/C)∫icdt,因Ui=UR+Uo,当t=to时，Uc=Oo.随后C充电，由于RC≥Tk,充电很慢，所以认为Ui=UR=Ric,即ic=Ui/R,故Uo=(1/c)∫icdt=(1/RC)∫icdt这就是输出Uo正比于输入Ui的积分（∫icdt）RC电路的积分条件：RC≥Tk一、矩形脉冲信号在数字电路中，经常会碰到如图4-16所示的波形，此波形称为矩形脉冲信号。
其中为脉冲幅度，为脉冲宽度，为脉冲周期。
当矩形脉冲作为RC串联电路的激励源时，选取不同的时间常数及输出端，就可得到我们所希望的某种输出波形，以及激励与响应的特定关系。
图4-16 脉冲信号二、微分电路在图4-17所示电路中，激励源为一矩形脉冲信号，响应是从电阻两端取出的电压，即，电路时间常数小于脉冲信号的脉宽，通常取。
图4-17 微分电路图因为t<0时，，而在t = 0 时，突变到，且在0< t < t1期间有：，相当于在RC串联电路上接了一个恒压源，这实际上就是RC串联电路的零状态响应：。
由于，则由图4-17电路可知。
所以，即：输出电压产生了突变，从0 V突跳到。
因为，所以电容充电极快。
当时，有，则。
故在期间内，电阻两端就输出一个正的尖脉冲信号，如图4-18所示。
在时刻，又突变到0 V，且在期间有：= 0 V，相当于将RC串联电路短接，这实际上就是RC串联电路的零输入响应状态：。