第三章 控制网平差
第三章监测网平差及基准点稳定性分析

剔除动点后,其余点构成统计量
F1
ˆF 2 ˆ02
ˆF
2
=
dFT
PFF fF
dF
当F1<F分析值,分析即结束,反之,继续 剔除动点,继续检验,直到原假设不再拒绝,
最后剩下的都是稳定的点。
• 当网中存在固定点时,采用这些固定点作 基准,应用经典平差;
• 当网中某些点具有相对的稳定性,它们相 互变动是随机的情况下,则用这些点作拟 稳点,用拟稳平差对成果进行分析;
• 当监测网所有网点具有微小的随机变动时, 自由网平差是一种有效的分析方法.
因此,要合理地确定监测网的参考系,首先要 确定哪些点是稳定的或相对稳定的点,哪些点是 不稳定的点。从20世纪70年代起,人们相继提出 了多种关于监测点稳定性分析方法,其中平均间 隙法是一种比较典型的方法。
m i=1
xi =0
xm
x
1 m
m i 1
xi
0, x为水准网的高程重心.
x =0说明水准网的自由网平差参考系是网的高程重心.
以测边网为例:自由网平差
x1
1
G
T
X=
0
- y10
0 1 x10
1 0 - y20
0 1 x20
…1 …0 … ym0
0 1 xm0
y1 xm
所以:对监测网进行稳定性分析,并 根据稳定性分析结果选择平差方法,确立 一个对变形分析比较有利的参考系,是变 形观测数据处理的一项重要任务。
§3—2 监测网的参考系及其平差
起算数据称为平差问题的基准:基准给出了控制网的位 置。
尺度和方位的定义 即控制网的参考系.
• 经典平差:采用选择固定基准的办法确定参考 系. (满足待估参数的求取要求) • 监测网平差:满足有多期复测的观测值估计的 位移 是一种“绝对的”或接近绝对的位移
高程控制网平差

i
i
i
h h V 改厕厕短的改正数, 代入上式,得:
i
i
i
V1 V2 V3 V4 W 0
W H A h1 h2 h3 h4 H B
1.附合水准路线的条件数和条件方程式组成
观测值5个,待定水准点2 个,所以条件有3个,可 以列出3个条件方程:
h1
H B h1 h2 H A 0
V 1 V 3 V 2 W a 0 V 2 V 4 V 6 W b 0 V 4 V 5 V 3 W c 0
(二)观测值权的确定:
1.各水准路线都进行了往返观测,每公里水准路线的观测中误差为 ,
则m:i
R mi2
1 4n
n i
2 i
i
式中,为测往返测高程不符值,以mm为单位;R为测段长度,以km为单位;n
H A h2 h3 h5 H D 0
H B h1 h3 h4 H C 0
一般以1个已知点为起点,其它已知点为终点,所构成的附合 水准路线为已知点数减1,这样可以列出的条件方程式为已知 水准点个数减1.
2.闭合水准路线的条件数和条件方程式的组成
从一个水准点出发,经过若干水准测段,又回到该 水准点,这样的水准路线称为闭合水准路线。
V 1 V 7 V 8 W b 0
V 2 V 8 V 7 W c 0
V 3 V 5 V 8 W d 0
V 4 V 6 V 5 W e 0
2.闭合水准路线的条件数和条件方程式的组 成
图(c)是四边形状水准网,网中有4个待定点,没有已知点, 在平差计算时,只能确定个待定水准点之间的相互关系,如 果确定一个水准点的高程,就可以确定其他点的高程。因此, 该网的必要观测是3个,观测值总数是6个,又3个多余观测, 可以列出3个条件方程。为了让所列立的条件方程式互相独 立,没个条件方程都要求有一个其他方程没有用到的观测值, 即:
GNSS控制网观测与平差

在GPS观测技术出现之前,一般平面控制网都是采用三角网、导线网等形式进行观测。
90年代我国引入了GPS观测技术,由于其精度高且控制点间不需通视的优点,很快就成为平面控制网的主要观测手段。
现在除美国的GPS以外,还有俄罗斯的格洛纳斯(GLONASS),欧盟的伽利略(Galileo)和中国的北斗(BD)等全球卫星导航系统,都可以为我们提供全球高精度的导航定位服务。
全球卫星导航系统简称GNSS,原来的GPS接收机发展到现在基本上都能同时接收GPS、GLONASS、Galileo、BD等卫星信号,所以现在在称为GPS接收机已经不太准确,一般称为GNSS接收机,原来的GPS观测技术也扩展为GNSS观测技术,采用GNSS技术进行观测的平面控制网则称为GNSS控制网。
本文就GNSS控制网的观测和平差进行介绍。
一、GNSS控制网的设计GNSS控制网设计最重要的是确定控制网的等级。
GNSS测量规范比较多,有国家标准也有行业标准。
由于不同的规范对等级的规定不一致,比如《全球定位系统(GPS)测量规范》中规定的等级为B、C、D、E(A级为连续运行参考站网),《全球定位系统(GPS)铁路测量规程》也是B、C、D、E四级,《卫星定位城市测量技术规范》、《城市测量规范》和《工程测量规范》中规定的精度级别为二等、三等、四等、一级、二级,《公路全球定位系统(GPS)测量规范》中规定的等级为一级、二级、三级、四级。
所以要确定GNSS控制网的等级,首先要确定采用的技术依据,也就是用哪个规范。
这个就要根据实际的需求来进行确定,如果实在不确定采用哪个规范,可以直接采用国家标准《全球定位系统(GPS)测量规范》。
图1 《全球定位系统(GPS)测量规范》中的精度等级规定图2 《工程测量规范》中的精度等级规定根据采用的规范确定好GNSS控制网的等级后,就可以根据规范的相关规定进行具体的技术设计。
主要有坐标系统的确定,起算点的选择,控制点点位及布网概略设计,采用的GNSS接收机与数据处理软件及平差软件,控制网观测、数据处理及平差技术要求及上交成果资料等内容。
第3讲(三角网条件平差

第三章 条件平差
第四节
二、条件方程的列立 条件方程的种类:图形条件(内角和条件)、水平条件(圆周条件)、极条件、 条件方程的种类:图形条件(内角和条件)、水平条件(圆周条件)、极条件、 )、水平条件 )、极条件 方位角条件、边长条件、坐标条件。 方位角条件、边长条件、坐标条件。 1. 图形条件(n=15 图形条件(n=15 t=8 r=7 哪7个?) 每个三角形内角平差值和等于180 每个三角形内角平差值和等于180
sin L1 sin L4 sin L7 sin L10 sin L13 sin L1 sin L4 sin L7 sin L10 sin L13 v v cot L1 1 − cot L2 2 sin L2 sin L5 sin L8 sin L11 sin L14 ρ ′′ sin L2 sin L5 sin L8 sin L11 sin L14 ρ ′′
第三章 条件平差
第四节
三角网平差的目的 求待定点平面坐标平差值, 求待定点平面坐标平差值,并进行精度 评定。 评定。 三角网件方程个数等于多余观测个数。 条件方程个数等于多余观测个数。
r=nr=n-t
测角网、测边网、边角同测网。无 关键在于确定必要观测个数 t 。 测角网、测边网、边角同测网。 论网型多么复杂, 论网型多么复杂,都是由三角形和 大地四边形相互邻接或重叠而组成。 当网中有2个或2 大地四边形相互邻接或重叠而组成。 1.当网中有2个或2个以上已知点时 t=2 t=2倍待定点数 当网中仅具备4个必要起算数据( 当网中仅具备4个必要起算数据(一点 坐标、一条边的方位、 坐标、一条边的方位、一条边的边 2.当网中少于2个已知点时 当网中少于2 长或已知两点坐标) 称为自由 长或已知两点坐标)时,称为自由 这四个数据成为必要起算数据。 网。这四个数据成为必要起算数据。 (1)测角网 t=2倍总点数t=2倍总点数-4 多余四个必要起算数据时,成为非自由 多余四个必要起算数据时,成为非自由 网。 (2)测边或边角网 t=2倍总点数t=2倍总点数-3
第三章 监测网平差及参考点稳定性检验

V T PV s nt d
求 ( NN ) : 可以在方阵中任意去掉d行、d列,把余下的式子 (已是满秩的)求出凯来逆,再在原来去掉的行、列补上0, 即为NN的一个广义逆。
因广义逆不唯一,但可以证明,用不同的广义 逆(NN)-代入上式后,求得的X向量却是相同的, 故X有唯一解!
3.3 秩亏自由网平差
2 X T 2K T N 0 X
X NK
X NK
T NNK A Pl 代入法方程,有:
NX AT Pl
K ( NN ) 1 AT Pl
X N ( NN ) 1 AT Pl
NN 仍是秩亏的,但
X N ( NN ) 1 AT Pl 却是惟一的
观测改正数: V AX l ( AN ( NN ) 1 AT P E )l 单位权方差:
3.3 秩亏自由网平差
四、 秩亏自由网平差——直接解法
问题的提出:在秩亏自由网平差中,如果像经典平差平差那样,只 要求遵循最小二乘原则求未知参数的解,将不可能取得唯一确定 的估计量; 解决方法:为了得唯一确定的估计量,需要在遵循最小二乘原则基 础上附加另外条件; 附加条件的前提:该条件的确定应保证所求得的未知数的估计量 是最优的. 这样的最优解是唯一存在的,它就是法方程的最小范数解!
3.2 监测网经典平差
一、间接平差原理
误差方程式:
L V AX
设观测值权为 P ,根据最小二乘原理:
V T PV min
求极值,有:
d (V T PdX
AT PV 0
3.2 监测网经典平差
AT P( AX l ) 0 AT PAX AT Pl
7.3mm
H P H P 0 H P 103.455m 7.3mm 103.4623
注册测绘师-综合-第三章第2节-工程控制网建立

第2节工程控制网建立大纲要求:工程控制网的设计重点:工程控制网的坐标系选择、工程控制网的施测方法、《工程测量规范》知识点一:工程控制网的分类控制测量包括平面控制测量、高程控制测量、三维控制测量;按照用途,工程控制网可分为测图控制网、施工控制网、安装控制网和变形监测网。
(1)按照网点性质,可分为一维网(水准网、高程控制网)、二维网(平面控制网)、三维网;(2)按照网形,可分为三角网、导线网、混合网、方格网等;(3)按照施测方法,可分为测角网、测边网、边角网、gps网等;(4)按照坐标系和基准,可分为附合网(约束网)、独立网、经典自由网、自由网等;(5)按照其他标准,还可分为首级网、加密网、特殊网、专用网(如隧道控制网、桥梁控制网、建筑方格网)等。
知识点二:工程控制网的特点测图控制网精度取决测图比例尺。
1.隧道控制网的点位布设要保证隧道两端都有控制点;2.桥梁控制网要求纵向精度高干其他方向精度;3.投影面的选择应满足“控制点坐标反算的两点间长度与实地两点间长度之差应尽可能小”;隧道控制网的投影面一般选在贯通平面上,或选在放样精度要求最高的平面上;知识点三:工程控制网建立过程(了解)工程控制网建立过程如下:(1)设计。
(2)选点埋石。
(3)观测。
(4)平差计算。
知识点四:工程控制网设计步骤工程控制网的设计步骤如下:(1)根据控制网建立目的、要求和控制范围,经过图上规划和野外踏勘,确定控制网的图形和参考基准(起算数据);(2)根据测量仪器条件,拟定观测方法和观测值先验精度;(3)根据观测所需的人力、物力,预算控制网建设成本;(4)根据控制网图形和观测值先验精度,估算控制网成果精度,改进布设方案;(5)根据需要,进行控制网优化设计。
知识点五:工程控制网的坐标系选择在满足工程精度的前提下,工程控制网一般采用国家统一的3°带高斯平面直角坐标系。
(考题)当不能满足工程对高斯投影长度变形的要求(通常不大于2.5 cm/km)时,可以自定义中央子午线和投影基准面,建立任意带的独立高斯平面直角坐标系,但应与国家坐标系衔接,建立双向的坐标转换关系。
第三章 控制网平差

能够唯一地确定一个几何模型所必要的元素, 称必要元素;确定必要元素的观测称为必要观
测。必要元素的个数用t 表示。
• 为了确定一个几何模型就必须进行观测。如果 观测个数 n 少于必要元素的个数,即 n<t,显 然无法确定该模型,出现了数据不足的情况; 若观测了 t 个独立量,n =t,则可唯一地确定 该模型。在这种情况下,如果观测结果中含有 错误,将无法发现。为了能及时发现错误,并 提高测量成果的精度,就必须使 n>t,即必须 进行多余观测。多余观测的个数在测量中又称 “自由度”。令
h1 h3 h2 0
h1 h6 h 4 0
(a)
h2 h5 h4 0
式中: h i 表示观测量 hi 的平差值。
这就是用平差值表达的条件方程。
由于平差值应该等于观测值与其改正数之和, 即:
hi hi vi
代入(a)式得:
其中:
v1 v2 v3 w1 0 v1 v4 v6 w2 0, v2 v4 v5 w3 0
P
. . .
p2 . .
. .
... .
. pn
显然 P 是一个对角阵,其逆存在,且:
1 . . .
p1
P 1
.
.
.
1 .
p2
.
. .
... .
. 1
p n
三、法方程的解
令
N = AP –1 AT
则法方程式的形式为
第3章 工程控制网布设的理论与方法
3.1 工程控制网的分类和作用
二、作用 工程控制网也具有控制全局、提供基准和控制
测量误差积累的作用。
三、建网步骤 遵循大地测量学的原理,如: 要有坐标系和基准 要构成网 要逐级布设等。
10
工程控制网的分类、作用和建网步骤
工程控制网的布设也遵循国家控制网建立的一些基本原 理,如要有坐标系和基准,要构成网,采用逐级布设方式等。
y y1 y1 y2 y2
2
2
x x1 x1 x2 x2
2
2
x1
O′
B
∆x
B′
A O ∆y A′
x1′
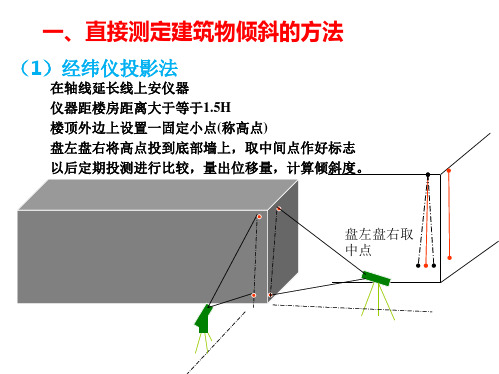
用矢量相加的方法,计 x2′
算出顶部中心O对底部中心
O′的总偏移值ΔD,即
y
y2
y1
y1′
y2′
D x 2 y2
arctan1( D)
H
(2)测水平角的方法
(2)测水平角的方法
主要内容
工程控制网的作用和分类 工程控制网的基准和建立方法 工程控制网的质量准则 工程控制网的优化设计 典型工程控制网 控制点的埋石与标志 控制测量内外业一体化
重点
工程控制网的质量准则
2
3.1 工程控制网的分类和作用
3.1.1 测量控制网的分类 全球控制网(地球、板块、运动) 国家控制网(测图、坐标框架、定点) 工程控制网(服务工程、参考框架)
二等三角测量有两种布网形式 •1、由纵横交叉的两条二等基本锁将一等锁环划分成
等 4个大致相等的部分,这4个空白部分用二等补充网填
三 充,称纵横锁系布网方案。
角 锁
•2、在一等锁环内布设全面二等三角网,称全面布网 方案。二等基本锁的边长为20~25公里,二等网的平
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
h2
C h4 h5 h3 h6
D
这个水准网可以列出7个条件方程,其中只有 3个是相互独立的,我们取:
h1 h3 h2 0 h1 h6 h4 0 h2 h5 h4 0
式中:
(a)
hi
表示观测量 hi 的平差值。
这就是用平差值表达的条件方程。
由于平差值应该等于观测值与其改正数之和, 即:
第三节 独立三角网条件平差
根据三角网中起算数据的多少,三角网有 独立三角网(网中仅有必要的起算数据)和非
独立三角网(网中具有多余的起算数据)之分。
三角网平差有按角度平差和按方向平差两种方
法。本节讨论独立三角网按角度进行条件平差
时,条件方程式列立、法方程式组成和解算的
详细步骤和方法。
条件平差时,关键是列出条件方程。独立 三角网的观测量主要是三角形的内角,这些角 在几何上应该满足一定的条件,这些条件就是 列立条件方程的基础。 根据几何条件的不同,独立三角网的条件 方程分为图形条件、圆周角条件、极条件、基 线条件四种类型。
P
1
三、法方程的解
令 N = AP –1 AT ( 3)
则法方程式的形式为
N K+W =0 其中N 称为法方程式系数矩阵,是一个满 秩二次型方阵,其逆存在。从而可解出联系 数向量: K = -N –1 W ( 4)
四、条件平差的一般过程
(1)列出条件方程 AV +W=0
(2)组成法方程系数矩阵 N = AP –1 AT
p1 . P . .
. p2 . .
. . ... .
. . . pn
显然 P 是一个对角阵,其逆存在,且:
1 p1 . . . . 1 p2 . . . . ... . . . . 1 pn
第三章 控制网平差
• 完成控制网测量的外业工作后要进行 内业计算,内业计算分为概算、平差计 算和编制控制点成果表。本章重点介绍 独立三角网的条件平差方法。 • 第一节 • 第二节 • 第三节 测量平差的数学模型 条件平差原理 独立三角网条件平差
第一节
测量平差的数学模型
一、必要观测与多余观测
在测量工作中,最常见的问题是要确定 某些几何量的大小。由各种几何量构成的模型 (测量中就是各种控制网)就是几何模型。 为了确定一个几何模型,并不需要知道该 模型中所有元素的大小,而只需要知道其中部 分元素,其它元素可以通过已知的元素确定。 能够唯一地确定一个几何模型所必要的元 素,称必要元素;确定必要元素的观测称为必 要观测。必要元素的个数用t 表示。
令其等于零,注意到 (PV )T = V T P,从而有: V T P =K T A 转置后左乘 P –1 得: V =P –1 ATK (1) 该公式表达了改正数 V 与联系数 K 的关系。
二、法方程式
将(1)式代入条件方程 AV +W=0 中得: AP –1 AT K+W=0 ( 2) 这就是条件平差的法方程式。式中,P为观测值 的权矩阵,设第 i 个观测值的权为 pi , 则
V -为n 1列阵,称为改正数向量; W-为r 1列阵,称为闭合差向量。
2、间接平差法
• 一个几何模型中,只会有 t 个独立量,如果平
差时就以这 t 个独立量为参数,模型中的所有
量都一定是这 t 个独立参数的函数,亦即每个
观测量都可表达成所选 t 个独立参数的函数。
• 选择几何模型中 t 个独立量为平差参数,将每
矩阵求导的两个公式:
(1) 设C为常数阵,X为列阵,则
d (CX ) C dX
(2)设Y、Z 均为列阵,则:
d (Y T Z ) T dZ T dY Y Z dX dX dX
一、改正数方程
函数 Ф = VTPV - 2 KT ( AV+W ) 对 V 求导:
d T T T V P ( PV ) 2 K A dV
例如: 为确定三角 形ABC,只需要3 个必要观测,它们 可以是: S1, a, b
或: S1, a, c
S2
C c
S3
或: S1, S2, b
或: S1, S2, S3
b a
……
B
S1
A
如果观测了所有六个元素,则有3 个多余观测
二、平差的数学模型
• 测量中是通过观测来确定控制网中的某些几 何量,因而考虑的模型总是数学模型。因为 观测量是一种随机变量,所以平差的数学模 型应同时包含函数模型和随机模型。函数模 型和随机模型总称为数学模型。 • 函数模型是由描述观测量和待求量间的函数 关系的模型,随机模型是描述观测量及其相 互间统计相关性质的模型。建立这两种模型 是测量平差中最基本而首先考虑的问题。
V=P –1 ATK
• 改正数
• 条件平差的一般过程
(1)列出条件方程 (2)组成法方程系数矩阵 AV +W=0 N = AP –1 AT K = - N –1 W V=P –1 ATK
(3)解法方程得到联系数
(4)计算改正数
(5)计算平差值
L L V
(6)精度评定(计算单位权方差、观测值中误 差、平差值函数的中误差等)
w限 2m n
式中, m 为角度观测中误差; n 为圆周角的个数。
三、极条件
以中点多边形为例,若从OA边出发, 依次解算三角形①、②、…,最后解算 出的OA边长应与出发边OA相等。即:
是确定条件方程满足VTPV=min 的唯
一解。
根据计算函数的条件极值的拉格朗 日乘数法则组成新函数: Ф = VTPV- 2KT(AV+W)
其中: K =(k1, k2,…,kr )T 是拉格 朗日乘数,测量平差中称之为联系数 向量。 显然,只要令Ф对V的一阶导数等于 零就可以求出 VTPV 的极值。
一个观测量表达成所选参数的函数,即列出 n
个这种函数关系式,以此为平差的函数模型,
称为间接平差法,又称参数平差法。
例如: △ABC中,观测量为其中的三个内角,选 定∠A和∠B为平差参数,设为X1和 X2,将 每一个观测量均表达为这两个平差参数的 函数,构成数学模型: C
L1 X 1 L2 X 2 L 3 X 1 X 2 180
• 为了确定一个几何模型就必须进行观测。如果 观测个数 n 少于必要元素的个数,即 n<t,显 然无法确定该模型,出现了数据不足的情况; 若观测了 t 个独立量,n =t,则可唯一地确定 该模型。在这种情况下,如果观测结果中含有 错误,将无法发现。为了能及时发现错误,并 提高测量成果的精度,就必须使 n>t,即必须 进行多余观测。多余观测的个数在测量中又称 “自由度”。令 r=n–t 显然, r 就是多余观测数。
2. 改正数表达的图形条件
平差值、观测值、改正数三者的关系为:
ai ai vai ;
bi bi vbi ; ci ci vci
代入用平差值表达的条件方程,整理后可得
(1)中点多边形和三角锁:
vai+vbi+vci+wi=0;
wi= ai+ bi +ci - 180º
(2)大地四边形:
各角度值之和不等于360°的现象,平差时
除了要满足三角形闭合条件外,还必须使中
心点处的角度满足下列条件:
a1
c
i
360 0
b1
c1 ci ai bi
用改正数表达的圆周角条件为:
v
ci
wo 0 ; wo ci 360
其中,wo 称为圆周角条件闭合差。 对wo应用误差传播定律,并以2倍中误差作 为限差,则圆周角闭合差的限差为:
• 测量平差通常是基于线性函数模型的, 当函数模型为非线性形式时,是将其用 泰勒公式展开,并取其一次项化为线性 形式。
• 对于一个实际平差问题,可建立不同形 式的函数模型,相应地就有不同的平差 方法。测量中常见的控制网平差方法有 条件平差和间接平差两种。
1、条件平差法
以观测量之间必须满足一定的条件方程为 函数模型的平差方法,称为条件平差法 。 例如:为了确定B、 C、D三点的高程, 其必要观测数 t =3, 实际观测了6 段高 差, 故多余观测数 r = n–t =3,应列出 3个线性无关条件 方程.
A
X1 L1
L3
X2 L2
B
令: L1 L1 v1 L L 2 L2 v2 L V v L3 L 3 3 0 1 0 X1 B 0 1 , X , d 0 X 2 1 1 180
1 0 1
1 0 0
0 1 1
0 0 1
0 w1 1 , W w2 w 0 3
V = ( v1
v2
v3
v4
v5
v6)T (c)
则条件方程可表达为以下矩阵形式: AV +W=0
这就是条件平差函数模型的一般形式。
条件方程
AV +W=0 中,
A -为r n 阶矩阵,称为系数矩阵;
则间接平差的函数模型可用以下矩阵形式表达:
L+V=BX+d 或: V=BX – l 此式称为间接平差误差方程。 式中,L 为观测值向量( n 1 阶); V 为改正数向量( n 1 阶) ; B 为系数矩阵( n t 阶) ; X 为未知数向量( t 1 阶) ;
l =L – d 为常数矩阵( n 1 阶) 。
bi ai
ci
an
bn
bi
cn
(a)
(b)
• 对于大地四边形,
