第二章 运动的守恒量和守恒定律
合集下载
动量和动量守恒定律解析
动量和动量守恒定律解析动量是物体运动的基本性质之一，它描述了物体在运动过程中的惯性和动力。
动量的大小与物体的质量和速度有关，定义为质量乘以速度。
而动量守恒定律则是描述了在没有外力作用下，物体的总动量保持不变的原理。
本文将对动量和动量守恒定律进行解析，探讨其在物理学中的重要性和应用。
一、动量的概念和性质动量是描述物体运动状态的物理量，它与物体的质量和速度有关。
动量的大小等于物体的质量乘以其速度，即p=mv。
其中，p表示动量，m表示物体的质量，v表示物体的速度。
动量是一个矢量量，具有大小和方向。
当物体的速度改变时，其动量也会相应改变。
动量具有一些重要的性质。
首先，动量是物体运动的量度，它能够描述物体的惯性。
质量越大，速度越快的物体，其动量也越大。
其次，动量是一个守恒量，即在没有外力作用下，物体的总动量保持不变。
这就是动量守恒定律。
二、动量守恒定律的原理动量守恒定律是描述物体在没有外力作用下动量保持不变的原理。
根据牛顿第二定律F=ma，可以推导出动量守恒定律。
如果物体在外力作用下的加速度为零，即a=0，那么根据牛顿第二定律可知，物体所受合力F=0。
根据动量的定义p=mv，可得到物体的动量变化量Δp=mΔv。
当物体的加速度为零时，它的速度不变，即Δv=0，所以动量的变化量Δp=0，即物体的总动量保持不变。
动量守恒定律适用于没有外力作用的系统。
在这种情况下，系统中各个物体之间的相互作用力互相抵消，不会改变物体的总动量。
例如，当两个物体发生碰撞时，它们之间的相互作用力会导致动量的转移，但总动量保持不变。
三、动量守恒定律的应用动量守恒定律在物理学中有广泛的应用。
首先，它可以用来解释和预测物体碰撞的结果。
根据动量守恒定律，当两个物体碰撞时，它们的总动量保持不变。
利用这一原理，可以计算碰撞后物体的速度和方向。
例如，当一个小球以一定的速度撞向一个静止的小球时，根据动量守恒定律可以计算出两个小球碰撞后的速度。
其次，动量守恒定律还可以用来解释流体的运动。
动量守恒定律
17
物理 （工）
2-2
动量守恒定律
应有 L 常矢量
即 J11 J 22
解 m绕O转动中， 所受力矩M=0．
r/2
O
r
v
m
F
2
mr0 0 mr
2
解得： r / r
2 0 0
2
第二章 守恒定律
18
物理 （工）
2-2
动量守恒定律
2011.04 6.如图，一质量为M的均匀直杆可绕通过O点的水平轴转动， 质量为m的子弹水平射入静止直杆的下端并留在直杆内， 则在射入过程中，由子弹和杆组成的系统（ ） A.动能守恒 B.动量守恒 C.机械能守恒 D.对O轴的角动量守恒
27
物理 （工）
2-2
动量守恒定律
2011.04
第二章 守恒定律
28
物理 （工）
2.6
2-2
动量守恒定律
一 保守力作功的特点
(1) 万有引力作功
m ' 对m 的万有引力为
m' m F G 2 er r
A
rA e
r
r
rB
m
dr
m'
dr r dr
B
m移动dr 时，F作元功为
x1
x2
x2
x1
1 2 1 2 kxdx ( kx2 kx1 ) 2 2
31
第二章 守恒定律
物理 （工）
2-2
动量守恒定律
F
dW
O
x1
x2
dx
x2 x
W Fdx
x1
x2
x1
1 2 1 2 kxdx ( kx2 kx1 ) 2 2
物理 （工）
2-2
动量守恒定律
应有 L 常矢量
即 J11 J 22
解 m绕O转动中， 所受力矩M=0．
r/2
O
r
v
m
F
2
mr0 0 mr
2
解得： r / r
2 0 0
2
第二章 守恒定律
18
物理 （工）
2-2
动量守恒定律
2011.04 6.如图，一质量为M的均匀直杆可绕通过O点的水平轴转动， 质量为m的子弹水平射入静止直杆的下端并留在直杆内， 则在射入过程中，由子弹和杆组成的系统（ ） A.动能守恒 B.动量守恒 C.机械能守恒 D.对O轴的角动量守恒
27
物理 （工）
2-2
动量守恒定律
2011.04
第二章 守恒定律
28
物理 （工）
2.6
2-2
动量守恒定律
一 保守力作功的特点
(1) 万有引力作功
m ' 对m 的万有引力为
m' m F G 2 er r
A
rA e
r
r
rB
m
dr
m'
dr r dr
B
m移动dr 时，F作元功为
x1
x2
x2
x1
1 2 1 2 kxdx ( kx2 kx1 ) 2 2
31
第二章 守恒定律
物理 （工）
2-2
动量守恒定律
F
dW
O
x1
x2
dx
x2 x
W Fdx
x1
x2
x1
1 2 1 2 kxdx ( kx2 kx1 ) 2 2
大学物理：2-2 动量守恒定律
y P
rP
F
O
地球
r
C
Q
rQ x
7
3、保守力 (conservation force)
物体在某种力的作用下， 沿任意闭合路径绕行一周所 作的功恒等于零，即
Q
CD
E
F
P
F dl 0
具有这种特性的力，称为保守力；不具有这种特 性的力称为非保守力。
8
四、 机械能守恒定律
1、功能原理 由 n 个相互作用着的质点所组成的质点系。系统中
Q
A
Q Q
AaPdFv,d
r
P
dr
ma d r
vdt
F
Q
m
d
vdtv
d
t
P dt
Q P
mv
d
v
1 2
mvQ2
1 2
P
mvP2
vdPr
质点的动能(kinetic energy)定义：质点的质量与
其运动速率平方的乘积的一半。
用Ek表示，即
Ek
1 2
mv2
5
所以有 A Ek Q Ek P 动能定理：作用于质点的合力所作的功，等于质点
0
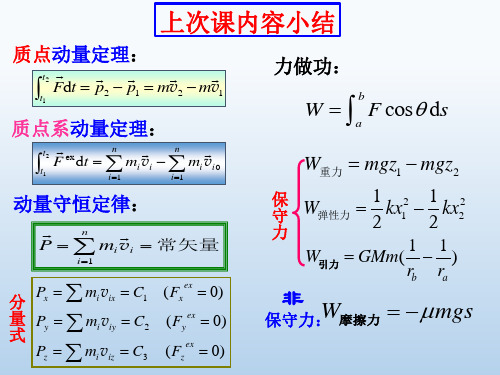
mivi 恒矢量
i 1
在外力的矢量和为零的情况下，质点系的总动量
不随时间变化——动量守恒定律。
其分量式
n
mi vix 恒量
i 1 n
mi viy 恒量
i 1 n
mi viz 恒量
i 1
n
(当 Fix 0 时)
i 1
n
(当 Fiy 0 时)
i 1
n
(当 Fiz 0 时)
i 1
大学物理第二章习题质点力学的基本规律 守恒定律
第2章 质点力学的基本规律 守恒定律
基本要求
掌握经典力学的基本原理及会应用其分析和处理质点动力学问题，理 解力学量的单位和量纲。掌握动量、冲量、动量定理，动量守恒定律。并 能分析和计算二维平面简单力学问题。理解惯性系概念及经典力学的基本 原理的适用范围。掌握功与功率、动能、势能（重力势能、弹性势能、引 力势能）概念，动能定理、功能原理、机械能守恒定律。
教学基本内容、基本公式
1.牛顿定律
解牛顿定律的问题可分为两类： 第一类是已知质点的运动，求作用于质点的力； 第二类是已知作用于质点的力，求质点的运动.
2.基本定理 动量定理
动能定理
I
t2 t1
F (t )dt
mv
mv0
A12
2
F
(r)
dr
1
1 2
mv
2 2
1 2
解：根据牛顿第二定律
f
k x2
m dv dt
m dv d x dx dt
mv
dv dx
k x2
mv
dv dx
v
dv
k
dx mx2
v
v
0
dv
A/4
A
k mx2
d
x
1v2 k (4 1) 3 k 2 m A A mA
另解：根据动能定理
v 6k /(mA)
(2)写出初末态系统的动量
t 时刻水平方向动量
dm m
t+dt时刻水平方向动量
O
x
(3)求出系统水平方向动量的增量
基本要求
掌握经典力学的基本原理及会应用其分析和处理质点动力学问题，理 解力学量的单位和量纲。掌握动量、冲量、动量定理，动量守恒定律。并 能分析和计算二维平面简单力学问题。理解惯性系概念及经典力学的基本 原理的适用范围。掌握功与功率、动能、势能（重力势能、弹性势能、引 力势能）概念，动能定理、功能原理、机械能守恒定律。
教学基本内容、基本公式
1.牛顿定律
解牛顿定律的问题可分为两类： 第一类是已知质点的运动，求作用于质点的力； 第二类是已知作用于质点的力，求质点的运动.
2.基本定理 动量定理
动能定理
I
t2 t1
F (t )dt
mv
mv0
A12
2
F
(r)
dr
1
1 2
mv
2 2
1 2
解：根据牛顿第二定律
f
k x2
m dv dt
m dv d x dx dt
mv
dv dx
k x2
mv
dv dx
v
dv
k
dx mx2
v
v
0
dv
A/4
A
k mx2
d
x
1v2 k (4 1) 3 k 2 m A A mA
另解：根据动能定理
v 6k /(mA)
(2)写出初末态系统的动量
t 时刻水平方向动量
dm m
t+dt时刻水平方向动量
O
x
(3)求出系统水平方向动量的增量
物理学 第二章 牛顿运动定律
g sin a2 tg( ) g cos
g sin a2 arc tg g cos
讨论：如果=0，a1=a2 ，则实际上是小车在水平 方向作匀加速直线运动；如果=0，加速度为零， 悬线保持在竖直方向。
例题2-3 一重物m用绳悬起，绳的另一端系在天花板上， 绳长l=0.5m，重物经推动后，在一水平面内作匀速率圆 周运动，转速n=1r/s。这种装置叫做圆锥摆。求这时绳 和竖直方向所成的角度。
2m1m2 T g m1 m2
（2）电梯加速下降时，a<0，即得到
m1 m2 ar ( g a) m1 m2
a=g，即得到
2m1m2 T ( g a) m1 m2
ar 0,
T 0
例题2-2 一个质量为m、悬线长度为l的摆锤，挂在架子上， 架子固定在小车上，如图所示。求在下列情况下悬线的方 向(用摆的悬线与竖直方向所成的角表示)和线中的张力： (1)小车沿水平方向以加速度a1作匀加速直线运动。 (2)当小车以加速度a2沿斜面(斜面与水平面成角)向上作 匀加速直线运动。
自然坐标系中的分量形式
2
dv Ft mat m dt
Fn man m
v
2
2、牛顿第二定律的微分形式
牛顿第二定律原文意思：运动的变化与所加的动力成正 比，并且发生在这力所沿直线的方向上。 这里的“运动”指物体的质量和速度矢量的乘积。
p mv
牛顿第二定律实质上是：
dp F dt
g cos 2 2 0.497 4 n l
60 13
可以看出，物体的转速n愈大， 也愈大，而 与重物的质量m无关。
l
大学物理第二章动能定理
例题3. 如图，一轻绳跨过一定滑轮，两边分别拴有质量
为m及M的物体，M离地面的高度为h: (1)若滑轮质量及
摩擦力不计，m与桌面的摩擦也不计，开始时两物体均静
止，求M落到地面时的速度(m始终在桌面上); (2)若m与
桌面的静摩擦系数和滑动摩擦系数均为，结果又如何？
解：
m
(1)不计摩擦,系统(m,M,地球)机械能守恒:
v
m
0 M f c
f
s
s
Wf Wf 0
N
v c
N
WN WN 0
质点系动能定理：
质点系的动能的增量等于作用于质点系的一切外力与
内力做功之和.
W ex
W in
n i1
1 2
mi vi2
n i1
1 2
mi vi20
2.2.1 质点系动量定理
作用于质点系的合外力的冲量等于质点系动量的增量.
t2
系统内所有质点对同一参考点角动量的矢量和称为
质点系的角动量.
L Li ri pi ri mivi
i
i
i
dL dt
d dt
Li
i
Mi外
i
Mi内
i
0
M外
M 外
dL dt
积分得：
t2 t1
M外dt
L2
L1
注意：只有外力矩对质点系的角动量变化有贡献，
内力矩对质点系的角动量变化没有贡献.
W
F dr
l
F dr
acb
F dr
bda
0
a
c
F dr F dr F dr
acb
adb
bda
d
2牛顿定律与守恒定律
i x, y, z
t0
t
F1
二、质点系的动量定理 以两个质点组成的质点系为例 内力(成对出现) 外力
F2
m1
I P P0 t I Fi dt表示质点系的合外力的冲量 t0 i P0 mi vi 0 ， P mi vi表示初、末时刻质
m m x l
M
T ( x x)
x
T ( x) (m) g T ( x x)
T ( x)
T T ( x x) T ( x)
O
x
x x
m, l
mg ( m ) g x (m) g l M T ( x x) mg x dT dx l Mg l mg （ x l 时， ） T Mg dT dx T x l
p mv
矢量 单位：kg m / s
b.低速情况下 (v c) ，m为常量
dp d (mv ) dv F m ma dt dt dt dp F ma dt
c.高速情况下(v接近c)，m为与速度v有关 的变量
(4)牛顿第二定律只适用于质点的运动 合外力 F 与加速度 a 之间是瞬时对应关系
A A
合力的功等于各分力的功的代数和
4．功率 W (1)平均功率 P
t
dW 功率 P dt
(2)描述了做功的快慢 (3) dW F dr cos
dt dt (4)单位： 1W 1J / s
P
Fv cos F v
练习：质量为m的质点在外力F的作用下沿x 轴运动，已知t=0时质点位于原点，且初 速度为零。设外力F随距离线性地减小，且 x=0时，F=F0；x=L时，F=0。求质点 从x=0运动到x=L处的过程中力F对质点 所做的功。 F0 解一：
t0
t
F1
二、质点系的动量定理 以两个质点组成的质点系为例 内力(成对出现) 外力
F2
m1
I P P0 t I Fi dt表示质点系的合外力的冲量 t0 i P0 mi vi 0 ， P mi vi表示初、末时刻质
m m x l
M
T ( x x)
x
T ( x) (m) g T ( x x)
T ( x)
T T ( x x) T ( x)
O
x
x x
m, l
mg ( m ) g x (m) g l M T ( x x) mg x dT dx l Mg l mg （ x l 时， ） T Mg dT dx T x l
p mv
矢量 单位：kg m / s
b.低速情况下 (v c) ，m为常量
dp d (mv ) dv F m ma dt dt dt dp F ma dt
c.高速情况下(v接近c)，m为与速度v有关 的变量
(4)牛顿第二定律只适用于质点的运动 合外力 F 与加速度 a 之间是瞬时对应关系
A A
合力的功等于各分力的功的代数和
4．功率 W (1)平均功率 P
t
dW 功率 P dt
(2)描述了做功的快慢 (3) dW F dr cos
dt dt (4)单位： 1W 1J / s
P
Fv cos F v
练习：质量为m的质点在外力F的作用下沿x 轴运动，已知t=0时质点位于原点，且初 速度为零。设外力F随距离线性地减小，且 x=0时，F=F0；x=L时，F=0。求质点 从x=0运动到x=L处的过程中力F对质点 所做的功。 F0 解一：
普通物理学(第六版)上册第二章第一节课件
1 2 1
§2.2
动量定理和动量守恒定律
（力与运动的过程关系研究）
一、动量定理
dp 由牛顿第二定律： F = Fdt = dp dt 1、冲量 1）微分形式： dI Fdt Fdt 表示力的时间累积，叫时间 d t 内合外力 F 的冲量。
2）积分形式： I
牛顿运动定律适用的参考系称为惯性参考系。 一切惯性系，对于描述机械运动的力学规律来说是完全 等价的。 在一个惯性系内部所作的任何力学实验都不能够确定这 一惯性系本身是在静止状态，还是在做匀速直线运动。这 个原理叫做力学的相对性原理，或伽利略相对性原理。
二、经典（牛顿）力学时空观
据伽利略变换，可得到经典时空观 同时的绝对性
牛顿力学
时间的测量 长度的测量
与惯性系无关
-----牛顿力学的绝对时空观
三、惯性参考系与非惯性参考系
乙 甲
F
m l0
a
观察者甲： 有力 F 和加速度 a 即
F ma
牛顿定律在该参照系中适用 — 惯性系
观察者乙：有力 F 但没有加速度 a 即 m a 0, F 0
P Mvc P mv dp dp F F dt dt F ma F Mac
质点
质点系
例3 一质量m1=50kg的人站在一条质量为m2=200kg， 长度l=4m的船头上，开始时船静止。求当人走到船尾 时船移动的距离。水的阻力不计。
f 惯的方向与非惯性系的加 速度反向。
注意
惯性力不是真实力，无施力物体，无反作用力。
2、非惯性系中的力学规律
a ' 为物体相对非惯性系的加速度
F f 惯 ma '
§2.2
动量定理和动量守恒定律
（力与运动的过程关系研究）
一、动量定理
dp 由牛顿第二定律： F = Fdt = dp dt 1、冲量 1）微分形式： dI Fdt Fdt 表示力的时间累积，叫时间 d t 内合外力 F 的冲量。
2）积分形式： I
牛顿运动定律适用的参考系称为惯性参考系。 一切惯性系，对于描述机械运动的力学规律来说是完全 等价的。 在一个惯性系内部所作的任何力学实验都不能够确定这 一惯性系本身是在静止状态，还是在做匀速直线运动。这 个原理叫做力学的相对性原理，或伽利略相对性原理。
二、经典（牛顿）力学时空观
据伽利略变换，可得到经典时空观 同时的绝对性
牛顿力学
时间的测量 长度的测量
与惯性系无关
-----牛顿力学的绝对时空观
三、惯性参考系与非惯性参考系
乙 甲
F
m l0
a
观察者甲： 有力 F 和加速度 a 即
F ma
牛顿定律在该参照系中适用 — 惯性系
观察者乙：有力 F 但没有加速度 a 即 m a 0, F 0
P Mvc P mv dp dp F F dt dt F ma F Mac
质点
质点系
例3 一质量m1=50kg的人站在一条质量为m2=200kg， 长度l=4m的船头上，开始时船静止。求当人走到船尾 时船移动的距离。水的阻力不计。
f 惯的方向与非惯性系的加 速度反向。
注意
惯性力不是真实力，无施力物体，无反作用力。
2、非惯性系中的力学规律
a ' 为物体相对非惯性系的加速度
F f 惯 ma '