高中数学 空间位置关系的判断与证明 板块四 垂直关系的判断与证明完整讲义(学生版)
空间位置关系的判断与证明.板块四.垂直关系的判断与证明.学生版

【例1】 下列说法正确的有 .①过一点有且只有一条直线垂直于已知直线.②若一条直线与平面内无数条直线垂直,则这条直线与这个平面垂直.③若一条直线平行于一个平面,则垂直于这个平面的直线必垂直于这条直线. ④若一条直线垂直于一个平面,则垂直于这条直线的另一条直线必平行于这个平面.⑤若一条直线平行于一个平面,则它和这个平面内的任何直线都不垂直. ⑥平行于同一个平面的两条直线可能垂直.【例2】 在空间四面体的四个面中,为直角三角形的最多有 个.【例3】 已知在三棱锥A BCD -中AC AD =,BD BC =,求证:AB ⊥CD .ABCE【例4】 如图,已知三棱锥P ABC -,90ACB ∠= ,D 为AB 的中点,且PDB ∆是正三角形,PA ⊥PC .求证:⑴ PA ⊥面PBC ;⑵平面PAC ⊥平面ABC .DPABC【例5】 如图,ABCD 是正方形,SA 垂直于平面ABCD ,过A 且垂直于SC 的平面交SB 、SC 、SD 分别于点E 、F 、G ,求证:AE SB ⊥,AG SD ⊥.典例分析板块四.垂直关系的判断与证明EBCFDGSA【例6】 如图,在四棱锥P ABCD-中,PA ⊥底面A B C ,60AB AD AC CD ABC ⊥⊥∠=,,°,PA AB BC ==,E 是PC 的中点.证明:面ABE ⊥面PCD .【例7】 如图,四面体P ABC -,PA ⊥面ABC ,AB ⊥BC ,过A 作AE ⊥PB 交PB 于E ,过A 作AF ⊥PC 交PC 于F .求证:PC ⊥EF .F EPABC【例8】 如图O 是正方体下底面ABCD 中心,B H D O ''⊥,H 为垂足.求证:B H '⊥平面AD C '.【例9】 如图所示,在正方体1111ABCD A B C D -中..求证:1BD ⊥面1AB C .A 1D 1C 1B 1DCBA【例10】 在长方体1111ABCD A B C D -中,点E ,F 分别在1AA ,1CC 上且1BE A B ⊥,1BF BC ⊥,求证:1BD ⊥面BEF【例11】 在正方体1111ABCD A B C D -中,P 为1DD 的中点,O 为底面ABCD 的中心.求证:1B O ⊥面PAC .【例12】 在四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥底面ABCD ,M ,N 分别为PC ,AB 的中点.⑴求证:MN ∥平面PAD ;⑵若45PDA ∠= ,求证:MN ⊥面PCD .QPD CAMN【例13】 已知平行六面体1111ABCD A B C D -的底面是菱形,且1160A AB A AD ∠=∠= .求证:1CC ⊥BD .OABCD A 1B 1C 1D 1【例14】 (2008深圳高三联考)如图,在直四棱柱1111ABCD A B C D -中,当底面四边形ABCD满足条件 时,有111AC B D ⊥.(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形)D 1C 1B 1A 1DCBA【例15】 如图,A 、B 、C 、D 是空间四点,在ABC △中,2AB =,AC BC ==,等边ADB △所在的平面以AB 为轴可转动.当ADB △转动过程中,是否总有AB CD ⊥?请证明你的结论ABC DO【例16】 在正方体1111ABCD A B C D -中,M 是1AA 的中点,问当点N 位于AB 上何处时,1MN MC ⊥?【例17】 如图,直三棱柱111ABC A B C -中,1AC BC ==,90ACB ∠=︒,1AA =,D 是11A B 的中点.⑴求证1C D ⊥平面1A B ;⑵当点F 在1BB 上什么位置时,会使得1AB ⊥平面1C DF ?并证明你的结论.C 1B 1A 1FEDC B A【例18】 (2000全国,文19)如图已知平行六面体1111ABCD A B C D -的底面A B C D 是菱形,且11C CB C CD BCD ∠=∠=∠.⑴ 证明1C C BD ⊥;⑵ 当1CDCD 的值为多少时,能使1AC ⊥平面1C BD ?请给出证明. 图 9-2-284D 1A 1C 1B 1DCBA【例19】 已知四面体ABCD ,①若棱AB CD ⊥,求证2222AC BD AD BC +=+②若2222AC BD AD BC +=+,求证棱AB CD ⊥.【例20】 已知三棱锥P ABC -中,PC ⊥底面ABC ,AB BC =,D F ,分别为AC PC ,的中点,DE AP ⊥于E .⑴求证:AP ⊥平面BDE ;⑵求证:平面BDE ⊥平面BDF ;⑶若:1:2AE EP =,求截面BEF 分三棱锥P ABC -所成两部分的体积比.【例21】 (2009扬州中学高三期末)在四棱锥P ABCD -中,90ABC ACD ∠=∠=︒,60BAC CAD ∠=∠=︒,PA ⊥平面ABCD ,E 为PD 的中点,22PA AB ==. ⑴求四棱锥P ABCD -的体积V ;⑵若F 为PC 的中点,求证PC ⊥平面AEF .【例22】 (2003京皖春)如图所示,正四棱柱1111ABCD AB C D -中,底面边长为侧棱长为4.E F ,分别为棱AB BC ,的中点,EF BD G = . ⑴求证:平面1B EF ⊥平面11BDD B ;⑵求点1D 到平面1B EF 的距离d ; ⑶求三棱锥11B EFD -的体积V .D 1C 1B 1A 1GFEDCB A。
高中数学常见题型解法归纳 空间直线、平面垂直位置关系的证明
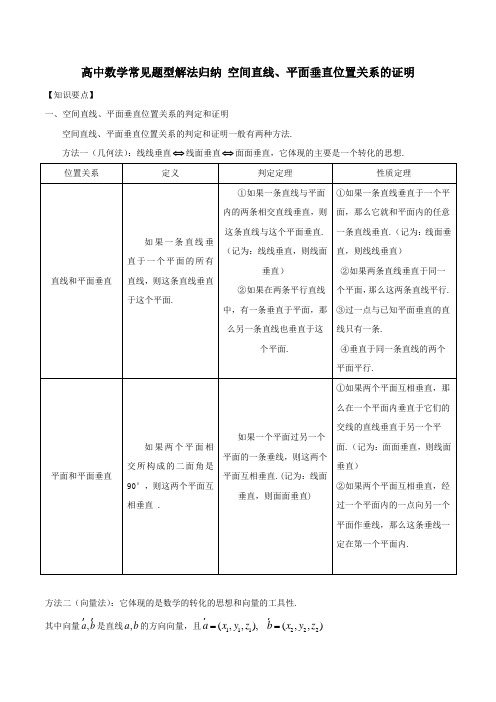
高中数学常见题型解法归纳 空间直线、平面垂直位置关系的证明【知识要点】一、空间直线、平面垂直位置关系的判定和证明空间直线、平面垂直位置关系的判定和证明一般有两种方法.方法一(几何法):线线垂直⇔线面垂直⇔面面垂直,它体现的主要是一个转化的思想.方法二(向量法):它体现的是数学的转化的思想和向量的工具性. 其中向量,a b 是直线,a b 的方向向量,且111222(,,),(,,)a x y z b x y z ==向量,m n 是平面,αβ的法向量,且333444(,,),(,,)m x y z n x y z ==1200(,1212z z a b a b a b x x y y a b a b +⊥⇔⊥⇔=⇔+=直线直线其中分别为直线,的方向向量),,31313(1x y y z z a a m x a a m λλλαα===⊥⇔⇔直线平面其中为直线的方向向量,为平面的法向量)3400(3434z z m n m n x x y y m αβαβ+⊥⇔⊥⇔=⇔+=平面平面其中,n 分别为平面,的法向量) 二、空间的几何元素的位置关系从低到高有三个层次:线线关系、线面关系和面面关系.三、空间垂直位置关系的证明,总是把要证明的垂直关系首先转化成最靠近它的位置关系去证明.如果要证明线线垂直,只能首先转化成证明线面垂直;如果要证明线面垂直,可以首先转化成证明线线垂直或者面面垂直;如果要证明面面垂直,只能首先转化成证明线面垂直. 【方法讲评】【例1】【2017北京,文18】如图,在三棱锥P –ABC 中,PA ⊥AB ,PA ⊥BC ,AB ⊥BC ,PA =AB =BC =2,D 为线段AC 的中点,E 为线段PC 上一点.(Ⅰ)求证:PA ⊥BD ;(Ⅱ)求证:平面BDE ⊥平面PAC ; (Ⅲ)当PA ∥平面BD E 时,求三棱锥E –BCD 的体积.(III )因为PA ∥平面BDE ,平面PAC平面BDE DE =,所以PA DE ∥.因为D 为AC 的中点,所以112DE PA ==,BD DC ==由(I )知,PA ⊥平面ABC ,所以DE ⊥平面PAC .所以三棱锥E BCD -的体积1163V BD DC DE =⋅⋅=. 【点评】(1)本题的第1问证明PA ⊥BD ,转化成证明PA ⊥平面ABC ,第2问证明平面BDE ⊥平面PAC 转化成证明BD ⊥平面PAC .(2)空间垂直位置关系的证明,总是把要证明的垂直关系首先转化成最靠近它的位置关系去证明.转化成哪一条线垂直哪一条线,哪一条线垂直哪一个平面,哪一个平面垂直哪一个平面,这取决于你的观察和分析,主要关注已知条件中的有垂直关系的线和面.【例2】如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,60AB ADAC CD ABC ⊥⊥∠=,,°,PA AB BC ==,E 是PC 的中点.(Ⅰ)证明CD AE ⊥; (Ⅱ)证明PD ⊥平面ABE ;(Ⅲ)求二面角A PD C --的大小.(Ⅲ)ABCDPEABCDPEM⊥的关键是证明CD垂直AE所在的平面PCD.(2)证明PD⊥平面ABE的【点评】(1)证明CD AEPC CD关键是证明PD垂直平面ABE内的两条相交直线,.【反馈检测1】【2017课标3,理19】如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.(1)证明:平面ACD⊥平面ABC;(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C 的余弦值.【例3】如图,已知正方体1AC 棱长为2,E 、F 、G 分别是1CC 、BC 和CD 的中点. (1)证明:1A G ⊥面EFD ;(2)求二面角E DF C --的余弦值.(2)由(1)知1(2,1,2)AG =--为面EFD 的法向量 ∵CE ⊥面CFD ,(0,0,1)CE =为面CFD 的法向量 设1AG 与CE 夹角为θ,则11cos A G CE A G CEθ⋅==⋅231-⋅23=- 由图可知二面角E DF C --的平面角为πθ- ∴二面角E DF C --的余弦值为23. 【点评】本题由于是正方体,所以方便建立空间直角坐标系,所以选择向量的方法比较直接. 当然,也可以选择几何法.【反馈检测2】如图,已知多面体ABCDEF 中,ABCD 为菱形,60ABC ∠=︒,AE ⊥平面ABCD ,,1,AE CF AB AE AF BE ==⊥.(1)求证:AF ⊥平面BDE ;(2)求二面角F BE D --的余弦值.高中数学常见题型解法归纳及反馈检测第60讲: 空间直线、平面垂直位置关系的证明参考答案【反馈检测1答案】(1)证明略;.(2)由题设及(1)知,,,OA OB OD 两两垂直,以O 为坐标原点,OA 的方向为x 轴正方向,OA 为单位长,建立如图所示的空间直角坐标系O xyz -.则()()()()1,0,0,,1,0,0,0,0,1A B C D -.由题设知,四面体ABCE 的体积为四面体ABCD 的体积的12,从而E 到平面ABC 的距离为D 到平面ABC 的距离的12,即E 为DB 的中点,得12E ⎛⎫ ⎪ ⎪⎝⎭.故()()11,0,1,2,0,0,2AD AC AE ⎛⎫=-=-=- ⎪⎪⎝⎭.【反馈检测2答案】(1)见解析;(2)所求二面角得余弦值为5. 【反馈检测2详细解析】(1)设AC BD O ⋂=以O 为空间直角坐标系原点,以OB 为x +轴,以OC 为y +轴,以过O 点平行于AE 的射线为z +轴建立空间直角坐标系xOy ∵1AB AE ==,且菱形ABCD 中60ABC ∠=︒∴1110,,0,,0,,0,,0,,122222A B C D E ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫--- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ ∵AECF 且()0,0,1AE =,∴设()()0,0,0CF λλ=> ∴10,,2F λ⎛⎫ ⎪⎝⎭又∵AF BE ⊥∴102AF BE λ⋅=-+=,∴12λ=,∴110,,22F ⎛⎫ ⎪⎝⎭又∵()10,1,02AF BD ⎛⎫⋅=⋅= ⎪⎝⎭∴AF BD ⊥,又AF BE ⊥且BD BE B = ∴AF ⊥平面BDE(2)设⊥m 平面BEF ,(),,x y z =m∴()11,,,1022BE x y z x y z ⎛⎫⋅=⋅-=-+= ⎪ ⎪⎝⎭m设所求二面角为θ,则有cosθ=.。
空间位置关系判断与证明.板块四.垂直关系判断与证明.教师版普通高中数学复习讲义Word版

板块五.垂直关系的判断与证明典例剖析【例1】以下说法正确的有.①过一点有且只有一条直线垂直于已知直线.②若一条直线与平面内无数条直线垂直,则这条直线与这个平面垂直.③若一条直线平行于一个平面,则垂直于这个平面的直线必垂直于这条直线.④若一条直线垂直于一个平面,则垂直于这条直线的另一条直线必平行于这个平面.⑤若一条直线平行于一个平面,则它和这个平面内的任何直线都不垂直.⑥平行于同一个平面的两条直线可能垂直.【考点】垂直关系的判断与证明【难度】1星【题型】填空【重点字】无【分析】①错误,过一点有一个平面垂直于已知直线,该平面内任一条过该点的直线都垂直于已知直线;②错误,若这无数条直线都是平行直线,则这条直线能够不垂直于这个平面,而且能够与这个平面订交,平行或在平面内;③正确,这条直线平行于这个平面,则必平行于该平面内的一条直线(过这条直线作一个与此平面订交的平面,交线即知足),而垂直于该平面的直线垂直于平面内任一条直线,故必垂直于这条与此平面平行的直线;④错误,能够在此平面内,或与此平面平行;⑤错误,在这个平面内有一组平行线与它异面垂直;⑥正确,比方正方体上底面的两条相邻的棱相互垂直,且都与下底面平行;【答案】正确的说法有③⑥.【例2】在空间四周体的四个面中,为直角三角形的最多有个.【考点】垂直关系的判断与证明【难度】2星【题型】填空【重点字】无【分析】一个可行的例子以下:ABC为直角三角形,B为直角,直线PA 面ABC,D为直线PA上异于A点的随意点,则四棱锥 D ABC的4个面均为直角三角形.(学生能够试着证明)【答案】4;【例3】已知在三棱锥A BCD中AC AD,BD BC,求证:AB⊥CD.AC BED【考点】垂直关系的判断与证明【难度】2星【题型】解答【重点字】无【分析】略【答案】设CD中点为E,连结AE,BE∵ACD为等腰三角形,∴AE⊥CD,同理BE⊥CD∴CD⊥平面ABE,又AB 面ABECD⊥AB.【例4】如图,已知三棱锥P ABC,ACB 90,D为AB的中点,且PDB是正三角形,PA⊥PC.求证:⑴PA⊥面PBC;⑵平面PAC⊥平面ABC.PCADB【考点】垂直关系的判断与证明【难度】3星【题型】解答【重点字】无【分析】略【答案】⑴由已知D是AB中点,PDB是正三角形,1APB为直角三角形∴PDAB,由平面几何知识可知,2∴PA⊥PB,又PA⊥PC,PB PC P,PA⊥面PBC⑵∵PA⊥面PBC又∵BC面PBC,∴PA⊥BC,又AC⊥BC,AC PA A BC⊥面PACBC面ABC∴平面PAC⊥平面ABC【例5】如图,ABCD 是正方形,垂直于平面ABCD,过A且垂直于SC的平面交SB、SASC、SD分别于点E、F、G,求证:AE SB,AG SD.SFGDCEA B【考点】垂直关系的判断与证明【难度】3星【题型】解答【重点字】无【分析】剖析:此题考察线面垂直的判断与性质定理,以及线线垂直和线面垂直相互转化的思想.因为图形的对称性,所以两个结论只需证一个即可.欲证AE SB,可证AE平面SBC,为此须证AE BC、AE SC,从而转变证明BC平面SAB、SC 平面AEFG.【答案】证明:∵SA平面ABCD,BC平面ABCD,∴SABC.又∵ABCD为正方形,∴BC AB.∴BC 平面.ASB∵AE 平面,∴BC AE.ASB又∵SC平面AEFG,∴SC AE.∴AE平面SBC.又∵SB平面SBC,∴AE SB,同理可证AG SD.【例6】如图,在四棱锥P ABCD中,PA底面ABCD,AB AD,AC CD,ABC,BC,E是PC的中点.证明:面60°PAABABE⊥面PCD.∵ 【考点】垂直关系的判断与证明 ∵ 【难度】3星 ∵ 【题型】解答 ∵ 【重点字】无 ∵ 【分析】略 ∵【答案】由PA A B BC ,ABC60°,可得ACPA .E 是PC 的中点,∴AE ⊥PC .在四棱锥PABCD 中,∵PA底面ABCD ,CD平面ABCD ,故P ACD .∵A CCD ,PAA CA ,∴CD ⊥平面PAC .而AE平面 PAC ,∴CD ⊥AE ,且PC CDC ,所以AE平面PCD .而AE 平面ABE ,∴平面ABE 平面PCD .【例7】如图,四周体PABC ,PA ⊥面ABC ,AB ⊥BC ,过A 作AE ⊥PB 交PB 于E ,过A 作AF ⊥PC 交PC 于F .求证:PC ⊥EF . P F E CA B【考点】垂直关系的判断与证明 【难度】3星 【题型】解答 【重点字】无 【分析】略 【答案】剖析:要证线线垂直,可转变为线面垂直,此题重点在于线 面垂直与线线 垂直的转变.可由剖析法下手:要证 PC ⊥EF PC ⊥面AEF PC ⊥AF(已知),PC ⊥AE AE ⊥面PBC AE ⊥PB (已知),AE ⊥BC BC ⊥面PABBC ⊥AB (已知),BC ⊥PA PA ⊥面ABC ,从而问题获得解决.PFE CBA∵PA⊥面ABC,且BC面ABC,∴BC⊥PA,且BC⊥AB∴BC⊥面ABE∴BC⊥AE,又PB⊥AE,且BC PB B∴AE⊥面PBC,且PC面PBC∴AE⊥PC,又AF⊥PC,且AF AE A∴PC⊥面AEF,且EF面AEF∴PC⊥EF此题能够分化出小题,表现中间的转变过程.【例8】如图O是正方体下底面ABCD中心,BH DO,H为垂足.求证:BH平面ADC.D'C'A'B'HD COA B【考点】垂直关系的判断与证明【难度】2星【题型】解答【重点字】无【分析】略【答案】因为BH DO,所以只需再证明BH垂直于面ADC上的此外一条直线即可.因为AC BD,AC BB,所以AC平面BDDB,又BH面BDDB,所以AC BH.于是BH垂直于订交直线AC,DO所在的平面ADC.【例9】以下图,在正方体ABCD A1B1C1D1中..求证:BD1⊥面AB1C.D1C1A1B1DCA B【考点】垂直关系的判断与证明【难度】2星【题型】解答【重点字】无【分析】略D1C1A1B1DCAB【答案】连结BD.∵DD1⊥底面ABCD,又AC面ABCD,∴DD1⊥AC,又底面ABCD为正方形,∴AC⊥BD,又BDDD1D,∴AC⊥面BDD1,又∵BD1面BDD1∴AC⊥BD1同理连结BC1可得BD1⊥B1C∴依据线面垂直的判断定理可得BD1⊥面AB1C.【例10】在长方体1111中,点E ,F分别在1,1上且BE1,ABCDABCD AA CC AB BF BC1,求证:BD1面BEF【考点】垂直关系的判断与证明【难度】2星【题型】解答【重点字】无【分析】略D1C1A1B1FEDA BC【答案】由A1D1A1B,B1E A1B,有B1E面A1BD1B1EBD1由C1D1BC1,B1F BC1,有B1F面BC1D1B1FBD1BD1面B1EF【例11】在正方体ABCD A1B1C1D1中,P为DD1的中点,O为底面ABCD的中心.求证:B1O⊥面PAC.【考点】垂直关系的判断与证明【难度】2星【题型】解答【重点字】无【分析】略D1C1A1B1PDCOA B【答案】(法一)因为AC⊥BD,且AC⊥BB1,∴AC⊥面BDD1B1,且B1O面BDD1B1.∴B1O⊥AC连结PB1,设AB a,则AB1CB1B1D12aD1C1A1B1PD QCOA B空间位置关系判断与证明.板块四.垂直关系判断与证明.教师版普通高中数学复习讲义Word 版∵OB 12OB2BB 12(2a)2a 23a 222 2221 2 29 2PB 1PD 1B 1D 1(a)(2a)a24OP2PD2DO2(1a)2( 2a)2 3a 222 4∴OB 12 OP 2 PB 12 .∴B 1O ⊥OP ,又POAC O ,∴B 1O ⊥平面PAC (法二)因为AC ⊥BD ,且AC ⊥BB 1,∴AC ⊥面BDD 1B 1,且B 1O面BDD 1B 1 ∴B 1O ⊥AC取CD 中点Q ,连结QC 1,OQ ,则OQ ∥B 1C 1在正方形CC 1D 1D 中,由P ,Q 分别为DD 1,CC 1 的中点,可知CP ⊥C 1Q ,又CP ⊥B 1C 1,且C 1QB 1C 1C 1∴CP ⊥面B 1C 1QO ,又B 1O面B 1C 1QOCP ⊥B 1O ∴B 1O ⊥面PAC【例12】在四棱锥PABCD 中,底面ABCD 为矩形,PA ⊥底面ABCD ,M ,N 分别为PC ,AB 的中点.⑴求证:MN ∥平面PAD ;⑵若PDA45,求证:MN ⊥面PCD .PM QDCANB【考点】垂直关系的判断与证明【难度】4星 【题型】解答 【重点字】无 【分析】略【答案】⑴取PD 中点Q ,连结MQ ,AQ , ∵M ,N 分别为AB ,PC 的中点 ∴MQ ∥AN 且MQ AN ∴MN ∥AQ ,从而获得 MN ∥平面PAD⑵(法一)空间位置关系判断与证明.板块四.垂直关系判断与证明.教师版普通高中数学复习讲义Word版PMD RCA NB∵PA⊥底面ABCD,且CD面ABCD∴CD⊥PA,又由底面是矩形有CD⊥AD∴CD⊥面PAD,又AQ面PADAQ⊥CD又∵PDA45,∴PAAD从而在等腰RtAPD中,又PQQDAQ⊥PD,又CDPDDAQ⊥面PAD,又MN∥AQMN⊥面PCD(法二)∵PA⊥底面ABCD,且CD面ABCD∴CD⊥PA,又由底面是矩形有CD⊥AD∴∴CD⊥面PAD,又PD面PAD∴PD⊥CD∴取CD中点R,连结MR,NR,则MR∥PD,NR∥AD CD⊥MR,又CD⊥AD,∴CD⊥NR,∴CD⊥面MNR,且MN面MNR,∴MN⊥CD∵PDA 45,∴PAAD,且BCAD∴PA BC,又A N BN,且PANCBN90∴依据三角形全等可知PN NC,又PM MC∴MN⊥PC∵CD P C C,∴MN⊥面PCD【例13】已知平行六面体 ABCD A1B1C1D1的底面是菱形,且A1AB A1AD60.求证:CC1⊥BD.D1A1C1DOA B B1 C【考点】垂直关系的判断与证明【难度】3星【题型】解答【重点字】无【分析】略【答案】∵底面ABCD是菱形,∴BD⊥AC连结BD,AC交于点O,连结A1B,A1D∵A1AB A1AD60,由A1AD≌A1AB可知,∴A1BD为等腰三角形,又BO OD∴AO⊥BD,又AC AO O,11∴BD⊥面A1AO,又AA1∥CC1,且CC1面A1AO.∴CC1⊥BD【例14】如图,在直四棱柱ABCD A1B1C1D1中,当底面四边形ABCD知足条件时,有AC BD.(注:填上你以为正确的一种条件即可,不用考虑全部可能的111情况)A1D1B1C1AB DC【考点】垂直关系的判断与证明【难度】2星【题型】解答【重点字】2008年,深圳高三联考【分析】略【答案】AC BD(或更特别的四边形ABCD是正方形或菱形);AC BD1BD平面ACCABDAC.1111故充要条件为AC BD,此题只需求写一个充足条件即可.【例15】如图,A、B、C、D是空间四点,在△ABC中,AB2,AC BC2,等边△ADB所在的平面以AB为轴可转动.当△ADB转动过程中,能否总有ABCD?请证明你的结论AOC BD【考点】垂直关系的判断与证明【难度】2星【题型】解答【重点字】无【分析】略【答案】当△ADB在转动过程中,总有OC AB,OD AB.AB平面COD,∴ABCD当△ADB转动到与△ABC共面时,仍旧有AB CD故△ADB转动过程中,总有AB CD.【例16】在正方体ABCD A1B1C1D1中,M是AA1的中点,问当点N位于AB上哪处时,MN MC1?【考点】垂直关系的判断与证明【难度】3星【题型】解答【重点字】无【分析】略【答案】若想MN MC1,只需MN MB1,只需△A1MB1∽△AMN,只需AN 1AM,N位于AN∶NB1∶3处,即AB的四平分点处.2【例17】如图,直三棱柱ABCA1B1C1中,AC BC1,ACB90,AA12,D是A1B1的中点.⑴求证C1D平面A1B;⑵当点F在BB1上什么地点时,会使得AB1平面C1DF?并证明你的结论.A CBFEA 1 C 1D B 1【考点】垂直关系的判断与证明 【难度】3星 【题型】解答 【重点字】无 【分析】略 A C BFEA 1C 1D【答案】 B 1⑴如图,∵ABCA 1B 1C 1是直三棱柱,∴ACBC1,且 ACB90.1111111又D 是A 1B 1的中点,∴C 1DA 1B 1.∵AA 1 平面A 1B 1C 1,C 1D 平面A 1B 1C 1, ∴AA 1 C 1D ,∴C 1D平面AA 1B 1B .⑵作DEAB 1交AB 1于E ,延伸DE 交BB 1于F ,连结C 1F ,则AB 1 平面C 1DF ,点F 即为所求.事实上,∵C 1D平面AA 1B 1B ,AB 1平面AA 1B 1B ,∴C 1DAB 1.又AB 1 DF ,DFC 1DD ,AB 1平面C 1DF .【例18】如图已知平行六面体ABCDA 1B 1C 1D 1的底面ABCD 是菱形,且C 1CBC 1CDBCD . ⑴证明C 1CBD ;⑵当CD的值为多少时,能使A 1C平面C 1BD ?请给出证明.CD 1B1A 1C 1D 1ABCD图9-2-284【考点】垂直关系的判断与证明 【难度】4星 【题型】解答【重点字】2000年,全国高考 【分析】略【答案】⑴连结A 1C 、AC ,AC 和BD 交于O ,连结C 1O .∵四边形ABCD 是菱形,∴ AC BD ,BCCD .又∵ BCC 1 DCC 1,C 1C C 1C ,∴C 1BC ≌C 1DC .∴C 1BC 1D .∵DO OB ,∴C 1OBD .又AC BD ,ACC 1OO ,∴BD平面AC 1.又C 1C 平面AC 1,∴C 1CBD .⑵当CDAC平面 CBD .1时,能使11CC 1证法一:∵CD1,∴BCCD C 1C .CC 1B 1A 1C 1D 1G BHACD图9-2-285C 1CD ,由此可推得BD C 1BC 1D .又BCDC 1CB∴三棱锥C C 1BD 是正三棱锥.设A 1C 与C 1O 订交于G .∵AC 11∥AC ,且AC 1 1:OC2:1,∴C 1G:GO 2:1.又C 1O 是正 C 1BD 的BD 边上的高和中线,∴点G 是正C 1BD 的中心.∴CG 平面C 1BD ,即A 1C 平面C 1BD .证法二:由 ⑴知BD 平面AC 1,∵A 1C 平面AC 1,∴BDAC 1.当CD时,平行六面体的六个面是全等的菱形,同BD AC 证法可得11CC 1BC1AC.又 BD BC1B,∴ACCBD.11平面1【例19】已知四周体ABCD ,①若棱AB2222CD ,求证ACBD AD BC②若AC 2 BD 2 AD 2 BC 2,求证棱 AB CD .【考点】垂直关系的判断与证明 【难度】3星 【题型】解答 【重点字】无 【分析】略 【答案】①过B 作CD 的垂线,垂足E ,连AE ,ABDEFC∵CDAB , CD 平面ABE ,∴CD AE .∴AC 2 AE 2 CE 2、BD 2BE 2 DE 2;又有AD 2AE 2DE 2、BC 2 BE 2 CE 2.∴AC 2 BD 2 AE 2 BE 2 CE 2DE 2,而AD 2 BC 2 AE 2 BE 2 CE 2 DE 2.∴AC 2 BD 2 AD 2 BC2. ②过A 点作CD 的垂线,垂足设为 F ,于是有:AD 2 AF 2 DF 2、BC 2 BE 2CE 2;AC 2 AF 2 CF 2、BD 2 BE 2DE 2;∵AD 2 BC 2 AC 2 BD 2;∴AF 2 DF 2BE 2 CE 2 AF 2 CF 2 BE 2 DE 2∴DF2 CE 2 CF 2 DE2,∴DF 2CF 2DE22CE ,∴DFCF DFCFDE CE DE CE ,∴DF CF DE CE .∴DF CE DE CF .∴E 、 F 只好重合于一点,故有 CD 平面ABE ,∴CD AB .【例20】已知三棱锥P ABC中,PC底面ABC,ABBC,D,F分别为AC,PC的中点,DE AP于E.⑴求证:AP⑵求证:平面⑶若AE:EP 平面BDE;BDE 平面BDF;1:2,求截面BEF分三棱锥P ABC所成两部分的体积比.【考点】垂直关系的判断与证明【难度】3星【题型】解答【重点字】无【分析】略PEFDACB【答案】⑴∵AB BC,D为AC中点,∴BD AC又PC底面ABC,∴PCBD∵PC AC C,∴BD平面PAC,∴BD AP.又DE AP,∴AP平面BDE.⑵∵D,F为AC,PC的中点,∴DF∥AP.联合⑴可知DF平面BDE.⑶∵S PEF:S PAC PE PF211,∴B PEF1BPAC.PA PC32V V33所以两部分的体积比为1:2.【例21】在四棱锥P ABCD中,ABC ACD 90,BAC CAD 60,PA平面ABCD,E为PD的中点,PA2AB2.⑴求四棱锥P ABCD的体积V;⑵若F为PC的中点,求证PC平面AEF.【考点】垂直关系的判断与证明【难度】3星【题型】解答【重点字】2009年,扬州中学高三期末【分析】略PE F AB【答案】DC⑴在Rt ABC 中,AB 1, BAC 60 ,∴BC3,AC 2 . 在Rt ACD 中,AC 2 , CAD 60,∴CD2 3,AD 4 .∴S BCD1ABBC1ACCD1 13 1 2 2 3 5 3.222 22则V1 532 5 3.3 2 3⑵∵PA CA ,F 为PC 的中点,∴AFPC .PA 平面ABCD ,∴PACD .∵AC CD ,PAAC A ,∴CD 平面PAC .∴CD PC . ∵E 为PD 中点,F 为PC 中点,∴EF ∥CD .则EFPC .∵AF EFF ,∴PC 平面AEF .【例22】以下图,正四棱柱ABCDA 1B 1C 1D 1中,底面边长为 22,侧棱长为4.E ,F分别为棱AB ,BC 的中点,EFBDG .⑴求证:平面B 1EF 平面BDD 1B 1; ⑵求点D 1到平面B 1EF 的距离d ; ⑶求三棱锥B 1 EFD 1的体积V .D 1C 1 A 1B 1D CG FAEB【考点】垂直关系的判断与证明 【难度】3星 【题型】解答【重点字】2003年,京皖春天高考 【分析】略【答案】⑴连结AC .∵正四棱柱ABCD A 1B 1C 1D 1的底面是正方形.∴ACBD ,又ACDD 1,故AC平面BDD 1B 1.∵E ,F 分别为AB ,BC 的中点,故EF ∥AC ,∴EF平面BDD 1B 1,∴平面B 1EF平面BDD 1B 1.⑵连结B 1G ,在对角面BDD 1B 1中,作D 1H B 1G ,垂足为H ,∵平面B 1EF 平面BDD 1B 1,且平面B 1EF平面BDD 1B 1 B 1G ,∴D 1H平面B 1EF ,且垂足为H ,∴点D 1到平面B 1EF 的距离dD 1H .法一:在Rt D 1HB 1中,D 1HD 1B 1sin D 1B 1H ,∵D 1B 12A 1B 14,sinD 1B 1HsinBB 14 4B 1GB4212,D 1GB 117B 1HDGB4 1617 .∴dD 1H4 1717法二:∵D 1HB 1∽B 1BG ,∴D 1HD 1B 1,B 1BB 1GBB216∴dD 1H117.B 1G 17法三:连结 D 1G ,则三角形 D 1GB 1的面积等于正方形DBB 1D 1面积的一半.即1B 1GD 1H1BB 12.∴d1617.2217⑶VV BEFD1V D BEF1dS BEF1 16 12 1716.111313 17 23。
空间位置关系的判断与证明.知识框架

高考要求模块框架空间位置关系的判断与证明平行.◆如果一个平面内的两条相交直线与另一个平面都平行,那么这两个平面平行.◆如果一条直线与一个平面内的两条相交直线都垂直,那么该直线与此平面垂直.◆如果一个平面经过另一个平面的垂线,那么这两个平面互相垂直.理解以下性质定理,并能够证明.◆如果一条直线与一个平面平行,经过该直线的任一个平面与此平面相交,那么这条直线就和交线平行.◆如果两个平行平面同时和第三个平面相交,那么它们的交线相互平行.◆垂直于同一个平面的两条直线平行.◆如果两个平面垂直,那么一个平面内垂直于它们交线的直线与另一个平面垂直.③能运用公理、定理和已获得的结论证明一些空间位置关系的简单命题.*公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内.公理2:过不在一条直线上的三点,有且只有一个平面.公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.公理4:平行于同一条直线的两条直线平行.定理:空间中如果两个角的两条边分别对应平行,那么这两个角相等或互补.知识内容1.集合的语言:我们把空间看做点的集合,即把点看成空间中的基本元素,将直线与平面看做空间的子集,这样便可以用集合的语言来描述点、直线和平面之间的关系:点A在直线l上,记作:A l∉;∈;点A不在直线l上,记作A l点A在平面α内,记作:Aα∉;∈;点A不在平面α内,记作Aα直线l在平面α内(即直线上每一个点都在平面α内),记作lα⊂;直线l不在平面α内(即直线上存在不在平面α内的点),记作lα⊄;直线l和m相交于点A,记作{}=;=,简记为l m Al m Aαβ=.平面α与平面β相交于直线a,记作a2.平面的三个公理:⑴公理一:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.图形语言表述:如右图:符号语言表述:,,,A l B l A B l ααα∈∈∈∈⇒⊂⑵ 公理二:经过不在同一条直线上的三点,有且只有一个平面,也可以简单地说成,不共线的三点确定一个平面. 图形语言表述:如右图,符号语言表述:,,A B C 三点不共线⇒有且只有一个平面α, 使,,A B C ααα∈∈∈.⑶ 公理三:如果不重合的两个平面有一个公共点,那么它们有且只有一条过这个点的公共直线. 图形语言表述:如右图:符号语言表述:,A a A a αβαβ∈⇒=∈.如果两个平面有一条公共直线,则称这两个平面相交,这条公共直线叫做两个平面的交线.3.平面基本性质的推论:推论1:经过一条直线和直线外的一点,有且只有一个平面. 推论2:经过两条相交直线,有且只有一个平面. 推论3:经过两条平行直线,有且只有一个平面.4.共面:如果空间中几个点或几条直线可以在同一平面内,那么我们说它们共面.<教师备案>1.公理1反映了直线与平面的位置关系,由此公理我们知道如果一条直线与一个平面有公共点,那公共点要么只有一个,要么直线上所有点都是公共点,即直线在平面内.2.公理2可以用来确定平面,只要有不在同一条直线上的三点,便可以得到一个确定的平面,后面的三个推论都是由这个公理得到的.要强调这三点必须不共线,否则有无数多个平面经过它们. 确定一个平面的意思是有且仅有一个平面.3.公理3反应了两个平面的位置关系,两个平面(一般都指两个不重合的平面)只要有公共点,它们的交集就是一条公共直线.此公理可以用来证明点共线或点在直线上,可以从后面的例题中看到.4.平面基本性质的三个公理是不需要证明的,后面的三个推论都可以由这三个公理得到.推论1与2直接在直线上取点,利用公理1与2便可得到结论,推论3是由平行的定义得到存在性的,再由公理2保证唯一性.线线关系与线面平行1.平行线:在同一个平面内不相交的两条直线.平行公理:过直线外一点有且只有一条直线与这条直线平行. 公理4(空间平行线的传递性):平行于同一条直线的两条直线互相平行;等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等.2.空间中两直线的位置关系:⑴共面直线:平行直线与相交直线;⑵异面直线:不同在任一平面内的两条直线.3.空间四边形:顺次连结不共面的四点所构成的图形.这四个点叫做空间四边形的顶点;所连结的相邻顶点间的线段叫做空间四边形的边;连结不相邻的顶点的线段叫做空间四边形的对角线.如右图中的空间四边形ABCD ,它有四条边,,,AB BC CD DA ,两条对角线,AC BD . 其中,AB CD ;,AC BD ;,AD BC 是三对异面直线.DCBA4.直线与平面的位置关系:⑴直线l 在平面α内:直线上所有的点都在平面内,记作l α⊂,如图⑴;⑵直线l 与平面α相交:直线与平面有一个公共点A ;记作l A α=,如图⑵; ⑶直线l 与平面α平行:直线与平面没有公共点,记作//l α,如图⑶.l3()2()1()lAαααl5.直线与平面平行的判定定理:如果不在一个平面内的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行.符号语言表述:,,////l m l m l ααα⊄⊂⇒. 图象语言表述:如右图:mlα6.直线与平面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和两平面的交线平行.符号语言表述://,,//l l m l m αβαβ⊂=⇒. 图象语言表述:如右图:βαl m<教师备案>1.画线面平行时,常常把直线画成与平面的一条边平行; 2.等角定理证明:已知:如图所示,BAC ∠和B A C '''∠的边//AB A B '',//AC A C '',且射线AB与A B ''同向,射线AC 与A C ''同向. 求证:BAC B A C '''∠=∠证明:对于BAC ∠和B A C '''∠在同一平面内的情形,在初中几何中已经证明,下面证明两个角不在同一平面内的情形.分别在BAC ∠的两边和B A C '''∠的两边上截取线段AD AE 、和A D A E ''''、,使,A D A D A E A E ''''==,因为//''AD A D ,所以AA D D ''是平行四边形 所以//AA DD ''.同理可得//AA EE '',因此//DD EE ''. 所以DD E E ''是平行四边形. 因此DE D E ''=. 于是ADE A D E '''∆≅∆. 所以BAC B A C '''∠=∠.E'E DC BAA'D 'B 'C '3.根据等角定理可以定义异面直线所成的角的概念:过空间一点作两异面直线的平行线,得到两条相交直线,这两条相交直线成的直角或锐角叫做两异面直线成的角.异面直线所成角的范围是π(0,]24.线面平行判定定理(,,////l m l m l ααα⊄⊂⇒),即线线平面,则线面平行.要证明这个定理可以考虑用反证法,因为线线平行(//l m ),所以它们可以确定一个平面β,β与已知平面α的交线恰为m ,若线面不平行,则线面相交于一点,此点必在两个平面的交线m 上,从而得到l 与m 相交,与已知矛盾.5.线面平行性质定理,即线面平行,则线线平行,这平行的定义立即可得(共面且无交点).面面平行的判定与性质1.两个平面的位置关系⑴两个平面,αβ平行:没有公共点,记为//αβ;画两个平行平面时,一般把表示平面的平行四边形画成对应边平行,如右图:⑵两个平面,αβ相交,有一条交线,l αβ=.2.两个平面平行的判定定理:如果一个平面内有两条相交直线平行于另一个平面, 那么这两个平面平行.符号语言表述:,,,//,////a b a b A a b ααββαβ⊂⊂=⇒.推论:如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线,则这两个平面平行.3.两个平面平行的性质定理:如果两个平面同时与第三个平面相交,那么它们的交线平行. 符号语言表述://,,//a b a b αβαγβγ==⇒. 图象语言表述:如右图:γbaβα<教师备案>1.画两个平面相交时,可以先画出交线,再补充其它,平面被遮住的部分画成虚线或不画. 如右图所示:2.面面平行的判定定理可以由线面平行的性质直接得到,如果满足定理条件的两个平面相交,则这两条相交直线都平行于平面的交线,与过直线外一点只能作一条直线与已知直线平行的公理矛盾.故这两个平面不相交,是平行平面.3.面面平行的性质定理可以直接由两条交线无交点且共面得到.4.在证明线面平行,线线平行和面面平行的题时,常常遇到平行关系的转化,要灵活运用两个性质定理与两个判定定理,证明要求的结论.由于空间中平行关系与垂直关系是高考的核心内容,因此在出题时经常会有所结合,本板块专门就平行知识的题目类型归纳,更综合的题目会在第十一讲中详细讲解.由于线面与面面问题之间都是互相转化的,因此本板块中的面面平行题目较少,多数都为线面平行问题.本板块题目多采用两种方法,事实上就是两种思路证明线面平行,一种方法线线平行⇒线面平行,另一种方法是面面平行⇒线面平行.线面垂直1.线线垂直:如果两条直线相交于一点或经过平移后相交于一点,并且交角为直角,则称 这两条直线互相垂直.由定义知,垂直有相交垂直和异面垂直. 2.直线与平面垂直:⑴概念:如果一条直线和一个平面相交于点O ,并且和这个平面内过交点的任何直线都垂直,则称这条直线与这个平面互相垂直.这条直线叫做平面的垂线,这个平面叫做直线的垂面,交点叫垂足. 垂线上任意一点到垂足间的线段,叫做这个点到这个平面的垂线段.垂线段的长度叫做这个点到平面的距离.如果一条直线垂直于一个平面,那么它就和平面内的任意一条直线垂直.画直线与平面垂直时,通常把直线画成和表示平面的平行四边形的一边垂直,如右图.αl直线l 与平面α互相垂直,记作l α⊥.⑵线面垂直的判定定理:如果一条直线与平面内的两条相交直线垂直,则这条直线与这个平面垂直.推论:如果在两条平行直线中,有一条垂直于平面,那么另一条直线也垂直于这个平面. ⑶线面垂直的性质定理:如果两条直线垂直于同一个平面,那么这两条直线平行.<教师备案>1.如果定义了异面直线所成角,则异面垂直即异面直线所成角为90︒.2.线面垂直的判定定理把定义中的与任意一条直线垂直这个很强的命题,转化为只需证明与两条相交直线垂直这个问题,从而大大简化了线面垂直的判断.n mA'EDCB Aβα要证明判定定理,只能用定义,若',',AA m AA n m n B ⊥⊥=,,m n α⊂,要证'AA α⊥,在平面α内任选一条直线g ,去证'AA g ⊥,结合右图,通过全等三角形的证明可得到,从而得到判定定理,具体的证法略. 3.线面垂直的性质定理,可以用同一法证明, 如图:laABm'mβα直线,l m αα⊥⊥,若直线,l m 不平行,则过直线l 与平面α的交点B 作直线'//m l ,从而有'm α⊥.又相交直线,'m m 可以确定一个平面β,记a αβ=,则因为,'m m 都垂直于平面α,故,'m m 都垂直于交线a .这与在一个平面内,过直线上一点有且只有一条直线与已知直线垂直相矛盾.故,'m m 重合,//m l ,性质定理得证.由同一法还可以证明:过一点与已知平面垂直的直线只有一条.点面距离与线面角 (一)主要方法:本板块所学内容为点面距离与线面角,求点面距离有两种方法,首先可以通过直接法作面的垂线,其次可以通过体积法转化,或者将问题转化为与面平行的直线上的点到面的距离;线面角问题属于线面关系的一种,是线面垂直与面面垂直定理的应用. 1.点、斜线、斜线段及射影⑴点在直线上的射影自点A 向直线l 引垂线,垂足1A 叫做点A 在直线l 上的射影.点A 到垂足的距离叫点到直线的距离.⑵点在平面内的射影自点A 向平面α引垂线,垂足1A 叫做点A 在平面α内的射影,这点和垂足间的线段叫做这点到平面的垂线段.垂线段的长度叫做这点到这个平面的距离. ⑶斜线在平面内的射影一条直线和一个平面相交,但不和这个平面垂直,这条直线叫做这个平面的斜线,斜线和平面的交点叫做斜足,斜线上一点和斜足间的线段,叫做这点到平面的斜线段.过斜线上斜足以外的一点向平面引垂线,过垂足和斜足的直线叫做斜线在这平面内的射影,垂足与斜足间的线段叫做这点到平面的斜线段在这个平面内的射影. 2.直线和平面所成的角直线和平面所成的角,应分三种情况:⑴直线和平面斜交时,线面所成的角是这条直线和它在平面内的射影所成的锐角; ⑵直线和平面垂直时,直线和平面所成的角的大小为90;。
2019-2020年高中数学 空间位置关系的判断与证明 板块四 垂直关系的判断与证明完整讲义(学生版)
2019-2020年高中数学 空间位置关系的判断与证明 板块四 垂直关系的判断与证明完整讲义(学生版)【例1】 下列说法正确的有 .①过一点有且只有一条直线垂直于已知直线.②若一条直线与平面内无数条直线垂直,则这条直线与这个平面垂直.③若一条直线平行于一个平面,则垂直于这个平面的直线必垂直于这条直线. ④若一条直线垂直于一个平面,则垂直于这条直线的另一条直线必平行于这个平面.⑤若一条直线平行于一个平面,则它和这个平面内的任何直线都不垂直. ⑥平行于同一个平面的两条直线可能垂直.【例2】 在空间四面体的四个面中,为直角三角形的最多有 个.【例3】 已知在三棱锥中,,求证:⊥.ABCDE【例4】 如图,已知三棱锥,,为的中点,且是正三角形,⊥.求证:⑴ ⊥面;⑵平面⊥平面.DPABC【例5】 如图,是正方形,垂直于平面,过且垂直于的平面交、、 分别于点、、,求证:,.EBCFDGSA典例分析【例6】如图,在四棱锥中,底面,60AB AD AC CD ABC⊥⊥∠=,,°,,是的中点.证明:面⊥面.【例7】如图,四面体,⊥面,⊥,过作⊥交于,过作⊥交于.求证:⊥.FEPA BC【例8】如图是正方体下底面中心,,为垂足.求证:平面.【例9】如图所示,在正方体中..求证:⊥面.A1D1C1B1DCBA【例10】在长方体中,点,分别在,上且,,求证:面【例11】在正方体中,为的中点,为底面的中心.求证:⊥面.【例12】在四棱锥中,底面为矩形,⊥底面,,分别为,的中点.⑴求证:∥平面;⑵若,求证:⊥面.QPD CAMN【例13】 已知平行六面体的底面是菱形,且.求证:⊥.OABCD A 1B 1C 1D 1【例14】 (xx 深圳高三联考)如图,在直四棱柱中,当底面四边形满足条件 时,有.(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形)D 1C 1B 1A 1DCBA【例15】 如图,、、、是空间四点,在中,,,等边所在的平面以为轴可转动.当转动过程中,是否总有?请证明你的结论ABC DO【例16】 在正方体中,是的中点,问当点位于上何处时,?【例17】 如图,直三棱柱中,,,,是的中点.⑴求证平面;⑵当点在上什么位置时,会使得平面?并证明你的结论.C 1B 1A 1FEDC B A【例18】 (xx 全国,文19)如图已知平行六面体的底面是菱形,且. ⑴ 证明;⑵ 当的值为多少时,能使平面?请给出证明.图 9-2-284D 1A 1C 1B 1DCBA【例19】 已知四面体,①若棱,求证 ②若,求证棱.【例20】 已知三棱锥中,底面,,分别为的中点,于.⑴求证:平面; ⑵求证:平面平面;⑶若,求截面分三棱锥所成两部分的体积比.【例21】 (xx 扬州中学高三期末)在四棱锥中,,,平面,为的中点,. ⑴求四棱锥的体积;⑵若为的中点,求证平面.【例22】 (xx 京皖春)如图所示,正四棱柱中,底面边长为,侧棱长为.分别为棱的中点,. ⑴求证:平面平面; ⑵求点到平面的距离; ⑶求三棱锥的体积.D 1C 1B 1A 1GFEDCB A2019-2020年高中数学 空间几何体 板块一 对空间几何体的初步认识完整讲义(学生版)空间几何体的几何特征【例23】 能保证棱锥是正棱锥的一个条件是( )A .底面是正多边形B .各侧棱都相等C .各侧棱与底面都是全等的正三角形D .各侧面都是等腰三角形【例24】 判断下面这个命题是否正确:由两个面互相平行,其余各面都是平行四边形的几何体是棱柱.【例25】 一个棱柱是正四棱柱的条件是( )A .底面是正方形,有两个侧面是矩形B .底面是正方形,有两个侧面垂直于底面C .每个侧面都是全等矩形的四棱柱D .底面是菱形,且有一个顶点处的三条棱两两垂直【例26】 (xx 全国II 理16)平面内的一个四边形为平行四边形的充要条件有多个,如两组对边分别平行,类似地,写出空间中的一个四棱柱为平行六面体的两个充要条件:充要条件① ; 充要条件② .(写出你认为正确的两个充要条件)典例分析【例27】(xx北京理10)设命题甲:“直四棱柱中,平面与对角面垂直”;命题乙:“直四棱柱是正方体”.那么甲是乙的()A.充分必要条件 B.充分非必要条件C.必要非充分条件 D.既非充分又非必要条件【例28】判断下列说法是否正确,并说明理由:①四边相等的四边形是菱形;②若四边形的两个对角都是直角,则这个四边形是圆内接四边形.③将一个矩形沿竖直方向平移一段距离可形成一个长方体;④平行四边形是一个平面.⑤多面体至少有四个面.【例29】下列命题不正确的有.⑴ 底面是矩形的平行六面体是长方体;⑵ 棱长相等的直四棱柱是正方体;⑶ 棱锥被平面分成的两部分不可能都是棱锥;⑷ 有一个面是多边形,其余各面都是三角形的几何体是棱锥.【例30】下列命题正确的有.⑴ 棱柱的侧面都是平行四边形;⑵ 有两个面平行,其余各面都是平行四边形的几何体叫做棱柱;⑶ 用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;⑷ 有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台.【例31】⑴ 一个棱柱至少有个面,面数最少的一个棱锥有个顶点,顶点最少的一个棱台有条侧棱.⑵ 一个正棱锥的侧棱长与底面边长相等,则该棱锥不可能是()A.三棱锥 B.四棱锥 C.五棱锥 D.六棱锥【例32】设表示平行六面体,表示直平行六面体,表示长方体,表示正四棱柱,表示正方体,则,,,,的关系是()A. B.C. D.【例33】设有四个命题:①底面是矩形的平行六面体是长方体;②棱长相等的直四棱柱是正方体;③有两条侧棱都垂直于底面一边的平行六面体是直平行六面体;④对角线相等的平行六面体是直平行六面体.以上四个命题中,真命题有_______.【例34】下列命题中正确的是()A.由五个平面围成的多面体只能是四棱锥B.棱锥的高线可能在几何体之外C.仅有一组对面平行的六面体是棱台D.棱长相等的直四棱柱是正方体【例35】下列说法正确是()A.圆台是直角梯形绕其一边旋转而成B.圆锥是直角三角形绕其一边旋转而成C.圆柱的母线和它的底面不垂直.D.圆台可以看作是平行于底面的平面截一个圆锥而得到的.【例36】(xx重庆)如题图,模块①-⑤均由个棱长为的小正方体构成,模块⑥由个棱长为的小正方体构成.现从模块①-⑤中选出三个放到模块⑥上,使得模块⑥成为一个棱长为的大正方体.则下列选择方案中,能够完成任务的为()模块⑥模块⑤模块④模块③模块②模块①A.模块①,②,⑤B.模块①,③,⑤C.模块②,④,⑥ D.模块③,④,⑤空间几何体的展开图【例37】将一个边长为和的矩形纸片卷成一个圆柱,则圆柱的底面半径为.【例38】根据图中所给的图形制成几何体后,哪些点重合在一起.NMJHGFED CB A【例39】 下面是一多面体的展开图,每个面内都给了字母,请根据要求回答问题:FEDCBA①如果在多面体的底面,那么哪一面会在上面?②如果面在前面,从左边看是面,哪一个面会在上面? ③如果从左面看是面,面在后面,哪一个面会在上面?【例40】 如图,右边哪一个长方体是由左边的平面图形围成的( )BDAC【例41】 右图是一个正方体,它的展开图可能是下面四个展开图中的( )4DC BA68468468864【例42】 圆锥的侧面展开图是半径为的半圆面,求圆锥的母线与轴的夹角的大小,轴截面的面积.【例43】 (xx 年宣武一模)若将下面的展开图恢复成正方体,则的度数为 .11题图CBA空间几何体的三视图和直观图【例44】根据下面的几何体的直观图画出相应的的三视图.⑴圆台⑵正三棱柱【例45】下列几何体中,主视图、左视图、俯视图相同的几何体是()A.球和圆柱 B.圆柱和圆锥 C.正方体的圆柱 D.球和正方体【例46】(xx年北京)一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如图所示,则该几何体的俯视图为侧(左)视图正(主)视图A. B.C. D.【例47】(xx年朝阳一模)一个简单几何体的正视图,侧视图如图所示,则其俯视图不可能为①长方形;②正方形;③圆;④椭圆.其中正确的是()A.①②B.②③C.③④D.①④侧视图正视图【例48】(xx年海淀一模)一个体积为的正三棱柱的三视图如图所示,则这个三棱柱的左视图的面积为()A. B. C. D.第 5 题【例49】(xx年崇文一模)有一个几何体的三视图及其尺寸如图(单位:),该几何体的表面积和体积为()A. B.C. D.以上都不正确俯视图侧(左)视图正(主)视图【例50】 (xx 年西城二模)如图,三棱柱的侧棱长和底面边长均为,且侧棱底面,其正(主)视图是边长为的正方形,则此三棱柱侧(左)视图的面积为( )A .B .C .D .【例51】 (xx 年朝阳一模)一个几何体的三视图如图所示,则此几何体的体积是 ( )A .112B .80C .72D .64俯视图侧视图正视图【例52】 如图,正方形的边长为,它是水平放置的一个平面图形的直观图.请画出原来的平面几何图形的形状,并求原图形的周长与面积.【例53】 (08广东)将正三棱柱截去三个角(如图所示分别是三边的中点)得到几何体如图,则该几何体按图中所示方向的侧视图(或称左视图)为( )F ED CB A F E D IH G CB ADC B A B BB B E E E E【例54】 (xx 海南宁夏)某几何体的一条棱长为,在该几何体的正视图中,这条棱的投影是长为的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为和的线段,则的最大值为( )A .B .C . 4D .【例55】 斜二测画法所得的直观图的多边形面积为, 那么原图多边形面积是_______.【例56】 如图,正方形的边长为,它是水平放置的一个平面图形的直观图.请画出原来的平面几何图形的形状,并求原图形的周长与面积.【例57】 根据下面几何体的三视图,描述这个几何体的大致形状,并用斜二测画法画出这个几何体的直观图,其中三视图中的主视图和左视图都是正三角形,俯视图是边长为的正方形.主视图 俯视图左视图。
高考数学复习考点知识与结论专题讲解46 空间垂直关系

高考数学复习考点知识与结论专题讲解第46讲 空间垂直关系通关一、直线与平面垂直的判定定理(1)自然语言:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂间(2)图形语言:如图所示.(3)符号语言:.,,,,ααα⊥⇒⊥⊥=⊂⊂l b l a l P b a b a通关二、直线与平面垂直的性质定理自然语言:垂直于同一个平面的两条直线平行.图形语言:如图所示.符号语言:.//,b a b a ⇒⊥⊥αα要点诠释:(1) 直线与平面垂直的定义常常逆用,即.,b a b a ⊥⇒⊂⊥ααoLB(2) 若平行直线中一条垂直于平面,则另一条也垂直于该平面.(3)垂直于同一条直线的两个平面平行.(4)过一点有且只有一条直线与已知平面垂直.(5)过一点有且只有一个平面与已知直线垂直. 通关三、平面与平面垂直的判定定理(1)两个平面垂直的定义如果两个相交平面所成的二面角是直二面角,那么就说这两个平面互相垂直.平面α与β垂直,记作βα⊥.(2)两个平面垂直的判定定理自然语言:一个平面过另一个平面的垂线,则这两个平面垂直.图形语言:如图所示.符号语言:βααβ⊥⇒⊂⊥AB AB ,.要点诠释:(1)两个平面互相垂直是两个平面相交的特殊情况,正方体中任意相邻的两个面都是互相垂直的;(2)由定理可知,要证明平面与平面垂直,可转化为从现有直线中寻找平面的垂线,即证明线面垂直;(3)面面垂直的判定定理提供了找出垂直于一个平面的另一个平面的依据.通关四、平面与平面垂直的性质定理自然语言:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直图形语言:如图所示.符号语言:,,,CD AB AB CD αβαβα⊥=⊂⊥⇒AB β⊥.要点诠释:(1)两个平面互相垂直是两个平面相交的特殊情况,正方体中任意相邻的两个面都是互相垂直的;(2)由定理可知,要证明平面与平面垂直,可转化为从现有直线中寻找平面的垂线,即证明线面垂直;(3)面面垂直的判定定理提供了找出垂直于一个平面的另一个平面的依据.结论一、线线垂直思考途径:1.转化为相交垂直;2.转化为线面垂直;3.转化为线与另一线的射影垂直;4.转化为线与形成射影的斜线垂直.支持定理:)三垂线定理及其逆定理;③②所成角为①(90;PA AO a a PO b a b a ⊥⇒⊥⊂⊥︒⊥⇒⊂⊥⎪⎭⎪⎬⎫⎭⎬⎫ααααα 配图助记:【例1】如图,ABCD 是正方形,SA 垂直于平面A BCD ,过A 且垂直于SC 的平面分别交SB ,SC ,SD 于点E ,F ,G ,求证:AE ⊥SB ,AG ⊥SD .【解析】证明因为SA ⊥平面ABCD ,BC ⊂平面ABCD ,所以SA ⊥BC .又因为ABCD 为正方形,所以BC⊥AB,所以BC⊥平面ASB.因为AE⊂平面ASB,所以BC⊥AE.又因为SC⊥平面AEFG,所以SC ⊥AE,所以AE上平面SBC.又因为SB⊂平面SBC,所以AE⊥SB,同理可证AG⊥SD.【变式】如图,四面体P-ABC中,P A上面ABC,AB上BC,过A作AE⊥PB交PB于E,过A作AF⊥PC交PC于F.求证:PC⊥EF.【解析】证明因为P A上面ABC,且BC⊂面ABC,所以BC⊥P A,且BC⊥AB,所以BC⊥面ABE,所以BC⊥AE.又PB⊥AE,且BC∩PB=B,所以AE⊥面PBC,且PC⊂面PBC,所以AE⊥PC.又AF ⊥PC,且AF∩AE=A,所以PC⊥面AEF ,且EF⊂面AEF,所以PC⊥EF.结论二、线面垂直思考途径:1.转化为该直线与平面内任一直线垂直;2.转化为该直线与平面内相交二直线垂直;3.转化为该直线与平面的任意一条垂线平行;4.转化为该直线垂直于另一个平行平面;5.转化为该直线与平面的垂线平行.支持定理.支持定理:ααβααβαβααβαβααα⊥⇒⊥⊥⇒⊥⊥⇒⊥⊂=⊥⊥⇒⊥⊥=⊂⊂⎭⎬⎫⎭⎬⎫⎪⎭⎪⎬⎫⎪⎭⎪⎬⎫b a b a a l a a l a l b l a l 0b a b a //;//;,;,,④③②① 配图助记:要点诠释:平面和平面垂直的判定定理的两个条件:,l l αβ⊂⊥,缺一不可.【例2】如图,在正方体1111ABCD A B C D -,P 为1DD 的中点,O 为底面ABCD 的中心.求证1B O ⊥面PAC .【解析】证法一由于AC BD ⊥,且AC BB ⊥,所以AC ⊥面11BDD B ,1B O ⊂11BDD B ,所以1B O AC ⊥连结1PB ,设AB a =,则1111.AB CB B D ==因为222222113,2OB OB BB a a ⎫=+=+=⎪⎪⎝⎭)22222211111924PB PD B D a a ⎛⎫=+=+= ⎪⎝⎭,2222221324OP PD DO a a ⎫⎛⎫=+=+=⎪ ⎪⎪⎝⎭⎝⎭, 所以22211OB OP PB +=,所以1B O OP ⊥,PO AC O =,所以1B O ⊥面PAC .证法二由于AC BD ⊥,且1AC BB ⊥,所以AC ⊥面11BDD B ,且1B O ⊂面11BDD B ,所以1B O AC ⊥.取CD 中点Q ,连结11,OC OQ ,则11//.OQ B C 在正方形11CC D D 中,由P ,Q 分别为1,DD CD 的中点,可知1CP C Q ⊥,又11,CP B C ⊥且1111=C Q B C C ,所以CP ⊥面11B QO C ,又1B O ⊂面11B QO C ,所以1,CP BO ⊥所以1B O ⊥面PAC .【变式】在四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥底面ABCD ,M N ,分别为PC ,AB 的中点.若45PDA ∠=︒,求证:MN ⊥面PCD【解析】证法一取PD 中点Q ,连结AQ MQ ,,则1,2MQ CD =1,2MQ CD所以MQ NA ⊥,所以四边形ANMQ 是平行四边形.因为PA ⊥底面ABCD ,且CD ⊂面ABCD ,所以CD PA ⊥.又由底面是矩形有CD AD ⊥,所以CD ⊥面PAD .又AQ ⊂面PAD ,所以AQ CD ⊥.又因为45PDA ∠=︒,所以APD △是等腰直角三角形.因为Q 为PD 中点,所以PQ QD =,所以AQ PD ⊥.又CDPD D =,AQ ⊥面PCD .又MN AQ ,所以MN ⊥面PCD .证法二先完全仿照证法一可证明CD ⊥面.PAD 取CD 中点R ,连接,,MR PN NC ,则//,MR PD //NR AD ,所以面//MRN 面PDA ,所以CD ⊥面MRN ,所以MN ⊥C D .因为∠PDA =45°,所以P A =AD ,又BC =AD ,所以P A =BC ,又AN =BN ,且PAN ∠=∠CBN =90°,所以根据三角形全等可知PN =NC ,又PM =MC ,所以.MN PC ⊥因为CD ∩PC =C ,所以MN ⊥面PCD结论三、面面垂直思考途径:1.转化为判断二面角是直二面角;2.转化为线面垂直.支持定理:① 二面角的平面角为90︒;②a a βαβα⊂⎫⇒⊥⎬⊥⎭;③a a βαβα⎫⇒⊥⎬⊥⎭配图助记:【例3】在四棱锥S -ABCD 中,底面ABCD 是正方形,SA ⊥底面ABCD ,SA =AB ,点M 是SD 的中点,AN ⊥SC ,且交SC 于点N .证明:平面SAC ⊥平面AMN .【解析】证明因为SA ⊥底面ABCD ,CDC 平面ABCD ,所以SA ⊥C D .又因为CD ⊥AD ,SAC 平面SAD ,ADC 平面SAD ,SA ∩AD =A ,所以CD ⊥平面SA D .AMC 平面SAD ,所以CD ⊥AM .又因为SA =AD =AB ,M 是SD 的中点,所以AM ⊥S D .SDC 平面SCD ,CDC 平面SCD ,SD ∩CD =D ,所以AM ⊥平面SC D .SCC 平面SCD ,所以AM ⊥S C .又因为AN ⊥SC ,AM ,ANC 平面AMNAM ∩AN =A ,所以SC ⊥平面AMN .又因为SCC 平面SAC ,所以平面SAC ⊥面AMN .【变式】如图,在直四棱柱1111ABCD A B C D -中,DB BC =,DB AC ⊥,点M 是棱BB 1,上一点(1)求证:11B D 面A 1BD ;(2)求证:MD AC ⊥(3)试确点M 的位置,使得平面DMC 1⊥平面CC 1D 1D .【解析】1)证明由直四棱柱,得11//,BB DD 11BB DD =所以11BB D D 是平行四边形,所以11B D BD 而BD ⊂平面111,A BD B D ⊂/平面1A BD ,所以11B D 面1.A BD(2)证明因为1BB ⊥面ABCD ,ACC 面ABCD ,所以1.BB AC ⊥又因为BD ⊥AC ,且1BD BB B =所以AC ⊥面1,BB D 而MD ⊂面1,BB D 所以MD ⊥AC (3)当点M 为棱1BB 的中点时,平面1DMC ⊥平面 D D 取DC 的中点11,N D C 的中点1,N 连结1NN 交DC 于O ,连结OM .因为N 是DC 中点,BD =BC ,所以BN ⊥D C .又因为DC 是面ABCD 与面11DC D 的交线,而面ABCD ⊥面11,DCC D 所以BN ⊥面11.DC D 又可证得O 是1NN 的中点,所以BM //NO 且BM =NO ,即BMON 是平行四边形,所以BN //OM ,所以OM ⊥平面 D D 因为OMC 平面1,DMC 所以平面1DMC ⊥ D D。
2019-2020年高中数学 空间位置关系的判断与证明 板块三 平行关系的判断与证明完整讲义(学生版)

2019-2020年高中数学空间位置关系的判断与证明板块三平行关系的判断与证明完整讲义(学生版)【例1】下列命题中,正确的个数是()①平行于同一条直线的两直线平行②平行于同一个平面的两直线平行③垂直于同一条直线的两直线平行④垂直于同一个平面的两直线平行⑤平行于同一条直线的两平面平行⑥平行于同一个平面的两平面平行A.1 B.2 C.3 D.4【例2】下列命题中,真命题有_______.①若,则;②若,则;③若,则;④若//,//,//,//,a ab b a b Aαβαβ=,则;【例3】平行于平面的,是两异面直线,且分别在平面的两侧,,若与平面交于点,与平面交于点.求证:.A BCD αab MN【例4】已知平面,,为夹在,间的异面线段,、分别为、的中点.求证:,.【例5】如图,线段分别交两个平行平面、于、两点,线段分别交、于、两点,线段分别交、于、两点,若,,,的面积为,求的面积.典例分析βD Q BEαPCAF【例6】 如图,在四棱锥中,,,是的中点. 求证:∥平面.EPDA B C【例7】 已知空间四边形,、、分别是、、的中点,求证:平面,平面.【例8】 如图,在四棱锥中,底面是平行四边 形,是的中点.求证:∥平面.OPD B CA E【例9】 已知空间四边形,、分别是和的重心,求证:平面.【例10】 已知分别是四面体的棱的中点,G F ED C BAMN求证:面.【例11】 如图,在底面是平行四边形的四棱锥中,点在上,且, 为棱的中点.求证:∥平面E PD AB C F【例12】 如图,四棱锥中,四边形是平行四边形,、分别是、的中点. 求证:∥平面.C AD E FP【例13】 如图,四边形是矩形,面,过作平面交于,交于,求证:四边形是梯形.PF ED B A【例14】 已知为空间四边形的边上的点,⑴若都分别是所在边的中点,求证:四边形为平行四边形;⑵若,求证:.H GF ED CBA【例15】 如图,为所在平面外一点,,,分别为,,的重心,⑴求证:平面平面;⑵求G F DC BAM NPH【例16】 如图,三棱柱中,是的中点. 求证://平面.EA B CA 1B 1C 1D【例17】 已知正方体,为与的交点,为与的交点,则的长度为_______.N MD 1C 1B 1A 1DC B A【例18】 如图,在正方体中,为的中点.求证:∥面.E F A B CDB 1C 1D 1A 1【例19】 如图,正方体中,点在上,点在上,且,求证:平面.D 1C 1B 1MBNF EC DA 1A【例20】 如图所示,正方体中,棱长为,分别为和上的点,.N MF E A B 1C 1D 1DC B A 1⑴求证:∥平面;⑵求的最小值.【例21】 设是单位正方体的面、的中心,如图,⑴证明:平面;⑵求线段的长.AB CD A 1B 1C 1D 1PQ【例22】 正方体中,、分别是、的中点,如下图.求证:平面.D 1C 1B 1A 1G ED CB A【例23】 如图,正方体中,分别是的中点.求证:平面∥平面.【例24】 如图,在正方体中,、、分别是、、的中点,求证:平面平面.D1C 1B 1A 1GF E D CBA【例25】 已知正方体,求证:平面平面.A B CD A 1B 1C 1D 1【例26】 如图,在五面体中,点是平行四边形的对角线的交点,面是等边三角形,棱.求证:∥平面F EDC B A O【例27】 已知长方体中,分别是的中点.求证:平面平面.A A'B B'C C'D D'EF【例28】 (xx 年湖南高考题·理3)过平行六面体任意两条棱的中点作直线,其中与平面平行的直线共有( ).A .4条B .6条C .8条D .12条【例29】 (xx 湖北,理10)如图,在三棱柱中,点、、、分别为、、、的中点,为的重心.从、、、中取一点作为,使得该棱柱恰有条棱与平面平行,则为( )A .B .C .D .A'B2019-2020年高中数学 空间位置关系的判断与证明 板块二 对空间位置关系的判断完整讲义(学生版)【例30】 直线和平面所成的角为,则( )A .B .C .D .【例31】 若直线平面,直线平面,则直线与的位置关系是【例32】 室内有一根直尺,无论怎么放置,在地面上总有这样的直线,它与直尺所在的直线A .异面B .相交C .平行D .垂直【例33】 若不共线的三点到平面的距离相等,则该三点确定的平面与之间的关系为( )A .平行B .相交C .平行或相交D .无法确定【例34】 设为两条直线,为两个平面,下列四个命题中,正确的命题是( ) 典例分析A .若与所成的角相等,则B .若,,,则C .若,,,则D .若,,,则【例35】 下列命题中,真命题有_______.①若,则;②若,则;③若,则;④若//,//,//,//,a a b b a b A αβαβ=,则;【例36】 ,是空间两条不同直线,,是空间两条不同平面,下面有四个命题:①,;m n m n αβαβ⊥⇒⊥, ②,,;m n m n αβαβ⊥⊥⇒ ③,,;m n m n αβαβ⊥⇒⊥ ③,,;m m n n ααββ⊥⇒⊥ 其中真命题的编号是________(写出所有真命题的编号).【例37】 (xx 广东五校)在下列关于直线、与平面、的命题中,真命题是( )A .若,且,则B .若,且,则C .若,且,则D .若,且,则【例38】 (xx 年二模·东城·文·题3)已知,为两条不同的直线,,为两个不同的平面,则下列命题中正确的是( )A .B .,,m n m n αβαβ⊂⊂⇒∥∥C .D .,,,m n m n ααββαβ⊂⊂⇒∥∥∥【例39】 (xx 年二模·宣武·理·题4)已知直线、与平面、,下列命题正确的是 ( )A .且,则B .且,则C .且,则D .且,则【例40】 (xx 浙江高考)设,是两条不同的直线,是一个平面,则下列命题正确的是A .若,,则B .若,,则C .若,则D .若,,则【例41】 (xx 新课标海南宁夏)已知平面平面,,点,,直线,直线,直线,,则下列四种位置关系中,不一定...成立的是( )A .B .C .D .【例42】已知直线与平面,下面三个命题中正确的有______.①;②;③.【例43】(05广东)给出下列关于互不相同的直线、、和平面、的四个命题:①若,,点,则与不共面;②若、是异面直线,,,且,,则;③若,,,则;④若,,点,,,则.其中为假命题的是()A.① B.② C.③ D.④【例44】(xx北江中学)已知是两个不同的平面,是两条不同的直线,给出下列命题:①若,则;②若,,则;③如果是异面直线,则与相交;④若,且,则且.其中正确的命题是()A.①②B.②③C.③④D.①④【例45】(05福建卷)已知直线、与平面,给出下列三个命题:①若,,则②若,,则③若,,则其中真命题的个数是()A.B. C. D.【例46】(xx年二模·朝阳·理·题5)已知平面,直线,直线,有下面四个命题:①②③④其中正确的命题是()A.①与② B.③与④ C.①与③ D.②与④【例47】(xx年二模·海淀·理·题6)已知,是不同的直线,,是不同的平面,则下列条件能使成立的是()A., B.,C., D.,【例48】(xx年二模·丰台·文·题7)设是空间三条不同的直线,是空间三个不同的平面,给出下列四个命题:①若,则;②若,则;③若,则;④若是在内的射影,且,则.其中正确的个数是()A.1 B.2 C.3 D.4【例49】 (xx 年一模·崇文·理·题5)(崇文·文·题6)已知是两条不同直线,是三个不同平面,下列命题中正确的为 ( )A .若则B .若则C .若,则D .若则【例50】 (09年西城区期末考试5)已知是平面的一条斜线,点,为过点的一条动直线,那么下列情形可能出现的是( )A . ,B . ,C . ,D . ,【例51】 (05江苏)设为两两不重合的平面,为两两不重合的直线,给出下列四个命题:①若,,则;②若,,,,则;③若,,则;④若,,,,则.其中真命题的个数是( )A .B .C .D .【例52】 (xx 浙江)对两条不相交的空间直线和,必定存在平面,使得( )A .,B .,C .,D .,【例53】 (xx 江苏12)设和为不重合的两个平面,给出下列命题:①若内的两条相交直线分别平行于内的两条直线,则平行于;②若外一条直线与内的一条直线平行,则和平行;③设和相交于直线,若内有一条直线垂直于,则和垂直;④直线与垂直的充分必要条件是与内的两条直线垂直.上面命题中,真命题的序号是 .(写出所有真命题的序号)【例54】 (xx 湖南文6)如图,在正四棱柱 中,、分别是、的中点,则以下结论中不成立的是( )A .与垂直B .与垂直C .与异面D .与异面A B CDE F A 1B 1C 1D 1【例55】 (xx 年二模·海淀·文·题7)在正四面体中,棱长为4,是BC 的中点,在线段上运动(不与、重合),过点作直【例56】 (xx 崇文一模)如图,在正方体中,是底面正方形的中心,是的中点,是上的动点,则直线、的位置关系是( )A .平行B .相交C .异面垂直D .异面不垂直O D 1C 1B 1A 1DC B A MN【例57】 (xx 山东文9)已知,表示两个不同的平面,为平面内的一条直线,则“”是“”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【例58】 对于直线、和平面,下面命题中的真命题是( )A .如果,、是异面直线,那么B .如果,、是异面直线,那么相交C .如果,、共面,那么D .如果,、共面,那么【例59】 (xx 福建文10)设是平面内的两条不同直线;,是平面内的两条相交直线.则的一个充分而不必要的条件是( )A .且B .且C .且D .且【例60】 已知、为不垂直的异面直线,是一个平面,则、在上的射影有可能是 .①两条平行直线 ②两条互相垂直的直线③同一条直线 ④一条直线及其外一点在上面结论中,正确结论的编号是 (写出所有正确结论的编号).【例61】 (xx 西城高三期末)在空间中,有如下四个命题:①平行于同一个平面的两条直线是平行直线;②垂直于同一条直线的两个平面是平行平面;③若平面内有不共线的三个点到平面距离相等,则;④过平面的一条斜线有且只有一个平面与平面垂直.其中正确的两个命题是( )A .①、③B .①、④C .②、④D .②、③【例62】 两个平面平行的条件是( )A .一个平面内一条直线平行于另一个平面B .一个平面内两条直线平行于另一个平面C .一个平面内的无数条直线平行于另一个平面D .一个平面内的任意一条直线平行于另一个平面【例63】 (xx 江苏12)设和为不重合的两个平面,给出下列命题:①若内的两条相交直线分别平行于内的两条直线,则平行于;②若外一条直线与内的一条直线平行,则和平行;③设和相交于直线,若内有一条直线垂直于,则和垂直;④直线与垂直的充分必要条件是与内的两条直线垂直.上面命题中,真命题的序号是 .(写出所有真命题的序号)【例64】 (05年北京卷6)在正四面体中,,,分别是,,的中点,下面四个结论中不成立...的是( )A .平面B .平面C .平面平面D .平面平面【例65】 判断下面命题的正误:⑴一条直线和一个平面平行,它就和这个平面内的任何直线平行.⑵如果一条直线垂直于平面内的两条直线,那么这条直线和这个平面垂直.⑶垂直于三角形两边的直线必垂直于第三边.⑷过点垂直于直线的所有直线都在过点垂直于的平面内.⑸如果三条共点直线两两垂直,那么其中一条直线垂直于另两条直线确定的平面.【例66】 (xx 年一模·朝阳·文·题8)如图,设平面,,EF AB CD αβαα=⊥⊥,垂足分别为,且,如果增加一个条件就能推出,给出四个条件:①;②;③与在内的正投影在同一条直线上;④与在平面内的正投影所在直线交于一点. 那么这个条件不可能...是( ) A .①② B .②③ C .③ D .④【例67】(xx四川)如图,已知六棱锥的底面是正六边形,平面,,则下列结论正确的是()A. B.平面平面C.直线平面 D.直线与平面所成的角为PFE DC A。
空间位置关系的判断与证明.板块四.垂直关系的判断与证明 普通高中数学复习讲义Word版

【例1】 下列说法正确的有 .①过一点有且只有一条直线垂直于已知直线.②若一条直线与平面内无数条直线垂直,则这条直线与这个平面垂直.③若一条直线平行于一个平面,则垂直于这个平面的直线必垂直于这条直线. ④若一条直线垂直于一个平面,则垂直于这条直线的另一条直线必平行于这个平面.⑤若一条直线平行于一个平面,则它和这个平面内的任何直线都不垂直. ⑥平行于同一个平面的两条直线可能垂直.【难度】 ★ 【解析】 ①错误,过一点有一个平面垂直于已知直线,该平面内任一条过该点的直线都垂直于已知直线;②错误,若这无数条直线都是平行直线,则这条直线可以不垂直于这个平面,并且可以与这个平面相交,平行或在平面内;③正确,这条直线平行于这个平面,则必平行于该平面内的一条直线(过这条直线作一个与此平面相交的平面,交线即满足),而垂直于该平面的直线垂直于平面内任一条直线,故必垂直于这条与此平面平行的直线; ④错误,可以在此平面内,或与此平面平行; ⑤错误,在这个平面内有一组平行线与它异面垂直;⑥正确,比如正方体上底面的两条相邻的棱互相垂直,且都与下底面平行; 综上知,正确的说法有③⑥.【例2】 在空间四面体的四个面中,为直角三角形的最多有 个. 【难度】 ★★【解析】 4;一个可行的例子如下:ABC ∆为直角三角形,B ∠为直角,直线PA ⊥面ABC ,D 为直线PA 上异于A 点的任意点,则四棱锥D ABC -的4个面均为直角三角形.(学生可以试着证明)【例3】 已知在三棱锥A BCD -中AC AD =,BD BC =,求证:AB ⊥CD .典例分析板块五.垂直个关系的判断与证明ABCE【难度】 ★★【解析】 设CD 中点为E ,连接AE ,BE∵ACD ∆为等腰三角形,∴AE ⊥CD , 同理BE ⊥CD∴CD ⊥平面ABE ,又AB ⊂面ABE ∴CD ⊥AB .【例4】 如图,已知三棱锥P ABC -,90ACB ∠=,D 为AB 的中点,且PDB ∆是正三角形,PA ⊥PC .求证:⑴ PA ⊥面PBC ;⑵平面PAC ⊥平面ABC .DPABC【难度】 ★★★【解析】 ⑴由已知D 是AB 中点,PDB ∆是正三角形,∴12PD AB =,由平面几何知识可知,APB ∆为直角三角形 ∴PA ⊥PB ,又PA ⊥PC ,PB PC P =, ∴PA ⊥面PBC ⑵∵PA ⊥面PBC 又∵BC ⊂面PBC ,∴PA ⊥BC ,又AC ⊥BC ,AC PA A =∴BC ⊥面PAC∵BC ⊂面ABC ∴平面PAC ⊥平面ABC【例5】 如图,ABCD 是正方形,SA 垂直于平面ABCD ,过A 且垂直于SC 的平面交SB 、SC 、SD 分别于点E 、F 、G ,求证:AE SB ⊥,AG SD ⊥.EBCFDGSA【难度】 ★★★【解析】 分析:本题考查线面垂直的判定与性质定理,以及线线垂直和线面垂直相互转化的思想.由于图形的对称性,所以两个结论只需证一个即可.欲证AE SB ⊥,可证AE ⊥平面SBC ,为此须证AE BC ⊥、AE SC ⊥,进而转化证明BC ⊥平面SAB 、SC ⊥平面AEFG .证明:∵SA ⊥平面ABCD ,BC ⊂平面ABCD ,∴SA BC ⊥. 又∵ABCD 为正方形,∴BC AB ⊥. ∴BC ⊥平面ASB .∵AE ⊂平面ASB ,∴BC AE ⊥.又∵SC ⊥平面AEFG ,∴SC AE ⊥.∴AE ⊥平面SBC . 又∵SB ⊂平面SBC ,∴AE SB ⊥, 同理可证AG SD ⊥.【例6】 如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,60AB AD AC CD ABC ⊥⊥∠=,,°,PA AB BC ==,E 是PC 的中点.证明:面ABE ⊥面PCD .【难度】 ★★★【解析】 由PA AB BC ==,60ABC ∠=°,可得AC PA =.∵E 是PC 的中点,∴AE ⊥PC . 在四棱锥P ABCD -中,∵PA ⊥底面ABCD ,CD ⊂平面ABCD ,故PA CD ⊥. ∵AC CD PAAC A ⊥=,,∴CD ⊥平面PAC .而AE ⊂平面PAC ,∴CD ⊥AE ,且PCCD C =,所以AE ⊥平面PCD .而AE ⊂平面ABE ,∴平面ABE ⊥平面PCD .【例7】 如图,四面体P ABC -,PA ⊥面ABC ,AB ⊥BC ,过A 作AE ⊥PB 交PB 于E ,过A 作AF ⊥PC 交PC 于F .求证:PC ⊥EF .F EPABC【难度】 ★★★【解析】 分析:要证线线垂直,可转化为线面垂直,本题关键在于线 面垂直与线线垂直的转化.可由分析法入手:要证PC ⊥EF ⇐PC ⊥面AEF ⇐PC ⊥AF (已知),PC ⊥AE ⇐AE ⊥面PBC ⇐AE ⊥PB (已知),AE ⊥BC ⇐BC ⊥面PAB ⇐BC ⊥AB (已知),BC ⊥PA ⇐PA ⊥面ABC ,从而问题得到解决. F EPABC∵PA ⊥面ABC ,且BC ⊂面ABC ,∴BC ⊥PA ,且BC ⊥AB ∴BC ⊥面ABE∴BC ⊥AE ,又PB ⊥AE ,且BC PB B = ∴AE ⊥面PBC ,且PC ⊂面PBC ∴AE ⊥PC ,又AF ⊥PC ,且AFAE A =∴PC ⊥面AEF ,且EF ⊂面AEF ∴PC ⊥EF 本题可以分化出小题,体现中间的转化过程.【例8】 如图O 是正方体下底面ABCD 中心,B H D O ''⊥,H 为垂足.求证:B H '⊥平面AD C '.【难度】 ★★【解析】OH DCBAD'C'B'A'因为B H D O ''⊥,所以只需再证明B H '垂直于面AD C '上的另外一条直线即可. 因为AC BD AC BB '⊥⊥,,所以AC ⊥平面BDD B '',又B H '⊂面BDD B '',因此AC B H '⊥.于是B H '垂直于相交直线AC D O ',所在的平面AD C '.【例9】 如图所示,在正方体1111ABCD A B C D -中..求证:1BD ⊥面1AB C .A 1D 1C 1B 1DCBA【难度】 ★★【解析】 连结BD .ABCDB 1C 1D 1A 1∵1DD ⊥底面ABCD ,又AC ⊂面ABCD ,∴1DD ⊥AC ,又底面ABCD 为正方形,∴AC ⊥BD ,又1BD DD D =,∴AC ⊥面1BDD ,又∵1BD ⊂面1BDD ∴AC ⊥1BD 同理连结1BC 可得1BD ⊥1B C∴根据线面垂直的判定定理可得1BD ⊥面1AB C .【例10】 在长方体1111ABCD A B C D -中,点E ,F 分别在1AA ,1CC 上且1BE A B ⊥,1BF BC ⊥,求证:1BD ⊥面BEF【难度】 ★★【解析】 FEC 1B 1D 1A 1AB C D由111A D A B ⊥,11B E A B ⊥,有1B E ⊥面11A BD ∴11B E BD ⊥由111C D BC ⊥,11B F BC ⊥,有1B F ⊥面11BC D ∴11B F BD ⊥ ∴1BD ⊥面1B EF【例11】 在正方体1111ABCD A B C D -中,P 为1DD 的中点,O 为底面ABCD 的中心.求证:1B O ⊥面PAC .【难度】 ★★【解析】P OA 1D 1C 1B 1D CA(法一)由于AC ⊥BD ,且AC ⊥1BB ,∴AC ⊥面11BDD B ,且1B O ⊂面11BDD B .∴1B O ⊥AC 连结1PB ,设AB a =,则1111AB CB B D ===QABCDB 1C 1D 1A 1PO∵222222113()22OB OB BB a a =+=+=222222111119())24PB PD B D a a =+=+=22222213())24OP PD DO a a =+=+=∴22211OB OP PB +=.∴1B O ⊥OP ,又POAC O =,∴1B O ⊥平面PAC (法二)由于AC ⊥BD ,且AC ⊥1BB ,∴AC ⊥面11BDD B ,且1B O ⊂面11BDD B ∴1B O ⊥AC 取CD 中点Q ,连结1QC ,OQ ,则OQ ∥11B C在正方形11CC D D 中,由P ,Q 分别为1DD ,1CC 的中点,可知CP ⊥1C Q , 又CP ⊥11B C ,且1111C QB C C =∴CP ⊥面11B C QO ,又1B O ⊂面11B C QO ∴CP ⊥1B O ∴1B O ⊥面PAC【例12】 在四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥底面ABCD ,M ,N 分别为PC ,AB 的中点.⑴求证:MN ∥平面PAD ;⑵若45PDA ∠=,求证:MN ⊥面PCD .QPD CAMN【难度】 ★★★★【解析】 ⑴取PD 中点Q ,连结MQ ,AQ ,∵M ,N 分别为AB ,PC 的中点 ∴MQ ∥AN 且MQ =AN∴MN ∥AQ ,从而得到MN ∥平面PAD ⑵(法一)R PDBCAM N∵PA ⊥底面ABCD ,且CD ⊂面ABCD ∴CD ⊥PA ,又由底面是矩形有CD ⊥AD ∴CD ⊥面PAD ,又AQ ⊂面PAD ∴AQ ⊥CD又∵45PDA ∠=,∴PA AD = 从而在等腰Rt APD ∆中,又PQ QD = ∴AQ ⊥PD ,又CD PD D =∴AQ ⊥面PAD ,又MN ∥AQ∴MN ⊥面PCD (法二)∵PA ⊥底面ABCD ,且CD ⊂面ABCD ∴CD ⊥PA ,又由底面是矩形有CD ⊥AD ∴CD ⊥面PAD ,又PD ⊂面PAD ∴PD ⊥CD取CD 中点R ,连结MR ,NR ,则MR ∥PD ,NR ∥AD ∴CD ⊥MR ,又CD ⊥AD ,∴CD ⊥NR ,∴CD ⊥面MNR ,且MN ⊂面MNR , ∴MN ⊥CD∵45PDA ∠=,∴PA AD =,且BC AD =∴PA BC =,又AN BN =,且90PAN CBN ∠=∠=∴根据三角形全等可知PN NC =,又PM MC =∴MN ⊥PC∵CDPC C =,∴MN ⊥面PCD【例13】 已知平行六面体1111ABCD A B C D -的底面是菱形,且1160A AB A AD ∠=∠=.求证:1CC ⊥BD .OABCD A 1B 1C 1D 1【难度】 ★★★【解析】 ∵底面ABCD 是菱形,∴BD ⊥AC连结BD ,AC 交于点O ,连结1A B ,1A D∵1160A AB A AD ∠=∠=,由1A AD ∆≌1A AB ∆可知,∴1A BD ∆为等腰三角形,又BO OD =∴1A O ⊥BD ,又1ACAO O =, ∴BD ⊥面1A AO ,又1AA ∥1CC ,且1CC ⊂面1A AO .∴1CC ⊥BD【例14】 (2008深圳高三联考)如图,在直四棱柱1111ABCD A B C D -中,当底面四边形ABCD满足条件 时,有111AC B D ⊥.(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形)D 1C 1B 1A 1DCBA【难度】 ★★【解析】 AC BD ⊥(或更特殊的四边形ABCD 是正方形或菱形);111AC B D ⊥⇔BD ⊥平面11ACC A ⇔BD AC ⇔⊥. 故充要条件为AC BD ⊥,本题只要求写一个充分条件即可.【例15】 如图,A 、B 、C 、D 是空间四点,在ABC △中,2AB =,AC BC =边ADB △所在的平面以AB 为轴可转动.当ADB △转动过程中,是否总有AB CD ⊥?请证明你的结论ABC DO【难度】 ★★【解析】 当ADB △在转动过程中,总有OC AB ⊥,OD AB ⊥.∴AB ⊥平面COD ,∴AB CD ⊥当ADB △转动到与ABC △共面时,仍然有AB CD ⊥ 故ADB △转动过程中,总有AB CD ⊥.【例16】 在正方体1111ABCD A B C D -中,M 是1AA 的中点,问当点N 位于AB 上何处时,1MN MC ⊥?【难度】 ★★【解析】 若想1MN MC ⊥,只需1MN MB ⊥,只需11A MB AMN ∽△△,只需12AN AM =,N 位于13AN NB =∶∶处,即AB 的四等分点处.【例17】 如图,直三棱柱111ABC A B C -中,1AC BC ==,90ACB ∠=︒,1AA =,D 是11A B 的中点.⑴求证1C D ⊥平面1A B ;⑵当点F 在1BB 上什么位置时,会使得1AB ⊥平面1C DF ?并证明你的结论.C 1B 1A 1FEDC B A【难度】 ★★★【解析】 C 1B 1A 1FEDCB A⑴如图,∵111ABC A B C -是直三棱柱,∴11111AC B C ==,且11190AC B ∠=︒. 又D 是11A B 的中点,∴111C D A B ⊥. ∵1AA ⊥平面111A B C ,1C D ⊂平面111A B C , ∴11AA C D ⊥,∴1C D ⊥平面11AA B B .⑵作1DE AB ⊥交1AB 于E ,延长DE 交1BB 于F ,连结1C F , 则1AB ⊥平面1C DF ,点F 即为所求.事实上,∵1C D ⊥平面11AA B B ,1AB ⊂平面11AA B B , ∴11C D AB ⊥.又1AB DF ⊥,1DF C D D =,∴1AB ⊥平面1C DF .【例18】 (2000全国,文19)如图已知平行六面体1111ABCD A B C D -的底面ABCD 是菱形,且11C CB C CD BCD ∠=∠=∠.⑴ 证明1C C BD ⊥;⑵ 当1CD CD 的值为多少时,能使1A C ⊥平面1C BD ?请给出证明.图 9-2-284D 1A 1C 1B 1DCBA【难度】 ★★★★【解析】 ⑴ 连结1A C 、AC ,AC 和BD 交于O ,连结1C O .∵四边形ABCD 是菱形,∴AC BD ⊥,BC CD =.又∵11BCC DCC ∠=∠,11C C C C =,∴11C BC C DC ∆∆≌.∴11C B C D =. ∵DO OB =,∴1C O BD ⊥. 又AC BD ⊥,1ACC O O =,∴BD ⊥平面1AC .又1C C ⊂平面1AC ,∴1C C BD ⊥. ⑵ 当11CD CC =时,能使1A C ⊥平面1C BD .证法一:∵11CDCC =,∴1BC CD C C ==.图 9-2-285HGA 1D 1ADCC 1B 1B又11BCD C CB C CD ∠=∠=∠,由此可推得11BD C B C D ==. ∴三棱锥1C C BD -是正三棱锥. 设1A C 与1C O 相交于G .∵11AC AC ∥,且11:2:1AC OC =,∴1:2:1C G GO =. 又1C O 是正1C BD ∆的BD 边上的高和中线,∴点G 是正1C BD ∆的中心.∴CG ⊥平面1C BD ,即1A C ⊥平面1C BD . 证法二:由⑴知BD ⊥平面1AC ,∵1A C ⊂平面1AC ,∴1BD AC ⊥. 当11CDCC =时,平行六面体的六个面是全等的菱形,同1BD AC ⊥证法可得11BC AC ⊥.又1BD BC B =,∴1A C ⊥平面1C BD .【例19】 已知四面体ABCD ,①若棱AB CD ⊥,求证2222AC BD AD BC +=+ ②若2222AC BD AD BC +=+,求证棱AB CD ⊥.【难度】 ★★★【解析】 ①过B 作CD 的垂线,垂足E ,连AE ,FEDCBA∵CD AB ⊥, ∴CD ⊥平面ABE , ∴CD AE ⊥.∴222AC AE CE =+、222BD BE DE =+; 又有222AD AE DE =+、222BC BE CE =+. ∴222222AC BD AE BE CE DE +=+++, 而222222AD BC AE BE CE DE +=+++. ∴2222AC BD AD BC +=+.②过A 点作CD 的垂线,垂足设为F ,于是有:222AD AF DF =+、222BC BE CE =+; 222AC AF CF =+、222BD BE DE =+;∵2222AD BC AC BD +=+;∴22222222AF DF BE CE AF CF BE DE +++=+++ ∴2222DF CE CF DE +=+, ∴2222DF CF DE CE -=-,∴()()()()DF CF DF CF DE CE DE CE +-=+-, ∴DF CF DE CE -=-. ∴DF CE DE CF +=+.∴E 、F 只能重合于一点,故有CD ⊥平面ABE , ∴CD AB ⊥.【例20】 已知三棱锥P ABC -中,PC ⊥底面ABC ,AB BC =,D F ,分别为AC PC ,的中点,DE AP ⊥于E .⑴求证:AP ⊥平面BDE ;⑵求证:平面BDE ⊥平面BDF ;⑶若:1:2AE EP =,求截面BEF 分三棱锥P ABC -所成两部分的体积比.【难度】 ★★★【解析】FEBDCAP⑴∵AB BC=,D为AC中点,∴BD AC⊥又PC⊥底面ABC,∴PC BD⊥∵PC AC C=,∴BD⊥平面PAC,∴BD AP⊥.又DE AP⊥,∴AP⊥平面BDE.⑵∵D F,为AC PC,的中点,∴DF AP∥.结合⑴可知DF⊥平面BDE.⑶∵211:323PEF PACPE PFS SPA PC∆∆⨯==⨯=⨯,∴13B PEF B PACV V--=.因此两部分的体积比为1:2.【例21】(2009扬州中学高三期末)在四棱锥P ABCD-中,90ABC ACD∠=∠=︒,60BAC CAD∠=∠=︒,PA⊥平面ABCD,E为PD的中点,22PA AB==.⑴求四棱锥P ABCD-的体积V;⑵若F为PC的中点,求证PC⊥平面AEF.【难度】★★★【解析】FEDCBAP⑴在Rt ABC∆中,1AB=,60BAC∠=︒,∴BC2AC=.在Rt ACD∆中,2AC=,60CAD∠=︒,∴CD=4AD=.∴1111122222BCDS AB BC AC CD∆=⋅+⋅=⨯⨯⨯.则123V=⑵∵PA CA=,F为PC的中点,∴AF PC⊥.∵PA⊥平面ABCD,∴PA CD⊥.∵AC CD⊥,PA AC A=,∴CD⊥平面PAC.∴CD PC⊥.∵E 为PD 中点,F 为PC 中点,∴EF CD ∥.则EF PC ⊥. ∵AFEF F =,∴PC ⊥平面AEF .【例22】 (2003京皖春)如图所示,正四棱柱1111ABCD A B C D -中,底面边长为侧棱长为4.E F ,分别为棱AB BC ,的中点,EF BD G =. ⑴求证:平面1B EF ⊥平面11BDD B ; ⑵求点1D 到平面1B EF 的距离d ; ⑶求三棱锥11B EFD -的体积V .D 1C 1B 1A 1GFEDCB A【难度】 ★★★ 【解析】 ⑴连接AC .∵正四棱柱1111ABCD A B C D -的底面是正方形. ∴AC BD ⊥,又1AC DD ⊥,故AC ⊥平面11BDD B . ∵E F ,分别为AB BC ,的中点,故EF AC ∥, ∴EF ⊥平面11BDD B , ∴平面1B EF ⊥平面11BDD B .⑵连结1B G ,在对角面11BDD B 中,作11D H B G ⊥,垂足为H , ∵平面1B EF ⊥平面11BDD B ,且平面1B EF平面11BDD B 1B G =,∴1D H ⊥平面1B EF ,且垂足为H ,∴点1D 到平面1B EF 的距离1d D H =. 法一:在11Rt D HB ∆中,11111sin D H D B D B H =⋅∠,∵11114D B B =,11111sin sin BB D B H B GB GB ∠=∠===HGDB B 1D 1∴14d D H ===法二:∵111D HB B BG ∆∆∽,∴11111D H D BB B B G =,∴2111B B d D H B G ==法三:连接1D G ,则三角形11D GB 的面积等于正方形11DBB D 面积的一半.即21111122B G D H BB ⋅=.∴d =⑶111111111623323B EFD D B EF B EF V V V dS --∆====⋅=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学而思高中完整讲义:空间位置关系的判断与证明.板块三.平行关系
的判断与证明.学生版
【例1】 下列说法正确的有 .
①过一点有且只有一条直线垂直于已知直线.
②若一条直线与平面内无数条直线垂直,则这条直线与这个平面垂直.
③若一条直线平行于一个平面,则垂直于这个平面的直线必垂直于这条直线. ④若一条直线垂直于一个平面,则垂直于这条直线的另一条直线必平行于这个平面.
⑤若一条直线平行于一个平面,则它和这个平面内的任何直线都不垂直. ⑥平行于同一个平面的两条直线可能垂直.
【例2】 在空间四面体的四个面中,为直角三角形的最多有 个.
【例3】 已知在三棱锥A BCD -中AC AD =,BD BC =,求证:AB ⊥CD .
A
B
C
E
【例4】 如图,已知三棱锥P ABC -,90ACB ∠= ,D 为AB 的中点,且PDB ∆是正三角
形,PA ⊥PC .
求证:⑴ PA ⊥面PBC ;⑵平面PAC ⊥平面ABC .
D
P
A
B
C
【例5】 如图,ABCD 是正方形,SA 垂直于平面ABCD ,过A 且垂直于SC 的平面交SB 、
SC 、SD 分别于点E 、F 、G ,求证:AE SB ⊥,AG SD ⊥.
典例分析
E
B
C
F
D
G
S
A
【例6】 如图,在四棱锥
P ABCD
-中,
PA ⊥底面A B C ,
60AB AD AC CD ABC ⊥⊥∠=,,°,PA AB BC ==,E 是PC 的中点.
证明:面ABE ⊥面PCD .
【例7】 如图,四面体P ABC -,PA ⊥面ABC ,AB ⊥BC ,过A 作AE ⊥PB 交PB 于E ,
过A 作AF ⊥PC 交PC 于F .求证:PC ⊥EF .
F E
P
A
B
C
【例8】 如图O 是正方体下底面ABCD 中心,B H D O ''⊥,H 为垂足.求证:B H '⊥平面
AD C '.
【例9】 如图所示,在正方体1111ABCD A B C D -中..求证:1BD ⊥面1AB C .
A 1
D 1
C 1
B 1
D
C
B
A
【例10】 在长方体1111ABCD A B C D -中,点E ,F 分别在1AA ,1CC 上且1B E A B ⊥,
1BF BC ⊥,求证:1BD ⊥面BEF
【例11】 在正方体1111ABCD A B C D -中,P 为1DD 的中点,O 为底面ABCD 的中心.求证:
1B O ⊥面PAC .
【例12】 在四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥底面ABCD ,M ,N 分别为PC ,
AB 的中点.⑴求证:MN ∥平面PAD ;⑵若45PDA ∠= ,求证:MN ⊥面PCD .
Q
P
D C
A
M
N
【例13】 已知平行六面体1111ABCD A B C D -的底面是菱形,且1160A AB A AD ∠=∠= .求证:
1CC ⊥BD .
O
A
B
C
D A 1
B 1
C 1
D 1
【例14】 (2008深圳高三联考)如图,在直四棱柱1111ABCD A B C D -中,当底面四边形ABCD
满足条件 时,有1
11AC B D ⊥.(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形)
D 1
C 1
B 1
A 1
D
C
B
A
【例15】 如图,A 、B 、C 、D 是空间四点,在ABC △中,2AB =
,AC BC ==,等
边ADB △所在的平面以AB 为轴可转动.当ADB △转动过程中,是否总有AB CD ⊥?请证明你的结论
A
B
C D
O
【例16】 在正方体1111ABCD A B C D -中,M 是1AA 的中点,问当点N 位于AB 上何处时,
1MN MC ⊥?
【例17】 如图,直三棱柱111ABC A B C -中,1AC BC ==,90ACB ∠=︒
,1AA =D 是11
A B 的中点.
⑴求证1C D ⊥平面1A B ;
⑵当点F 在1BB 上什么位置时,会使得1AB ⊥平面1C DF ?并证明你的结论.
C 1
1A 1
F
E
D
C B A
【例18】 (2000全国,文19)
如图已知平行六面体1111ABCD A B C D -的底面A B C D 是菱形,且11C CB C CD BCD ∠=∠=∠.
⑴ 证明1C C BD ⊥;
⑵ 当1
CD CD 的值为多少时,能使1
AC ⊥平面1C BD ?请给出证明. 图 9-2-284
D 1
A 1
C 1
B 1
D
C
B
A
【例19】 已知四面体ABCD ,
①若棱AB CD ⊥,求证2222AC BD AD BC +=+
②若2222AC BD AD BC +=+,求证棱AB CD ⊥.
【例20】 已知三棱锥P ABC -中,PC ⊥底面ABC ,AB BC =,D F ,
分别为AC PC ,的中点,DE AP ⊥于E .
⑴求证:AP ⊥平面BDE ;
⑵求证:平面BDE ⊥平面BDF ;
⑶若:1:2AE EP =,求截面BEF 分三棱锥P ABC -所成两部分的体积比.
【例21】 (2009扬州中学高三期末)
在四棱锥P ABCD -中,90ABC ACD ∠=∠=︒,60BAC CAD ∠=∠=︒,PA ⊥平面ABCD ,E 为PD 的中点,22PA AB ==. ⑴求四棱锥P ABCD -的体积V ;
⑵若F 为PC 的中点,求证PC ⊥平面AEF .
【例22】 (2003京皖春)
如图所示,正四棱柱1111ABCD A B C D -中,
底面边长为侧棱长为4.E F ,
分别为棱AB BC ,
的中点,EF BD G = . ⑴求证:平面1B EF ⊥平面11BDD B ;
⑵求点1D 到平面1B EF 的距离d ; ⑶求三棱锥11B EFD -的体积V .
D 1
C 1
B 1
A 1
G
F
D
C
B A。
