流体静力学方程的应用
流体静力学方程式
流体静力学方程式流体静力学是研究流体在静止状态下的力学性质的学科。
它是流体力学的一个分支，研究流体静止时的压力、密度、重力等因素对流体的影响。
本文将介绍流体静力学的方程式及其应用。
正文流体静力学方程式是描述流体静止时的力学行为的数学表达式。
主要包括两个方程式：流体静力平衡方程和流体连续性方程。
一、流体静力平衡方程流体静力平衡方程是基于力的平衡原理得出的。
它可以用来描述流体内外压力的均衡状态。
在一个封闭的容器中，流体的压力在各个方向上必须保持平衡。
这个平衡关系可以用以下方程式表示：P = ρg其中，P是压力场的梯度，ρ是流体的密度，g是重力加速度。
这个方程式表明流体中各个点的压力梯度与密度和重力加速度之间存在着一定的关系。
二、流体连续性方程流体连续性方程是基于流体质量守恒原理得出的。
它描述了流体在任意两个点之间质量的守恒关系。
对于一个不可压缩的流体（密度恒定），流体连续性方程可以用以下方程式表示：·v = 0其中，·v表示流体速度场的散度。
这个方程式表明流体在任意两个点之间的流量守恒，流出的质量等于流入的质量。
这两个方程式是流体静力学中的基本方程，通过它们可以计算流体静止时的压力分布和速度分布。
在实际的工程应用中，它们被广泛用于分析和设计涉及流体静力学的系统，如水坝、水管等。
总结起来，流体静力学方程式是描述流体静止时力学行为的基本数学表达式。
通过流体静力平衡方程和流体连续性方程，我们可以了解流体静态时的压力分布和速度分布，进而应用于实际工程中的设计和分析。
这些方程式为我们提供了深入理解流体静力学的基础，有助于我们更好地应对与流体静力学相关的问题。
流体静力学方程的应用条件
流体静力学方程的应用条件流体静力学是流体力学的一个分支，研究的是静止流体的力学性质和行为。
在实际应用中，流体静力学方程经常用于解决各种与静止流体相关的问题。
下面将介绍流体静力学方程的应用条件及其在不同领域的具体应用。
流体静力学方程适用于稳定的静止流体系统，即系统中的流体没有运动。
这意味着流体的速度、加速度等都为零，只存在压力和重力。
当流体系统处于平衡状态时，流体静力学方程可以用来描述和分析流体的力学性质。
在建筑工程领域，流体静力学方程被广泛应用于水压力计算。
例如，在水坝工程中，需要计算水坝底部受到的压力，以确保水坝的稳定性。
通过应用流体静力学方程，可以计算出水坝底部受到的水压力，并据此设计水坝的结构和厚度，确保其能够承受水压力的作用。
在航空航天领域，流体静力学方程的应用条件也得到了充分利用。
例如，在航空器的燃油系统中，需要保证燃油能够平稳地供给到发动机。
通过应用流体静力学方程，可以计算出燃油供给系统中的压力分布，并据此设计和优化燃油管道的布局和尺寸，以确保燃油能够稳定地输送到发动机。
在地质学领域，流体静力学方程被用于地下水的流动分析。
地下水是地球内部的一种重要水资源，对于地下水的合理开发和利用具有重要意义。
通过应用流体静力学方程，可以计算地下水的压力分布和流速，进而预测地下水的流动方向和速率。
这对于地下水资源的管理和保护具有重要的参考意义。
除了以上几个领域，流体静力学方程还被广泛应用于液压系统、水污染控制、海洋工程等领域。
在液压系统中，流体静力学方程被用于计算液压缸中的压力和力的分布，以实现液压系统的运动控制。
在水污染控制中，流体静力学方程被用于计算污水处理设备中的压力和流速，以实现污水的处理和净化。
在海洋工程中，流体静力学方程被用于计算海洋结构物受到的水压力和力的分布，以确保结构物的安全性和稳定性。
流体静力学方程在各个领域都有着广泛的应用。
通过应用流体静力学方程，可以计算出流体系统中的压力分布和力的分布，进而实现对流体系统的分析和设计。
流体静力学基本方程式的应用
ρρAC、：ρ9B
：指示液的密度 流体的密度
9
第一节 流体静力学基本方程式
(3)斜管压差计 ❖ 当被测量的流体的压差更小时，可采用斜管压差计。
R'=R/sinα
10
10
第一节 流体静力学基本方程式
2.液位的测量
h =（ρ0－ρ）R/ρ
11
11
5
5
第一节 流体静力学基本方程式
三、流体静力学基本方程式
p ＝ p0 ＋ g h
（1）液体内静压强随液体的深度的增大而增大， 等深处形成等压面。
（2）当液面上方的压力p0有改变时，液体内部各
点的压力p也发生同样大小的改变，称为帕斯卡原
理。
6
第一节 流体静力学基本方程式
四、流体静力学基本方程式的应用 ❖ 1.压力与压力差的测量
第一章 流体流动
目录
第一节 流体静力学基本方程式 第二节 流体流动的基本方程式 第三节 流体在管内的流动 第四节 流速和流量的测量
第一节 流体静力学基本方程式
一、流体的密度
❖ 1.混合液体的密度
1 xwA xwB xwn
m A B
n
❖ 2.混合气体的密度
3
m AxVA A xVB AxVn
(1)U形管压差计 (2)微差压差计 ❖ 2.液位的测量
7
7
图1-3 U型管压差计
第一节 流体静力学基本方程式
(1)U形管压差计
p1- p2=(ρA-ρ)gR
ρA：指示液的密度 ρ： 流体的密度
8
8
第一节 流体静力学基本方程式
(2)微差压差计 ❖ 若所测的压力差很小，可采用微差压差计。
流体静力方程应用
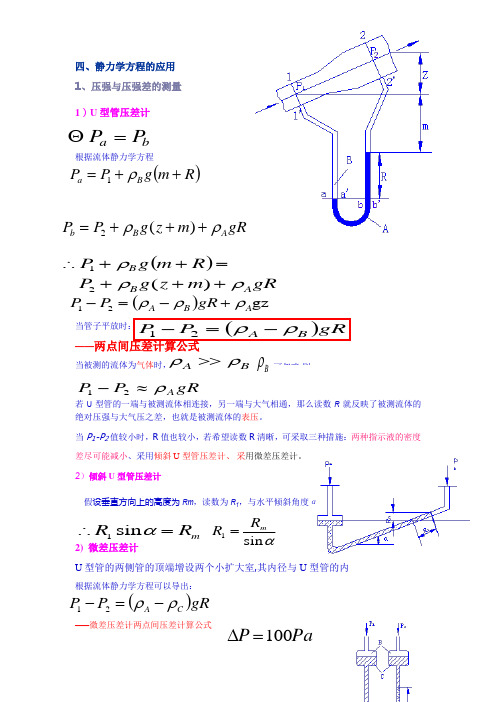
四、静力学方程的应用 1、压强与压强差的测量 1）U 型管压差计根据流体静力学方程当管子平放时： ——两点间压差计算公式当被测的流体为气体时， 若U 型管的一端与被测流体相连接，另一端与大气相通，那么读数R 就反映了被测流体的绝对压强与大气压之差，也就是被测流体的表压。
当P 1-P 2值较小时，R 值也较小，若希望读数R 清晰，可采取三种措施：两种指示液的密度差尽可能减小、采用倾斜U 型管压差计、 采用微差压差计。
2）倾斜U 型管压差计假设垂直方向上的高度为Rm ，读数为R 1，与水平倾斜角度α2) 微差压差计 U 型管的两侧管的顶端增设两个小扩大室,其内径与U 型管的内根据流体静力学方程可以导出： ——微差压差计两点间压差计算公式 ba P P =Θ()R m g P P B a ++=ρ1gRm z g P P A B b ρρ+++=)(2())( 21gR m z g P R m g PA B B ρρρ+++=++∴()gz 21A B A gR P P ρρρ+-=-可忽略,则 B ρB A ρρ>>， gRP P A ρ≈-21()gRP P B A ρρ-=-21m R R =∴αsin 1αsin 1m R R =()gRP P C A ρρ-=-21PaP 100=∆例：用3种压差计测量气体的微小压差试问：1）用普通压差计，以苯为指示液，其读数R 为多少？2）用倾斜U 型管压差计，θ=30°，指示液为苯，其读数R’为多少？3）若用微差压差计，其中加入苯和水两种指示液，扩大 室截面积远远大于U 型管截面积，此时读数R 〃为多少？ R 〃为R 的多少倍？ 已知：苯的密度 水的密度计算时可忽略气体密度的影响。
解：1）普通管U 型管压差计U 型管的两侧管 3/879m kg c=ρg P RC ρ∆=807.9879100⨯=m 0116.0=。
流体静力学方程的应用条件(一)
流体静力学方程的应用条件(一)流体静力学方程的应用条件1. 理论背景在研究流体行为时，流体静力学是其中的一个重要方面。
流体静力学是研究流体在静止状态下的行为和力学性质的学科。
通过应用流体静力学方程，我们可以分析和解决许多与流体静停止状态有关的问题。
2. 流体静力学方程的概述流体的静平衡在流体静力学中，我们考虑的是流体处于静止状态，并且没有流动的情况。
这意味着流体内部的每一点都保持静止，并且没有速度梯度存在。
流体静力学方程流体静力学方程是描述流体静力学行为的基本方程，它包括了质量守恒、动量守恒和能量守恒定律。
流体静力学方程可以用来计算流体内的压力分布、压力力学、力的传递以及其他与流体在静止状态下相关的物理量。
3. 流体静力学方程的应用条件根据流体静力学方程的性质和适用范围，我们可以得出以下应用条件：•流体应为牛顿流体：流体力学方程适用于牛顿流体，即粘度随剪切速率保持恒定。
如果流体具有非牛顿性质，例如塑性流体或非牛顿粘性流体，流体静力学方程将不再适用。
•流体应为静止状态：流体静力学方程适用于流体处于静止状态下的情况。
如果流体具有流动或速度梯度，流体动力学方程将更适用于分析此类情况。
•流体应为恒定密度流体：流体静力学方程假设流体具有恒定的密度。
如果流体的密度随位置或时间变化，流体静力学方程将不再适用。
•流体应为亚音速流体：流体静力学方程适用于亚音速流体，即流体的速度小于声速。
如果流体处于超音速流动状态，流体动力学方程将更适合分析。
4. 结论流体静力学方程是解决与流体在静态条件下相关问题的基本工具。
然而，我们必须注意应用流体静力学方程的条件，以确保结果的准确性和可靠性。
只有在满足适用条件的情况下，我们才能有效地利用流体静力学方程解决实际问题。
以上是流体静力学方程的应用条件的简要介绍。
通过理解并应用这些条件，我们可以更好地利用流体静力学方程分析和解决与静态流体行为有关的问题。
5. 应用举例下面列举几个典型的应用例子，展示在何种情况下可以应用流体静力学方程：•管道内的压力分布：当液体在管道内静止时，可以使用流体静力学方程来计算管道内的压力分布。
4-第一节 流体静力学方程应用
2、学会应用方程式的步骤并计算简单问题
3、静力学基本方程式的解题思路、方法及应用
教学难点
静力学基本方程式的解题思路、方法及应用
教学方法
习题法
使用教具
多媒体教学平台
板书设计
主要教学内容及步骤
复习：
1、静止流体的特性
2、流体静力学基本方程式的推导及意义
3、应用公式进行计算的方法及简单应用
若U管一端与设备或管道某一截面连接，另一端与大气相通，这时读数R所反映的是管道中某截面处的绝对压强与大气压强之差，即为表压强或真空度，从而可求得该截面的绝压。
二、液面测定：
液柱压差计是于容器底部器壁及液面上方器壁处各开一小孔，用玻璃管将两孔相连接。玻璃管内所示的液面高度即为容器内的液面高度。这种构造（图1－7所示）易于破损，而且不便于远距离观测。
备课时间
授课时间
授课课时
2
授课形式
讲授
授课章节
名称
第一章第一节
四、静力学基本方程式的应用举例
静力学基本方程式的应用
教学目的
1、熟悉静力学基本方程式
2、学会应用方程式的步骤并计算简单问题
3、知道液柱压强计、液面测定的基本原理及
4、通过例题的讲解，进一步熟悉静力学基本方程式的解题思路、方法及应用
教学重点
根据静力学基本方程：PC=P1+（H+R）ρg
PC，=p2+Hρg+RρAg
因C-C，是等压面，PC= PC，
P1+（H+R）ρg = P2+Hρg+RρAg
2、压强的测定：
选１-１，为等压面，Ｐ1＝Ｐ1，
P1= PＰ1，= Pa + RgρA
第二讲流体静力学基本方程及其应用
第二讲流体静力学基本方程及其应用【学习要求】1．理解流体静力学方程的意义；2．掌握流体静力学方程的应用。
【预习内容】1．在均质流体中，流体所具有的与其所占有的之比称为。
任何流体的密度都随它的和而变化，但对液体的密度影响很小，可忽略，故常称液体为的流体。
2．流体静压力的两个重要特性分别是：（1）；（2）。
3．1atm = mmHg = Pa = mH2O【学习内容】一、流体静力学基本方程式1．流体静力学基本方程式的形式p2 = p1+ ρ ( z1—z2 )g 或p2 = p1+ hρg流体静力学方程表明：在重力作用下静止液体内部的变化规律。
即在液体内部任一点的流体静压力等于。
2．流体静力学基本方程式的意义流体静力学方程表明：（1）当作用于流体面上方的压强有变化时；（2）当流体面上方的压强一定时，静止流体内部任一点压强的大小与流体本身的和有关，因此在的的同一液体处，处在都相等。
二、流体静力学基本方程式的应用1．流体进压强的测量（1）U形管压差计①U形管压差计由、及管内指示液组成。
②指示液要与被测流体不，不起，其密度要，通常采用的指示液有、、及等。
③U形管压差计可用来测量压强差，也可以用来测量或。
【典型例题】例1用U形管测量管道中1、2两点的压强差。
已知管内流体是水，指示液是密度为1595 kg／m3的CCl4，压差计读数为40cm，求压强差(p1– p2)。
若管道中的流体是密度为2.5kg／m3的气体，指示液仍为CCl4，U形管读数仍为40cm，则管道中1、2两点的压强差是多少Pa？【例2】某蒸汽锅炉用本题附图中串联的汞-水U形管压差计以测量液面上方的蒸气压。
已知汞液面与基准面的垂直距离分别为h1 = 2.3 m，h2 = 1.2 m,h3 = 2.5 m,h4 = 1.4m,两U形管间的连接管内充满了水。
锅炉中水面与基准面的垂直距离h5 = 3.0m，大气压强p a = 99kPa。
试求锅炉上方水蒸汽的压强p0为若干（Pa）？【随堂练习】1．大气压强为750mmHg时，水面下20m深处水的绝对压强为多少Pa？2．水平导管上的两点接一盛有水银的U形管压差计（如图所示），压差计读数为26mmHg。
流体静力学方程的应用
液面测定
生产中经常需要了解容器内液体的贮存量，或需 要控制设备里液体的液面，因此要对液面进行测定。
有些液面测定方法，是以静力学基本方程为依据的。
确定液封高度
液封的目的：防治气体泄漏、倒流或有毒气体 溢出；有时则是防止压力过高而起到泄压作用， 以保护设备。
安全水封：当设备内压力超过规定值时，气体就 会从水封管排出，以确保设备操作安全。
水封管插入液面下的深度：
h P1
水g
切断水封:正常操作时，水封不灌水，气体可以绕过 隔板出入储罐，需要切断时，向水封内注入一定高度的水， 使隔板进入水的深度大于两侧可能的压差即可。
溢流水封 用水洗涤的气体设备，通常设备内还有气体，洗
涤液在不断流进的同时还会不断地流出，同时还要 保证设备的气体不外泄。
2.斜管压差计
当被测量的流体压力或压差不大时，读数H很小， 为得到精确读数，可采用斜管压差计，此时：
H H
sin
斜管压差计
注意：倾斜角越小，其值越小，则H值放大为H’的倍数越大。
3.微差压差计
由静力学方程可知：
P1 P2 P ( A B )gH
双液柱微差计
对于一定的压差，密度差越小则H越大，所以应该选 择两种密度接近的指示液。
流体静力学方程的应用
㈠ 压力测量
1.U形管液柱压差计
P2
P1
P2
P1
Hale Waihona Puke L HP1=P2两边液面相等
P1＞P2
两边液面不等
P2
P1
L ba H
P1＞P2
两边液面不等
Pa P1 g(L H ) Pb P2 gL 0 gH
Pa Pb
P1 P2 (0 )gH 0
流体静力学方程的应用
A
所以
h 0 R
流体静力学基本方程式的应用(二)
三. 液封高度的计算 液封作用：
确保设备安全：当设备 内压力超过规定值时，气 体从液封管排出；
防止气柜内气体泄漏。 液封高度： h p(表)
g
切断水封有些常压可燃气体贮罐前 后安装切断水封以代替笨重易漏 的截止阀 .正常操作时，水封不 充水，气体可以顺利绕过隔板出 入贮罐；需要切断时（如检修）， 往水封内注入一定高度的水，使 隔板在水中的水封高度大于水封 两侧最大可能的压差值。（图b所 示）
流体静力学基本方程式的应用（一）
▪ 例2 如附图所示，水在管道中 流动。为测得a、b两点的压力差， 在管路上方安装一U形压差计， 指示液为汞。已知压差计的读数 R＝100mm，试计算ａ、ｂ截面的 压力差。已知水与汞的密度分别 为1000kg/m3和13600 kg/m3。
流体静力学基本方程式的应用（一）
溢流水封许多用水（或其他液 体）洗涤气体的设备内，通常 维持在一定压力p下操作，水不 断流入同时必须不断排出，为 了防止气体随水一起泄出设备， 采用图c所示的溢流水封装置 。
* 本节主要内容：
在重力场中的静止流体内部压强的变化规律及其 实际工程应用。
* 本节的重点 :
重点掌握流体静力学基本方程式的适用条件及工 程应用实例。
流体静力学基本方程式的应用（一）
▪ 例3:采用如图所示的复式U 形管压差计测定设备内C点 的压力,压差计中的指示液 为汞.两U管间的连接管内充 满了被测流体—水.两U形水 银测压计中汞柱的读数分别 R1=0.3m,R2=0.6m.h1=0.4m； h2=0.3m;指示液的其他液面 与设备内C点的垂直距离如 图所示,求C点压强.
流体静力学基本方程式的应用（一）
3 流体静力学基本方程式的应用
p p1 p2 (A C )gR RC g
式中 ΔR=R(d/D)2为小室的液面差，d为U管内径，D为小室内径。
结构：如图示。于容器底部器
壁及液面上方器壁处各开一
小孔，用玻璃管将两孔相连
接。玻璃管内所示的液面高
H
度即为容器内的液面高度。
缺点：易于破损，而且不便于 远距离观测。
（2）液柱压差计：压差法测量液位
结构：于容器或设备外边设一个称为平衡器的小室，用一装有
指示液的U管压差计将容器与平
衡器连通起来，小室内装的液体
与容器内的相同，其液面的高度
维持在容器液面允许到达的最大
高度处。 由： pA' pA
则： g(m h) g(m R) AgR
h A R
m A A’
由此可见，容器内液面越高，h越小，压差计读数R越小；
当容器内的液面达到最大高度时，h为零，压差计读数R亦为零。
（3）鼓泡式液柱测量装置：若容器离操作室较远或埋在地下，
⑤ 复式U形管压差计 应用：适用于压差较大，而测量空间高度有限，这样， 通过串联方式可以在有限高度空间范围内拓宽测量范围。 A（顺置）
指示液ρ0>被测流体ρ，则：
Pa
p0=p4-ρg(h5-h4)
3 1
p4=p3+ρ0g(h3-h4) p3=p2-ρg(h3-h2)
1.2.3 流体静力学基本方程式的应用
流体静力学原理应用非常广泛，它是连通器和液柱压差计 工作原理的基础，还用于容器内液位的测量，液封装置等。解 题的基本要领是正确确定等压面。 1、压强或压强差的测量
流体静力学方程的适用条件(一)
流体静力学方程的适用条件(一)流体静力学方程的适用条件引言流体静力学是研究流体在静力平衡状态下的行为规律的学科，描述了流体静力学方程的适用条件对于理解和解决流体的静态问题非常重要。
适用条件在研究流体静力学方程的适用条件时，需要考虑以下几个方面：1.静态平衡条件–流体必须处于静力平衡状态，即没有加速度和剪切力的存在。
–流体内部各点之间的压强相等，即存在等压面。
这要求流体没有外力或外压作用。
2.宏观尺度–流体静力学方程适用于宏观尺度，即适用于大尺度上对流体进行整体平均的情况。
–该方程不适用于涉及微观尺度或有明显界面效应的情况。
3.不可压缩性–流体静力学方程假设流体是不可压缩的，即流体密度在空间和时间上保持不变。
–在某些特殊情况下，对于可压缩流体，可以通过适当的近似方法将其视为不可压缩流体进行处理。
4.没有动力学效应–流体静力学方程适用于没有动力学效应的情况，即流体中没有涡旋运动或渗透流存在。
总结流体静力学方程的适用条件主要包括静态平衡、宏观尺度、不可压缩性和没有动力学效应等。
在理解和应用流体静力学方程时，我们必须考虑这些条件，并根据具体情况进行适当的近似和简化。
这些适用条件是我们研究和解决流体静态问题的基础。
以上是针对流体静力学方程的适用条件的相关介绍，希望能对读者有所帮助。
应用范围流体静力学方程的适用条件在很多领域都有广泛的应用，包括但不限于以下几个方面：1.工程液压学–在液压系统中，通过流体静力学方程可以计算液压系统中的压力分布、液体高度等参数。
–这有助于优化液压系统的设计和运行，提高系统的效率和安全性。
2.建筑水力学–在水资源工程中，流体静力学方程可用于计算大坝、堤坝和水闸等结构的承压能力。
–这可以帮助工程师评估工程结构的稳定性，并制定相应的安全措施。
3.管道输送–在管道系统中，流体静力学方程可用于计算流体在管道中的流速和压力分布。
–这对于优化管道输送系统的设计和运行非常重要，能够提高流体的输送效率和节约能源。
流体静力学方程的适用条件
流体静力学方程的适用条件
流体静力学方程的适用条件
引言
在研究流体力学中，流体静力学是一个重要的方面。
它研究了静止流体的性质和行为，特别是在没有外力作用的情况下。
本文将阐述流体静力学方程的适用条件。
1. 稳定静态条件
•流体静力学方程适用于稳定的静态条件。
•流体在空间中处于平衡状态，不发生任何小范围的扰动。
2. 不可压缩性条件
•流体静力学方程适用于不可压缩的流体。
•不可压缩流体指的是密度不随位置变化而变化的流体。
3. 液体和气体的适用条件
液体的适用条件
•流体静力学方程适用于液体的静态条件。
•液体的体积相对固定，在流体内部不存在可压缩性。
气体的适用条件
•流体静力学方程适用于稳定条件下的气体。
•气体的压力与体积之间存在一定的关系，可以通过状态方程来描述。
4. 假设条件
•流体静力学方程的适用条件基于一些假设，例如忽略流体的黏性、温度变化等因素。
•在实际应用时，需要根据具体情况评估这些假设对结果的影响。
结论
流体静力学方程适用于稳定的静态条件下的不可压缩液体和气体。
然而，在应用时需要注意各种假设条件，并根据实际情况进行修正。
只有在适用条件下，我们才能准确地利用流体静力学方程进行研究和
实践应用。
注意：本文仅介绍了流体静力学方程的适用条件，对于流体动力学、复杂流体等其他方面的内容未作深入探讨。
流体静力学方程的适用条件
流体静力学方程的适用条件流体静力学是研究静止流体的力学性质和行为的学科。
在流体静力学中，流体被认为是不可压缩和不可扩展的，即密度不随时间和位置的变化而变化。
流体静力学方程描述了流体在静止状态下的力学行为，它由质量守恒方程和动量守恒方程组成。
流体静力学方程的适用条件如下：1. 静止流体：流体静力学方程适用于描述静止的流体。
在这种情况下，流体中的速度为零，因此动量守恒方程中的惯性项可以忽略。
2. 不可压缩流体：流体静力学方程假设流体是不可压缩的，即流体的密度在空间和时间上保持不变。
这意味着质量守恒方程中的质量流入和流出项可以忽略。
3. 重力场：流体静力学方程考虑了重力场对流体静力学行为的影响。
重力场可以通过引入重力加速度来描述，它是一个向下的常矢量。
4. 无粘性：流体静力学方程忽略了流体的粘性效应。
粘性是指流体内部分子之间的相互作用力，它导致了流体的黏滞和摩擦。
在流体静力学中，我们假设流体是无粘性的，即没有黏滞和摩擦效应。
基于以上适用条件，流体静力学方程可以用于求解静止流体中的压力分布、浮力、液压力等问题。
通过质量守恒方程可以得到流体中的压力梯度，即单位面积上的力。
重力场对流体的影响可以通过引入重力加速度来描述，从而得到流体中的压力分布。
此外，通过应用流体静力学方程，还可以计算浸没体的浮力，即液体对浸没体的向上的力。
液压力是由于流体静力学方程中的压力梯度引起的，它可以用于求解液体对容器壁的作用力。
流体静力学方程是研究静止流体行为的重要工具。
它适用于描述静止、不可压缩、无粘性流体在重力场中的力学行为。
通过应用流体静力学方程，我们可以求解流体中的压力分布、浮力、液压力等问题，为工程和科学领域提供了重要的理论基础。
流体静力学基本方程式的适用条件是
流体静力学基本方程式的适用条件流体静力学是研究静止的流体力学现象的学科，主要研究流体静力学基本方程式的解法和应用。
流体静力学基本方程式包括质量守恒方程、动量守恒方程和能量守恒方程。
这些方程式适用于静止的流体，即不受外力而处于平衡状态的流体。
下面我们将详细介绍流体静力学基本方程式的适用条件。
一、质量守恒方程质量守恒方程是研究流体静力学的基本方程式之一，它描述了流体内质量的守恒。
质量守恒方程的适用条件如下：1. 流体是静止的，即流体的速度为零。
2. 流体是连续的，即流体是连续的物质，不存在空隙。
3. 流体是不可压缩的，即流体的密度不随时间和位置的变化而变化。
4. 流体是单相的，即流体内的物理和化学性质是均匀的。
二、动量守恒方程动量守恒方程是研究流体静力学的基本方程式之一，它描述了流体内动量的守恒。
动量守恒方程的适用条件如下：1. 流体是静止的，即流体的速度为零。
2. 流体是连续的，即流体是连续的物质，不存在空隙。
3. 流体是不可压缩的，即流体的密度不随时间和位置的变化而变化。
4. 流体是单相的，即流体内的物理和化学性质是均匀的。
5. 流体是粘性的，即流体内存在摩擦力。
三、能量守恒方程能量守恒方程是研究流体静力学的基本方程式之一，它描述了流体内能量的守恒。
能量守恒方程的适用条件如下：1. 流体是静止的，即流体的速度为零。
2. 流体是连续的，即流体是连续的物质，不存在空隙。
3. 流体是不可压缩的，即流体的密度不随时间和位置的变化而变化。
4. 流体是单相的，即流体内的物理和化学性质是均匀的。
5. 流体是绝热的，即流体内不存在热传导。
以上是流体静力学基本方程式的适用条件，下面我们将通过实例来进一步说明。
实例：一艘船停泊在湖面上，船底面积为10平方米，船重为50吨，水的密度为1000千克/立方米。
求船底受到的水的压力。
解析：根据质量守恒方程可知，流体在静止状态下，密度不随位置和时间的变化而变化，因此可以将水的密度视为恒定值1000千克/立方米。
工程流体力学2.4流体静力学基本方程的应用
第四节 流体静力学基本方程的应用
一、测压管 适用范围
测压管适用于测量较小的压强，但不适合测真空。 一般不超过9800Pa，相当于1mH2O。
如果被测压强较高，则需加长测压管的长度，使用 就很不方便。
测压管中的工作介质就是被测容器中的流体，所以 测压管只能用于测量液体的压强。
第四节 流体静力学基本方程的应用
M点的绝对压强为
p pa gh
M点的计示压强为 pe p pa gh
用测得的液柱高度h，可得到容器中液体的计示压强 及绝对压强。
第第四四节节 流流体体静静力力学学基基本本方方程程的的应应用用
一、测压管
测量容器中的真空
pV pa p gh
pv
h
pa
一、测压管
1.结构 测压管是一种最简单的液柱式测压计，是以液柱高度 为表征测量点压强的连通管。一端与被测点容器壁的孔口 相连，另一端直接和大气相通的直管。
为了减少毛细现象所造成的误差，采用一根内径为 10mm左右的直玻璃管。
图（2-9）测压管
第四节 流体静力学基本方程的应用
一、测压管 2.测量原理
n 1
sin
当Θ=300时
h2 Lsin30
1 2
L
压强差的液柱读数放大了两倍；
当Θ=100时
n 1/ sin10 5.75 倾斜微压计可使读数更精确。
但若Θ过小（如小于50）时，倾斜玻璃管内的液体将 产生较大的波动，位置不易确定。
应用静力学基本方程式的步骤:
(1)选择正确的等压面
当A、s和ρ 一定时，K仅是倾斜角Θ 的函数。改变 Θ 的大小，可得到不同的K值，即将被测压强差的L值 放大了不同的倍数。倾斜微压计的放大倍数
流体力学流体静力学和动力学的应用
流体力学流体静力学和动力学的应用在工程领域中，流体力学是一门重要的学科，它包括了流体静力学和动力学的研究。
流体力学的应用十分广泛，涵盖了各个领域，如航空、航天、汽车、能源、环境等。
本文将介绍流体力学在不同领域中的应用。
一、流体静力学的应用流体静力学主要研究静止流体的力学性质，其中最基本的定律是帕斯卡定律。
根据帕斯卡定律，静止流体各点的压力相等。
这一定律在水压机、液压升降机、液压起重机等设备中得到广泛应用。
例如，在液压升降机中，通过调节液压系统的压力来实现起升或下降的操作。
当液压系统中的液体受到外力作用时，根据帕斯卡定律，液体会沿着静控定理传递压力，从而使升降机实现相应的运动。
这种液压系统广泛应用于工业生产、物流运输等领域，提高了生产效率和工作效益。
此外，流体静力学还应用于水坝、水闸等水利工程中。
在水坝工程中，根据流体静力学原理进行结构设计，以保证水坝的安全稳定。
流体静力学的研究方法和理论为水利工程的设计、施工和运营提供了基础。
二、流体动力学的应用流体动力学主要研究流体的运动规律和力学性质，其中最重要的方程是连续性方程、动量方程和能量方程。
通过这些方程，可以研究流体的流速分布、压力分布等参数。
在航空领域，流体动力学的应用非常广泛。
例如，研究飞机在空气中飞行时的气动特性，需要通过数值模拟或实验方法来计算飞机表面的气动力，以设计出低阻力、稳定的飞行器。
此外，流体动力学也应用于喷气发动机、风力发电机、水轮发电机等设备的设计与优化。
在车辆领域，流体动力学的应用主要体现在空气动力学方面。
通过研究车辆表面的气流分布，可以降低车辆的风阻，提高燃油利用率。
同时，流体动力学对于汽车制动系统、悬挂系统等的设计也具有重要意义，可以减少制动时的飘移、提高悬挂系统的舒适性。
此外，流体动力学还应用于地下水资源开发与管理、天气预报与气候研究等领域。
例如，地下水资源开发中需要通过研究地下水流动的规律，确定井点位置和开采量，以合理利用地下水资源。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
二. 液位测量 （1）近距离液位测量装置 压差计读数R反映出容器 内的液面高度。
ρ0 − ρ h= R ρ
液面越高，h越小，压差计读数R越小；当液 面达到最高时，h为零，R亦为零。
（2）远距离液位测量装置 管道中充满氮气， 其密度较小，近似 认为 而
p A ≈ pB
p A = p a + ρБайду номын сангаасh
流体静力学基本方程式的应用 三、液位测量
近距离液位测量装置
远距离液位测量装置
ρ0 − ρ h= R ρ
ρ0 h= R ρ
1-4 流体静力学基本方程式的应用
被测流体是气体
p1 − p 2 ≈ Rgρ 0
一端与被测点连接 ， 另一端与大气相通， 另一端与大气相通，则 测得的是表压或真空度。 测得的是表压或真空度。 图中R 问:图中R表示表压还是 真空度? 真空度?
流体静力学基本方程式的应用
例2 如附图所示， 如附图所示 ， 水在管道中
流动。 为测得a 两点的压力差， 流动 。 为测得 a、b 两点的压力差 ， 在管路上方安装一U 形压差计， 在管路上方安装一 U 形压差计 ， 指示液为汞。 指示液为汞 。 已知压差计的读数 R＝100mm， 试计算 ａ 、 ｂ 截面的 100mm， 试计算ａ mm 压力差。 压力差 。 已知水与汞的密度分别 为1000kg/m3和13600 kg/m3。 1000kg/m
流体静力学基本方程式的应用
解:取等压面1-1′,2-2′ 取等压面1
p1 = p1'
p 2 = p 2'
p1' = pa − ρgx
p1 = p2 + ρ0 gR = p2' + ρ0 gR = pb − ρg ( x + R) + ρ0 gR
pa − pb = ( ρ 0 − ρ ) gR （ = 13600 − 1000） 9.81× 0.1 × = 12360.6Pa
p B = p a + ρ 0 gR
A B
所以
ρ0 h= R ρ
流体静力学基本方程式的应用
三. 液封高度的计算 液封作用： 确保设备安全：当设备 内压力超过规定值时，气 体从液封管排出； 防止气柜内气体泄漏。 液封高度： h = p (表) ρg
切断水封有些常压可燃气体贮罐前 后安装切断水封以代替笨重易漏 的截止阀 .正常操作时，水封不 正常操作时， 充水， 充水，气体可以顺利绕过隔板出 入贮罐；需要切断时（如检修）， 入贮罐；需要切断时（如检修）， 往水封内注入一定高度的水， 往水封内注入一定高度的水，使 隔板在水中的水封高度大于水封 两侧最大可能的压差值。（图b所 两侧最大可能的压差值。（图 。（ 示）
流体静力学基本方程式的应用
解: p C = p1 + ρ H 2 O gh1
p1 = p 2 = p 3
p3 = p4 + ρ Hg gR1
p4 = p5
p5 + ρ H 2O g ( R1 + h1 − h2 ) = p6
p6 = p7 = pa + ρ Hg gR2
解得 P = 223725 Pa (绝压) C
实际上， 实际上，不论两测压点 位置如何， 位置如何，Ｕ形压差计 的读数所反映的实际上 是两测压点之间的总势 能差。 能差。
流体静力学基本方程式的应用
p1
p2
ρ 02
a b R1
R
a
b
ρ0
(a)
p1 (b)
p2
ρ0
α (c)
ρ 01
R Ra = b sin α
'
(d)
p1 − p2 = ( ρ A − ρ B ) gR
p1 − p2 = Rg ( ρ B − ρ A )
p1 − p2 ≈ RgρA
p1 − p2 ≈ RgρB
2、压力测量： 、压力测量： U形压差计可测系统内两点的压力差 ， 当将 形管一 形压差计可测系统内两点的压力差， 当将U形管一 形压差计可测系统内两点的压力差 端与被测点连接、另一端与大气相通时， 端与被测点连接、另一端与大气相通时，也可测得流 体的表压或真空度； 体的表压或真空度；
p1 p1 pa
pa
表压
真空度
复合U形压差计 复合 形压差计
双液体微差计
流体静力学基本方程式的应用 结论： 形压差计所测压差（压力） 结论：U形压差计所测压差（压力）的大小只 与被测流体及指示剂的密度、读数R有关， 与被测流体及指示剂的密度、 读数R 有关， 而与U形压差计的粗细及放置的位置无关 而与U
溢流水封许多用水（或其他液 溢流水封许多用水（ 体）洗涤气体的设备内，通常 洗涤气体的设备内， 维持在一定压力p下操作，水不 维持在一定压力p下操作， 断流入同时必须不断排出，为 断流入同时必须不断排出， 了防止气体随水一起泄出设备， 了防止气体随水一起泄出设备， 采用图c所示的溢流水封装置 。 采用图c
流体静力学基本方程式的应用
静力学问题解题步骤: 静力学问题解题步骤:
选择等压面（三个条件：同一种流体，连通， ( 1 ) 选择等压面 （ 三个条件 ： 同一种流体 ， 连通 ， 同一 水平面） 水平面） 利用静力学原理求等压面不同点处的压强， ( 2 ) 利用静力学原理求等压面不同点处的压强 ， 使其中 一个包含的全是已知条件或已求出的量， 一个包含的全是已知条件或已求出的量 ， 另一个包含 有未知量，。 有未知量， 注意：计算时，方程中各项物理量的单位必须一致。 ( 3 ) 注意 ： 计算时 ， 方程中各项物理量的单位必须一致 。
1-4 流体静力学基本方程式的应用
U形压差计安装在倾斜管路中 形压差计安装在倾斜管路中
p1 − p2 = ( ρ 0 − ρ ) gR + ρ ( z2 − z1 ) g ( ρ 0 − ρ ) gR = ( p1 − p2 ) − ρ ( z2 − z1 ) g = ( p1 + ρgz1 ) − ( p2 + ρgz2 )
流体静力学基本方程式的应用
利用静力学基本原理可以测量: 利用静力学基本原理可以测量: 流体压差与压力（表压或是真空度） 流体压差与压力（表压或是真空度） 容器中的液位 液封高度计算
流体静力学基本方程式的应用
一、1、压差测量（U形管压差计） 压差测量（ 形管压差计）
p1 p2 p1 p2
ρ0
a b R
流体静力学基本方程式的应用
例3:采用如图所示的复式U 形管压差计测定设备内C点 的压力,压差计中的指示液 为汞.两U管间的连接管内充 满了被测流体—水.两U形水 银测压计中汞柱的读数分别 R1=0.3m,R2=0.6m.h1=0.4m； h2=0.3m;指示液的其他液面 与设备内C点的垂直距离如 图所示,求C点压强.
流体静力学基本方程式的应用
例1 如附图所示，水在水平管道内流动。为测量流体 在某截面处的压力，直接在该处连接一U形压差计， 指示液为水银，读数 R＝250mm，m＝900mm。 已知当地大气压为101.3kPa， 水 的 密 度 1000kg/m3， 水 银 的 密度13600kg/m3。试计算该截 面处的压力。