洛伦兹变换的四维形式1四维空间的转动变换
洛伦兹变换的四维形式1四维空间的转动变换
( x1 i x4 ) x1 x2 x2
a x x
x3 x3 (i x1 x4 ) x4
x1 x2 0 x3 0 i x 4 0 0 i x1 x 1 0 0 2 0 1 0 x3 0 0 x4
( , v 1 4)
4 4
j k,l,m ,n, 代表1—3 英文小写字母 i,, 希腊小写字母 ,,,,, , 代表1—4
变换表示式: 正交条件为:
a x x
aa I a a aa
机动 目录 上页 下页 返回 结束
机动 目录 上页 下页 返回 结束
三、洛伦兹变换的四维形式
1、四维空间的转动变换(三维情况的推广)
转动中的不变量:
2 x2 2 x3 2 x4 2 x12 x22 x32 x42 x x xv xv x1
1
v 1
x xv xv x
原 则
机动
目录
上页
下页
返回
结束
变换关系
a dx , d d dx
a U U
四维速度与三维速度间的关系
dxi 三维速度 ui dt
用dt度量三维空间的位移 dxi 它不满足洛仑兹变换,也不是四维速度的前三个分量。
机动 目录 上页 下页 返回 结束
令某物体沿∑系正方向运动,它 的三维速度大小为u,固有时为 dτ,∑系上度量时间为dt ,
例如:速度、加速度、力、电场强度、 ▽算符等。
•
aik a jlTkl Tij 方式变换的具有9个分量的物理量,记为 T。
相对论质点力学方程
2m
O' uB ' v
BA x
uA ' v
一、相对论质量
SS'
v
uB ' v 2m O'
BA x
uA ' v
在S系:分裂前总动量 (mA mB )v 2mv
分裂后 uB 0
2v uA 1 v2 / c2
ux
u 'x v
1
v c2
u 'x
一、相对论质量
动量守恒要求:
(mA
mB )v
——质速关系
物体的运动质量m与其静止质量m0和速度v 的关系。
电子质量随速度变化:
理4
论 结
3 2
果1
考夫曼的 实验结果
0 0.2 0.4 0.6 0.8 1.0
二、四维动量矢量
(1) 意义:质量具有相对性,揭示了物 质与运动的不可分割的属性。
(2) 极限速度原理:
m m0 1 (v )2 c
P后
mA uA
mA
2v
(1
v c
2 2
)
ex
m0' 1 uA2
/ c2
2v
(1
v c
2 2
)
e
x
m0'
1
1
2v v2 /
c
2
2
1 c2
(1
2v v
c
2 2
)
e
x
2m0' v
1
v2 c2
ex
2m前后仍有动量守恒。
二、四维动量矢量
讨论
m
m0 1 v2 / c2
1.不存在极限速度;
045-6第6章 狭义相对论-4-相对论理论的四维形式-1

(5)
x3
a31x1
a32 x2
a33 x3
OP2 x12 x22 x32 x12 x22 x32 不变量
(6)
3
可简写为
由(5)式 xi aij xj
xi aij x j
(7)
j 1
将式中对重复下标求和的求和号省略,是现代物理通用
约定,称为爱因斯坦求和约定。(7)式中重复下标为 j。
u'u
₪ 狭义相对论
2. 物理量按空间变换性质的分类
(2)矢量:不仅有大小,而且有空间取向的量,称为矢量。 例如:电场强度、磁感应强度、力、速度、动量等等。 矢量在三维空间用3个分量表示。同一个矢量在不同 的转动坐标系中的变换关系满足(7)式。
3
v 'i aijvj v 'i aijv j
(20)
₪ 狭义相对论
3. 洛伦兹变换的四维形式
为了方便和统一起见,对于上述四维时空线性变换,形 式上引入第四维虚数坐标:
x4 ict
则间隔不变性(20)式可改写为:
(21)
x12 x22 x32 x42 x12 x22 x32 x42 不变量
4
4
x 2 x2 不变量
1
1
3
3
aij
x
j
3
aik
xk
3
xi2 (10)
i1 j1
k1
i1
从(10)式左边的爱因斯坦求和约定简写式可见:相邻的
相同哑元下标可以消去!从而大大地简化书写过程。
₪ 狭义相对论
1. 三维空间的正交变换
定义符号
ij
1 0
若i j 若i j
(11)
洛伦兹变换坐标系

洛伦兹变换坐标系在狭义相对论中,洛伦兹变换是描述不同惯性参考系之间的时空坐标变换关系的数学表达式。
这种变换是由荷兰物理学家亨德里克·洛伦兹于1903年提出的,为描述高速运动下的物体和光传播等现象提供了重要的数学工具。
洛伦兹变换的基本原理狭义相对论认为,物体的运动状态和时间的流逝速度取决于观察者的参考系选择。
因此,为了描述同时存在的不同惯性参考系下的物理现象,需要进行坐标系之间的变换。
洛伦兹变换是这种坐标变换的数学表达形式。
洛伦兹变换的公式洛伦兹变换可以描述时间和空间坐标之间的转换关系。
在特殊相对论中,洛伦兹变换的一般形式可以表示为:x' = γ(x - vt)y' = yz' = zt' = γ(t - vx/c^2)其中,x、y、z、t是原来参考系中的空间坐标和时间,x’、y’、z’、t’是新的参考系中的空间坐标和时间,v表示两个参考系相对速度,c是光速,γ是洛伦兹因子。
洛伦兹因子洛伦兹因子γ定义为:γ = 1 / √(1 - v^2 / c^2)其中,v是参考系之间的相对速度。
当物体的速度远小于光速时,γ接近1,此时洛伦兹变换退化为经典的伽利略变换。
洛伦兹变换的重要性洛伦兹变换在描述高速运动下的物体以及光的传播等情况下起着重要作用。
它揭示了时空的弯曲性,探讨了观察者在不同惯性参考系中背景下所看到的物理现象之间的联系。
洛伦兹变换为狭义相对论的建立奠定了坚实的数学基础。
总结洛伦兹变换是描述不同惯性参考系之间的时空坐标变换关系的重要工具。
通过公式和洛伦兹因子,我们可以准确地描述高速运动物体和光的传播等现象,揭示了时空的规则和物质之间的联系。
因此,洛伦兹变换在现代物理学中具有重要的地位和作用。
洛伦兹变换是一种线性变换它体现了四维时空的变换关系

事件2:鸟死
S ´系中:开枪在先 ,鸟死在后
S 系中: 开枪在先, 鸟死在后
3、同时不同地事件 (类空事件)
t1 t2 , x1 x2
若 x2 x1 若 x2 x1
t1 (t 0) t2 t1 (t 0) t2
结论:同时不同地两事件,在其他惯 性系中一般为不同时、不同地事件 。 同时的相对性:不同的惯性系时间不 再统一,否定了绝对时空
分析: 1. v << c时洛仑兹速度变换退化为伽利略变换
v c v / c 0 ( 0) u x / c 0
uy u y , u u x ux v , z uz ,
2. 速度变换满足光速不变原理
若 u = c , 则可推出
cv uv cv c c u 2 2 1 vc / c cv 1 vu / c
z' z
t'
t vx / c 2 1 2
dt vdx c 2 1 2
dx'
dx vdt 1
2
dy' dy
dz' dz
uy 1 2 1 uxv / c2
dt '
u x
ux v 1 uxv / c
2
u y
u z
uz 1 2 1 uxv / c2
§6.3 相对论时空理论
一 相对论时空结构 设第一个事件时空坐标(0,0,0,0),第二个事件时空坐标(x, y,z,t) 。则 S 2 c 2t 2 r 2, r 2 x 2 y 2 z 2 为空间间隔。 两事件的间隔根据取值分三种情况 (1)若两事件可以用光波联系,有r = ct,因而s2 = 0; (2)若两事件可用低于光速的作用相联系,有r < ct,因
(完整版)洛伦兹变换的详细推导

第三节 洛伦兹变换式教学内容:1. 洛伦兹变换式的推导;2. 狭义相对论的时空观:同时性的相对性、长度的收缩和时间的延缓; 重点难点:狭义相对论时空观的主要结论。
基本要求:1. 了解洛伦兹坐标变换和速度变换的推导;2. 了解狭义相对论中同时性的相对性以及长度收缩和时间延缓概念;3. 理解牛顿力学中的时空观和狭义相对论中的时空观以及两者的差异。
三、洛伦兹坐标变换的推导()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧--='='='--='22211c v c vx t t z z y y c v vt x x 或 ()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-'+'='='=-'+'=22211c v c x v t t z z y y c v t v x x据狭义相对论的两个基本假设来推导洛仑兹变换式。
1. 时空坐标间的变换关系作为一条公设,我们认为时间和空间都是均匀的,因此时空坐标间的变换必须是线性的。
对于任意事件P 在S 系和S '系中的时空坐标(x ,y ,z ,t )、(x ',y ',z ',t '),因S ' 相对于S 以平行于 x 轴的速度v 作匀速运动,显然有y '=y , z '=z 。
在S 系中观察S 系的原点,x =0;在S '系中观察该点,x '=-v t ',即x '+v t '=0。
因此x =x '+v t '。
在任意的一个空间点上,可以设:x =k (x '+v t '),k 是—比例常数。
同样地可得到:x '=k '(x -v t )= k '(x +(-v )t )根据相对性原理,惯性系S 系和S '系等价,上面两个等式的形式就应该相同(除正、负号),所以k =k '。
洛伦兹变换推导过程详细

洛伦兹变换推导过程详细全文共四篇示例,供您参考第一篇示例:洛伦兹变换(Lorentz transformation)是狭义相对论中的重要概念,描述了不同惯性参考系之间的时空坐标变换关系。
由荷兰物理学家亨德里克·安杰洛·洛伦兹(Hendrik Antoon Lorentz)首先提出,并由爱因斯坦在他的狭义相对论中进一步发展。
洛伦兹变换不仅在相对论中有着广泛的应用,而且也成为了后来爱因斯坦提出的广义相对论中的基础之一。
在这篇文章中,我们将详细推导洛伦兹变换的过程,并探讨其物理意义。
我们从狭义相对论的两个基本假设开始。
第一个假设是等效原理,即在加速度为零的惯性参考系中的物理定律是相同的。
第二个假设是光速不变原理,即光在真空中的传播速度对于所有惯性观察者都是相同的,不受光源或观察者的运动状态的影响。
根据这两个假设,我们可以推导出洛伦兹变换。
假设有两个惯性参考系S和S',S'相对于S以速度v沿x轴方向匀速运动。
在S参考系中,事件的时空坐标为(x, y, z, t),而在S'参考系中为(x', y', z', t')。
我们希望通过洛伦兹变换找到这两个参考系之间的坐标变换关系。
首先考虑S'参考系中的时间坐标t'和空间坐标x'之间的变换。
由光速不变原理可知,在S'参考系中静止的光源发出的光信号在空间中传播的速度是恒定不变的,即光速c。
假设光源在S参考系中坐标为(x, t),在S'参考系中坐标为(x', t'),那么光信号在S参考系中的传播距离为c(t-t'),在S'参考系中的传播距离为c(t'-t)。
根据光速不变原理,这两个传播距离应该相等,即:c(t-t') = c(t'-t)整理得到:t' = γ(t - vx/c^2)其中γ为洛伦兹因子,定义为1/√(1-v^2/c^2),即:γ = 1/√(1-v^2/c^2)这个式子描述了S'参考系中事件的时间与S参考系中事件的时间之间的关系。
洛伦兹变换

洛伦兹变换编辑由于爱因斯坦提出的假说否定了伽利略变换,因此需要寻找一个满足相对论基本原理的变换式。
洛伦兹导出了这个变换式,一般称它为洛伦兹变换式。
中文名洛伦兹变换外文名Lorentz transformation别称洛伦兹变换式提出者亨德里克·洛伦兹提出时间1904年应用学科数学适用领域范围狭义相对论目录1简介2理论3释义4推导▪公设一▪公设二▪过程▪另一种方式5区别6四维矢量改写1简介编辑洛伦兹变换(Lorentz transformation)是观测者在不同惯性参照系之间对物理量进行测量时所进行的转换关系,在数学上表现为一套方程组。
洛伦兹变换因其创立者——荷兰物理学家亨德里克·洛伦兹而得名。
洛伦兹变换最初用来调和19世纪建立起来的经典电动力学同牛顿力学之间的矛盾,后来成为狭义相对论中的基本方程组。
2理论编辑洛伦兹变换(Lorentz transformation)是狭义相对论中关于不同惯性系之间物理事件时空坐标变换的基本关系式。
设两个惯性系为S系和S′系,它们相应的笛卡尔坐标系彼此平行,S′系相对于S系沿x 方向运动,速度为v,且当t=t′=0时,S′系与S系的坐标原点重合,则事件在这两个惯性系的时空坐标之间的洛伦兹变换为式中,;c为真空中的光速。
其逆变换形式为不同惯性系中的物理定律必须在洛伦兹变换下保持形式不变。
19世纪后期建立了麦克斯韦方程组,标志着经典电动力学取得了巨大成功。
然而麦克斯韦方程组在经典力学的伽利略变换下并不是协变的。
由麦克斯韦方程组可以得到电磁波的波动方程,由波动方程解出真空中的光速是一个常数。
按照经典力学的时空观,这个结论应当只在某个特定的惯性参照系中成立,这个参照系就是以太。
其它参照系中测量到的光速是以太中光速与观察者所在参照系相对以太参照系的速度的矢量叠加。
然而1887年的迈克耳孙-莫雷实验测量不到地球相对于以太参照系的运动速度。
1904年,洛伦兹提出了洛伦兹变换用于解释迈克耳孙-莫雷实验的结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
viwi aij v j aik wk jkv j wk v j w j vi wi
例二: 张量与矢量点积
v w vi wi
无自由指标为标量
T v Tij v j
一个自由指标为矢量
Tijvj aik a jlTkla jmvm aik lmTklv m aikTklv l
2、洛伦兹变换为复四维空间的转动变换 与转动变换不变
洛伦兹变换下间隔为不变量,即:
量表示形式不同
2 x2 2 x3 2 c2t2 x12 x22 x32 c2t 2 x1 ict 定义:x4 ict , x4
2 x1
x3 x4 x2
例如:速度、加速度、力、电场强度、 ▽算符等。
•
aik a jlTkl Tij 方式变换的具有9个分量的物理量,记为 T。
二阶张量:空间转动变换下按
例如:应力张量,电四极矩张量等。
机动 目录 上页 下页 返回 结束
使用自由指标判断物理量 标量:没有自由指标,又称为零阶张量; 矢量:一个自由指标,又称为一阶张量; 张量:两个自由指标,又称为二阶张量。 例一:两矢量点积
xi aij x j
j 1 3
不变量
(i 1, 2,3)
2 2 x x i i i 1 i 1
3
3
机动
目录
上页
下页
返回
结束
aij aik jk (1)
3 aij aik jk i 1
(1)与(2) 为正交条件
写成矩阵
机动 目录 上页 下页 返回 结束
( x1 i x4 ) x1 x2 x2
a x x
x3 x3 (i x1 x4 ) x4
x1 x2 0 x3 0 i x 4 0 0 i x1 x 1 0 0 2 0 1 0 x3 0 0 x4
正交变换条件
cos sin cos aa sin cos sin
sin 1 0 I aa cos 0 1
2、三维空间坐标转动变换 a11x1 a12 x2 a13x3 a11 a12 a13 x1 x1 x1 x2 a21x1 a22 x2 a23 x3 a21 a 22 a 23 x 2 a x 2 x a x a x a x a x x a a 3 31 1 32 2 33 3 31 32 33 3 3
( , v 1 4)
4 4
j k,l,m ,n, 代表1—3 英文小写字母 i,, 希腊小写字母 ,,,,, , 代表1—4
变换表示式: 正交条件为:
a x x
aa I a a aa
机动 目录 上页 下页 返回 结束
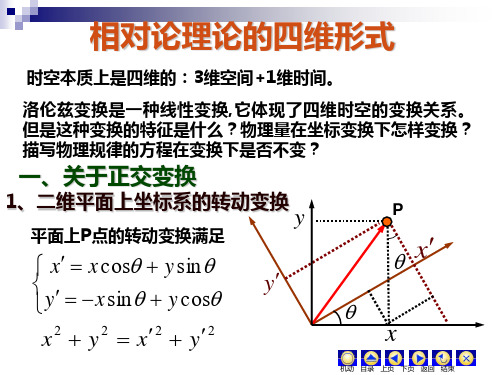
相对论理论的四维形式
时空本质上是四维的:3维空间+1维时间。 洛伦兹变换是一种线性变换 ,它体现了四维时空的变换关系。 但是这种变换的特征是什么?物理量在坐标变换下怎样变 换?描写物理规律的方程在变换下是否不变?
一、关于正交变换
1、二维平面上坐标系的转动变换
平面上P点的转动变换满足
y
P
x x cos y sin y x sin y cos x 2 y 2 x 2 y 2
y
机动 目录
x
x
上页 下页 返回 结束
x cos sin x a11 a12 x y sin cos y a a y 21 22
2 2 2
2 x1
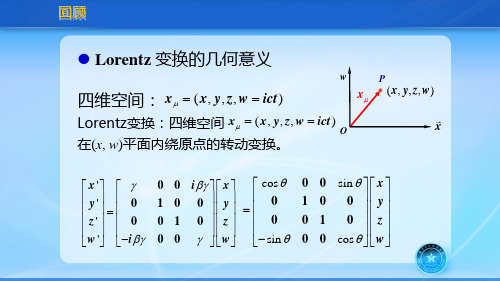
x x x x2 x3 x4 x
2, x2 , x3 , x4 ict) 的“转动”变换
该空间又称为闵可夫斯基空间。
ict x2 , x3 x3 ( x1 t ) x1 x1 x1 i x4 x2 c i ict ic (t 2 x1 ) x4 i x1 i x1 x 4 x4 c
% = aa % aa = I L L L (2)
机动
目录
上页
下页
返回
结束
二、物理量按空间变换性质分类
• 标量: 空间转动变换中不变的量称为标量。 u u 例如:质量,电荷,空间距离。 • 矢量:空间转动变换中按 vi aij v j i 1,2,3 方式变换的量称为矢量,记为 v 。
机动
矩 阵 形 式
( x ax) ~ ( x a x)
目录 上页 下页 返回 结束
四、四维协变量
协变性:在某种变换下数学方程形式保持不变的性质。 洛伦兹协变性:在洛伦兹变换下物理规律的数学方程保持不变 的性质。
1、四维协变量
在洛伦兹变换下具有确定变换性质的物理量。即在变换下方 程不变,方程中同一类物理量按相同形式变换,这样的物理量 统称为四维协变量。 ⑴ 洛伦兹标量:洛伦兹变换下保持不变的物理量 例如:电荷Q,时空间隔,固有长度,固有时间隔,静止质 量m0 ,四维空间的体积元等 固有时间隔dτ为不变量的说明: ds 2 c2 dt 2 dr 2 而间隔dS2为不变量,所以 时间间隔dt 在洛仑兹变换下是一个可变量 dt dt .
机动 目录 上页 下页 返回 结束
三、洛伦兹变换的四维形式
1、四维空间的转动变换(三维情况的推广)
转动中的不变量:
2 x2 2 x3 2 x4 2 x12 x22 x32 x42 x x xv xv x1
1
v 1
x xv xv x
