理论力学课后习题答案-第8章--动量定理及其应用
理论力学课后习题答案-第8章--动量定理及其应用

论力学课后习题答案-第8章--动量定理及其应用第8章 动量定理及其应用8-1 计算下列图示情况下系统的动量。
(1) 已知OA =AB =l ,θ=45°,ω为常量,均质连杆AB 的质量为m ,而曲柄OA 和滑块B 的质量不计(图a )。
(2) 质量均为m 的均质细杆AB 、BC 和均质圆盘CD 用铰链联结在一起并支承如图。
已知AB = BC = CD = 2R ,图示瞬时A 、B 、C 处于同一水平直线位置,而CD 铅直,AB 杆以角速度ω转动(图b )。
(3) 图示小球M 质量为m 1,固结在长为l 、质量为m 2的均质细杆OM 上,杆的一端O 铰接在不计质量且以速度v 运动的小车上,杆OM 以角速度ω绕O 轴转动(图c )。
解:(1)p = mv C =ωm l 25,方向同Cv (解图(a ));(2)p = mv C 1 + mv C 2 = mv B = 2Rm ω,方向同Bv ,垂直AC (解图(b )); (3)j i p )60sin 260sin ()]60cos 2()60cos ([2121︒+︒+︒-+︒-=ωωωωlm l m l v m l v m j i 423]42)[(212121m m l l m m v m m +++-+=ωω(解图(c ))。
习题8-1图ABOθω ABCDωOMvω 60˚(a)(b)(c)8-2 图示机构中,已知均质杆AB 质量为m ,长为l ;均质杆BC 质量为4m ,长为2l 。
图示瞬时AB 杆的角速度为ω,求此时系统的动量。
解:杆BC 瞬时平移,其速度为v Bωωωm l m l l m p p p BCAB 2942=+=+= 方向同v B 。
8-3 两均质杆AC 和BC 的质量分别为m 1和m 2,在C 点用铰链连接,两杆立于铅垂平面内,如图所示。
设地面光滑,两杆在图示位置无初速倒向地面。
问:当m 1= m 2和m 1= 2m 2时,点C 的运动轨迹是否相同。
理论力学习题集
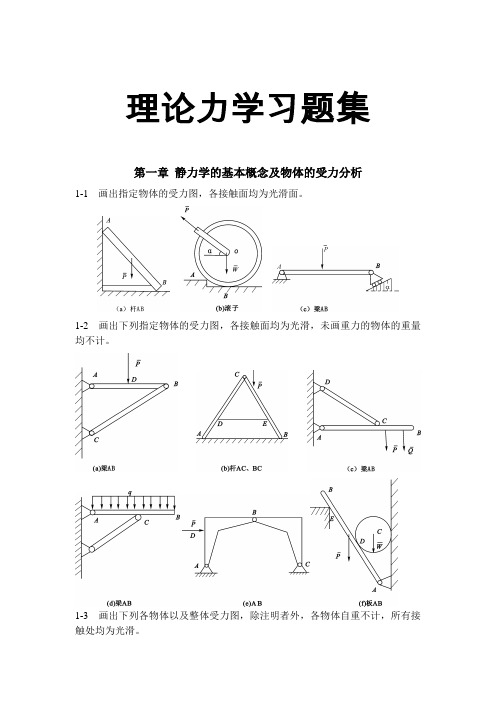
理论力学习题集第一章静力学的基本概念及物体的受力分析1-1 画出指定物体的受力图,各接触面均为光滑面。
1-2 画出下列指定物体的受力图,各接触面均为光滑,未画重力的物体的重量均不计。
1-3 画出下列各物体以及整体受力图,除注明者外,各物体自重不计,所有接触处均为光滑。
(a) (b)(c) (d)(e) (f)第二章平面一般力系2-1 物体重P=20kN,用绳子挂在支架的滑轮B上,绳子的另一端接在铰车D 上,如图所示。
转动铰车,物体便能升起,设滑轮的大小及滑轮转轴处的摩擦忽略不计,A、B、C三处均为铰链连接。
当物体处于平衡状态时,试求拉杆AB和支杆CB所受的力。
2-2 用一组绳悬挂重P=1kN的物体,求各绳的拉力。
2-3 某桥墩顶部受到两边桥梁传来的铅直力P1=1940kN,P2=800kN及制动力T=193kN,桥墩自重W=5280kN,风力Q=140kN。
各力作用线位置如图所示,求将这些力向基底截面中心O简化的结果,如能简化为一合力,试求出合力作用线的位置。
2-4 水平梁的支承和载荷如图所示,试求出图中A、B处的约束反力。
2-5 在图示结构计算简图中,已知q=15kN/m,求A、B、C处的约束力。
2-6 图示平面结构,自重不计,由AB、BD、DFE三杆铰接组成,已知:P=50kN,M=40kN·m,q=20kN/m,L=2m,试求固定端A的反力。
图2-6 图2-72-7 求图示多跨静定梁的支座反力。
2-8 图示结构中各杆自重不计,D、E处为铰链,B、C为链杆约束,A为固定端,已知:q G=1kN/m,q=1kN/m,M=2kN·m,L1=3m,L2=2m,试求A、B、C 处约束反力。
图2-8 图2-92-9 支架由两杆AO、CE和滑轮等组成,O、B处为铰链,A、E是固定铰支座,尺寸如图,已知:r=20cm,在滑轮上吊有重Q=1000N的物体,杆及轮重均不计,试求支座A和E以及AO杆上的O处约束反力。
理论力学答案
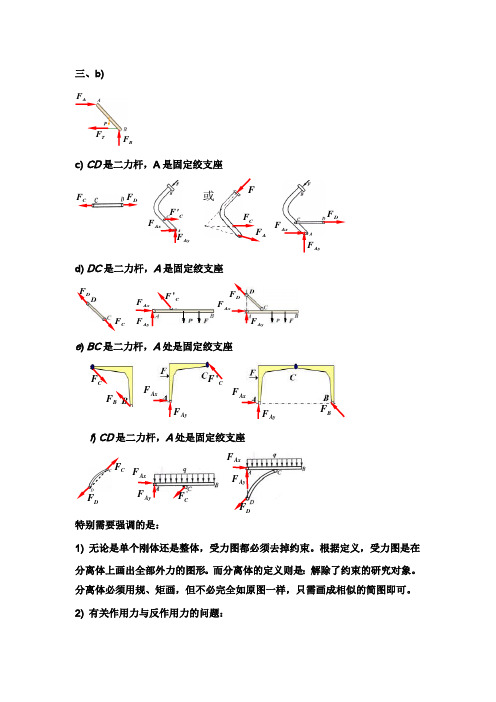
三、b)c) CD 是二力杆,A 是固定绞支座d) DC 是二力杆,A 是固定绞支座e ) BC 是二力杆,A 处是固定绞支座f ) CD 是二力杆,A 处是固定绞支座特别需要强调的是:1) 无论是单个刚体还是整体,受力图都必须去掉约束。
根据定义,受力图是在分离体上画出全部外力的图形。
而分离体的定义则是:解除了约束的研究对象。
分离体必须用规、矩画,但不必完全如原图一样,只需画成相似的简图即可。
2) 有关作用力与反作用力的问题:AyF Ax F 'C F CDF AyF AxF DF CF BFAyF AxF CF 'AyF AxF BF CF 'AyF Ax F DF AyF AxF DF CF AF FCF 或AyF AxF C 'F AyF AxF DF DF CF AF B F TFa ) 习惯上,先找出二力杆,并标示一约束反力(如F D ,将其认为是作用力)。
在另一受力图上的相联点(如D 点),然后根据作用力与反作用力定律确定的约束反力当作反作用力,标示为F'D 。
其中,符号 ' 是为了表示它是F D 的反作用力。
所以,它是有确切含义的。
标注符号时,要注意先后顺序,先确定的约束反力不标注 ' 符号,后确定的约束反力一定要标注符号 ' 。
两者必须成对、反向画。
b ) 为了明确地表示两者的作用力与反作用力关系,两个力的下脚标必须一致,如上述的D 。
不能随手写其它符号,以免产生误解。
下脚标通常用该点的符号表示,不宜象中学物理中那样,标示成数字。
3) 整体受力图一般最后画,整体受力图上的约束反力,应该与各单个刚体上已经画出的约束反力方向一致,以免产生岐义。
一、b ) k 点是光滑面约束,A 是光滑铰链,B 、O 是固定铰支座。
c ) 先确定斜杆(标注为DE )是二力杆,A 是固定绞支座,B 是可动绞支座。
BC 杆带铰,C 铰与AC 杆上C 孔铰接,力F 作用在铰上。
理论力学(金尚年-XXX编著)课后习题答案详解

理论力学(金尚年-XXX编著)课后习题答案详解高等教育出版社的《理论力学课后题答案》一书中,第一章包含了以下三个问题的解答:1.2 题目要求写出在铅直平面内的光滑摆线,并分方程。
解答中使用了微积分和力学原理,得出了运动微分方程。
最后证明了质点在平衡位置附近作振动时,振动周期与振幅无关。
1.3 题目要求证明单摆运动的振动周期与摆长无关。
解答中使用了微积分和力学原理,得出了运动微分方程。
最后通过进一步计算,得出了单摆运动的振动周期公式。
1.5 题目要求使用拉格朗日方程计算质点的运动。
解答中使用了拉格朗日方程,并通过进一步计算得出了质点的运动轨迹。
如图,在半径为R时,地球表面的重力加速度可以由万有引力公式求得:g=\frac{GM}{R^2}$$其中M为地球的质量。
根据广义相对论,地球表面的重力加速度还可以表示为:g=\frac{GM}{R^2}\left(1-\frac{2GM}{c^2R}\right)$$其中c为光速。
当半径增加到R+ΔR时,总质量仍为M,根据XXX展开,可以得到:frac{1}{(R+\Delta R)^2}=\frac{1}{R^2}-\frac{2\DeltaR}{R^3}+\mathcal{O}(\Delta R^2)$$代入上式可得:g'=\frac{GM}{R^2}\left(1-\frac{2GM}{c^2R}\right)\left(1+\frac{2\Delta R}{R}\right)$$ 化简后得:g'=g-\frac{2g\Delta R}{R}$$因此,当半径改变时,表面的重力加速度的变化为:Delta g=-\frac{2g\Delta R}{R}$$2.在平面极坐标系下,设质点的加速度的切向分量和法向分量都是常数,即$a_t=k_1$,$a_n=k_2$(其中$k_1$和$k_2$为常数)。
根据牛顿第二定律,可以得到质点的运动方程:r\ddot{\theta}+2\dot{r}\dot{\theta}=k_2$$ddot{r}-r\dot{\theta}^2=k_1$$其中$r$为极径,$\theta$为极角。
理论力学 第8章 动力学普遍定理

xC
mi
M
xi
,
yC
mi
M
yi
,
zC
mi
M
zi
10
在均匀重力场中,质点系的质心与重心的位置重合。可采 用静力学中确定重心的各种方法来确定质心的位置。但是,质 心与重心是两个不同的概念,质心比重心具有更加广泛的力学 意义。 二、质点系的内力与外力 外力:所考察的质点系以外的物体作用于该质点系中各质点的力。 内力:所考察的质点系内各质点之间相互作用的力。
应用质点运动微分方程,可以求解质点动力学的两类问题。
6
1.第一类:已知质点的运动,求作用在质点上的力(微分问题) 2.第二类:已知作用在质点上的力,求质点的运动(积分问题) 已知的作用力可能是常力, 也可能是变力。变力可能是时间、 位置、速度或者同时是上述几种变量的函数。
7
例1 曲柄连杆机构如图所示.曲柄OA以匀角速度 转
只有外力才能改变质点系的动量,内力不能改变整个质点系 的动量,但可以引起系统内各质点动量的传递。
20
[例3] 质量为M的大三角形柱体, 放于光滑水平面上, 斜面上另 放一质量为m的小三角形柱体,求小三角形柱体滑到底时,大三角 形柱体的位移。
解:选两物体组成的系统为研究对象。
受力分析, Fx(e) 0, 水平方向 Px 常量。
l2 r2 l
得 F mr2 2 l 2 r 2
9
质点系的质心,内力与外力
一.质点系的质心 质点系的质量中心称为质心。是表征质点系质量分布情况的 一个重要概念。
质心 C 点的位置: (M mi )
rC
mi
M
ri
或 MrC mi ri
理论力学第8章_动量定理_48

第八章 动量定理
Page 1
NCEPU
8.1 动量与冲量
一、质点的动量
物体的质量和它的质心速度的乘积。
r r 质点m的动量: p mv
r v
m
动量为矢量!
u r p
单位是 kg m s
Page 2
vC
C
p = pABx + pCDx + pBCx = 3mlw
Page 6
NCEPU
8.2 动量定理与动量守恒
m
z
r v
r a
y
一、质点动量定理 1、微分形式的动量定理
由牛顿第二定律 r d (mv) r F dt
x
r r
r F
o
r r 即: d (mv) Fdt r u dp r 或: F dt
2、积分形式 r t2 r r r p2 p1 Fdt I
t1
即:质点系的动量在一段有限时间间隔内的改变, 等于作用在质点系的所有外力在同一时间间隔内的 冲量的矢量和。 在 直角坐标轴上的投影式:
p2 x p1x I x p2 y p1 y I y p2 z p1z I z
A2
pCDDC ( A V t ) q tV V2 v 2 2 2 pABBA ( A1V1t )V1 qv tV1
mv2 x mv1x Fx dt I x
t1
t2
mv2 y mv1 y Fy dt I y
t1
t2
mv2 z mv1z Fz dt I z
t1
t2
Page 8
NCEPU
《理论力学Ⅰ》第八版课后习题解析

理论力学Ⅰ第 8 版课后习题答案目录:
第一章静力学公理和物体的受力分析
第二章平面力系
第三章空间力系
第四章摩擦
第五章点的运动学
第六章刚体的简单运动
第七章点的合成运动第
八章刚体的平面运动
第九章质点动力学的基本方程
第十章动量定理
第十一章动量矩定理
第十二章动能定理
第十三章达朗贝尔定理
第十四章虚位移定理
第一章
后面章节的课后答案请关注.微-.信.公众号:学糕
后面章节的课后答案请关注.微-.信.公众号:学糕
第二章
后面章节的课后答案请关注.微-.信.公众号:学糕
后面章节的课后答案请关注.微-.信.公众号:学糕
后面章节的课后答案请关注.微-.信.公众号:学糕
后面章节的课后答案请关注.微-.信.公众号:学糕
后面章节的课后答案请关注.微-.信.公众号:学糕
后面章节的课后答案请关注.微-.信.公众号:学糕
后面章节的课后答案请关注.微-.信.公众号:学糕。
理论力学课本及习题集答案
西北工业大学理论力学教研室
2009年7月
第一章:静力学的基本概念
第二章:平面基本力系
第三章:平面任意力系
第五章:空间基本力系
第六章:空间任意力系
第七章:重 心
第八章:点的运动
第九章:刚体的基本运动
第十章:点的复合运动
日
啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊
第十一章:刚体的平面运动
第十二章:刚体的转动合成
第十四章:质点动力学基础
第十五章:质点的振动
第七章:动能定理
第十八章:动量定理
第十九章:动量矩定理
第二十章:碰撞理论
第二十一章:达朗伯原理
第二十二章:虚位移原理
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第8章 动量定理及其应用
8-1 计算下列图示情况下系统的动量。
(1) 已知OA =AB =l ,θ=45°,ω为常量,均质连杆AB 的质量为m ,而曲柄OA 和滑块B 的质量不计(图a )。
(2) 质量均为m 的均质细杆AB 、BC 和均质圆盘CD 用铰链联结在一起并支承如图。
已知AB = BC = CD = 2R ,图示瞬时A 、B 、C 处于同一水平直线位置,而CD 铅直,AB 杆以角速度ω转动(图b )。
(3) 图示小球M 质量为m 1,固结在长为l 、质量为m 2的均质细杆OM 上,杆的一
端O 铰接在不计质量且以速度v 运动的小车上,杆OM 以角速度ω绕O 轴转动(图c )。
解:(1)p = mv C =
ωml 2
5
,方向同C v (解图(a )
); (2)p = mv C 1 + mv C 2 = mv B = 2Rm ω,方向同B v ,垂直AC (解图(b ));
(3)j i p )60sin 2
60sin ()]60cos 2()60cos ([2121︒+︒+︒-+︒-=ωωωωl m l m l v m l v m
j i 4
23]42)[(2
12121m m l l m m v m m +++-
+=ωω(解图(c )
)。
8-2 图示机构中,已知均质杆AB 质量为m ,长为l ;均质杆BC 质量为4m ,长为2l 。
图示瞬时AB 杆的角速度为ω,求此时系统的动量。
解:杆BC 瞬时平移,其速度为v B
ω
ωωml ml l m p p p BC
AB 29
42=+=+= 方向同v B 。
习题8-1解图
(a)
(b)
(c)
习题8-1图
v
(a)
(b)
(c)
C
习题8-2解图
8-3 两均质杆AC 和BC 的质量分别为m 1和m 2,在C 点用铰链连接,两杆立于铅垂平面内,如图所示。
设地面光滑,两杆在图示位置无初速倒向地面。
问:当m 1= m 2和m 1= 2m 2时,点C 的运动轨迹是否相同。
解:根据受力分析知:∑
=0x F ,故系统的质心在水平方向运动守恒。
当m 1= m 2时,系统关于y 轴对称,质心位于y 轴上,且沿y 轴作铅垂直线运动,点C 的运动轨迹亦为铅垂直线。
当m 1= 2m 2时,质心位于y 轴左侧,且作铅垂直线运动,点C 的运动轨迹必为曲线。
故两种情况下,点C 的运动轨迹不相同。
8-4 图示水泵的固定外壳D 和基础E 的质量为m 1,曲柄OA =d ,质量为m 2,滑道B 和活塞C 的质量为m 3。
若曲柄OA 以角速度ω作匀角速转动,试求水泵在唧水时给地面的动压力(曲柄可视为匀质杆)。
解:以整个水泵为研究对象,受力如图(a ): 解法1:用动量定理求解 瞬时t ,系统动量 p = p 2+p 3
ω2
2222d m v m p C ⋅==,方向如图 ϕωsin 3333 d m v m p C ==,方向如图 由质系动量应理:
∑==y y y
F F t p d d (1)
∑==x x x
F F t
p d d (2)
ϕωϕωsin sin 23232d m d m p p p y y y +⋅=+= ϕωcos 2
232d
m p p p x
x x ⋅=+=
x x x F F F ==∑
g m m m F F F )(321++-==∑y y y 代入(1)、(2),并注意到t ωϕ=得:
g m m m F t d m t d m t y )(sin sin 2d d 32132++-=⎪⎭⎫
⎝⎛+⋅ωωωω x F t d m t =⎪⎭
⎫
⎝⎛⋅ωωcos 2d d 2
得t ωd m m g m m m F 2y ωcos 2
2)(3
2321++++= (3) t m d F 2x ωωsin 2
2-= (4)
解法2:用质心运动定理解 研究对象及受力同前: R F a =C M 32p p p +=
3322C C C m m M v v v +=
t
d d
:3322C C C a a a m m M +=
习题8-4图
习题8-3解图
p
(a)
习题8-6图 2
22
ωd a =
C ,方向指向O 点; t d a C ωωcos 23=,方向向上。
写出质心运动定理的投影形式:
g m m m F t d m t d m y 2)(cos cos 2
321322++-=+ωωωω x F t d m -=⋅ωωsin 2
22
t d
-m F x ωωsin 2
22⋅=
t d m m g m m m F 2y ωωcos 2
2)(3
2321++++= 结果同解法1。
8-5 图示均质滑轮A 质量为m ,重物M 1、M
2质量分别为m 1和m 2,斜面的倾角为θ,忽略摩擦。
已知重物M 2的加速度a ,试求轴承O 处的约束力(表示成a 的函数)。
解:以系统整体为研究对象,应用动量定理 θθsin cos d d N 2F F a m t p Ox x
+== g
m m m F F a m a m t
p Oy y )(cos sin d d 21N 21++-+=-=θθ分析M 2可知:θ
cos 2N g m F =
则有
θ
θθθθcos )sin (sin cos cos 222m g a g m a m F Ox -=-=
g
m m m g m a m m F Oy )(cos )sin (212221+++--=θθ
8-6 板AB 质量为m ,放在光滑水平面上,其上用铰链连接四连杆机构OCDO 1(如图示)。
已知OC = O 1D = b ,CD = OO 1,均质杆OC 、O 1D 质量皆为m 1,均质杆CD 质量为m 2,当杆OC 从与铅垂线夹角为θ由静止开始转到水平位置时,求板AB 的位移。
解:以系统整体为研究对象,根据受力分析知:
∑=0x
F
,
故系统的质心在水平方向运动守恒。
若初始时(设CD = l ):
m
m m l b
m l m l b m b m x C +++++++=
211210
2)sin 2(2)2sin (sin 2θθθ 设杆OC 转到水平位置时板AB 的位移为s ,
m
m m l s b
m s l m l s b m s b m x C +++-+-++-+-=
211212)2()2()2()2(x C 0 = x C
)sin 1(2212
1θ-+++=b m
m m m m s
习题8-5图
M 习题8-5解图
M m 1
习题8-6解图
习题8-7图
习题8-8图
v x
(a) B F g
m 8-7 匀质杆AB 长2l ,B 端放置在光滑水平面上。
杆在图示位置自由倒下,试求A 点轨迹方程。
解:杆水平受力为零,水平动量守恒;初始静止、质心位置C x 守恒: 0cos αl x C =
ϕcos l x x C A +=
ϕsin 2l y A =由(1),
ϕcos l x x C A =- 即 ϕαcos cos 0l l x A =- (3) 由(2)
ϕsin 2
l y A
= (4)
(3)、(4)两边平方后相加,得
222
04
)cos (l y l x A A =+-α
此为椭圆方程。
*8-8自动传送带如图所示,其运煤量恒为20kg/s ,传送带速度为1.5m/s 。
试求匀速传送时传送带作用于煤块的总水平推力。
解:设皮带作用煤块的总水平推力为F x ,皮带在d t 时间内输送量为t q V d ,由动量定理微分形式: t F v t q x V d d =⋅
305120=⨯==.v q F V x N。
