中间时刻中间位置的瞬时速度求解
瞬时速度的计算公式

瞬时速度的计算公式
瞬时速度,是表示物体在某一时刻或经过某一位置时的速度,该时刻
相邻的无限短时间内的位移与通过这段位移所用时间的比值v=△x╱△t。
瞬时速度是矢量,某一时刻(或经某一位置时)瞬时速度的方向,即
是这一时刻(或经过一位置时)物体运动的方向。
瞬时速度是理想状态下
的量。
如果物体做匀速直线运动,他在运动过程中速度保持不变,那么他
任何时刻的瞬时速度和整个运动过程的平均速度也相同。
注意事项:
物体从t到t+△t的时间间隔内的平均速度为△s/△t,如果△t无
限接近于0,就可以认为△s/△t表示的是物体在t时刻的速度。
在匀变
速直线运动中,某一段时间的平均速度等于中间时刻的瞬时速度(即中间
时刻的瞬时速度)。
平均速度与路程或时间相对应,瞬时速度与位置或时刻相对应。
做匀
速直线运动的物体,平均速度等于瞬时速度。
当运动物体通过的路程或所用的时间短到物体运动快慢的改变可以忽
略的时候,平均速度就转化为了瞬时速度;反之,瞬时速度也可以看成是
在极短时间内的平均速度。
(完整版)匀变速直线运动的推论及推理

罗老师总结匀变速直线运动常用公式 (附匀变速直线运动的推论及推理过程)一、基本公式速度公式 at v v t +=0 当00=v 时,at v t = 位移公式 2021at t v s += 221at s = 二、几个常用的推论1.位移推导公式 2022v v as t -=, t v v s t20+=2.平均速度v 、中间时刻的瞬时速度2/t v 、中间位置的瞬时速度2/s v 为:0/22t t v v xv v t +===, 22202/t s v v v += 3.做匀变速直线运动的物体,在各个连续相等的时间T 内的位移分别是s 1、s 2、s 3…s n ,则Δs =s 2-s 1=s 3-s 2=…=s n -s n-1=aT 2.4.V 0=0的匀加速直线运动中的几个常用的比例公式(1)等分运动时间,以T 为单位时间.①1T 末,2T 末,3T 末…,n T 末的速度之比v 1:v 2:v 3:…:v n =1:2:3…:n②1T 内、2T 内、3T 内…n T 内通过的位移之比s 1:s 2:s 3:…:s n =1:4:9…:n 2③第1个T 内、第2个T 内、第3个T 内…、第n 个T 内通过的位移之比s Ⅰ:s Ⅱ:s Ⅲ:…:s N =1:3:5…:(2n —1)④第1个T 内、第2个T 内、第3个T 内…、第n 个T 内的平均速度之比v Ⅰ:v Ⅱ:v Ⅲ:…:v N =1:3:5…:(2n —1) (2)等分位移,以x 为位移单位. ①通过1x 、2x 、3x …、n x 所需时间之比t 1:t 2:t 3:…:t n =1:3:2…:n②通过第1个x 、第2个x 、第3个x 、…第n 个x 所需时间之比t Ⅰ:t Ⅱ:t Ⅲ:…:t N =1::23:12--…:1--n n③1x 末,2x 末,3x 末…,n x 末的速度之比v 1:v 2:v 3:…:v n =1:3:2…:n对匀变速直线运动公式作进一步的推论,是掌握基础知识、训练思维、提高能力的一个重要途径,掌握运用的这些推论是解决一些特殊问题的重要手段。
中间时刻的瞬时速度的计算公式

中间时刻的瞬时速度的计算公式
瞬时速度是指物体在某一时刻的瞬间速度,是速度的一种表现形式。
瞬时速度与平均速度是密切相关的,平均速度是物体在一段时间内的平均速度,而瞬时速度是在某一时刻的速度。
在研究物体运动时,我们往往需要计算中间时刻的瞬时速度,这对于解决运动学问题具有重要意义。
中间时刻的瞬时速度计算公式为:v = (v0 + vt) / 2,其中v0 是初始速度,vt 是末速度,t 是时间。
这个公式是通过平均速度的计算公式v = (s - s0) / t 推导得出的,其中s 是物体的位移。
我们可以通过已知的初始速度、末速度和时间来计算中间时刻的瞬时速度。
中间时刻的瞬时速度计算公式在解决运动学问题中有着广泛的应用。
例如,在研究物体在一段时间内的位移时,我们可以通过计算中间时刻的瞬时速度,结合位移公式s = vt 来求解。
此外,在交通速度监控中,我们也可以通过计算车辆在一段时间内的中间时刻瞬时速度,来了解车辆的实时速度,以便进行交通管理和调度。
速度对运动成绩也有很大的影响。
例如,在田径比赛中,运动员的速度是决定比赛成绩的关键因素。
教练员可以通过观察运动员在比赛过程中的速度变化,找出影响成绩的原因,并制定相应的训练计划。
总之,中间时刻的瞬时速度的计算公式在解决运动学问题、交通管理和运动成绩提高等方面具有重要意义。
3.求瞬时速度和加速度
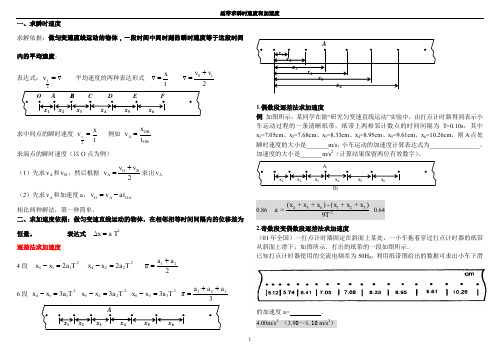
1一、求瞬时速度求解依据:做匀变速直线运动的物体,一段时间中间时刻的瞬时速度等于这段时间内的平均速度。
表达式:v v t =2平均速度的两种表达形式 t xv = 20t v v v +=求中间点的瞬时速度 t xv t =2例如 OBOB A t x v = 求端点的瞬时速度(以O 点为例) (1)先求A v 和B v ,然后根据 2BO A v v v +=求出A v (2)先求A v 和加速度a ,OA A O at v v -=相比两种解法,第一种简单。
二、求加速度依据:做匀变速直线运动的物体,在相邻相等时间间隔内的位移差为恒量。
表达式 2a T x =∆ 逐差法求加速度4段 21132T a x x =- 22242T a x x =- 221a a a +=6段 21143T a x x =- 22253T a x x =- 23363T a x x =- 3321a a a a ++=1.偶数段逐差法求加速度例 如图所示,某同学在做“研究匀变速直线运动”实验中,由打点计时器得到表示小车运动过程的一条清晰纸带,纸带上两相邻计数点的时间间隔为T =0.10s ,其中x 1=7.05cm 、x 2=7.68cm 、x 3=8.33cm 、x 4=8.95cm 、x 5=9.61cm 、x 6=10.26cm ,则A 点处瞬时速度的大小是_______m/s ,小车运动的加速度计算表达式为________________,加速度的大小是_______m/s 2(计算结果保留两位有效数字)。
2.奇数段变偶数段逐差法求加速度(01年全国)一打点计时器固定在斜面上某处,一小车拖着穿过打点计时器的纸带从斜面上滑下,如图所示.打出的纸带的一段如图所示.已知打点计时器使用的交流电频率为50H Z ,利用纸带图给出的数据可求出小车下滑的加速度a = . 4.00m/s 2 (3.90~4.10 m/s 2)23.已知不相邻的两段相等时间内的位移求加速度一条残缺的纸带如图所示,打点计时器所用交流电频率为50 Hz 。
必修一物理匀变速直线运动的推论及推理过程

匀变速直线运动常用公式(附匀变速直线运动的推论及推理过程)一、 基本公式 速度公式 at v v t +=0 当00=v 时,at v t =位移公式 2021at t v s+= 221at s =二、 几个常用的推论 1.位移推导公式 2022v v ast -=, t v v s t20+=2.平均速度v 、中间时刻的瞬时速度2/t v 、中间位置的瞬时速度2/s v 为:0/22tt v v xv v t +===, 22202/t s v v v +=3.做匀变速直线运动的物体,在各个连续相等的时间T 内的位移分别是s 1、s 2、s 3…s n ,则Δs =s 2-s 1=s 3-s 2=…=s n -s n-1=aT 2.4.V 0=0的匀加速直线运动中的几个常用的比例公式 (1)等分运动时间,以T 为单位时间. ①1T 末,2T 末,3T 末…,n T 末的速度之比v 1:v 2:v 3:…:v n =1:2:3…:n②1T 内、2T 内、3T 内…n T 内通过的位移之比s 1:s 2:s 3:…:s n =1:4:9…:n 2③第1个T 内、第2个T 内、第3个T 内…、第n 个T 内通过的位移之比s Ⅰ:s Ⅱ:s Ⅲ:…:s N =1:3:5…:(2n —1)④第1个T 内、第2个T 内、第3个T 内…、第n 个T 内的平均速度之比v Ⅰ:v Ⅱ:v Ⅲ:…:v N =1:3:5…:(2n —1)(2)等分位移,以x 为位移单位. ①通过1x 、2x 、3x …、n x 所需时间之比t 1:t 2:t 3:…:t n =1:3:2…:n②通过第1个x 、第2个x 、第3个x 、…第n 个x 所需时间之比t Ⅰ:t Ⅱ:t Ⅲ:…:t N =1::23:12--…:1--n n③1x 末,2x 末,3x 末…,n x 末的速度之比v 1:v 2:v 3:…:v n =1:3:2…:n对匀变速直线运动公式作进一步的推论,是掌握基础知识、训练思维、提高能力的一个重要途径,掌握运用的这些推论是解决一些特殊问题的重要手段。
专题二:中间时刻速度与中间位置速度

• (2)火车中点经过此路标时的速度v。
• (3)整列火车通过此路标所用的时间t。
目标升华
匀变速直线运动两个重要推论:
1、中间时刻速度公式 :
vt
2
v=
1 2
v0
v
2、中点位置瞬时速度公式 :
vx =
2
v
2 0
v2
2
当堂诊学
诊学1、(基础题)(四川理综)假设战机起飞前从静止
独立自学
1.做匀变速直线运动的物体在一段时间t内的平均速度等于这段 时间的中间时刻的瞬时速度,还等于这段时间初、末速度矢量和的 一半.即
2
.
做
匀
变
速
直
线
运
动
的
物
体
,
在
某v x
段
位
移
内
中
间
位
置
的
速
度vvx 2
x
2
2
等于这段位移的初、末速度的方均根.即
引导探究一
中间时刻的瞬时速度 前提条件:质点做匀变速直线运 动。vt2 Nhomakorabeav0
vt 2
vs
2
1 2
(v02
vt2 )
v2 2 t v2 2 s(v 0 4 v t)2 v 0 2 2v t2 v 0 2 v t4 2 2 v 0 v t
14(v02vt22v0vt) 由于 (v t v 0 )2 v 0 2 v t2 2 v 0 v t 0 (v 0 v t)
开始做匀变速直线运动,达到起飞速到v所需时间为t,则
起飞运动的距离为(
)
答案:B
• 诊学2、(基础题)做匀加速直线运动的列车 出站时,车头经过站台时的速度为1 m/s,车 尾经过站台时的速度为7 m/s,则车身的中部 经过站台时的速度为( )
中间时刻的瞬时速度的计算公式

中间时刻的瞬时速度的计算公式中间时刻的瞬时速度的计算公式中间时刻的瞬时速度是指某一物体在某一时刻的瞬时速度。
瞬时速度是物体在某一时刻的瞬时速度。
计算中间时刻的瞬时速度可以使用以下公式:1.瞬时速度的定义公式:瞬时速度= lim(△t→0)(△s / △t) 其中,lim 表示极限操作,△t表示时间变化的极小量,△s表示位移变化的极小量。
2.几何法计算瞬时速度:瞬时速度 = ds / dt 其中,ds表示位移的微小变化,dt表示时间的微小变化。
3.导数计算瞬时速度:瞬时速度 = dx / dt 其中,dx表示质点位置的微小变化。
举例说明:假设有一辆汽车沿直线行驶,其位移函数为 s(t) = 2t^2 + 3t - 4,其中t表示时间。
1.使用瞬时速度的定义公式来计算中间时刻的瞬时速度:根据定义公式可知,瞬时速度= lim(△t→0) (△s / △t) 我们选择一个具体的时刻,例如t=2,此时位移为 s(2) = 2(2^2)+ 32 - 4 = 10 然后我们再选取一个极小的时间变化△t,例如△t=,计算在 t=2 附近的位移变化△s:△s = s(2 + △t) - s(2) = [2(2 + △t)^2 + 3(2 + △t) - 4] - 10 最后,带入公式即可计算出中间时刻的瞬时速度。
2.使用几何法计算瞬时速度:几何法的公式是瞬时速度 = ds / dt,我们选择同样的时刻t=2,并计算其相邻的位移微小变化ds和时间微小变化dt。
然后带入公式即可计算出中间时刻的瞬时速度。
3.使用导数计算瞬时速度:导数计算瞬时速度的公式是瞬时速度 = dx / dt,同样选择时刻t=2,计算质点位置微小变化dx和时间微小变化dt。
然后带入公式即可计算出中间时刻的瞬时速度。
以上就是中间时刻的瞬时速度的计算公式及其举例解释。
不同的公式可以根据具体情况选择使用,但都能准确计算物体在中间时刻的瞬时速度。
中间时刻的瞬时速度公式

中间时刻的瞬时速度公式瞬时速度可以通过计算物体位置随时间的导数来得到。
在中间时刻的瞬时速度公式可以通过以下步骤来推导:1.瞬时速度的定义:瞬时速度是物体在其中一时刻的速度,可以用以下公式表示:v(t) = lim Δt→0 [ (x(t+Δt) - x(t)) / Δt ]其中,v(t)表示在时刻t的瞬时速度,x(t)表示在时刻t的位置,Δt表示时间的微小变化量。
2.物体的位置函数:如果我们已知物体在其中一时刻t的位置函数x(t),则可以将其代入上述公式中计算得到瞬时速度。
v(t) = lim Δt→0 [ (x(t+Δt) - x(t)) / Δt ]3.导数的定义:根据导数的定义,我们可以将上述公式重新表达为:v(t) = dx(t) / dt其中,dx(t) 表示位置函数 x(t) 的微分,dt 表示时间的微小变化量。
4.求解位置函数的导数:为了求解位置函数x(t)的导数,我们需要对其进行微分。
这是一个涉及函数微积分的问题,具体求解过程将超过1200字的限制,因此我们可以通过讨论几个常见的位置函数来展示中间时刻的瞬时速度公式。
a.匀速直线运动:对于匀速直线运动,物体的位置函数可以表示为x(t)=x0+v0*t,其中x0是初始位置,v0是初始速度。
对位置函数进行微分:dx(t) / dt = v0因此,在匀速直线运动中,瞬时速度恒定,等于初始速度。
b.自由落体运动:对于自由落体运动,物体的位置函数可以表示为x(t)=1/2*g*t^2,其中g是重力加速度。
对位置函数进行微分:dx(t) / dt = g * t在自由落体运动中,瞬时速度是与时间成正比的,并且随着时间的增加而增加。
c. 简谐振动:对于简谐振动,物体的位置函数可以表示为 x(t) = A * cos(ω * t + φ),其中 A 是振幅,ω 是角频率,φ 是相位。
对位置函数进行微分:dx(t) / dt = -A * ω * sin(ω * t + φ)在简谐振动中,瞬时速度既与时间有关,也与振幅、角频率和相位有关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第8讲 中间时刻、中间位置的瞬时速度求解
【技巧点拨】
一、两个中间速度
匀变速直线运动中某段时间中点的瞬时速度:2
02t v v
v v +==
匀变速直线运动中某段位移中点的瞬时速度:2
x v = 【特别提醒】无论匀加速直线运动还是匀减速直线运动,中间时刻的瞬时速度
小于位移中点的瞬时速度
:22
02t x v v v v +=<=
【对点题组】
1.光滑斜面长为L ,一物体自斜面顶端由静止开始匀加速下滑到底端经历的时间为t ,则( )
A .物体在2
t 时刻的瞬时速度是t
L 2
B .物体全过程的平均速度是t
L
C .物体到斜面中点时的瞬时速度小于t
L
D .物体从开始运动到斜面中点经历的时间为2
t
2.一个做匀加速直线运动的物体,先后经过A 、B 两点的速度分别是v 和7v ,经过AB 的时间是t ,则下列判断中正确的是( )
A .经过A
B 中点的速度是4v B .经过AB 中间时刻的速度是4v
C .前2
t 时间通过的位移比后2
t 时间通过的位移少1.5vt D .前2
x 位移所需时间是后2
x 位移所需时间的2倍
3.物体做直线运动,在t 时间内通过的路程为x ,在中间位置x /2处的速度为v 1,且在中间时刻t /2处的速度为v 2,则v 1和v 2的关系错误的是( ) A .当物体做匀加速直线运动时,v 1>v 2 B .当物体做匀减速直线运动时,v 1>v 2 C .当物体做匀速直线运动时,v 1=v 2 D .当物体做匀减速直线运动时,v 1<v 2
4.做匀加速直线运动的列车出站后,车头经过某标牌时的速度为1 m/s ,车尾经过该牌时的速度为7 m/s ,则车身的中部经过该牌时的速度大小为( ) A .4 m/s B .5 m/s C .3.5 m/s
D .5.5 m/s
5.某人用手表估测火车的加速度.先观测3 min ,发现火车前进540 m ;隔3 min 后又观察1 min ,发现火车前进360 m.若火车在这7 min 内做匀加速直线运动,则火车的加速度为( )
2
2
C.0.5 m/s 2
D.0.6 m/s 2
6.沿直线作匀变速直线运动的质点在第一个0.5秒内的平均速度比它在第一个
1.5秒内的平均速度大
2.45m/s ,以质点的运动方向为正方向,则该质点的加速度为( )
A .2.45m/s 2
B .-2.5m/s 2
C .4.90m/s 2
D .-4.90m/s 2
7.汽车自O 点出发从静止开始在平直公路上做匀加速直线运动,途中在6 s 内分别经过P 、Q 两根电线杆,已知P 、Q 电线杆相距60 m ,车经过电线杆Q 时的速率是15 m/s ,则下列说法正确的是( ) A .经过P 杆时的速率是5 m/s B .车的加速度是1.5 m/s 2 C .P 、O 间的距离是7.5 m
D .车从出发到经过Q 所用的时间是9 s
答案精析
【对点题组】
1.【答案】B
【解析】物体从顶端下滑到底端的平均速度为v =t L ,物体在2
t
时刻的瞬时速度
2t
v =v =t
L ,故A 错、B 对.物体的速度随时间增大,所以在前一半位移的平均速度小于在后一半位移的平均速度,即在前一半位移用的时间长,大于2
t
;后一
半位移的时间短,小于2t ,故2x v =at ′>2at =v 2t =t
L ,即物体在斜面中点时的瞬时速度大于t
L ,故C 、D 两项都错.
2.【答案】 BCD
3.【答案】D
【解析】物体做匀变速直线运动,有22
02t v v ax -=知2
2
x v -
=2a 2
x
由以上两式得2
22
02x v v v +=
讨论:由于2t
v =20t v v +,2x
v =
2
2
20t v v + 则
2
x v 2
-
2
t
v 2
=2
2
2
0t
v v +-20)2(t v v +=2
04)(t v v -≥0, 当且仅当v 0=v t 时等号成立,故只要物体做匀变速运动,则一定有 2
2
x t v v >.
4.【答案】B
【解析】由车头到列车中心通过:
-=22
x a ;由列车中心到车尾通过:
v 2
-
=22
x
a 解得v 中= 2
2
2
0v v +=
27122+m/s =5 m/s. 5.【答案】B
【解析】第一个3min 内中间时刻的瞬时速度1540
m /s 3m /s 180
x v t ===,1min 内中间时刻的瞬时速度2360
m /s 6m /s 60
v ==,两个时刻之间的时间间隔为300s ,所以,21
20.01m /s v v t
a -==
故B 正确,A 、C 、D 错误。
答案为B
6.【答案】D
【解析】时间中点的瞬时速度等于平均速度。
所以第0.25秒的瞬时速度v 1比0.75秒的瞬时速度v 2大2.45m/s ,则122 2.45
0.750.25
4.90m /s v v t a -=
-=-=﹣所以选D 7.【答案】 ACD
【解析】 由于汽车在P 、Q 间的平均速度等于它经过两点时瞬时速度的平均值,即2
p Q
v v x
t
+=
,故25m/s p Q x v v t =
-=,A 对.车的加速度25
m/s 3
Q p v v a t -==,B 错.从O 到P 用时'
3p v t s a
=
=,P 、O 间距离1'7.5m 2
p v x t =
=,C 对.O 到Q 用时t ′+t
=3 s +6 s =9 s ,D 对.。
