倍长中线法
倍长中线法经典例题较难

倍长中线法经典例题较难在说到倍长中线法,大家可能会觉得这是什么神秘的东西,其实并没有那么复杂。
想象一下,我们在课堂上,老师拿着一个三角形,指着那根中线,眼睛闪闪发光,像是在说:“看,这就是你们的未来!”这时的我们,或许有点懵,心里想着:“我能干嘛呢?”可这玩意儿就像一块儿美味的蛋糕,切开来让大家分享,越吃越觉得香。
倍长中线法的核心就像是我们生活中的很多道理,简单明了。
想象一个三角形,边边角角都各有千秋,老师告诉我们,长的那条中线就像是三角形的心脏,连接着两个顶点,恰到好处。
这时候,你可能会想:“这和我有什么关系?”可实际上,这就是几何的魅力所在!你看,学习数学就像是打怪升级,每个定理、每条公式都是你在游戏中的技能点,越多越好。
说到倍长中线,得先搞清楚中线是啥。
简单来说,三角形的中线是连接一个顶点和对边中点的线段。
它像个桥,把三角形的两边连成一体,真是个绝佳的搭档。
老师总爱用“中线”来解释一些深奥的道理,仿佛在说:“只要你找到这个点,生活就会变得简单。
”可这条中线可不止是个连接的角色,它还能让我们看见美丽的几何图形之舞,优雅而又有趣。
再说说倍长的意思。
倍长中线法的“倍长”其实就是中线的长度变成了原来的两倍。
这时候,想象一下我们平常买的衣服,如果腰围从30寸变成了60寸,那可就得赶紧去找裁缝了。
这种变化让我们不仅能观察到三角形的变化,更能思考背后隐藏的数学美感。
倍长中线法就像是一种魔法,把简单的三角形变成了充满可能的世界。
有人会问,倍长中线法到底有什么用呢?这就像问“为什么要吃水果”,答案是让我们更健康。
用倍长中线法,我们可以求得三角形的周长、面积,还能算出各种角度。
学会这招,就像拥有了打开数学大门的钥匙。
数学不仅仅是书本上的公式,更是我们生活中的每一个细节。
在解题时,倍长中线法也特别好用。
拿个简单的例子来说,给你个三角形,让你找出它的面积。
用倍长中线法,你只需简单几步,仿佛在解密一样,轻松搞定,心里那种成就感,简直就像是打通了一个难关,爽得不行。
倍长中线法(经典例题)
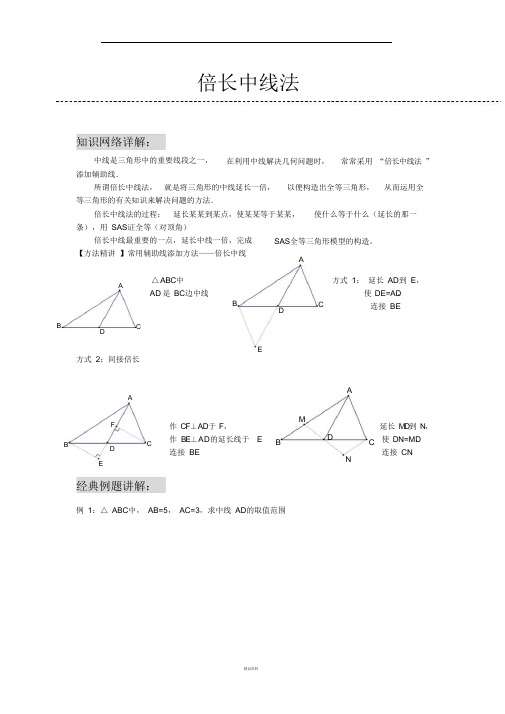
倍长中线法例 1:△ ABC 中, AB=5, AC=3,求中线 AD 的取值范围知识网络详解:中线是三角形中的重要线段之一, 添加辅助线.在利用中线解决几何问题时, 常常采用 “倍长中线法 ”所谓倍长中线法, 就是将三角形的中线延长一倍, 以便构造出全等三角形, 从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程: 延长某某到某点,使某某等于某某, 使什么等于什么(延长的那一条),用 SAS 证全等(对顶角)倍长中线最重要的一点,延长中线一倍,完成 【方法精讲 】常用辅助线添加方法——倍长中线SAS 全等三角形模型的构造。
AA△ ABC 中 AD 是 BC 边中线BDC方式 1: 延长 AD 到 E ,使 DE=AD ,连接 BEB DCE方式 2:间接倍长AAF 作 CF ⊥ AD 于 F , MDB D C作 BE ⊥ AD 的延长线于 连接 BEE BC 延长 MD 到 N , 使 DN=M ,D 连接 CNEN经典例题讲解:例2:已知在△ABC中,AB=AC,D 在AB上,E 在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CEADBFCE例3:已知在△ ABC中,AD是BC边上的中线, E 是AD上一点,且BE=AC,延长BE交AC于F,求证:AF=EFAFEBD C例4:已知:如图,在ABC 中,AB 交AE于点F,DF=AC.求证:AE平分BAC AC ,D、E 在BC上,且DE=EC,过D作DF // BAAFB D E C例5:已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,求证:∠C=∠BAEABCE D自检自测:1、如图,△ABC中,BD=DC=AC,E是DC的中点,求证,AD平分∠BAE.2、在四边形ABCD中,AB∥DC,E 为BC边的中点,∠BAE=∠EAF,AF 与DC的延长线相交于点F。
试探究线段AB与AF、CF之间的数量关系,并证明你的结论.ADBE CF3、如图,AD为ABC 的中线,DE平分BDA 交AB于E,DF平分ADC 交AC于F. 求证:BE CF EFAEFB CD第14 题图4、已知:如图,ABC中,C=90 ,CM AB于M,AT 平分BAC交CM于D,交BC于T,过D作DE//AB 交BC于E,求证:CT=BE.A MD BETCWelcome To Download !!!欢迎您的下载,资料仅供参考!。
中考数学几何辅助线:倍长中线法

中考数学几何添加辅助线:倍长中线中线或中点是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线。
所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法。
此法常用于构造全等三角形,利用中线的性质、辅助线、对顶角进而用“SAS”证明对应边之间的关系。
常规的倍长中线可以出全等,但需要证明“三点共线”,遇到“中点+平行”,我们“延长出全等”,而非“倍长出全等”. 用“倍长中线法”作辅助线解几何题,是一种重要的技巧套路。
它可以有效地生发出全等、平行等基本条件,关联好多基本图形,帮助解题,大家务必好好掌握。
也给我们解题的启示:抓住核心,找到关键,才能快速解题。
逢中点,便倍长,全等观,平行现.倍长中线法:是指加倍延长中线,使所延长部分与中线相等,然后连接相应的顶点,构造“8字形”的全等三角形。
在与中点有关的线段尤其是涉及线段的等量关系时,倍长中线应用较常见,常见添加如图(AD是底边中线)典例1.已知:AD是ΔABC的中线,AE=EF.求证:AC=BF.名师指点:延长AD到M,使AD=DM,连接BM,根据SAS证△ADC≌△MDB,推出BM=AC,∠CAD=∠M,根据AE=EF,推出∠CAD=∠AFE=∠BFD,求出∠BFD=∠M,再根据等腰三角形的性质证明即可.满分解答:证明:延长AD 到M ,使AD =DM ,连接BM ,∵AD 是△ABC 中线,∴CD =BD ,∵在△ADC 和△MDB 中,{CD =BD∠ADC =∠MDB AD =DM,∴△ADC ≌△MDB (SAS ),∴BM =AC ,∠CAD =∠M ,∵AE =EF ,∴∠CAD =∠AFE ,∵∠AFE =∠BFD ,∴∠BFD =∠CAD =∠M ,∴BF =BM =AC ,即AC =BF .名师点评:倍长中线是常见的辅助线、全等中相关的角、线段的代换是解决问题的关键. 1.如图,在平行四边形ABCD 中,28CD AD ==,E 为AD 上一点,F 为DC 的中点,则下列结论中正确的是( )A .4BF =B .2ABC ABF ∠>∠。
倍长中线法(初二)

全等三角形的构造方法---常用辅助线搞清了全等三角形的证题思路后,还要注意一些较难的一些证明问题,只要构造合适的全等三角形,把条件相对集中起来,再进行等量代换,就可以化难为易了.下面举例说明几种常见的构造方法,供同学们参考.(一)倍长中线法:题中条件若有中线,可延长一倍,以构造全等三角形,从而将分散条件集中在一个三角形内。
例1.如图(1)AD 是△ABC 的中线,BE 交AC 于E ,交AD 于F ,且AE=EF . 求证:AC=BF 证明:延长AD 至H 使DH=AD ,连BH ,∵BD=CD, ∠BDH=∠ADC ,DH=DA , ∴△BDH ≌△CDA ,∴BH=CA ,∠H=∠DAC ,又∵AE=EF , ∴∠DAC=∠AFE ,∵∠AFE=∠BFD ,∴∠AFE= 图(1) ∠BFD=∠DAC=∠H ,∴BF=BH ,∴AC=BF .小结:涉及三角形中线问题时,常采用延长中线一倍的办法,即倍长中线法。
它可以将分居中线两旁的两条边AB 、AC 和两个角∠BAD 和∠CAD 集中于同一个三角形中,以利于问题的获解。
中线一倍辅助线作法△ABC 中 延长AD 到E ,AD 是BC 边中线DE=AD ,连⊥AD 于F ,延长MD AD 的延长线于使DN=MD , 连接例2、△ABC 中,AB=5,AC=3,求中线AD 的取值范围E AB C DF H例3、已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE课堂练习:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF例4、已知:如图,在ABC ∆中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC.求证:AE 平分BAC ∠课堂练习:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAEB第 1 题图 A B F D EC作业:1、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
中线倍长法

中线倍长法
中线倍长法是指使用一组具备特定功能的几何形状,并把它们重复堆叠起来,形成空间结构的设计方式。
它是以传统中国建筑中拱形拱门为设计元素,融合了现代空间建筑技术,以达成建筑空间效果的独特技术。
它最初由中国老牌建筑设计师陆文厦在上世纪八十年代提出,他基于传统的中国建筑拱形结构,提出了一种使用若干倍长的中线构建空间结构的设计方案,以此来巧妙地解决复杂的建筑空间布局问题。
中线倍长法以中线作为基本框架,通过倍长来模拟建筑拱形结构,既可以满足复杂的建筑空间布局,又可以达到拱形的空间效果,使空间变得更加宽敞、完美,并使之有着舒适的感受。
中线倍长法在其设计方法上也有着一些特点,主要体现在通过中线的使用,可以实现把传统的圆形结构形状“堆叠”,从而形成一种
较为宽敞的“拱门”形状,使建筑空间布局更加自由,不受传统拱形结构的限制。
中线倍长法由于具有灵活、高效以及适用性强等特点,被广泛运用于现代建筑空间设计,尤其是在大型建筑中,由于高度和空间结构上的复杂,中线倍长法则成为解决空间布置问题的有效方式。
中线倍长法的应用也被越来越多的应用于工业制造和现代建筑
空间设计中,可以有效地降低工程施工时间,提高工作效率。
特别是在大型建筑项目中,则可以有效地使用中线倍长法的方式简化工作,提高建筑质量,节省建筑施工费用。
因此,中线倍长法在现代建筑空
间设计中,是一个非常有用的技术工具,可以帮助建筑设计师有效地实现空间效果。
总而言之,中线倍长法是一种特定的建筑空间设计方式,它既可以满足复杂的建筑空间布局,又可以实现空间效果的最佳展示,所以在现代建筑空间设计中,中线倍长法是非常有效的工具。
倍长中线法经典例题

倍长中线法经典例题倍长中线法是一种加法运算技巧,有效地提高了大数加法的运算复杂度,其思想是利用“倍数方法”和“中线方法”相结合,让大数加法运算变得更加容易、快捷。
今天,我们就来认真研究一下倍长中线法的经典例题,深入了解它的奥妙之处,为今后的加法运算奠定坚实的理论基础。
例题一:计算788 + 883首先,我们来看倍长中线法的思路:首先用“倍数方法”,将两个加数乘以1000,即78800 + 883000;然后,用“中线方法”,将两个乘以1000后的数放在中线上,形成一条倍长的中线,即| 7880000 | 8830000 |;最后,从右往左数,总计8位,从右往左加即可得出结果。
由于是从右往左加,所以从右边开始计算,第8位末位数相加,结果为1,但此时不进位;再加第7位,结果为8,该位也不进位;继续加第6位,结果为3,也不进位;最终结果为1671000。
即788 + 883 = 1671。
例题二:计算486 + 879先用“倍数方法”,将两个加数乘以1000,即486000 + 879000;然后,用“中线方法”,将两个乘以1000后的数放在中线上,形成一条倍长的中线,即| 4860000 | 8790000 |;最后,从右往左数,总计8位,从右往左加即可得出结果。
从右往左加,第8位末位数相加,结果为2,不进位;继续加第7位,结果为8,该位也不进位;再加第6位,结果为7,此时需要进位;最终结果为1365000。
即486 + 879 = 1365。
通过上面的两个例题,相信读者对倍长中线法的思想及操作方法已经有了一定的了解,下面我们将再来讨论一个关键概念:“倍数方法”与“中线方法”之间如何结合?其实“倍数方法”与“中线方法”之间的相互结合,就是倍长中线法的关键点所在。
前面的例题中,我们都是“倍数方法”将加数乘以1000;然后用“中线方法”将乘以1000的结果放在中线上,然后从右往左依次加数,最终得到结果。
倍长中线法

倍长中线法知识网络详解:中线是三角形中的重要线段之一,在利用中线解决几何问题时,经常采纳“倍长中线法”增添协助线.所谓倍长中线法,就是将三角形的中线延伸一倍,以便结构出全等三角形,进而运用全等三角形的相关知识来解决问题的方法.倍长中线法的过程:延伸某某到某点,使某某等于某某,使什么等于什么(延伸的那一条),用 SAS证全等(对顶角)倍长中线最重要的一点,延伸中线一倍,达成SAS全等三角形模型的结构。
【方法精讲】常用协助线增添方法——倍长中线AAB CD △ ABC中方式1:延伸AD到E,AD 是 BC边中线使DE=AD,B C连结BED方式 2:间接倍长AFB D CEEA作 CF⊥ AD于 F,M 延伸 MD到N,作 BE⊥ AD的延伸线于 E BD使 DN=MD,C连结 BEN连结 CN经典例题解说:例 1:△ ABC中, AB=5, AC=3,求中线 AD的取值范围例2:已知在△ ABC中, AB=AC, D 在 AB上, E 在 AC的延伸线上, DE交 BC于 F,且DF=EF,求证: BD=CEADBCFE例3:已知在△ ABC中,AD是 BC边上的中线, E 是 AD上一点,且 BE=AC,延伸 BE交 AC于 F,求证: AF=EFAFEBD C例 4:已知:如图,在ABC 中, AB AC ,D、E在BC上,且DE=EC,过D作 DF // BA交AE于点 F, DF=AC.A求证: AE均分BACFB D E C例5:已知 CD=AB,∠ BDA=∠BAD, AE是△ ABD的中线,求证:∠ C=∠ BAEAB CE D自检自测:1、如图,△ ABC 中, BD=DC=AC,E是 DC的中点,求证,A D均分∠ BAE.2、在四边形 ABCD中, AB∥ DC, E 为 BC边的中点,∠ BAE=∠ EAF, AF 与 DC的延伸线订交于点 F。
尝试究线段 AB与 AF、CF之间的数目关系,并证明你的结论 .ADBE CF3、如图, AD为ABC 的中线,DE均分BDA 交AB于E,DF均分ADC 交AC于F.求证:BE CF EFAEFB CD第 14 题图4、已知:如图,ABC中,C=90,CM AB于M,AT均分BAC交 CM于 D,交 BC于 T,过D 作 DEMAD BETC。
倍长中线法(经典例题)教学内容

倍长中线法知识网络详解:中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用SAS 证全等(对顶角)倍长中线最重要的一点,延长中线一倍,完成SAS 全等三角形模型的构造。
【方法精讲】常用辅助线添加方法——倍长中线△ABC 中 方式1: 延长AD 到E ,AD 是BC 边中线 使DE=AD ,连接BE方式2:间接倍长作CF ⊥AD 于F , 延长MD 到N ,作BE ⊥AD 的延长线于E 使DN=MD , 连接BE 连接CN经典例题讲解:例1:△ABC 中,AB=5,AC=3,求中线AD 的取值范围D ABCEDAB C F EDC B AN D C B AM例2:已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF例4:已知:如图,在ABC ∆中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC.求证:AE 平分BAC ∠FE DA B CFEC ABD AB F D E C例5:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE自检自测:1、如图,△ABC 中,BD=DC=AC,E 是DC 的中点,求证,AD 平分∠BAE.2、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论.E D ABCF EAB C D3、如图,AD 为ABC ∆的中线,DE 平分BDA ∠交AB 于E ,DF 平分ADC ∠交AC 于F. 求证:EF CF BE >+4、已知:如图,∆ABC 中,∠C=90︒,CM ⊥AB 于M ,AT 平分∠BAC 交CM 于D ,交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE.第 14 题图 DF CBEADABCMTE。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
倍长中线法
知识网络详解:
中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采纳“倍长中线
法”增添辅助线.
所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.
倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用 SAS证全等(对顶角)
倍长中线最重要的一点,延长中线一倍,完成SAS全等三角形模型的构造。
【方法精讲】常用辅助线增添方法——倍长中线
A
A
B C
D △ ABC中方式1:延长AD到E,AD 是 BC边中线使DE=AD,
B C连接BE
D
方式 2:间接倍长
A
F
B D C
E
E
A
作 CF⊥ AD于 F,
M延长 MD到
N,
作 BE⊥ AD的延长线于 E B
D
使 DN=MD,
C
连接 BE
N
连接 CN
经典例题讲解:
例 1:△ ABC中, AB=5, AC=3,求中线 AD的取值范围
例 2:已知在△ ABC中, AB=AC, D 在 AB上, E 在 AC的延长线上, DE交 BC于 F,且 DF=EF,
求证: BD=CE
A
D
B
C
F
E
例 3:已知在△ ABC中,AD是 BC边上的中线, E 是 AD上一点,且 BE=AC,延长 BE交 AC于 F,
求证: AF=EF
A
F
E
B
D C
例 4:已知:如图,在ABC 中, AB AC ,D、E在BC上,且DE=EC,过D作 DF // BA
交 AE于点 F, DF=AC.
A
求证: AE均分BAC
F
B D E C
例 5:已知 CD=AB,∠ BDA=∠BAD, AE是△ ABD的中线,求证:∠ C=∠ BAE
A
B C
E D
自检自测:
1、如图,△ ABC 中, BD=DC=AC,E是 DC的中点,求证,A D均分∠ BAE.
2、在四边形 ABCD中, AB∥ DC, E 为 BC边的中点,∠ BAE=∠ EAF, AF 与 DC的延长线订
交于点 F。
尝试究线段 AB与 AF、CF之间的数目关系,并证明你的结论 .
A
D
B
E C
F
3、如图, AD为ABC 的中线,DE均分BDA 交AB于E,DF均分ADC 交AC于F.求证:
BE CF EF
A
E
F
B C
D
第14 题图
4、已知:如图,ABC中,C=90,CM AB于M,AT均分BAC交 CM于 D,交 BC于 T,
过D作DE
M
A
D B
E
T
C。
