回归分析练习题
数学建模竞赛统计回归分析相关练习题

1. 一个班有7名男性工人,他们的身高和体重列于下表
请把他们分成若干类并指出每一类的特征。
这里身高以米为单位,体重以千克为单位。
2. 有两种跳蚤共10只,分别测得它们四个指标值如表。
1)用距离判别法建立判别准则。
2)问(192, 287, 141, 198)和(197, 303, 170, 205)各属于哪一种?
求y 关于x 的线性回归方程,检验回归效果是否显著,并预测x=42℃时产量的估值
4.在研究化学动力学反应过程中,建立了一个反应速度和反应物 含量的数学模型,形式为
3
423125
3
211x x x x x y βββββ+++-
=
其中51,,ββ 是未知参数,321,,x x x 是三种反应物(氢,n 戊烷, 异构戊烷)的含量,y 是反应速度.今测得一组数据如表,试由 此确定参数51,,ββ
序号反应速度y 氢x1 n戊烷x2 异构戊烷x3
1 8.55 470 300 10
2 3.79 285 80 10
3 4.82 470 300 120
4 0.02 470 80 120
5 2.75 470 80 10
6 14.39 100 190 10
7 2.54 100 80 65
8 4.35 470 190 65
9 13.00 100 300 54
10 8.50 100 300 120
11 0.05 100 80 120
12 11.32 285 300 10
13 3.13 285 190 120 5.主成分与卡方检验已课件为主。
第七章 相关回归分析 思考题及练习题

实用价值越小。
13、在相关分析中,要求相关的两个变量( )
A、都是随机变量
B、都不是随机变量
C、其中因变量是随机变量 D、其中自变量是随机变量
14、在简单回归直线
中,
表示( ) A、当
增加一个单位时,
增加
的数量 B、当
增加一个单位时,
增加
的数量 C、当
增加一个单位时,
的平均增加值 D、当
增加一个单位时,
按一定数额变化时,变量
也随之近似地按固定的数额变化,那么,这时变量
和
之间存在着( )
A、正相关关系
B、负相关关系
C、直线相关关系 D、曲线相关关系
18、两个变量间的相关关系称为( )
A、单相关
B、无相关
C、复相关
D、多相关
19、如果两个变量之间的相关系数
,说明这两个变量之间存在( )。 A、低度相关关系 B、高度相关关系 C、完全相关关系 D、显著相关关系 20、已知
第七章 思考题及练习题
(一) 填空题
1、 1、 在相关关系中,把具有因果关系相互联系的两个变
量中起影响作用的变量称为_______,把另一个说明观察结果的
变量称为________。
2、 2、 现象之间的相关关系按相关的程度分有________相
关、________相关和_______相关;按相关的方向分有________
E、 E、回归方程实用价值大小的指标 10、现象之间相互联系的类型有( )
A、函数关系 B、回归关系 C、相关关系 D、随机关系 E、结构关系 11、相关关系种类( ) A、从相关方向分为正相关和负相关 B、从相关形态分为线性相关和非线性相关 C、从相关程度分为完全相关、不完全相关和零相关
第七章回归与相关分析练习及答案

第七章回归与相关分析一、填空题1.现象之间的相关关系按相关的程度分为、和;按相关的形式分为和;按影响因素的多少分为和。
2.两个相关现象之间,当一个现象的数量由小变大,另一个现象的数量,这种相关称为正相关;当一个现象的数量由小变大,另一个现象的数量,这种相关称为负相关。
3.相关系数的取值X围是。
4.完全相关即是关系,其相关系数为。
5.相关系数,用于反映条件下,两变量相关关系的密切程度和方向的统计指标。
6.直线相关系数等于零,说明两变量之间;直线相关系数等1,说明两变量之间;直线相关系数等于—1,说明两变量之间。
7.对现象之间变量的研究,统计是从两个方面进行的,一方面是研究变量之间关系的,这种研究称为相关关系;另一方面是研究关于自变量和因变量之间的变动关系,用数学方程式表达,称为。
8.回归方程y=a+bx中的参数a是,b是。
在统计中估计待定参数的常用方法是。
9. 分析要确定哪个是自变量哪个是因变量,在这点上它与不同。
10.求两个变量之间非线性关系的回归线比较复杂,在许多情况下,非线性回归问题可以通过化成来解决。
11.用来说明回归方程代表性大小的统计分析指标是。
12.判断一条回归直线与样本观测值拟合程度好坏的指标是。
二、单项选择题1.下面的函数关系是( )A销售人员测验成绩与销售额大小的关系 B圆周的长度决定于它的半径C家庭的收入和消费的关系 D数学成绩与统计学成绩的关系2.相关系数r的取值X围( )A -∞<r<+∞B -1≤r≤+1C -1<r<+1D 0≤r≤+13.年劳动生产率z(干元)和工人工资y=10+70x,这意味着年劳动生产率每提高1千元时,工人工资平均( )A增加70元 B减少70元 C增加80元 D减少80元4.若要证明两变量之间线性相关程度是高的,则计算出的相关系数应接近于( )A+1 B 0 C 0.5 D [1]5.回归系数和相关系数的符号是一致的,其符号均可用来判断现象( ) A线性相关还是非线性相关 B正相关还是负相关C完全相关还是不完全相关 D单相关还是复相关6.某校经济管理类的学生学习统计学的时间(x)与考试成绩(y)之间建=a+b x。
回归分析练习试题和参考答案解析

1 下面是7个地区2000年的人均国内生产总值(GDP)和人均消费水平的统计数据:求:(1)人均GDP作自变量,人均消费水平作因变量,绘制散点图,并说明二者之间的关系形态。
(2)计算两个变量之间的线性相关系数,说明两个变量之间的关系强度。
(3)求出估计的回归方程,并解释回归系数的实际意义。
(4)计算判定系数,并解释其意义。
α=)。
(5)检验回归方程线性关系的显著性(0.05(6)如果某地区的人均GDP为5000元,预测其人均消费水平。
(7)求人均GDP为5000元时,人均消费水平95%的置信区间和预测区间。
解:(1)可能存在线性关系。
(2)相关系数:系数a模型非标准化系数标准系数t Sig.相关性B标准误差试用版零阶偏部分1(常量).003人均GDP.309.008.998.000.998.998.998 a. 因变量: 人均消费水平有很强的线性关系。
(3)回归方程:734.6930.309y x=+系数a模型非标准化系数标准系数t Sig.相关性回归系数的含义:人均GDP没增加1元,人均消费增加元。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型非标准化系数标准化系数t显著性B标准误Beta1(常量)人均GDP(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(4)模型汇总模型R R 方调整 R 方标准估计的误差1.998a.996.996a. 预测变量: (常量), 人均GDP。
人均GDP对人均消费的影响达到%。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
模型摘要模型R R 方调整的 R 方估计的标准差1.998(a)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(5)F检验:Anova b模型平方和df均方F Sig.1回归.6801.680.000a 残差5总计.7146a. 预测变量: (常量), 人均GDP。
回归分析练习题及参考答案
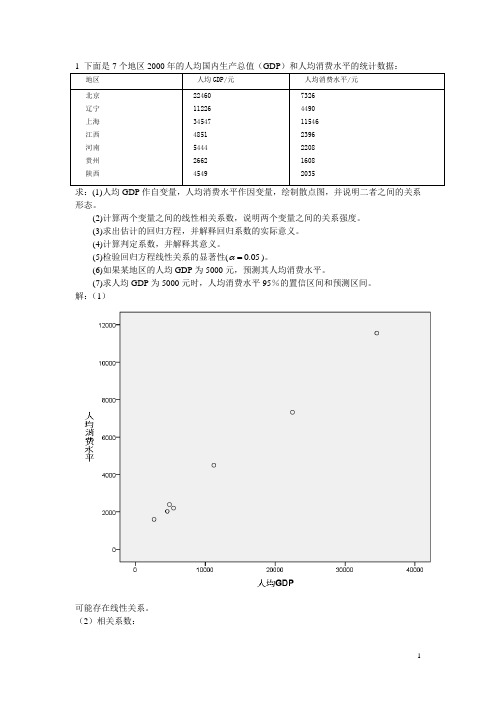
1 下面是7个地区2000年的人均国内生产总值(GDP)和人均消费水平的统计数据:地区人均GDP/元人均消费水平/元北京辽宁上海江西河南贵州陕西 224601122634547485154442662454973264490115462396220816082035求:(1)人均GDP作自变量,人均消费水平作因变量,绘制散点图,并说明二者之间的关系形态。
(2)计算两个变量之间的线性相关系数,说明两个变量之间的关系强度。
(3)求出估计的回归方程,并解释回归系数的实际意义。
(4)计算判定系数,并解释其意义。
(5)检验回归方程线性关系的显著性(0.05α=)。
(6)如果某地区的人均GDP为5000元,预测其人均消费水平。
(7)求人均GDP为5000元时,人均消费水平95%的置信区间和预测区间。
解:(1)可能存在线性关系。
(2)相关系数:(3)回归方程:734.6930.309y x=+回归系数的含义:人均GDP没增加1元,人均消费增加0.309元。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型非标准化系数标准化系数t 显著性B 标准误Beta1 (常量)734.693 139.540 5.265 0.003人均GDP(元)0.309 0.008 0.998 36.492 0.000 a. 因变量: 人均消费水平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(4)模型汇总模型R R 方调整 R 方标准估计的误差1 .998a.996 .996 247.303a. 预测变量: (常量), 人均GDP。
人均GDP对人均消费的影响达到99.6%。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
5相关分析和回归分析练习题

第五章相关分析和回归分析练习题一、单项选择题1、相关分析研究的是()。
A、变量间的相互依存关系B、变量间的因果关系C、变量间严格的一一对应关系D、变量间的线性关系2、测定变量之间相关关系密切程度的主要方法是()。
A、相关表B、相关图C、相关系数D、定性分析3、下列情况中,称为正相关的是()。
A、随一个变量增加,另一个变量相应减少B、随一个变量减少,另一个变量相应增加C、随一个变量增加,另一个变量相应增加D、随一个变量增加,另一个变量不变4、相关系数r取值范围()。
A、︱r︱<∞B、︱r︱≤1C、r<1D、r≤0.55、相关系数等于零表明两个变量()。
A、是严格的函数关系B、不存在相关关系C、不存在线性相关关系D、存在曲线相关关系6、现象之间相互依存关系的程度是对等的,则相关系数()。
A、越小于0B、越接近-1C、越接近于1D、越接近于07、相关关系中,两个变量的关系是对待的,从而变更x对变量y的相关,同变量y对变量x的相关()。
A、是同一问题B、不一定相同C、有联系但是不是一个问题D、完全不同8、若居民收入增加,居民消费额也增加,则居民收入和居民消费额之间()。
A、无相关B、存在正相关C、存在负相关D、无法判断是否相关9、产品产量与单件成本的相关系数是-0.80,单位成本与利润率的相关系数是-0.94,产量与利润率之间的相关系数是0.89,因此()。
A、产量与利润率的相关程度最高B、单位成本与利润率的相关程度最高C、产量与单位成本的相关程度最高D、反映不出哪对变量的相关程度最高10、在回归分析中,自变量同因变量的地位不同,两变量y和x回归和x对y回归()。
A、是同一问题B、不一定相同C、有联系但不是一个问题D、完全不同11、回归分析中的简单回归是指()。
A、两上变量之间的回归B、变量之间的线性回归C、两个变量之间的线性回归D、变量之间的简单回归12、当自变量的数值确定后,因变量的数值也随之完全确定,这种关系属于()。
01练习题6(相关系数与回归分析)
练习题6(相关系数与回归分析)1某电视台非常关心新闻节目的受欢迎程度;电视节目的受欢迎程度由一套评估体系来决定,这个评估体系对每个被评估的节目评级:由1(最低)到10(最高)。
某电视台认为在新闻节目之前的节目的受欢迎程度会影响到新闻节目的受欢迎程度。
为此,他们搜集了一组30个样本,其中包含两个变量:x-新闻节目之前的节目评级;y-新闻节目的评级,数据列于为研究x与y二者之间的关系,计算相关系数,并对其进行检验。
3 使用四川绵阳地区3年生中山柏的数据“中山柏.sav”,分析月生长量与平均气温、月降雨量、月平均日照时数、月平均湿度这4个气候因素哪个因素有关?回归分析:4 零售商要了解每周的广告费X及消费额Y之间关系,记录如下数据:画出散点图,并在Y对X回归为线性的假定下,用最小二乘法算出一元回归方程.5 某厂生产某产品,其成本费用(Y,万元)与劳动量(X1,千小时)及原材料价格(X 2,万元/万吨)有密切关系。
下面列出了2002年1月~2003年6月的成本、劳动量、原材料价格资料。
要求:(1)建立二元线性回归方程,对回归系数b1、b2进行合理的解释。
(2)对所建立的回归方程进行显著性检验;(3)假定2003年7月份劳动量X1=1.19千小时,X2=2.31万元/万吨,试预测2003年7月份的成本费用。
6 用第2题资料,计算身高与坐高、体重、胸围、肩宽和骨盆宽等变量的Pearson相关关系,并用逐步回归建立方程。
(引入原则P<0.05,剔除原则P>0.051)7用第1题资料,假定模型为:y=β0+β1Xi+εi i= 1,…,30用最小二乘法估计模型参数,建立线性回归模型,对回归系数进行显著性检验,对β1的置信水平作95%的区间估计。
对x=8时的y值作预测,并作95%的预测区间。
8 家庭信用卡消费多寡与家庭年收入及家庭人口有关,具体数据如下表,要求:①做消费金额与家庭人口,消费金额与年收入的散点图;②因变量、自变量分别是什么;③建立回归方程,讨论这三者之间的关系;④讨论哪个因素对因变量影响大,理由是什么?被调查对象的家庭年收入(万元)、家庭人口和信用卡消费的金额(元)。
回归方程大题练习题
回归方程大题练习题回归方程大题练习题回归分析是一种统计方法,用于研究变量之间的关系。
通过建立回归方程,我们可以预测一个因变量如何随着一个或多个自变量的变化而变化。
在实际应用中,回归分析常用于预测销售额、人口增长率、股票价格等。
下面我们来看几个回归方程的大题练习题,通过解答这些问题,我们可以更好地理解回归方程的应用。
1. 一家餐馆想预测每天的顾客数量与广告投入之间的关系。
他们收集了过去一年的数据,发现每天的广告投入(以元为单位)与顾客数量(以人数为单位)之间存在一定的关系。
现在他们想知道,如果他们每天投入1000元的广告费用,预计会有多少顾客光顾餐馆?解答:我们可以建立一个简单的线性回归方程来预测顾客数量。
假设顾客数量(Y)是广告投入(X)的线性函数,即Y = a + bX。
通过回归分析,我们可以得到回归方程的系数a和b。
根据给定的问题,我们已经知道广告投入为1000元,那么代入回归方程即可得到预测的顾客数量。
2. 一家电子产品公司想预测某款产品的销量与价格之间的关系。
他们收集了过去一年的数据,发现产品的价格(以元为单位)与销量(以件为单位)之间存在一定的关系。
现在他们想知道,如果他们将产品的价格降低10%,预计会有多少增加的销量?解答:同样地,我们可以建立一个线性回归方程来预测销量。
假设销量(Y)是价格(X)的线性函数,即Y = a + bX。
通过回归分析,我们可以得到回归方程的系数a和b。
根据给定的问题,我们已经知道价格降低10%,那么代入回归方程即可得到预测的销量增加。
3. 一家保险公司想预测客户的保险费用与年龄之间的关系。
他们收集了一组数据,包括客户的年龄和保险费用。
现在他们想知道,如果一个客户的年龄增加一岁,预计保险费用会增加多少?解答:同样地,我们可以建立一个线性回归方程来预测保险费用。
假设保险费用(Y)是年龄(X)的线性函数,即Y = a + bX。
通过回归分析,我们可以得到回归方程的系数a和b。
回归分析与独立性检验练习
回归分析与独立性检验综合训练回归分析: 热身练习1. 在画两个变量的散点图时,下面哪个叙述是正确的( )(A)预报变量在x 轴上,解释变量在y 轴上 (B)解释变量在x 轴上,预报变量在y 轴上 (C)可以选择两个变量中任意一个变量在x 轴上 (D)可以选择两个变量中任意一个变量在y 轴上 2. 一位母亲记录了儿子3~9岁的身高,由此建立的身高与年龄的回归模型为y=7.19x+73.93用这个模型预测这个孩子10岁时的身高,则正确的叙述是( ) A.身高一定是145.83cm; B.身高在145.83cm 以上; C.身高在145.83cm 以下; D.身高在145.83cm 左右.3. 两个变量y 与x 的回归模型中,分别选择了4个不同模型,它们的相关指数2R 如下 ,其中拟合效果最好的模型是( )A.模型1的相关指数2R 为0.98 B.模型2的相关指数2R 为0.80 C.模型3的相关指数2R 为0.50 D.模型4的相关指数2R 为0.254. 若有一组数据的总偏差平方和为100,相关指数为0.5,则期残差平方和为_______ 回归平方和为____________5.工人月工资(元)依劳动生产率(千元)变化的回归直线方程为ˆ6090yx =+,下列判断正确的是() A.劳动生产率为1000元时,工资为50元 B.劳动生产率提高1000元时,工资提高150元 C.劳动生产率提高1000元时,工资提高90元 D.劳动生产率为1000元时,工资为90 独立性检验: 热身练习1.下面是一个2×2列联表:则表中a 、b 处的值分别为( )A .94、96B .52、50C .52、60D .54、52 2.下列关于等高条形图的叙述正确的是( ).A .从等高条形图中可以精确地判断两个分类变量是否有关系B .从等高条形图中可以看出两个变量频数的相对大小C .从等高条形图可以粗略地看出两个分类变量是否有关系D .以上说法都不对3.关于分类变量x 与y 的随机变量K 2的观测值k ,下列说法正确的是( ).A .k 的值越大,“X 和Y 有关系”可信程度越小B .k 的值越小,“X 和Y 有关系”可信程度越小C .k 的值越接近于0,“X 和Y 无关”程度越小D .k 的值越大,“X 和Y 无关”程度越大 4.若由一个2×2列联表中的数据计算得k =4.013,那么在犯错误的概率不超过________的前提下认为两个变量之间有关系.5.为了判断高中三年级学生是否选修文科与性别的关系,现随机抽取50名学生,得到如下2×2列联表:理科 文科 男 13 10 女720已知P (K 2≥3.841)≈0.05,P (K 2≥5.024)≈0.025.根据表中数据,得到k =50×13×20-10×7223×27×20×30≈4.844.则认为选修文科与性别有关系出错的可能性约为________.6.第16届亚运会于2010年11月12日至27日在中国广州进行,为了搞好接待工作,组委会招幕了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余人不喜爱运动.(1)根据以上数据完成以下2×2列联表:喜爱运动 不喜爱运动 总计 男 10 16 女 614 总计30(2) 基础练习1.下列变量间的关系,不是函数关系的是( ) A .角度和它的余弦值 B .正方形的边长和面积C .正多边形的边数和顶点的角度之和D .人的年龄和身高2. “回归”一词是在研究子女的身高与父母的身高之间的遗传关系时,由高尔顿提出的.他的研究结果是子代的平均身高向中心回归.根据他提出的结论,在儿子的身高y 与父亲的身高x 的回归方程ˆya bx =+中,b ( )A .在(-1,0)内B .等于0C .在(0,1)内D .在[1,)+∞内 3.已知回归直线斜率的估计值为1.23,样本的中心点为(4,5),则回归直线方程为( )A .ˆ 1.234yx =+ B .ˆ 1.235y x =+ C .ˆ 1.230.08y x =+ D .ˆ0.08 1.23y x =+ 4.对于回归直线方程ˆ 4.67 2.85yx =+,当21x =时,y 的估计值为 5.一所大学图书馆有6台复印机供学生使用管理人员发现,每台机器的维修费用与其使用的时间有一定的关系,根据去年一年的记录,得到每周使用时间(单位:小时)与年维修费用(单位:元)的数据如下:时间 33 21 31 37 46 42 费用 16 14 25 29 38 34则使用时间与维修费用之间的相关系数为6.某种产品的广告支出与销售额(单位:百万元)之间有如下的对应关系x 2 4 5 6 8 y3040605070(1)假定x 与y 之间具有线性相关关系,求回归直线方程.(2)若实际销售额不少于60百万元,则广告支出应该不少于多少?7.下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x (吨)与相应的生产能耗y (吨标准煤)的几组对照数据(1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程ˆˆy bxa =+; (3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值:32.5435464.566.5⨯+⨯+⨯+⨯=) 8.下表为收集到的一组数据:(1)作出x 与y 的散点图,猜测(2)建立x 与y 的关系,预报回归模型并计算残差; (3)利用所得模型,预报x =40时y 的值.综合练习:一、选择题1.已知回归直线的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是( ) Ay ∧=1.23x +4 By ∧=1.23x+5 C y ∧=1.23x+0.08 D y ∧=0.08x+1.232.回归分析中,相关指数R 2的值越大,说明残差平方和( )A 越小B 越大C 可能大也可能小D 以上都不对3.为研究变量x 和y 的线性相关性,甲、乙二人分别作了研究,利用线性回归方法得到回归直线方程1l 和2l ,两人计算知x 相同,y 也相同,下列正确的是()A 1l 与2l 一定平行B 1l 与2l 相交于点),(y xC 1l 与2l 重合D 无法判断1l 和2l 是否相交 4.变量x 与y 具有线性相关关系,当x 取值16,14,12,8时,通过观测得到y 的值分别为11,9,8,5,若在实际问题中,y 的预报最大取值是10,则x 的最大取值不能超过( )A 16B 17C 15D 12二、填空题5.在回归分析中,代表了数据点和它在回归直线上相应位置的差异的是____________6.利用独立性检验来考虑两个分类变量X 和Y 是否有关系时,通过查阅下表来确定断言“X 和Y 有关系”的可信度。
第八章-相关与回归分析练习题
第八章-相关与回归分析练习题第八章相关与回归分析一、单选题1.相关分析研究的是()A、变量间相互关系的密切程度B、变量之间因果关系C、变量之间严格的相依关系D、变量之间的线性关系2.若变量X的值增加时,变量Y的值也增加,那么变量X和变量Y之间存在着()。
A、正相关关系 B、负相关关系 C、直线相关关系 D、曲线相关关系3.若变量X的值增加时,变量Y的值随之下降,那么变量X和变量Y之间存在着()。
A、正相关关系 B、负相关关系 C、直线相关关系 D、曲线相关关系4.相关系数等于零表明两变量()。
A.是严格的函数关系B.不存在相关关系C.不存在线性相关关系D.存在曲线线性相关关系5.相关关系的主要特征是()。
A、某一现象的标志与另外的标志之间的关系是不确定的B、某一现象的标志与另外的标志之间存在着一定的依存关系,但它们不是确定的关系C、某一现象的标志与另外的标志之间存在着严格的依存关系D、某一现象的标志与另外的标志之间存在着不确定的直线关系 6.时间数列自身相关是指()。
A、两变量在不同时间上的依存关系 B、两变量静态的依存关系C、一个变量随时间不同其前后期变量值之间的依存关系D、一个变量的数值与时间之间的依存关系7.如果变量X和变量Y之间的相关系数为负1,说明两个变量之间()。
A、不存在相关关系 B、相关程度很低 C、相关程度很高 D、完全负相关8.若物价上涨,商品的需求量愈小,则物价与商品需求量之间()。
A、无相关 B、存在正相关 C、存在负相关 D、无法判断是否相关 9.相关分析对资料的要求是()。
A.两变量均为随机的 B.两变量均不是随机的 C、自变量是随机的,因变量不是随机的 D、自变量不是随机的,因变量是随机的 10.回归分析中简单回归是指()。
A.时间数列自身回归 B.两个变量之间的回归 C.变量之间的线性回归 D.两个变量之间的线性回归11.已知某工厂甲产品产量和生产成本有直线关系,在这条直线上,当产量为1000时,其生产成本为30000元,其中不随产量变化的成本为6000元,则成本总额对产量的回归方程为()A. y=6000+24xB. y=6+0.24xC. y=24000+6xD. y=24+6000x12.直线回归方程中,若回归系数为负,则() A.表明现象正相关 B.表明现象负相关C.表明相关程度很弱D.不能说明相关方向和程度二、多项选择题1.下列属于相关关系的有()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
万元.
8、(2015·重庆卷)随着我国经济的发展,居民的 储蓄存款逐年增长.设某地区城乡居民人民币储 蓄存款(年底余额)如下表:
年份
2010 2011 2012 2013 2014
时间代号t
1 2 3 45
储蓄存款y(千亿元 5 6 7 8 10
主题班会
珍爱河湖 保护生态
--------高二(31)班
1.在两个变量的回归分析中,作散点图是为了(C )
A.直接求出回归直线方程 B.直接求出回归方程 C.根据经验选定回归方程的类型 D.估计回归方程的参数
2、四名同学根据各自的样本数据研究变量x,y
之间的相关关系,并求得回归直线方程,分别 得到以下四个结论:
4、已知x和y之间的一组数据 x0123
y1357
则y与x的线性回归方程 yˆ bˆx aˆ必过点(D)
A.(2,2)
B.( 3 , 0) 2
C.(1,2)
3 D.(2
, 4)
5、(2014·重庆卷)已知变量x与y正相关,且由观
测数据算得样本平均数 x =3, y =3.5,则
由该观测数据算得的线性回归方程可能是(A)
根据上表可得回归直线方程 yˆ bˆx aˆ,其
中 bˆ =0.76,据此估计,该社区一户年收入为
15万元家庭的年支出为(B )
A.11.4万元
B.11.8万元
C.12.0万元
D.12.2万元
7、为了均衡教育资源,加大对偏远地区的教育 投入,调查了某地若干户家庭的年收入x(单位: 万元)和年教育支出y(单元:万元),调查显示年 收入x与年教育支出y具有线性相关关系,并由 调查数据得到y到x的回归直线方程: y=0.15x+0.2.由回归直线方程可知,家庭年收
A. yˆ=0.4x+2.3
B. yˆ=2x-2.4
C. yˆ=-2x+9.5
D. yˆ=-0.3x+4.4
6、(2015·福建卷)为了解某社区居民的家庭年收入 与年支出的关系,随机调查了该社区5户家庭,得 到如下统计数据表:
收入x(万元) 8.2 8.6 10.0 11.3 11.9
支出y(万元) 6.2 7.5 8.0 8.5 9.8
i 1
5
b
ti yi 5t y
i 1
5
ti 2
2
5t
120 5 55
3 5
7.2 32
1.2
i 1
a y b t 7.2 1.2 3 3.6
y 1.2t 3.6
(2)2017年对应的时间代号t=8,即:
y 1.28 3.6 13.2(千亿元)
答:2017年的人民币储蓄存款为13.2千亿元。
ቤተ መጻሕፍቲ ባይዱ
(1)求y关) 于t的回归方程 yˆ bˆt aˆ ; (2)用所求回归方程预测该地区2017年的人 民币储蓄存款.
解:(1)
t 1 2 3 4 5 3, y 5 6 7 8 10 7.2
5
5
5
ti yi 1 5 2 6 3 7 48 510 120
i 1
5
ti2 12 22 32 42 52 55
变量研究得到一组随机样本数据,
运用Excel软件计算得 yˆ =0.577x-0.448(x为
人的年龄,y%为人体脂肪含量).对年龄为37岁
的人来说,下面说法正确的是(C )
A.年龄为37岁的人体内脂肪含量都为20.90% B.年龄为37岁的人体内脂肪含量为21.0% C.年龄为37岁的人群中的大部分人的体内脂肪 含量为20.90% D.年龄为37岁的大部分的人体内脂肪含量为31.5%
①y与x负相关且 yˆ =2.347x-6.423 ②y与x负相关且 yˆ =-3.476x-5.648; ③y与x正相关且 yˆ =5.437x+8.493; ④y与x正相关且 yˆ =-4.326x-4.578.
其中一定不正确的结论的序号是(D )
A.①② B.②③ C.③④ D.①④
3、某医学科研所对人体脂肪含量与年龄这两个
