2007年北京市中学生数学竞赛初二
4. B.
由[ 3
x+ 7
7
]
=
4
,知
4
≤3 x + 7
7
<
5
,得
7
≤
x
<
28 3
.
故
x
=7
,8
,9.
5. A.
如图 6 ,过 E 作 EF
⊥BD 于 F. 易 知 点 F
为 BD 中点.
又 A 、B 、F、E 四点
共圆 ,故
DE·DA = DF·DB ,
图6
即 DE·8 = 2 5 ×4 5 ] DE = 5.
令 t=
a b
,则 4 t2 + (8 -
k) t + 4 = 0.
解得
t
=
1 8
[
(k
-
8)
+
k ( k - 16) ] .
9. 6 223.
设正方形边长 a = 2 007 , ∠D′DC =α. 则 ∠BD′E = 2α, CD′= atan α, BD′= a (1 - tan α) .
所以 , △BD′E 的周长为
2 ac
2 ab
之和恰等于 1 ,求证 :这三个分数的值有两个
为1 ,一个为 - 1.
41
四 、( 10 分) 如 图
5 , 在 △ABC 中 ,
∠ABC = 46°, D 是 边
BC 上 的 一 点 , DC =
AB , ∠DAB = 21°. 试
确定 ∠CAD 的度数.
图5
五 、(15 分) 若对于任意 n 个连续正整数
AC 、AB 上的点 ,且 A P
= PQ = QB = BC. 则
图3
∠PCQ = .
4. 化简
1 a
+
1 b
1
+
1 a
+
1 c
1
+
1 a
1
+
1 b
+
1 d
1
+
1 a
1+
1 b
1
+
1 c
-
1
+
1 a
1
+
1 b
1+
1 c
1
+
1 d
的值为 .
5. 如图 4 ,在长
方 形 ABCD 中 , E、
191 504
.
则这三个数之和等于
(
)
.
(A) 27 (B) 24 (C) 21 (D) 18 3. 分母是 2 007 的正的最简真分数有 ( ) 个.
(A) 675 (B) 1 326 (C) 1 329 (D) 1 332 4. 对于实数 x ,符号 [ x ] 表示不大于 x
的最大整数 , 例如 , [ 3114 ] = 3 , [ - 7159 ] =
© 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved.
42
中等数学
故
S △BDE
=
1 2
D E·AB
= 10.
二 、1. 1 008 017.
设第 i 个拐角处的数为 ai . 显然 ,
a1 = 2 , a2 i = a2 i - 1 + i ,
a2 i + 1 = a2 i + ( i + 1) . 因 2 007 = 2 ×1 003 + 1 ,所以 ,
a2 007 = 1 + 2 (1 + 2 + …+ 1 003) + 1 004 = 1 0042 + 1 = 1 008 017.
a (1 - tan α) (1 + tan 2α+ sec 2α)
=
a·cos
αcos
sin α
α·cos
2α+ sin 2α+ 1 cos 2α
=
a·cos
αcos
sin α
α·2cos2coαs2 +α2-sinsiαn2·αcos
α
= 2 a = 6 223. 10. 20 或 119. 设 x2 + ( x + 1) 2 = v2 ,则(2 x + 1) 2 = 2v2 - 1. 令 u = 2 x + 1 ,则 u2 - 2 v2 = - 1. 其为佩 尔方程 ,其基本解为 ( u0 , v0 ) = (1 ,1) . 其全部正整数解可由
(1 +
1) c
=
-
1+
(1 +
1 a
)
(1
+
1 b
)
(1
+
1 c
)
(1
+
1 d
)
.
519. 联结 FP 并延长交 AD 于点 Q ,显然 ,点 Q 是 AD 的中点. 则
PQ =
1 2
AE =
1 4
AB
, FP =
3 4
AB .
所以
, MN
=
3 5
BC.
故
= S 四边形MFNP
1 2
FP·MN
=
-
1.
(2) 若 c + a - b = 0 ,同理可得
b2 + c2 2 bc
a2
=1
, c2
+ a2 2 ac
b2 =
- 1,
a2 + b2 2 ab
c2
= 1.
(3) 若 b + c - a = 0 ,同理可得
b2 + c2 2 bc
a2 =
-
1 , c2
+ a2 2 ac
b2 = 1 ,
a2 + b2 2 ab
=
1 2
×3 4
×3 5
S 长方形ABCD
= 9.
三 、由题设
b2 + c2 2 bc
a2
+
c2
+ a2 2 ac
b2 +
a2 + b2 2 ab
c2 = 1 ,
即
b2 + c2 2 bc
a2 - 1
+
a2 + c2 2 ac
b2 - 1
+
a2 + b2 2 ab
c2
+1
=0
]
b2 + c2 - a2 - 2 bc 2 bc
- 8. 则关于
x 的方程
3x +7 7
= 4 的整数根
有 ( ) 个.
(A) 4 (B) 3 (C) 2 (D) 1 5. 如图 1 ,已知长方形的长为 8 ,宽为 4 , 将长方形沿一条对角线折起压平. 则重叠部 分 (阴影三角形) 的面积是 ( ) .
图1
7.
2 3
,
2 - 1 ,1 - 2
2. B. 设此三个连续正整数为 n - 1 , n , n + 1. 则
191 504
=
1 n-
1
+
1 n
+
n
1 +
1
=
3 n2 n ( n2 -
1 1)
,
即 191 n3 - 1 512 n2 - 191 n + 504 = 0.
因式分解得( n - 8) (191 n2 + 16 n - 63) = 0.
c2
= 1.
综合 (1) 、(2) 、(3) 可得 ,三个分数
b2 + c2 - a2 、c2 + a2 - b2 、a2 + b2 - c2
2 bc
2 ac
2 ab
的值有两个为 1 ,一个为 - 1.
2.
令 x = 2 y ,代入原方程得
6 2 y3 + 4 2 y2 - 17 2 y + 18y - 6 + 5 2 = 0.
易知
y=
1 3
满足条件.
故
x1
=
2 3
.
于是
,
3 x3 + 2 2 x2 - (17 - 9 2) x - (6 - 5 2)
= (x-
2 3
)
(3
x2
+
3
2x +9
2 - 15) .
c-
b) +
c ( a +
b + c) ( a + 2 abc
b-
c)
=0
]
(a+ b-
c) ( ab -
ac -
a2 + ab 2 abc
bc -
b2 +
ac +
bc + c2)
=0
]
(a+ b-
c) ( c2 2 abc
(a-
b) 2 ] = 0
]
(a+ b-
c) ( c + a 2 abc
b) ( c -
2008 年第 1 期
(1) 若 a + b - c = 0 ,则
b2 + c2 2 bc
a2
=
b2
+
c2 - ( b 2 bc
-
c) 2 = 1 ;
c2 + a2 2 ac
(2021年整理)分式的化简求值经典练习题(带答案)
分式的化简求值经典练习题(带答案)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（分式的化简求值经典练习题(带答案)）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为分式的化简求值经典练习题(带答案)的全部内容。
分式的化简一、比例的性质:⑴比例的基本性质:a c ad bc bd=⇔=，比例的两外项之积等于两内项之积.⑵更比性(交换比例的内项或外项）: ( ) ( )( )a bc d a c d cb d b a d bc a ⎧=⎪⎪⎪=⇒=⎨⎪⎪=⎪⎩交换内项 交换外项 同时交换内外项 ⑶反比性(把比例的前项、后项交换）:a c b d b d a c=⇒=⑷合比性：a c a b c d b d b d ±±=⇒=，推广：a c a kb c kd b d b d±±=⇒=(k 为任意实数）⑸等比性:如果....a c m b d n ===，那么......a c m a b d n b+++=+++（...0b d n +++≠）二、基本运算分式的乘法：a c a c b d b d⋅⋅=⋅分式的除法：a c a d a db d bc b c⋅÷=⨯=⋅乘方：()n n n nn a a aa a aa ab b bb b bb b ⋅=⋅=⋅个个n 个＝（n 为正整数）知识点整数指数幂运算性质： ⑴mnm na a a +⋅=(m 、n 为整数） ⑵()m nmna a =（m 、n 为整数) ⑶()n n nab a b =(n 为整数）⑷m n m na a a -÷=（0a ≠，m 、n 为整数)负整指数幂：一般地,当n 是正整数时，1nnaa -=（0a ≠)，即na -（0a ≠)是na 的倒数分式的加减法法则：同分母分式相加减，分母不变，把分子相加减，a b a b ccc+±=异分母分式相加减,先通分，变为同分母的分式再加减，a c ad bc ad bc bdbdbdbd±±=±=分式的混合运算的运算顺序：先算乘方，再算乘除，后算加减，如有括号，括号内先算．结果以最简形式存在。
分式的恒等变形精讲精练
一、化分式为部分分式的和【例1】 （4级）(第10届华罗庚金杯决赛)下面的等式成立：22465()()x y x y x y A x y B -+--=--++，求A 、B .【例2】 （4级）若代数式(1)(2)(3)x x x x p ++++恰好能分解为两个二次整式的乘积(其中二次项系数均为1，且一次项系数相同)，则p 的最大值是 .【例3】 （5级）若213111a M Na a a -=+--+，求M 、N 的值.【例4】 （3级）(06年宁波市重点中学提前考试招生试题)已知2a x +与2b x -的和等于244xx -，求a ，b .【例5】 （4级）(2004年第15届培训题)已知正整数,a b 满足1114a b +=，则a b +的最大值是 ．【例6】 （4级）若对于3±以外的一切数，28339m n xx x x -=+--均成立，求mn .【例7】 （5级）若关于x 的恒等式222Mx N c x x x a x b +=-+-++中，22Mx Nx x ++-为最简分式，且有a b >，a b c +=， 求N .【例8】 （4级）将269x -化为部分分式.分式恒等变形（竞赛部分）【例9】 （4级）化21(1)(2)x x x ---为部分分式．【例10】 （4级）将下列分式写成部分分式的和的形式：2342x x x +--.【例11】 （4级）将下列分式写成部分分式的和的形式：32222361(1)(3)x x x x x -++++.【例12】 （5级）将下列分式写成部分分式的和的形式：32241338(1)(2)(1)x x x x x x -+++--.【例13】 （4级）计算：2132x x x -++262x x ---2104x x ---．【例14】 （4级）将下列分式写成部分分式的和的形式：4322231(1)(1)x x x x x ++-+-.二、分式的恒等证明【例15】 （4级）（1994广东潮州市初中数学竞赛）求证：()()332222222222a a a ab b a ab b a ab b a ab b a b a b ⎛⎫⎛⎫++--+-=++-+ ⎪⎪-+⎝⎭⎝⎭【例16】 （5级）已知x 、y 、z 为三个不相等的实数，且111x y z y z x+=+=+，求证：2221x y z =.【例17】 （5级）已知：a c b d=，求证：22222222a b c d a b c d abcd ----++++++=.【例18】 （5级）若a b x a b -=+，b c y b c -=+，c az c a-=+，求证：(1)(1)(1)(1)(1)(1)x y z x y z +++=---【例19】 （5级）若1abc =，求证：1111a b ca ab b bc c ca++=++++++.【例20】 （5级）(2003年第1届“创新杯”数学邀请赛初中二年级第二试试题)已知1111a b ca ab b bc c ca++=++++++，求证：1abc =.【例21】 （6级）(1986年中国数学奥林匹克竞赛赛前培训试题) 已知2220a b cbc a ca b ab c ++=---，求证：()()()2222220a b cbc a ca b ab c ++=---.【例22】 （6级）已知0a b cb c c a a b++=---，求证：2220()()()a b c b c c a a b ++=---.【例23】 (5级)(2002年北京市中学生数学竞赛初二复赛题二)已知0abc ≠，证明：下列四个数3333()()()(),,,a b c b c a c a b a b c abc abc abc abc++------中至少有一个不小于6．【例24】 （5级）已知223344371642a b a b a b a b x y x y x x x y +=+=+=+=，，，，求证：5520a bx y+=。
2007年初二数学竞赛答案
2007年江干区数学小能手竞赛8年级解答一、选择题（40分）题号 1 2 3 4 5 6 7 8 答案DABDCCAB二、填空题（40分）题号 9 10 11 12 13 14 15 16 答案 1711921237.444110或914.44，提示：如图，连接OC ，就有（x+10）: y =20: 16,(16+y ):x =20:10,可求得x =20, y =24.三、解答题（40分） 17．18．解：由题意知△DEF 为等腰直角三角形，△ABE ≌△BFE ， ∵DE =1，∴DF =1，AE =EF =2,AD=BC =2+1（4分） 设AB=x ，则CF = x －1 ∵222BF CF BC =+∴222(1)(12)x x =-++，解得x =2+2（4分）∴矩形ABCD 的面积=（2+2）（2+1）=4+32（2分）（第17题）（第18题）19.解：设两辆公交车发车的间隔时间x为分。
（1分）由题意得方程11113()105x x-=-，（5分）解得x=8，（2分）经检验，x=8是原方程的解且符合题意。
（1分）答：（略）（1分）（本题解法多样，本解法的关键是把两车的间隔距离看作1，利用速度的3倍关系列方程）20．如图，将相邻的圆圈染成一黑一白，则16个圆圈染成如图的颜色.（4分）由题意，旅游的路线必为：白→黑→白→黑→白→黑…，或黑→白→黑→白→黑→白….（3分）由于有 16个城市，因此，应是黑点、白点各8个.但图中的白点有7个，黑点有9个，所以，不可能找到一条不重复地走遍这16个城市的旅游路线.（3分）（20题）。
2018年北京市中学生数学竞赛初二试题(含答案)
2018年北京市中学生数学竞赛初二试题一、选择题（每小题5分，共25分）1．在1～100这100个自然数中，质数所占的百分比是（）．（A）25% （B）24% （C）23% （D）22%2．一个三角形的三边长都是整数，它的周长等于10，则这个三角形是（）．（A）直角三角形（B）钝角三角形（C）恰有两边相等的三角形（D）恰有一个内角为60°的三角形3．已知n为正整数，S=1+2+…+n．则S的个位数字不能取到的数字是（）．（A）0，1，2，3 （B）3，4，5，6（C）3，5，6，8 （D）2，4，7，94．如图1，四边形ABCD的对角线AC、BD相交于点O．S△AOB=4，S△COD=9．则S四边形的最小值是（）．ABCD（A）22 （B）25 （C）28 （D）32（1）(2) (3)5．如果│a-b│=1，│b+c│=1，│a+c│=2，则│a+b+2c│等于（）．（A）3 （B）2 （C）1 （D）0二、填空题（每小题7分，共35分）1．如图2，大圆的两条直线AC、BC垂直相交于点O，分别以边AB、BC、CD、DA为直径向大圆外侧作四个半圆，图中四个“月形”阴影的总面积是2cm2．•则大圆的半径等于_______cm．2．2 005被两位的自然数去除，可能得到的最大余数是_______．3．已知a2+bc=14，b2-2bc=-6．则3a2+4b2-5bc=_________．4．如图3，在凸六边形ABCDEF中，AD、BE、CF三线共点于O，•每相邻三个顶点所组成的三角形的面积都等于1，则S六边形ABCDEF=_______．5．有6个被12除所得余数都相同的自然数，它们的连乘积为971 425．则这6•个自然数之和的最小值是________．三、（15分）已知非零实数a、b、c满足a+b+c=0.求证：（1）a3+b3+c3=3abc；（2）（a bc-+b ca-+c ab-）（ca b-+ab c-+bc a-）=9.四、（15分）如图，在△ABC中，∠BAC=∠BCA=44°，M为△ABC形内一点，•使得∠MCA=30°，∠MAC=16°，求∠BMC的度数．五、（10分）某学生在黑板上写出了17个自然数，•每个自然数的个位数码只能是0，1，2，3，4这5个数字中的一个．证明：从这17个数中可以选出5个数，•它们的和能被5整除．参考答案一、1．A在1～100这100个自然数中，有质数2，3，5，7，11，13，17，19，23，29，31，37，41，43，47，53，59，61，67，71，73，79，83，89，97共25个，所以，其中质数所占的百分比是25%．2．C将10分拆成三个正整数之和，有10=1+1+8=1+2+7=1+3+6=1+4+5=2+2+6=2+3+5=2+4+4=3+3+4共八种情况．由“三角形两边之和大于第三边”可知，只有（2，4，4），（3，3，4）两组可构成三角形．由于等腰三角形两个底角都是锐角，于是，以2、4、4为边的等边三角形中，最小边2对的顶角也是锐角．以3、3、4为边的等腰三角形中，由32+32>42，•知顶角也是锐角．所以，以2、4、4为边的等腰三角形以及以3、3、4为边的等腰三角形都是锐角三角形，排除选项（A）、（B）•．•又由于等腰三角形中恰有一个内角为60°时变为等边三角形，与边为（2，4，4）、（3，3，4）的条件矛盾，排除选项（D）．由（2，4，4）、（3，3，4）为边的三角形是恰有两边相等的三角形．3．D．由S=(1)2n n+，又n、n+1是两个连续的自然数，知n（n+1）的个位数字只能取0，2，6．•所以，S的个位数字只能是0，1，3，5，6，8这六个数字．因此，S的个位数字不能取到的是2，4，7，9．4．B如图1，设S△AOD=x，S△BOC=y，则S四边形ABCD=4+9+x+y≥13+2xy．由49xy=，有xy=36．所以，S四边形ABCD≥13+2xy=13+12=25．故S四边形ABCD的最小值是25．此时，AB∥DC，即四边形ABCD是梯形．5．A．由│a-b│=1，知a-b=1或a-b=-1；由│b+c│=1，知b+c=1或b+c=-1；由│a+c│=2，知a+c=2或a+c=-2．这样，可以得到23=8个三元一次方程组：（1）a-b=1，b+c=1，a+c=2；（2）a-b=1，b+c=1，a+c=-2；（3）a-b=1，b+c=-1，a+c=2；（4）a-b=1，b+c=-1，a+c=-2；（5）a-b=-1，b+c=1，a+c=2；（6）a-b=-1，b+c=1，a+c=-2；（7）a-b=-1，b+c=-1，a+c=2；（8）a-b=-1，b+c=-1，a+c=-2．对于（2）～（7），将前两个方程相加得到的a+c的值与后一个方程不同，所以，不会出现这六种情况．对于（1），有a=2-c，b=1-c，所以，a+b+2c=3．对于（8），有a=-2-c，b=-1-c，所以，a+b+2c=-3．故│a+b+2c│=3．二、1．1．由勾股定理知AD2+CD2=AC2．所以，上面半个大圆的面积等于以AD、CD为直径的两个半圆的面积．同理，下面半个大圆的面积等于以AB、BC为直径的两个半圆的面积．•因此，正方形ABCD的面积等于四个“月形”的总面积．容易计算，大圆的半径OD是1cm．2．85．由2 005依次被99，98，97，…去除，观察所得余数的值变化得2 005=99×20+25=98×20+45=97×20+65=96×20+85=95×21+10=94×21+31=93×21+52=92×21+73=91×22+3=90×22+25=89×22+47=88×22+69=87×23+4=86×23+27=85×23+50．以下的余数不会大于84，故可能得到的最大余数是85．3．18．3a2+4b2-5bc=3（a2+bc）+4（b2-2bc）=3×14+4×（-6）=18．4．6．如图5，连结BD、CE．因为S△BCD=S△ECD=1，所以，BE∥CD．因为S△BAF=S△EAF，所以，BE∥AF．因此，BE∥AF∥CD．同理，CF∥DE∥BA，AD∥FE∥BC．由AD、BE、CF三线共点于O，可知四边形OCDE、四边形OEFA、四边形OABC 都是平行四边形，易知，每个平行四边形的面积都等于2．5．150．因为971 425被12除余1，而971 425=5×5×7×7×13×61，其中被12除余5、余7、余1的质因数各都是两个，由于两个被12除余5（余7）的数的乘积被12除余1，而971 425与若干个1的积仍为971 425，被12除余1，所以，•只能是6个被12除余1的数的乘积为971 425．计算得知：971 425=1×1×1×1×1×971 425，这6个因数之和为1+1+1+1+1+971 425=971 430；971 425=1×1×1×1×13×74 725，这6个因数之和为1+1+1+1+13+74 725=74 742；971 425=1×1×1×13×25×2 989，这6个因数之和为1+1+1+13+25+2 989=3 030．事实上，设a、b都是被12除余1的大于1的自然数，且a≥b，则a≥b>2，易知ab>a×2=a+a>a+b．①根据式①得971 425=13×74 725>13+74 725=13+25×2 989>13+25+2 989=13+25+49×61>13+25+49+61．因为971 425=52×72×13×61=1×1×13×25×49×61，所以，971 425表为6•个被12除余1的自然数，它们和的最小值等于1+1+13+25+49+61=150．三、（1）由a+b+c=0，得a+b=-c，因此，（a+b）3=-c3．于是，有a3+3a2b+3ab2+b3=-c3．故a3+b3+c3=-3ab（a+b）=-3ab（-c）=3abc．（2）．（a bc-+b ca-+c ab-）·ca b-=1+（b ca-+c ab-）·ca b-=1+22cab．同理，（a bc-+b ca-+c ab-）·ab c-=1+22abc．（a bc-+b ca-+c ab-）·bc a-=1+22bac故（a bc-+b ca-+c ab-）（ca b-+ab c-+bc a-）=1+22cab+1+22abc+1+22bac=3+3332()a b cabc++=3+23abcabc⨯=9．四、在△ABC中，由∠BAC=∠BCA=44°，得AB=BC，∠ABC=92°．如图6，作BD⊥AC于点D，延长CM交BD于点O，连结OA，则有∠OAC=∠MCA=30°，∠BAO=∠BAC-∠OAC=44°-30°=14°．∠OAM=∠OAC-∠MAC=30°-16°=14°．所以，∠BAO=∠MAO．又∠AOD=90°-∠OAD=90°-30°=60°=∠COD，所以，∠AOM=120°=∠AOB．又AO=AO，因此，△ABO≌△AMO．故OB=OM．由于∠BOM=120°，从而，∠OMB=∠OBM=1802BOM︒-∠=30°．所以，∠BMC=180°-∠OMB=150°．五、如果17个数的末位数字0，1，2，3，4每个都有，可选出5•个数的末位数字恰分别为0，1，2，3，4，则这5个数之和的末位数字为0，其和被5整除．如果17个数的末位数字不是0，1，2，3，4每个都有，则最多只有4•种不同的末位数字．这时，根据轴屉原理，这17个数中至少有5个数的末位数字一样．于是，这5•个数之和被5整除．。
2007年北京市初二数学竞赛试题
2007年北京市初二数学竞赛试题一、选择题（每小题5分，共25分）1、若c b a 、、是三个不同的正整数，并且16=abc ，则a c b c b a +-可能的最大值是（ ）.（A ）249 （B ）253 （C ）263 （D ）2642、已知三个连续的正整数的倒数和等于504191. 则这三个数之和等于（ ）. （A ）27 （B ）24 （C ）21（D ）18 3、分母是2007的正的最简真分数有（ ）个. （A ）675 （B ）1326 （C ）21329（D ）1332 4、对于实数x ，符号[]x 表示不大于x 的最大整数，例如，[][]859.7,314.3-=-=. 则关于x 的方程4773=+x 的整数根有（ ）个. （A ）4 （B ）3 （C ）2 （D ）15、如图1，已知长方形的长为8，宽为4，将长方形沿一条对角线折起压平. 则重叠部分（阴影三角形）的面积是（ ）.（A ）10 （B ）12 （C ）14 （D ）16二、填空题（每小题7分，共35分）1、将正整数从1开始依次按如图2所示的规律排成一个数阵，其中，2在第一个拐角处，3在第2个拐角处，5在第3个拐角处，7在第4个拐角处，……，那么，在第2007个拐角处的数是 .2、在一个3×3的方格表中填有1,2,3,4,5,6,7,8,9九个数，每格只填一个数. 现将每行中放有最大数的格子染成红色，放有最小数的格子染成绿色. 设M 是红格中的最小数，m 是绿格中的最大数. 则M －m 可以取到 个不同的值.3、如图3，已知在等腰三角形ABC 中，AB ＝AC ，P 、Q 分别是边AC 、AB 上的点，且AP ＝PQ ＝QB ＝BC. 则∠PCQ ＝ .4、化简⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛++d c b a c b a d b a c a b a 111111111111111111111111的值为 .5、如图4，在长方形ABCD 中，E 、F 、G 分别是边AB 、BC 、CD 的中点. 已知长方形ABCD 的面积是40cm 2. 则四边形MFNP 的面积是 cm 2.三、（15分）已知c b a 、、是实数. 若abc b ac b a bc a c b 2a 2c 2222222222-+-+-+、、之和恰等于1，求证：这三个分数的值有两个为1，一个为－1.四、（10分）如图5，在△ABC 中，∠ABC ＝46°，D 是边BC 上的一点，DC ＝AB ，∠DAB ＝21°. 试确定∠CAD 的度数。
2018年北京市中学生数学竞赛初二年级获奖名单
2018年北京市中学生数学竞赛初二年级获奖名单一等奖（94名）姓名学校年级姓名学校年级唐锦琪人大附中初一樊骏一人大附中初一袁浩然人大附中初二杨丽鸿清华附中初二陈竞帆人大附中初二段睿思清华附中初二关乃粼人大附中早六宋知轩清华附中初一张世奇人大附中初二沈芸伍清华附中初二张世潇北师大实验中学初一许易清华附中初二赵亦阳十一学校初二张一锐清华附中初二王浩霖人大附中初一潘宇锐北京一零一中初二廖昱博人大附中初一陈昕宇北京一零一中初二李永一人大附中初一李昊轩人大附中初一王原北大附中初二苗硕人大附中初二邹听雨十一学校初一黄安辀人大附中初一张书豪十一学校初二梁恒睿人大附中分校初一黄亦骐人大附中早六王俣涵北大附中初二宋嘉玺人大附中初二武正坤人大附中初一胡殊闻人大附中早六卢远人大附中初一王誉墨北师大实验中学初二谢昊霖人大附中初一贾博暄人大附中初二黄鹤鸣人大附中初一黄子萌北师大实验中学初二曲兆轩牛栏山一中实验学校初二张涵之人大附中初二阮宗泽人大附中初一陈嘉雪人大附中初二王慕涵人大附中初二徐健十一学校初一许睿泽北师大实验中学初二徐文昕人大附中初一许远航北京一零一中初二周亚琪清华附中初二刘若易北师大实验中学初二肖子健清华附中初一李海峰清华附中初一孙胤博人大附中初一许子涵人大附中初一王小龙人大附中早六朱祎然北京二中分校初二陈吉轲人大附中初二张元之清华附中初二李思学北大附中初二郭逸远北京一零一中初一廖原北京五中分校初二吴迪北师大实验中学初二王默涵清华附中初一钟沐阳人大附中初二刘星彤清华附中初二陈宇轩人大附中早六张皓翔北京一零一中初一蓝漩十一学校初二张章北京一零一中初二邓宇晨人大附中初一修时雨人大附中初二邓怡馨人大附中初一游天宇人大附中初一刘馨阳人大附中初一孙晓森清华附中初二吕博涵清华附中初二刘睿韬清华附中初一高子昂清华附中初一邹岳桐人大附中初二虞明达清华附中初一何翰韬十一学校初一李祖豫人大附中早六徐烨堃十一学校初二王中天人大附中初二张翔宇人大附中初二左泽成北师大实验中学初二张皓天北师大实验中学初一吴紫菱北师大实验中学初二张远洋人大附中初一罗天择人大附中初二高梓博人大附中初二卢天戈北大附中初二陈坤宁人大附中初二范唯楚清华附中初一张庭语人大附中初一付紫成人大附中初一二等奖（144名）姓名学校年级姓名学校年级范天舒人大附中初二齐锴人大附中初一张家铭人大附中初二李安之北京二中分校初二蔡振浩人大附中初二肖翊宸人大附中初一王凤怡人大附中初二袁籁人大附中初一孟博彰人大附中初一张泰然人大附中初一晁一沣人大附中初二彦昕人大附中初一王培阳清华附中初一孙嘉鸿人大附中初一毛嘉琛人大附中初一郭尉含章人大附中初二刘一铭清华附中初一栗选丞人大附中早六陈胤彤清华附中初二葛皓天人大附中初一李汝诚清华附中初二董亦麟人大附中初二曾广宇清华附中初二查益清华附中初二曹硕清华附中六年顾芸萌北师大实验中学初二张邵博清华附中初一丛诗雨北京一零一中初二张智清人大附中初二于天润北京一零一中初二王梓畅人大附中初一王梓翔人大附中初一杨昊源北京一零一中初二刘俊宏人大附中初一李宗润北师大实验中学初二洪维清华附中初一张一博北师大实验中学初二蒋辰昊人大附中初一刘以诺清华附中初二高慈欣北京一零一中初二吴梦晗清华附中初二董昀翱人大附中初一刘嫁新清华附中初二张天意北师大实验中学初二孙嘉阳清华附中初一翟凌飞人大附中早六夏海闻北师大实验中学初一朱泽睿人大附中初二陈宇奇人大附中初一周以端十一学校初二董天诺人大附中初二张煦恒人大附中初一吴飞扬人大附中初二李易铭人大附中初一段文博人大附中初二李飞跃十一学校初二郑元彬人大附中初二王羽健十一学校初二夏一桐人大附中初一斯文人大附中初二苗可明人大附中初一吴奕涵人大附中初一钱海天人大附中初一赵宸宇北京二中分校初二陆雪松人大附中初二李佳俊清华附中初二肖旭磊十一学校初一陈彦旭清华附中初二李春进人大附中早六王子兮清华附中初二乔铎北京亦庄实验中学初二李子豪清华附中初一郭俊游人大附中早六常三思人大附中初一黄俊维人大附中早六吕逍依人大附中初一王雨晗十一学校初二王镜廷人大附中早六龙韬智十一学校初二祝世博十一学校初二吴青阳人大附中初二陆洲锋北京二中分校初二龚云锋牛栏山一中实验学校初二黄兆屹人大附中分校初二方郑琦牛栏山一中实验学校初二张广源清华附中初一徐定坤人大附中初二刘一晨北京一零一中初二周蔚然人大附中初二张致远北京二中分校初二崔焱扬北京二中分校初二陈炫东北大附中初二张逸轩北大附中初一赵泽昕人大附中分校初二陈灵钧北京五中分校初二肖惠文清华附中六年黎丹宇北大附中初二张殊赫北京一零一中初二申君皓清华附中初二李依桐北京一零一中初二赵培源清华附中初二汪远北京一零一中初二韩羽霄清华附中初二姚亦嵩北京一零一中初二关清元人大附中初一李思颖北京一零一中初二余凌越清华附中初二李奕含北师大实验中学初二卞皓晨北师大实验中学初二吕彦荣北师大实验中学初二陈霁芸人大附中早六田昊霖人大附中初一耳昶玮人大附中初二孟晙阳北京二中分校初二王子初北京二中分校初二刘语玹人大附中初二刘任达北京四中初二郭晟毓十一学校初二申奕坤人大附中初二徐皓天人大附中初二马迹昀十一学校初一胡晓君人大附中初二阮家琪人大附中初一张子睿人大附中分校初一王子鸣人大附中初一徐金人大附中初二吴雨轩人大附中初二王子涵人大附中早六李铭泽清华附中初一陈智谦人大附中初二徐启鑫清华附中初一董雪瑞北大附中初二郑睿阳清华附中初二杨子谦北京五中分校初二杨舒涵清华附中初二付浩辰十一学校初二刘语涵清华附中初一赵柯人大附中初一荆明健清华附中初二蒋穆清人大附中初一李浩明北师大实验中学初一许景粟人大附中初一张涵钰清华附中初一郑睿阳清华附中初二三等奖（123名）姓名学校年级姓名学校年级刘相卿清华附中初二赵天珺十一学校-初二杜胤臻清华附中初二杨成科人大附中初一钱铭阳清华附中初二李卓言北京五中分校初二张文健清华附中初二李天圣北大附中初一陈楚瑜清华附中初二陈桢懿北大附中初二董予人大附中初一陈灿首师大附中初二赵一辰北师大实验中学初二张逸扬北京二中分校初二陈誉霄人大附中初二蔡泊屹北大附中初一周子昂人大附中初二马昊宇十一学校初二张雪桢北京二中分校初二苗瀚文人大附中初一王帅烨人大附中早六鲍俊辰清华附中初二张冰喆人大附中初一张宁远清华附中初二王泽尘人大附中初二张天翼清华附中初二田笑冰北京五中分校初二贺家琦北师大实验中学初一李昀濠清华附中初一张雨桐北京一零一中初二李金宸清华附中初一余瑶北师大实验中学初二孙一文清华附中初一张杰辰北京一零一中初二陆宜行十一学校初二杨谨毓北京一零一中初一周雪阳清华附中初一梁毓北师大实验中学初二孙家瑞人大附中初二杨博涵北师大实验中学初二李一申北京五中分校初二诸晨岳清华附中初二韩沛瑾人大附中初一郭馨锴清华附中初二康恺文牛栏山实验中学初二王一飞清华附中初二梁宸菲牛栏山实验中学初二关澜清华附中初二张喆人大附中初二宋清岳清华附中初二李诗均北大附中初一许赫男清华附中初一杜恒奕北京二中分校初二杨凡楷清华附中初二卢思翰人大附中早六吕桉驰清华附中初二杨紫雄人大附中初二汪佳萱北师大实验中学初二朱炯亦首师大附中初一李子闻北师大实验中学初一匡天一北京二中分校初二杨润欣北师大实验中学初一王彦翔北京四中初二刘孟歆北师大实验中学初一石家霖人大附中初二徐鼎新人大附中分校初一徐隽镕人大附中早六姬奕晨北京一零一中初二罗嘉祺北京一零一中初二高飞人大附中初二张亦鑫人大附中初一张沁月北大附中初二汪宁北京二中分校初二贾天歌人大附中初一王雨桉北京四中初二吴道宁人大附中初一张童开首师大附中初二李思海人大附中初一丁牧云北京市第十二中学初二魏梦萱人大附中初一刘涵柞人大附中初二邢琬瑜人大附中早六高欢瑜人大附中早六方大容人大附中初一何思远清华附中初二陈瑞泽首师大附中初一任墨也人大附中初二郑文博首师大附中初二王禹腾清华附中初二里正阳北京四中初二陈禹铭清华附中初二何阳松人大附中初二侯博文十一学校初一许昊翔人大附中早六东紫昭十一学校初二丁天岚人大附中初一王润山十一学校初一王泽芃北京四中初二隋远昊十一学校初一陈子璐北京一零一中初二史洪毓人大附中初一高江山清华附中初二杨佳营北京五中分校初二纪明悦清华附中初二迟嘉会北京五中分校初二李熙民北师大实验中学初二张语轩人大附中初二战治成师达中学初二王众一人大附中初二张斗和人大附中初二温雪岭人大附中初二王心睿人大附中初二刘羿镝人大附中初二孟繁钰人大附中初二张皓翔人大附中初二张婧婷十一学校初一刘俊扬人大附中初一闫岳霖牛栏山一中实验学校初二张戈飞人大附中早六张天艺牛栏山一中实验学校初二侯梓超人大附中初二杨卓然首师大附中初二陈含哲北京一零一中初二。
北京市初二数学竞赛学生版
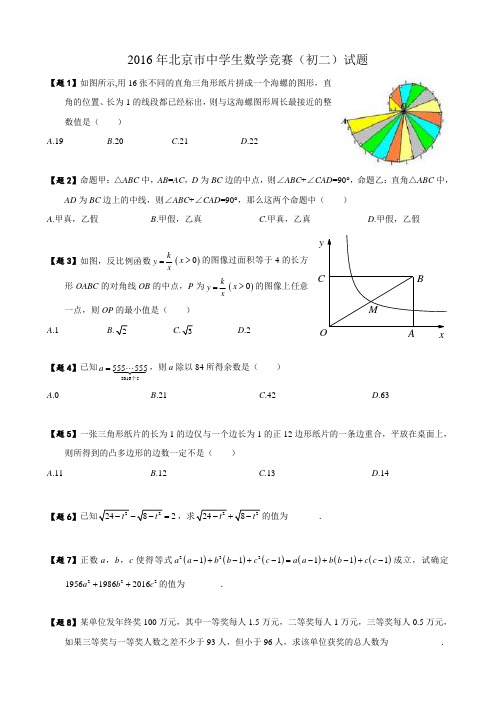
【题 9】△ABC 中，∠BAC=45°，∠ABC=60°，高线 AD 与 BE 相交于 H，若 AB=1，求四边形 CDHE 的面 积_________．
x
一点，则 OP 的最小值是（ ）
A.1
B. 2
C. 3
D.2
O
B M
Ax
【题 4】已知 a 555555 ，则 a 除以 84 所得余数是（ ）
2016个5
A.0
B.21
C.42
D.63
【题 5】一张三角形纸片的长为 1 的边仅与一个边长为 1 的正 12 边形纸片的一条边重合，平放在桌面上， 则所得到的凸多边形的边数一定不是（ ）
A.11
B.12
C.13
D.14
【题 6】已知 24 t2 8 t2 2 ，求 24 t2 8 t2 的值为_______．
【题 7】正数 a，b，c 使得等式 a2 a 1 b2 b 1 c2 c 1 a a 1 bb 1 c c 1 成立，试确定
1956a2 1986b2 2016c2 的值为________．
A C1 C2
B2 B1
B A1 A2 C
【题 13】一个自然数 n 若能表示为若干个正整数的和，且这些正整数的倒数和也恰等于 1，则称 n 为“金 猴数”，比如 2 4 8 8 22 且 1 1 1 1 1 ，22 就是一个“金猴数” 2488
（1）证明：11 与 28 是两个“金猴数”； （2）证明：如果 n 是“金猴数”，则 2n 2 、 2n 9 也是“金猴数”； （3）请你判定：2016 也是“金猴数”．
北京市中学生数学竞赛初二年级获奖名单
2018年北京市中学生数学竞赛初二年级获奖名单一等奖（94名）姓名学校年级姓名学校年级唐锦琪人大附中初一樊骏一人大附中初一袁浩然人大附中初二杨丽鸿清华附中初二陈竞帆人大附中初二段睿思清华附中初二关乃粼人大附中早六宋知轩清华附中初一张世奇人大附中初二沈芸伍清华附中初二张世潇北师大实验中学初一许易清华附中初二赵亦阳十一学校初二张一锐清华附中初二王浩霖人大附中初一潘宇锐北京一零一中初二廖昱博人大附中初一陈昕宇北京一零一中初二李永一人大附中初一李昊轩人大附中初一王原北大附中初二苗硕人大附中初二邹听雨十一学校初一黄安辀人大附中初一张书豪十一学校初二梁恒睿人大附中分校初一黄亦骐人大附中早六王俣涵北大附中初二宋嘉玺人大附中初二武正坤人大附中初一胡殊闻人大附中早六卢远人大附中初一王誉墨北师大实验中学初二谢昊霖人大附中初一贾博暄人大附中初二黄鹤鸣人大附中初一黄子萌北师大实验中学初二曲兆轩牛栏山一中实验学校初二张涵之人大附中初二阮宗泽人大附中初一陈嘉雪人大附中初二王慕涵人大附中初二徐健十一学校初一许睿泽北师大实验中学初二徐文昕人大附中初一许远航北京一零一中初二周亚琪清华附中初二刘若易北师大实验中学初二肖子健清华附中初一李海峰清华附中初一孙胤博人大附中初一许子涵人大附中初一王小龙人大附中早六朱祎然北京二中分校初二陈吉轲人大附中初二张元之清华附中初二李思学北大附中初二郭逸远北京一零一中初一廖原北京五中分校初二吴迪北师大实验中学初二王默涵清华附中初一钟沐阳人大附中初二刘星彤清华附中初二陈宇轩人大附中早六张皓翔北京一零一中初一蓝漩十一学校初二张章北京一零一中初二邓宇晨人大附中初一修时雨人大附中初二邓怡馨人大附中初一游天宇人大附中初一刘馨阳人大附中初一孙晓森清华附中初二吕博涵清华附中初二刘睿韬清华附中初一高子昂清华附中初一邹岳桐人大附中初二虞明达清华附中初一何翰韬十一学校初一李祖豫人大附中早六徐烨堃十一学校初二王中天人大附中初二张翔宇人大附中初二左泽成北师大实验中学初二张皓天北师大实验中学初一吴紫菱北师大实验中学初二张远洋人大附中初一罗天择人大附中初二高梓博人大附中初二卢天戈北大附中初二陈坤宁人大附中初二范唯楚清华附中初一张庭语人大附中初一付紫成人大附中初一二等奖（144名）姓名学校年级姓名学校年级范天舒人大附中初二齐锴人大附中初一张家铭人大附中初二李安之北京二中分校初二蔡振浩人大附中初二肖翊宸人大附中初一王凤怡人大附中初二袁籁人大附中初一孟博彰人大附中初一张泰然人大附中初一晁一沣人大附中初二彦昕人大附中初一王培阳清华附中初一孙嘉鸿人大附中初一毛嘉琛人大附中初一郭尉含章人大附中初二刘一铭清华附中初一栗选丞人大附中早六陈胤彤清华附中初二葛皓天人大附中初一李汝诚清华附中初二董亦麟人大附中初二曾广宇清华附中初二查益清华附中初二曹硕清华附中六年顾芸萌北师大实验中学初二张邵博清华附中初一丛诗雨北京一零一中初二张智清人大附中初二于天润北京一零一中初二王梓畅人大附中初一王梓翔人大附中初一杨昊源北京一零一中初二刘俊宏人大附中初一李宗润北师大实验中学初二洪维清华附中初一张一博北师大实验中学初二蒋辰昊人大附中初一刘以诺清华附中初二高慈欣北京一零一中初二吴梦晗清华附中初二董昀翱人大附中初一刘嫁新清华附中初二张天意北师大实验中学初二孙嘉阳清华附中初一翟凌飞人大附中早六夏海闻北师大实验中学初一朱泽睿人大附中初二陈宇奇人大附中初一周以端十一学校初二董天诺人大附中初二张煦恒人大附中初一吴飞扬人大附中初二李易铭人大附中初一段文博人大附中初二李飞跃十一学校初二郑元彬人大附中初二王羽健十一学校初二夏一桐人大附中初一斯文人大附中初二苗可明人大附中初一吴奕涵人大附中初一钱海天人大附中初一赵宸宇北京二中分校初二陆雪松人大附中初二李佳俊清华附中初二肖旭磊十一学校初一陈彦旭清华附中初二李春进人大附中早六王子兮清华附中初二乔铎北京亦庄实验中学初二李子豪清华附中初一郭俊游人大附中早六常三思人大附中初一黄俊维人大附中早六吕逍依人大附中初一王雨晗十一学校初二王镜廷人大附中早六龙韬智十一学校初二祝世博十一学校初二吴青阳人大附中初二陆洲锋北京二中分校初二龚云锋牛栏山一中实验学校初二黄兆屹人大附中分校初二方郑琦牛栏山一中实验学校初二张广源清华附中初一徐定坤人大附中初二刘一晨北京一零一中初二周蔚然人大附中初二张致远北京二中分校初二崔焱扬北京二中分校初二陈炫东北大附中初二张逸轩北大附中初一赵泽昕人大附中分校初二陈灵钧北京五中分校初二肖惠文清华附中六年黎丹宇北大附中初二张殊赫北京一零一中初二申君皓清华附中初二李依桐北京一零一中初二赵培源清华附中初二汪远北京一零一中初二韩羽霄清华附中初二姚亦嵩北京一零一中初二关清元人大附中初一李思颖北京一零一中初二余凌越清华附中初二李奕含北师大实验中学初二卞皓晨北师大实验中学初二吕彦荣北师大实验中学初二陈霁芸人大附中早六田昊霖人大附中初一耳昶玮人大附中初二孟晙阳北京二中分校初二王子初北京二中分校初二刘语玹人大附中初二刘任达北京四中初二郭晟毓十一学校初二申奕坤人大附中初二徐皓天人大附中初二马迹昀十一学校初一胡晓君人大附中初二阮家琪人大附中初一张子睿人大附中分校初一王子鸣人大附中初一徐金人大附中初二吴雨轩人大附中初二王子涵人大附中早六李铭泽清华附中初一陈智谦人大附中初二徐启鑫清华附中初一董雪瑞北大附中初二郑睿阳清华附中初二杨子谦北京五中分校初二杨舒涵清华附中初二付浩辰十一学校初二刘语涵清华附中初一赵柯人大附中初一荆明健清华附中初二蒋穆清人大附中初一李浩明北师大实验中学初一许景粟人大附中初一张涵钰清华附中初一郑睿阳清华附中初二三等奖（123名）姓名学校年级姓名学校年级刘相卿清华附中初二赵天珺十一学校-初二杜胤臻清华附中初二杨成科人大附中初一钱铭阳清华附中初二李卓言北京五中分校初二张文健清华附中初二李天圣北大附中初一陈楚瑜清华附中初二陈桢懿北大附中初二董予人大附中初一陈灿首师大附中初二赵一辰北师大实验中学初二张逸扬北京二中分校初二陈誉霄人大附中初二蔡泊屹北大附中初一周子昂人大附中初二马昊宇十一学校初二张雪桢北京二中分校初二苗瀚文人大附中初一王帅烨人大附中早六鲍俊辰清华附中初二张冰喆人大附中初一张宁远清华附中初二王泽尘人大附中初二张天翼清华附中初二田笑冰北京五中分校初二贺家琦北师大实验中学初一李昀濠清华附中初一张雨桐北京一零一中初二李金宸清华附中初一余瑶北师大实验中学初二孙一文清华附中初一张杰辰北京一零一中初二陆宜行十一学校初二杨谨毓北京一零一中初一周雪阳清华附中初一梁毓北师大实验中学初二孙家瑞人大附中初二杨博涵北师大实验中学初二李一申北京五中分校初二诸晨岳清华附中初二韩沛瑾人大附中初一郭馨锴清华附中初二康恺文牛栏山实验中学初二王一飞清华附中初二梁宸菲牛栏山实验中学初二关澜清华附中初二张喆人大附中初二宋清岳清华附中初二李诗均北大附中初一许赫男清华附中初一杜恒奕北京二中分校初二杨凡楷清华附中初二卢思翰人大附中早六吕桉驰清华附中初二杨紫雄人大附中初二汪佳萱北师大实验中学初二朱炯亦首师大附中初一李子闻北师大实验中学初一匡天一北京二中分校初二杨润欣北师大实验中学初一王彦翔北京四中初二刘孟歆北师大实验中学初一石家霖人大附中初二徐鼎新人大附中分校初一徐隽镕人大附中早六姬奕晨北京一零一中初二罗嘉祺北京一零一中初二高飞人大附中初二张亦鑫人大附中初一张沁月北大附中初二汪宁北京二中分校初二贾天歌人大附中初一王雨桉北京四中初二吴道宁人大附中初一张童开首师大附中初二李思海人大附中初一丁牧云北京市第十二中学初二魏梦萱人大附中初一刘涵柞人大附中初二邢琬瑜人大附中早六高欢瑜人大附中早六方大容人大附中初一何思远清华附中初二陈瑞泽首师大附中初一任墨也人大附中初二郑文博首师大附中初二王禹腾清华附中初二里正阳北京四中初二陈禹铭清华附中初二何阳松人大附中初二侯博文十一学校初一许昊翔人大附中早六东紫昭十一学校初二丁天岚人大附中初一王润山十一学校初一王泽芃北京四中初二隋远昊十一学校初一陈子璐北京一零一中初二史洪毓人大附中初一高江山清华附中初二杨佳营北京五中分校初二纪明悦清华附中初二迟嘉会北京五中分校初二李熙民北师大实验中学初二张语轩人大附中初二战治成师达中学初二王众一人大附中初二张斗和人大附中初二温雪岭人大附中初二王心睿人大附中初二刘羿镝人大附中初二孟繁钰人大附中初二张皓翔人大附中初二张婧婷十一学校初一刘俊扬人大附中初一闫岳霖牛栏山一中实验学校初二张戈飞人大附中早六张天艺牛栏山一中实验学校初二侯梓超人大附中初二杨卓然首师大附中初二陈含哲北京一零一中初二。
初中数学竞赛专题6：因式分解
专题6：因式分解第1讲 因式分解赛题练习一、选择题1．（第17届希望杯竞赛题）若22222006200620072007m =+⨯+，则m （ ） A ．是完全平方数，还是奇数 B ．是完全平方数，还是偶数 C ．不是完全平方数，但是奇数D ．不是完全平方数，但是偶数2．（第17届希望杯竞赛题）There is a two-placed number 10ab a b =+satisfying that ab ba + is a complete square number ，then total number of those like ab is （ ） A ．4B ．6C ．8D ．10（英汉词典：two-placed number 两位数；number 数；to satisfy 满足；complete square 完全平方（数）；total 总的，总数）3．（2005年全国初中数学竞赛题）若223894613M x xy y x y =-+-++（x ，y 是实数），则M 的值一定是（ ） A ．正数B ．负数C ．零D ．整数4.（北京市竞赛题）44a +分解因式的结果是（ ） A.()()222222a a a a +--+ B.()()222222a a a a +--- C.()()222222a a a a ++--D.()()222222a a a a ++-+5.（2006年希望杯竞赛题）实数320052005m =-，下列各数中不能整除m 的是（ ） A.2006B.2005C.2004D.20036.（2005年武汉市竞赛题）若3234x kx -+被31x -除后余3，则k 的值为（ ） A.2B.4C.9D.107.（第13届希望杯竞赛题）已知a b c >>，222M a b b c c a =++，222N ab bc ca =++，则M 与N 的大小关系是（ ） A.M N <B.M N >C.M N =D.不能确定8.（美国犹他州竞赛题）322136x x x +-+的因式是（ ） A.21x - B.2x + C.3x -D.21x +E.21x +9.（2005年全国初中数学竞赛题）若22389M x xy y =-+-4613x y ++（x 、y 是实数），则M 的值一定是（ ） A.正数B.负数C.零D.整数10.（武汉市竞赛题）如果328x ax bx +++有两个因式1x +和2x +，则a b +=（ ） A.7 B.8C.15D.21二、填空题11．（第7届五羊杯竞赛题）把()()()()16a b c d b c a d c a b d a b c d abcd ++++--+--+--+因式分解为________．12．（第18届五羊杯竞赛题）在实数范围内分解因式：432344x x x x +---=________． 13．（第18届五羊杯竞赛题）分解因式：2226773x xy y x y --+++=________．14．（2004年全国初中数学竞赛题）已知实数a ，b ，x ，y 满足2a b x y +=+=，5ax by +=，则()()2222ab xy ab x y +++=________．15．（2007年全国初中数学联赛题）若10064a +和20164a +均为四位数，且均为完全平方数，则整数a 的值是________．16.（北京市竞赛题）已知222246140x y z x y z ++-+-+=，则2002()x y z --=__________. 17.（2004年广西竞赛题）已知()22210x y x y +--+=，则()999x y +=__________.18.（北京市竞赛题）1~100若存在整数n ，使2x x n +-能分解为两个整系数一次式的乘积，这样的n 有____________个.19.（郑州市竞赛题）分解因式：22423a b a b -+++=_______________________________________. 20.（2004年河南省竞赛题）分解因式：229643x x y y --+-=_______________________________. 21.（第16届希望杯竞赛题）分解因式：()()221ab a b a b +-++=_____________________________. 22.（2004年全国初中数学竞赛题）已知实数a 、b 、x 、y 满足2a b x y +=+=，5ax by +=，则()()2222ab xy ab x y +++=___________________.23.（第15届江苏省竞赛题）已知26x x +-是多项式43221x x ax bx a b +-+++-的因式，则a =___________，b =___________.24.（第18届五羊杯竞赛题）在实数范围内分解因式：432344x x x x +---=___________. 25.（大连市第8届育英杯竞赛题）分解因式：()()112x x y y xy -++-=____________. 三、解答题26．（1991年黄冈初中数学竞赛题）已知a 是自然数，且3221215a a a +-+表示质数，求这个质数．27．（1999年天津市数学竞赛题）当k 为何值时，多项式222352x xy ky x y -++-+能分解成两个一次因式的积？28．（第9届华杯赛总决赛题）计算；()()()()()()()()()()444444444476415642364316439643641164196427643564++++++++++．29．（第10届希望杯竞赛题）272-1能被500与600之间的若干整数整除，请找出三个这样的整数，它们是________．30．（第10届希望杯竞赛题）若233x x x k +-+有一个因式是x +1，求k 的值．31．（第6届希望杯竞赛题）计算：2211100.010.01101001000⎛⎫⎛⎫++++- ⎪ ⎪⎝⎭⎝⎭．32．（第9届五羊杯竞赛题）当n =1，x =2时，求多项式51n n x x ++的两个因式的和．33．（2000年美国犹他州中学数学竞赛题）如果328x ax bx +++有两个因式x +1和x +2，求a +b 的值．34．（第5届美国数学邀请赛试题）计算：()()()()()()()()()()44444444441032422324343244632458324432416324283244032452324++++++++++．35．（第37届美国中学生数学竞赛题）设543269569106910695691N =+⨯+⨯+⨯+⨯+．问：有多少个正整数是N 的因数？36．（第9届莫斯科奥林匹克试题）证明：对任何整数x 和y ，343223453515412x x y x y x y xy y +--++的值都不会等于33．37．（第37届美国中学生数学竞赛题）已知b ，c 是整数，二次三项式2x bx c ++既是42625x x ++的一个因式，也是4234285x x x +++的一个因式，求当x =1时，2x bx c ++的值．38.（祖冲之杯竞赛题）分解因式：32539x x x ++-.39.（北京市竞赛题）证明恒等式：()244422()2a b a b a ab b +++=++.40.（江苏省竞赛题）已知x 、y 为正偶数，且2296x y xy +=，求22x y +的值.41.（希望杯竞赛题）分解因式：()()()2221x y xy x y xy +-+-+-.42.（第12届五羊杯竞赛题）分解因式：()()42424310x x x x +-+++.43（2006年希望杯培训题）计算：32322007220072005200720072008-⨯-+-.44.（太原市竞赛题）已知关于x 、y 的二次式22754324x xy ay x y ++-+-可分解为两个一次因式的乘积，求a 的值.45.（2005年莫斯科市竞赛题）对方程22222004a b a b ++=，求出至少一组整数解.46.（2006年创新杯培训题）已知n 是正整数，且4216100n n -+是质数，求n .47.（2006年全国初中数学竞赛题）计算 (252)(472)(692)(8112)(200420072)(142)(362)(582)(7102)(200320062)⨯+⨯+⨯+⨯+⨯⨯⨯+⨯+⨯+⨯+⨯+⨯⨯⨯+48.计算：（1）（第15届希望杯竞赛题）2220034004200320024008200320042003300520032003200520053005-⨯+⨯-⨯-⨯-⨯+⨯；（2）（第九届华杯赛竞赛题）()()()()()()()()()()444444444476415642364316439643641164196427643564++++++++++49.分解因式： （1）4464a b +； （2）4224x x y y ++； （3）()2222(1)x x x x ++++；（4）（昆明市竞赛题）()()()24c a b c a b ----；（5）（第15届希望杯竞赛题）432234232a a b a b ab b ++++； （6）（重庆市竞赛题）32256x x x +--.50.（重庆市竞赛题）分解因式： （1）224443x x y y --+-； （2）343115x x -+.问题解决例1.分解因式：()()()3332332125x y x y x y -+---=______. 例2.把下列各式分解因式： （1）()()22525312x x x x ++++-； （2）()()()()21236x x x x x +++++； （3）()()()()211x y x y xy xy xy +++++-.例3.阅读理解：观察下列因式分解的过程： （1）244x xy x y -+-原式()()()()()()24444x xy x y x x y x y x y x =-+-=-+-=-+. （2）2222a b c bc --+原式()()()()222222a b c bc a b c a b c a b c =-+-=--=+--+.第（1）题分组后能直接提公因式，第（2）题分组后能直接运用公式.仿照上述分解因式的方法，把下列各式分解因式： （1）2a ab ac bc -+-； （2）22244x y z yz --+.例4.分解因式：326116x x x +++.例5.把下列各式分解因式： （1）261110y y --； （2）22823x xy y --.数学冲浪 知识技能广场1.分解因式：（1）()()22162x x x ---=______； （2）()()4a b a b ab --+=______； （3）276ax ax a -+=______. 2.分解因式：（1）3222a ab a b +-=______；（2）()()21211x x ---+=______； （3）2221a ab b -+-=______； （4）2244x y x --+=______. 3.分解因式：（1）323412x x x +--=______； （2）()()2223238x xx x +-+-=______.4.若()()23x x m x x n ++=-+对x 恒成立，则n =______.5.把多项式22344x y xy x --分解因式的结果是（ ）. A.()34xy x y x --B.()22x x y --C.()2244x xy y x --D.()2244x xy y x --++6．()()()()()()656565323322134x x x x x x x xx +-+++-+++-与下列哪一个式子相同（ ）.A.()()653421x x x -+ B.()()653423x x x -+ C.()()653421x x x --+D.()()653423x x x --+7．把多项式22243x y x y ----因式分解之后，正确的结果是（ ） A.()()31x y x y ++-- B.()()13x y x y +--+ C.()()31x y x y +--+D.()()13x y x y ++--8．已知212x ax +-能分解成两个整系数的一次因式的乘积，则符合条件的整数a 的个数是（ ） A.3个B.4个C.6个D.8个9．先阅读以下材料，然后解答问题.分解因式：()()()()mx nx my ny mx nx my ny x m n y m n +++=+++=+++=()()m n x y ++；也可以()()()()()()mx nx my ny mx my nx ny m x y n x y m n x y +++=+++=+++=++. 以上分解因式的方法称为分组分解法. 请用分组分解法分解因式：3322a b a b ab -+-.10.分解因式：（1）22463a b a b -+-；（2）222944a b bc c -+-； （3）()()()2a c a c b b a +-+-； （4）()()221212x x x x ++++-； （5）()22223122331x x x x -+-+-； （6）()()()213512x x x -+++.思维方法天地11.分解因式：()()()()()12345x x x x x x ++++++=______. 12.分解因式：()()()33322x y x y -----=______.13.已知()()()()1931131713171123x x x x -----可因式分解为()()8ax b x c ++，其中a ，b ，c 均为整数，则a b c ++=______.14.已知1x -得多项式33x x k -+的一个因式，那么k =______；将这个多项式分解因式，得______. 15.44a +分解因式的结果是（ ）.A.()()222222a a a a +--+B.()()222222a a a a +---C.()()222222aa a a ++-- D.()()222222aa a a ++-+16．实数320052005m =-，下列各数中不能整除m 的是（ ） A.2006B.2005C.2004D.200317．已知3a b -=，5b c +=-，则代数式2ac bc a ab -+-的值为（ ） A.15-B.2-C.6-D.618．已知a ，b ，c 是ABC ∆的三边长，且满足()222220a b c b a c ++-+=，则此三角形是（ ）. A.等腰三角形 B.等边三角形 C.直角三角形 D.不能确定19．分解因式：（1）224443x x y y --+-；（2）()()()2221x y xy x y xy +-+-+-； （3）343115x x -+； （4）32539x x x ++-.应用探究乐园20.已知在ABC ∆中，三边长a ，b ，c 满足等式222166100a b c ab bc --++=.求证：2a c b +=.21.下金蛋的鸡法国数学家费马（1601-1665）一生中提出了不少猜想，最著名的是“费马大定理”：关于x ，y ，z 的方程n n n x y z +=（n 为大于2的整数）没有正整数解.直到350年之后，这个猜想才由英国数学家怀尔斯（1953— ）于1994年证明.德国数学家希尔伯特（1862-1943）将费马大定理称为“一只会下金蛋的鸡”，因为在攻克它的漫漫征程中，不但引出了许多数学概念和方法，而且促进了一些新的分支的创立和发展.这些远比证明定理本身更重要！不过费马的猜想并不总是正确的.他考察了12215+=，222117+=，3221257+=，422165537+=，发现结果都是素数（也称质数），于是猜想：对任意正整数n ，221n+（即()221n+）都是素数.瑞士数学家欧拉（1707-1783）指出，5221+并不是素数.我国数学家华罗庚（1910—1985）在他的著作《数论导引》中给出一种简明的证法：设72a =，5b =，可算得()524442111ab a a b +=++-，可见5221+必有除1和本身以外的约数______（填较简单的一个，用含a ，b 的式子表示），即5221+能被______整除（填入具体数值），所以不是素数.第2讲 因式分解的应用赛题练习1.（2004年重庆市竞赛题）已知2310x x x +++=，则220041x x x ++++的值为（ ）A.0B.1C.1-D.20042.（第19届江苏省竞赛题）若432237x x ax x b -+++能被22x x +-整除，则:a b 的值是 （ ） A.2-B.12-C.6D.43.（第14届希望杯竞赛题）若1x y +=-，则43222234585x x y x y x y xy xy y ++++++的值为（ ） A.0B.1-C.1D.34.（第17届江苏省竞赛题）a 、b 、c 是正整数，a b >，且27a ab ac bc --+=，则a c -的值为（ ） A.1-B.1-或7-C.1D.1或75.（中学生智能通讯赛试题）设()()322320042003200420052003200220012002a -⨯+=⨯--，()()322320052004200520062004200320022003b -⨯+=⨯--，则a 、b 的大小关系是（ ） A.a b >B.a b =C.a b <D.不能确定6.（湖北省竞赛题）设a 是正数，且21a a -=，那么224a a-的值为（ ） A.3-B.1C.3D.57.（2005年全国初中数学竞赛题）已知2221114834441004A ⎛⎫=⨯+++⎪---⎝⎭，则与A 最接近的正整数是（ ） A.18B.20C.24D.258.（2007年全国初中数学竞赛题）方程323652x x x y y ++=-+的整数解(),x y 的个数是（ ） A.0B.1C.3D.无穷多9.（第17届希望杯竞赛题）若22222006200620072007m =+⨯+，则m （ ） A.是完全平方数，还是奇数 B.是完全平方数，还是偶数 C.不是完全平方数，但是奇数D.不是完全平方数，但是偶数10.（2002年全国初中数学联赛题）若22m n =+，22()n m m n =+≠，则332m mn n -+的值为（ ） A.1B.0C.1-D.2-11.（2003年全国初中数学联赛题）满足等式2003=的正整数对(),x y 的个数是（ ）A.1B.2C.3D.412.（第14届希望杯竞赛题）已知54410a a b a a b --+--=，且231a b -=，则33a b +的值为___________.13.（全国初中数学竞赛题）已知a 、b 、x 、y 满足2a b x y +=+=，5ax by +=，则()()2222ab xy ab x y +++=___________.14.（第17届希望杯竞赛题）A 、n 都是自然数，且21526A n n =++是一个完全平方数，则n =_____________.15.（四川省竞赛题）对一切大于2的正整数n ，数5354n n n -+的最大公约数是____________. 16.（2001年全国初中数学联赛题）一个正整数，若分别加上100和168，则可得到两个完全平方数，这个正整数为___________.17.（第9届华杯赛试题）a 、b 、c 是正整数，并且满足等式12004abc ab ac bc a b c +++++++=，那么a b c ++的最小值是__________.18.（祖冲之杯竞赛题）整数a 、b 满足6910303ab a b =-+，则a b +=___________.19.（第18届五羊杯竞赛题）若P 是两位的正整数，则以下等式中有可能成立的式子的个数是______________.①22006(34)(59)x Px x x ++=--； ②22006(17)(118)x Px x x ++=--； ③22006(34)(59)x Px x x --=+-； ④22006(17)(118)x Px x x --=+-； ⑤22006(1)(2006)x Px x x +-=-+.20.（2001年全国初中数学联赛题）若214x xy y ++=，228y xy x ++=，则x y +的值为___________. 21.（2005年四川省竞赛题）对于一个正整数n ，如果能找到正整数a 、b ，使得n a b ab =++，则称n 为一个“好数”，例如31111=++⨯，3就是一个“好数”，那么，在1~20这20个正整数中，好数有___________个.22.（2004年北京市竞赛题）已知x 、y 为正整数，且满足22222341x y x y +=+，则22x y +__________. 23.（第10届希望杯竞赛题）7221-能被500与600之间的若干整数整除，请找出3个这样的整数，它们是__________.24.（2008年天津市竞赛题）已知4个实数a 、b 、c 、d ，且a b ≠，c d ≠.若4个关系式：22a ac +=，22b bc +=，24c ac +=，24d ad +=同时成立，则6232a b c d +++的值为___________. 25.（五城市联赛题）若a 是自然数，则4239a a -+是质数还是合数？给出你的证明.26.（全国初中数学联赛题）某校在向“希望工程”捐款活动中，甲班的m 个男生和11个女生的捐款总数与乙班的9个男生和n 个女生的捐款总数相等，都是()911145mn m n +++元，已知每人的捐款数相同，且都是整数，求每人的捐款数.27.（2006年俄罗斯萨温市竞赛题）（1）证明：19992000200120032004200536⨯⨯⨯⨯⨯+是一个完全平方数.（2）证明：数848497n n ++-对于任何自然数n 都能被20整除.28.（江苏省竞赛题）（1）证明：791381279--能被45整除；（2）证明：当n 为自然数时，()221n +形式的数不能表示为两个整数的平方差；（3）计算：44444444441111124681044444111111357944444⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++++ ⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++++ ⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭29.（2005年太原市竞赛题）二次三项式22x x n --能分解为两个整系数一次因式的乘积. （1）若130n ≤≤，且n 是整数，则这样的n 有多少个？ （2）当2005n ≤时，求最大的整数n .30.（重庆市竞赛题）按下面规则扩充新数：已有两数a 、b ，可按规则c ab a b =++扩充一个新数，在a 、b 、c 三个数中任取两数，按规则又可扩充一个新数，…，每扩充一个新数叫做一次操作.现有数1和4. （1）求按上述规则操作三次得到扩充的最大新数； （2）能否通过上述规则扩充得到新数1999，并说明理由.问题解决例1.方程2270xy x y --+=的整数解（x y ≤）为______. 例2.1621-能分解成n 个质因数的乘积，n 的值是（ ）. A.6 B.5 C.4 D.3例3.计算：（1）2220034004200320024008200320042003300520032003200520053005-⨯+⨯-⨯-⨯-⨯+⨯；（2）()()()()()()()()()()444444444476415642364316439643641164196427643564++++++++++. 例4.设9310382a =+-，证明：a 是37的倍数.例5.已知n 是正整数，且4216100n n -+是质数，求n 的值.例6.（1）实数x ，y 满足221252810x xy y y ++-+=，则22x y -=______.（2）在平面直角坐标系中，满足不等式2222x y x y +≤+的整数点坐标(),x y 的个数为（ ）. A.10B.9C.7D.5数学冲浪 知识技能广场1.设y ax =，若代数式()()()23x y x y y x y +-++化简的结果为2x ，则a =______.2.如图，有三种卡片，其中边长为a 的正方形卡片1张，边长分别为a ，b 的长方形卡片6张，边长为b 的正方形卡片9张，用这16张卡片拼成一个正方形，则这个正方形的边长为______. 3.如果实数x ，y 满足方程组1,2225,x y x y ⎧-=-⎪⎨⎪+=⎩那么22x y -的值为______.4.已知2m ≥，2n ≥，且m ，n 均为正整数，如果将n m 进行如下方式的“分解”，那么下列三个叙述：（1）在52的“分解”中最大的数是11； （2）在34的“分解”中最小的数是13；（3）若3m 的“分解”中最小的数是23，则m 等于5. 其中正确的是______.5.若实数x ，y ，z 满足()()()240x z x y y z ----=，则下列式子一定成立的是（ ） A.0x y z ++= B.20x y z +-= C.20y z x +-=D.20z x y +-=6．边长为a ，b 的矩形的周长为14，面积为10，则22a b ab +的值为（ ） A.140B.70C.55D.247．设n 为某一自然数，代入代数式3n n -计算其值时，四个学生算出了下列四个结果，其中正确的结果是（ ）. A.5814B.5841C.8415D.84518．a ，b ，c 是正整数，a b >，27a ab ac bc --+=，则a c -等于（ ） A.1- B.1-或7- C.1 D.1或79．计算：（1）32322004220042002200420042005-⨯-+-； （2）44444444441111124681044444111111357944444⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++++ ⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++++ ⎪⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭.10.选取二次三项式()20ax bx c a ++≠中的两项，配成完全平方式的过程叫配方. ①选取二次项和一次项配方：()224222x x x -+=--；②选取二次项和常数项配方：(()22424x x x x -+=+，或((32424x x x x -+=-+；③选取一次项和常数项配方：22242x x x -+=-.根据上述材料，解决下面的问题.（1）写出284x x -+的两种不同形式的配方；（2）已知22330x y xy y ++-+=，求y x 的值.思维方法天地11.若两个不等实数m ，n 满足22m m a -=，22n n a -=，225m n +=，则实数a 的值为______. 12.已知a ，b ，x ，y 满足2a b x y +=+=，5ax by +=，则()()2222a b xy ab x y +++=______. 13.整数x ，y 满足方程283xy x y ++=，则x y +=______.14.A ，n 都是自然数，且21526A n n =++是一个完全平方数，则n =______. 15.若22222006200620072007m =+⨯+，则m （ ）. A.是完全平方数，还是奇数 B.是完全平方数，还是偶数 C.不是完全平方数，但是奇数D.不是完全平方数，但是偶数16．设n 为某一正整数，代入代数式2n n -计算其值时，四个学生算出了下列四个结果，其中仅有一个是正确的，则这个正确的结果是（ ） A.7770B.7775C.7776D.777917．方程222334x xy y ++=的整数解(),x y 的组数为（ ）. A.3B.4C.5D.618．黑板上写有1，12，…，1100共100个数字，每次操作先从黑板上的数中选取两个数a ，b ，然后删去a ，b ，并在黑板上写上数a b ab ++，则经过99次操作后黑板上剩下的数是（ ）. A.2012B.101C.100D.9919．已知()()222012a b c b a c +=+=，且a b ≠，求()2c a b +的值.20.计算：()()()()()()()()()()424242424242424242422214416618881010133155177199111111++++++++++++++++++++.应用探究乐园21.当我们看到下面这个数学算式333337133713503724613724++==++时，大概会觉得算题的人错用了运算法则吧，因为我们知道3333a b a bc d c d++≠++，但是，如果你动手计算一下，就会发现上式并没有错，不仅如此，我们还可以写出任意多个这种等式：333331313232++=++，333352525353++=++，333373737474++=++，3333107107103103++=++，…，你能发现以上等式的规律吗？22.按下面规则扩充新数：已有两数a ，b ，可按规则c ab a b =++扩充一个新数，在a ，b ，c 三个数中任取两数，按规则又可扩充一个新数……每扩充一个新数叫做一次操作.现有数1和4. （1）求按上述规则操作三次得到扩充的最大新数； （2）能否通过上述规则扩充得到新数1999，并说明理由.。
2007年初中数学竞赛试题赏析(含解答)-
2007年初中数学竞赛试题赏析2007年春末夏初，国内的初中数学竞赛基本告一段落，暑假期间，在放松避暑纳凉的同时，对数学爱好者来说，把玩一下新的试题，也是一件乐事．下面为大家选析一些试题，供同学们玩赏．一、代数问题例1 已知a ，b ，c 是实数，若2222b c a bc +-，2222c a b ac +-，2222a b c ab+-之和恰等于1，求证：这三个分数的值有两个为1，一个为-1．（2007年北京市初二数学竞赛试题三）证明 由题设2222b c a bc +-+2222c a b ac +-+2222a b c ab+-=1， 即（2222b c a bc +--1）+（2222a c b ac +--1）+（2222a b c ab+-+1）=0， 通分，分子部分因式分解，（请自己完成演算）可得()()()2a b c c a b c a b abc+-+--+=0． 所以，或者a+b-c=0或者c+a-b=0或者b+c-a=0．①若a+b-c=0，则222222222222222222()21;222()21;222()2 1.222b c a b c b c bc bc bc bcc a b c a c a ac ac ac cab c a a b a b ab bc ab ab+-+--===+-+--===+-+-+-===- ②若c+a-b=0，同理可得2222b c a bc +-=1，2222c a b ac +-=-1，2222a b c ab+-=1， ③若c+a-b=0，同理可得2222b c a bc +-=-1，2222c a b ac +-=1，2222a b c ab+-=1． 综合①、②、③可得，三个分数2222b c a bc +-，2222c a b ac +-，2222a b c ab+-的值有两个为1，一个为-1．评析：由题设2222b c a bc +-+2222c a b ac +-+2222a b c ab+-=1，要证这三个分数的值有两个为1，一个为-1，想到证（2222b c a bc +--1）+（2222a c b ac +--1）+（2222a b c ab+-+1）=0 是关键．其中分子部分的因式分解，可检验你的代数式恒等变形的基本功是否过硬． 例2 设a 是正整数，二次函数y=x 2+（a+17）x+38-a ，反比例函数y=56x，•如果这两个函数的图象的交点都是整点（横坐标和纵坐标都是整数的点），求a 的值．（2007年全国初中数学联合竞赛（B 组）试题第三大题）解 联立方程组2(17)38,56,y x a x a y x ⎧=+++-⎪⎨=⎪⎩消去y 得x 2+（a+17）x+38-a=56x， 即x 3+（a+17）x 2+（38-a ）x-56=0，分解因式得（x-1）[x 2+（a+18）x+56]=0． （1）显然x 1=1是方程（1）的一个根，（1，56）是两个函数的图象的一个交点， 因为a 是正整数，所以关于x 的方程x 2+（a+18）x+56=0 （2）的判别式△=（a+18）2-224>0，它一定有两个不同的实数根．而两个函数的图象的交点都是整点，所以方程（2）的根都是整数，•因此它的判别式△=（a+18）2-224应该是一个完全平方数．设（a+18）2-224=k 2（其中k 为非负整数），则（a+18）2-k 2=224，即（a+18+k ）（a+18-k ）=224．显然a+18+k 与a+18-k 的奇偶性相同，且a+18+k ≥8，而224=112×2=56×4=28×8，18112,1856,1828,182,184,188.39,12,0,55,26,10.a k a k a k a k a k a k a a a k k k ++=++=++=⎧⎧⎧⎨⎨⎨+-=+-=+-=⎩⎩⎩===⎧⎧⎧⎨⎨⎨===⎩⎩⎩所以或或解得或或 而a 是正整数，所以只可能39,12,55,26,a a k k ==⎧⎧⎨⎨==⎩⎩或 当a=39时，方程（2）即x 2+57x+56=0，它的两根分别为-1和-56，此时两个函数的图象还有两个交点（-1，-56）和（-56，-1）．当a=12时，方程（2）即x 2+30x+56=0，它的两根分别为-2和-28，此时两个函数的图象还有两个交点（-2，-28）和（-28，-2）．评析：这是初中数学的重点知识与方法高度综合的题目，要求会自行演算独立解答．二、几何问题在初中阶段，图形的运动主要是合同变换，包含平移、轴对称、旋转和中心对称．另外，在我国的几何教学中，对等积变换的知识日益普及，主要是利用“同底等高的两个三角形面积相等”和三角形面积公式来证题、计算，包括解决线段的比例问题．例3 如图1所示，△ABC 中，∠ABC=46°，D 是BC 边上一点，DC=AB ，∠DAB=21°，•试确定∠CAD 的度数．（2007年北京市中学生数学竞赛初二年级试题四）图1 图2解如图2，作△ABD关于AD的轴对称图形△AED，即∠EAD=21°，AE=AB，•所以DE=BD．易知∠ADC=21°+46°=67°，所以∠ADE=∠ADB=180°-67°=113°，∠CDE=113°-67°=46°，连接CE，DC=AB，△ABD≌△CDE≌△ADE．设O为AE与DC的交点，由于∠ODE=∠OED=46°，所以OD=OE．又DC=AE，所以AO=CO ∠OCA=∠OAC ∠COE=2∠ACO．易知∠COE=2×46°=92°，因此2∠ACO=∠COE=92°∠ACO=46°=∠OAC．所以∠DAC=∠DAE+∠EAC=21°+46°=67°．例4如图3，已知等腰△ABC中，AB=AC，P、Q分别为AC、AB上的点，且AP=PQ=•QB=BC，则∠PCQ=______．（2007年北京市中学生数学竞赛初二年级试题）图3 图4解：如图4，过P作AB的平行线，过B作PQ的平行线，二平行线相交于O，则PQBO•是个菱形．连接CO．由AB=AC，AP=QB，则PC=AQ，AP=QB=PO，∠CPO=∠PAQ，所以△PQC≌△APQ，因此CO=PQ=CB=OB，可知△BCO为等边三角形，∠BCO=∠CBO=60°，•设∠CAB=θ，•则∠PCO=∠QBO=θ，由三角形内角和定理，得3θ+2×60°=180°⇒θ=20°，因此∠PCQ=80°-•50°=30°．例5 如图5，四边形ABCD 是梯形，点E 是上底AD 边上一点，CE 的延长线与BA 的延长线交于点F ，过点E 作BA 的平行线CD 交的延长线于点M ，BM 与AD 交于点N ．证明：∠AFN=∠DME ．（2007全国初中数学联合竞赛试题）例5分析 延长BF ，CM 相交于Q ，因为EM ∥AF ，所以∠DME=∠DQA ．要证∠AFN=∠DME ，只需证∠AFN=∠DQA 即可．为此，只需证FN ∥MC ．证明 （面积法）连接FM ，BE ，CN ，因为EM ∥AF ，所以S △PFM =S △PBE ，因为AD ∥BC ，S △BNE =S △CNE ，因此S △BNE +S △PNE =S △CNE +S △PNE ．即S △PBE =S △PNC ，所以S △PFM =S △PNC ．两边同加S △PMC 得S △FMC =S △NMC ，所以FN ∥MC ，又已知FB ∥ME ，所以∠AFN=∠DME ．至于其它的证法我们就不再例举了．例6 试问：18能否表示为3个互异的正整数的倒数的和？18能否表示为3•个互异的完全平方数的倒数的和？如果能，请给出一个例子；如果不能，请说明理由． （第12届华杯赛初一组决赛试题14）解：（1）由于18=14×12=14×（112+16+14）=114824++116，所以18能表示为3个互异的正整数的倒数的和．（2）不妨设三个正整数a<b<c ，满足18=21a +21b +21c． 由于a ，b ，c 是互异的正整数，则21c <21b <21a， 从而18=21a +21b +21c <23a ，所以a 2>24．又18>21a，所以a 2>8，故a 2=9或16． 若a 2=9，则21b +21c =18-19=172，于是172>21b，有b 2>72； 又因为21c <21b ，所以172=21b +21c <22b ， 因此b 2<144，所以72<b 2<144．故b 2=81，100或121，将b 2=81，100，121分别代入c 2=227272b b -，没有一个是完全平方数，此时无解．若a 2=16，则21b +21c =18-116=116， 同上讨论可得：16<b 2<32，所以b 2=25，c 2=22161625169b b ⨯=-不是整数． 综上所述，18不能表示为3个互异的完全平方数的倒数之和． 例7 已知a ，b 都是正整数，试问关于x 的方程x 2-abx+12（a+b ）=0是否有两个整数解？如果有，请把它们求出来；如果没有，请给出证明．解 不妨设a ≤b ，且方程的两个整数根为x 1，x 2（x 1≤x 2），则有12121()2x x ab x x a b +=⎧⎪⎨=+⎪⎩ 所以x 1x 2-x 1-x 2=12a+12b-ab ，4（x 1-1）（x 2-1）+（2a-1）（2b-1）=5． 因为a ，b 都是正整数，所以x 1，x 2均是正整数．于是x 1-1≥0，x 2-1≥0，2a-1≥1，2b-1≥1，所以12(1)(1)0(21)(21)5x x a b --=⎧⎨--=⎩或12(1)(1)1(21)(21)1x x a b --=⎧⎨--=⎩ （1）当12(1)(1)0(21)(21)5x x a b --=⎧⎨--=⎩时，由于a ，b 都是正整数，且a ≤b ，可得a=1，b=3． 此时，一元二次方程为x 2-3x+2=0，它的两个根为x=1，x=2．（2）当12(1)(1)1(21)(21)1x x a b --=⎧⎨--=⎩时，可得a=1，b=1，此时，一元二次方程为x 2-x+1=0，它无整数解．综上所述，当且仅当a=1，b=3时，题设方程有整数解，且它的两个整数解为x 1=1，x 2=2．例8 （1）是否存在正整数m ，n ，使得m （m+2）=n （n+1）？（2）设k （k ≥3）是给定的正整数，是否存在正整数m ，n ，使得m （m+k ）=n （n+1）？ 解:（1）答案是否定的．若存在正整数m ，n ，使得m （m+2）=n （n+1）． 则（m+1）2=n 2+n+1，显然n>1．于是n 2<n 2+n+1<（n+1）2，所以n 2+n+1不是平方数，矛盾．（2）当k=3时，若存在正整数m ，n ，使得m （m+3）=n （n+1），则4m 2+12m=4n 2+4n ⇔（2m+3）2=（2n+1）2+8即（2m+3-2n-1）（2m+3+2n+1）=8⇔ （m-n+1）（m+n+2）=2， 而m+n+2>2，故上式不可能成立．当k ≥4时，若k=2t （t 是不小于2的整数）为偶数，取m=t 2-t ，n=t 2-1，则m （m+k ）=（t 2-t ）（t 2+t ）=t 4-t 2，n （n+1）=（t 2-1）t 2=t 4-t 2，因此这样的（m ，n ）满足条件．若k=2t+1（t是不小于2的整数）为奇数，取m=22t t-，n=222t t+-，则m（m+k）=22t t-（22t t-+2t+1）=14（t4+2t3-t2-2t）n（n+1）=222t t+-·22t t+=14（t4+2t3-t2-2t），因此这样的（m，n）满足条件．综上所述，当k=3时，答案是否定的；当k≥4时，答案是肯定的．（注：当k≥4时，构造的例子不是唯一的．）四、组合与极值组合问题对锻炼思维意义重大，初中只适宜分类计数、加法原理、乘法原理的简单运用，简单的包含排除原理，基本的抽屉原理也是重要的内容．但在初中阶段，不应提前引入排列组合的计算公式．特别是提前较大范围的培训高中的排列组合知识，会激起大范围超前学习的竞争热，从而影响基础教育，并且也影响竞赛的公平性．建议命一些以几何元素为背景的构造性的问题，容易引发学生兴趣，又使套用组合公式的人容易出错，这类问题的研制特别引人注目．例9 平面上有6个点，其中任何3个点不在同一条直线上，以这6个点为顶点可以构造多少个不同的三角形？从这些三角形中选出一些，如果要求其中任何两个三角形没有公共点，则最多可以选出多少个三角形？（第12届华杯赛初一组决赛试题12）解答:（1）先从6个点中选取1个做三角形的一个顶点，有6种取法；•再从余下的5点中选取1个做三角形的第二个顶点，有5种取法；再从余下的4个点中选取1个点做三角形的第三个顶点者，有4种取法．因为任何3个点不在同一条直线上，所以，这样选出的三个点可以做出一个三角形．但是，如果选出的三个点相同的话，则做出的三角形相同，•三个点相同的取法有3×2×1=6种，所以，以这6个点为顶点可以构造654321⨯⨯⨯⨯=20个不同的三角形．（2）每个三角形有3个顶点，所以，6个点最多只能做出2个三角形，•它们没有公共顶点，如图4（1）．（3）用英文大写字母A，B，C，D，E，F记这6个点，如果可以选出5个三角形，它们共有15个顶点，需要15个英文大写字母．但是，不同的英文大写字母仅有6个，因此，这5•个三角形中至少有三个三角形有同一个顶点，不妨设为点A．根据题目条件，这三个三角形没有公共边，即除去公共顶点A之外，其余6•个顶点互不相同，即表示这6个顶点的字母不相同．否则，根据题目条件，它们将有公共边．但是，除A之外，我们仅有5个不同的字母，所以，不可能存在5个三角形，它们没有公共边．如图4（2）所示，△ABC，△ADE，△BDF和△CEF这4个三角形没有公共边，所以，最多可以选出4个三角形，它们没有公共边．例10 若对于任意n个连续正整数中，总存在一个数的数字之和8是的倍数．试确定n的最小值，并说明你的理由．（2007北京市中学生数学竞赛初二年级试题五）解先证n≤14时题设的性质不成立．因为，当n=14时，对于9999993，9999994，…，999999，…，10000006这14个连续整数中，任意一个数字的数字之和均不能被8整除．所以n≤14时题设的性质不成立．因此要使题设的性质成立，应有n≥15．再证n=15时，题设的性质成立．设a1，a2，…，a15为任意的连续15个正整数，则这15个正整数中，个位数字为0•的整数最多有两个，最少有一个，可分为：（1）当a1，a2，…，a15中个位数字为0的整数有两个时，设a i<a j，且a i，a j的个位数字为0．则满足a i，a i+1，a i+2，…，a i+9，a j为连续的11个整数，其中a i，a i+1，a i+2，…，a i+9无进位设n i表示a i各位数字之和．则前10个数的各位数字之和分别为n i，n i+1，…，n i+9则这连续的10个数中至少有一个被8整除．（2）当a1，a2，…，a15中个位数字为0的整数只有一个时，设其中的a i的个位数字为0，•①若整数满足1≤i≤8，则在a i后面至少有7个连续整数，则a i，a i+1，a i+2，…，a i+7这8个连续整数的各位数字和也为8个连续整数，所以必有一个数能被8整除．②若整数i满足9≤i≤15，则在a前面至少有8个连续整数，不妨设为a i-8，a i-7，a i-5，a i-4，a i-3，a a-2，a a-2，a i-1，这8个连续整数的各位数字和也为8个连续整数，所以必有一个数能被8整除．由①、②可知，当a1，a2，…，a15中个位数字为0的整数只有一个时，必有一个数，其各位数字之和是8的倍数．综上（1）、（2）所述，对于任意15个连续整数中，必有一个数，•其各位数字之和是的倍数．而小于15个的任意连续整数不成立此性质，所以n的最小值是15．例11 平面上有若干个点，其中任意三点都不在同一直线上，将这些点分成三组，并按下面的规则用线段连接：①在同一组的任意两点都没有线段连接；②不在同一组的任意两点间一定有线段连接．（1）若平面上恰好有9个点，且平均分成三组，那么平面上有多少条线段？（2）若平面上恰好有9个点，且点数分成2，3，4三组，那么平面上有多少条线段？（3）若平面上共有192条线段，那么平面上至少有多少个点？（第十八届“希望杯”全国数学邀请赛初二第2试23题）解：（1）平面上恰好有9个点，且平均分成三组，每组3个点，•按题设规则用线段连接，可以连出3×3+3×3+3×3=27条线段．（2）平面上恰好有9个点，且点数分成2，3，4三组，按题设规则用线段连接，可以连出2×3+2×4+3×4=26条线段．（3）设平面上三组点数为m，n，p个，s=m+n+p，目标求s的最小值？按题设规则用线段连接，可以连出mn+mp+np=192条线段．由于s2=（m+n+p）2=m2+n2+p2+2mn+2mp+2np≥mn+mp+np+2mn+2mp+2np=3mn+3mp+3np=•3（mn+mp+np）=3×192=576=242所以s≥24．s的最小值是24．事实上，当这24个点平分为3组，每组8个点，按题设规则用线段连接，恰可以连出8×8+8×8+8×8=3×64=192条线段．因此平面上至少有24个点．- 11 -。