锐角的三角比知识讲解
沪教版初三上册397914锐角的三角比 知识讲解

沪教版初三数学上册知识点梳理重点题型(常考知识点)巩固练习锐角的三角比 知识讲解【学习目标】1.结合图形理解记忆锐角三角函数的定义;2.会推算30°、45°、60°角的三角函数值,并熟练准确的记住特殊角的三角函数值;3.理解并能熟练运用“同角三角函数的关系”及“锐角三角函数值随角度变化的规律”.【要点梳理】要点一、锐角三角函数的概念如图所示,在Rt △ABC 中,∠C =90°,∠A 所对的边BC 记为a ,叫做∠A 的对边,也叫做∠B 的邻边,∠B 所对的边AC 记为b ,叫做∠B 的对边,也是∠A 的邻边,直角C 所对的边AB 记为c ,叫做斜边.锐角A 的对边与斜边的比叫做∠A 的正弦,记作sinA ,即;锐角A 的邻边与斜边的比叫做∠A 的余弦,记作cosA ,即;锐角A 的对边与邻边的比叫做∠A 的正切,记作tanA ,即;锐角A 的邻边与对边的比叫做∠A 的余切,记作cotA ,即.同理;;;要点诠释:(1)正弦、余弦、正切、余切函数是在直角三角形中定义的,反映了直角三角形边与角的关系,是两条线段的比值.角的度数确定时,其比值不变,角的度数变化时,比值也随之变化.(2)sinA ,cosA ,tanA ,cotA 分别是一个完整的数学符号,是一个整体,不能写成,,,不能理解成sin 与∠A ,cos 与∠A ,tan 与∠A ,cot 与∠A 的乘积.书写时习惯上省略∠A 的角的记号“∠”,但对三个大写字母表示成的角(如∠AEF),其正切应写成“tan ∠AEF ”,不能写成“tanAEF ”;另外,、、、常写成、、、.(3)任何一个锐角都有相应的锐角三角函数值,不因这个角不在某个三角形中而不存在.(4)由锐角三角函数的定义知:当角度在0°<∠A<90°间变化时,,,tanA >0 cotA >0.要点二、特殊角的三角函数值C a b要点诠释:(1)通过该表可以方便地知道30°、45°、60°角的各三角函数值,它的另一个应用就是:如果知道了一个锐角的三角函数值,就可以求出这个锐角的度数,例如:若,则锐角.(2)仔细研究表中数值的规律会发现:、、的值依次为、、,而、、的值的顺序正好相反,、、的值依次增大,其变化规律可以总结为:①正弦、正切值随锐角度数的增大(或减小)而增大(或减小)②余弦、余切值随锐角度数的增大(或减小)而减小(或增大).要点三、锐角三角函数之间的关系如图所示,在Rt△ABC中,∠C=90°.(1)互余关系:,;tanA=cot(90°-∠A)=cotB , tanB=cot(90°-∠B)=cotA.(2)平方关系:;(3)倒数关系:或;(4)商的关系:要点诠释:锐角三角函数之间的关系式可由锐角三角函数的意义推导得出,常应用在三角函数的计算中,计算时巧用这些关系式可使运算简便.【典型例题】类型一、锐角三角函数值的求解策略1.(2016•安顺)如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是()A.2 B. C. D.【思路点拨】根据勾股定理,可得AC、AB的长,根据正切函数的定义,可得答案.【答案】D.【解析】解:如图:,由勾股定理,得AC=,AB=2,BC=,∴△ABC为直角三角形,∴tan∠B==,故选:D.【总结升华】本题考查了锐角三角函数的定义,先求出AC、AB的长,再求正切函数.举一反三:【高清课堂:《锐角三角函数》专题第一讲:锐角三角函数---例1(1)】【变式】在Rt△ABC中,,若a=3,b=4,则,,,,.【答案】5 ,,,,.类型二、特殊角的三角函数值的计算2.求下列各式的值:(1)(2015•茂名校级一模)6tan230°﹣sin60°﹣2sin45°;(2)(2015•乐陵市模拟)sin60°﹣4cos230°+sin45°•tan60°;(3)(2015•宝山区一模)+cot30°﹣.【答案与解析】解:(1)原式==﹣.(2)原式=×﹣4×()2+×=﹣3+=;(3)原式=+﹣=2+﹣=3﹣2+2=+2.【总结升华】熟记特殊角的三角函数值或借助两个三角板推算三角函数值,先代入特殊角的三角函数值,再进行化简.举一反三:【高清课堂:《锐角三角函数》专题第一讲:锐角三角函数---例1(3)】【变式】在Rt△ABC中,,若∠A=45°,则,,,,.【答案】45°,,,,.类型三、锐角三角函数之间的关系3.(2015•河北模拟)已知△ABC中的∠A与∠B满足(1﹣tanA)2+|sinB﹣|=0(1)试判断△ABC的形状.(2)求(1+sinA)2﹣2﹣(3+tanC)0的值.【答案与解析】解:(1)∵|1﹣tanA)2+|sinB﹣|=0,∴tanA=1,sinB=,∴∠A=45°,∠B=60°,∠C=180°﹣45°﹣60°=75°,∴△ABC是锐角三角形;(2)∵∠A=45°,∠B=60°,∠C=180°﹣45°﹣60°=75°,∴原式=(1+)2﹣2﹣1=.【总结升华】本题考查的是特殊角的三角函数值,熟记各特殊角度的三角函数值是解答此题的关键.类型四、锐角三角函数的拓展探究与应用4.如图所示,AB是⊙O的直径,且AB=10,CD是⊙O的弦,AD与BC相交于点P,若弦CD=6,试求cos∠APC的值.【答案与解析】连结AC,∵ AB是⊙O的直径,∴∠ACP=90°,又∵∠B=∠D,∠PAB=∠PCD,∴△PCD∽△PAB,∴.又∵ CD=6,AB=10,∴在Rt△PAC中,.【总结升华】直角三角形中,锐角的三角函数等于两边的比值,当这个比值无法直接求解,可结合相似三角形的性质,利用对应线段成比例转换,间接地求出这个比值.锐角的三角函数是针对直角三角形而言的,故可连结AC,由AB是⊙O的直径得∠ACB=90°,,PC、PA均为未知,而已知CD=6,AB=10,可考虑利用△PCD∽△PAB得.5.通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图1①,在△ABC中,AB=AC,顶角A的正对记作sadA,这时.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:(1)sad60°=________.(2)对于0<A<180°,∠A的正对值sadA的取值范围是_______.(3)如图1②,已知sinA=,其中∠A为锐角,试求sadA的值.【答案与解析】(1)1;(2)0<sadA<2;(3)如图2所示,延长AC到D,使AD=AB,连接BD.设AD=AB=5a,由得BC=3a,∴,∴ CD=5a-4a=a,,∴.【总结升华】(1)将60°角放在等腰三角形中,底边和腰相等,故sadA=1;(2)在图①中设想AB=AC 的长固定,并固定AB让AC绕点A旋转,当∠A接近0°时,BC接近0,则sadA接近0但永远不会等于0,故sadA>0,当∠A接近180°时,BC接近2AB,则sadA接近2但小于2,故sadA <2;(3)将∠A放到等腰三角形中,如图2所示,根据定义可求解.。
《求锐角的三角比的值》 讲义

《求锐角的三角比的值》讲义一、锐角三角比的定义在直角三角形中,锐角的三角比包括正弦(sin)、余弦(cos)、正切(tan)。
正弦(sin)等于锐角的对边与斜边的比值;余弦(cos)等于锐角的邻边与斜边的比值;正切(tan)等于锐角的对边与邻边的比值。
例如,在一个直角三角形 ABC 中,∠C 为直角,∠A 为锐角,其对边为 a,邻边为 b,斜边为 c。
那么,sin A = a / c,cos A = b / c,tan A = a / b。
二、特殊锐角的三角比值我们先来了解一些特殊锐角(30°、45°、60°)的三角比值,这些是需要大家牢记的。
1、 30°角对于 30°角的直角三角形,假设斜边为 2,对边为 1,根据勾股定理可得邻边为√3。
所以,sin 30°= 1 / 2,cos 30°=√3 / 2,tan 30°=√3 / 3。
2、 45°角在等腰直角三角形中,两个直角边相等,假设直角边为 1,斜边为√2。
则 sin 45°= cos 45°=√2 / 2,tan 45°= 1。
3、 60°角与30°角相对应,60°角的直角三角形中,假设斜边为2,邻边为1,对边为√3。
所以,sin 60°=√3 / 2,cos 60°= 1 / 2,tan 60°=√3。
三、利用三角函数定义求三角比值当已知直角三角形的边长时,我们可以直接根据三角比的定义来求出相应锐角的三角比值。
例如,在直角三角形中,∠C 为直角,∠A 为锐角,已知∠A 的对边为 4,邻边为 3,斜边为 5。
则 sin A = 4 / 5,cos A = 3 / 5,tanA = 4 / 3。
再比如,一个直角三角形的斜边为 10,一个锐角的对边为 6,那么这个锐角的正弦值就是 6 / 10 = 3 / 5。
锐角的三角比

锐角的三角比一、介绍在数学中,三角比是指三角函数中的比值,用于描述三角形的各个边与角之间的关系。
锐角是指小于90度的角,因此在本文中,我们将讨论关于锐角的三角比。
三角比一共有六个,分别是正弦(sin)、余弦(cos)、正切(tan)、余切(cot)、正割(sec)和余割(csc)。
这些三角比在数学和物理等科学领域中都有广泛的应用,例如解决三角函数方程、测量角度和距离等。
二、正弦(sin)在锐角三角形中,正弦表示三角形的对边与斜边之间的比值。
数学表达式如下:sin(A) = 对边 / 斜边其中,A表示锐角的大小。
正弦的取值范围是-1到1之间,当A接近0度时,正弦的值接近0;而当A接近90度时,正弦的值接近1。
三、余弦(cos)余弦代表锐角三角形的邻边与斜边之间的比值。
数学表达式如下:cos(A) = 邻边 / 斜边同样地,余弦的取值范围也是-1到1之间。
在锐角三角形中,当A接近0度时,余弦的值接近1;当A接近90度时,余弦的值接近0。
四、正切(tan)正切是锐角三角形中对边与邻边之间的比值。
数学表达式如下:tan(A) = 对边 / 邻边正切的取值范围是无穷,当A接近0度时,正切的值接近0;当A接近90度时,正切的值趋于无穷大。
五、余切(cot)余切是锐角三角形中邻边与对边之间的比值。
数学表达式如下:cot(A) = 邻边 / 对边余切的取值范围也是无穷,当A接近0度时,余切的值趋于无穷大;当A接近90度时,余切的值接近0。
六、正割(sec)正割表示斜边与邻边之间的比值。
数学表达式如下:sec(A) = 斜边 / 邻边正割的取值范围是大于等于1的实数。
当A接近0度时,正割的值趋于无穷大;当A接近90度时,正割的值接近1。
七、余割(csc)余割代表斜边与对边之间的比值。
数学表达式如下:csc(A) = 斜边 / 对边余割的取值范围也是大于等于1的实数。
当A接近0度时,余割的值接近无穷大;当A接近90度时,余割的值趋近于1。
锐角三角比的意义

儒洋教育学科教师辅导讲义课 题 锐角三角比的意义教学目标1、理解锐角的正切、余切、正弦、余弦的概念;2、能正确使用锐角的正切、余切、正弦、余弦的符号语言;3、培养观察、归纳、总结数学问题的能力。
教学内容一、新课讲解:1、操作:(1)任作锐角∠。
(2)在上任取B 1、B 2、B 3,分别过B 1、B 2、B 3作的垂线。
垂足为C 1、C 2、C 3。
(3)量出B 1C 1和1,B 2C 2和2,B 3C 3和3的长度,并计算出111B C AC ,222B CAC ,333B C AC 的值。
2、探究:由以上操作可得到:△1C 1、△2C 2、△3C 3。
显然有1C 12C 23C 3,于是可得:331122123B C B C B CAC AC AC ==3、结论:在放大和缩小时,当锐角A 的大小固定不变后,无论△的边长怎么变化,两条直角边的比值总是不变的。
大写字母C 表示△的直角,小写字母a 表示∠A 的对边,b 表示∠B 的对边,c 表示斜边。
(如上图) 同理,通过分析可知在放大和缩小时,当锐角A 的大小固定不变后, 无论△的边长怎么变化,直角边与斜边的比值总是不变的。
二、知识要点:锐角A 的对边()与邻边()的比叫做锐角A 的正切,记作。
如图△中,∠900,baAC BC A A A ===的邻边锐角的对边锐角tan锐角A 的邻边()与对边()的比叫做锐角A 的余切,记作。
如图△中,∠900,abBC AC A A A ===的对边锐角的邻边锐角cot锐角A 的对边()与斜边()的比叫做锐角A 的正弦,记作。
如图△中,∠900,caAB BC A A A ===的斜边锐角的对边锐角sinCBC 1B 3B 2B 1C 3C 2AbacACB锐角A 的对边()与斜边()的比叫做锐角A 的余弦,记作。
如图△中,∠900,cbAB AC A A A ===的斜边锐角的邻边锐角cos在直角三角形中,锐角A 的正切()、余切()、正弦()、余弦()统称为锐角A 的三角比,简称三角比。
锐角三角比讲义
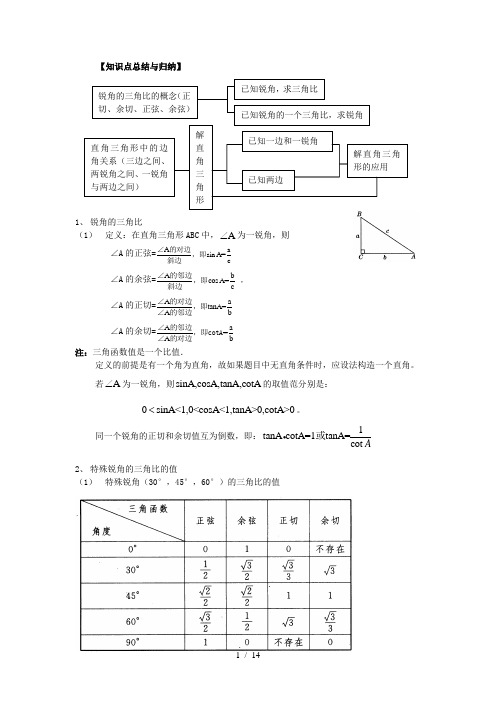
【知识点总结与归纳】1、锐角的三角比(1)定义:在直角三角形ABC中,A∠为一锐角,则∠A的正弦=A asin A=c∠的对边,即斜边∠A的余弦=A bcos A=c∠的邻边,即斜边,∠A的正切=A atanA=A b∠的对边,即∠的邻边∠A的余切=A a=A b∠的邻边,即cotA∠的对边注:三角函数值是一个比值.定义的前提是有一个角为直角,故如果题目中无直角条件时,应设法构造一个直角。
若A∠为一锐角,则sinA,cosA,tanA,cotA的取值范分别是:0sinA<1,0<cosA<1,tanA>0,cotA>0<。
同一个锐角的正切和余切值互为倒数,即:1tanA cotA=1tanA=cot A或2、特殊锐角的三角比的值(1)特殊锐角(30°,45°,60°)的三角比的值锐角的三角比的概念(正切、余切、正弦、余弦)已知锐角,求三角比已知锐角的一个三角比,求锐角直角三角形中的边角关系(三边之间、两锐角之间、一锐角与两边之间)解直角三角形已知一边和一锐角已知两边解直角三角形的应用(2) 同角,互余的两角多的三角比之间的关系: 倒数关系:1tanA=cot A平方关系:22sin A+cos A=1 积商关系:sin cos tanA=,cot cos sin A AA A A=余角和余函数的关系:如果090A B ∠+∠=,那么sinA=cosB, tanA=cotB (正弦和余弦,正切和余切被称为余函数关系)。
注意:求锐角三角比的值问题(1) 在直角三角形中,给定两边求锐角的三角比,关键是搞清某锐角的“对边”“邻边”,掌握三角比的定义。
(2) 给出锐角的度数,求这个锐角的三角比特殊锐角,一般情况下,使用精确值;在实际应用中,根据问题要求处理。
求非特殊锐角的三角比的值,使用计算器或查表求值。
(3) 当锐角不是直角三角形的内角,首先观察有否相等的锐角可代换,而且可代换的锐角含在某直角三角形中,如果没有可代换的相等的锐角,可作适当的垂线构建含有这个锐角的直角三角形。
锐角三角比

锐角三角比:知识点一:锐角三角比的定义: 一、 锐角三角比定义:在Rt △ABC 中,∠C=900, ∠A 、∠B 、∠C 的对边分别为a 、b 、c , 则∠A 的正弦可表示为:sinA= , ∠A 的余弦可表示为cosA=∠A 的正切:tanA= ,它们弦称为∠A 的锐角三角比 2、取值范围 <sinA< cosA< tanA> 】 例1.如图所示,在Rt △ABC 中,∠C =90°.第1题图①斜边)(sin =A =______, 斜边)(sin =B =______;②斜边)(cos =A =______,斜边)(cos =B =______;③的邻边A A ∠=)(tan =______,)(tan 的对边B B ∠==______.例2. 锐角三角函数求值:在Rt △ABC 中,∠C =90°,若a =9,b =12,则c =______,sin A =______,cos A =______,tan A =______, sin B =______,cos B =______,tan B =______.例3.已知:如图,Rt △TNM 中,∠TMN =90°,MR ⊥TN 于R 点,TN =4,MN =3.求:sin ∠TMR 、cos ∠TMR 、tan ∠TMR .例题:类型一:直角三角形求值1.已知Rt △ABC 中,,12,43tan ,90==︒=∠BC A C 求AC 、AB 和cos B .2.如图,⊙O 的半径OA =16cm ,OC ⊥AB 于C 点,⋅=∠43sin AOC 求AB 及OC 的长.3.已知:⊙O 中,OC ⊥AB 于C 点,AB =16cm ,⋅=∠53sin AOC(1)求⊙O 的半径OA 的长及弦心距OC ; (2)求cos ∠AOC 及tan ∠AOC .4. 已知A ∠是锐角,178sin =A ,求A cos ,A tan 的值针对训练:1.在Rt △ABC 中,∠ C =90°,若BC =1,AB =5,则tan A 的值为A .55 B .255 C .12D .2 2.在△ABC 中,∠C =90°,sin A=53,那么tan A 的值等于( ).A .35B . 45C . 34D . 43类型二. 利用角度转化求值:1.已知:如图,Rt △ABC 中,∠C =90°.D 是AC 边上一点,DE ⊥AB 于E 点.DE ∶AE =1∶2.求:sin B 、cos B 、tan B .2.如图,直径为10的⊙A经过点(05)C,和点(00)O,,与x轴的正半轴交于点D,B是y轴右侧圆弧上一点,则cos∠OBC的值为()A.12B.32C.35D.453.如图,角α的顶点为O,它的一边在x轴的正半轴上,另一边OA上有一点P(3,4),则sinα=.4.如图,菱形ABCD的边长为10cm,DE⊥AB,3sin5A=,则这个菱形的面积= cm2.5.如图,O⊙是ABC△的外接圆,AD是O⊙的直径,若O⊙的半径为32,2AC=,则sin B的值是()A.23B.32C.34D.436. 如图6,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处.已知8AB=,10BC=,AB=8,则tan EFC∠的值为 ( )A.34B.43C.35D.457. 如图7,在等腰直角三角形ABC∆中,90C∠=︒,6AC=,D为AC上一点,若1tan5DBA∠=,则AD 的长为( )A.2 B.2 C.1 D.228. 如图8,在Rt△ABC中,∠C=90°,AC=8,∠A的平分线AD=3316求∠B的度数及边BC、AB的长.DCBAOyx第8题图A DECBFDABC类型三. 化斜三角形为直角三角形例1 如图,在△ABC中,∠A=30°,∠B=45°,AC=23,求AB的长.例2.已知:如图,在△ABC中,∠BAC=120°,AB=10,AC=5.求:sin∠ABC的值.针对训练1.如图,在Rt△ABC中,∠BAC=90°,点D在BC边上,且△ABD是等边三角形.若AB=2,求△ABC的周长.(结果保留根号)2.已知:如图,△ABC中,AB=9,BC=6,△ABC的面积等于9,求sin B.3. ABC中,∠A=60°,AB=6 cm,AC=4 cm,则△ABC的面积是A.23 cm 2 .43 cm 2 C.63 cm 2 D.12 cm 2类型四:利用网格构造直角三角形例1 如图所示,△ABC 的顶点是正方形网格的格点,则sinA 的值为( ) A .12 B .55 C .1010D .255对应练习:1.如图,△ABC 的顶点都在方格纸的格点上,则sin A =_______.2.如图,A 、B 、C 三点在正方形网络线的交点处,若将ABC ∆绕着点A 逆时针旋转得到''B AC ∆,则'tan B 的值为 A.41 B. 31 C.21D. 13.正方形网格中,AOB ∠如图放置,则tan AOB ∠的值是( )A .5 5 B. 2 5 5 C.12D. 2 特殊角的三角函数值当 时,正弦和正切值随着角度的增大而 余弦值随着角度的增大而 例1.求下列各式的值. 1).计算:︒-︒+︒60tan 45sin 230cos 2. 2)计算:︒-︒+︒30cos 245sin60tan 2.锐角α 30° 45° 60° sin α cos α tan αCBAABO3)计算:3-1+(2π-1)0-33tan30°-tan45°4.计算:30tan 2345sin 60cos 221⎪⎪⎭⎫ ⎝⎛︒-︒+︒+.5.计算: tan 45sin 301cos 60︒+︒-︒;家庭作业:1.已知:如图,在菱形ABCD 中,DE ⊥AB 于E ,BE =16cm ,⋅=1312sin A 求此菱形的周长.2.已知:如图,Rt △ABC 中,∠C =90°,3==BC AC ,作∠DAC =30°,AD 交CB 于D 点,求:(1)∠BAD ;(2)sin ∠BAD 、cos ∠BAD 和tan ∠BAD .3. 已知:如图△ABC 中,D 为BC 中点,且∠BAD =90°,31tan =∠B ,求:sin ∠CAD 、cos ∠CAD 、tan ∠CAD .4. 如图,在Rt △ABC 中,∠C=90°,53sin =B ,点D 在BC 边上,DC= AC = 6,求tan ∠BAD 的值.5.如图,△ABC 中,∠A=30°,3tan 2B =,43AC =.求AB 的长.签字确认 学员 教师 班主任DCBAACB。
初中数学:锐角的三角比知识清单

初中数学:锐角的三角比知识清单1.锐角的三角比定义:一个锐角的正切、余切、正弦、余弦统称为这个锐角的三角比.正切:把直角三角形中一个锐角的对边与邻边的比叫这个锐角的正切.即tan A A A ∠=∠的对边的邻边;余切:把直角三角形中一个锐角的邻边与对边的比叫这个锐角的余切.即cot A A A ∠=∠的邻边的对边;正弦:把直角三角形中一个锐角的对边与斜边的比叫这个锐角的正弦.即sin A A ∠=的对边斜边;余弦:把直角三角形中一个锐角的邻边与斜边的比叫这个锐角的余弦.即cos A A ∠=的邻边斜边;2.性质①当锐角增大时,这个锐角的正切与正弦值都增大,这个锐角的余切与余弦值都减小;②若90A B ∠+∠=︒,则tan ;cot cos sin B B A A ==;③1tan cot A A ⋅=.3.特殊角的三角比30α=︒60α=︒45α=︒tan α3331cot α3331sin α123222cos α3312224.锐角的三角比.⎧⎨⎩已知锐角,求三角比;已知锐角的三角比,求锐角1.解直角三角形:在直角三角形中,由已知元素求出所有未知元素的过程.2.直角三角形的边角关系(ABC ∆中,90C ∠=︒)222;90;tan ;cot ;sin .a b c A B a b a b A A A A b a c c ⎧⎪+=⎪∠+∠=︒⎨⎪⎪====⎩①三边关系:②锐角关系:③边角关系:3.解直角三角形的应用(1)仰角与俯角在视线与水平线所成的角中,视线在水平线上方的角叫仰角;视线在水平线下方的角叫俯角;(2)坡度:坡面的铅垂高度h和水平宽度l 的比叫做坡面的坡度,记作i ,即hi l=;坡度表示形式:1:i m =.坡面与水平面的夹角叫坡角,记为α;坡度i 与坡角α的关系:tan hi l==α一、锐角的三角比1.如图,在Rt △ABC 中,90C ∠= ,直角边BC 和AC 分别叫做A ∠的对边和邻边.2.(1)直角三角形中一个锐角的对边与斜边的比叫做这个锐角的正弦.===A BC a sinA AB c角的斜锐对边边.(2)直角三角形中一个锐角的邻边与斜边的比叫做这个锐角的余弦.===A AC b cosA AB c角的斜锐邻边边.(3)直角三角形中一个锐角的对边与邻边的比叫做这个锐角的正切.===A BC a tanA A AC b角的角的锐对边锐邻边.(4)直角三角形中一个锐角的邻边与对边的比叫做这个锐角的余切.===A AC bcotA A BC a角的角的锐邻边锐对边.【记忆技巧】正(正对)弦(斜边):对边比斜边;余(余邻—“鱼鳞”)弦(斜边):邻边比斜边.二、特殊角的三角比1.特殊角的锐角三角比:【记忆技巧】1.图形推导法2.表格记忆法α30°45°60°sin α122232cos α322212tan α3313cot α3133α30°45°60°sin α122232cos α322212tan α3313cot α3133三、解直角三角形1.在直角三角形中,由已知元素求未知元的过程叫做解直角三角形.2.在Rt △ABC 中,C ∠=90°,则它的三条边和两个锐角这五个元素间有以下关系:(1)锐角之间的关系:=A B ∠+∠90°;(2)三边之间的关系:222a b c +=;(3)边角之间的关系:A sinA ∠=的斜对边边;A cosA ∠=的斜邻边边;A tanA A ∠=∠的的对边邻边;A cotA A ∠=∠的的邻边对边.3.解直角三角形的类型与解法:类型一︰已知一边一角(角为两锐角之一)类型二︰已知两边(两直角边或一条直角边与斜边)四、解直角三角形的应用1.水平线:水平面上的直线以及和水平面平行的直线.2.铅垂线:垂直于水平面的直线,我们通常称为铅垂线.3.在测量时,如图,在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,视线在水平线下方的角叫做俯角.4.如图,坡面的铅垂高度(h )和水平宽度(l )的比叫做坡面的坡度(或坡比),记作i ,即h i l=.坡度通常写成1:m 的形式,如i =1︰1.5.5.坡面与水平面的夹角叫做坡角,记作α.坡度i 与坡角α之间的关系:hi tan lα==.1.方向角:以观测者的位置为中心,将正北或正南方向作为起始方向,旋转到目标的方向线所成的小于90°的角,通常表达成北(南)偏东(西)*度.若正好为45°,则表示为西(东)南(北)方向.2.方位角:从标准方向的北端起,顺时针方向到直线的水平角称为该直线的方位角.方位角θ的取值范围为0360θ≤< .。
锐角三角比2015

锐角三角比第一节 锐角的三角比1.锐角的三角比的定义如图 ,Rt △ABC 中,∠C =90°,锐角A 的四个三角比为: tanA =b aAC BC A A ==∠∠的邻边的对边cotA =abBC AC A A ==∠∠的对边的邻边sinA =c aAB BC A ==∠斜边的对边cosA =cbAB AC A ==∠斜边的邻边2.三角比的值(1)特殊角的三角比的值(30°、45°、60°)(2)锐角α三角比的值都是正数,并且有0<sin α<1,0<cos α<1 (3)同角三角比的关系:AA cot 1tan =(4)互余两角的三角比的关系:tan (90°—A )= cotA ,sin (90°—A )= cosA 注意点:1、要熟记30°、45°、60°等特殊角的三角比值;2、会使用计算器求锐角的三角比的值;3、要善于运用锐角三角比的定义求出锐角的三角比或边长,当所给的图形中没有直角三角形,会构造直角三角形;当图形较复杂,求一个角的三角比不方便时,会分析图形、条件,观察图形中是否有与所求角相等的角,然后转化成求另一个角的三角比. 例题精讲[例题1] 如图24—1,在△PQR 中,∠R =90°,tan P =3,RQ =12.求QR 和sin Q 的值.[例题分析]由已知在直角三角形中一个角的正切和一条直角边, 就可直接运用三角比的定义求出另一条直角边,再由勾股定理, 求出斜边,然后求出锐角的正弦或余弦.[解题过程] 在△PQR 中,∠R =90°,tan P =3,∴312==PRPR RQ ,∴4=PR 又∵222RQ PR PQ +=,∴5=PQ ∴53sin ==PQ PR Q [例题2] 如图24—2,在直角坐标平面内有一点),2(b A )0(>b .OA 与x 轴正半轴的┒R P Q 图24—1CAB夹角为α.(1)用含α的式子表示b . (2)用含b 的式子表示αcos .[例题分析]轴的距离有关,所以,只要过点A 作x 轴的垂线,就 可构造直角三角形,再运用三角比求解.[解题过程](1) 过点A 作x 轴的垂线,垂足为C ,则 ∠ACO =90°,∠AOC =α,由点),2(b A )0(>b ,得,,2b AC OC ==∴OCAC=αtan ,∴αtan 2=b . (2)∵22224b AC OC AO +=+=,∴42+=b AO∴44242cos 222++=+==b b b AO OC α. [例题3] 如图24—3,在△ABC 中,∠C =90°,DE ⊥AB 于点E ,交AC 于点D ,AC =5,BC =12. 求sin ∠ADE 的值.[例题分析]要求sin ∠ADE 的值,由正弦的定义即要求出AD DE的值,由于点D 、E 不确定,无法求DE 、AD 的值, 从题中的信息可以证明△ADE ∽△ABC ,得AB AC AD DE = 并可求ABAC 的值,但比较复杂,由于∠ADE 与∠B 都是∠A 的余角,所以∠ADE =∠B ,那么求sin ∠ADE 的值就转化为求sin ∠B 的值.[解题过程]∵ DE ⊥AB ∴∠AED =90°,又∠C =90°, ∴∠ADE =90°-∠A ==∠B在△ABC 中,∠C =90°, AC =5,BC =12,∴169222=+=BC AC AB ∴13=AB∴135sin ==∠AB AC B ∴sin ∠ADE =135. 锐角三角比的意义练习1.在Rt △ABC 中,∠C = 90°,AC = 4,BC = 5,则tan A = ,cot A = . 2.在Rt △MNP 中,∠P =90°,MP =10,52cot =N ,那么NP = ,MN = .3.如图24—4,在△PQR 中,∠R =90°,点M 在边PR 上. 设∠P =β,∠QMR =α,QR =a .用含a 和α、β的式子表示PM 的长.图24—2┒EC B A 图24—3DβαMRQP图24—44.如图24—5,在△ABC 中,∠ACB =90°,AC =6,AB =10,CD ⊥AB ,垂足为点D . 求(1) tan A ;(2)cot ∠ACD .5.在Rt △ABC 中,∠C =90°,a 、b 、c 分别是∠A 、∠B 、∠C 的对边,下列关系中,正确的是( ) (A)c b A =sin ; (B)a c B =cos ; (C) b a A =tan ; (D)ab B =cot . 6.如果Rt △ABC 中,∠C =90°,各边的长都扩大到原来的2倍,那么锐角A 的各三角比的值( )(A)都扩大到原来的2倍; (B)都缩小到原来的2倍; (C)没有变化; (D) 不能确定. 7.在Rt △SQR 中,∠R =90°,如果tanS =512 ,那么sinQ 的值等于( )(A)135; (B) 1312 ; (C) 125 ; (D) 512 . 8.在直角坐标平面内有一点)4,(a P )0(>a .OP 与x 轴正半轴的夹角为α. (1)用含α的式子表示a .(2)用含a 的式子表示αsin .9.若3tan α=3,则锐角α = 度. 10.求下列各式的值:(1)3cot60°-tan45°+2sin45°-2cos30°;(2)0060cos 160sin 30tan -+.第二节 解直角三角形解直角三角形与直角三角形的概念、性质、判定和作图有着密切的联系,是在深入研究几何图形性质的基础上,根据已知条件,计算直角三角形未知的边长、角度和面积,以及与之相关的几何图形的数量.1.明确解直角三角形的依据和思路在直角三角形中,我们是用三条边的比来表述锐角三角函数定义的.因此,锐角三角函数的定义本质揭示了直角三角形中边角之间的关系,是解直角三角形的基础.2.解直角三角形的基本类型和方法事实上,解直角三角形跟直角三角形的判定与作图有着本质的联系,因为已知两个元素(至少有一个是边)可以判定直角三角形全等,也可以作出直角三角形,即此时直角三角形┒DC A 图24—5是确定的,所以这样的直角三角形是可解的.解直角三角形就分为两大类,即已知一条边及一个锐角或已知两条边解直角三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
锐角的三角比-知识讲解————————————————————————————————作者:————————————————————————————————日期:锐角的三角比 知识讲解【学习目标】1.结合图形理解记忆锐角三角函数的定义;ﻫ2.会推算30°、45°、60°角的三角函数值,并熟练准确的记住特殊角的三角函数值;3.理解并能熟练运用“同角三角函数的关系”及“锐角三角函数值随角度变化的规律”.【要点梳理】要点一、锐角三角函数的概念如图所示,在Rt △ABC 中,∠C=90°,∠A 所对的边BC 记为a,叫做∠A 的对边,也叫做∠B 的邻边,∠B 所对的边AC 记为b,叫做∠B 的对边,也是∠A 的邻边,直角C 所对的边AB记为c,叫做斜边.ﻫ锐角A 的对边与斜边的比叫做∠A 的正弦,记作sinA,即sin A a A c∠==的对边斜边; 锐角A 的邻边与斜边的比叫做∠A 的余弦,记作cos A,即cos A b A c∠==的邻边斜边; 锐角A的对边与邻边的比叫做∠A 的正切,记作tanA ,即tan A a A A b ∠==∠的对边的邻边; 锐角A 的邻边与对边的比叫做∠A 的余切,记作c otA,即cot A b A A a∠==∠的邻边的对边. 同理sin B b B c ∠==的对边斜边;cos B a B c∠==的邻边斜边;tan B b B B a ∠==∠的对边的邻边; cot B a B B b∠==∠的邻边的对边ﻫ要点诠释: (1)正弦、余弦、正切、余切函数是在直角三角形中定义的,反映了直角三角形边与角的关系,是两条线段的比值.角的度数确定时,其比值不变,角的度数变化时,比值也随之变化.ﻫ (2)sinA,c osA,tanA,cotA 分别是一个完整的数学符号,是一个整体,不能写成A B C a b c,,ﻫ,cot A•不能理解成sin与∠A,cos与∠A,tan与∠A,cot与∠A的乘积.书写时习惯上省略∠A的角的记号“∠”,但对三个大写字母表示成的角(如∠AEF),其正切应写成“tan∠AEF”,不能写成“tanAEF”;另外,、、、2()常写成cot A、、、2cot A.ﻫ(3)任何一个锐角都有相应的锐角三角函数值,不因这个角不在某个三角形中而不存在.(4)由锐角三角函数的定义知:当角度在0°<∠A<90°间变化时,,,tanA>0 cotA>0.要点二、特殊角的三角函数值利用三角函数的定义,可求出30°、45°、60°角的各三角函数值,归纳如下:锐角cot30°145° 160°要点诠释:(1)通过该表可以方便地知道30°、45°、60°角的各三角函数值,它的另一个应用就是:如果知道了一个锐角的三角函数值,就可以求出这个锐角的度数,例如:若,则锐角. (2)仔细研究表中数值的规律会发现:、、的值依次为、、,而、、的值的顺序正好相反,、、的值依次增大,其变化规律可以总结为:①正弦、正切值随锐角度数的增大(或减小)而增大(或减小)②余弦、余切值随锐角度数的增大(或减小)而减小(或增大).ﻫ要点三、锐角三角函数之间的关系如图所示,在Rt△ABC中,∠C=90°.(1)互余关系:,;tanA=cot(90°-∠A)=cotB , tanB=cot(90°-∠B)=cotA.ﻫ(2)平方关系:;(3)倒数关系:或;ﻫ(4)商的关系:sin cos tan,cotcos sinA AA AA A==要点诠释:ﻫ锐角三角函数之间的关系式可由锐角三角函数的意义推导得出,常应用在三角函数的计算中,计算时巧用这些关系式可使运算简便.【典型例题】类型一、锐角三角函数值的求解策略1.如图所示,在Rt△ABC中,∠C=90°,AB=13,BC=5,求∠A,∠B的正弦、余弦、正切、余切值.【答案与解析】在Rt△ABC中,∠C=90°.∵ AB=13,BC=5.∴ 222213512AC AB BC =-=-=. ∴ 5sin 13BC A AB ==,12cos 13AC A AB ==,5tan 12BC A AC ==,12cot 5AC A BC ==; 12sin 13AC B AB ==,5cos 13BC B AB ==,12tan 5AC B BC ==,5cot 12BC B AC ==. 【总结升华】先运用勾股定理求出另一条直角边,再运用锐角三角函数的定义求值.举一反三:【变式】在Rt △ABC 中,∠C =90°,若a=3,b =4,则c = ,sinA = , cosA = ,sinB = , cosB = .【答案】c = 5 ,sinA =35 , cosA =45,sinB =45, cosB =35. 类型二、特殊角的三角函数值的计算2.求下列各式的值:(1)s in30°-2cos 60°+c ot45°; (2)tan 30sin 30cot 45tan 60••°°°°; (3)101(13)|1sin 30|2-⎛⎫---+ ⎪⎝⎭°. 【答案与解析】(1)原式11121222=-⨯+=; (2)原式31132613⨯==⨯; (3)原式11511212222=--+=-+=. A B C a b c【总结升华】熟记特殊角的三角函数值或借助两个三角板推算三角函数值,先代入特殊角的三角函数值,再进行化简.举一反三:【变式】在Rt△ABC中,∠C=90°,若∠A=45°,则∠B=,sinA=,cosA=,sinB= , cosB= .【答案】∠B=45°,sinA=22,cosA=22,sinB=22, cosB=22.类型三、锐角三角函数之间的关系3.(1)求锐角;(2)已知求锐角. 【答案与解析】(1)先将已知方程变形后再求解.ﻫ∴锐角=30°.ﻫ(2)先将已知方程因式分解变形.∴锐角=45°.【总结升华】要求等式中的锐角,只需求得这个角的三角函数值,运用换元的方法,把角的三角函数看作未知数,解方程求得它的解(值),然后再求这个锐角.类型四、锐角三角函数的拓展探究与应用4.如图所示,A B是⊙O的直径,且A B=10,CD 是⊙O 的弦,AD 与B C相交于点P,若弦CD =6,试求c os ∠A PC的值.【答案与解析】连结A C,∵ A B是⊙O 的直径,∴ ∠AC P=90°,又∵ ∠B =∠D,∠PAB=∠P CD,∴ △PCD ∽△P AB,∴ PC CD PA AB =. 又∵ CD=6,A B=10,∴在Rt△PAC 中,63cos 105PC CD APC PA AB ∠====. 【总结升华】直角三角形中,锐角的三角函数等于两边的比值,当这个比值无法直接求解,可结合相似三角形的性质,利用对应线段成比例转换,间接地求出这个比值.锐角的三角函数是针对直角三角形而言的,故可连结AC,由AB 是⊙O 的直径得∠ACB =90°,cos PC APC PA∠=,P C、PA 均为未知,而已知CD =6,AB=10,可考虑利用△PCD ∽△PA B得PC CD PA AB =. 5.通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sa d).如图1①,在△A BC 中,AB =AC ,顶角A的正对记作sadA,这时sadA BC AB==底边腰.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:(1)sad60°=________.(2)对于0<A<180°,∠A 的正对值sa dA 的取值范围是_______.(3)如图1②,已知sin A=35,其中∠A为锐角,试求sadA 的值.【答案与解析】(1)1;(2)0<sadA<2;(3)如图2所示,延长A C到D ,使AD =A B,连接BD.设AD =AB=5a,由3sin 5BC A AB ==得BC=3a, ∴ 22(5)(3)4AC a a a =-=,∴ C D=5a -4a=a ,22(3)10BD a a a =+=,∴ 10sadA 5BD AD ==. 【总结升华】(1)将60°角放在等腰三角形中,底边和腰相等,故sadA =1;(2)在图①中设想A B=AC的长固定,并固定AB 让AC 绕点A 旋转,当∠A 接近0°时,BC 接近0,则sadA 接近0但永远不会等于0,故sadA >0,当∠A接近180°时,BC 接近2AB ,则sa dA接近2但小于2,故sadA<2;(3)将∠A放到等腰三角形中,如图2所示,根据定义可求解.。
