南京市鼓楼区2019年中考一模数学试卷(含答案)
2019年江苏省南京市鼓楼区中考一模数学试卷
2019鼓楼区中考数学一模一、选择题（共6小题，共12分）1.4的算术平方根是（）A.2±B .2C .-2D .162.鼓楼区公益项目“在线伴读”平台开通以来，累计为学生在线答疑15000次，用科学计数法表示15000是（）A.61015.0⨯B .5105.1⨯C .4105.1⨯D .31015⨯3.计算()()322-a a ⋅的结果是（）A .8aB .8-aC .7aD .7-a4.若顺次连接四边形ABCD 各边中点所得的四边形是菱形，则下列结论中正确的是（）A .AB //CD B .AB ⊥BC C .AC ⊥BD D .AC =BD 5.下图是某家庭2018年每月交通费支出的条形统计图，若记该家庭2018年月交通费平均支出为a 元，则下列结论中正确的是（）A.220200≤≤a B .042022≤≤a C .062042≤≤a D .082062≤≤a6.A 、B 两地相距900km ，一列快车以200km /h 的速度从A 地匀速驶往B 地，到达B 地后立刻原路原速返回A 地，一列慢车以75km /h 的速度从B 地匀速驶往A 地，两车同时出发，截止到它们都到达中点时，两车恰好相距200km 的次数是（）A.5B .4C .3D .2二、填空题（共10小题，共20分）7.-3的绝对值是.8.若式子1+x 在实数范围内有意义，则x 的取值范围是.9.计算26-27的结果是.10.方程xx 221=+的解是.11.正五边形的每个外角的大小是.12.已知关于x 的方程022=-+mx x 有一根是2，则另一根是，m =.13.如图，AB //EG //CD ,EF 平分∠BED ,若∠D =69°，∠GEF =21°，则∠B =.14.如图，圆锥底面圆心为O ，半径OA =1，顶点为P ，将圆锥置于平面上，若保持顶点P 位置不变，将圆锥顺时针滚动三周后点A 恰好回到原处，则圆锥的高OP =.15.如图，点A ，B ，C ，D 在圆上，B 是弧AC 的中点，过C 做圆的切线交AB 的延长线于点E ，若∠AEC =84°，则∠ADC =.16.在∆ABC 中，AB =5，AC =4,BC =3,若点P 在∆ABC 内部（含边界）且满足PB PA PC ≤≤,则所有点P 组成的区域的面积为.三、解答题（共11小题，共88分）17.（7分）解不等式组()⎩⎨⎧≥--->423223x x x x18.（7分）计算⎪⎭⎫ ⎝⎛--+÷--312a a 19.（8分）（1）解方程012=--x x （2）在实数范围内分解因式12--x x 的结果为.20.（8分）如图，AB =AD ,AC =AE ,BC =DE ,点E 在BC 上.（1）求证ADE ABC ∆≅∆;（2）求证∠EAC =∠DEB .21.（8分）（1）两只不透明的袋子中均有红球、黄球、白球各1个，这些球除颜色外无其它差别。
【鼓楼区数学】2019~2020年初三(下)一模试卷+答案
南京学而思初中教研部
11 / 15
咨询电话 10108899
(2)连接 OA，分别过 O 作 OG⊥BC，OH⊥AD，垂足为 G、H. ∴BG=GC=5 ∴OG=5 ∴GD=BD-BG=6-5=1 易得四边形 OGDH 是矩形 ∴HD=OG=5, OH=GD=1
∴ OA = 5 2 , AH = OA2 − OH 2 = 7
过
3
程
当 DB、AM 相交于 F 时，即要折出对角线上的 DF = 1 DB . 那么…… 4
折 ①折出 DB；对折纸片，使 D、B 重合，得到的折痕与 DB 相交于点 E；继续折叠
叠 纸片，使 D、B 与 E 重合，得到的折痕与 DB 分别相交于点 F、G；
方 ②折出 AF、CG，分别交边 CD、AB 于 M、Q；
⑴若产品 A 的总成本为 yA ，则 yA 关于 x 的函数表达式为 ▲ . ⑵当 x = 1 000 时，产品 A、B 的总成本相同.
①求 a；
②当 x2 000 时，产品 C 的总成本最低，求 b 的取值范围.
24.（8 分）如图，△ABC 内接于⊙O，∠BAC =45° ，AD ⊥ BC ，垂足为 D，BD = 6 ， DC = 4 .
8. 若式子 x −1在实数范围内有意义，则 x 的取值范围是 ▲ .
9. 计算 3 +
1的结果是Fra bibliotek▲.
22
10. 方程 2 = 3 的解是 ▲ . x−3 x
11. 已知方程 2x2 + 4x − 3 =0 的两根分别为 x1 、 x2 ，则 x1 + x2 = ▲ ，
x1x2 = _____▲ .
12. 数据 2，3，2，3，5 的方差是 ▲ .
江苏省南京市2019-2020学年中考一诊数学试题含解析
江苏省南京市2019-2020学年中考一诊数学试题一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．如图，在△ABC中，∠C=90°，AC=BC=3cm.动点P从点A出发，以2cm/s的速度沿AB方向运动到点B．动点Q同时从点A出发，以1cm/s的速度沿折线AC→CB方向运动到点B．设△APQ的面积为y（cm2）.运动时间为x（s），则下列图象能反映y与x之间关系的是（）A．B．C．D．2．如图是几何体的俯视图，所表示数字为该位置小正方体的个数，则该几何体的正视图是（）A．B．C．D．3．在某校“我的中国梦”演讲比赛中，有9名学生参加决赛，他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名，不仅要了解自己的成绩，还要了解这9名学生成绩的( )A．众数B．方差C．平均数D．中位数4．下列图案中，是轴对称图形但不是中心对称图形的是（）A．B．C．D．a-3，则a的值可以是（）5．若22A ．﹣7B ．163C ．132D ．126．已知二次函数2y ax bx c =++的图象与x 轴交于点()2,0-、()1,0x ，且112x <<，与y 轴的正半轴的交点在()0,2的下方．下列结论：①420a b c -+=；②0a b c -+<；③20a c +>；④210a b -+>．其中正确结论的个数是（ ）个．A ．4个B ．3个C ．2个D ．1个7．如图已知⊙O 的内接五边形ABCDE ，连接BE 、CE ，若AB ＝BC ＝CE ，∠EDC ＝130°，则∠ABE 的度数为（ ）A ．25°B ．30°C ．35°D ．40°8．如图，将Rt ∆ABC 绕直角项点C 顺时针旋转90°，得到∆A' B'C ，连接AA'，若∠1=20°，则∠B 的度数是( )A ．70°B ．65°C ．60°D ．55°9．2019年4月份，某市市区一周空气质量报告中某项污染指数的数据是：31，35，31，34，30，32，31，这组数据的中位数、众数分别是（ ）A ．32，31B ．31，32C ．31，31D ．32，3510．下列各数：1.414213，0，其中是无理数的为（ ） A ．1.414 B ． 2C ．﹣13 D ．011．将抛物线2 21y x =-+向右平移 1 个单位长度，再向下平移 3 个单位长度，所得的抛物线的函数表达式为（ ）A ．()2212y x =---B ．()2212y x =-+-C ．()2214y x =--+D ．()2214y x =-++ 12．下列各式计算正确的是（ ）A ．2223a a +=B ．()236b b -=-C ．235c c c ⋅=D ．()222m n m n -=-二、填空题：（本大题共6个小题，每小题4分，共24分．）13．一组数据4，3，5，x，4，5的众数和中位数都是4，则x=_____．14．一等腰三角形，底边长是18厘米，底边上的高是18厘米，现在沿底边依次从下往上画宽度均为3厘米的矩形，画出的矩形是正方形时停止，则这个矩形是第_____个．15．如图，将直线y＝x向下平移b个单位长度后得到直线l，l与反比例函数y＝5x（x＞0）的图象相交于点A，与x轴相交于点B，则OA2﹣OB2的值为_____．16．如图是由大小完全相同的正六边形组成的图形，小军准备用红色、黄色、蓝色随机给每个正六边形分别涂上其中的一种颜色，则上方的正六边形涂红色的概率是_______.17．如图，正方形ABCD边长为3，连接AC，AE平分∠CAD，交BC的延长线于点E，FA⊥AE，交CB延长线于点F，则EF的长为__________．18．若x a y与3x2y b是同类项，则ab的值为_____．三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．（6分）海中有一个小岛P，它的周围18海里内有暗礁，渔船跟踪鱼群由西向东航行，在点A测得小岛P在北偏东60°方向上，航行12海里到达B点，这时测得小岛P在北偏东45°方向上．如果渔船不改变航线继续向东航行，有没有触礁危险？请说明理由．20．（6分）如图，在四边形ABCD中，E是AB的中点，AD//EC，∠AED=∠B．求证：△AED≌△EBC；当AB=6时，求CD的长．21．（6分）如图，大楼AB的高为16m，远处有一塔CD，小李在楼底A处测得塔顶D处的仰角为60°，在楼顶B处测得塔顶D处的仰角为45°，其中A、C两点分别位于B、D两点正下方，且A、C两点在同一水平线上，求塔CD的高．（3=1.73，结果保留一位小数．）22．（8分）如今很多初中生购买饮品饮用，既影响身体健康又给家庭增加不必要的开销，为此数学兴趣小组对本班同学一天饮用饮品的情况进行了调查，大致可分为四种：A：自带白开水；B：瓶装矿泉水；C：碳酸饮料；D：非碳酸饮料．根据统计结果绘制如下两个统计图（如图），根据统计图提供的信息，解答下列问题：（1）请你补全条形统计图；（2）在扇形统计图中，求“碳酸饮料”所在的扇形的圆心角的度数；（3）为了养成良好的生活习惯，班主任决定在自带白开水的5名同学（男生2人，女生3人）中随机抽取2名同学担任生活监督员，请用列表法或树状图法求出恰好抽到一男一女的概率．23．（8分）当前，“精准扶贫”工作已进入攻坚阶段，凡贫困家庭均要“建档立卡”．某初级中学七年级共有四个班，已“建档立卡”的贫困家庭的学生人数按一、二、三、四班分别记为A1，A2，A3，A4，现对A1，A2，A3，A4统计后，制成如图所示的统计图．（1）求七年级已“建档立卡”的贫困家庭的学生总人数；（2）将条形统计图补充完整，并求出A1所在扇形的圆心角的度数；（3）现从A1，A2中各选出一人进行座谈，若A1中有一名女生，A2中有两名女生，请用树状图表示所有可能情况，并求出恰好选出一名男生和一名女生的概率．24．（10分）解方程(1)x 1﹣1x ﹣1＝0(1)(x+1)1＝4(x ﹣1)1．25．（10分）如图，在平面直角坐标系xOy 中，A 、B 为x 轴上两点，C 、D 为y 轴上的两点，经 过点A 、C 、B 的抛物线的一部分C 1与经过点A 、D 、B 的抛物线的一部分C 2组合成一条封闭曲线，我们把这条封闭曲线称为“蛋线”．已知点C 的坐标为（0，），点M 是抛物线C 2：2y mx 2mx 3m =--（m ＜0）的顶点．（1）求A 、B 两点的坐标；（2）“蛋线”在第四象限上是否存在一点P ，使得△PBC 的面积最大？若存在，求出△PBC 面积的最大值；若不存在，请说明理由；（3）当△BDM 为直角三角形时，求m 的值．26．（12分）已知：如图，AB ＝AC ，点D 是BC 的中点，AB 平分∠DAE ，AE ⊥BE ，垂足为E ． 求证：AD ＝AE ．27．（12分）解不等式组4623x x x x +>⎧⎪+⎨≥⎪⎩并写出它的所有整数解．参考答案一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．D【解析】【分析】在△ABC中，∠C=90°，AC=BC=3cm，可得AB=32，∠A=∠B=45°，分当0＜x≤3（点Q在AC上运动，点P在AB上运动）和当3≤x≤6时（点P与点B重合，点Q在CB上运动）两种情况求出y与x的函数关系式，再结合图象即可解答.【详解】在△ABC中，∠C=90°，AC=BC=3cm，可得AB=32，∠A=∠B=45°，当0＜x≤3时，点Q在AC上运动，点P在AB上运动（如图1），由题意可得AP=2x，AQ=x，过点Q作QN⊥AB于点N，在等腰直角三角形AQN中，求得QN=22x，所以y=12AP QN⋅=21212=222x x x⨯⨯（0＜x≤3），即当0＜x≤3时，y随x的变化关系是二次函数关系，且当x=3时，y=4.5；当3≤x≤6时，点P与点B重合，点Q在CB上运动（如图2），由题意可得PQ=6-x，AP=32，过点Q作QN⊥BC于点N，在等腰直角三角形PQN中，求得QN=22(6-x)，所以y=12AP QN⋅=12332(6)=9222x x⨯⨯--+（3≤x≤6），即当3≤x≤6时，y随x的变化关系是一次函数，且当x=6时，y=0.由此可得，只有选项D符合要求，故选D.【点睛】本题考查了动点函数图象，解决本题要正确分析动线运动过程，然后再正确计算其对应的函数解析式，由函数的解析式对应其图象，由此即可解答．2．B【解析】【分析】根据俯视图中每列正方形的个数，再画出从正面看得到的图形即可．【详解】解：主视图，如图所示：．故选B．【点睛】本题考查由三视图判断几何体；简单组合体的三视图．用到的知识点为：主视图是从物体的正面看得到的图形；看到的正方体的个数为该方向最多的正方体的个数．3．D【解析】【分析】根据中位数是一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数）的意义，9人成绩的中位数是第5名的成绩．参赛选手要想知道自己是否能进入前5名，只需要了解自己的成绩以及全部成绩的中位数，比较即可．【详解】由于总共有9个人，且他们的分数互不相同，第5的成绩是中位数，要判断是否进入前5名，故应知道中位数的多少.故本题选：D.【点睛】本题考查了统计量的选择，熟练掌握众数，方差，平均数，中位数的概念是解题的关键.4．D【解析】分析：根据轴对称图形与中心对称图形的概念分别分析得出答案．详解：A．是轴对称图形，也是中心对称图形，故此选项错误；B．不是轴对称图形，也不是中心对称图形，故此选项错误；C．不是轴对称图形，是中心对称图形，故此选项错误；D．是轴对称图形，不是中心对称图形，故此选项正确．故选D．点睛：本题考查了轴对称图形和中心对称图形的概念．轴对称图形的关键是寻找对称轴，图形沿对称轴折叠后可重合；中心对称图形是要寻找对称中心，图形旋转180°后与原图形重合．5．C【解析】【分析】根据已知条件得到4＜a-2＜9，由此求得a 的取值范围，易得符合条件的选项．【详解】解：∵2＜2a -＜3，∴4＜a-2＜9，∴6＜a ＜1．又a-2≥0，即a≥2．∴a 的取值范围是6＜a ＜1．观察选项，只有选项C 符合题意．故选C ．【点睛】考查了估算无理数的大小，估算无理数大小要用夹逼法．6．B【解析】分析：根据已知画出图象，把x=−2代入得：4a−2b+c=0，把x=−1代入得：y=a−b+c>0，根据122c x x a ⋅=<-，不等式的两边都乘以a(a<0)得：c>−2a ，由4a−2b+c=0得22c a b -=-，而0<c<2,得到102c -<-<即可求出2a−b+1>0.详解：根据二次函数y=ax 2+bx+c 的图象与x 轴交于点(−2,0)、(x 1,0),且1<x 1<2,与y 轴的正半轴的交点在(0,2)的下方，画出图象为：如图把x=−2代入得：4a−2b+c=0，∴①正确；把x=−1代入得：y=a−b+c>0，如图A 点，∴②错误；∵(−2,0)、(x 1,0),且1<x 1，∴取符合条件1<x 1<2的任何一个x 1,−2⋅x 1<−2， ∴由一元二次方程根与系数的关系知122c x x a ⋅=<-， ∴不等式的两边都乘以a(a<0)得：c>−2a ，∴2a+c>0，∴③正确；④由4a−2b+c=0得22c a b -=-，而0<c<2,∴102c -<-< ∴−1<2a−b<0∴2a−b+1>0，∴④正确.所以①③④三项正确．故选B.点睛：属于二次函数综合题，考查二次函数图象与系数的关系, 二次函数图象上点的坐标特征, 抛物线与x 轴的交点，属于常考题型.7．B【解析】【分析】如图，连接OA ，OB ，OC ，OE ．想办法求出∠AOE 即可解决问题．【详解】如图，连接OA ，OB ，OC ，OE ．∵∠EBC+∠EDC ＝180°，∠EDC ＝130°，∴∠EBC ＝50°，∴∠EOC ＝2∠EBC ＝100°，∵AB ＝BC ＝CE ，∴弧AB ＝弧BC ＝弧CE ，∴∠AOB ＝∠BOC ＝∠EOC ＝100°，∴∠AOE ＝360°﹣3×100°＝60°，∴∠ABE ＝12∠AOE ＝30°．故选：B．【点睛】本题考查圆周角定理，圆心角，弧，弦之间的关系等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．8．B【解析】【分析】根据图形旋转的性质得AC=A′C，∠ACA′=90°，∠B=∠A′B′C，从而得∠AA′C=45°，结合∠1=20°，即可求解．【详解】∵将Rt∆ABC绕直角项点C顺时针旋转90°，得到∆A' B'C，∴AC=A′C，∠ACA′=90°，∠B=∠A′B′C，∴∠AA′C=45°，∵∠1=20°，∴∠B′A′C=45°-20°=25°，∴∠A′B′C=90°-25°=65°，∴∠B=65°．故选B．【点睛】本题主要考查旋转的性质，等腰三角形和直角三角形的性质，掌握等腰三角形和直角三角形的性质定理，是解题的关键．9．C【解析】分析：找中位数要把数据按从小到大的顺序排列，位于最中间的一个数（或两个数的平均数）为中位数；众数是一组数据中出现次数最多的数据，注意众数可以不只一个．解答：解：从小到大排列此数据为：30、1、1、1、32、34、35，数据1出现了三次最多为众数，1处在第4位为中位数．所以本题这组数据的中位数是1，众数是1．故选C．10．B【解析】试题分析：根据无理数的定义可得是无理数．故答案选B.考点：无理数的定义.11．A根据二次函数的平移规律即可得出．【详解】解：221y x =-+向右平移 1 个单位长度，再向下平移 3 个单位长度，所得的抛物线的函数表达式为()2212y x =---故答案为：A ．【点睛】本题考查了二次函数的平移，解题的关键是熟知二次函数的平移规律．12．C【解析】【分析】【详解】解：A ．2a 与2不是同类项，不能合并，故本选项错误；B ．应为()236b b -=，故本选项错误；C ．235·c c c =，正确；D ．应为()2222m n m n mn -=+-，故本选项错误．故选C ．【点睛】本题考查幂的乘方与积的乘方；同底数幂的乘法．二、填空题：（本大题共6个小题，每小题4分，共24分．）13．1【解析】【分析】一组数据中出现次数最多的数据叫做众数，由此可得出答案．【详解】∵一组数据1，3，5，x ，1，5的众数和中位数都是1，∴x=1，故答案为1．【点睛】本题考查了众数的知识，解答本题的关键是掌握众数的定义．14．5根据相似三角形的相似比求得顶点到这个正方形的长，再根据矩形的宽求得是第几张.【详解】解：已知剪得的纸条中有一张是正方形，则正方形中平行于底边的边是3，所以根据相似三角形的性质可设从顶点到这个正方形的线段为x，则＝，解得x=3，所以另一段长为18-3=15，因为15÷3=5，所以是第5张．故答案为：5.【点睛】本题主要考查了相相似三角形的判定和性质，关键是根据似三角形的性质及等腰三角形的性质的综合运用解答.15．1．【解析】解：∵平移后解析式是y=x﹣b，代入y=5x得：x﹣b=5x，即x2﹣bx=5，y=x﹣b与x轴交点B的坐标是（b，0），设A的坐标是（x，y），∴OA2﹣OB2=x2+y2﹣b2=x2+（x﹣b）2﹣b2=2x2﹣2xb=2（x2﹣xb）=2×5=1，故答案为1．点睛：本题是反比例函数综合题，用到的知识点有：一次函数的平移规律，一次函数与反比例函数的交点坐标，利用了转化及方程的思想，其中利用平移的规律表示出y=x平移后的解析式是解答本题的关键.16．1 3【解析】试题分析：上方的正六边形涂红色的概率是，故答案为．考点：概率公式．17．6【解析】【分析】利用正方形的性质和勾股定理可得AC的长，由角平分线的性质和平行线的性质可得∠CAE=∠E，易得CE=CA，由FA⊥AE，可得∠FAC=∠F，易得CF=AC，可得EF的长．【详解】解：∵四边形ABCD为正方形，且边长为3，∴2∵AE平分∠CAD，∴∠CAE=∠DAE，∵AD∥CE，∴∠DAE=∠E，∴∠CAE=∠E，∴2，∵FA⊥AE，∴∠FAC+∠CAE=90°，∠F+∠E=90°，∴∠FAC=∠F，∴2，∴22218．2【解析】试题解析：∵x a y与3x2y b是同类项，∴a=2，b=1，则ab=2.三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．有触礁危险，理由见解析.【解析】试题分析：过点P作PD⊥AC于D，在Rt△PBD和Rt△PAD中，根据三角函数AD，BD就可以用PD 表示出来，根据AB=12海里，就得到一个关于PD的方程，求得PD．从而可以判断如果渔船不改变航线继续向东航行，有没有触礁危险．试题解析：有触礁危险．理由：过点P作PD⊥AC于D．设PD 为x ，在Rt △PBD 中，∠PBD=90°-45°=45°．∴BD=PD=x ．在Rt △PAD 中，∵∠PAD=90°-60°=30°∴AD=330x x tan ＝︒∵AD=AB+BD 3∴3+131-（） ∵63）＜18∴渔船不改变航线继续向东航行，有触礁危险．【点睛】本题主要考查解直角三角形在实际问题中的应用，构造直角三角形是解题的前提和关键． 20．（1）证明见解析；（2）CD =3【解析】分析: （1）根据二直线平行同位角相等得出∠A=∠BEC ，根据中点的定义得出AE=BE ，然后由ASA 判断出△AED ≌△EBC ；（2）根据全等三角形对应边相等得出AD=EC ，然后根据一组对边平行且相等的四边形是平行四边形得出四边形AECD 是平行四边形，根据平行四边形的对边相等得出答案.详解:（1）证明 ：∵AD ∥EC∴∠A=∠BEC∵E 是AB 中点，∴AE=BE∵∠AED=∠B∴△AED ≌△EBC（2）解：∵△AED≌△EBC ∴AD=EC∵AD∥EC∴四边形AECD是平行四边形∴CD=AE∵AB=6∴CD= 12AB=3点睛: 本题考查全等三角形的判定和性质、平行四边形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型.21．塔CD的高度为37.9米【解析】试题分析：首先分析图形，根据题意构造直角三角形．本题涉及两个直角三角形，即Rt△BED和Rt△DAC，利用已知角的正切分别计算，可得到一个关于AC的方程，从而求出DC．试题解析：作BE⊥CD于E．可得Rt△BED和矩形ACEB．则有CE=AB=16，AC=BE．在Rt△BED中，∠DBE=45°，DE=BE=AC．在Rt△DAC中，∠DAC=60°，DC=ACtan60°=3AC．∵16+DE=DC，∴16+AC=3AC，解得：AC=83+8=DE．所以塔CD的高度为（83+24）米≈37.9米，答：塔CD的高度为37.9米．22．（1）详见解析；（2）72°；（3）【解析】【分析】（1）由B类型的人数及其百分比求得总人数，在用总人数减去其余各组人数得出C类型人数，即可补全条形图；（2）用360°乘以C类别人数所占比例即可得；（3）用列表法或画树状图法列出所有等可能结果，从中确定恰好抽到一男一女的结果数，根据概率公式求解可得．【详解】解：（1）∵抽查的总人数为：（人）∴类人数为：（人）补全条形统计图如下：（2）“碳酸饮料”所在的扇形的圆心角度数为：（3）设男生为、，女生为、、，画树状图得：∴恰好抽到一男一女的情况共有12 种，分别是∴（恰好抽到一男一女）．【点睛】本题考查的是条形统计图和扇形统计图的综合运用以及概率的求法，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．23．（1）15人;(2)补图见解析.（3）.【解析】【分析】（1）根据三班有6人，占的百分比是40%，用6除以所占的百分比即可得总人数；（2）用总人数减去一、三、四班的人数得到二班的人数即可补全条形图，用一班所占的比例乘以360°即可得A1所在扇形的圆心角的度数；（3）根据题意画出树状图，得出所有可能，进而求恰好选出一名男生和一名女生的概率．【详解】解:（1）七年级已“建档立卡”的贫困家庭的学生总人数：6÷40%=15人；（2）A2的人数为15﹣2﹣6﹣4=3（人）补全图形，如图所示，A1所在圆心角度数为：×360°=48°；（3）画出树状图如下：共6种等可能结果,符合题意的有3种∴选出一名男生一名女生的概率为：P=.【点睛】本题考查了条形图与扇形统计图，概率等知识，准确识图，从图中发现有用的信息，正确根据已知画出树状图得出所有可能是解题关键．24．（1）x13，x1=13（1）x1=3，x1=13．【解析】【分析】(1)配方法解；(1)因式分解法解.【详解】（1）x 1﹣1x ﹣1=2，x 1﹣1x+1=1+1，（x ﹣1）1=3，x ﹣1=3± ， x=13±，x 1=13+，x 1=1﹣3， （1）（x+1）1=4（x ﹣1）1．（x+1）1﹣4（x ﹣1）1=2．（x+1）1﹣[1（x ﹣1）]1=2．（x+1）1﹣（1x ﹣1）1=2．（x+1﹣1x+1）（x+1+1x ﹣1）=2．（﹣x+3）（3x ﹣1）=2．x 1=3，x 1=13． 【点睛】考查了解一元二次方程的应用，解此题的关键是能把一元二次方程转化成一元一次方程．25．（1）A （，0）、B （3，0）． （2）存在．S △PBC 最大值为2716（3）2m =1m =-时，△BDM 为直角三角形． 【解析】【分析】 （1）在2y mx 2mx 3m =--中令y=0，即可得到A 、B 两点的坐标．（2）先用待定系数法得到抛物线C 1的解析式，由S △PBC = S △POC + S △BOP –S △BOC 得到△PBC 面积的表达式，根据二次函数最值原理求出最大值．（3）先表示出DM 2，BD 2，MB 2，再分两种情况：①∠BMD=90°时；②∠BDM=90°时，讨论即可求得m 的值．【详解】解：（1）令y=0，则2mx 2mx 3m 0--=，∵m ＜0，∴2x 2x 30--=，解得：1x 1=-，2x 3=．∴A （，0）、B （3，0）．（2）存在．理由如下：∵设抛物线C 1的表达式为()()y a x 1x 3=+-（a 0≠），把C （0，32-）代入可得，12a =． ∴Ｃ1的表达式为：()()1y x 1x 32=+-，即213y x x 22=--． 设P （p ，213p p 22--）， ∴ S △PBC = S △POC + S △BOP –S △BOC =23327p 4216--+（）． ∵3a 4=-<0，∴当3p 2=时,S △PBC 最大值为2716． （3）由C 2可知： B （3，0），D （0，3m -），M （1，4m -），∴BD 2=29m 9+，BM 2=216m 4+，DM 2=2m 1+．∵∠MBD<90°, ∴讨论∠BMD=90°和∠BDM=90°两种情况：当∠BMD=90°时，BM 2+ DM 2= BD 2，即216m 4+＋2m 1+=29m 9+，解得：12m =22m =(舍去)． 当∠BDM=90°时，BD 2+ DM 2= BM 2，即29m 9+＋2m 1+=216m 4+，解得：1m 1=-，2m 1=(舍去) ．综上所述，2m =或1m =-时，△BDM 为直角三角形． 26．见解析【解析】试题分析：证明简单的线段相等，可证线段所在的三角形全等，结合本题，证△ADB ≌△AEB 即可． 试题解析：∵AB=AC,点D 是BC 的中点,∴AD ⊥BC,∴∠ADB=90°.∵AE ⊥EB,∴∠E=∠ADB=90°.∵AB 平分∠DAE,∴∠BAD=∠BAE.在△ADB 和△AEB 中,∠E=∠ADB,∠BAD=∠BAE,AB=AB,∴△ADB ≌△AEB(AAS),∴AD=AE.27．不等式组的整数解有﹣1、0、1．【解析】【分析】先解不等式组，求得不等式组的解集，再确定不等式组的整数解即可.【详解】4623x x x x +>⎧⎪⎨+≥⎪⎩①②， 解不等式①可得，x ＞-2；解不等式②可得，x≤1；∴不等式组的解集为：﹣2＜x≤1，∴不等式组的整数解有﹣1、0、1．【点睛】本题考查了解一元一次不等式组，正确求出每一个不等式解集是基础， 熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则求不等式组的解集是解答本题的关键．。
2019年南京市鼓楼区中考数学一模试卷解析版
2019年江苏省南京市鼓楼区中考数学一模试卷解析版一、选择题1．4的算术平方根是（）A．±2B．2C．﹣2D．±16【解答】解：∵22＝4，∴4的算术平方根是2．故选：B．2．鼓楼区公益项目“在线伴读”平台开通以来，累计为学生在线答疑15000次．用科学记数法表示15000是（）A．0.15×106B．1.5×105C．1.5×104D．15×105【解答】解：用科学记数法表示15000是：1.5×104．故选：C．3．计算（﹣a）2•（a2）3（）A．a8B．﹣a8C．a7D．﹣a7【解答】解：（﹣a）2•（a2）3＝a2•a6＝a8，故选：A．4．若顺次连接四边形ABCD各边中点所得的四边形是菱形，则下列结论中正确的是（）A．AB∥CD B．AB⊥BC C．AC⊥BD D．AC＝BD【解答】解：如图，连接AC，BD，点E、F、G、H分别为四边形ABCD各边中点，∴EH＝AC，EH∥AC，FG＝AC，FG∥AC，∴四边形EFGH为平行四边形，当EH＝EF时，四边形EFGH为菱形，又∵EF＝BD，若EH＝EF，则AC＝BD．故选：D．【点评】本题考查了菱形的判定定理：邻边相等的平行四边形是菱形．也考查了平行四边形的判定以及三角形中位线的性质．5．如图是某家庭2018年每月交通费支出的条形统计图，若该家庭2018年月交通费平均支出为a元，则下列结论中正确的是（）A．200≤a≤220B．220≤a≤240C．240≤a≤260D．260≤a≤280【分析】首先根据条形统计图得出每个月交通费的取值范围，再根据平均数的定义求出a 的范围即可．【解答】解：设i月份的交通费为x i（1≤i≤12，且i为整数）．由图可知，240＜x1≤250，260＜x2＜270，280＜x3＜300，280＜x4＜290，260＜x5＜280，240＜x6＜250，240＜x7＜260，230＜x8＜240，180＜x9＜190，200＜x10＜210，240＜x11＜250，270＜x12＜280，则（240+260+280+280+260+240+240+230+180+200+240+270）＜a＜（250+270+300+290+280+250+260+240+190+210+250+280），解得243＜a＜255，综观各选项，只有C符合．故选：C．【点评】本题考查的是条形统计图的综合运用．读懂统计图，从统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据．也考查了算术平均数．6．A、B两地相距900km，一列快车以200km/h的速度从A地匀速驶往B地，到达B地后立刻原路返回A地，一列慢车以75km/h的速度从B地匀速驶往A地．两车同时出发，截止到它们都到达终点时，两车恰好相距200km的次数是（）A．5B．4C．3D．2【分析】相距200km要从相遇前和相遇后；追及前和追及后，快车已到终点几个方面考虑，共计5种情况，经计算检验数据是否符合题意．【解答】解：设两车相距200km时，行驶的时间为t小时，依题意得：①当快车从A地开往B地，慢车从B地开往A地，相距200km时，则有：200t+75t+200＝900，解得：t＝；②当快车继续开往B地，慢车继续开往A地，相遇后背离而行，相距200km时，200t+75t﹣200＝900，解得：t＝4；③快车从A地到B地全程需要4.5小时，此时慢车从B地到A地行驶4.5×75＝337.5km，∵337.5＞200∴快车又从B地返回A地是追慢车，追上前相距200km，则有：75t＝200+200（t﹣4.5），解得：t＝；④快车追上慢车后并超过慢车相距200km，则有：200（t﹣4.5）﹣75t＝200解得：t＝8.8⑤快车返回A地终点所需时间是9小时，此刻慢车行驶了9×75＝675km，距终点还需行驶25km，则有：75t＝900﹣200解得：t＝．综合所述两车恰好相距200km的次数为5次．故选：A．【点评】本题考查了一元一次方程行程方面的应用题，主要是相遇和追及问题，同时需分类要做到不重不漏．二、填空题7．﹣3的绝对值是3．【分析】计算绝对值要根据绝对值的定义求解．第一步列出绝对值的表达式；第二步根据绝对值定义去掉这个绝对值的符号．【解答】解：﹣3的绝对值是3．【点评】规律总结：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．8．若式子在实数范围内有意义，则x的取值范围是x≥﹣1．【分析】根据二次根式的定义可知被开方数必须为非负数，列不等式求解．【解答】解：根据题意得：x+1≥0，解得x≥﹣1，故答案为：x≥﹣1．【点评】主要考查了二次根式的意义和性质．概念：式子（a≥0）叫二次根式．性质：二次根式中的被开方数必须是非负数，否则二次根式无意义．9．计算﹣的结果是2．【分析】先二次根式的除法法则运算，然后化简后合并即可．【解答】解：原式＝3﹣＝3﹣＝2．故答案为2．【点评】本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后进行二次根式的乘除运算，再合并即可．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．10．方程＝的解是x＝﹣4．【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．【解答】解：去分母得：x＝2x+4，解得：x＝﹣4，经检验x＝﹣4是分式方程的解，故答案为：x＝﹣4【点评】此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验．11．正五边形每个外角的大小是72度．【分析】根据n边形取n个外角，无论边数是几，其外角和永远为360°，求出正五边形每个外角的大小是多少度即可．【解答】解：∵360÷5＝72（度），∴正五边形每个外角的大小是72度．故答案为：72．【点评】此题主要考查了多边形的内角与外角的计算，解答此题的关键是要明确：多边形的外角和指每个顶点处取一个外角，则n边形取n个外角，无论边数是几，其外角和永远为360°．12．已知关于x的方程x2+mx﹣2＝0有一根是2，则另一根是x＝﹣1，m＝﹣1．【分析】直接把x＝2代入方程x2+mx﹣2＝0求出m的值，利用根与系数的关系求得方程的另一根．【解答】解：把x＝2代入，得22+2m﹣2＝0．解得m＝﹣1．设方程的另一根为x，则2x＝﹣2．所以x＝﹣1．故答案是：x＝﹣1；﹣1．【点评】本题考查的是一元二次方程的根即方程的解的定义．一元二次方程的根就是一元二次方程的解，就是能够使方程左右两边相等的未知数的值．即用这个数代替未知数所得式子仍然成立．13．如图，AB∥EG∥CD，EF平分∠BED，若∠D＝69°，∠GEF＝21°，则∠B＝27°．【分析】根据平行线的性质求出∠GED＝∠D，∠B＝∠BEG，根据角平分线的定义求出∠BEF＝∠DEF，即可求出答案．【解答】解：∵AB∥EG∥CD，∠D＝69°，∴∠GED＝∠D＝69°，∵∠GEF＝21°，∴∠DEF＝∠GED﹣∠GEF＝48°，∵EF平分∠BED，∴∠BEF＝∠DEF＝48°，∴∠BEG＝∠BEF﹣∠GEF＝48°﹣21°＝27°，∵ABB∥EG，∴∠B＝∠BEG＝27°，故答案为：27．【点评】本题考查了角平分线的定义和平行线的性质，能根据平行线的性质求出∠GED ＝∠D和∠B＝∠BEG是解此题的关键．14．如图，圆锥底面圆心为O，半径OA＝1，顶点为P，将圆锥置于平面上，若保持顶点P 位置不变，将圆锥顺时针滚动三周后点A恰好回到原处，则圆锥的高OP＝2或．【分析】先利用圆的周长公式计算出P A的长，然后利用勾股定理计算PO的长．【解答】解：当A点第一次回到A点：2π×P A＝3×2π×1，所以P A＝3，所以圆锥的高OP＝＝＝2．当A点第二次回到A点：2×2π×P A＝3×2π×1，所以P A＝，所以圆锥的高OP＝＝＝．故答案为2或．【点评】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．15．如图，点A、B、C、D在⊙O上，B是的中点，过C作⊙O的切线交AB的延长线于点E．若∠AEC＝84°，则∠ADC＝64°．【分析】连接BD、BC，根据圆周角定理得出，根据圆内接四边形的性质得出∠EBC＝∠ADC，根据切线的性质得出∠BCE＝∠BDC＝∠ADC，然后根据三角形内角和定理得出84°+∠ADC+∠ADC＝180°，解得即可．【解答】解：连接BD、BC，∵B是的中点，∴＝，∴，∵四边形ABCD是圆内接四边形，∴∠EBC＝∠ADC，∵EC是⊙O的切线，切点为C，∴∠BCE＝∠BDC＝∠ADC，∵∠AEC＝84°，∠AEC+∠BCE+∠EBC＝180°，∴84°+∠ADC+∠ADC＝180°，∴∠ADC＝64°．故答案为64．【点评】本题考查了切线的性质，圆内接四边形的性质，圆周角的定理等，熟练掌握性质定理是解题的关键．16．在△ABC中，AB＝5，AC＝4，BC＝3．若点P在△ABC内部（含边界）且满足PC≤P A≤PB，则所有点P组成的区域的面积为．【分析】分别作AB，AC的垂直平分线，交AB于点E，交AC于点F，交AC于点D，利用线段垂直平分线的性质，结合PC≤P A≤PB的条件，判断点P在△DEF内部（含边界），再利直角三角形的性质求解；【解答】解：分别作AB，AC的垂直平分线，交AB于点E，交AC于点F，交AC于点D，∵若点P在△ABC内部（含边界）且满足PC≤P A≤PB，∴点P在△DEF内部（含边界），∵DE⊥AC，EF⊥AB，∴△DEF是直角三角形，△AEF是直角三角形，∵AB＝5，AC＝4，BC＝3，∴AD＝2，AE＝2.5，DE＝1.5，∵AE2＝AD•AF，∴AF＝，∴DF＝，∴△DEF的面积为××＝；【点评】本题考查动点轨迹，直角三角形性质，线段垂直平分线性质；能够结合条件判断点的运动轨迹是直角三角形是解题的关键．三、解答题17．解不等式组．【分析】先求出两个不等式的解集，再求其公共解．【解答】解：，由①得，x＞﹣2，由②得，x≤1，所以不等式组的解集为﹣2＜x≤1．【点评】本题主要考查了一元一次不等式组解集的求法，其简便求法就是用口诀求解．求不等式组解集的口诀：同大取大，同小取小，大小小大中间找，大大小小找不到（无解）．18．计算【分析】原式括号中两项通分并利用同分母分式的减法法则变形，同时利用除法法则变形，约分即可得到结果．【解答】解：原式＝÷＝•＝．【点评】此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．19．（1）解方程x2﹣x﹣1＝0．（2）在实数范围内分解因式x2﹣x﹣1的结果为＝（x﹣）（x﹣）．【分析】（1）先求出b2﹣4ac的值，再代入公式求出即可；（2）根据（1）中方程的解分解即可．【解答】解：（1）x2﹣x﹣1＝0，b2﹣4ac＝（﹣1）2﹣4×1×（﹣1）＝5，x＝，x1＝，x2＝；（2）∵方程x2﹣x﹣1＝0的解x1＝，x2＝；∴x2﹣x﹣1＝（x﹣）（x﹣），故答案为：（x﹣）（x﹣）．【点评】本题考查了分解因式和解一元二次方程，能求出方程的解是解此题的关键．20．如图，AB＝AD，AC＝AE，BC＝DE，点E在BC上．（1）求证：△ABC≌△ADE；（2）求证：∠EAC＝∠DEB．【分析】（1）用“SSS”证明即可；（2）借助全等三角形的性质及角的和差求出∠DAB＝∠EAC，再利用三角形内角和定理求出∠DEB＝∠DAB，即可说明∠EAC＝∠DEB．【解答】解：（1）∵AB＝AD，AC＝AE，BC＝DE，∴△ABC≌△ADE（SSS）；（2）由△ABC≌△ADE，则∠D＝∠B，∠DAE＝∠BAC．∴∠DAE﹣∠ABE＝∠BAC﹣∠BAE，即∠DAB＝∠EAC．设AB和DE交于点O，∵∠DOA＝BOE，∠D＝∠B，∴∠DEB＝∠DAB．∴∠EAC＝∠DEB．【点评】本题主要考查了全等三角形的判定和性质，解题的关键是利用全等三角形的性质求出相等的角，体现了转化思想的运用．21．（1）两只不透明的袋子中均有红球、黄球、白球各1个，这些球除颜色外无其他差别．分别从每个袋子中随机摸出一个球，求摸出两个球都是红球的概率．（2）鼓楼区实施全面均衡分班，某校为七年级各班随机分配任课教师．已知该校七年级共有10个班，语文洪老师、数学胡老师都执教该年级，则他俩都任教七（1）班的概率为．【分析】（1）根据概率公式即可得出结果；（2）根据概率公式即可得出结果．【解答】解：（1）摸出两个球都是红球的概率＝＝；答：摸出两个球都是红球的概率为；（2）他俩都任教七（1）班的概率＝×＝，答：他俩都任教七（1）班的概率为．故答案为：．【点评】本题考查了概率，熟练掌握概率公式是解题的关键．22．妈妈准备用5万元投资金融产品，她查询到有A、B两款“利滚利”产品，即上一周产生的收益将计入本金以计算下一周的收益．例如：投资100元，第一周的周收益率为5%，则第一周的收益为100×5%＝5元，第二周投资的本金将变为100+5＝105元．如图是这两款产品过去5周的周收益率公告信息．（第一周：3月1日～3月7日）（1）若妈妈3月1日投资产品B，到第二周结束时会不赚不赔，这种说法对吗？请判断并说明理由．（2）请运用学过的统计知识，为妈妈此次投资金融产品提出建议并简要说明理由．【分析】（1）根据题意和统计图中的信息可以计算出到第二周结束时是赚还是赔，本题得以解决；（2）根据统计图中的信息可以帮助妈妈此次投资金融产品提出合理性建议．【解答】解：（1）这种说法不对，理由：设开始投资x元，则两周结束时的总资产为：x（1+2%）（1﹣2%）＝0.9996x≠x，故到第二周结束时会不赚不赔，这种说法不对；（2）选择A产品，理由：由图可以看出两个产品平均收益率相近，但A产品波动较小，方差较小，且一直是正收益，说明收益比较稳定，故选择A产品．【点评】本题考查折线统计图，解答本题的关键是明确题意，利用数形结合的思想解答．23．已知点A（1，1），B（2，3），C（4，7），请用两种不同的方法判断这三点是否在一条直线上．（写出必要的推理过程）【分析】方法一：设AB两点所在直线的解析式为y＝kx+b，将A（1，1），B（2，3）代入可得函数解析式，进而得出点C也在直线AB上即可；方法二：依据两点间距离公式即可得到AB+BC＝AC，进而得出A、B、C三点在一条直线上．【解答】解：A、B、C三点在一条直线上．方法一：设AB两点所在直线的解析式为y＝kx+b，将A（1，1），B（2，3）代入可得，，解得，∴y＝2x﹣1，当x＝4时，y＝7，∴点C也在直线AB上，即A、B、C三点在一条直线上．方法二：∵A（1，1），B（2，3），C（4，7），∴AB＝＝，AC＝＝3，BC＝＝2，∴AB+BC＝AC，∴A、B、C三点在一条直线上．【点评】本题考查了一次函数图象上点的坐标特征：一次函数y＝kx+b，（k≠0，且k，b为常数）的图象是一条直线．直线上任意一点的坐标都满足函数关系式y＝kx+b．24．已知：如图，在▱ABCD中，G、H分别是AD、BC的中点，AE⊥BD，CF⊥BD，垂足分别为E、F．（1）求证：四边形GEHF是平行四边形；（2）已知AB＝5，AD＝8．求四边形GEHF是矩形时BD的长．【分析】（1）根据平行四边形的性质得出AD∥BC，AD＝BC，求出∠GDE＝∠FBH，根据直角三角形斜边上中线性质求出EG＝FH，求出EG∥FH，根据平行四边形的判定得出即可；（2）根据矩形的性质得出∠EHF＝∠BFC＝90°，证△EFH∽△CBF，根据相似得出＝，求出BE，证△ABE≌△CDF，求出BE＝DF，即可得出答案．【解答】（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∴∠GDE＝∠FBH，∵G、H分别是AD、BC的中点，AE⊥BD，CF⊥BD，∴在Rt△AED和Rt△CFB中，EG＝AD＝GD，FH＝BC＝HB，∴EG＝FH，∠GED＝∠GDE，∠FBH＝∠BFH，∴∠GED＝∠BFH，∴EG∥FH，∴四边形GEHF是平行四边形；（2）解：连接GH，当四边形GEHF是矩形时，∠EHF＝∠BFC＝90°，∵∠FBH＝∠BFH，∴△EFH∽△CBF，∴＝，由（1）可得：GA∥HB，GA＝HB，∴四边形GABH是平行四边形，∴GH＝AB＝5，∵在矩形GEHF中，EF＝GH，且AB＝5，AD＝8，∴＝，解得：BF＝，∴BE＝BF﹣EF＝﹣5＝，在△ABE和△CDF中∴△ABE≌△CDF（AAS），∴BE＝DF＝，∴BD＝BF+DF＝+＝．【点评】本题考查了矩形的性质，全等三角形的性质和判定，相似三角形的性质和判定，平行四边形的性质等知识点，能综合运用知识点进行推理是解此题的关键．25．某商品的进价是每件40元，原售价每件60元．进行不同程度的涨价后，统计了商品调价当天的售价和利润情况，以下是部分数据：售价（元/件）60616263…利润（元）6000609061606210…（1）当售价为每件60元时，当天售出300件；（2）若对该商品原售价每件涨价x元（x为正整数）时当天售出该商品的利润为y元．①用所学过的函数知识直接写出y与x之间满足的函数表达式：y＝﹣10x2﹣500x+6000．②如何定价才能使当天的销售利润不低于6200元？【分析】（1）销售件数＝当天销售利润÷每件利润的单价；（2）①先通过已知数据，找出每增加1元，减少的销售件数，然后销售利润＝每件利润×销售件数；②根据①中的关系，列出不等式即可．【解答】解：（1）6000÷（60﹣40）＝300件；故答案为：300（2）①当每件售价61元，销售件数：6090÷（61﹣40）＝290件；当每件收件62元，销售件数：6160÷（62﹣40）＝280件；当每件收件63元，销售件数：62100÷（63﹣40）＝270件；可以看出，售价每增加1元，销售减少10件，y＝（60+x﹣40）（300﹣10x）＝﹣10x2+100x+6000．故答案为：y＝﹣10x2+100x+6000．②﹣10x2+100x+6000≥6200，当＜x＜5+，∵x为正整数整数解，故当定价为3，4，5，6，7，都能使天的销售利润不等于6200元【点评】本题考查了二次函数的实际应用，将实际问题转化成函数关系式解答此题的关键．26．如图①，一座石拱桥坐落在秦淮河上，它的主桥拱为圆弧形．如图②，乔宽AB为8米，水面BC宽16米，表示的是主桥拱在水面以上的部分，点P表示主桥拱拱顶．小明乘坐游船，沿主桥拱的中轴线向主桥拱行驶．（1）图③是主桥拱在水面以上部分的主视图，请用直尺和圆规作出主桥拱在静水中的倒影．（保留作图痕迹，不写作法）．（2）已知小明眼睛距离水平1.6米，游船的速度为0.2米/秒．某一时刻，小明看拱顶P的仰角为37°，4秒后，小明看拱顶P的仰角为45°．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75．）①求桥拱P到水面的距离；②船上的旗杆高1米，某时刻游船背对阳光形式，小明发现旗杆在阳光下的投影所在直线与航线平行且长为2米．请估计此刻桥的正下方被阳光照射到的部分的面积（需画出示意图并标注必要数据）．【分析】（1）在上取一点D，作线段BD，BC的垂直平分线交于点O，作点O关于BC的对称点O′，以O′为圆心，O′B为半径画弧即可解决问题．（2）①如图2中，当小明刚到拱顶正下方时，设拱顶P到小明的眼睛距离即PC为x米．构建方程求出x即可解决问题．②如图红色曲线与BC构成的图形即可所求的区域（面积为S），与阴影部分弓形相比，水平长度相同，竖着高度变为其两倍，所以可以认为S为弓形面积的两倍．【解答】解：（1）如图所示：（2）①如图2中，当小明刚到拱顶正下方时，设拱顶P到小明的眼睛距离即PC为x米．∵tan37°＝＝，∴AC＝x，∵tan45°＝＝1，∴BC＝PC＝x，∴AB＝AC﹣BC＝x﹣x＝0.2×4，解得x＝2.4，∴PE＝2.4+1.6＝4（米）．②如图红色曲线与BC构成的图形即可所求的区域（面积为S），与阴影部分弓形相比，水平长度相同，竖着高度变为其两倍，所以可以认为S为弓形面积的两倍．由①可知：OB＝10，∠BOC＝106°，∴S弓形＝﹣×16×＝﹣48，∴S＝2S弓形＝﹣96．【点评】本题考查的是解直角三角形的应用﹣仰角俯角问题，掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键．27．把一个函数图象上每个点的纵坐标变为原来的倒数（原函数图象上纵坐标为0的点除外）、横坐标不变，可以得到另一个函数的图象，我们称这个过程为倒数变换．例如：如图，将y＝x的图象经过倒数变换后可得到y＝的图象．特别地，因为y＝x图象上纵坐标为0的点是原点，所以该点不作变换，因此y＝的图象上也没有纵坐标为0的点．（1）请在下面的平面直角坐标系中画出y＝﹣x+1的图象和它经过倒数变换后的图象．（2）观察上述图象，结合学过的关于函数图象与性质的知识，①猜想：倒数变换得到的图象和原函数的图象之间可能有怎样的联系？写出两个即可．②说理：请简要解释你其中一个猜想．（3）请画出函数y＝（c为常数）的大致图象．【分析】（1）画出y＝的图象；（2）猜想一：倒数变换得到的图象和原函数的图象之间如果存在交点，则其纵坐标为1或﹣1；猜想二：倒数变换得到的图象和原函数的图象的对称性相同，比如原函数是轴对称图形，则倒数变换的图象也是轴对称图象；（3）分三种情况画图：①c＝0②c＞0③c＜0；【解答】解：（1）在平面直角坐标系中画出y＝﹣x+1的图象和它经过倒数变换后的图象如图：图中去掉（1，0）的点（2）①猜想一：倒数变换得到的图象和原函数的图象之间如果存在交点，则其纵坐标为1或﹣1；猜想二：倒数变换得到的图象和原函数的图象的对称性相同，比如原函数是轴对称图形，则倒数变换的图象也是轴对称图象；②猜想一：因为只有1和﹣1的倒数是其本身，所以如果原函数存在一个点的纵坐标为1或﹣1，那么倒数变换得到的图象上必然也存在这样对应的纵坐标为1或﹣1，即两个函数图象的交点．（3）当c＝0时，当c＞0时，当c＜0时，【点评】本题考查函数的变换．理解倒数函数的定义是解题的基础，能够熟练用描点法画图是正确画出图象的关键．。
2019年鼓楼区初三一模卷
九年级（下）期中试卷英语 2018.04注意事项：1．本试卷共10页。
全卷满分为90分。
考试时间90分钟。
试题包含选择题和非选择题。
考生答题全部在答题卡上，答在本试卷上无效。
2．请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合，再将自己的姓名、考试证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上。
3．答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑。
如需改动，请用橡皮擦干净后，再选涂其它答案。
答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡的指定位置，在其它位置答题一律无效。
选择题（共40分）一、单项填空（共15小题；每小题1分，满分15分）从A、B、C、D四个选项中，选出可以填入空白处的最佳选项。
1. —It’s reported that Nanjing Metro Line 3 was in service April 1, 2018.—What exciting news! I believe the public transport system of Nanjing will be much better.A. on; anB. on; /C. in; anD. in; /2. —What did you talk about last night?—She told me about her job, her family and .A. somethingB. anythingC. everythingD. nothing3. —Excuse me, is the price of the iPhone 6 Plus?—It costs about ￥5,700.A. whatB. how manyC. how muchD. which4. I think that “Duang” must be one of the words on the Internet this year.A. deepestB. widestC. hottestD. highest5.—Do you think if I’m suitable for this job?—You can’t get the job you have experience in the computer industry.A. ifB. unlessC. sinceD. when6. Beijing plans to control the of its population and to have no more than 23 million peopleby the year 2020.A. sizeB. styleC. formD. shape7. —Tom, I told you how to solve the math problem in the last lesson.—I’m sorry, Mr. Lin. I about the plan for the class trip.A. thinkB. thoughtC. was thinkingD. have thought8. —Have you seen the watch my uncle gave me as my birthday present last year?—Sorry, I haven’t.A. whatB. whichC. whoD. when9. —Where is Jason? I want to tell him about the result of the singing competition.—Oh, you . He has known it already.A. needn’tB. can’tC. mustn’tD. shouldn’t10. More and more couples would rather a second baby their first child can feel lesslonely.A. have; in order toB. to have; in order toC. have; so thatD. to have; so that11. —Excuse me, sir. When can we have a swim in the pool?—Not until it next month.A. repairsB. will repairC. is repairedD. will be repaired12. —Mr. Ma has gone to Guangzhou on business.—Really? Do you know ?A. who did he go withB. when he came backC. how soon will he be backD. whether he went there by train13. Jack is dishonest. He always some excuses for doing something wrong.A. makes upB. sets upC. takes upD. picks up14. —How do you like the movie Cinderella?— .A. I watched it onlineB. I’ve seen it twiceC. It was shown last monthD. It’s a fantastic romantic film15. —Liu Xiang has announced the end of his sporting career.— . But I think he is still one of the greatest athletes in China.A. Don’t mention itB. That’s such a pityC. I can’t agree moreD. I’m afraid he couldn’t二、完形填空（共10小题；每小题1分，满分10分）阅读下面短文，从各题所给的A、B、C和D四个选项中，选出可以填入空白处的最佳选项。
2019年南京市鼓楼区初三中考一模数学试卷及评分标准
价当天的售价和利润情况，以下是部分数据：
售价（元/件）
60
61
62
63
···
利润（元）
6000
6090
6160
6210
···
⑴当售价为每件 60 元时，当天售出
件；
当售价为每件 60 元时，当天售出
件.
⑵若对该商品原售价每件涨价 x 元（ x 为正整数）时当天售出该商品的利润为 y 元.
①用所学过的函数知识直接写出 y 与 x 之间满足的函数表达式：
3．计算 a2 a2 3 的结果是（ ）
A． a8
B． a8
C． a7
D． a7
4．若顺次连接四边形 ABCD 各边中点所得的四边形是菱形，则下列结论中正确的是（ ）
A． AB∥CD
B． AB BC
C． AC BD
D． AC BD
5．下图是某家庭 2018 年每月交通费支出的条形统计图，若该家庭 2018 年月交通费平均支
变换，因此 y 1 的图像上也没有纵坐标为 0 的点. x
⑴请在下面的平面直角坐标系中画出 y x 1的图像和它经过倒数变换后的图像.
⑵观察上述图像，结合学过的关于函数图像与性质的知识， ①猜想：倒数变换得到的图像和原函数的图像之间可能有怎样的联系？写出两个即可.
②说理：请简要解释你其中一个猜想.
7． 3的绝对值是
．
8．若式子 x 1 在实数范围内有意义，则 x 的取值范围是
．
9．计算
27
6 的结果是 2
．
1 / 10
10．方程
x
1
2
2 x
的解是
．
11．正五边形的每个外角的大小是
南京鼓楼区2018—2019数学一模试卷
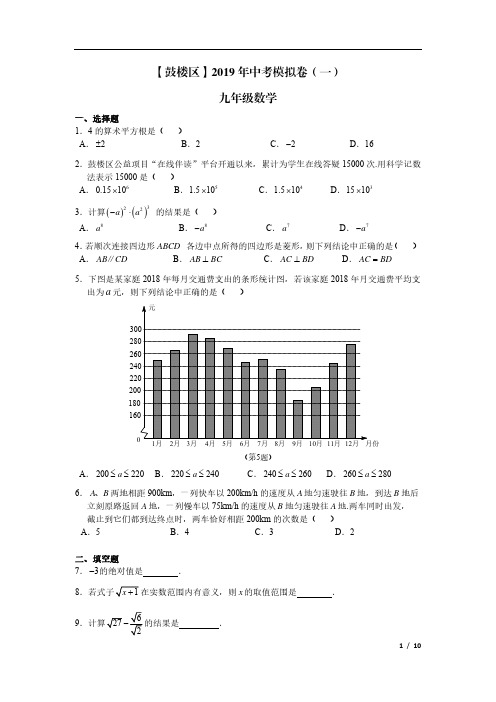
300 280 260 240 220 200 180 160一、选择题【鼓楼区】2019 年中考模拟卷（一）九年级数学1．4 的算术平方根是（ ）A ． ±2B ．2C ． -2D ．162. 鼓楼区公益项目“在线伴读”平台开通以来，累计为学生在线答疑 15000 次.用科学记数法表示 15000 是（ ）A ． 0.15 ⨯106 3．计算(-a )2⋅ (a2)3B ．1.5 ⨯105的结果是（ ）C ．1.5 ⨯104D ．15 ⨯103A ． a 8B ． -a 8C ． a 7D ． -a 74.若顺次连接四边形 ABCD 各边中点所得的四边形是菱形，则下列结论中正确的是（ ）A. AB ∥CDB. AB ⊥ BCC. AC ⊥ BDD. AC = BD5.下图是某家庭 2018 年每月交通费支出的条形统计图，若该家庭 2018 年月交通费平均支出为 a 元，则下列结论中正确的是（ ）1月2月 3月4月 5月 6 月 7 月 8 月9月 10月 11月 12月 月份A ． 200 ≤ a ≤ 220B ． 220 ≤ a ≤ 240（第5题）C ． 240 ≤ a ≤260D ． 260 ≤ a ≤ 2806.A 、B 两地相距 900km ，一列快车以 200km/h 的速度从 A 地匀速驶往 B 地，到达 B 地后立刻原路返回 A 地，一列慢车以 75km/h 的速度从 B 地匀速驶往 A 地.两车同时出发， 截止到它们都到达终点时，两车恰好相距 200km 的次数是（ ） A ．5B ．4C ．3D ．2二、填空题 7. -3的绝对值是．8. 若式子 在实数范围内有意义，则 x 的取值范围是．⎨⎪x - 3( x - 2) ≥ 49.计算 - 的结果是 ．10. 方程 1 x + 2 = 2的解是 ．x11.正五边形的每个外角的大小是°．12.已知关于 x 的方程 x 2 + mx - 2 = 0 有一根是 2，则另一根是， m = ．13．如图，AB ∥EG ∥CD ，EF 平分∠BED ，若∠D =69°，∠GEF =21°，则∠B =°．14.如图，圆锥底面圆心为 O ，半径 OA =1，顶点为 P ，将圆锥置于平面上，若保持顶点 P位置不变，将圆锥顺时针滚动三周后点 A 恰好回到原处，则圆锥的高 OP = ． 15.如图，点 A 、B 、C 、D 在⊙O 上，B 是 AC 的中点，过 C 作⊙O 的切线交 AB 的延长线于点 E .若∠AEC =84°，则∠ADC =°．A GACD（第13题）（第14题）DEC（第15题）16.在△ ABC 中，AB =5，AC =4，BC =3.若点 P 在△ ABC 内部（含边界）且满足PC ≤ PA ≤ PB ,则所有点 P 组成的区域的面积为 ．三、解答题17．（7 分）解不等式组⎧⎪3x > 2x - 2 ．⎩19．（8 分）⑴解方程 x 2 - x - 1 = 0 ．⑵在实数范围内分解因式 x 2 - x - 1 = 0 的结果为 ．2720．（8分）如图，AB=AD，AC=AE，BC=DE，点E在BC上⑴求证△ABC≌△ADE；A⑵求证∠EAC =∠DEB.DB E C(第20题）21.（8 分）⑴两只不透明的袋子中均有红球、黄球、白球各 1 个，这些球除颜色外无其他差别.分别从每个袋子中随机摸出一个球，求摸出两个球都是红球的概率.⑵鼓楼区实施全面均衡分班，某校为七年级各班随机分配任课教师.已知该校七年级共有10 个班，语文洪老师、数学胡老师都执教该年级，则他俩都任教七⑴班的概率为.22．（8分）妈妈准备用5万元投资金融产品，她查询到有A、B两款“利滚利”产品，即上一周产生的收益将计入本金以计算下一周的收益。
2019年中考数学模拟测试卷及答案(鼓楼一模)
2019年中考数学模拟考试（鼓楼一模）全卷满分120分．一、选择题（本大题共6小题，每小题2分，共12分．） 1．4的算术平方根是A ．±2B ． 2C ．－2D ．162．鼓楼区公益项目“在线伴读”平台开通以来，累计为学生在线答疑15 000次．用科学记数法表示15 000是A ．0.15×106B ．1.5×105C ．1.5×104D ．15×1033．计算(－a )2·(a 2)3的结果是A ．a 8B ．－a 8C ．a 7D ．－a 7 4．若顺次连接四边形ABCD 各边中点所得的四边形是菱形，则下列结论中正确的是A ．AB ∥CDB ．AB ⊥BCC ．AC ⊥BDD ．AC ＝BD5．下图是某家庭2018年每月交通费支出的条形统计图，若记该家庭2018年月交通费平均支出为a 元，则下列结论中正确的是A ．200≤a ≤220B ．220≤a ≤240C ．240≤a ≤260D ．260≤a ≤2806．A 、B 两地相距900 km ，一列快车以200 km/h 的速度从A 地匀速驶往B 地，到达B 地后立刻原速原路返回A 地，一列慢车以75 km/h 的速度从B 地匀速驶往A 地．两车同时出发，截止到它们都到达终点时，两车恰好相距200 km 的次数是A ．5B ．4C ．3D ．2二、填空题（本大题共10小题，每小题2分，共20分．）7．－3的绝对值是 ▲ ．8．若式子x ＋1在实数范围内有意义，则x 的取值范围是 ▲ ． 9．计算 27－62的结果是 ▲ ． 10．方程1x ＋2＝2x的解是 ▲ ． 11．正五边形的每个外角的大小是 ▲ °．12．已知关于 x 的方程x 2＋mx －2＝0有一根是2，则另一根是 ▲ ，m ＝ ▲ ． 13．如图，AB ∥EG ∥CD ，EF 平分∠BED ．若∠D ＝69°，∠GEF ＝21°，则∠B ＝ ▲ °．14．如图，圆锥底面圆心为O ，半径OA ＝1，顶点为P ．将圆锥置于平面上，若保持顶点P 位置不变，将圆锥顺时针滚动三周后点A 恰回到原处，则圆锥的高OP ＝ ▲ ．（第5题）15．如图，点A 、B 、C 、D 在⊙O 上，B 是 AC ︵的中点，过C 作⊙O 的切线交AB 的延长线于点E ．若∠AEC ＝84°，则∠ADC ＝ ▲ °．16．在△ABC 中，AB ＝5，AC ＝4，BC ＝3．若点P 在△ABC 内部（含边界）且满足 PC ≤P A ≤PB ，则所有点P 组成的区域的面积为 ▲ ．三、解答题（本大题共11小题，共88分．）17．（7分）解不等式组 ⎩⎪⎨⎪⎧3x ＞2x －2，x －3(x －2)≥4．18．（7分）计算 a －2a －1÷(a ＋1－3a －1)．19．（8分）（1）解方程x 2－x －1＝0．（2）在实数范围内分解因式x 2－x －1＝ ▲ ．（第13题）（第15题） （第14题）20．（8分）如图，AB ＝AD ，AC ＝AE ，BC ＝DE ，点E 在BC 上． （1）求证△ABC ≌△ADE ； （2）求证∠EAC ＝∠DEB ．21．（8分）（1）两只不透明的袋子中均装有红球、黄球、白球各1个，这些球除颜色外无其他差别．分别从每个袋子中随机摸出一个球，求摸出的两个球都是红球的概率．（2）鼓楼区实施全面均衡分班，某校为七年级各班随机分配任课教师．已知该校七年级共有10个班，语文洪老师、数学胡老师都只执教该年级的某一个班，则他俩都任教七（1）班的概率为 ▲ ．ABDCE（第20题）22．（8分）妈妈准备用5万元投资金融产品，她查询到有A 、B 两款“利滚利”产品，即上一周产生的收益将计入本金以计算下一周的收益．例如：投资100元，第一周的周收益率为5%，则第一周的收益为100×5%＝5元，第二周投资的本金将变为100＋5＝105元．下图是这两款产品过去．．5．周．的周收益率公告信息．（第1周：3月1日~3月7日）（1）若妈妈3月1日投资产品B ，到第二周结束时会不赚不赔，这种说法对吗？请判断并说明理由． （2）请运用学过的统计知识，为妈妈此次投资金融产品提出建议并简要说明理由．23．（8分）已知点A （1，1），B （2，3），C （4，7）．请用两种不同的方法判断这三点是否在一条直线上．（写出必要的推理过程）－－第二周 第三周 第四周 第一周 第五周（第22题）产品A24．（8分）已知：如图，在□ABCD 中，G 、H 分别是AD 、BC 的中点，AE ⊥BD ，CF ⊥BD ，垂足分别为E 、F ．（1）求证：四边形GEHF 是平行四边形；（2）已知AB ＝5，AD ＝8．求四边形GEHF 是矩形时BD 的长．25．（8分）某商品的进价是每件40元，原售价每件60元．进行不同程度的涨价后，统计了商品调价当天的售价和利润情况，以下是部分数据：（1）当售价为每件60元时，当天可售出 ▲ 件；当售价为每件61元时，当天可售出 ▲ 件．（2）若对该商品原售价每件涨价x 元（x 为正整数）时当天售出该商品的利润为y 元． ①用所学过的函数知识直接写出y 与x 满足的函数表达式： ▲ ． ②如何定价才能使当天的销售利润不低于6 200元？ABCDGH E F（第24题）26．（9分）如图①，一座石拱桥坐落在秦淮河上，它的主桥拱是圆弧形．如图②，桥宽AB 为8米，水面BC 宽16米，BC ︵表示的是主桥拱在水面以上的部分，点P 表示主桥拱拱顶．小明乘坐游船，沿主桥拱的中轴线向主桥拱行驶．（1） 图③是主桥拱在水面以上部分的主视图，请用直尺和圆规作出主桥拱在静水中的倒 影（保留作图痕迹，不写作法）．（2）已知小明眼睛距离水面1.6米，游船的速度为0.2米/秒．某一时刻，小明看拱顶P 的仰角为37°，4秒后，小明看拱顶P 的仰角为45°，整个过程中，游船未经过主桥拱的正下方． （参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75．） ①求拱顶P 到水面的距离；②船上的旗杆高1米，某时刻游船背对阳光行驶，小明发现旗杆在阳光下的投影所在直线与航线平行且长为2米．请估计此刻桥的正下方被阳光照射到的部分的面积（需画出示意图）．第26题①BC 水第26题③第26题②27．（9分）把一个函数图像上每个点的纵坐标变为原来的倒数（原函数图像上纵坐标为0的点除外）、横坐标不变，可以得到另一个函数的图像，我们称这个过程为倒数变换．例如：如图，将y ＝x 的图像经过倒数变换后可得到y ＝1x 的图像．特别地，因为y ＝x 图像上纵坐标为0的点是原点，所以该点不作变换，因此 y ＝1x 的图像上也没有纵坐标为0的点．（1）请在同一个平面直角坐标系中画出y ＝－x ＋1的图像和它经过倒数变换后的图像．（2）观察上述图像，结合学过的关于函数图像与性质的知识，①猜想：倒数变换得到的图像和原函数的图像之间可能有怎样的联系？写出两个即可．②说理：请简要解释你其中一个猜想．（3）请画出y ＝1x 2＋c （c 为常数）的大致图像．＝1x（第27题）2019年中考数学模拟考试（鼓楼一模）参考答案及评分标准一、选择题（本大题共6小题，每小题2分，共12分．）二、填空题（本大题共10小题，每小题2分，共20分．）7．3 8．x ≥－1 9．2 3 10．x ＝－4 11．72° 12．－1，－1 13．27° 14．22或52 15．64° 16． 2732三、解答题（本大题共11小题，共88分．） 17．（本题7分）解：由①，得x ＞－2． .................................................................................................. 2分由②，得x ≤1． ...................................................................................................... 5分 ∴ 不等式组的解集为－2＜x ≤1． ...................................................................... 7分18．（本题7分）解：a －2a －1÷(a ＋1－3a －1) ＝a －2a －1÷⎣⎡⎦⎤(a ＋1)(a －1)a －1－3a －1 ........................................ 2分＝a －2a －1÷a 2－1－3a －1 ＝a －2a －1•a －1 (a ＋2)(a －2) ........................................................... 5分 ＝1a ＋2． .................................................................................................................. 7分 19．（本题8分） （1）解： x 2－x ＝1 x 2－x ＋( 1 2)2＝ 54(x － 1 2)2＝ 54 ................................................................................................................ 2分x － 1 2＝±52.............................................................................................................. 4分x 1＝1＋5 2，x 2＝1－52． ................................................................................. 5分（2）(x －1＋5 2)(x －1－52)． ..................................................................................... 8分20．（本题8分）（1）证明：∵ AD ＝AB ，AE ＝AC ，DE ＝BC ，∴ △ABC ≌△ADE （SSS ）． ....................................................................................... 4分 （2）证明：∵ AC ＝AE ，∴ ∠AEC ＝∠C ．∵ △ABC ≌△ADE ，∴ ∠AED ＝∠C ．∴ ∠AEC ＝∠AED ． 设 ∠EAC ＝x °，则∠AEC ＝180°－x °2． ∴∠BED ＝180°－180°－x °2•2＝x °．∠EAC ＝∠DEB ． ............................................................................................................ 8分 21．（本题8分）解：（1）记两个袋子中的球分别为红1、黄1、白1，红2、黄2、白2．可能结果如下：（红1，红2），（红1，黄2），（红1，白2），（黄1，红2），（黄1，黄2），（黄1，白2）， （白1，红2），（白1，黄2），（白1，白2）．所有可能的结果共9种，它们出现的可能性相同， 其中“摸出的两个球都是红球”（记为事件A ）包含其中1种结果．所以P (A )＝19． ............................................................................................................... 6分（2）1100． ........................................................................................................................... 8分22．（本题8分）解：（1）不对． ............................................................................................................... 1分 设投资B 产品a 元，则第一周的收益为2%a 元，第二周投资的本金变为(1＋2%)a 元， 第二周结束时的余额为a (1＋2%)(1－2%)＝0.9996a ＜a ，所以赔了． .................... 4分 （2）答案不唯一，自圆其说即可得分． ....................................................................... 8分答案1：建议妈妈买产品A ，因为产品A 收益比较稳定，风险较小． 答案2：建议妈妈买产品B ，因为产品B 虽然风险高但收益同样也非常高． 23．（本题8分）答案不唯一，例如： 法1：直线AB 的函数表达式为y ＝2x －1．当x ＝4时，y ＝7，∴C 点在直线AB 上． ........................................................ 5分法2：如图，分别过点B 、C 作x 轴的垂线，分别过点A 、B 分别作x 轴的平行线，它们交于D 、E ．由题意得：AD ＝1，BD ＝2，BE ＝2，CE ＝4，∠D ＝∠E ＝∠DBE ＝90°． ∵AD BE ＝ BD CE ＝ 12且∠ADB ＝∠BEC ， ∴ △ABD ∽△BCE ． ∴ ∠A ＝∠CBE ． ∵ ∠A ＋∠ABD ＝90°， ∴ ∠CBE ＋∠ABD ＝90°．∴ ∠CBE ＋∠DBE ＋∠ABD ＝180°．∴ A 、B 、C 三点共线． ................................................................................... 8分 法3：同法2作辅助线．由勾股定理可得：AB ＝12＋22＝5，BC ＝22＋42＝25，AC ＝32＋62＝35． ∴ AB ＋BC ＝AC ．∴ A 、B 、C 三点共线． ................................................................................... 8分 24．（本题8分）（1）证明：∵ AE ⊥BD ，CF ⊥BD ， ∴ ∠AED ＝∠CFB ＝90°．∵ G 、H 分别是AD 、BC 的中点，∴ EG ＝DG ＝12AD ，FH ＝BH ＝12B C ．∴ ∠1＝∠2，∠3＝∠4． ∵ 四边形ABCD 是平行四边形， ∴ AD ＝BC ，AD ∥B C ． ∴ EG ＝FH ，∠2＝∠4. ∴ ∠1＝∠3．∴ EG ∥FH ．∴ 四边形GEHF 是平行四边形． ................................................................. 5分（2）解：连接GH ．当□GEHF 是矩形时，EF ＝GH ．易证四边形ABHG 是平行四边形． ∴GH ＝AB ＝5．AB CD E（法2）ABCDGH EF（第24题）1234易证△ABE ≌△CDF ． ∴BE ＝DF ．设 BE ＝x ，则DF ＝x ，ED ＝5＋x ．∴52－x 2＝82－(5＋x )2 x ＝1.4∴BD ＝7.8． ......................................................................................................... 8分25．（本题8分）解：（1）300，290． ........................................................................................................... 2分 （2）①y ＝－10x 2＋100x ＋6000． ............................................................................... 5分 ②y ＝－10x 2＋100x ＋6000＝－10(x －5)2＋6250． 当y ＝6200时，－10(x －5)2＋6250＝6200． 解得 x 1＝5－5，x 2＝5＋5． ∵ －10＜0，∴ 该二次函数的图像开口向下． ∴ 当y ≥6200时，5－5≤x ≤5＋5． 即 当y ≥6200时，3≤x ≤7（x 为正整数）．答：定价为：63，64，65，66，67．.................................................................. 8分 26．（本题9分）解：（1）如图即为所求（作法不唯一）； ......................................................................... 3分（2）①如图，设PE ＝xm ． 在△PED 中，∠PED ＝90°，则tan∠PDE ＝PE DE． ∴ DE ＝xtan45°＝x ．在△PEM 中，∠PEM ＝90°，则tan ∠PME ＝ PE ME ．∴ ME ＝xtan37°．∵ ME －DE ＝MD ， ∴ xtan37°－x ＝0.8． 解得x ＝2.4．∴ PH ＝1.6＋2.4＝4．答：拱顶P 到水面的距离是4 m ． ............................................................................ 6分 ②太阳照射到的部分如图所示．PEHMDBC 水面27．（本题9分）（1）如图所示．2分（2）①答案不唯一，以下作为参考．4分猜想1：原函数图像在x轴上（下）方的部分，经过倒数变换后的图像也在x轴上（下）方．猜想2：若原函数图像经过x轴上的点A（a，0），则经过倒数变换后的图像无限接近直线x＝a猜想3：原函数图像在x轴上方的部分，若y随x增大而增大（减小），经过倒数变换后的该部分图像y随x的增大而减小（增大）；原函数图像在x轴下方的部分，若y随x增大而增大（减小），经过倒数变换后的该部分图像y随x的增大而减小（增大）．猜想4：若原函数的图像和它经过倒数变换后的图像有公共点，则公共点纵坐标为1或－1．②答案不唯一，以下作为参考． ........................................................................................... 6分解释1：互为倒数的两个数符号相同．解释2：0没有倒数，纵坐标的绝对值越小，倒数变换后的对应点的纵坐标绝对值越大．解释3：y1•y2＝1，一个增大时，另外一个必然减小．解释4：y1•y2＝1且y1＝y2，可求得y＝±1．（3）y＝1x2＋c（c为常数）的大致图像如下图所示． .................................................. 9分当c＞0时当c＝0时当c＜0时数学试卷第11 页（共11 页）。
江苏省南京市2019-2020学年中考数学一模考试卷含解析
江苏省南京市2019-2020学年中考数学一模考试卷一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．） 1．已知△ABC ，D 是AC 上一点，尺规在AB 上确定一点E ，使△ADE ∽△ABC ，则符合要求的作图痕迹是（ ）A ．B ．C ．D ．2．如图，在ABC 中，D 、E 分别在边AB 、AC 上，//DE BC ，//EF CD 交AB 于F ，那么下列比例式中正确的是( )A ．AF DEDF BC= B ．DF AFDB DF= C ．EF DECD BC= D ．AF ADBD AB= 3．定义：若点P （a ，b ）在函数y=的图象上，将以a 为二次项系数，b 为一次项系数构造的二次函数y=ax 2+bx 称为函数y=的一个“派生函数”．例如：点（2， ）在函数y=的图象上，则函数y=2x 2+称为函数y=的一个“派生函数”．现给出以下两个命题：（1）存在函数y=的一个“派生函数”，其图象的对称轴在y 轴的右侧（2）函数y=的所有“派生函数”的图象都经过同一点，下列判断正确的是（ ） A ．命题（1）与命题（2）都是真命题 B ．命题（1）与命题（2）都是假命题 C ．命题（1）是假命题，命题（2）是真命题D ．命题（1）是真命题，命题（2）是假命题4．给出下列各数式，①2?--（） ②2-- ③2 2- ④22-（） 计算结果为负数的有（ ） A ．1个 B ．2个 C ．3个 D ．4个5．一、单选题如图，△ABC 中，AD 是BC 边上的高，AE 、BF 分别是∠BAC 、∠ABC 的平分线，∠BAC=50°，∠ABC=60°，则∠EAD+∠ACD=（ ）A ．75°B ．80°C ．85°D ．90°6．如图 1 是某生活小区的音乐喷泉， 水流在各个方向上沿形状相同的抛物线路径落下，其中一个喷水管喷水的最大高度为 3 m ，此时距喷水管的水平距离为 1 m ，在如图 2 所示的坐标系中，该喷水管水流喷出的高度y （m ）与水平距离x （m ）之间的函数关系式是（ ）A ．()213y x =--+ B ．()2213y x =-+ C ．()2313y x =-++D ．()2313y x =--+7．如图，将Rt ABC △绕直角顶点C 顺时针旋转90，得到A B C ''，连接'A A ，若120︒∠=，则B 的度数是（ ）A ．70︒B ．65︒C ．60︒D ．55︒8．关于x 的一元二次方程x 2-2x-（m-1）=0有两个不相等的实数根，则实数m 的取值范围是（ ） A ．0m >且1m ≠ B ．0m >C ．0m ≥且1m ≠D ．0m ≥9．如图，AB 是O 的直径，弦CD AB ⊥，垂足为点E ，点G 是AC 上的任意一点，延长AG 交DC 的延长线于点F ，连接,,GC GD AD .若25BAD ∠=︒，则AGD ∠等于（ ）A ．55︒B ．65︒C ．75︒D ．85︒10．如图，在ABCD 中，E 为CD 上一点，连接AE 、BD ，且AE 、BD 交于点F ，DE ：EC=2:3，则S △DEF :S △ABF =（ ）A ．2：3B ．4：9C ．2：5D ．4：2511．当x=1时，代数式x 3+x+m 的值是7，则当x=﹣1时，这个代数式的值是（ ） A ．7B ．3C ．1D ．﹣712．实数6 的相反数是 （ ） A ．-6B ．6C ．16D ．6-二、填空题：（本大题共6个小题，每小题4分，共24分．）13．如图，将ABC △的边AB 绕着点A 顺时针旋转()090a α︒︒<<得到AB '，边AC 绕着点A 逆时针旋转()090ββ︒︒<<得到AC '，联结B C ''．当90αβ︒+=时，我们称AB C ''△是ABC △的“双旋三角形”．如果等边ABC △的边长为a ，那么它的“双旋三角形”的面积是__________（用含a 的代数式表示）．14．若|a|=20160，则a=___________.15．如图，已知∠A+∠C=180°，∠APM=118°，则∠CQN=_____°．16．如图，在平面直角坐标系中，已知抛物线y=x2+bx+c过A，B，C三点，点A的坐标是（3，0），点C 的坐标是（0，-3），动点P在抛物线上． b =_________，c =_________，点B的坐标为_____________；（直接填写结果）是否存在点P，使得△ACP是以AC为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由；过动点P作PE垂直y轴于点E，交直线AC于点D，过点D作x轴的垂线．垂足为F，连接EF，当线段EF的长度最短时，求出点P的坐标．17．若分式15x-有意义，则实数x的取值范围是_______．18．11201842-⎛⎫+- ⎪⎝⎭=_____．三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．（6分）某种蔬菜的销售单价y1与销售月份x之间的关系如图（1）所示，成本y2与销售月份之间的关系如图（2）所示（图（1）的图象是线段图（2）的图象是抛物线）分别求出y1、y2的函数关系式（不写自变量取值范围）；通过计算说明：哪个月出售这种蔬菜，每千克的收益最大？20．（6分）如图，在△ABC中，∠ACB=90°，O是AB上一点，以OA为半径的⊙O与BC相切于点D，与AB交于点E，连接ED并延长交AC的延长线于点F．（1）求证：AE=AF；（2）若DE=3，sin∠BDE=13，求AC的长．21．（6分）计算：025(3)tan 45π︒+--.化简：2(2)(1)x x x ---.22．（8分）已知：如图，抛物线y=ax 2+bx+c 与坐标轴分别交于点A （0，6），B （6，0），C （﹣2，0），点P 是线段AB 上方抛物线上的一个动点． （1）求抛物线的解析式；（2）当点P 运动到什么位置时，△PAB 的面积有最大值？（3）过点P 作x 轴的垂线，交线段AB 于点D ，再过点P 做PE ∥x 轴交抛物线于点E ，连结DE ，请问是否存在点P 使△PDE 为等腰直角三角形？若存在，求出点P 的坐标；若不存在，说明理由．23．（8分）如图1，点P 是平面直角坐标系中第二象限内的一点，过点P 作PA ⊥y 轴于点A ，点P 绕点A 顺时针旋转60°得到点P'，我们称点P'是点P 的“旋转对应点”．（1）若点P （﹣4，2），则点P 的“旋转对应点”P'的坐标为 ；若点P 的“旋转对应点”P'的坐标为（﹣5，16）则点P 的坐标为 ；若点P （a ，b ），则点P 的“旋转对应点”P'的坐标为 ； （2）如图2，点Q 是线段AP'上的一点（不与A 、P'重合），点Q 的“旋转对应点”是点Q'，连接PP'、QQ'，求证：PP'∥QQ'；（3）点P 与它的“旋转对应点”P'的连线所在的直线经过点（3，6），求直线PP'与x 轴的交点坐标．24．（10分）如图，在平面直角坐标系中，矩形OABC 的顶点B 坐标为（4，6），点P 为线段OA 上一动点（与点O 、A 不重合），连接CP ，过点P 作PE ⊥CP 交AB 于点D ，且PE ＝PC ，过点P 作PF ⊥OP 且PF ＝PO （点F 在第一象限），连结FD 、BE 、BF ，设OP ＝t ．（1）直接写出点E 的坐标（用含t 的代数式表示）： ；（2）四边形BFDE 的面积记为S ，当t 为何值时，S 有最小值，并求出最小值； （3）△BDF 能否是等腰直角三角形，若能，求出t ；若不能，说明理由．25．（10分）某制衣厂某车间计划用10天加工一批出口童装和成人装共360件,该车间的加工能力是：每天能单独加工童装45件或成人装30件．（1）该车间应安排几天加工童装,几天加工成人装，才能如期完成任务；（2）若加工童装一件可获利80元, 加工成人装一件可获利120元, 那么该车间加工完这批服装后，共可获利多少元．26．（12分）如图，矩形ABCD 的两边AD 、AB 的长分别为3、8，E 是DC 的中点，反比例函数my x=的图象经过点E ，与AB 交于点F .若点B 坐标为(6,0)-，求m 的值及图象经过A 、E 两点的一次函数的表达式；若2AF AE -=，求反比例函数的表达式.27．（12分）如图，已知抛物线y ＝x 2﹣4与x 轴交于点A ，B （点A 位于点B 的左侧），C 为顶点，直线y ＝x+m 经过点A ，与y 轴交于点D ．求线段AD 的长；平移该抛物线得到一条新拋物线，设新抛物线的顶点为C′．若新抛物线经过点D ，并且新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD ，求新抛物线对应的函数表达式．参考答案一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．A【解析】【分析】以DA为边、点D为顶点在△ABC内部作一个角等于∠B，角的另一边与AB的交点即为所求作的点．【详解】如图，点E即为所求作的点．故选：A．【点睛】本题主要考查作图-相似变换，根据相似三角形的判定明确过点D作一角等于∠B或∠C，并熟练掌握做一个角等于已知角的作法式解题的关键．2．C【解析】【分析】根据平行线分线段成比例定理和相似三角形的性质找准线段的对应关系，对各选项分析判断．【详解】A、∵EF∥CD，DE∥BC，∴AF AEDF EC=，AE DEAC BC=，∵CE≠AC，∴AF DEDF BC≠，故本选项错误；B、∵EF∥CD，DE∥BC，∴AF AEDF EC=，AE ADEC BD=，∴AF ADDF BD=，∵AD≠D F，∴DF AFDB DF≠，故本选项错误；C、∵EF∥CD，DE∥BC，∴DE AEBC AC=，EF AECD AC=，∴EF DECD BC=，故本选项正确；D、∵EF∥CD，DE∥BC，∴AD AEAB AC=，AF AEAD AC=，∴AF ADAD AB=，∵AD≠DF，∴AF ADBD AB≠，故本选项错误.故选C.【点睛】本题考查了平行线分线段成比例的运用及平行于三角形一边的直线截其它两边，所得的新三角形与原三角形相似的定理的运用，在解答时寻找对应线段是关健．3．C【解析】试题分析：（1）根据二次函数y=ax2+bx的性质a、b同号对称轴在y轴左侧，a、b异号对称轴在y轴右侧即可判断．（2）根据“派生函数”y=ax 2+bx ，x=0时，y=0，经过原点，不能得出结论． （1）∵P （a ，b ）在y=上， ∴a 和b 同号，所以对称轴在y 轴左侧， ∴存在函数y=的一个“派生函数”，其图象的对称轴在y 轴的右侧是假命题． （2）∵函数y=的所有“派生函数”为y=ax 2+bx ， ∴x=0时，y=0， ∴所有“派生函数”为y=ax 2+bx 经过原点，∴函数y=的所有“派生函数”，的图象都进过同一点，是真命题． 考点：（1）命题与定理；（2）新定义型 4．B 【解析】∵①(2)2--=；②22--=-；③224-=-；④2(2)4-=； ∴上述各式中计算结果为负数的有2个. 故选B. 5．A 【解析】分析：依据AD 是BC 边上的高，∠ABC=60°，即可得到∠BAD=30°，依据∠BAC=50°，AE 平分∠BAC ，即可得到∠DAE=5°，再根据△ABC 中，∠C=180°﹣∠ABC ﹣∠BAC=70°，可得∠EAD+∠ACD=75°． 详解：∵AD 是BC 边上的高，∠ABC=60°， ∴∠BAD=30°，∵∠BAC=50°，AE 平分∠BAC ， ∴∠BAE=25°， ∴∠DAE=30°﹣25°=5°，∵△ABC 中，∠C=180°﹣∠ABC ﹣∠BAC=70°， ∴∠EAD+∠ACD=5°+70°=75°， 故选A ．点睛：本题考查了三角形内角和定理：三角形内角和为180°．解决问题的关键是三角形外角性质以及角平分线的定义的运用． 6．D 【解析】 【分析】根据图象可设二次函数的顶点式，再将点（0,0）代入即可． 【详解】解：根据图象，设函数解析式为()2y a x h k =-+ 由图象可知，顶点为（1,3） ∴()213y a x =-+，将点（0,0）代入得()20013a =-+ 解得3a =- ∴()2313y x =--+ 故答案为：D ． 【点睛】本题考查了是根据实际抛物线形，求函数解析式，解题的关键是正确设出函数解析式． 7．B 【解析】 【分析】根据旋转的性质可得AC ＝A′C ，然后判断出△ACA′是等腰直角三角形，根据等腰直角三角形的性质可得∠CAA′＝45°，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠A′B′C ，最后根据旋转的性质可得∠B ＝∠A′B′C ． 【详解】解：∵Rt △ABC 绕直角顶点C 顺时针旋转90°得到△A′B′C ， ∴AC ＝A′C ，∴△ACA′是等腰直角三角形， ∴∠CAA′＝45°，∴∠A′B′C ＝∠1＋∠CAA′＝20°＋45°＝65°， ∴∠B ＝∠A′B′C ＝65°． 故选B ． 【点睛】本题考查了旋转的性质，等腰直角三角形的判定与性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记各性质并准确识图是解题的关键． 8．A 【解析】 【分析】根据一元二次方程的系数结合根的判别式△＞1，即可得出关于m 的一元一次不等式，解之即可得出实数m 的取值范围． 【详解】∵关于x的一元二次方程x2﹣2x﹣（m﹣1）=1有两个不相等的实数根，∴△=（﹣2）2﹣4×1×[﹣（m﹣1）]=4m ＞1，∴m＞1．故选B．【点睛】本题考查了根的判别式，牢记“当△＞1时，方程有两个不相等的实数根”是解题的关键．9．B【解析】【分析】连接BD，利用直径得出∠ABD=65°，进而利用圆周角定理解答即可．【详解】连接BD，∵AB是直径，∠BAD=25°，∴∠ABD=90°-25°=65°，∴∠AGD=∠ABD=65°，故选B．【点睛】此题考查圆周角定理，关键是利用直径得出∠ABD=65°．10．D【解析】试题分析：先根据平行四边形的性质及相似三角形的判定定理得出△DEF∽△BAF，从而DE：AB=DE：DC=2：5，所以S△DEF:S△ABF=4：25试题解析:∵四边形ABCD是平行四边形，∴AB∥CD，BA=DC∴∠EAB=∠DEF，∠AFB=∠DFE，∴△DEF∽△BAF，∴DE：AB=DE：DC=2：5，∴S△DEF：S△ABF=4：25，考点：1.相似三角形的判定与性质；2.三角形的面积；3.平行四边形的性质．11．B【解析】【分析】【详解】因为当x=1时，代数式的值是7，所以1+1+m=7，所以m=5，当x=-1时，=-1-1+5=3， 故选B ．12．A【解析】【分析】根据相反数的定义即可判断.【详解】 6 的相反数是6故选A.【点睛】此题主要考查相反数的定义，解题的关键是熟知相反数的定义即可求解.二、填空题：（本大题共6个小题，每小题4分，共24分．）13．214a . 【解析】【分析】首先根据等边三角形、“双旋三角形”的定义得出△A B'C'是顶角为150°的等腰三角形，其中AB'=AC'=a ．过C'作C'D ⊥AB'于D ，根据30°角所对的直角边等于斜边的一半得出C'D 12=AC'12=a ，然后根据S △AB'C'12=AB'•C'D 即可求解． 【详解】∵等边△ABC 的边长为a ，∴AB=AC=a ，∠BAC=60°．∵将△ABC 的边AB 绕着点A 顺时针旋转α（0°＜α＜90°）得到AB'，∴AB'=AB=a ，∠B'AB=α． ∵边AC 绕着点A 逆时针旋转β（0°＜β＜90°）得到AC'，∴AC'=AC=a ，∠CAC'=β，∴∠B'AC'=∠B'AB+∠BAC+∠CAC'=α+60°+β=60°+90°=150°．如图，过C'作C'D ⊥AB'于D ，则∠D=90°，∠DAC'=30°，∴C'D 12=AC'12=a ，∴S △AB'C'12=AB'•C'D 12=a•12a 14=a 1． 故答案为：14a 1．【点睛】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了含30°角的直角三角形的性质，等边三角形的性质以及三角形的面积． 14．±1【解析】试题分析：根据零指数幂的性质（01(0)a a =≠），可知|a|=1，座椅可知a=±1. 15．1【解析】【分析】先根据同旁内角互补两直线平行知AB ∥CD ，据此依据平行线性质知∠APM=∠CQM=118°，由邻补角定义可得答案．【详解】解：∵∠A+∠C=180°，∴AB ∥CD ，∴∠APM=∠CQM=118°，∴∠CQN=180°-∠CQM=1°，故答案为：1．【点睛】本题主要考查平行线的判定与性质，解题的关键是掌握平行线的判定是由角的数量关系判断两直线的位置关系．平行线的性质是由平行关系来寻找角的数量关系． 16．（1）2-，3-，（-1,0）；（2）存在P 的坐标是(14)-，或(-25)，；（1）当EF 最短时，点P 的坐标是：（2102+，32-210-，32-） 【解析】【分析】（1）将点A 和点C 的坐标代入抛物线的解析式可求得b 、c 的值，然后令y=0可求得点B 的坐标； （2）分别过点C 和点A 作AC 的垂线，将抛物线与P 1，P 2两点先求得AC 的解析式，然后可求得P 1C和P 2A 的解析式，最后再求得P 1C 和P 2A 与抛物线的交点坐标即可；（1）连接OD ．先证明四边形OEDF 为矩形，从而得到OD=EF ，然后根据垂线段最短可求得点D 的纵坐标，从而得到点P 的纵坐标，然后由抛物线的解析式可求得点P 的坐标．【详解】解：（1）∵将点A 和点C 的坐标代入抛物线的解析式得：3930c b c =-⎧⎨++=⎩， 解得：b=﹣2，c=﹣1，∴抛物线的解析式为223y x x =--．∵令2230x x --=，解得：11x =-，23x =，∴点B 的坐标为（﹣1，0）．故答案为﹣2；﹣1；（﹣1，0）．（2）存在．理由：如图所示：①当∠ACP 1=90°．由（1）可知点A 的坐标为（1，0）．设AC 的解析式为y=kx ﹣1．∵将点A 的坐标代入得1k ﹣1=0，解得k=1，∴直线AC 的解析式为y=x ﹣1，∴直线CP 1的解析式为y=﹣x ﹣1．∵将y=﹣x ﹣1与223y x x =--联立解得11x =，20x =（舍去），∴点P 1的坐标为（1，﹣4）．②当∠P 2AC=90°时．设AP 2的解析式为y=﹣x+b ．∵将x=1，y=0代入得：﹣1+b=0，解得b=1，∴直线AP 2的解析式为y=﹣x+1．∵将y=﹣x+1与223y x x =--联立解得1x =﹣2，2x =1（舍去），∴点P 2的坐标为（﹣2，5）．综上所述，P 的坐标是（1，﹣4）或（﹣2，5）．（1）如图2所示：连接OD ．由题意可知，四边形OFDE 是矩形，则OD=EF ．根据垂线段最短，可得当OD ⊥AC 时，OD 最短，即EF 最短．由（1）可知，在Rt △AOC 中，∵OC=OA=1，OD ⊥AC ，∴D 是AC 的中点．又∵DF ∥OC ，∴DF=12OC=32， ∴点P 的纵坐标是32-， ∴23232x x --=-，解得：x=2102±， ∴当EF 最短时，点P 的坐标是：（2102+，32-）或（2102-，32-）． 17．【解析】 由于分式的分母不能为2，x-1在分母上，因此x-1≠2，解得x ．解：∵分式15x -有意义， ∴x-1≠2，即x≠1．故答案为x≠1．本题主要考查分式有意义的条件：分式有意义，分母不能为2．18．1【解析】分析：第一项根据非零数的零次幂等于1计算，第二项根据算术平方根的意义化简，第三项根据负整数指数幂等于这个数的正整数指数幂的倒数计算.详解：原式=1+2﹣2=1．故答案为：1．点睛：本题考查了实数的运算，熟练掌握零指数幂、算术平方根的意义，负整数指数幂的运算法则是解答本题的关键.三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．（1）y1＝273x-+;y2＝13x2﹣4x+2；（2）5月出售每千克收益最大，最大为73．【解析】【分析】（1）观察图象找出点的坐标，利用待定系数法即可求出y1和y2的解析式；（2）由收益W=y1-y2列出W与x的函数关系式，利用配方求出二次函数的最大值．【详解】解：（1）设y1＝kx+b，将（3，5）和（6，3）代入得，3563k bk b+=⎧⎨+=⎩，解得237kb⎧=-⎪⎨⎪=⎩．∴y1＝﹣23x+1．设y2＝a（x﹣6）2+1，把（3，4）代入得，4＝a（3﹣6）2+1，解得a＝13．∴y2＝13（x﹣6）2+1，即y2＝13x2﹣4x+2．（2）收益W＝y1﹣y2，＝﹣23x+1﹣（13x2﹣4x+2）＝﹣13（x﹣5）2+73，∵a＝﹣13＜0，∴当x＝5时，W最大值＝73．故5月出售每千克收益最大，最大为73元．【点睛】本题考查了一次函数和二次函数的应用，熟练掌握待定系数法求解析式是解题关键，掌握配方法是求二次函数最大值常用的方法20．（1）证明见解析；（2）1．【解析】【分析】（1）根据切线的性质和平行线的性质解答即可；（2）根据直角三角形的性质和三角函数解答即可．【详解】（1）连接OD，∵OD=OE，∴∠ODE=∠OED．∵直线BC为⊙O的切线，∴OD⊥BC．∴∠ODB=90°．∵∠ACB=90°，∴OD∥AC．∴∠ODE=∠F．∴∠OED=∠F．∴AE=AF；（2）连接AD，∵AE是⊙O的直径，∴∠ADE=90°，∵AE=AF，∴DF=DE=3，∵∠ACB=90°，∴∠DAF+∠F=90°，∠CDF+∠F=90°，∴∠DAF=∠CDF=∠BDE，在Rt△ADF中，DFAF=sin∠DAF=sin∠BDE=13，∴AF=3DF=9，在Rt△CDF中，CFDF=sin∠CDF=sin∠BDE=13，∴CF=13DF=1，∴AC=AF﹣CF=1．【点睛】本题考查了切线的性质，解直角三角形的应用，等腰三角形的判定等，综合性较强，正确添加辅助线、熟练掌握和灵活运用相关知识是解题的关键.21．（1）5；（2）-3x+4【解析】【分析】(1)第一项计算算术平方根，第二项计算零指数幂，第三项计算特殊角的三角函数值，最后计算有理数运算. （2）利用完全平方公式和去括号法则进行计算，再进行合并同类项运算.【详解】（1）解：原式5115=+-=（2）解：原式224434x x x x x =-+-+=-+【点睛】本题考查实数的混合运算和整式运算，解题关键是熟练运用完全平方公式和熟记特殊角的三角函数值. 22．（1）抛物线解析式为y=﹣12x 2+2x+6；（2）当t=3时，△PAB 的面积有最大值；（3）点P （4，6）． 【解析】【分析】（1）利用待定系数法进行求解即可得；（2）作PM ⊥OB 与点M ，交AB 于点N ，作AG ⊥PM ，先求出直线AB 解析式为y=﹣x+6，设P （t ，﹣12t 2+2t+6），则N （t ，﹣t+6），由S △PAB =S △PAN +S △PBN =12PN•AG+12PN•BM=12PN•OB 列出关于t 的函数表达式，利用二次函数的性质求解可得；（3）由PH ⊥OB 知DH ∥AO ，据此由OA=OB=6得∠BDH=∠BAO=45°，结合∠DPE=90°知若△PDE 为等腰直角三角形，则∠EDP=45°，从而得出点E 与点A 重合，求出y=6时x 的值即可得出答案．【详解】（1）∵抛物线过点B （6，0）、C （﹣2，0），∴设抛物线解析式为y=a （x ﹣6）（x+2），将点A （0，6）代入，得：﹣12a=6，解得：a=﹣12， 所以抛物线解析式为y=﹣12（x ﹣6）（x+2）=﹣12x 2+2x+6； （2）如图1，过点P 作PM ⊥OB 与点M ，交AB 于点N ，作AG ⊥PM 于点G ，设直线AB 解析式为y=kx+b ，将点A （0，6）、B （6，0）代入，得：660b k b =⎧⎨+=⎩， 解得：16k b =-⎧⎨=⎩， 则直线AB 解析式为y=﹣x+6，设P （t ，﹣12t 2+2t+6）其中0＜t ＜6， 则N （t ，﹣t+6）， ∴PN=PM ﹣MN=﹣12t 2+2t+6﹣（﹣t+6）=﹣12t 2+2t+6+t ﹣6=﹣12t 2+3t ， ∴S △PAB =S △PAN +S △PBN=12PN•AG+12PN•BM =12PN•（AG+BM ） =12PN•OB =12×（﹣12t 2+3t ）×6 =﹣32t 2+9t =﹣32（t ﹣3）2+272， ∴当t=3时，△PAB 的面积有最大值；（3）△PDE 为等腰直角三角形，则PE=PD ，点P （m ，-12m 2+2m+6）， 函数的对称轴为：x=2，则点E 的横坐标为：4-m ，则PE=|2m-4|，即-12m 2+2m+6+m-6=|2m-4|， 解得：m=4或-2或5+17或5-17（舍去-2和5+17）故点P 的坐标为：（4，6）或（5-17，317-5）．【点睛】本题考查了二次函数的综合问题，涉及到待定系数法、二次函数的最值、等腰直角三角形的判定与性质等，熟练掌握和灵活运用待定系数法求函数解析式、二次函数的性质、等腰直角三角形的判定与性质等是解题的关键.23．（1）（﹣2，2+23），（﹣10，16﹣53），（2a ，b ﹣32a ）；（2）见解析；（3）直线PP'与x 轴的交点坐标（﹣3，0）【解析】【分析】（1）①当P （-4，2）时，OA=2，PA=4，由旋转知，∠P'AH=30°，进而P'H=12P'A=2，AH=3P'H=23，即可得出结论；②当P'（-5，16）时，确定出P'A=10，AH=53，由旋转知，PA=PA'=10，OA=OH-AH=16-53，即可得出结论；③当P （a ，b ）时，同①的方法得，即可得出结论；（2）先判断出∠BQQ'=60°，进而得出∠PAP'=∠PP'A=60°，即可得出∠P'QQ'=∠PAP'=60°，即可得出结论；（3）先确定出y PP '=3x+3，即可得出结论．【详解】解:（1）如图1，①当P （﹣4，2）时，∵PA ⊥y 轴，∴∠PAH=90°，OA=2，PA=4，由旋转知，P'A=4，∠PAP'=60°，∴∠P'AH=30°，在Rt △P'AH 中，P'H=12P'A=2， ∴AH=3P'H=23，∴OH=OA+AH=2+23，∴P'（﹣2，2+23），②当P'（﹣5，16）时，在Rt △P'AH 中，∠P'AH=30°，P'H=5， ∴P'A=10，AH=53，由旋转知，PA=PA'=10，OA=OH ﹣AH=16﹣53， ∴P （﹣10，16﹣53），③当P （a ，b ）时，同①的方法得，P'（a 2，b ﹣32a ）， 故答案为：（﹣2，2+23），（﹣10，16﹣53），（2a ，b ﹣32a ）； （2）如图2，过点Q 作QB ⊥y 轴于B ，∴∠BQQ'=60°，由题意知，△PAP'是等边三角形，∴∠PAP'=∠PP'A=60°，∵QB ⊥y 轴，PA ⊥y 轴，∴QB ∥PA ，∴∠P'QQ'=∠PAP'=60°，∴∠P'QQ'=60°=∠PP'A ，∴PP'∥QQ'；（3）设y PP '=kx+b'，由题意知，3，∵直线经过点（3，6），∴b'=3，∴y PP'=3x+3，令y=0，∴x=3∴直线PP'与x30）．【点睛】此题是几何变换综合题，主要考查了含30度角的直角三角形的性质，旋转的性质，等边三角形的判定和性质，待定系数法，解本题的关键是理解新定义．24．(1)、（t+6，t）；(2)、当t=2时，S有最小值是16；(3)、理由见解析．【解析】【分析】【详解】（1）如图所示，过点E作EG⊥x轴于点G，则∠COP=∠PGE=90°，由题意知CO=AB=6、OA=BC=4、OP=t，∵PE⊥CP、PF⊥OP，∴∠CPE=∠FPG=90°，即∠CPF+∠FPE=∠FPE+∠EPG，∴∠CPF=∠EPG，又∵CO⊥OG、FP⊥OG，∴CO∥FP，∴∠CPF=∠PCO，∴∠PCO=∠EPG，在△PCO和△EPG中，∵∠PCO=∠EPG，∠POC=∠EGP，PC=EP，∴△PCO≌△EPG（AAS），∴CO=PG=6、OP=EG=t，则OG=OP+PG=6+t，则点E的坐标为（t+6，t），（2）∵DA∥EG，∴△PAD∽△PGE，∴AD PAGE PG=，∴46AD tt-=，∴AD=16t（4﹣t），∴BD=AB﹣AD=6﹣16t（4﹣t）=16t2﹣23t+6，∵EG⊥x轴、FP⊥x轴，且EG=FP，∴四边形EGPF为矩形，∴EF⊥BD，EF=PG，∴S四边形BEDF=S△BDF+S△BDE=12×BD×EF=12×（16t2﹣23t+6）×6=12（t﹣2）2+16，∴当t=2时，S有最小值是16；（3）①假设∠FBD为直角，则点F在直线BC上，∵PF=OP＜AB，∴点F不可能在BC上，即∠FBD不可能为直角；②假设∠FDB为直角，则点D在EF上，∵点D在矩形的对角线PE上，∴点D 不可能在EF 上，即∠FDB 不可能为直角；③假设∠BFD 为直角且FB=FD ，则∠FBD=∠FDB=45°，如图2，作FH ⊥BD 于点H ，则FH=PA ，即4﹣t=6﹣t ，方程无解，∴假设不成立，即△BDF 不可能是等腰直角三角形．25． (1) 该车间应安排4天加工童装，6天加工成人装；(2) 36000元．【解析】【分析】（1）利用某车间计划用10天加工一批出口童装和成人装共360件，分别得出方程组成方程组求出即可；（2）利用（1）中所求，分别得出两种服装获利即可得出答案．【详解】解：（1）设该车间应安排x 天加工童装，y 天加工成人装，由题意得：104530360x y x y +=⎧⎨+=⎩， 解得：46x y =⎧⎨=⎩， 答：该车间应安排4天加工童装，6天加工成人装；（2）∵45×4=180，30×6=180， ∴180×80+180×120=180×（80+120）=36000（元），答：该车间加工完这批服装后，共可获利36000元．【点睛】本题考查二元一次方程组的应用．26．（1）12=-m ，43y x =-；（2）4y x =-. 【解析】分析：（1）由已知求出A 、E 的坐标，即可得出m 的值和一次函数函数的解析式；（2）由34AD DE ==，，得到5AE =，由2AF AE -=，得到71AF BF ，==．设E 点坐标为()4a ，，则点F 坐标为()31a -，，代入反比例函数解析式即可得到结论．详解：（1）∵()6038B AD AB E -==，，，，为CD 的中点， ∴()()3468E A --，，，． ∵反比例函数图象过点()34E ，-， ∴3412m =-⨯=-．设图象经过A 、E 两点的一次函数表达式为：y kx b =+，∴6834k b k b -+=⎧⎨-+=⎩， 解得430k b ⎧=-⎪⎨⎪=⎩：， ∴43y x =-． （2）∵34AD DE ==，，∴5AE =．∵2AF AE -=，∴7AF =，∴1BF =．设E 点坐标为()4a ，，则点F 坐标为()31a -，．∵E F ，两点在m y x=图象上， ∴43a a =-，解得：1a =-， ∴()14E -，， ∴4m =-，∴4y x=-．点睛：本题考查了矩形的性质以及反比例函数一次函数的解析式．解题的关键是求出点A 、E 、F 的坐标．27．（1） ;(1) y ＝x 1﹣4x+1或y ＝x 1+6x+1．【解析】【分析】（1）解方程求出点A 的坐标，根据勾股定理计算即可；（1）设新抛物线对应的函数表达式为：y ＝x 1+bx+1，根据二次函数的性质求出点C′的坐标，根据题意求出直线CC′的解析式，代入计算即可．【详解】解：（1）由x 1﹣4＝0得，x 1＝﹣1，x 1＝1，∵点A 位于点B 的左侧，∴A （﹣1，0），∵直线y ＝x+m 经过点A ，∴﹣1+m ＝0，解得，m ＝1，∴点D 的坐标为（0，1），∴AD ；（1）设新抛物线对应的函数表达式为：y ＝x 1+bx+1，y ＝x 1+bx+1＝（x+2b ）1+1﹣24b ， 则点C′的坐标为（﹣2b ，1﹣24b ）， ∵CC′平行于直线AD ，且经过C （0，﹣4），∴直线CC′的解析式为：y ＝x ﹣4，∴1﹣24b ＝﹣2b ﹣4， 解得，b 1＝﹣4，b 1＝6，∴新抛物线对应的函数表达式为：y ＝x 1﹣4x+1或y ＝x 1+6x+1．【点睛】本题考查的是抛物线与x 轴的交点、待定系数法求函数解析式，掌握二次函数的性质、抛物线与x 轴的交点的求法是解题的关键．。
2019--2020南京鼓楼区中考一模数学试卷
③是否存在实数 m, n(m n) ，使得当 m x n 时， m y n ？若存在，请求出 m, n ；
若不存在，请说明理由.
27. （9 分）如图，已知矩形纸片 ABCD ，折叠，能是边 AB 被三等分？
以下是小红的研究过程.
要使边 AB 被三等分，若从边 DC 上考虑，就是要折出 DM 1 DC ， 3
说法正确的是
A. ①较长
B. ②较长
C. ①②一样长
D. 以上皆有可能
二、填空题（本大题共 10 小题，每小题 2 分，共 20 分不需写出解答过程，请
把答案直接填写在答题纸相应位置上）
7. 写出一个数，使这个数等于它的倒数：
．
8. 若式子 x 1 在实数范围内有意义，则 x 的取值范围
．
9. 计算 3 1 的结果是
k2 x
的解是
．
14. 如图，点 O 是正五边形 ABCDE 的中心，连接 BD 、 OD 、则∠BDO
．
15. 如图， BC 是 O 的切线， D 是切点.连接 OB 并延长，交 O 于点 E 、 A ，过 A 作
AC⊥BC ，垂足为 C .若 BD 8, BE 4 ， AC
．
16. 用若干个相同的小正方体搭一个几何体，该几何体的主视图、俯视图如图所示.若小正
思 也就是要折出 DM 1 DC ，
3
考 当 DB, AM 相交于 F 时，即要折出对角线上的 DF 1 DB ，么……
过
4
程
1 折出 DB ；对折纸片，使 D, B 重合，得到折痕与 DB 相交于点 E ；继续折叠纸
片，使 D, B 与 E 重合，得到的折痕与 DB 分别相交于点 F ,G ；
2019年江苏省南京市中考数学第一次联合测评试卷附解析
2019年江苏省南京市中考数学第一次联合测评试卷学校：__________ 姓名：__________ 班级：__________ 考号：__________注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上一、选择题1．如图，在A 、B 两座工厂之间要修建一条笔直的公路，从A 地测得B 地的走向是南偏东52°，现A 、B 两地要同时开工，若干天后公路准确对接，则B 地所修公路的走向应该是（ ）A ．北偏西52°B ．南偏东52°C ．西偏北52°D ．北偏西38°2．某人沿坡度为 26°的斜坡行进了 100 米，他的垂直高度上升了（ ）A ．0100sin 6米B ．0100cos 26米C ．0100tan 26米D ．0100tan 26米 3．若⊙O 的半径为6，如果一条直线和圆相切，P 为直线上的一点，则OP 的长度（ ）A ．OP=6B ．OP ＞6C ．OP ≥6D ．OP ＜6 4．下列各组数中成比例的是（ ） A ．3,4,5,6B ．1,3,3,5C ．1,4,4,2D ．1,4,2，8 5．已知213y x x =−，226y x =−，当12y y =时，x 的值为（ ） A ．2x =或3x =B ．1x =或6x =C ．1x =−或6x =D ．2x =−或3x =− 6．如果代数式32a−的值大于 一3 且小于 7，那么 a 的取值范围是（ ）A ．0a <B ．20a >C ．020a <<D ．20a o a <>或7．如图，某同学把一块三角形的玻璃打碎成三片，现在他要到玻璃店去配一块形状完全一样的玻璃.那么最省事的办法是带（ ）A ．①B ．②C ．③D ．①和②8．下列事件中，属于随机事件的是（ ）A ．掷一枚普通正六面体骰子所得点数不超过 6B ．买一张体育彩票中奖C ．太阳从西边落下D ．口袋中只装有 10个红球，从中摸出一个白球二、填空题9．把大小和形状一模一样的6张卡片分成两组，每组3张，分别标上1，2，3.将这两组卡片分别放入两个盒子中搅匀，再从中各随机抽取一张，试求取出的两张卡片数字之和为偶数的概率（要求用树状图或列表方法求解）.10．已知⊙O的半径为5㎝，弦AB的长为8㎝，则圆心O到AB的距离为㎝.11．已知反比例函数y＝－8ｘ的图象经过点P（a+1，4），则a=_____．－312．已知AD∥BC，要使四边形ABCD为平行四边形，需要增加的条件是__________（•填一个你认为正确的条件）．13．平行四边形的面积为S，边长为5,该边上的高为h，则S与h的关系为；当h=2时，S= ；当S=40时，h= ．14．一个直棱柱有 16个顶点，则它的棱数是 .15．如图，在长方形ABCD中，AB＝1，BC＝2则AC＝___________.16．当12s t=+时，代数式222s st t−+的值为．17．（23a4b7-19a2b6）÷（-13ab3）2=_ ．18．若一个长方形的面积等于(3346mn m n+)cm2，其中长是（2223n m+）cm，则该长方形的宽是．三、解答题19．如图，某幢大楼顶部有一块广告牌CD，甲、乙两人分别在相距8m的A、B两处测得D 点和C点的仰角分别为45°和60°，且A、B、E三点在一条直线上．若BE=15m，求这块广告牌的高度．(取3≈1.73，计算结果保留整数）20．如图所示是由小立方块所搭成几何体的俯视图，小正方形中的数字表示在该位置小立方块的个数．请画出相应几何体的主视图和左视图．A B P Q M N21．如图，已知AB ∥CD ，AF= FB ，EC = EB ，试说明：(1)△OCF ∽△OAE ；(2)OC OF CD OC =(第 11 颧 )22．如图，已知等腰梯形ABCD 中，AD ∥BC ，AB=DC ，AC 与BD 相交于点O ．请在图中找出一对全等的三角形，并加以证明．23．如图，已知PQ ∥MN ，夹在两条平行线间的线段AB 长为 3 cm ，∠ABM ＝60°.求PQ 与MN 之间的距离.D B A O C24．如图是一个食品包装盒的展开图．(1)请写出这个包装盒的多面体形捩的名称；(2)请根据图中所标的尺寸，计算这个多面体的侧面积．25．解不等式组523483x xxx−<+⎧⎪+⎨≥−⎪⎩，并写出它的非负整数解．26．如图，在△ABC中，AB =AC，D 为 BC边上的一点，∠BAD = ∠CAD，BD = 6cm，求BC的长.27．如图是4个小正方形连在一起，试再拼接2个同样大小的正方形，使它可以折成正方体．请画出两种拼法：28．如图，∠1 =75°，请你添加一个条件，使直线 AB与直线 CD平行，并说明理由．.29．利用计算器计算： 4413343− 1115(结果保留3个有效数字) 358−结果保留3个有效数字) 352结果保留3个有效数字)30．计算：2007200645()()54⨯−．45【参考答案】学校：__________ 姓名：__________ 班级：__________ 考号：__________注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上一、选择题1．A2．A3．C4．D5．A6．C7．C8．B二、填空题9．510．9311．12．AD=BC （答案不惟一）13．S=5h ，10，814．2415． 516．41 17． 162−b a 18．2mn三、解答题19．解：∵AB=8，BE=15，∴AE=23．在R t △ADE 中，︒=∠45DAE ，∴DE=AE=23．在R t △BCE 中，︒=∠60CBE ，∴31560tan ·=︒=BE CE，∴395.223315≈≈−=−=DE CE CD ．∴这块广告牌的高度约为3米． 20．如图．21．（1）∵AF= FB,∴∠A=∠B.∵ EC=EB ，∴∠B=∠OCF.∴∠A=∠OCF.∵∠AOE=∠COF ，∴△OCF ∽△OAE ；(2）∵AB ∥CD,∠A=∠D.∵∠A=∠OCF ，∠OCF=∠D.∵∠COF=∠COD ， ∵△OCF ∽△ODC ，∴OC OF CD OC =22．解：△ABC ≌△DCB ．证明：∵在等腰梯形ABCD 中，AD ∥BC ，AB=DC ，∴∠ABC=∠DCB ． 在∆ABC 与∆DCB 中AB DC ABC DCB BC CB =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△DCB ．（注：答案不唯一）23． 32cm ． 24．(1)直六棱柱 (2)6ab25．-2≤x<3，x=0，l ，226．∵∠BAD=∠CAD ，∴AD 是∠BAC 的平分线．∵AB=AC ，∴△ABC 是等腰三角形．∴AD 是△ABC 的BC 边上的中线，∴BD=CD=12BC ． ∵BD=6cm ，∴BC=12(cm) 27．答案不唯一，如28．不唯一，如∠2=105°，理由略29．(1)21 (2)-7 (3)0. 856 (4)-0.721 (5)0.29630．45。
南京市2019中考一模数学试卷含答案
初三学情调研试卷（Ⅰ）数 学注意事项：1．本试卷共6页．全卷满分120分．考试时间为120分钟．考生答题全部答在答题卡上，答在本试卷上无效．2．请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合，再将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上． 3．答选择题必须用2B 铅笔将答题卡上对应的答案标号涂黑．如需改动，请用橡皮擦干净后，再选涂其他答案．答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上的指定位置，在其他位置答题一律无效．4．作图必须用2B 铅笔作答，并请加黑加粗，描写清楚．一、选择题（本大题共6小题，每小题2分，共12分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡．．．相应位置．．．．上） 1．下列计算结果为负数的是A ．－1＋2B ．|－1|C ．(－2)2D ．－2－12．计算a 5·(－1a)2的结果是A ．－a 3B ．a 3C ．a 7D ．a 103．若a ＜22＜b ，其中a 、b 为两个连续的整数，则ab 的值为A ．2B ．5C ．6D ．124．如图是一几何体的三视图，这个几何体可能是A ．三棱柱B ．三棱锥C ．圆柱D ．圆锥5．如图，已知a ∥b ，∠1＝115°，则∠2的度数是A ．45°B ．55°C ．65°D ．85°6．在学习“一次函数与二元一次方程”时，我们知道了两个一次函数图像的交点坐标与其相应的二元一次方程组的解之间的关系．请通过此经验推断：在同一平面直角坐标系中，函数y ＝5x 2－3x ＋4与y ＝4x 2－x ＋3的图像交点个数有A ．0个B ．1个C ．2个D ．无数个二、填空题（本大题共10小题，每小题2分，共计20分．不需写出解答过程，请把答案主视图左视图俯视图（第4题）a b12（第5题）直接填写在答题卡．．．相应位置．．．．上） 7．若式子x －2在实数范围内有意义，则x 的取值范围是 ． 8．若a －b ＝3， a ＋b ＝－2，则a 2－b 2＝ ．9．据统计，2016年春节“黄金周”（2月7日至13日）期间，南京共接待游客4 880 000人． 将4 880 000用科学记数法表示为 ．10．若△ABC ∽△A'B'C'，相似比为1:3，则△ABC 与△A'B'C'的面积比为 ． 11．已知圆锥的底面半径为1cm ，母线长为3cm ，则其侧面积为 cm 2（结果保留π）．12．已知关于x 的方程x 2＋mx －3＝0的一个根是1，则它的另一个根是 ．13．某校射击队从甲、乙、丙、丁四人中选拔一人参加市运会射击比赛．在选拔赛中，每人射击10次，他们10次成绩的平均数及方差如下表所示．请你根据表中数据选一人参加比赛，最合适的人选是 ．14．在同一平面直角坐标系中，正比例函数y ＝k 1x 的图像与反比例函数y ＝k 2x的图像一个交点的坐标是（－2，3），则它们另一个交点的坐标是 ．15．如图，在正十边形A 1A 2A 3A 4A 5A 6A 7A 8A 9A 10中，连接A 1A 4、A 1A 7，则∠A 4A 1A 7＝ °．16．如图①，在等边△ABC中，CD⊥AB，垂足为D，⊙O的圆心与点D重合，⊙O与线段CD交于点E，且CE＝4cm．将⊙O沿DC方向向上平移1cm后，如图②，⊙O恰与△ABC的边AC、BC相切，则等边△ABC的边长为cm．A5A6A7A8A910A1A2A3 A4（第15题）三、解答题（本大题共有11小题，共计88分．请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）17．（6分）先化简，再求值：(1a －1b )÷a 2－b 2ab，其中a ＝2＋1，b ＝2－1．18．（6分）解不等式组⎩⎪⎨⎪⎧ x ＋92≥4，2x －3＜0，并写出不等式组的整数解．19．（7分）如图，在四边形ABCD 中，AB ∥CD ，点E 、F 在对角线AC 上，且∠ABF ＝∠CDE ，AE ＝CF ．（1）求证：△ABF ≌△CDE ；（2）当四边形ABCD 满足什么条件时，四边形BFDE 是菱形?为什么?20．（8分）“低碳环保，你我同行”．近两年，南京市区的公共自行车给市民出行带来了极大的方便．图①是公共自行车的实物图，图②是公共自行车的车架示意图，点A 、D 、C 、E 在同一条直线上，CD ＝30cm ，DF ＝20cm ，AF ＝25cm ，FD ⊥AE 于点D ，座杆CE ＝15cm ，且∠EAB ＝75°． （1）求AD 的长；（2）求点E 到AB 的距离．（参考数据：sin75°≈0.97，cos75°≈0.26，tan75°≈3.73）21．（7分）甲、乙两名同学从《奔跑吧兄弟》、《极限挑战》、《最强大脑》三个综艺节目中随机选择一个观看．图①图②（第20题）MFE DCBA（1）甲同学观看《最强大脑》的概率是 ；（2）求甲、乙两名同学观看同一节目的概率．22．（8分）“世界那么大，我想去看看”一句话红遍网络，随着国际货币基金组织正式宣布人民币2016年10月1日加入SDR （特别提款权），以后出国看世界更加方便.为了解某区6 000名初中生对“人民币加入SDR ”知晓的情况，某校数学兴趣小组随机抽取区内部分初中生进行问卷调查，将问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不了解”四个等级，并将调查结果整理分析，得到下列图表：某区抽取学生对“人民币加入SDR ”知晓情况频数分布表某区抽取学生对“人民币加入SDR ”知晓情况扇形统计图非常了解 26%比较了解基本了解不了解（1）本次问卷调查抽取的学生共有人，其中“不了解”的学生有人；（2）在扇形统计图中，学生对“人民币加入SDR”基本了解的区域的圆心角为°；（3）根据抽样的结果，估计该区6000名初中生对“人民币加入SDR”了解的有多少人（了解是指“非常了解”、“比较了解”和“基本了解”）？23．（8分）某商场将进货价为每只30元的台灯以每只40元售出，平均每月能售出600只．调查表明，这种台灯的售价每上涨1元，其销售量将减少10只.当这种台灯的售价定为多少元时，每个月的利润恰为10 000元？24．（9分）货车和轿车分别从甲、乙两地同时出发，沿同一公路相向而行．轿车出发2.4h 后休息，直至与货车相遇后，以原速度继续行驶．设货车出发x h后，货车、轿车分别到达离甲地y1km和y2 km的地方，图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系．（1）求点D的坐标，并解释点D的实际意义；（2）求线段DE所在直线的函数表达式；（3）当货车出发h时，两车相距200km25．（8分）数学活动课上，小君在平面直角坐标系中对二次函数图像的平移进行了研究. 图①是二次函数y ＝(x －a )2＋a3（a 为常数）当a ＝－1、0、1、2时的图像.当a 取不同值时，其图像构成一个“抛物线簇”.小君发现这些二次函数图像的顶点竟然在同一条直线上！（1）小君在图①中发现的“抛物线簇”的顶点所在直线的函数表达式为 ；（2）如图②，当a ＝0时，二次函数图像上有一点P (2,4).将此二次函数图像沿着（1）中发现的直线平移，记二次函数图像的顶点O 与点P 的对应点分别为O 1、P 1.（第25题）若点P1到x轴的距离为5，求平移后二次函数图像所对应的函数表达式.26．（10分）如图，直线AB交⊙O于C、D两点，CE是⊙O的直径，CF平分∠ACE交⊙O于点F，连接EF，过点F作FG∥ED交AB于点G．（1）求证：直线FG是⊙O的切线；（2）若FG＝4，⊙O的半径为5，求四边形FGDE27．（11分）问题提出平面上，若点P与A、B、C三点中的任意两点均构成等腰三角形，则称点P是A、B、C三点的巧妙点．若A、B、C三点构成三角形，也称点P是△ABC的巧妙点．初步思考（1）如图①，在等边△ABC的内部和外部各作一个△ABC的巧妙点．（尺规作图，不写作法，保留作图痕迹）（2）如图②，在△ABC中，AB＝AC，∠BAC＝36°，点D、E是△ABC的两个巧妙点，深入研究（3）在△ABC中，AB＝AC，若存在一点P，使PB＝BA，P A＝PC．点P可能为△ABC 的巧妙点吗？若可能，请画出示意图，并直接写出∠BAC的度数；若不可能，请说明理由．数学参考答案及评分标准说明：本评分标准每题给出了一种或几种解法供参考，如果考生的解法与本解答不同，参照本评分标准的精神给分．一、选择题（每小题2分，共计12分）二、填空题（每小题2分，共计20分）7．x ≥2 8．－6 9．4.88×106 10．1: 9 11．3π 12．－3 13．丁 14．（2，－3） 15．54° 16．1433三、解答题（本大题共11小题，共计88分）17．（本题6分）解：原式＝(b －a ab )·ab(a ＋b )(a －b )································································· 2分＝－1a ＋b． ···················································································· 4分当a ＝2＋1，b ＝2－1时，原式＝－ 1 (2＋1)＋(2－1)＝－ 1 22＝－ 24． ···································· 6分18．（本题6分）解：解不等式①，得x ≥－1． ···································································· 2分解不等式②，得x ＜32． ······································································· 4分所以不等式组的解集是－1≤x ＜32． ························································ 5分不等式组的整数解为－1、0、1． ·························································· 6分19．（本题7分）解：（1）∵AB ∥CD ，∴∠BAC ＝∠DCA ．∵AE ＝CF ，∴AE ＋EF ＝CF ＋EF ，即AF ＝CE ．又∵∠ABF ＝∠CDE ，∴△ABF ≌△CDE ． ····································································· 3分（2）当四边形ABCD 满足AB ＝AD 时，四边形BEDF 是菱形． ·················· 4分连接BD 交AC 于点O ，由（1）△ABF≌△CDE 得AB＝CD，BF＝DE，∠AFB＝∠CED,∴BF∥DE．∵AB∥CD，AB＝CD，∴四边形ABCD是平行四边形．又∵AB＝AD，∴□ABCD是菱形．∴BD⊥AC．∵BF＝DE，BF∥DE，∴四边形BEDF是平行四边形，∴□BEDF是菱形．······································································ 7分20．（本题8分）解：（1）在Rt△ADF中，由勾股定理得，AD＝AF 2－FD2＝252－202＝15（cm）． ······································· 3分（2）AE＝AD＋CD＋EC＝15＋30＋15＝60（cm）． ···································· 4分过点E作EH⊥AB于H，在Rt△AEH中，sin∠EAH＝EHAE， ··················································· 6分∴EH ＝AE ·sin ∠EAH ＝AB ·sin75°≈ 60×0.97＝58.2（cm ）．答：点E 到AB 的距离为58.2 cm ． ·················································· 8分21．（本题7分）解：（1）13 ． ·························································································· 2分（2）分别用A ，B ，C 表示《奔跑吧兄弟》、《极限挑战》、《最强大脑》三个综艺节目，用表格列出所有可能出现的结果：一共有9种可能的结果，它们是等可能的，其中符合要求的有3种． P (甲、乙两名同学观看同一节目)＝ 39 ＝ 13．答：甲、乙两名同学观看同一节目的概率为 13． ································· 7分22．(本题8分)解：（1）100，20． ··················································································· 2分（2）72． ·························································································· 4分（3）6 000×80%＝4 800人．答：估计该校6 000名初中生中对“人民币加入SDR”了解的有4 800人．···· 8分23．(本题8分)解法一：设这种台灯的售价上涨x元，( 600－10x ) ( 40＋x－30)＝10 000， ················································· 4分解得x1 ＝10，x2＝40，·································································· 6分∴当x＝10时，40＋x＝50，当x＝40时，40＋x＝80； ························ 7分解法二：设这种台灯的售价为x元，[600－10(x－40)] (x－30)＝10 000，·················································· 4分解得x1 ＝50，x2＝80，·································································· 7分答：当这种台灯的售价定为50或80元时，每个月的利润恰为10 000元．··········· 8分24．(本题9分)解：（1）求出点坐标D ( 4，300 )．······························································ 2分点D是指货车出发4h后，与轿车在距离A地300 km处相遇．·············· 3分（2）求出点坐标E ( 6.4，0 )．······························································· 4分设DE 所在直线的函数表达式为y ＝kx ＋b ，将点D ( 4，300 )，E ( 6.4，0)代入y ＝kx ＋b 得：⎩⎪⎨⎪⎧4k ＋b ＝300，6.4k ＋b ＝0， 解得 ⎩⎪⎨⎪⎧b ＝800，k ＝－125， ∴DE 所在直线的函数表达式为y ＝－125x ＋800． ····························· 7分(3) 2或5. ····················································································· 9分25．(本题8分)解：（1）y ＝ 13x ． ··················································································· 2分（2）点O 1的坐标为 ( 3，1) 或 (－27，－9) ············································· 4分平移后的二次函数的表达式为y ＝(x －3)2 ＋1或y ＝(x ＋27)2 －9． ·········· 8分26．(本题10分)证明：（1）连接FO ，∵ OF ＝OC ，∴ ∠OFC ＝∠OCF ．∵CF 平分∠ACE ，∴∠FCG ＝∠FCE ．∴∠OFC ＝∠FCG ．E∵ CE 是⊙O 的直径，∴∠EDG ＝90°，又∵FG ∥ED ，∴∠FGC ＝180°－∠EDG ＝90°，∴∠GFC ＋∠FCG ＝90°∴∠GFC ＋∠OFC ＝90°，即∠GFO ＝90°，∴OF ⊥GF ， ···················································································· 4分又∵OF 是⊙O 半径，∴FG 与⊙O 相切． ··········································································· 5分（2）延长FO ，与ED 交于点H ， 由(1)可知∠HFG ＝∠FGD ＝∠GDH ＝90°，∴四边形FGDH 是矩形．∴FH ⊥ED ，∴HE ＝HD ．又∵四边形FGDH 是矩形，FG ＝HD ，（第26题）DGCBA（第26题）∴HE＝FG＝4.∴ED＝8. ·························································································7分∵在R t△OHE中，∠OHE＝90°，∴OH＝OE2－HE2＝52－42＝3．∴FH＝FO＋OH＝5＋3＝8． ·······························································9分S四边形FGDH＝12(FG＋ED)·FH＝12×(4＋8)×8＝48． ································ 10分27．(本题11分)解：（1）画对1个巧妙点给一分． ······························································· 2分（2）∵AB＝AC，∠BAC＝36°，∴∠ABC＝∠ACB＝72°，∵AD＝AB，AB＝AC，BD＝BC，∴△ADB≌△ABC．同理：△ACE≌△ABC．∴∠BAD＝∠BAC＝∠CAE＝36°，∠ADB＝∠ABD＝∠ABC＝72°，∴∠DAE＝∠BAD＋∠BAC＋∠CAE＝108°，∵AD＝AB＝AC＝AE，∴∠ADE ＝∠AED ＝36°＝∠BAD ，∴∠BDM ＝∠BDA －∠MDA ＝36°，∠BMD ＝∠ADM ＋∠DAM ＝72°＝∠ABD ，∴DB ＝DM ． ············································································· 5分 ∵∠DBM ＝∠ABD ，∠AED ＝∠BAD ，∴△DAM ∽△DEA ，∴DM DA ＝DA DE，DA 2 ＝D M ·DE ， ∵DM ＝DB ，∴DA 2 ＝D B ·DE ． ··················································· 7分（3）第一种如图①或图②(只需画一个即可)，∠BAC ＝60°．B A CPC第二种如图③，∠BAC ＝36°； 第三种如图④，∠BAC ＝108°； 第四种如图⑤，∠BAC ＝120°．以上共四种：60°、36°、108°、120°． ········································ 11分（第27题） 图⑤ 图④ 图③ （第27题） 图② 图① B AC PB ACP CB P。
2019年南京市中考一模数学试卷与答案试题试卷
D
F
F
C
O
A
B
B
C
A
B
（第14题）
（第15题）
（第16题）
15、如图，在矩形 ABCD 中， AB 4 ， BC 6 ， E 为 AD 中点，CED 的外接圆与 BE 交于 点 F ，则 BF 的长度为____________．
16、如图， AB 是 O 的弦，若 O 的半径长为 6， AB 6 2 ，在 O 上取一点 C ，使得 AC 8 2 ，则弦 BC 的长度为____________．
C． 3
D． 3
C． ab2 3 ab6
D． a2a3 a5
3、已知 a 为整数，且满足 5＜a＜ 10 ，则 a 的值为
A．4
B．3
C．2
D．1
k 4、已知反比例函数 y
的图像经过点 1,3 ，若 x＜-1，则 y 的取值范围为
x
A． y＞ 3
B． y＜3
C． 3＜y＜0
D． 0＜y＜3
三、解答题（本大题共 11 小题，共 88 分，请在答题卡指定区域内作答，解答时应写出文
字说明、证明过程或演算步骤）
3 m 1
17、（7
分）计算
m
2
m
2
2m
4
.
x 2＜5， 18、（7 分）解不等式组 x x 1 并把不等式组的解集在数轴上表示出来． 3 2 ＜1.
-4 -3 -2 -1 0 1 2 3 4
13、某校九年级（1）班 40 名同学期末考试成绩统计如下．
成绩 x （单位：分） 60 x 70 70 x 80
80 x 90 90 x 100
人数
4
14
(完整版)2019年南京市鼓楼区数学一模试卷
九年级（下）期中试卷数学注意事项：1．本试卷共6页．全卷满分120分，考试时间为120分钟．考生答题全部答在答题卡上，答在本试卷上无效．2．请将自已的姓名、准考证号用0．5毫米黑色墨水签字笔填写在答题卡及本试卷上．3．答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑．如需改动，请用橡皮擦干净后，再选涂其他答案，答非选择题必须用0．5毫米黑色墨水签字笔写在答题卡上的指定位置，在其他位置答题一律无效．4．作图必须用2B铅笔作答，并请加黑加粗，描写清楚．一、选择题（本大题共6小题，每小题2分，共12分．在毎小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）1．4的算术平方根是（）A．±2 B．2 C．-2 D．162．鼓楼区公益项目“在线伴读”平台开通以米，累计为学生在线答疑15000次用科学记数法表示15000是（）A．0．15×106B．1．5×105C．1．5×104D．15×1033．计算（－a）2・（a2）3的结果是（）A．a8 B．-a8 C． a7 D． -a74．若顺次连接四边形ABCD各边中点所得的四边形是菱形，则下列结论中正确的是（）A．AB∥ CD B．AB⊥ BC C．AC⊥ BD D．AC=-BD5．下图是某家庭2018年每月交通费支出的条形统计图，若记该家庭2018年月交通费平均支出为a元，则下列结论中正确的是（）A．200≤a≤220 B．220≤a≤240c．240≤a≤260D．260≤2806．A、B两地相距900km一列快车以200km／h的速度从A地匀速驶往B地，到达B地后立刻原路原速返回A地，一列慢车以75km／h的速度从B地匀速驶往A地两车同时出发，截止到它们都到达终点时，两车恰好相距200km的次数是（）A．5 B．4 C．3 D．2二、填空题（本大题共10小题，每小題2分，共20分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）7．一3的绝对值是．9的结果是 ．10．方程122x x=+的解是 ． 11．正五边形的每个外角的大小是 ．12．已知关于x 的方程220x mx +-=有一根是2，则另一根是 ，m ＝ ． 13．如图，AB∥EG∥CD，EF 平分∠BED．若∠D＝69°，∠CE F ＝21°，则∠B＝ °．14．如图，圆锥底面圆心为O ，半径OA ＝1，顶点为P ．将圆锥置于平面上，若保持顶点P 位置不变，将圆锥顺时针滚动三周后点A 恰好回到原处，则圆锥的高OP ＝ ．15．如图，点A 、B 、C 、D 在⊙O 上，B 是AC 的中点，过C 作⊙0的切线交AB 的延长线于点E ．若∠AEC＝84°，则∠ADC＝ °．ABG FECDD（第13题） （第14题） （第15题）16．在△ABC 中，AB ＝5，AC ＝4，BC ＝3．若点P 在△ABC 内部（含边界）且满足PC≤PA≤PB，则所有点P 组成的区域的面积为 ．三、解答题（本大题共11小题，共88分．请在答题卡指定区域内作答，解答时应写出文字说明、证明 过程或演算步骤）17．（7分）解不等式组322324x x x x -⎧⎨-≥⎩＞，（－）．18．（7分）计算3(a 1)11a a a -÷+---2．19．（8分）（1）解方程210x x --=．（2）在实数范围内分解因式21x x --的结果为 ． 20．（8分）如图，AB ＝AD ，ACE ，BC ＝DE ，点E 在EC 上． （1）求证△ABC≌△ADE； （2）求证∠EAC＝∠DEB．B C AED（第20题）21．（8分）（1）两只不透明的袋子中均有红球、黄球、白球各1个，这些球除颜色外无其他差别，分别从每个袋子中随机摸出个球，求摸出的两个球都是红球的概率．（2）鼓楼区实施全面均衡分班，某校为七年级各班随机分配任课教师已知该校七年级共有10个班，语文洪老师、数学胡老师都执教该年级，则他俩都任教七（1）班的概率为 ． 22．（8分）妈妈准备用5万元投资金融产品，她查询到有A 、B 两款“利滚利”产品，即上一周产生的收益将计入本金以计算下一周的收益．例如投资100元，第一周的周收益率为5％，则第一周的收益为100×5％＝5元，第二周投资的本金将变为100＋5＝105元，下图是这两款产品过去5周的周收益率公告信息．（第1周：3月1日～3月7日）（1）若妈妈3月1日投资产品B，到第二周结東时会不不赔，这种说法对吗？请判断并说明理由． （2）请运用学过的统计知识，为妈妈此次投资金融产品提出建议并简要说明理由．23．（8分）已知点A （1，1），B （2，3），C （4，7）．请用两种不同的方法判断这三点是否在一条直线上．（写出必要的推理过程）24．（8分）已知：如图，在口ABCD 中，G 、H 分別是AD 、BC 的中点，AE⊥BD，CF⊥BD，垂足分别为E 、F ． （1）求证：四边形GEHF 是平行四边形；（2）已知AB ＝5，AD ＝8．求四边形GEHF 是矩形时BD 的长．DC BG HEA F（第24题）25．（8分）某商品的进价是每件40元，原售价每件60元，进行不同程度的涨价后，统计了商品调价当天（1）当售价为每件60元时，当天可售出 件； 当售价为每件61元时，当天可售出 件．（2）若对该商品原售价每件涨价x 元（x 为正整数）时当天售出该商品的利润为y 元． ①用所学过的函数知识直接写出y 与x 之同满足的函数表达式： ． ②如何定价才能使当天的销售利润不低于6200元？ 26．（9分）如图①，一座石拱桥坐落在秦淮河上，它的主桥拱是圆弧形．如图②，桥宽AB 为8米，水面BC 宽16米，BC 表示的是主桥拱在水面以上的部分，点P 表示主标拱拱顶小明乘坐游船，沿主桥拱的中轴线向主桥拱行驶．（1）图③是主桥拱在水面以上部分的主视图，请用直尺和圆规作出主桥拱在静水中的倒影（保留作图痕迹，不写作法）．（2）已知小明眼睛距离水面1．6米，游船的速度为0．2米／秒．某一时刻，小明看拱顶P 的仰角为37°，4秒后，小明看拱顶P 的仰角为45°．参考数据：sin37°≈0．60，cos37°≈0．80，tan37°≈0．75．） ①求拱顶P 到水面的距离；②船上的旗杆高1米，某时刻游船背对阳光行驶，小明发现旗杆在阳光下的投影所在直线与航线平行且长为2米．请估计此刻桥的正下方被阳光照射到的部分的面积（需画出示意图并标注必要数据）． 27．（9分）把一个函数图像上每个点的纵坐标变为原来的倒数（原函数图像上纵坐标为0的点除外）、横坐标不变，可以得到另一个函数的图像，我们称这个过程为倒数变换． 例如：如图，将y ＝x 的图像经过倒数变换后可得到y ＝1x的图像．特别地，因为x 图像上纵坐标为0的点是原点、所以该点不作变换，因此y ＝1x的图像上也没有纵坐标为0的点． xyO（第27题）（1）请在下面的平面直角坐标系中画出y ＝-x ＋1的图像和它经过倒数变换后的图像． （2）观察上述图像，结合学过的关于函数图像与性质的知识，①猜想：倒数变换得到的图像和原函数的图像之间可能有怎样的联系？写出两个即可． ②说理：请简要解释你其中一个猜想． （3）请画出函数y ＝1（c 为常数）的大致图像．。
2019学年江苏省南京市鼓楼区中考一模数学试卷【含答案及解析】
2019学年江苏省南京市鼓楼区中考一模数学试卷【含答案及解析】姓名___________ 班级____________ 分数__________一、选择题1. 4的算术平方根是（）A、2B、-2C、-D、±22. 下列图形中，既是轴对称图形又是中心对称图形的是（）3. 计算（-）÷×cos60°-20150的结果是（）A、 B、 C、 D、4. 已知，△ABC∽△DEF，△ABC与△DEF的面积之比为1：2，当BC=1，对应边EF的长是（）A、 B、2 C、3 D、45. 在二次函数y=ax2+bx+c，x与y的部分对应值如下表：6. x…-2023…y…8003…td7. 如图，以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE，使AD=DE=CE，∠DEC=90°，且点E在平行四边形内部，连接AE、BE，则∠AEB的度数是（）A、120°B、135°C、150°D、45°二、填空题8. -3的倒数是，-3的绝对值是．9. 红细胞是人体中血液运输氧气的主要媒介，人体中红细胞的直径约为0．0000077m，将0．0000077用科学记数法表示为．10. 若式子有意义，则x的取值范围是．11. 某同学6次引体向上的测试成绩（单位：个）分别为16、18、20、17、16、18，这组数据的中位数是．12. 计算的结果是．13. 已知Rt△ABC，∠C=90°，AB=13，AC=12，以AC所在直线为轴，将此三角形旋转1周，所得圆锥的侧面积是．14. 如图，反比例函数y=的图象经过△ABO的顶点A，点D是OA的中点，若反比例函数y=的图象经过点D，则k的值为．15. 如图，⊙O的直径为10，弦AB长为8，点P在AB上运动，则OP的最小值是．16. 在直角坐标系中，点A、B的坐标分别为（-2，4）、（-5，2），点M在x轴上，点N 在y轴上．如果以点A、B、M、N为顶点的四边形是平行四边形，那么符合条件的点M有个．17. 如图，矩形纸片ABCD中，AB=4，AD=6，点P是边BC上的动点，现将纸片折叠，使点A与点P重合，折痕与矩形边的交点分别为E、F，要使折痕始终与边AB、AD有交点，则BP的取值范围是．三、解答题18. 解方程：19. 先化简：，再选取一个恰当的x的值代入求值．20. 如图，点A、F、C、D在同一直线上，点B和点E分别在直线AD的两侧，且AB=DE，∠A=∠D，AF=DC．（1）求证：四边形BCEF是平行四边形，（2）若∠ABC=90°，AB=4，BC=3，当AF为何值时，四边形BCEF是菱形．21. 在不透明的袋子中有四张标着数字1，2，3，4 的卡片，这些卡片除数字外都相同．甲同学按照一定的规则抽出两张卡片，并把卡片上的数字相加．如图是他所画的树状图的一部分．（1）由如图分析，甲同学的游戏规则是：从袋子中随机抽出一张卡片后（填“放回”或“不放回”），再随机抽出一张卡片；（2）帮甲同学完成树状图；（3）求甲同学两次抽到的数字之和为偶数的概率．22. “低碳环保，你我同行”，两年来，南京市区的公共自行车给市民出行带来切实方便，电视台记者在某区街头随机选取了市民进行调查，调查的问题是“您大概多九使用一次公共自行车？”，将本次调查结果归为四种情况：A 每天都用；B 经常使用；C 偶尔使用；D 从未使用．将这次调查情况整理并绘制如下两幅统计图：根据图中的信息，解答下列问题：（1）本次活动共有位市民参与调查；（2）补全条形统计图；（3）根据统计结果，若该区有46万市民，请估算每天都用公共自行车的市民约有多少人？23. 学校举行数学知识竞赛，设立了一、二、三等奖，计划共购买45件奖品，其中二等奖奖品件数比一等奖奖品件数的2倍还少5件，已知购买一等奖奖品x件．各种奖品的单价如下表：24. 奖品一等奖奖品二等奖奖品三等奖奖品单价（元）12108td25. 如图，平地上一幢建筑物AB与铁塔CD相距40m，在建筑物的顶部测得铁塔底部的俯角为37°，测得铁塔顶部的仰角为26．6°，求铁塔的高度．（参考数据：sin26．6°≈0．45，tan26．6°≈0．50；sin37°≈0．60，tan37°≈0．75）26. 如图，四边形ABCD是平行四边形，以AB为直径的⊙0经过点D，E是⊙O上一点，且∠AED=45°，（1）求证：CD是⊙O的切线．（2）若⊙O的半径为3，AE=5，求∠DAE的正弦值．27. 甲乙两地相距400千米，一辆货车和一辆轿车先后从甲地出发驶向乙地，如图，线段OA表示货车离甲地的路程y（千米）与所用时间x（小时）之间的函数关系，折线BCD表示轿车离甲地的路程y（千米）与x（小时）之间的函数关系，根据图象解答下列问题：（1）求线段CD对应的函数表达式；（2）求E点的坐标，并解释E点的实际意义；（3）若已知轿车比货车晚出发2分钟，且到达乙地后在原地等待货车，则当x= 小时，货车和轿车相距30千米．28. 在初中数学中，我们学习了“两点间的距离”、“点到直线的距离”、“平行线之间的距离”，距离的本质是“最短”，图形之间的距离总可以转化为两点之间的距离，如“垂线段最短”的性质，把点到直线的距离转化为点到点（垂足）的距离．一般的，一个图形上的任意点A与另一个图形上的任意点B之间的距离的最小值叫做两个图形的距离．（1）如图1，过A，B分别作垂线段AC、AD、BE、BF，则线段AB和直线l的距离为垂线段的长度．（2）如图2，Rt△ABC中，∠ACB=90°，∠B=30°，CD⊥AB，AD=2，那么线段AD与线段BC的距离为．（3）如图3，若长为1cm的线段CD与已知线段AB的距离为1．5cm，请用适当的方法表示满足条件的所有线段CD．注：若满足条件的线段是有限的，请画出；若满足条件的线段是无限的，请用阴影表示其所在区域．（保留画图痕迹）29. 【问题提出】如图1，四边形ABCD中，AD=CD，∠ABC=120°，∠ADC=60°，AB=2，BC=1，求四边形ABCD的面积．【尝试解决】旋转是一种重要的图形变换，当图形中有一组邻边相等时，往往可以通过旋转解决问题．（1）如图2，连接 BD，由于AD=CD，所以可将△DCB绕点D顺时针方向旋转60°，得到△DAB′，则△BDB′的形状是．（2）在（1）的基础上，求四边形ABCD的面积．[类比应用]如图3，四边形ABCD中，AD=CD，∠ABC=75°，∠ADC=60°，AB=2，BC=，求四边形ABCD的面积．参考答案及解析第1题【答案】第2题【答案】第3题【答案】第4题【答案】第5题【答案】第6题【答案】第7题【答案】第8题【答案】第9题【答案】第10题【答案】第11题【答案】第12题【答案】第13题【答案】第14题【答案】第15题【答案】第16题【答案】第17题【答案】第18题【答案】第19题【答案】第20题【答案】第21题【答案】第22题【答案】第23题【答案】第24题【答案】第25题【答案】第26题【答案】第27题【答案】。
19南京鼓楼一模数学(含答案)
19南京鼓楼一模数学(含答案)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIANx + 1 6 2元300 280 260 240 220 200 180 160一、选择题南京市鼓楼区2019 年中考第一次一模拟卷九年级数学1．4 的算术平方根是（ ）A ． ±2B ．2C ． -2D ．162. 鼓楼区公益项目“在线伴读”平台开通以来，累计为学生在线答疑 15000 次.用科学记数法表示 15000 是（ ） A ． 0.15 ⨯10 3．计算(-a )⋅ (a ) B ．1.5 ⨯10的结果是（ ）C ．1.5 ⨯10D ．15 ⨯10A ． aB ． -aC ． aD ． -a4.若顺次连接四边形 ABCD 各边中点所得的四边形是菱形，则下列结论中正确的是（ ）A. AB ∥CDB. AB ⊥ BCC. AC ⊥ BDD. AC = BD5.下图是某家庭 2018 年每月交通费支出的条形统计图，若该家庭 2018 年月交通费平均支出为 a 元，则下列结论中正确的是（ ）A ． 200 ≤ a ≤ 220B ． 220 ≤ a ≤ 240（第5题）C ． 240 ≤ a ≤ 260D ． 260 ≤ a ≤ 2806.A 、B 两地相距 900km ，一列快车以 200km/h 的速度从 A 地匀速驶往 B 地，到达 B 地后立刻原路返回 A 地，一列慢车以 75km/h 的速度从 B 地匀速驶往 A 地.两车同时出发， 截止到它们都到达终点时，两车恰好相距 200km 的次数是（ ） A ．5B ．4C ．3D ．2二、填空题 7. -3的绝对值是．8.若式子 在实数范围内有意义，则 x 的取值范围是 ．9.计算 -的结果是．27BEF⎨⎪x - 3( x - 2) ≥ 410. 方程 1 x + 2 = 2的解是 ．x11.正五边形的每个外角的大小是°．12.已知关于 x 的方程 x + mx - 2 = 0 有一根是 2，则另一根是， m = ．13．如图，AB ∥EG ∥CD ，EF 平分∠BED ，若∠D =69°，∠GEF =21°，则∠B =°．14.如图，圆锥底面圆心为 O ，半径 OA =1，顶点为 P ，将圆锥置于平面上，若保持顶点 P位置不变，将圆锥顺时针滚动三周后点 A 恰好回到原处，则圆锥的高 OP = ． 15.如图，点 A 、B 、C 、D 在⊙O 上，B 是 AC 的中点，过 C 作⊙O 的切线交 AB 的延长线于点 E .若∠AEC =84°，则∠ADC =°．A GACD16.在△ ABC 中，AB =5，AC =4，BC =3.若点 P 在△ ABC 内部（含边界）且满足PC ≤ PA ≤ PB ,则所有点 P 组成的区域的面积为 ．三、解答题17．（7 分）解不等式组 ⎧⎪3x > 2x - 2 ．⎩18．（7 分）计算 a - 2 ÷ ⎛ a + 1 - 3 ⎫． a -1 a - 1 ⎪⎝⎭19．（8 分）⑴解方程 x 2 - x - 1 = 0 ．⑵在实数范围内分解因式 x 2 - x - 1 = 0 的结果为 ．PAOB20．（8分）如图，AB=AD，AC=AE，BC=DE，点E在B C上⑴求证△ABC≌△ADE；A⑵求证∠EAC=∠DEB.DB E C(第20题）21.（8 分）⑴两只不透明的袋子中均有红球、黄球、白球各 1 个，这些球除颜色外无其他差别.分别从每个袋子中随机摸出一个球，求摸出两个球都是红球的概率.⑵鼓楼区实施全面均衡分班，某校为七年级各班随机分配任课教师.已知该校七年级共有10 个班，语文洪老师、数学胡老师都执教该年级，则他俩都任教七⑴班的概率为.22．（8分）妈妈准备用5万元投资金融产品，她查询到有A、B两款“利滚利”产品，即上一周产生的收益将计入本金以计算下一周的收益。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
62南京市鼓楼区2019年中考一模试卷九年级数学2019.04一、选择题1．4 的算术平方根是（ ） A ． ±2 B ．2C ． -2D ．162. 鼓楼区公益项目“在线伴读”平台开通以来，累计为学生在线答疑 15000 次.用科学记数法表示 15000 是（ ）A ． 0.15 ⨯106 3．计算(-a )2⋅ (a2 )3A. a 8B ．1.5 ⨯105的结果是（ ）B. -a8C ．1.5 ⨯104C. a7D ．15 ⨯103D. -a 74.若顺次连接四边形 ABCD 各边中点所得的四边形是菱形，则下列结论中正确的是（ ）A. AB ∥CDB. AB ⊥ BCC. AC ⊥ BDD. AC = BD5.下图是某家庭 2018 年每月交通费支出的条形统计图，若该家庭 2018 年月交通费平均支出为 a 元，则下列结论中正确的是（ ）1月 2 月3 月 4 月5 月 6 月7 月8 月 9月10月11月12月A ． 200 ≤ a ≤ 220B ． 220 ≤ a ≤ 240（第5题）C ． 240 ≤ a ≤ 260D ． 260 ≤ a ≤ 2806. A 、B 两地相距 900km ，一列快车以 200km/h 的速度从 A 地匀速驶往 B 地，到达 B 地后立刻原路返回 A 地，一列慢车以 75km/h 的速度从 B 地匀速驶往 A 地.两车同时出发， 截止到它们都到达终点时，两车恰好相距 200km 的次数是（ ） A ．5 B ．4 C ．3 D ．2二、填空题 7. -3的绝对值是．8.在实数范围内有意义，则 x 的取值范围是 ．9.计算 -的结果是 ．27⎨⎪x - 3( x - 2) ≥ 4 10. 方程 1 x + 2 = 2的解是 ．x11.正五边形的每个外角的大小是°．12.已知关于 x 的方程 x 2 + mx - 2 = 0 有一根是 2，则另一根是， m = ．13．如图，AB ∥EG ∥CD ，EF 平分∠BED ，若∠D =69°，∠GEF =21°，则∠B =°．14.如图，圆锥底面圆心为 O ，半径 OA =1，顶点为 P ，将圆锥置于平面上，若保持顶点 P位置不变，将圆锥顺时针滚动三周后点 A 恰好回到原处，则圆锥的高 OP = ． 15.如图，点 A 、B 、C 、D 在⊙O 上，B 是 AC 的中点，过 C 作⊙O 的切线交 AB 的延长线于点 E .若∠AEC =84°，则∠ADC =°．A BEGFACD（第13题）（第14题）（第15题）16.在△ ABC 中，AB =5，AC =4，BC =3.若点 P 在△ ABC 内部（含边界）且满足PC ≤ PA ≤ PB ,则所有点 P 组成的区域的面积为 ．三、解答题17．（7 分）解不等式组 3x > 2x - 2． ⎩18．（7 分）计算19．（8 分）⑴解方程 x 2 - x - 1 = 0 ．⑵在实数范围内分解因式 x 2 - x - 1 = 0 的结果为．O20．（8 分）如图，AB =AD ，AC =AE ，BC =DE ，点 E 在 BC 上⑴求证△ABC ≌△ADE ；A⑵求证∠EAC =∠DEB .DBEC(第20题）21.（8 分）⑴两只不透明的袋子中均有红球、黄球、白球各 1 个，这些球除颜色外无其他差别.分别从每个袋子中随机摸出一个球，求摸出两个球都是红球的概率.⑵鼓楼区实施全面均衡分班，某校为七年级各班随机分配任课教师.已知该校七年级共有 10 个班，语文洪老师、数学胡老师都执教该年级，则他俩都任教七⑴班的概率为 .22．（8 分）妈妈准备用 5 万元投资金融产品，她查询到有 A 、B 两款“利滚利”产品，即上一周产生的收益将计入本金以计算下一周的收益。
例如：投资 100 元，第一周的周收益率为 5%，则第一周的收益为 100×5%=5 元，第二周投资的本金将变为 100+5=105 元. 下图是这两款产品过去 5 周的周收益率公告信息.（第一周：3 月 1 日~3 月 7 日） ⑴若妈妈 3 月 1 日投资产品 B ，到第二周结束时会不赚不赔，这种说法对吗？请判断并说明理由. ⑵请运用学过的统计知识，为妈妈此次投资金融产品提出建议并简要说明理由。
产品A B7%6%2%2%2.9%1%第一周 第二周 第三周 第四周 第五周（第22题）23．（8分）已知点A（1,1），B（2,3），C（4,7），请用两种不同的方法判断这三点是否在一条直线上.（写出必要的推理过程）24．（8分）已知：如图，在□ABCD中，G、H分别是AD、BC的中点，AE⊥BD，CF⊥BD，垂足分别为E、F.⑴求证：四边形GEHF 是平行四边形；⑵已知AB=5，AD=8。
求四边形GEHF 是矩形时BD 的长.25.某商品的进价是每件40 元，原售价每件60 元.进行不同程度的涨价后，统计了商品调价当天的售价和利润情况，以下是部分数据：⑴当售价为每件60 元时，当天售出件；当售价为每件60 元时，当天售出件.⑵若对该商品原售价每件涨价x 元（x 为正整数）时当天售出该商品的利润为y 元.①用所学过的函数知识直接写出y 与x 之间满足的函数表达式：.②如何定价才能使当天的销售利润不等于6200 元？26.如图①，一座石拱桥坐落在秦淮河上，它的主桥拱为圆弧形.如图②，乔宽AB 为8 米，水面BC宽16米，B C 表示的是主桥拱在水面以上的部分，点P表示主桥拱拱顶.小明乘坐游船，沿主桥拱的中轴线向主桥拱行驶.⑴图③是主桥拱在水面以上部分的主视图，请用直尺和圆规作出主桥拱在静水中的倒影（保留作图痕迹，不写作法）.第26题图③⑵已知小明眼睛距离水平1.6 米，游船的速度为0.2 米/秒.某一时刻，小明看拱顶P 的仰角为37°，4 秒后，小明看拱顶P 的仰角为45°.（参考数据：sin 37 ≈ 0.60 ，cos 37 ≈ 0.80 ，tan 37 ≈ 0.75 .）①求桥拱P 到水面的距离；②船上的旗杆高1 米，某时刻游船背对阳光形式，小明发现旗杆在阳光下的投影所在直线与航线平行且长为2 米.请估计此刻桥的正下方被阳光照射到的部分的面积（需画出示意图并标注必要数据）.27 . （9 分）把一个函数图像上每个点的纵坐标变为原来的倒数（原函数图像上纵坐标为 0 的点除外）、横坐标不变，可以得到另一个函数的图像，我们称这个过程为倒数变换.例如：如图，将 y = x 的图像经过倒数变换后可得到 y = 1的图像.x特别地，因为 y = x 图像上纵坐标为 0 的点是原点，所以该点不作变换，因此 y = 1的图像上也没有纵坐标为 0 的点.x⑴请在下面的平面直角坐标系中画出 y = -x + 1 的图像和它经过倒数变换后的图像.⑵观察上述图像，结合学过的关于函数图像与性质的知识，①猜想：倒数变换得到的图像和原函数的图像之间可能有怎样的联系？写出两个即可.②说理：请简要解释你其中一个猜想.⑶请画出函数 y = 1x 2 + c（c 为常数）的大致图像.1- 5 1+ 5 九年级数学答案一、选择题题号123456答案B C A D C A二、填空题题号78910 11 答案3x ≥-1 2 3 x =-4 72 题号12 13 14 15 16答案x =-1 ，-1 27 2 2 64 27 32三、解答题17．-2 <x ≤ 1÷18.=19．⑴x1 =2 x2=2(2)（x--）(x-+）20 ．⑴证明：∵AB=AD，AC=AE，BC=DE∴△ABC≌△ADE⑵∵△ABC≌△ADE∴∠DAE=∠BAC∴∠DAE -∠BAE =∠BAC -∠BAE∴∠EAC=∠DEB21 ．⑴P =1⨯1=1 3 3 9⑵P =22 ．⑴这种说法不对。
设开始投资x 元，则两周结束后总资产为：（x1+2%）（⋅1-2%）=0.9996x≠x，所以并不是不赚不赔，而是赔了。
⑵选择A 产品，因为由图可看出两个产品平均收益率相近，但A 产品波动较小，方差较小，且一直是正收益，说明收益比较稳健。
23.结论：A、B、C 三点共线。
证明：方法一：设AB 两点所在直线的解析式为y =kx +b(k ≠ 0）55 ⎨ 将 A 、B 两点坐标代入可求得 y = 2x - 1，将 C 点坐标代入验证，当 x = 4 时， y = 7 ，说明点 C 也在直线 AB 上，即 A 、B 、C 三点共线。
方法二：通过点坐标求出线段长度，结合三边关系来证明ABBC∴A 、B 、C 三点共线= ， AC == 3 = 2 ，∴AB +BC =AC24. ⑴∵在□ABCD 中,AD ∥BC 且 AD =BC∴∠GDE =∠FBH∵AE ⊥BD ，CF ⊥BD ，且 G 、H 分别是 AD 、BC 的中点∴在 Rt △ADE 与 Rt △BCF 中， EG = AD = GD , FH =BC = HB∴EG =FH ,∠GED =∠GDE ，∠FBH =∠BFH ∴∠GED =∠BFH ∴EG ∥FH∴四边形 GEHF 是平行四边形 ⑵连接 GH当四边形 GEHF 是矩形时，∠EHF =∠BFC =90°， 又∵∠FBH =∠BFH ∴△EFH ∽△CBF ∴EF = FH CB BF由(1)可得，GA ∥HB ,GA =HB ∴四边形 GABH 是平行四边形 ∴GH =AB =5∵在矩形 GEHF 中，EF =GH ，且 AB =5，AD =8 ∴ 5 =4 8 BF∴ BF = ∴BE =BF -EF =在△ABE 和△CDF 中 ⎧∠AEB = ∠CFD ⎪∠ABE = ∠CDF ⎪⎩AB = CD ∴△ABE ≌△CDF (AAS ) ∴BE =DF = ∴BD =BF +DF =25．⑴300；290⑵① y = -10x 2 + 100x + 600055 5②由题意，令y ≥ 6200 ，即-10x2 +100x + 6000 ≥ 6200 ，解得5 -≤x ≤ 5 +.又x 为正整数，所以x = 3、4、5、6、7.故定价为63、64、65、66、67 元. 26．⑴如图所示.⑵①当小明刚到桥拱顶正下方时，设桥拱顶到小明眼睛距离（即PC）为x 米.tan 37 ==⇒AC =x ； tan 45 == 1 ⇒BC =x ；AB =AC -BC =x -x = 0.2 ⨯ 4 ；解得：x = 2.4 .则拱桥P 到水面的距离PE 为： 2.4 + 1.6 = 4 米.②如图，红色曲线与BC 构成的图形即为所求区域（面积设为S），与阴影部分弓形相比，水平长度不变，竖直距离变为其两倍，所以可以认为S 为弓形的面积两倍由①可得OB = 10 ，∠BOC = 106∴ S弓形=106⨯π⨯102 -1⨯16 ⨯ 6=265 π- 48 360 2 9∴S = 2S弓形=530 π- 96 927 ．⑴⑵①猜想一：倒数变换得到的图像和原函数的图像之间如果存在交点，则其纵坐标为1 或-1 ；猜想二：倒数变换得到的图像和原函数的图像的对称性相同，比如原函数是轴对称图形，则倒数变换的图像也是轴对称图形。