长安大学814信号与系统A卷(含标准答案)2014年考研真题试题
2014年解放军信大硕士入学真题信号与系统80%、电路分析20%
2
2、 （12 分）有一线性时不变系统如图所示，其中子系统 H 2 ( s )
803 信号与系统 80%、电路分析 20% 科目试题
（共九大题，满分 150 分）
电路分析部分（共三题，满分 30 分）
一、 （10 分）如图所示电路中，A 元件伏安关系为 u 20i1 50 ，试问： 1、R 为多少时可获得最大功率？并计算此最大功率。 2、若 R 80 ，欲使流过 R 的电流 i 为零，则 a、b 之间应接什么元件？ 其参数为多少？并画出电路图。
9、信号 f (t ) t (t 1) 的拉普拉斯变换是（ A
1 s2
B
1 s e s2
C
1 s s2
D
1 s s e s2
10、离散系统差分方程为 y (k 1) y (k 1) f (k 1) f (k ) ，则该系统状态变 量的个数是（ A 一个 二、 （共 18 分）
6、一线性时不变系统的 H ( j ) 2[ ( 100) ( 100)] , ( ) 4 ,则下 面哪个信号通过此系统不发生线性失真( A sin 200t cos100t B sin10t cos 50t ） ) C cos 50t cos 60t D (cos 60t )2
7、双边序列 f (k ) 1 的 Z 变换为（
第2页 共5页
A
z z 1
B 0
C 不存在
D 以上答案都不对
8、某系统的系统函数为 H ( z ) （ A ）
z <0.5
z 1 ，为因果系统，则其收敛域为 ( z 0.5)( z 2)
B z >2
长安大学信号与系统期末试卷
长安大学试题
课程 系别 专业班号 姓名
信号与系统
考试日期 2006 年 6 月 25 日 学号
一 、(10 分)已知某连续时间信号如图所示。
1.绘出信号
x1 (t
)
=
x(4
−
t) 2
的波形；
2.若 x(t ) 的频谱是 X (ω) ，试用 X (ω) 表
示信号 x1(t)(n) = ∑δ (n − 8k) ；
k =−∞
3. y(n) 是如图所示的方波序列
七 、(10 分)已知 x(t) 是一个最高频率为 3kHz 的带限连续时间信号，y(t) 是最高频率为 2kHz
的带限连续时间信号。试确定对下列信号理想抽样时，允许的最低抽样频率。
1. f (t) = x(t) ； 2. f (t) = x(t)∗ y(t) ； 3. f (t) = x(t) y(t) ； 4. f (t) = x(t) + y(t) ； 5. f (t) = y(2t) 。
， X (Ω) 是信号 x(n) 的傅立叶变换。
1.求 X (0) 的值;
π
∫ 2.求 X (Ω)dΩ 的值; −π
∫ 3.求 π X (Ω) 2dΩ 的值. −π
七、(13 分)已知某离散时间序列 x(n) ，其傅立叶变换 X (Ω) 如图所示。
⎧x(n) , n = 2k
x1(n) = x(2n) ， x2 (n) = ⎨ ⎩
二、(10 分)已知某离散时间 LTI 系统的单位脉冲响应为 h(n) = u(n) ，该系统对输入信号
x(n)
的输出响应为
y(n)
=
⎜⎛
1
n
⎟⎞ u(n)
长安大学《信号与系统》考研真题
共4页 第2页
5.已知信号 f (t) 的傅里叶变换 F( jω) = δ (ω −ω0) ，则 f (t) 为( )
A
1 e jω0
2π
B
1 e6=30 分）
C 1 e jω0 ε (t ) 2π
D 1 e− ε jω0 (t ) 2π
1.命题：离散的 LTI 系统的所有极点都在单位圆内是判定系统稳定性的充要条
件。请判断该命题的对错，并说明原因。
2.简述什么是解析信号以及构造解析信号的作用。
3.信号 f (t)的最高频率为 fmaxHz ，请说明对信号 f (3t) * f 2 (t ) 进行采样所需的最
小采样频率，并说明原因。 4.命题：连续信号的傅立叶变换具有共轭对称性。请判断该命题的对错，并说 明原因。 5.简述什么是线性时不变系统的无失真传输，其条件是什么？ 6.什么是 Gibbs 现象？说明其产生的原因。 三、计算题（60 分）
y' (t) + 4y' (t ) + 3y(t ) = f ' (t ) − 3 f (t )
求该系统的系统函数 H (s) 和冲激响应 h(t) 。
四、综合题（40 分）
1.（20 分）线性时不变因果系统，当输入信号为 f1[n] = δ [n] 时，全响应为：
y1[ n]
=
2(
1)n 4
ε [ n]
sin π t f (t ) =
，
πt
∞
∑ δ T (t) = δ (t − nTs ), Ts =0.5 秒
n= −∞
答案必须写在答题纸上，写在试题或草稿纸上不给分。
试题代码：814 试题名称：信号与系统
共4页 第4页
2014年信号与系统A卷-供学生用含答案
四川大学期末考试试题（A卷）（2013——2014 学年第二学期）课程号：303123040课序号：课程名称：信号与系统任课教师：任小梅邓丽华余勤王忠罗伟钟俊蒲明刘亚梅成绩：注：1试题字迹务必清晰，书写工整。
本题5 页，本页为第 1 页2 题间不留空，一般应题卷分开教务处试题编号：学号： 姓名6、 一个周期为N 的离散时间信号，其傅里叶级数表示式是一个N +1项的有限级数。
（ F ）7、 一个非因果稳定的离散信号，其z 变换收敛域包含z =∞。
（ F ）8、 一个因果的连续时间系统的系统函数X (s )，若其极点都在虚轴以左，那么该系统一定稳定。
（ T ）9、 一个稳定的连续系统，其系统函数为2()(1)(2)s e H s s s =++，收敛域为Re{}1s >-，那么该系统是因果的。
（ F ）10、 单位冲激响应为6()th t e-=的系统是非因果稳定的。
（ T ）二、单项选择题：（共10小题，每题1.5分，共15分）1、 三个连续时间系统S 1、S 2和S 3，它们对于输入jt e 的响应分别是：312(1), , sin()S S S jt jt jt j t jt e te e e e t -−−→−−→−−→以下说法正确的是：（ C ）A ．都是非线性系统B ．S 1是非线性系统C ．S 1、S 2是线性系统D ．S 2和S 3是非线性系统 2、 已知x (t ) ，为求x (3-2t ) 则下列运算正确的是（ D ）A ．x (-2t ) 左移3B ．x (-2t ) 右移3C ．x (-2t ) 左移3/2D ．x (-2t ) 右移3/2 3、 已知信号1()x t 和2()x t 分别如右图所示，且12()()()y t x t x t =*，则(1)y =（ C ）。
A ．1B ．2C ．4D ．0 4、 下列各式正确的是（ B ）。
A.1(2)()2δδt t -=-B.1(2)()2δδt t -=C ．(2)()δδt t -=-D. (2)()δδt t -=5、 系统的幅频特性|H (j ω)|和相频特性如右图所示，则下列信号通过该系统时，不产生失真的是( B ) 。
西安交大电信学院自动化2014考研真题回忆版811自控与信号与系统
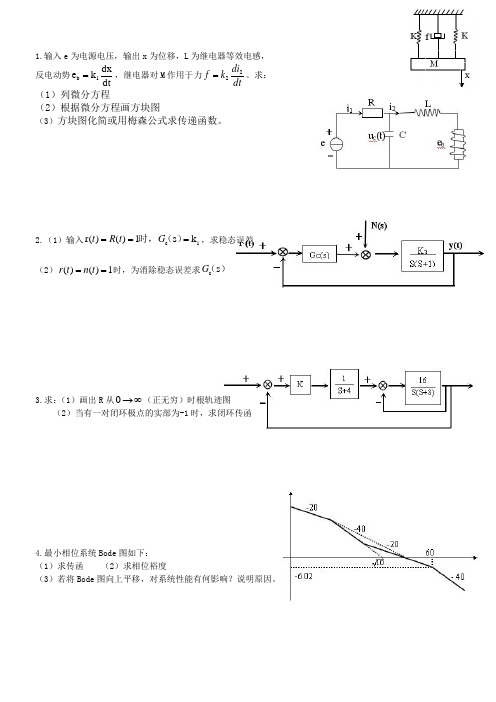
1.输入e 为电源电压，输出x 为位移，L 为继电器等效电感， 反电动势dt dx k e 1b =，继电器对M 作用于力dtdi k f 22=。
求： （1）列微分方程（2）根据微分方程画方块图（3）方块图化简或用梅森公式求传递函数。
2.（1）输入1c k s 1)()(r ===）（时，G t R t ，求稳态误差 （2）1)()(==t n t r 时，为消除稳态误差求）（s c G3.求：（1）画出R 从∞→0（正无穷）时根轨迹图（2）当有一对闭环极点的实部为-1时，求闭环传函4.最小相位系统Bode 图如下：（1）求传函 （2）求相位裕度（3）若将Bode 图向上平移，对系统性能有何影响？说明原因。
5.n 阶系统有p 个极点在左平面（p<n ）,奈奎斯特路径如图，+∞→=0,从w jw s 232,,Re s ππθθ→+∞→=从R j 0,→∞-=从w jw s则：（1）奈奎斯特稳定判据如何表述？（2）若含积分积分环节，则奈奎斯特路径如何选取？《信号与系统》6.)1()()(--=t u t u t x )3()1(u 2)(t h -+--=t u t t u ）（ )h *t )(t x t y （）（=用图解法求y(t)7.求)(]cos [)(02t u t w et x t -=的拉普拉斯变换X （s ），并指出ROC8.不记得9.用长除法求出211)211(1z (----=z z X ）的反变换前5项，写成：+-+-+-+-+-+=)5()5()4()4()3()3()2()2()1()1()()0()(n x n x n x n x n x n x n x δδδδδδ形式。
10.（1）求P （t ）的傅里叶系数及拉氏变化）（jw p X（2）不记得（图没画完整）（注：素材和资料部分来自网络，供参考。
请预览后才下载，期待你的好评与关注！）。
汽车理论试题长安大学考研题目及答案
汽车理论试题长安大学考研题目及答案汽车理论试题（长安大学考研题目）1.汽车行驶时，地面对驱动轮的切向反作用力不应小于（滚动阻力）、（空气阻力）与（坡度阻力）之和，同时也不可能大于（汽车重力）与（附着系数）的乘积。
2.变速器各相邻档位速比理论上应按（等比）分配，为的是（充分利用发动机提供的功率），提高汽车的（动力性）。
3.研究平顺性的目的是（控制汽车振动系统的动态特性），使乘坐者不舒服的感觉不超过一定界限，平顺性的评价方法有（基本评价）方法和（辅助评价）方法两种。
4.汽车采用自动防抱死装置为的是使车辆在制动时保持（车轮滚动）的状态，以获得（较高制动力）和（较高侧向力系数）因而提高汽车的（方向稳定性）和（转向操控能力）。
5.货车采用拖挂运输，使得分摊到（每吨货物）的百公里油耗（降低），其原因是（发动机负荷率增加，燃油消耗率下降）和（汽车列车的质量利用系数较大）。
6.等速百公里油耗正比于等速行驶时的（行驶阻力）和（燃油消耗率），反比于（传动效率）。
7.确定最大传动比时，要考虑三方面的问题：（最大爬坡度）、（附着率）以及（汽车最低稳定车速）。
8.同步附着系数w0是（前后制动器制动力分配线（β线）与理想的前后制动器制动力分配曲线（I线）交点处的附着系数）。
在同步附着系数的路面上最大制动减速度是（φ0g）；在大于w0的路面上制动时，汽车将会出现（后轮抱死），而当全部车轮都抱死时，其最大制动减速度应（大于）同步附着系数路面上的最大制动减速度。
9.轮胎侧偏角是（轮胎接触印迹中心位移方向与X轴的夹角），当前轮侧偏角小于后轮侧偏角时，汽车有（过多转向）特性。
10.汽车直接档的经济车速通常处于（接近低速的中等车速）范围。
这是因为，在高速行驶时由于（行驶阻力）迅速增加，使百公里油耗（增加），在低速行驶时，由于（发动机负荷率）较低，以至（燃油消耗率）显著上升，故百公里油耗（增加）。
11.降低车身固有频率，会使车身垂直振动加速度（较低），使悬架动挠度（增加）。
信号与系统2014A(答案)
华北电力大学2013～2014学年第 二 学期考试试卷（A ）班级: 姓名: 学号:一．填空题（共20分） 1.0j j 0e [()()]d 1e t t t t t t ωωδδ∞---∞--=-⎰（1分）2. 判断如下所示系统是否具有线性、时不变性、因果性：()sin[()]()y t f t t ε= 非线性 ， 时变 ， 因果 。
（3分） 3. 连续周期信号傅里叶级数的两种形式011cos()n n n A A n t ωϕ∞=++∑，1j 1e n t n n F ω∞=∑（如果写指数形式和三角形式，也算对吧）。
（2分）4. 调制的实质是 频谱搬移 ，频分复用的关键是将信号与不同频率的 载波信号（三角信号） 相乘。
（2分）5. 序列0.5()[(2)(6)]t f t e t t εε-=---拉普拉斯变换的收敛域 整个s 平面 。
（2分）6. 连续因果系统的系统函数H (s )的零、极点分布图如图1-1所示，且H (∞)=1，则系统的冲激响应h (t ) = ()2()t t δε+。
（2分）图1-1 图1-27. 判断序列()sin(0.4)2cos(0.5)x k k k =π+是否具有周期性 否 ，若具有周期性则周期为 无 （若不具有周期性则写“无”）。
（2分）8. 图1-2所示的信号是功率信号还是能量信号 能量 ，其功率或能量为 0.5 。
（2分）9. 已知序列x (k )的Z 变换为2()(1)(2)z X z z z =--，则x (0)与x (1)为 1，3 。
（2分）10. 序列(2)(1)kk ε--+的单边Z 变换1212z z z---=。
（2分） 二．作图与简答（共30分）1. （6分）已知信号f (t )的波形如图2-1所示，画出(12)(1)f t t ε--的波形图。
2. （6分）f 1(t )与f 2(t )的波形如图2-2所示，作出f 1(t )*f 2(t )的波形。
信号与系统(A卷规范标准答案)
淮南师范学院201 -201学年第 学期《信号与系统》A 卷参考答案及评分标准一、填空题（每题2分，共10分） 1．离散信号2．()f t 3．冲激信号或()t δ 4．可加性 5．()t δ 二、选择题（每题2分，共10分） 1. (B) 2. (C) 3. (C) 4. (A) 5. (C)三、判断题（每题2分，共10分） 1. × 2. √ 3. √ 4. √ 5. √四、简答题（每题5分，共10分）1. 简述根据数学模型的不同，列出系统常用的几种分类。
（本题5分）答：根据数学模型的不同,系统可分为4种类型. -----------------------(1分) (1) 即时系统与动态系统 -----------------------(1分) (2) 连续系统与离散系统 -----------------------(1分)(3) 线性系统与非线性系统 -----------------------(1分) (4) 时变系统与时不变系统 -----------------------(1分)2. 简述稳定系统的概念及连续时间系统时域稳定的充分必要条件。
（本题5分）答：（1）一个系统（连续的或离散的）如果对任意的有界输入，其零状态响应也是有界的则称该系统是有界输入有界输出稳定系统。
-----------------------(2分)（2）连续时间系统时域稳定的充分必要条件是()h t dt M ∞-∞≤⎰-----------------------(3分)五、计算题（每题10分，共60分） 1、如有两个序列11,0,1,2()0,k k f k +=⎧=⎨⎩ 其余21,0,1,2()0,k f k =⎧=⎨⎩ 其余试求卷积和12()()()f k f k f k =*（本题10分）解： 1 1 1⨯ 1 2 3-------------------------- 3 3 3 2 2 21 1 1---------------------------------1 3 6 5 3 -----------------------(5分){}12()()()0,1,3,6,5,3,00f k f k f k k =*=↑= -----------------------(5分)2、求象函数2()(2)(4)sF s s s =++的拉普拉斯逆变换()f t （本题10分）解：12()24k k F S s s =+++2424s s =-+++ -----------------------(5分) 24()(24)()tt f t ee t ε--∴=-+ -----------------------(5分)3. 已知某LTI 离散系统的差分方程为()(1)2(2)2()y k y k y k f k +---=, 求单位序列响应()h k （本题10分）解：12()()2()2()Y Z Z Y Z Z Y Z F Z --+-= -----------------------(2分)()()()Y Z H Z F Z =12212z Z --=+-2222Z Z Z =+- -----------------------(2分) ()2(2)(1)H Z Z Z Z Z =+-21413132Z Z =⋅+⋅-+ -----------------------(2分) 24()3132Z Z H Z Z Z =⋅+⋅-+ -----------------------(2分)24()[(2)]()33k h k k ε=+⋅- -----------------------(2分)4. 已知02,()0,F jw ωωωω⎧<⎪=⎨>⎪⎩ ，求()F jw 的傅里叶逆变换（本题10分）解：1 ()()2j tf t F j e dωωωπ+∞=-∞⎰011j te dωωωωπ=⋅-⎰-----------------------(5分)11j tejtωωωπ=⋅⋅-2sin()ttωπ=-----------------------(5分)5. 已知某系统框图其中()()f t tε=(1) 求该系统的冲激响应()h t(2) 求该系统的零状态响应()zsy t（本题10分）解：''()3'()2()4'()()y t y t y t f t f t++=+2(32)()(41)()S S Y S S F S++=+-----------------------(2分)2()(41)()()(32)Y S SH SF S S S+==++113712S S=-⋅+⋅++-----------------------(2分)(1) 冲激响应2()[(3)7]()t th t e e tε--=-⋅+-----------------------(2分)(2)41()()()(1)(2)zsSY S H S F SS S S+=⋅=++-----------------------(1分)1117132122S S S=⋅+⋅-⋅++-----------------------(1分)零状态响应217()(3)()22t tzsy t e e tε--=+------------------------(2分)6.如图所示的电路，写出以)(tus为输入，以)(tuc为响应的微分方程。