车削二包蜗杆宏程序【基于宏程序的椭圆车削】
宏程序车削蜗杆的应用

取槽宽为进刀宽度!利用两个循环语句!第一个循环沿斜线径 向单边以 "0# 77的吃刀深度进行循环切削!第二个循环切削 蜗杆槽宽度的部分! 4P方向以 "0! 77进给量进行循环切削0 这种方案最大的特点就是切削力非常小!不会出现扎刀'打刀 情况$
图 2&方法一&蜗杆螺纹粗车刀图
"#
创新与实践
!"#$%&'&() *%+ ,*-."! -./0!%!1.0%!!"#$
&引言 蜗杆在各类大型机械的减速机构上都有广泛应用!但蜗杆
的加工!特别是大模数的蜗杆的加工是比较棘手的问题!在普 车上车削要求工人要有比较熟练的操作技巧!其加工的精度和 生产效率受人为因素和操作技术水平影响比较大$ 虽然数控 车床具有较高的精度和稳定的加工性能!为蜗杆齿形的车削提 供了良好的加工基础!但是其程序的编制与操作控制均有较高 的难度$
技术与市场 !"#$ 年第!蜗 杆和大导程螺 纹零件 的齿形$ ) 用这个方法时!在数控车床能承受的范围内!可尽可能选择较 高的切削速度!比如(在车削模数 7Ub' 时!选用 2%" ;S789$ &蜗杆数控车削走刀方式设计
方法一(走刀路线如图 ! ) C* 所示$ 采用刀头宽小于齿形 槽宽的车刀如图 2 所示!采用 !0' 77的刀头宽加工 !03$$ 77 槽宽的蜗杆螺纹!巧妙地结合普通车床车削蜗杆时应用的左右 赶刀工艺技巧!采用左右分层车削斜面的方法取代成形刀法来
!+`!"`共六种!而蜗杆螺纹的齿形角度为 '"`!由于现在的数控 车床多数有 宏 变 量 编 程! 可 采 用 宏 变 量 控 制 走 刀 方 式! 结 合 R2! 或 R$! 螺纹指令完成蜗杆的加工$ &刀具的选择
宏程序椭圆教程

宏程序椭圆教程在数控加工领域,宏程序是一种强大的编程工具,能够实现复杂形状的加工,其中椭圆的加工就是一个常见的应用。
接下来,就让我们一起深入了解宏程序椭圆的相关知识和编程方法。
一、椭圆的基础知识在数学中,椭圆的标准方程有两种形式:中心在原点,焦点在 x 轴上时,方程为:$\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1$中心在原点,焦点在 y 轴上时,方程为:$\frac{y^2}{a^2} +\frac{x^2}{b^2} = 1$其中,a 表示椭圆的长半轴,b 表示椭圆的短半轴。
在数控加工中,我们通常需要根据给定的椭圆参数(如长半轴、短半轴、中心坐标等)来编写宏程序。
二、宏程序编程的基本思路要使用宏程序加工椭圆,首先需要确定编程的坐标系和加工的起点、终点。
然后,根据椭圆的方程,通过变量来计算每个加工点的坐标值。
以焦点在x 轴上的椭圆为例,假设椭圆的长半轴为a,短半轴为b,中心坐标为(Xc,Yc),我们可以定义变量1 为角度θ(从 0 到 360度变化),然后通过以下公式计算加工点的坐标:X = Xc +a cos(θ)Y = Yc +b sin(θ)三、宏程序示例以下是一个使用 FANUC 系统编写的椭圆宏程序示例:O0001 (程序名)G90 G54 G00 X0 Y0 S1000 M03 (设定初始状态)1=0 (角度初始值设为 0 度)2=30 (长半轴)3=20 (短半轴)4=100 (椭圆中心 X 坐标)5=50 (椭圆中心 Y 坐标)WHILE 1 LE 360 DO1 (当角度小于等于 360 度时,执行循环)6=4 + 2 COS1 (计算 X 坐标)7=5 + 3 SIN1 (计算 Y 坐标)G01 X6 Y7 F200 (直线插补到计算出的坐标点)1=1 + 1 (角度增加 1 度)END1 (循环结束)G00 X0 Y0 (回到原点)M30 (程序结束)在这个示例中,我们通过角度的变化,不断计算出椭圆上的点的坐标,并通过直线插补的方式进行加工。
数控车床车削宏程序

例6 抛物线与椭圆的混合运用。
%8002 (程序名) G92 X50 Z0 (起点坐标) U32 V40 W55 A8 B5 C4 M98 P8001(定义#20=32、#21=40、#22=55、#0=8、#1=5、#2=4) W G36 G90 X50 Z0(到起点位置) M30 V %8001 (子程序名) U #10=0 #11=0 (抛物线起点X、 Z轴坐标值) #12=0 #13=0 (椭圆起点在X、Z轴方向增量值) G64 G37 (小线段连续加工、半径编程) WHILE #11 LE #20 (抛物线方程:Z=-X*X/C ) G01 X[2*#10] Z[-[#11]] F1500 #10=#10+0.08 (计算各段抛物线X轴坐标) #11=#10*#10/#2 (计算各段抛物线Z轴坐标) 抛物线 ENDW Z=-X² /c G01 X[2*[SQRT[#20*#2]]] Z[-#20] (到达抛物线终点) G01 Z[-#21] (到达直线终点) 椭 圆 X a / b b2 z 2 : WHILe #13 LE #1 (椭圆方程:X*X/A*A+Z*Z/B*B=1) 图4 #16=#1*#1-#13*#13 #15=SQRT[#16] #12=#15*[#0/#1] (计算椭圆X轴方向的增量) G01 X[2*[SQRT[#20*#2]+#0-#12]] Z[-#21-#13] #13=#13+0.08 (确定椭圆Z轴方向的增量) ENDW G01 X [2*[SQRT[#20*#2]+#0] ]Z[-#21-#1] (到达椭圆终点) 抛物线 椭圆 G01 Z[-#22] 2 2 Z=-X² /c X a / b b z U12 G00 Z0 m99
数控车削加工椭圆的粗车方法

( 山学 院 , 唐 唐山 0 3 2 ) 6 0 0
Ro g u nn t o n n me ia t e u e lp e ma hn n u h t r ig me h d o u r la h s d i el s c i ig c l n i
+ c ) () 1
R- 2
( ) 算半 径 R = C 2计 0,
三 角形 M AO 中
图 1椭圆的近似画法 图2 C D作图 A
。 , A = c- , A 争 争A c x A cF O ±
=
() 中心线 A 1画 B和 C D分 别 等 于椭 圆 长轴 尺 寸 和短 轴 尺 寸
2 和 2 ;2连接 A 在 A 0 b() C, C线上取点 F, C = 0 C ;3作 使 FA 一 O () ,垂直平分线交 O A于 0 点 ,其延长交 C 。 D延长线与 0 点 ; : () 0 为圆点 0 1 4以  ̄ 为半径画弧 , 以 0 为圆点 以 0C为半径 再 。 。
3 圆弧代 替 椭 圆 的坐标 值得 确定 用
3 1 绘 图 法 .用
利用 C D软件 按 照 1 1 比例 ,. 1 的精 度 绘 图 , A :的 0 0 mm 0 然
★来稿 日期:0 0 0 - 0 2 1- 6 2
() 3 计算 G点 Z坐 标 , v一 E Z= G
c = c [ E =
机 械 设 计 与 制 造
1 68
文章 编 号 :0 13 9 ( 0 )4 0 6 - 2 10 — 9 7 2 1 0 — 180 1
M a h n r De in c iey sg
&
M a u a t r n fcue
数控车床加工椭圆的宏程序

数控车床加工椭圆的宏程序随着数控技术不断进步,数控车床加工中各种复杂形面也日渐增多,如椭圆、抛物线、正弦曲线、余弦曲线、双曲线等各种非圆曲面。
对于上述各种复杂成形面,利用CAM软件进行自动编程相对简单,但由于种种原因,在绝大多数情况下数控车床主要还是依靠手工编程。
椭圆轴线与数控车床Z轴重合的情形相对比较简单,其解决方案也多见于各类文献,但在本例中椭圆轴线与数控车床Z轴呈一定夹角,编程和加工难度陡增,主要原因如下:①机床数控系统本身既不存在加工椭圆等非圆曲线的G指令,更没有类似G68这样的旋转指令,使编程难度大大增加。
②加工中变量的参数直接影响着加工的效率以及质量,很容易产生过切报警,即使程序正确无误,实际加工时的参数调整也非常困难,直接影响着加工能否顺利进行,以及加工精度能否保证。
总而言之,目前尚未见有表述类似实例的文章。
本实例进行了有益的尝试和探索,给出了切实可行的解决方案,为类似问题提供了难得的参考及借鉴。
椭圆宏程序的编制如下。
1.椭圆方程宏程序主要利用各种数学公式进行运算加工,因此编制旋转椭圆程序操作者必须要掌握椭圆方程和旋转公式等各种数学公式的计算方法并加以灵活运用。
椭圆方程有两种形式,分别是椭圆的标准方程和参数方程。
椭圆标准方程:椭圆参数方程:其中a、b分别为X、Z所对应的椭圆半轴。
2.旋转公式由于数控车床并不像加工中心那样存在着旋转指令,所以要利用旋转公式来进行椭圆的旋转。
旋转公式的定义:如图1所示,平面上绕点O旋转,使平面上任意一对对应点P和P′与一个定点O连接的线段都相等,即OP=OP′,且角∠POP′等于角θ,点O称为旋转中心,角θ称为旋转角。
旋转公式:如图1所示,取直角坐标系,以原点O为旋转中心,旋转角为θ,平面上任意一点P(x,z)旋转到P′(x′,z′),令∠XOP=α,则∠XOP′=α+θ,且OP=OP′。
于是X′=OPx′=|OP′|cos(α+θ)=|OP′|(cosα×cosθ-sinα×sinθ)=|OP|cosα×cosθ-|OP|sinα×sinθ=OPxcosθ-PxPsinθ=xcosθ-zsinθ同理Z′=xsinθ+zcosθ车床旋转公式为其中,X′、Z′为旋转后的坐标,X、Z为旋转之前的坐标值,θ为旋转角度。
基于宏程序的椭圆车削加工
基 于 宏程 序 的椭 圆车削加 工
周 虹 , 斌 周 文 军 宁 ,
(. 南铁 道 职 业 技 术 学 院 , 南 株 洲 4 20 ;. 洲 电 力 机 车 有 限 公 司 , 南 株 洲 4 20 ) 1湖 湖 10 12 株 湖 1 0 1
回转轴 的交 点处 从 右 到 左粗 、 加 工 椭 圆部 分 , 精 采 用 主/ 子程 序指 令编 程 。
刀具 选 择 : O - 车 刀 , 偏 角 为 9 。副 偏 角 T 1粗 主 3,
XO 若 长 轴 方 Z,
向为 Z 轴 , 轴 短 方 向为 X 轴 , 已 知 椭 圆上节 点 的 Z 坐 标 , 根 据 则
用直 线 段 去 逼 近 椭 圆 , 这
、
、
、
- ~
—
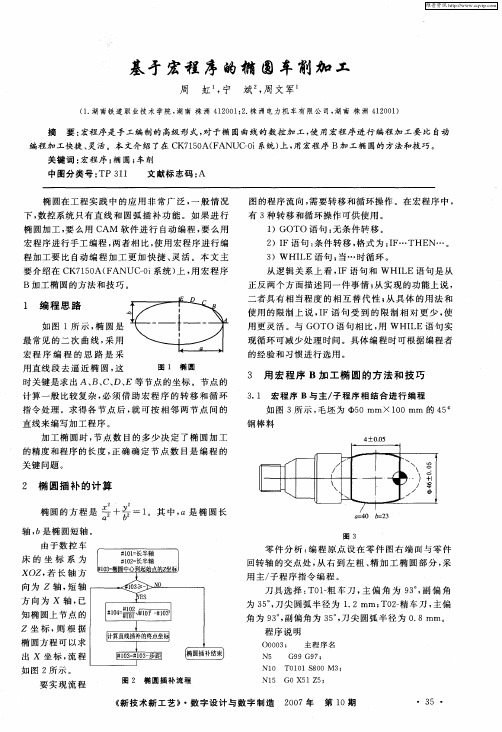
图 1 椭 圆
时关 键是求 出 A、 c、 E 等节 点 的坐标 。节点 的 B、 D、 计 算 一般 比较 复杂 , 须 借 助 宏 程 序 的 转 移 和循 环 必
3 用 宏 程 序 B加 工 椭 圆的 方 法 和 技 巧
3 1 宏程 序 B与 主/ . 子程序 相 结合 进行 编程 如 图 3所 示 , 毛坯 为 0 0mm×1 0mm 的 4 5 0 5 钢棒 料
椭 圆在工 程 实践 中 的应 用 非 常 广 泛 , 般 情 况 一
图 的程序 流 向 , 要转 移 和循环 操作 。在宏程 序 中 , 需 有 3 转 移 和循 环 操作 可供 使用 。 种
I )GOTO语 句 : 条 件转 移 。 无
下 , 控 系统 只有 直 线 和 圆 弧 插 补 功 能 。如 果 进 行 数 椭 圆加工 , 么用 C 要 AM 软件 进 行 自动 编程 , 么 用 要 宏程 序进 行手 工编 程 , 者相 比 , 两 使用 宏程 序 进行 编
椭圆零件在数控车床上的加工方法

椭圆零件在数控车床上的加工方法【摘要】轴类零件上一些高精度的曲面如椭圆、正弦曲线等,用普车难以加工,必须采用数控车床才可以加工。
本文根据平时加工中总结出的一些经验,简单谈下在广州数控系统数控车床上车削椭圆的一些看法,就编制步骤、宏程序组成、编程实例等几方面进行了探讨。
【关键字】数控加工椭圆宏程序编程椭圆加工,普通机床很难完成,而数控机床确实能够轻松的加工出来,主要是因为椭圆加工的时候X、Z两坐标是同时变化的,数控机床是通过程序控制的方式来驱动两轴,实现两轴的共同运动。
但数控车床只具有直线插补和圆弧插补两种基本插补功能,不具备椭圆插补功能,所以加工椭圆时可以采用直线逼近法的方式进行加工,即把曲线用许多小段的直线来代替,无限接近椭圆轮廓的加工方法。
下面选用广州数控980TB数控车削系统,结合教学工作实践谈谈如何巧用宏程序解决椭圆编程问题。
一、椭圆宏程序的编制步骤1.标准方程。
2.对标准方程进行转化成车床椭圆方程。
3.求值公式推导有些零件的椭圆中心不在工件原点处,就要根据实际椭圆写出正确的方程。
为编程方便,一般用Z作为变量。
二、宏程序组成1.变量的类型变量号#0,空变量;变量号#1~#33,局部变量;变量号#100~#109、#500~#999,公共变量;变量号#1000以上,系统变量。
2.变量的运算定义#1=#2;加法#1=#2+#3、减法#1=#2-#3、乘法#1=#2*#3、除法#1=#2/#3;正弦#1=SIN[#2]、余弦#1=COS[#2]、正切#1=TAN[#2];平方根#1=SQRT[#2]、绝对值#1=ABS[#2]。
3.运算符EQ(=)、GE(≥)、NE(≠)、LT()、LE(≤)。
按照优先的先后顺序依次是函数→乘和除运算→加和减运算。
4.条件转移(IF)功能语句IF[表达式]GOTO n。
指定的条件不满足时,转移到标有顺序号n的程序段。
三、980TB系统宏指令加工椭圆曲线编程实例1.凸椭圆中心不在零件轴线上例:毛坯直径为Ф40,总长为40,用变量进行编程,经计算椭圆起点的X 轴坐标值为10.141。
数控车削中椭圆宏程序的编制
号 O外 编 制椭 圆宏程序 要熟悉 椭 圆标 准方程 和参数 方程 ,它们 选择 1 3 。 圆车 刀加工 外轮廓 。切 削用量 的选择 :粗加 工 0 rm n .5 / ,精加工主轴转速 为 均表达 出 了椭 圆上 点的坐 标及两 坐标 之 司的关系 。例如 :图 主轴转速 为6 0/ ,进给 量为02 mmr
三 、以 参数 ( 角度 ) 为初始 变量
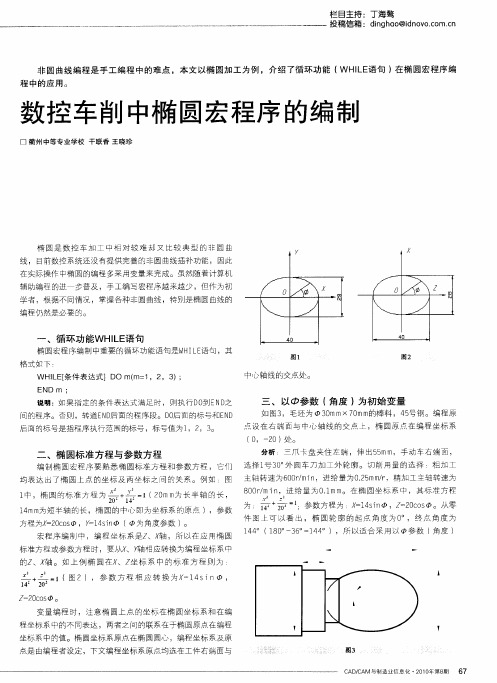
如 图3 ,毛坯 为 3 mm×7 mm 0 0 的棒 料 ,4 号钢。编程原 5 点设 在右 端面 与中心 轴线 的交点 上 ,椭 圆原点 在编 程坐标 系
( ,- 0) 。 0 2 处
二 、椭 圆标 准方程与参数方程
分析 :三爪卡 盘夹住左 端 ,伸 出5 mm,手 动车右端面 , 5
C DC M与制造业信息化 ・ 0 0 A /A 2 1年第8 期 6 7
T
为初始变量, 应用参数方程来表达椭圆上点的坐标。编制程 一半,长半轴长1m 钩 ) 短半轴长1m 轴 ) ( 5 m , 0 m( ,
序如下 。 O1 3 2 4:
G 0T01 3¥6 0; 4 01M0 0
2)。
编制 程 序 如 下 一
O1 3 2 5:
G7 0 Q20U1W O. 0 2 3 P1 05F 5:
N1 OGO 0×0. : G4 2 G01 Z F . ; 0, 0 1
G 0T0 01 M0 ¥6 0; 4 1 3 0 GOO 4 Z2 0: X3 G73 U1 4W 0 R7:
中心轴线 的交点处 。
说 明 :如 果 指 定 的条 件 表 达 式 满 足 时 ,则 执 行 D 到 E 之 0 D N 间 的 程序 。否 则 ,转 道 E D 面 的程 序 段 。 D 后 面 的 标 号 和 E D N后 0 N 后 面 的标 号 是 指 程 序 执 行 范 围 的标 号 ,标 号 值 为 1 ,3 ,2 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
车削二包蜗杆宏程序【基于宏程序的椭圆车削】
本文结合工作实践对编制椭圆轨迹通用程序的宏程序进行探讨。
一、编程原理使用宏程序编程,大部分零件尺寸和工艺参数通过
参数传递到宏程序中,程序修改方便,图样改变时,仅需修改相应参数,不需要重新编程。
同时在宏程序中利用数控系统自身的计算功能,尽可能地消除了数据计算误差,相应的也保证了加工工件的精度。
对于非圆曲线,我们可以对数据进行密集化处理,使直线尽可
能地逼近曲线。
这样应用宏程序中的变量和计算功能,使得数控系统自动计算出曲线上的点。
我们只需要指定曲线的起点和终点,以及相邻两数据之间的步长,并制定变量的运算方式就可以了。
由图1可以看到,步长越小,逼近曲线越接近理论曲线。
但在
实际编程中,无限缩小步长会增加系统的运算量,可能会造成加工时间延长。
需要根据加工工件的要求合理地设定步长。
二、编程方法
椭圆的方程有两种,一种是,还有一种参数方程:。
以为例,可以设定X为自变量,根据X值和椭圆方程,确定y 值。
需要特别注意的是,在数控车床中,编程时对应的是直径编程,
需要根据数控车床的坐标轴和坐标方向,根据图纸,对X,y值进行转变。
下面列出宏程序编制方法的流程图。
要实现图2所示的程序流向,需要在程序中对变量进行多次复制,并可以通过转移和循环语句实现。
在宏程序中,有以下几个语句可以使用:
GOTO语句:无条件转移;
IF语句:条件转移;
WHILE语句:当…时循环。
从功能上说,IF语句和WHILE语句具有一定的相互替代性;从具体的用法和使用的限制上说,IF语句受到的限制相对更少,使用更灵活。
与GOTO语句相比,用WHILE语句实现循环可减少处理时间。
具体编程时可根据编程者的经验和习惯进行选用。
三、加工程序
以图3为例,说明椭圆的加工程序。
图中椭圆长轴为50,短轴为25。
数控车床中X方向为直径编程,在加工时需要注意。
图中X的取值范围为[0,25],Z的取值范围为[-50,50],需要注意的是,每一个X值对应两个Z值,而每一个Z 值,只对应一个X值,所以在编程中以Z值为自变量,以X值为因变量。
程序如下:
O1234;
N10 M03 S500 T0101 F0.2;
N20 G00X52 Z52;
N30 G00X0;
N40 G01 Z0;
N50 #1=50;#1表示Z;
N60 #2=25*SQRT[1-#1*#1/2500];#2表示X值,半径值;
N70 G01X[2*#2] Z[#1];
N80 #1=#1-0.2;
N90 IF[#1GE-50] GOTO N60;
N100 G00X100;
N120 G00 Z150;
……
使用参数方程进行编程时,需要确定的起始角和结束角的角度,需要设定三个变量,X和Z值根据角度的大小发生变化,这里不在赘述。
(:山东省济南技师学院)
本文为全文原貌未安装PDF浏览器用户请先下载安装原版全文内容仅供参考。
