第三章 计算力学习题
简明理论力学第三章例题作业
平衡稳定性分析
平衡稳定性是指物体在平衡状态 下受到微小扰动后恢复到原平衡 状态的能力。
•·
平衡稳定性分析主要通过研究物
体的势能和动能来确定。
分析物体在平衡状态下受到微小 扰动后的稳定性。
如果势能曲线在平衡点附近是凸 的，则该平衡是稳定的；如果是 凹的，则是不稳定的。
04
动量与动量守恒
动量与冲量
三角形法则
三角形法则是一种更直观的力的 合成方法，通过将两个力首尾相 接，形成一个三角形，合力方向 沿三角形第三边的方向。
力的分解
正交分解法
正交分解法是一种常用的力的分解方 法，将力分解为相互垂直的两个分力 ，便于计算和解决实际问题。
余弦定理
余弦定理是一种解决力的分解问题的 数学工具，通过余弦定理可以求出分 力的具体数值。
动量守恒定律
动量守恒定律表述为
在没有外力作用或合外力为零 的系统中，系统的总动量保持 不变。
适用范围
适用于封闭系统，不受外力或 合外力为零的情况。
实例
碰撞、火箭发射、行星运动等 。
05
角动量与角动量守恒
角动量
01
02
03
定义
角动量是描述物体绕固定 点旋转运动的物理量，等 于物体质量、速度和到旋 转轴的距离的乘积。
力矩是力和力臂的乘积，表示力对物体转动效果的量度。力矩的公 式为M=FL，其中F为力，L为力臂。
力偶
力偶是两个大小相等、方向相反且作用线平行的力，其作用效果使 物体产生旋转运动。力偶的公式为M=(F1-F2)d，其中F1和F2为作 用在物体上的两个力，d为两力之间的距离。
力的合成
平行四边形法则
力的合成遵循平行四边形法则， 即两个力的合力等于以这两个力 为邻边的平行四边形的对角线。
初三物理力学计算练习题
初三物理力学计算练习题题目一：力的计算1.一个物体的质量是5kg，受到的作用力是10N，求物体的加速度。
解析：根据牛顿第二定律可知：F = m * a其中，F表示作用力，m表示物体的质量，a表示物体的加速度。
将已知数据带入公式：10N = 5kg * a解得：a = 2m/s²2.一个物体的质量是2kg，受到的作用力是20N，求物体的加速度。
解析：根据牛顿第二定律可知：F = m * a将已知数据带入公式：20N = 2kg * a解得：a = 10m/s²3.一个物体的质量是10kg，受到的作用力是50N，求物体的加速度。
解析：根据牛顿第二定律可知：F = m * a将已知数据带入公式：50N = 10kg * a解得：a = 5m/s²题目二：力的合成与分解1.有两个力分别为10N和20N，它们的合力大小是多少？解析：合力即为根据平行四边形法则绘制得到的对角线的长度，可以通过三角形法则计算：设两个力大小分别为F₁和F₂，合力大小为F₃，合力与力F₁的夹角为θ。
根据三角形法则可得：F₃² = F₁² + F₂² + 2F₁F₂cosθ已知F₁ = 10N，F₂ = 20N，角度θ为180°（因为两个力同向），代入计算得：F₃² = 10² + 20² + 2 * 10 * 20 * cos(180°)F₃² = 100 + 400 + 400F₃² = 900F₃ = 30N2.有两个力分别为15N和25N，它们的合力大小是多少？解析：根据同样的计算方法，代入已知数据进行计算：F₃² = 15² + 25² + 2 * 15 * 25 * cos(180°)F₃² = 225 + 625 + 750F₃² = 1600F₃ = 40N3.有两个力分别为12N和18N，它们的合力大小是多少？解析：同样地，代入已知数据进行计算：F₃² = 12² + 18² + 2 * 12 * 18 * cos(180°)F₃² = 144 + 324 + 432F₃² = 900F₃ = 30N题目三：斜面上的物体1.质量为20kg的物体放在一个倾斜角度为30°的斜面上，斜面的摩擦系数为0.1，求物体沿斜面下滑的加速度。
《建筑力学习题》-结构位移计算
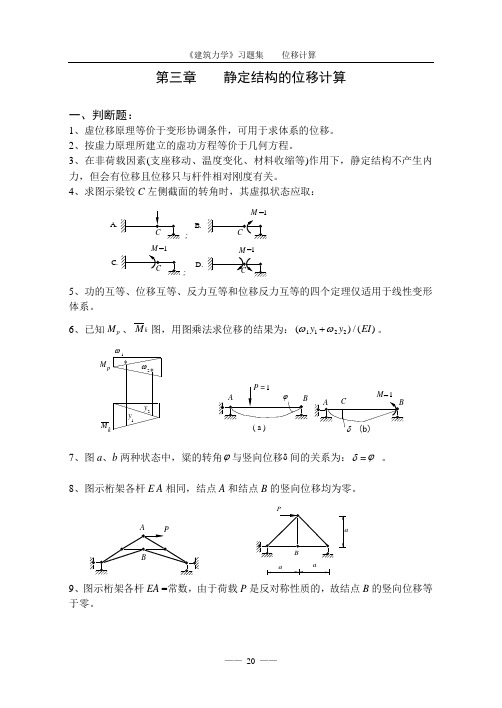
第三章 静定结构的位移计算一、判断题：1、虚位移原理等价于变形协调条件，可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下，静定结构不产生内力，但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时，其虚拟状态应取：A.;; B.D.C.=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图，用图乘法求位移的结果为：()/()ωω1122y y EI +。
M k M p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中，粱的转角ϕ与竖向位移δ间的关系为：δ=ϕ 。
8、图示桁架各杆E A 相同，结点A 和结点B 的竖向位移均为零。
9、图示桁架各杆EA =常数，由于荷载P 是反对称性质的，故结点B 的竖向位移等于零。
二、计算题：10、求图示结构铰A两侧截面的相对转角ϕA，EI = 常数。
q11、求图示静定梁D端的竖向位移∆DV。
EI = 常数，a = 2m 。
10kN/m12、求图示结构E点的竖向位移。
EI = 常数。
q13、图示结构，EI=常数，M=⋅90kN m, P = 30kN。
求D点的竖向位移。
P14、求图示刚架B端的竖向位移。
q15、求图示刚架结点C的转角和水平位移，EI = 常数。
q16、求图示刚架中Ｄ点的竖向位移。
EI ＝ 常数 。
l/217、求图示刚架横梁中Ｄ点的竖向位移。
EI ＝ 常数 。
18、求图示刚架中D 点的竖向位移。
E I = 常数 。
ql l l/219、求图示结构Ａ、Ｂ两截面的相对转角，EI ＝ 常数 。
l/23l/320、求图示结构A 、B 两点的相对水平位移，E I = 常数。
21、求图示结构B 点的竖向位移，EI = 常数 。
l l22、图示结构充满水后，求A 、B 两点的相对水平位移。
E I = 常数 ，垂直纸面取1 m 宽，水比重近似值取10 kN / m 3。
计算固体力学第三章_1
8. 可处理大变形和非线形材料带来的非线形问题.
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
3 协调模型分析
1. 建立协调模型的一般方法
大部分有限单元,都是根据虚功原理, 或由它导出的能量 原理建立的, 这类单元统称为“协调模型”或“相容模 型”（Conforming model)。
每个节点有三个转动 分量和三个位移分量.
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
如图1.4, 用120个节点和297个平面应变三角形单 元模拟. 将对称性应用于整个杆端的一半. 此分析 的目的是找出杆端应力集中最高的位置.
TSINGHUA UNIVERSITY
TSINGHUA UNIVERSITY
有限元法无论对什么样的结构（杆系，平面，三维， 板壳）分析过程是一样的，一般为：
有限元法基本步骤:
TSINGHUA UNIVERSITY
有限元法基本步骤
将物体划分为具体有相关节点的等价系统,选择最适当 的单元类型来最接近的模拟实际的物理性能. 所用的单元总 数和给顶物体内单元大小和类型的变化是需要工程判断的 主要问题. 单元必须小到可以给出有用的结果,又必须足够大以节省 计算费用.
一点的位移列阵： 一点的应变列阵：
一点的应力列阵：
一点的体积力列阵： 一点的表面力列阵：
边界外法线方向余弦矩阵：
其中：
平衡方程：（内力与体积力的关系方程）
写成矩阵形式：
其中
A - 微分算子矩阵
几何方程：(应变与位移的关系方程)
写成矩阵形式：
物理方程（应力与应变的关系方程)
计算力学大作
以下确定 Q(y)，和 R(x)； 将 u，V 代入 exy 表达式得
PLx PLx 2 dQ( y) vPy 2 dR( x) (1 v) P h 2 ( y2 ) EJ 2 EJ dy 2 EJ dx EJ 4
再分别对 x 和 y 求导并积分有
Q( y )
vPy 3 (1 v) Py 3 (1 v) Pyh 2 Ay B 6 EJ 3EJ 4 EJ PLx 2 Px3 R( x) Ax C 2 EJ 6 EJ
{
联立解得：
c1 2P h3
c2 0
c3
3P 2h
c4
P 2
故： 有上式求解应力：
A
P y y3 ( L x)(1 3 4 3 ) 2 h h
X
2 A P( L x) y y 2 J
{ 利用广义 Hooked 定律
eij
2 A y 0 x 2 2 A P h2 xy ( y2 ) yx 2J 4
目录
计算力学大作业 ......................................................................................................... 1 一． 解析部分 ................................................................................................... 1 二． 数值计算结果 ............................................................................................ 4 第一组： ..................................................................................................... 4 第二组 ......................................................................................................... 8 第三组 ......................................................................................................... 9 第四组 ....................................................................................................... 10 三． COMSOL 计算 .......................................................................................... 11 1x16 网格................................................................................................... 11 1x20 网格................................................................................................... 13 Finer 网格（由 COMSOL 自动生成） ....................................................... 14 较短梁讨论 ....................................................................................................... 15
力学第二版习题答案第三章
第三章基本知识小结⒈牛顿运动定律适用于惯性系、质点，牛顿第二定律是核心。
矢量式：22dtr d m dt v d m a m F=== 分量式：（弧坐标）（直角坐标）ρτττ2,,,vm ma F dt dv mma F ma F ma F ma F n n z z y y x x =======⒉动量定理适用于惯性系、质点、质点系。
导数形式：dt pd F =微分形式：p d dt F=积分形式：p dt F I∆==⎰)( （注意分量式的运用）⒊动量守恒定律适用于惯性系、质点、质点系。
若作用于质点或质点系的外力的矢量和始终为零，则质点或质点系的动量保持不变。
即∑==恒矢量。
则，若外p F0 （注意分量式的运用）⒋在非惯性系中，考虑相应的惯性力，也可应用以上规律解题。
在直线加速参考系中：0*a m f-=在转动参考系中：ωω⨯=='2,*2*mv f r m f k c⒌质心和质心运动定理 ⑴∑∑∑===i i c i i c i i ca m a m v m v m r m r m⑵∑=c a m F（注意分量式的运用）3.5.1 质量为2kg 的质点的运动学方程为j t t i t r ˆ)133(ˆ)16(22+++-= （单位：米，秒）， 求证质点受恒力而运动，并求力的方向大小。
解：∵j i dt r d a ˆ6ˆ12/22+== , j ia m F ˆ12ˆ24+== 为一与时间无关的恒矢量，∴质点受恒力而运动。
F=(242+122)1/2=125N ，力与x 轴之间夹角为：'34265.0/︒===arctg F arctgF x y α3.5.2 质量为m 的质点在o-xy 平面内运动，质点的运动学方程为：j t b i t a r ˆsin ˆcos ωω+= ，a,b,ω为正常数，证明作用于质点的合力总指向原点。
证明：∵rj t b i t a dt r d a2222)ˆsin ˆcos (/ωωωω-=+-==r m a m F2ω-==, ∴作用于质点的合力总指向原点。
计算力学试题答案
计算力学试题答案一、选择题1. 计算力学中，下列哪个方法常用于求解结构的静态响应？A. 有限元法B. 边界元法C. 有限差分法D. 谱方法答案：A2. 在材料力学中，弹性模量的定义是：A. 应力与应变的比值B. 应变与应力的比值C. 应力与变形的比值D. 变形与应力的比值答案：A3. 下列哪种材料在受力时表现出塑性变形？A. 弹性材料B. 塑性材料C. 粘弹性材料D. 脆性材料答案：B4. 在动力学问题中，阻尼力通常与什么参数有关？A. 速度B. 位移C. 力的大小D. 时间答案：A5. 根据牛顿第二定律，力与加速度的关系是：A. 力等于质量与加速度的乘积B. 力等于质量与速度的乘积C. 力等于加速度与时间的乘积D. 力等于速度与时间的乘积答案：A二、填空题1. 在平面应力问题中，最大应位移发生在距离________最远的点。
答案：载荷点2. 根据能量守恒原理，当一个系统的总势能减少时，其________能会增加。
答案：动3. 材料的泊松比是指在单轴拉伸时，横向应变与________应变的比值。
答案：纵向4. 在结构动力学中，自然频率是指结构在无阻尼情况下的________频率。
答案：固有5. 根据虚功原理，当一个力对一个位移的虚功等于零时，该位移可以是系统的一个________。
答案：振型三、简答题1. 请简述有限元法的基本思想及其在工程中的应用。
答：有限元法是一种数值分析工具，通过将连续体划分为有限数量的单元，并在每个单元内假设位移的近似函数，建立整个结构的方程系统。
该方法在工程中广泛应用于结构分析、热传导、流体力学等领域，能够有效处理复杂的几何形状和边界条件问题。
2. 描述材料的屈服准则，并举例说明其在工程设计中的重要性。
答：屈服准则是描述材料从弹性状态过渡到塑性状态的条件。
常用的屈服准则包括冯·米塞斯准则和特雷斯准则。
在工程设计中，了解和应用屈服准则对于确保结构在预期载荷下的安全性至关重要，可以避免因材料屈服导致的结构破坏。
结构力学(王焕定第三版)教材习题第三章答案全解——哈工大老师提供
结构力学(王焕定第三版)教材习题答案全解第三章习题答案3-1 (a) 答：由图（a ）、（b ）可知结构对称（水平反力为零）荷载对称，因此内力对称。
所以可只对一半进行积分然后乘以 2 来得到位移。
如图示F P R (1−cos θ)M P = θ∈[0,π/2]；M =R sin θ θ∈[0,π/2]2 代入位移计算公式可得M P M1 π2 M P M2 π2 F P R (1−cos θ)∆Bx = ∑∫ EId s = 2⋅ EI ∫0EI R d θ= EI ∫02 R sin θR d θ=F P R 3 =(→)2EI3-1 (b) 答： 如图（a ）、（b ）可建立如下荷载及单位弯矩方程EIBARRF P( a )1pR ∆Bx =∑∫ MEIM d s =∫0π2 MEI P M R d θ= q EI 4∫0π2(1−2cos θ+cos 2 θ)R d θqR 4 ⎡ θ 1⎤3π⎞ qR 4= EI ×⎢θ−2sin θ+ 2 + 4sin2θ⎥⎦0 =⎝⎜ 4 − 2⎠⎟ 2EI (→)2 ⎣3-2 答：作M P 图和单位力弯矩图如下图： 由此可得内力方程根据题意EI (x ) = EI (l + x )代入位移公式积分可得 2 2 P 0s i n ( ) d (1 c o s ) (1 c o s ) q M R q R M R θθ α α θθ − = = − = − ∫AqRBα θ1( a ) θ( b )ABlq 03 0 p 6 x q M M xl = = xP M 图2 0 6q l1lM 图 x5 83 82l 代入位移公式并积分（查积分表）可得M P M l 2 q0x4∆Bx =∑∫ EI d x =∫0 6EI(l + x) d x7q0l40.07 ql4= (ln 2−)× = (→)123EI EI3-3 答：分别作出荷载引起的轴力和单位力引起的轴力如下图所示：由此可得C 点的竖向为移为：F NP F N1F NP F N1 ∆Cy =∑∫EA d s=∑ EA l =65112.5 kN× ×6 m+2×(62.5 kN× ×5 m+125 kN× ×5 m+75 kN× ×6 m)= 88EA=8.485×10−4 m当求CD 和CE 杆之间的夹角改变使：施加如图所示单位广义力并求作出F N2 图，则F∆=∑∫ F NP EA F N2 ds =∑ NP EAF N2 l2×62.5 kN ×(−0.15)×5 m +(−112.5 kN)×0.25×6 m =EA=−1.4×10−4 rad( 夹角减小）3-4 （a）答：先作出M p和M 如右图所示。
土力学 第三章习题答案
3.1解：当第四层为坚硬的石时，该层为不透水层，处于地下水位以下的土体不受浮力作用，计算自重应力时，地下水位以下的土体采用其饱和重度。
地下水位以下的土体其天然状态就是饱和状态，故其天然重度即是其饱和重度。
计算中第一层素填土γ1=18.0kN/m3，第二层粉土γ2=19.4kN/m3，第三层中砂γ3=19.8kN/m3。
此时，岩顶处的自重应力为σcz=γ1h1＋γ2h2＋γ3h3=18×1.5＋19.4×3.6＋19.8×1.8=132.5kPa当第四层为强风化岩石，该层为透水层，处于地下水位的土体会受到浮力作用，计算自重应力时，地下水位以下的土体采用浮重度；地下水位以上的土体采用天然重度。
地下水位在第一层素填土和第二层粉土的分界面处，计算中第一层素填土γ1=18.0kN/m3，第二层粉土γ/2=9.4kN/m3，第三层中砂γ/3=9.8kN/m3。
此时，岩顶处的自重应力为σcz=γ1h1＋γ/2h2＋γ/3h3=18×1.5＋9.4×3.6＋9.8×1.8=78.5kPa3.2解：根据题意知，地下水位以上的粉土处于饱和状态，其饱和重度即是其天然重度。
计算中，地下水位以上1.1m范围的粉土采用天然重度γ=20.1kN/m3，地下水位以下3.7m范围的粉土采用浮重度γ/=10.1kN/m3。
粉土底面的自重应力为σcz=γh1＋γ/h2=20.1×1.1＋10.1×3.7=59.48kPa3.3解：偏心荷载下，在计算中心点下的附加应力时，可将梯形分布的基底压力简化为均布荷载，均布荷载p0的大小等于基底附加压力最大值p max和最小值p min 之和的一半，即：p0=(p max＋p min)/2=100kPa。
故本题可简化为条形基础作用均布荷载p0=100kPa，基础中心点下附加应力的计算，公式为：σz=αz p0，附加应力系数αz查P98页表3.5，计算列表如下：3.4解：为计算基础短边中心点下的附加应力，沿矩形基础长边方向，添加一块与原面积等大的荷载面，新的矩形基础长为原基础的2倍，宽不变。
工程力学习题 及最终答案
第一章第二章第三章绪论思考题1) 现代力学有哪些重要的特征？2) 力是物体间的相互作用。
按其是否直接接触如何分类？试举例说明。
3) 工程静力学的基本研究内容和主线是什么？4) 试述工程力学研究问题的一般方法。
第二章刚体静力学基本概念与理论习题2-1 求图中作用在托架上的合力F R。
12030200N习题2-1图页脚内容页脚内容2-2 已知F 1=7kN ，F 2=5kN, 求图中作用在耳环上的合力F R 。
2-3 求图中汇交力系的合力F R 。
2-4 求图中力F 2的大小和其方向角。
使 a )合力F R =1.5kN, 方向沿x 轴。
b)合力为零。
2-5 二力作用如图，F 1=500N 。
为提起木桩，欲使垂直向上的合力为F R =750N ，且F 2力尽量小，试求力F 2的大小和角。
245601习题2-2图(b)xy4530F 1=30NF 2=20NF3=40N A xy4560F 1=600NF 2=700NF 3=500NA 习题2-3图(a )x70F 2F 1=1.25kN A习题2-4图30F 1=500NAF 2页脚内容2-6 画出图中各物体的受力图。
(b)B (a )A (c)(d)DACDB页脚内容2-7 画出图中各物体的受力图。
2-8 试计算图中各种情况下F 力对o 点之矩。
习题2-6图(d)习题2-7图(a )C DB DABCBABC页脚内容2-9 求图中力系的合力F R 及其作用位置。
习题2-8图P (d)PF( a )F 3M =6kN m F 3F 2页脚内容2-10 求图中作用在梁上的分布载荷的合力F R 及其作用位置。
( a )q 1=600N/mq=4kN/m( b )q A =3kN/m习题2-9图( c ) F 4F 3页脚内容2-11 图示悬臂梁AB 上作用着分布载荷，q 1=400N/m ，q 2=900N/m, 若欲使作用在梁上的合力为零，求尺寸a 、b 的大小。
《工程力学》第三章平面一般力系试卷
1.当驱动外力的合力作用线与摩擦面法线所成的夹角不大于摩擦角时,物体总是处于状态。
(2 分)A.平衡B.运动C. 自由D. 自锁2.一力作平行移动后,新作用点的附加力偶矩一定。
(2 分)A.存在且与平移距离无关B.存在且与平移距离有关C.不存在3.平面一般力系的平衡条件是。
(2 分)A.合力为零B.合力矩为零C.各分力对某坐标轴投影的代数和为零D.合力和合力矩均为零4.若某刚体在平面一般力系作用下平衡,则此力系各分力对刚体的矩的代数和必为零。
(2 分)A.特定点B.重心C.任意点D.坐标原点5.这便于解题,力矩平衡方程的矩心应取在上。
(2 分)A.坐标原点B.未知力作用点C.任意点D.未知力作用线交点6.力矩平衡方程中的每一个单项必须是。
(2 分)A.力B.力矩C.力偶D.力对坐标轴上的投影7.一力向新作用点平移后,新点上有。
(2 分)A.一个力B.一个力偶C.一个力与一个力偶8.若平面一般力系向某点简化后合力矩为零,则其合力。
(2 分)A.一定为零B.不一定为零C.一定不为零9.为便于解题,力的投影平衡方程的坐标轴方向一般应按方向取定。
(2 分)A.水平或铅垂B.任意C.与多数未知力平行或垂直10.摩擦角是物体作用线与接触面法线间的夹角。
(2 分)A.全反力B.最大静摩擦力C.最大全反力D.驱动力11.( )平面一般力系的合力和合力偶的方向均与简化中心位置有关;合力和合力偶的大小均与简化中心位置无关。
(2 分)12.( )滚动摩擦力小于滑动摩擦力。
(2 分)13.( )作用于刚体上的力,其作用线可在刚体上任意平行移动,其作用效果不变。
(2 分)14.( )只要正确列出平衡方程,则无论坐标轴方向及矩心位置如何取定,未知量的最终计算结果总应一致。
(2 分)15.()对于受平面一般力系作用的物体系统,最多只能列出三个独立方程,求解三个未知量。
( )(2 分)16.( )对受平面一般力系作用的刚体列平衡方程时,三种形式的方程的使用条件均相同,每种形式均可求解三个未知量。
东南大学计算力学习题及答案汇总(2011版)
第三章1如图所示一三角形钢板，两个结点固定，对第三个结点施以单位水平位移，测出所施加的力，从而得出相应的刚度系数。
其他点依此类推，这样测得的刚度系数所组成的刚度矩阵，是否与按照常规三角形单元刚度矩阵计算公式所得结果一样？用这样实测所得的刚度矩阵能否进行有限元分析？为什么？解：不一样。
单元刚度矩阵中每个元素的物理意义：ij k 表示单元第j 个自由度产生单位位移，其它自由度固定时，第i 个自由度产生的节点力。
单元刚度矩阵是在单元处于平衡状态的前提下得出的，单元作为分离体看待，作用在它上面的外力（单元力）必是平衡力系，然而研究单元平衡时没有引入约束承受平衡力系作用的无约束单元，其变形是确定，但位移是不能确定的，即单元可发生任意的刚体位移。
不能。
因为与有限元中单元与单元之间的约束情况不一样，不能进行有限元分析。
2以位移为基本未知量的有限元法其解具有下限性质，试证明之。
解：系统总位能的离散形式{}{}{}{}12T Tp a K a a P ∏=- 将求解的方程[]{}{}K a P =带入可得{}[]{}{}[]{}{}[]{}1122T T Tp a K a a K a a K a U ∏=-=-=- 在平衡情况下，系统总位能等于负的应变能。
在有限元解中，由于假定的近似位移模式一般来说总与精确解有差别的。
设近似解为p ∏、U 、[]K 、{}a 、{}{}K a P ⎡⎤=⎣⎦，真实解为p ∏、U 、[]K 、{}a 、[]{}{}K a P = 且根据最小势能原理，得到的系统的总位能总会比真正的总位能要大，故p p ∏≥∏则U U ≤{}{}{}[]{}{}{}{}{}TT TTa K a a K a a P a P ⎡⎤≤⇒≤⎣⎦则近似解的位移总体上小于精确解的位移解释如下：单元原是连续体的一部分，具有无限多个自由度，在假定了单元的位移函数后，自由度限制为只有以结点位移表示的有限自由度，引入了更多的约束和限制，使得单元刚度较实际连续体加强了，连续体的整体刚度随之增加，所以有限元解整体上较真实解偏小。
土力学地基基础章节计算题及答案
土力学地基基础章节计算题及答案本页仅作为文档封面，使用时可以删除This document is for reference only-rar21year.March章节习题及答案第一章 土的物理性质1 有一块体积为60 cm 3的原状土样，重 N, 烘干后 N 。
已只土粒比重（相对密度）s G =。
求土的天然重度、天然含水量w 、干重度d 、饱和重度sat 、浮重度’、孔隙比e 及饱和度S r解：分析：由W 和V 可算得，由W s 和V 可算得d ，加上G s ，共已知3个指标，故题目可解。
363kN/m 5.1710601005.1=⨯⨯==--V W γ 363s d kN/m 2.1410601085.0=⨯⨯==--V W γ3w sws kN/m 7.261067.2=⨯===∴γγγγs s G G%5.2385.085.005.1s w =-==W W w 884.015.17)235.01(7.261)1(s =-+=-+=γγw e (1-12) %71884.06.2235.0s =⨯=⋅=e G w S r (1-14) 注意：1．使用国际单位制； 2．w 为已知条件，w =10kN/m3；3．注意求解顺序，条件具备这先做； 4．注意各的取值范围。
2 某工地在填土施工中所用土料的含水量为5%，为便于夯实需在土料中加水，使其含水量增至15%，试问每1000 kg 质量的土料应加多少水 解：分析：加水前后M s 不变。
于是：加水前： 1000%5s s =⨯+M M （1） 加水后： w s s 1000%15M M M ∆+=⨯+ （2） 由（1）得：kg 952s =M ，代入（2）得： kg 2.95w =∆M 注意：土料中包含了水和土颗粒，共为1000kg ，另外，swM M w =。
3 用某种土筑堤，土的含水量w ＝15％，土粒比重G s ＝。
分层夯实，每层先填0.5m ，其重度等＝16kN/ m 3，夯实达到饱和度r S ＝85%后再填下一层，如夯实时水没有流失，求每层夯实后的厚度。
初二物理第三章练习题
初二物理第三章练习题一、选择题1. 下列选项中，哪一个是力的三要素之一？A. 大小B. 方向C. 作用点D. 所有以上2. 物体受到的力是10N，且力的方向与物体运动方向成30°角，求该力在水平方向上的分力大小。
A. 5NB. 8.66NC. 10ND. 无法确定3. 一个物体在水平面上受到的摩擦力是5N，要使物体沿水平面运动，需要施加的最小推力是：A. 0NB. 5NC. 10ND. 20N4. 根据牛顿第二定律，下列哪一项不是力的计算公式？A. F = maB. F = mvC. F = ma^2D. F = m(v^2)5. 一个物体从静止开始做匀加速直线运动，初速度为0，加速度为2m/s²，经过4秒后的速度是多少？A. 4m/sB. 8m/sC. 16m/sD. 32m/s二、填空题6. 牛顿第一定律表明，物体在没有受到外力作用时，将保持________状态。
7. 力的合成遵循________原理，而力的分解遵循________原理。
8. 当一个物体受到多个力的作用时，这些力的合力等于这些力的________。
9. 牛顿第二定律的表达式是________，其中F表示力，m表示质量，a 表示加速度。
10. 一个物体做匀速直线运动时，其加速度为________。
三、简答题11. 解释什么是惯性，并给出一个生活中的例子。
12. 描述牛顿第三定律，并举例说明。
13. 说明力的平衡状态有哪些，并给出一个例子。
四、计算题14. 一辆汽车以20m/s的速度行驶，突然刹车，刹车加速度为-5m/s²。
求汽车从开始刹车到完全停止所需的时间。
15. 一个质量为10kg的物体，从高度为5m的平台上自由落下，忽略空气阻力，求物体落地时的速度。
五、实验题16. 设计一个实验来验证牛顿第二定律。
17. 描述如何使用弹簧秤测量物体的重力。
六、论述题18. 讨论力的合成与分解在实际生活中的应用，并给出两个不同的例子。
工程力学__第3章力系的平衡习题解
sin ( ) 3 cos )
即 3 sin cos sin cos cos sin
习题 3－4 图
即 2 tan tan
1
O
2
注：在学完本书第 3 章后，可用下法求解： Fx 0 ， FRAG sin 0
Fy 0 ， FRBG cos 0
M A (F ) 0
，G
l s3in(
)
FRB
l
解：（a），CD 为二力杆； 图（c）— 力偶系
ΣMi = 0
FRA FRC M 2 M
2
d
d
2
习题 3－11 图
— 11 —
（b）AB 为二力杆
图（d）：ΣMi = 0， FRC FD M ，
d
FRA FD M d
FD
D
A
45
D BM
M
FRA
FRC
C
FRC
FRA
A
FD' B
D
(d)
(e)
(c)
F
q
5 (6 2l) 340l 0
3
l = 1m 即 lmax = 1m
C 6 l (a)
D FR D
l
3－18 木支架结构的尺寸如图所示，各杆在 A、D、E、
F 处均以螺栓连接，C、D 处用铰链与地面连接，在水平杆 AB
的 B 端挂一重物，其重 W = 5kN。若不计各杆的重，试求 C、
G、A、E 各点的约束力。
3－10 试求图示结构中杆 1、2、3 所受的力。 解：杆 3 为二力杆 图（a）：
ΣMi = 0
F3 dM 0 M
F3 d
F = F3 （压） 图（b）：
现代计算力学智慧树知到答案章节测试2023年北京理工大学
第一章测试1.根据计算力学定义可知，力学是基础，现代计算机技术是工具。
（）A:错B:对答案:B2.传染病传播模型之-SEIR模型具有局限性，是因为它受到（）等多种因素的影响。
A:患者自身抵抗B:再感染率C:信息传播的网络D:病毒自身的进化答案:BCD3.针对我国目前国产自主计算力学软件发展现状，我们所提出的对策是（）。
A:软件开发模式以研究为主B:加强力学软件发展趋势与规划的战略研讨C:软件开发指导思想的转变D:软件推广模式的转变答案:BCD第二章测试1.Euler描述适合描述变形小的介质。
（）A:对B:错答案:A2.物质导数是Euler描述。
（）A:错B:对答案:A3.下面属于Euler描述的流体模型是（）。
A:移动控制体B:移动微元体C:固定控制体D:固定微元体答案:CD4.静止的流体依然有黏性力。
（）A:对B:错答案:B5.一阶变系数矢量偏微方程可以通过特征分解解耦成m个独立的标量偏微分方程。
（）A:对B:错答案:B6.下面属于抛物型方程的是（）。
A:一维单波方程B:拉普拉斯方程C:一维热传导方程D:泊松方程答案:C7.以下是欧拉方程的模型方程的是（）。
A:扩散方程B:单波方程C:有黏Burgers方程D:无黏Burgers方程答案:BD第三章测试1.拟合不要求得到的函数穿过已知的数据点。
（）A:错B:对答案:B2.拉格朗日多项式插值的计算量大于牛顿多项式插值的计算量。
（）A:错B:对答案:B3.当新增一个插值点时，拉格朗日插值需要重新计算全部的基函数，而牛顿插值只需计算均差表中新的一行的值即可。
（）A:错B:对答案:B4.给定4个离散的数据点，且任意两个不同点上的值都互不相同，则构造的插值多项式的精度最高是4阶。
（）A:对B:错答案:B5.分片线性插值多项式中，某一点上的斜率可以通过向前差分获得，也可以通过向后差分获得，优选哪一个?（）A:其他都可以B:斜率绝对值大的C:斜率绝对值小的D:斜率绝对值为零的答案:C第四章测试1.差分方程是修正方程的近似。
工程力学第3章习题解答
3-3在图示刚架中，已知kN/m 3=m q ，26=F kN ，m kN 10⋅=M ，不计刚架自重。
求固定端A 处的约束力。
m kN 12kN 60⋅===A Ay Ax M F F ，，3-4杆AB 及其两端滚子的整体重心在G 点，滚子搁置在倾斜的光滑刚性平面上，如图所示。
对于给定的θ角，试求平衡时的β角。
B解：解法一：AB 为三力汇交平衡，如图所示ΔAOG 中 βs i n l AO =， θ-︒=∠90AOG ，β-︒=∠90OAG ，βθ+=∠AGO由正弦定理：)90sin(3)sin(sin θβθβ-︒=+ll ，)cos 31)sin(sin θβθβ=+l 即 βθβθθβs i n c o s c o s s i n c o s s i n 3+=即 θβt a n t a n 2=)t a n21a r c t a n (θβ= 解法二：：0=∑x F ，0sin R =-θG F A （1） 0=∑y F ，0cos R =-θG F B（2） 0)(=∑F A M ，0sin )sin(3R =++-ββθl F l G B（3）解（1）、（2）、（3）联立，得 )t a n21a r c t a n (θβ=3-5 由AC 和CD 构成的组合梁通过铰链C 连接。
支承和受力如图所示。
已知均布载荷强度kN/m 10=q ，力偶矩m kN 40⋅=M ，不计梁重。
kN 15kN 5kN 40kN 15===-=D C B A F F F F ；；；解：取CD 段为研究对象，受力如图所示。
0)(=∑F CM，024=--q M F D ；kN 15=D F取图整体为研究对象，受力如图所示。
0)(=∑F AM ，01682=--+q M F F D B；kN 40=B F0=∑yF ，04=+-+D BAyF q F F ；kN 15-=Ay F0=∑x F ，0=AxF3-6如图所示，组合梁由AC 和DC 两段铰接构成，起重机放在梁上。
弹性力学第三版 第三章例题
(7 )
(8)
q0 q0 l q0l q0 h 3, F 由此可解得： D 10lh 3h 4h 80l
h 2 h 2
( x ) x l ydy 0
Al 2 Bh2 D 0
4、应力分量为：
2 q0 3 3 2 2 2 x 3 xy(2 y x l h ) lh 10 q y 0 3 x(3h 2 y 4 y 3 h 3 ) 2lh q0 h2 2 2 2 2 2 xy (4 y h )(3x y l 3 4lh 20
1 ( x y ) E 1 y ( y x ) E 2(1 ) xy xy E
x
v u x y
f 2 ( x) f1 ( x) 3F y 2 x y 4 Eb
练习
36
x 0, y
4.分析：
2qy 3x qx 3x (1 ) gy , xy (2 ) h h h h
f （1） (x)中的 Cx不能略去，因为 Cx 对剪应力有影响。 （2）在上端部，首先应使应力分量精确满足边界条件，如不 能，则可运用圣维南原理放松满足。本题 ( y ) y0 0 能精确满 足，因此， y 在此处是精确解，而 xy 在上端部是近似解。 （3）若设 xy f (x)，则导出的应力函数 和应力分量为：
q0 x l
q0
h l
q0l 6
O l
q0l 3
x
y 解：1、由满足相容方程确定系数A与B的关系：
4 4 4 0, 120Bxy, 36Axy 4 4 2 2 x y x y
72Axy 120Bxy 0
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一简述题
1如图所示一三角形钢板，两个结点固定，对第三个结点施以单位水平位移，测出所施加的力，从而得出相应的刚度系数。
其他点依此类推，这样测得的刚度系数所组成的刚度矩阵，是否与按照常规三角形单元刚度矩阵计算公式所得结果一样？用这样实测所得的刚度矩阵能否进行有限元分析？为什么？
2以位移为基本未知量的有限元法其解具有下限性质，试证明之。
3 请分别阐述单元刚度矩阵和整体刚度矩阵中任一元素的物理意义。
4 简述虚功原理，且使用虚功原理导出外荷载与节点荷载的等效关系式。
5试述弹性力学中按位移求解与有限单元法中按位移求解之间的异同点。
6 如果三节点三角形单元绕其中某一个节点作小的刚体转动，其转角为 ，证明单元内所有的应力均为零。
7二维单元在x,y坐标内平面平移到不同位置，单元刚度矩阵相同吗？在平面内旋转时又怎样？试证明之。
二分析计算题
1 判断有限元网格离散合理性
a) 对图1(a)所示的有限元网格，评论网格的优劣性，指出模型中的错误，并加以改正。
b) 评论图1(b)的网格划分合理吗?为什么?请加以改正。
图1
2 如图2所示，平面三角形构件以x-y坐标系表示的刚度矩阵方程如下：
图3
⎥⎥⎥⎥
⎥⎦
⎤
⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢
⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢
⎢
⎣⎡------221122
114
5.25
.25
.25
.25.25.25.45.25.20.55.283.15.283.15.21010y x y x y x y x P P P P v u v u
试建立以1x u ,1y u ,,
2x u (与图中,
2x P 同向的位移)及1x P ,1y P ,,
2x P 来表示的刚度矩阵方程。
3 某平面结构采用四节点矩形单元和三节点三角形单元建立有限元计算模型，其如图3所示。
试求结点2的等效荷载列阵{}2R 。
4 试求如图4所示的有限元网格的整体刚度矩阵，假设每个节点的自由度数为1，且设e K 表示第e 个单元的单元刚度矩阵（注意：结果应该用e
ij
k 表示）。
图2
图5
图6
5. 图5中两个三角形单元组成平行四边形，已知单元①按局部编码i ，j ，m 的单元刚度矩阵K ①和应力矩阵S ①是
K ①
=⎪⎪⎪⎪
⎪⎪
⎪⎪⎭⎫
⎝
⎛-----------5.53
5
.95.135
.1335.795
.134612616
6
26608称
对
S ①=⎪⎪⎪⎭
⎫ ⎝
⎛- 1.50.5
-1.5
-5
.10
2103040
030300
－－－ 按图5示单元②的局部编码写出K ②，S ②。
5 如图6所示8结点矩形单元(每边中点为结点), 3点为坐标原点，a=b=2，单元厚为t 。
○
1 求该单元的位移函数和形函数和并检验其是否满足收敛性条件。
○2 求在2-6-3边作用均布水平荷载q 时的等效结点荷载。
图4。