信号与系统—第七章习题讲解 PPT
合集下载
信号与系统第七章 系统函数

=
K
N1N 2 " N m e j(ψ1+ψ2 +"ψm ) M1 M2 " Mn ej(θ1+θ2 +"θn )
H (jω)
=
K
N1N2 " Nm M1M2 "Mn
ϕ (ω) = (ψ1 +ψ2 + "ψm ) − (θ1 +θ 2 + "θ n )
当ω 沿虚轴移动时,各复数因子(矢量)的模和辐角都
①H(z)在单位圆内的极点所对应的响应序列为衰减的。 即当k→∞时,响应均趋于0。 ②H(z)在单位圆上的一阶极点所对应的响应函数为稳 态响应。
③H(z)在单位圆上的高阶极点或单位圆外的极点,其 所对应的响应序列都是递增的。即当k→∞时,响应 均趋于∞。
第 19 页
三、由系统函数零、极点分布 决定频响特性
v1(t ) −
R
+
C v2(t )
−
写出网络转移函数表达式
H (s)
=
V2 (s) V1 (s )
=
1 RC
⎜⎛ ⋅⎜ ⎜⎜⎝
s
1 +1
RC
⎟⎞ ⎟ ⎟⎟⎠
=
1 RC
1 M1 ejθ1
= V2 ejϕ (ω) V1
M1
θ1
−1 RC
jω
O
σ
第 28 页
频响特性
jω
M1
V2 1 V1 1
2 θ1
−1 RC
O
σ
O1 RC
( ) H
jω
=
1 RC
1 M1 e jθ1
= V2 ejϕ (ω) V1
信号与系统第七章课后答案
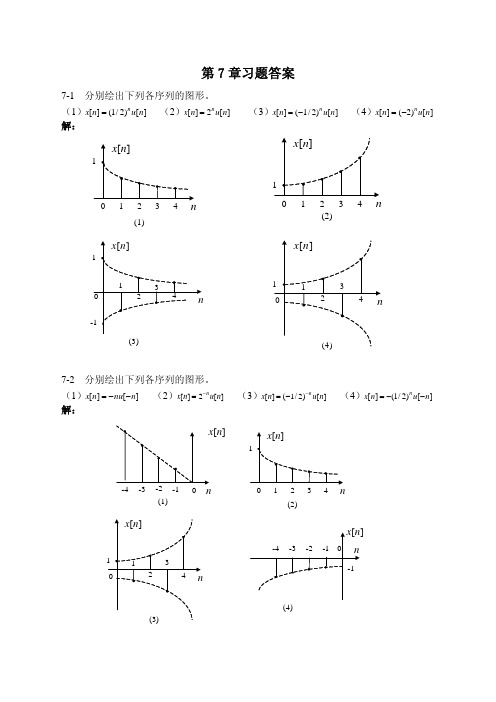
第 7 章习题答案
7-1 分别绘出下列各序列的图形。 (2)x[n] 2n u[n] (3)x[n] (1/ 2)n u[n] (4)x[n] (2) n u[ n] (1)x[n] (1/ 2)n u[n] 解:
x[ n ]
1
x[n]
1
0 1 2 (1) 3 4
n
0
1
2 3 (2)
x[n]
1
x[n]
-4
-3
-2 (1)
-1
0
n
0
1
2 (2)
3
4
n
x[n]
-4 1 0 1 2 3 4 -3 -2 -1 0
x[n] n
-1
n
(4)
(3)
7-3
分别绘出下列各序列的图形。 (2) x[n] cos
n 10 5
n (1) x[n] sin 5
1 z2 X (z) ( 1 1 2 z 1 )( 1 2 z 1 ) ( z 1 2 )( z 2 ) X (z) z 1 4 z ( z 1 2 )( z 2 ) 3( z 1 2 ) 3( z 2 )
X (z)
z 4z 3( z 1 2 ) 3 ( z 2 )
N
)
由于 x[n] 、 h[n] 均为因果序列,因此 y[n] 亦为因果序列,根据移位性质可求得
y [ n ] Z 1 [Y ( z )]
1 1 (1 a n 1 ) u [ n ] (1 a n 1 N ) u [ n N ] 1 a 1 a
7-24 计算下列序列的傅里叶变换。
(2)
7-1 分别绘出下列各序列的图形。 (2)x[n] 2n u[n] (3)x[n] (1/ 2)n u[n] (4)x[n] (2) n u[ n] (1)x[n] (1/ 2)n u[n] 解:
x[ n ]
1
x[n]
1
0 1 2 (1) 3 4
n
0
1
2 3 (2)
x[n]
1
x[n]
-4
-3
-2 (1)
-1
0
n
0
1
2 (2)
3
4
n
x[n]
-4 1 0 1 2 3 4 -3 -2 -1 0
x[n] n
-1
n
(4)
(3)
7-3
分别绘出下列各序列的图形。 (2) x[n] cos
n 10 5
n (1) x[n] sin 5
1 z2 X (z) ( 1 1 2 z 1 )( 1 2 z 1 ) ( z 1 2 )( z 2 ) X (z) z 1 4 z ( z 1 2 )( z 2 ) 3( z 1 2 ) 3( z 2 )
X (z)
z 4z 3( z 1 2 ) 3 ( z 2 )
N
)
由于 x[n] 、 h[n] 均为因果序列,因此 y[n] 亦为因果序列,根据移位性质可求得
y [ n ] Z 1 [Y ( z )]
1 1 (1 a n 1 ) u [ n ] (1 a n 1 N ) u [ n N ] 1 a 1 a
7-24 计算下列序列的傅里叶变换。
(2)
信号与系统第七、八章课后习题

N k
当
2
2.线性时不变离散时间系统 ①线性 线性=叠加性+均匀性(齐次性)
c1 x1 (n) c2 x2 (n)
系统
c1 y1 (n) c2 y2 (n)
②时不变
x(n N )
系统
y (n N )
x ( n)
1 E
y ( n)
y ( n)
a
ay(n)
单位延时
1 T D z ( )
已知激励初始状态y(-1)=0,y(-2)=1/2, fk=2ku(k),求系统 的零输入响应,零状态响应和全响应. 解: (1) 零输入响应 根据定义,零输入响应满足方程:
yx (k ) 3 yx (k 1) 2 yx (k 2) 0
其初始状态
1 yx (1) y (1) 0, yx 2 y 2 2
x(n)(n n0 ) x(n0 )(n n0 )
n
x(n)(n) x(0) (n) x(0)
n
n
x(n)(n n ) x(n ) (n n ) x(n )
0 0 n 0 0
x ( n)
k k 零状态响应
2 1 k k k (1) (2) (2) , k 0 3 3
离散时间系统的单位样值响应
(n)
零状态系统
h( n)
单位样值响应h(n)是系统在零状态时,由单位样值信 号作用之下产生的响应。因此,它是一个零状态响应。
同样,单位样值信号δ(n)仅在n=0时刻等于1,其它时 刻δ(n)=0,因此系统在n>0时的响应是零输入响应。
信号与系统—第七章习题讲解PPT课件

(1)x(n),h(n),见题图731(a) (2)x(n),h(n),见题图731(b)
(3)x(n)anu(n) 0<a<1;h(n)nu(n) 0<<1;a (4)x(n)u(n);h(n)(n2)(n3)
解 :(1)由 图7-3(1 a) 可 知 : x(n) (n) 2 (n 1) (n 2) h(n) (n) (n 1) (n 2) y(n) x(n)* h(n) [ (n) 2 (n 1) (n 2)] *[ (n) (n 1) (n 2)] (n) (n 1) (n 2) 2 (n 1) 2 (n 2) (n 3) (n 2) 2 (n 3) (n 4) (n) 3 (n 1) 4 (n 2) 3 (n 3) (n 4)
解 : (3) (n 4);非 因 果 , 稳 定 (5) u(3 n); 非 因 果 , 不 稳 定 (7) 3n u ( n);非 因 果 , 稳 定 (9) 0.5n u (n); 因 果 , 稳 定
7 30对 应 于 线 性 时 不 变 系 统 : (1)已 知 激 励 为 单 位 阶 跃 信 号 之 零 状 态 响 应 ( 阶 跃 响 应 ) 是 g (n),试 求 冲 击 响 应 h(n); ( 2 )已 知 冲 激 响 应 h ( n ), 试 求 阶 跃 响 应 g ( n )。
(2)单位阶跃信号u(n)可表示为:u(n)(nk) k0
由系统的线性时不变特性可得对(nk)的响应为
h(nk)。故阶跃响应g(n)h(nk)。 k0
731 以 下 各 序 列 中 , x(n)是 系 统 的 激 励 函 数 , h(n)是 线 性 时 不 变 系 统 的 单 位 样 值 响 应 。 分 别 求 出 各 y(n),画 出 y(n) 图 形 ( 用 卷 积 方 法 ) 。
信号与系统第七章(2)系统稳定性

Y (z) 1 2z1 3z2 z2 2z 3
H(z)
F(z)
1 z1 Kz2
z2 z K
其极点
1 1 4K
p1,2
2
பைடு நூலகம்
当 1 4K 0,即 为K实极1点,为使极点在单位圆
4
内,必须同时满足不等式
1 1 4K 1, 1 1 4K 1,
复习
连续系统稳定性的判断方法: ——罗斯-霍尔维兹判断准则 1、系统稳定的充分必要条件是什么? 2、什么样的多项式是霍尔维兹多项式? 3、怎样判断霍尔维兹多项式? 4、罗斯阵列的形式? 5、罗斯准则的要点是什么?
【例1】 已知三个线性连续系统的系统函数 分别为:
H1(s)
s4
s2 2s3 3s2
容易推出其根均在单位圆内的条件是
A(1) 0 A(1) 0
a2 a0
例7.2-5 设图示的离散因果系统,当K满足什么条
件时,系统是稳定的?
Fz
X z
1
z 1
Y z
2
k
3
z 1
Y (z) 1 2z1 3z2 z2 2z 3
11
定。 根据以上条件,当K<0时系统为稳定系统。
四、离散(因果)系统的稳定性准则----朱里准则
为要判别离散系统的稳定性,就需要判别系统函数
H(z) B(z) A( z )
的特征方程 A(z)所 0有根的绝对值是否都小于1。 朱里提出了一种列表的检验方法,称为朱里准则。
设 H (z的) 特征多项式为
信号与系统PPT全套课件

T T
T
f (t ) dt
f (t ) dt
2
2
(1.1-1)
1 P lim T 2T
T
T
( 1.1-2 )
上两式中,被积函数都是f ( t )的绝对值平方,所以信号能量 E 和信号功率P 都是非负实数。 若信号f ( t )的能量0 < E < , 此时P = 0,则称此信号 为能量有限信号,简称能量信号(energy signal)。 若信号f ( t )的功率0 < P < , 此时E = ,则称此信 号为功率有限信号,简称功率信号(power signal)。 信号f ( t )可以是一个既非功率信号,又非能量信号, 如单位斜坡信号就是一个例子。但一个信号不可能同时既是 功率信号,又是能量信号。
1.3 系统的数学模型及其分类
1.3.1 系统的概念 什么是系统( system )?广义地说,系统是由若干相互作用 和相互依赖的事物组合而成的具有特定功能的整体。例如, 通信系统、自动控制系统、计算机网络系统、电力系统、水 利灌溉系统等。通常将施加于系统的作用称为系统的输入激 励;而将要求系统完成的功能称为系统的输出响应。 1.3.2 系统的数学模型 分析一个实际系统,首先要对实际系统建立数学模型,在数 学模型的基础上,再根据系统的初始状态和输入激励,运用 数学方法求其解答,最后又回到实际系统,对结果作出物理 解释,并赋予物理意义。所谓系统的模型是指系统物理特性 的抽象,以数学表达式或具有理想特性的符号图形来表征系 统特性。
2.连续信号和离散信号 按照函数时间取值的连续性划分,确定信号可分为连续时 间信号和离散时间信号,简称连续信号和离散信号。 连续信号( continuous signal)是指在所讨论的时间内,对 任意时刻值除若干个不连续点外都有定义的信号,通常用f ( t ) 表示。 离散信号(discrete signal)是指只在某些不连续规定的时刻 有定义,而在其它时刻没有定义的信号。通常用 f(tk) 或 f(kT) [简写 f(k )] 表示,如图1.1-2所示。图中信号 f (tk) 只在t k = -2, -1, 0, 1, 2, 3,…等离散时刻才给出函数值。
郑君里信号与系统课件

2 an T1
T1 2 T 1 2
f ( t )dt
余弦分量 系数 正弦分量 系数
T1 2 T 1 2
f ( t ) cos(n1t )dt
2 bn T1
T1 2 T 1 2
f ( t ) sin( n1t )dt
注意!
傅立叶级数与傅立叶系数的联系与区别
指数形式傅立叶级数的傅里叶系数
尺度变换、初值、终值
卷积特性 拉氏逆变换
部分分式展开法(求系数)
系统函数H(s)
定义(两种定义方式)
求解(依据两种定义方式)
第四章 拉普拉斯变换、 连续时间系统的s域分析
收敛域:实际上就是拉氏变换存在的条件;
σ t
lim f (t ) e
t
0
σ σ0
三.一些常用函数的拉氏变换
t n st n n1 st e t e dt s 0 s 0
n n1 st t e dt s 0 n n 1 n 所以 L t L t s n1
Lt t e d t
st 0
1 1 st 1 e s2 s s 0 n2 2 2 1 2 2 L t Lt 2 3 s s s s n3 3 2 3 2 6 3 Lt Lt 3 4 s s s s
1 sin( t ) (e jt e jt ) 2j 1 cos(t ) (e jt e jt ) 2
推出 公式
第一章 绪论
关于冲激信号
(at )
1 (t ) a
尺度变换特性
(t ) f (t ) f (0) (t )
T1 2 T 1 2
f ( t )dt
余弦分量 系数 正弦分量 系数
T1 2 T 1 2
f ( t ) cos(n1t )dt
2 bn T1
T1 2 T 1 2
f ( t ) sin( n1t )dt
注意!
傅立叶级数与傅立叶系数的联系与区别
指数形式傅立叶级数的傅里叶系数
尺度变换、初值、终值
卷积特性 拉氏逆变换
部分分式展开法(求系数)
系统函数H(s)
定义(两种定义方式)
求解(依据两种定义方式)
第四章 拉普拉斯变换、 连续时间系统的s域分析
收敛域:实际上就是拉氏变换存在的条件;
σ t
lim f (t ) e
t
0
σ σ0
三.一些常用函数的拉氏变换
t n st n n1 st e t e dt s 0 s 0
n n1 st t e dt s 0 n n 1 n 所以 L t L t s n1
Lt t e d t
st 0
1 1 st 1 e s2 s s 0 n2 2 2 1 2 2 L t Lt 2 3 s s s s n3 3 2 3 2 6 3 Lt Lt 3 4 s s s s
1 sin( t ) (e jt e jt ) 2j 1 cos(t ) (e jt e jt ) 2
推出 公式
第一章 绪论
关于冲激信号
(at )
1 (t ) a
尺度变换特性
(t ) f (t ) f (0) (t )
信号与系统第7章(陈后金)3

一、系统函数
2. H(z)与h[k]的关系
[k]
h[k] yzs [k] = [k]*h[k] h[k ]
Z { yzs [k ]} Z {h[k ]} H ( z) Z {h[k ]} Z { [k ]} 1
H ( z ) Z {h[k ]}
h[k ] Z [H ( z)]
H(z)
2.5 1.25 z 1 0.5 z 2 H ( z) 1 0.25 z 2
二、系统函数的零极点分布
系统函数可以表达为零极点增益形式,即
( z r1 )( z r2 )( z rm ) N ( z) H ( z) K D( z ) ( z z1 )( z z2 )( z zn )
-
-
-
W(z)
an-1 an
z域框图
二、离散系统的模拟框图
2. 级联型结构
将系统函数的N(z) 和D(z)分解为一阶或二阶实系
数因子形式,将它们组成一阶和二阶子系统,即
H(z) = H1(z) H2(z) ….. Hn(z)
画出每个子系统直接型模拟流图,然后将各 子系统级联。
X(z)
H1(z)
H2(z)
D(z)=0的根是H(z)的极点,在z平面用表示。 N(z)=0的根是H(z)的零点,在z平面用 表示。 例如
(2) 1 Im (z) j 0. 5j (3) 0. 5 0 0. 5j j Re (z) 0. 5 1
H (z)
z3(z 1 j)(z 1 j)
(z 0.5)(z 1)2(z 0.5 j0.5)(z 0.5 j0.5)
w[k ] a j w[k j ] x[k ]
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解 : (1) 特 征 方 程 2+ 3 + 2= 0 1 1, 2 2
齐 次 解 : y (n ) C1(1)n C 2 (2)n
由 y (1)
2, y(2) 1
C
1
C
1
1 4
1C 2 C2
2
1
2
C C
1 2
4
1
2
y (n) 4(1)n 12(2)n
解:(2)特征方程2+2+1=01 2 1
(1)x(n),h(n),见题图731(a) (2)x(n),h(n),见题图731(b)
(3)x(n)anu(n) 0<a<1;h(n)nu(n) 0<<1;a (4)x(n)u(n);h(n)(n2)(n3)
解 :(1)由 图7-3(1 a) 可 知 : x(n) (n) 2 (n 1) (n 2) h(n) (n) (n 1) (n 2) y(n) x(n)* h(n) [ (n) 2 (n 1) (n 2)] *[ (n) (n 1) (n 2)] (n) (n 1) (n 2) 2 (n 1) 2 (n 2) (n 3) (n 2) 2 (n 3) (n 4) (n) 3 (n 1) 4 (n 2) 3 (n 3) (n 4)
1 3
y (1)
1
4 9
30
31 32
32
........
y(n)
30
31
32 3n
3n
3 3n点累了,稍作休息
大家有疑问的,可以询问和交流
7-12 解 差 分 方 程 。 (1) y ( n ) 3 y ( n 1) 2 y ( n 2 ) 0 , y ( 1) 2 , y ( 2 ) 1 (2)y (n) 2 y (n 1) y (n 2) 0, y(0) y(1) 1
解 : (3) (n 4);非 因 果 , 稳 定 (5) u(3 n); 非 因 果 , 不 稳 定 (7) 3n u ( n);非 因 果 , 稳 定 (9) 0.5n u (n); 因 果 , 稳 定
7 30对 应 于 线 性 时 不 变 系 统 : (1)已 知 激 励 为 单 位 阶 跃 信 号 之 零 状 态 响 应 ( 阶 跃 响 应 ) 是 g (n),试 求 冲 击 响 应 h(n); ( 2 )已 知 冲 激 响 应 h ( n ), 试 求 阶 跃 响 应 g ( n )。
解 : ( 1 ) 单 位 激 励 信 号 ( n) 可 表 示 为 ( n) u ( n ) u ( n 1) 系 统 对 u ( n )的 响 应 是 g ( n ), 又 由 系 统 的 线 性 时 不 变 特 性 可 得 对 u ( n 1)的 响 应 是 g ( n 1), 故 系 统 的 冲 激 响 应 为 : (h n) g ( n ) g ( n 1)
试确定其周期。
(1) x ( n )
A cos( 3
n
);( 2 ) x ( n )
j(n )
e8
78
解 : 如 果 对 于 整 数 N , 有 x ( n N ) x ( n ), 则 x ( n )是 周 期 序 列 。
由 于 x(n N ) A cos[ 3 (n N ) ] A cos[ 3 n 3 N ]
3
3
y ( 2 ) x ( 2 ) 1 y (1) ( 1 ) 2
3
3
........
y(n) (1 )nu(n) 3nu(n) 3
(2)x(n) u(n)
y (0 )
x(0)
1 3
y ( 1)
1
30 30
y (1)
x (1)
1 3
y (0 )
1
1 3
30 31 31
y(2)
x(2)
7
8
77 8
如 果 3 N 是 2 的 整 数 倍 , 则 由 余 弦 函 数 的 性 质 有 7
x ( n N ) x ( n ), 显 然 , 满 足 此 条 件 的 最 小 整 数 值
为 N 14, 故 x (n )为 周 期 序 列 , 其 周 期 为 14。
j( n )
(2)x(n) e 8
(1)x(n)(n);
(2)x(n)u(n)
解:由图可得系统差分方程为
y(n) x(n) 1 y(n 1) 3
(1) x ( n ) ( n ) 根 据 系 统 差 分 方 程 及 边 界 条 件 y(1) 0进 行 迭 代 求 解 :
y(0) x(0) 1 y(1) 1 3
y (1) x (1) 1 y (0 ) 1
齐次解:y(n) (C1nC2)(1)n
由y(0)
y(1)
1C(2C11 C2)
1CC12
2 1
y(n) (2n1)(1)n
7 2 8以 下 各 序 列 是 系 统 的 单 位 样 值 响 应 h ( n ), 试 分 别 讨论各系统的因果性与稳定性。 (3) (n 4); (5) u(3 n); (7) 3n u ( n); (9) 0.5n u (n)
(2)单位阶跃信号u(n)可表示为:u(n)(nk) k0
由系统的线性时不变特性可得对(nk)的响应为
h(nk)。故阶跃响应g(n)h(nk)。 k0
731 以 下 各 序 列 中 , x(n)是 系 统 的 激 励 函 数 , h(n)是 线 性 时 不 变 系 统 的 单 位 样 值 响 应 。 分 别 求 出 各 y(n),画 出 y(n) 图 形 ( 用 卷 积 方 法 ) 。
解:由于x(n
N)
e
j[(
1(nN 8
)
]
j( n ) j N
e 8 .e 8
jN
x(n)e 8
若x(n N)
x(n),则要求e
j
N 8
1,即 N
2k,为无理数,
8
故不存在满足此式的整数N, k,所以x(n)不是周期序列。
7-5列出题图7-5所示系统的差分方程,已知边界条件 y(1)0。分别求以下输入序列时的输出y(n),并绘出其 图形(用逐次迭代方法求)
第七章习题讲解
7- 2分 别 给 出 以 下 各 序 列 的 图 形 。 (1) x ( n ) n u ( n ) (2)x(n) 2nu(n)
(3)x(n) ( 1 )n u(n) 2 (1)
(2)
(3)
7 4判 断 以 下 各 序 列 是 否 周 期 性 的 , 如 果 是 周 期 性 的 ,
