空间几何体的三视图、表面积、体积专题练习
高三高考数学复习练习82空间几何体的表面积与体积

821.一个球的表面积是16π,那么这个球的体积为( )A.163π B.323π C .16π D .24π【解析】 设球的半径为R ,因为表面积是16π,所以4πR 2=16π,解得R =2,所以体积为43πR 3=32π3. 【答案】 B2.某几何体的三视图如图所示,则其表面积为( )A .πB .2πC .3πD .4π【解析】 由三视图可知,该几何体为半径为r =1的半球体,表面积为底面圆面积加上半球面的面积,所以S =πr 2+12×4πr 2=π×12+12×4π×12=3π.故选C. 【答案】 C3.在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2.将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.2π3B.4π3C.5π3 D .2π【解析】 过点C 作CE 垂直AD 所在直线于点E ,梯形ABCD 绕AD 所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径,线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径,ED 为高的圆锥,如图所示,该几何体的体积为V =V圆柱-V 圆锥=π·AB 2·BC -13·π·CE 2·DE =π×12×2-13π×12×1=5π3,故选C. 【答案】 C4.一个四面体的三视图如图所示,则该四面体的表面积是( )A .1+ 3B .2+ 3C .1+2 2D .2 2 【解析】 由空间几何体的三视图可得该空间几何体的直观图,如图所示,∴该四面体的表面积为S 表=2×12×2×1+2×34×(2)2=2+3,故选B. 【答案】 B5.(2018·太原一模)某几何体的三视图如图所示,则该几何体的表面积为( )A .6π+1B.(24+2)π4+1C.(23+2)π4+12D.(23+2)π4+1 【解析】 由几何体的三视图知,该几何体为一个组合体,其中下部是底面直径为2,高为2的圆柱,上部是底面直径为2,高为1的圆锥的四分之一,所以该几何体的表面积为4π+π+3π4+2π4+1=(23+2)π4+1,故选D. 【答案】 D6.甲几何体(上)与乙几何体(下)的组合体的三视图如图所示,甲、乙几何体的体积分别为V 1,V 2,则V 1∶V 2等于( )A .1∶4B .1∶3C .2∶3D .1∶π【解析】 由三视图知,甲几何体是半径为1的球,乙几何体是底面半径为2,高为3的圆锥,所以球的体积V 1=43π,V 2=13π×22×3=4π,所以V 1∶V 2=1∶3.故选B. 【答案】 B7.(2017·全国Ⅲ卷)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A .πB.3π4C.π2D.π4【解析】 设圆柱的底面半径为r ,球的半径为R ,且R =1,由圆柱两个底面的圆周在同一个球的球面上可知,r ,R 及圆柱的高的一半构成直角三角形.∴r = 12-⎝⎛⎭⎫122=32.∴圆柱的体积为V =πr 2h =34π×1=3π4. 故选B.【答案】 B8.(2017·襄阳调研)如图是一个空间几何体的三视图,则该几何体的表面积为________.【解析】 由三视图可知,该几何体是一个正四棱柱挖掉一个半球所得的几何体,其中半球的底面就是正四棱柱上底面的内切圆,正四棱柱的底面边长为4,高为2,半球所在球的半径为2.所以该几何体的表面由正四棱柱的表面与半球的表面积之和减去半球的底面构成,故其表面积为(4×4×2+2×4×4)+12×(4π×22)-π×22=64+4π. 【答案】 64+4π9.(2018·乌鲁木齐二诊)已知四面体ABCD 满足AB =CD =6,AC =AD =BC =BD =2,则四面体ABCD 的外接球的表面积是________.【解析】 (图略)在四面体ABCD 中,取线段CD 的中点为E ,连接AE ,BE .∵AC =AD =BC =BD =2,∴AE ⊥CD ,BE ⊥C D.在Rt △AED 中,CD =6,∴AE =102.同理BE =102.取AB 的中点为F ,连接EF .由AE =BE ,得EF ⊥A B.在Rt △EF A 中,∵AF =12AB =62,AE =102,∴EF =1.取EF 的中点为O ,连接OA ,则OF =12.在Rt △OF A 中,OA =72.∵OA =OB =OC =OD ,∴该四面体的外接球的半径是72,∴外接球的表面积是7π. 【答案】 7π10.(2018·贵州适应性考试)已知球O 的表面积是36π,A ,B 是球面上的两点,∠AOB =60°,C 是球面上的动点,则四面体OABC 体积V 的最大值为________.【解析】 设球的半径为R ,由4πR 2=36π,得R =3.显然在四面体OABC 中,△OAB 的面积为定值,S △OAB =12×R ×32R =34R 2=934.要使三棱锥的体积最大,只需球上的点到平面OAB 的距离最大,显然,到平面OAB 距离的最大值为球的半径,所以四面体OABC 的体积的最大值V =13×934×R =934. 【答案】 93411.(2016·全国丙卷)如图,四棱锥P -ABCD 中,P A ⊥底面ABCD ,AD ∥BC ,AB =AD =AC =3,P A =BC =4,M 为线段AD 上一点,AM =2MD ,N 为PC 的中点.(1)证明:MN ∥平面P AB ;(2)求四面体N -BCM 的体积.【解析】 (1)证明 由已知得AM =23AD =2. 如图,取BP 的中点T ,连接AT ,TN ,由N 为PC 中点知TN ∥BC ,TN =12BC =2. 又AD ∥BC ,故TN 綊AM ,所以四边形AMNT 为平行四边形,于是MN ∥AT .因为AT ⊂平面P AB ,MN ⊄平面P AB ,所以MN ∥平面P AB .(2)因为P A ⊥平面ABCD ,N 为PC 的中点,所以N 到平面ABCD 的距离为12P A. 取BC 的中点E ,连接AE .由AB =AC =3得AE ⊥BC ,AE =AB 2-BE 2= 5.由AM ∥BC 得M 到BC 的距离为5,故S △BCM =12×4×5=2 5. 所以四面体N -BCM 的体积V N -BCM =13×S △BCM ×P A 2=453. 12.如图所示,在空间几何体ADE -BCF 中,四边形ABCD 是梯形,四边形CDEF 是矩形,且平面ABCD ⊥平面CDEF ,AD ⊥DC ,AB =AD =DE =2,EF =4,M 是线段AE 上的动点.(1)试确定点M 的位置,使AC ∥平面MDF ,并说明理由;(2)在(1)的条件下,平面MDF 将几何体ADE -BCF 分成两部分,求空间几何体M -DEF 与空间几何体ADM -BCF 的体积之比.【解析】(1)当M 是线段AE 的中点时,AC ∥平面MDF .理由如下:连接CE 交DF 于点N ,连接MN .因为M ,N 分别是AE ,CE 的中点,所以MN ∥AC .又因为MN ⊂平面MDF ,AC ⊄平面MDF ,所以AC ∥平面MDF .(2)将几何体ADE -BCF 补成三棱柱ADE -B ′CF ,如图所示,三棱柱ADE -B ′CF 的体积为V =S △ADE ·CD =12×2×2×4=8,则几何体ADE -BCF 的体积V ADE BCF =V ADE B ′CF -V F BB ′C=8-13×⎝⎛⎭⎫12×2×2×2=203. 因为三棱锥M -DEF 的体积V M DEF =13×⎝⎛⎭⎫12×2×4×1=43, 所以V ADM BCF =203-43=163, 所以两几何体的体积之比为43∶163=1∶4.。
专题四 4.1空间几何体的三视图、表面积与体积题型及解法汇总(教师版)
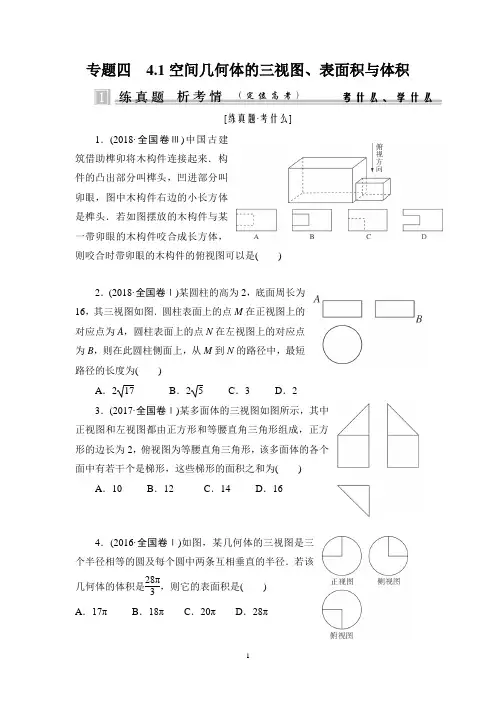
专题四 4.1空间几何体的三视图、表面积与体积[练真题·考什么]1.(2018·全国卷Ⅲ)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )2.(2018·全国卷Ⅰ)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为( )A .217B .25C .3D .23.(2017·全国卷Ⅰ)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )A .10B .12C .14D .164.(2016·全国卷Ⅰ)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3,则它的表面积是( ) A .17π B .18π C .20π D .28π5.(2017·全国卷Ⅱ)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )A .90πB .63πC .42πD .36π6.(2017·全国卷Ⅲ)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A .πB .3π4 C.π2 D .π4[析命题·学什么]●考点一 空间几何体的三视图【例1】 (1)(2018·兰州模拟)如图所示,四面体ABCD 的四个顶点是长方体的四个顶点(长方体是虚拟图形,起辅助作用),则四面体ABCD 的正视图、侧视图、俯视图是(用①②③④⑤⑥代表图形)( )A .①②⑥B .①②③C .④⑤⑥D .③④⑤(2)(2018·西安模拟)把边长为1的正方形ABCD 沿对角线BD 折起,使得平面ABD ⊥平面CBD ,形成的三棱锥C -ABD 的正视图与俯视图如图所示,则侧视图的面积为( )A.12 B .22 C.24 D .14(3)(2018·太原模拟)某几何体的三视图如图所示,则该几何体中最长的棱长为( )A .3 3B .26 C.21 D .2 5规 律 方 法1.由直观图确定三视图,一要根据三视图的含义及画法和摆放规则确认.二要熟悉常见几何体的三视图.2.由三视图还原到直观图的思路 (1)根据俯视图确定几何体的底面.(2)根据正视图或侧视图确定几何体的侧棱与侧面的特征,调整实线和虚线所对应的棱、面的位置.(3)确定几何体的直观图形状. 「对 点 训 练」1.(2018·长沙模拟)如图是一个正方体,A ,B ,C 为三个顶点,D 是棱的中点,则三棱锥A -BCD 的正视图、俯视图是(注:选项中的上图为正视图,下图为俯视图)( )2.某几何体的正视图与俯视图如图所示,若俯视图中的多边形为正六边形,则该几何体的侧视图的面积为( )A.152 B .6+3 C.32+3 3 D .4 33.(2018·北京卷)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为()A.1 B.2 C.3 D.4●考点二空间几何体的表面积与体积【例2】(1)(2018·长沙模拟)某几何体的三视图如图所示,其俯视图中的曲线部分为半圆,则该几何体的体积是()A.192+96π B.256+96πC.192+100πD.256+100π(2)(2018·辽宁五校联合体模拟)一个长方体被一平面截去一部分后,所剩几何体的三视图如图所示,则该几何体的体积为()A.36 B.48 C.64 D.72(3)某三棱锥的三视图如图所示,该三棱锥的表面积是( )A .28+6 5B .60+125C .56+125D .30+6 5规 律 方 法1.求几何体的表面积的方法(1)求表面积问题的基本思路是将立体几何问题转化为平面几何问题,即空间图形平面化,这是解决立体几何的主要出发点.(2)求不规则几何体的表面积时,通常将所给几何体分割成基本的柱、锥、台体,先求这些柱、锥、台体的表面积,再通过求和或作差得几何体的表面积.2.求空间几何体体积的常用方法(1)公式法:直接根据相关的体积公式计算.(2)等积法:根据体积计算公式,通过转换空间几何体的底面和高使得体积计算更容易,或是求出一些体积比等.(3)割补法:把不能直接计算体积的空间几何体进行适当分割或补形,转化为易计算体积的几何体.「对 点 训 练」1.(2018·沈阳模拟)已知一个三棱锥的三视图如图所示,则该三棱锥的体积为( )A.23 B .43 C .2 D .832.(2018·西安八校联考)某几何体的三视图如图所示,则该几何体的体积是( )A.4π3 B .5π3 C .2+2π3 D .4+2π33.(2018·天津卷)已知正方体ABCD -A 1B 1C 1D 1的棱长为1,除面ABCD 外,该正方体其余各面的中心分别为点E ,F ,G ,H ,M (如图),则四棱锥M -EFGH 的体积为________.●考点三 多面体与球的外接、内切的问题【例3】 (1)在封闭的直三棱柱ABC -A 1B 1C 1内有一个体积为V 的球.若AB ⊥BC ,AB =6,BC =8,AA 1=3,则V 的最大值是( )A .4πB .9π2C .6πD .32π3(2)(2018·沈阳模拟)若三棱锥S -ABC 的底面是以AB 为斜边的等腰直角三角形,AB =SA =SB =SC =2,则该三棱锥的外接球的表面积为( )A.16π3 B .8π3 C.43π3D .4π3规律方法“切”“接”问题的处理方法(1)“切”的处理:解决与球有关的内切问题主要是指球内切多面体与旋转体,解答时要先找准切点,通过作截面来解决.如果内切的是多面体,则多通过多面体过球心的对角面来作截面(2)“接”的处理:把一个多面体的几个顶点放在球面上即球的外接问题.解决这类问题的关键是抓住外接的特点,即球心到多面体的顶点的距离等于球的半径. 两种方法:构成正(长)方体,或者构成直角三角形「对点训练」1.若正四棱锥P-ABCD内接于球O,且底面ABCD过球心O,则球O的半径与正四棱锥P-ABCD内切球的半径之比为()A.3+1 B.2 C. 3 D.3-12.(2018·全国卷Ⅲ)设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为93,则三棱锥D-ABC体积的最大值为() A.12 3 B.183C.24 3 D.54 3专题四 4.1空间几何体的三视图、表面积与体积(答案)[练真题·考什么]1.解析:两木构件咬合成长方体时,榫头完全进入卯眼,易知咬合时带卯眼的木构件的俯视图为A.故选A.答案:A2.解析:由圆柱的三视图及已知条件可知点M 与点N 的位置如图1所示,设ME 与FN 为圆柱的两条母线,沿FN 将圆柱的侧面展开,如图2所示,连接MN ,MN 即为从M 到N 的最短路径,由题意知,ME =2,EN =4,∴MN =42+22=2 5.故选B.答案:B3.解析:由多面体的三视图还原直观图如图:该几何体由上方的三棱锥A -BCE 和下方的三棱柱BCE -B 1C 1A 1构成,其中面CC 1A 1A 和面BB 1A 1A 是梯形,则梯形的面积之和为2×(2+4)×22=12.故选B.答案:B4.解析:由三视图可知,该几何体是一个球被截去18后剩下的部分,设球的半径为R ,则该几何体的体积为78×43πR 3,即283π=78×43πR 3,解得R =2.故其表面积为78×4π×22+3×14×π×22=17π.故选A.答案:A5.解析:由三视图可知两个同样的几何体可以拼成一个底面直径为6,高为14的圆柱,所以该几何体的体积V =12×32×π×14=63π.故选B.答案:B6.解析:设圆柱的底面半径为r ,则222121=⎪⎭⎫ ⎝⎛+r ,解得r =32, ∴ππ4312322=⨯⎪⎪⎭⎫ ⎝⎛⨯=圆柱V,故选B. 答案:B●考点一 空间几何体的三视图【例1】[解析] (1)正视图应为边长为3和4的长方形,且正视图中右上到左下的对角线应为实线,故正视图为①;侧视图应为边长为4和5的长方形,且侧视图中左上到右下的对角线应为实线,故侧视图为②;俯视图应为边长为3和5的长方形,且俯视图中左上到右下的对角线应为实线,故俯视图为③,故选B.(2)由三棱锥C -ABD 的正视图、俯视图得三棱锥C -ABD 的侧视图为直角边长是22的等腰直角三角形,如图所示,所以三棱锥C -ABD 的侧视图的面积为14,故选D.(3)由三视图得,该几何体是四棱锥P -ABCD ,如图所示,ABCD 为矩形,AB =2,BC =3,平面P AD ⊥平面ABCD ,过点P 作PE ⊥AD ,则PE =4,DE =2,所以CE =22,所以最长的棱PC =PE 2+CE 2=26,故选B.[答案] (1)B (2)D (3)B 「对 点 训 练」1.解析:正视图和俯视图中棱AD 和BD 均看不见,故为虚线,易知选A.答案:A2.解析:由题图可知该几何体的侧视图如图,则该几何体的侧视图的面积为3×2+12×3×3=152,故选A.答案:A3.解析:由三视图得几何体的直观图,如图. 其中SD ⊥底面ABCD ,AB ⊥AD ,AB ∥CD ,SD =AD =CD =2,AB =1,故△SDC ,△SDA 为直角三角形.∵AB ⊥AD ,AB ⊥SD ,AD ∩SD =D ,∴AB ⊥平面SDA ,∴AB ⊥SA ,故△SAB 是直角三角形,从而SB =SD 2+AD 2+AB 2=3,易知BC =22+12=5,SC =22+22=22,则SB 2≠BC 2+SC 2,故△SBC 不是直角三角形,故选C.答案:C●考点二 空间几何体的表面积与体积【例2】[解析] (1)题中的几何体是由一个直三棱柱和一个半圆柱构成的几何体,其中直三棱柱的底面是两直角边分别为8和6的直角三角形,高为8,该半圆柱的底面圆的半径为5,高为8,因此该几何体的体积为()ππ1001928521868212+=⨯⨯+⨯⎪⎭⎫ ⎝⎛⨯⨯,故选C. (2)由几何体的三视图可得几何体如图所示,将几何体分割为两个三棱柱,所以该几何体的体积为12×3×4×4+12×3×4×4=48,故选B.(3)如图,在长方体ABCD -A 1B 1C 1D 1中,还原该三棱锥P -BCD ,易得BD =PB =41,PD =25,∴S △PBD =12×25×(41)2-⎝⎛⎭⎪⎫2522=65, 又易得S △BCD =12×4×5=10,S △BCP =12×BC ×PC =10,S △PCD =12×CD ×CC 1=10,∴该三棱锥的表面积是30+6 5.[答案] (1)C (2)B (3)D「对 点 训 练」1.解析:根据该三棱锥的三视图可以看出该三棱锥底面三角形一边长是2,该边上的高也是2,三棱锥的高也是2,其直观图如图为三棱锥A -BCD ,则其体积V =13×12×2×2×2=43.故选B.答案:B2.解析:由三视图可知,该几何体为一个半径为1的半球与一个底面半径为1,高为2的半圆柱组合而成的组合体,故其体积V =23π×13+12π×12×2=53π.故选B.答案:B3.解析:由题意知四棱锥的底面EFGH 为正方形,其边长为22,即底面面积为12,由正方体的性质知,四棱锥的高为12.故四棱锥M -EFGH 的体积V =13×12×12=112.答案:112●考点三 多面体与球的外接、内切的问题【例3】[解析] (1)由AB ⊥BC ,AB =6,BC =8,得AC =10.要使球的体积V 最大,则球与直三棱柱的部分面相切,若球与三个侧面相切,设底面△ABC 的内切圆的半径为r .则12×6×8=12×(6+8+10)·r ,所以r =2. 2r =4>3,不合题意.球与三棱柱的上、下底面相切时,球的半径R 最大. 此时2R =3,即R =32.故球的最大体积V =43πR 3=92π.故选B.(2)在等腰直角三角形ABC 中,AB 是斜边且AB =2,取AB 的中点D ,连接CD ,SD .∴CD =AD =BD =1.又SA =SB =SC =2,∴SD ⊥AB ,且SD =3,在△SCD 中,SD 2+CD 2=SC 2,∴SD ⊥CD ,∴SD ⊥平面ABC .∴三棱锥S -ABC 的外接球球心在SD 上,记为O ,设球半径为R ,连接OA ,则SO =OA =R ,∴在Rt △AOD 中,AD =1,OD =3-R ,AO =R ,∴12+(3-R )2=R 2⇒R =233,∴三棱锥S -ABC 的外接球的表面积3163324422πππ=⎪⎪⎭⎫ ⎝⎛⨯==R S .故选A. [答案] (1)B (2)A 「对 点 训 练」1.解析:如图,设球O 的半径为R ,由题意知OA =OB =OC =OD =OP =R .设正四棱锥P -ABCD 的内切球半径为r,由等体积法得()R R r R R r S V ABCD P ABCDP 22223142323131=⋅⎪⎪⎭⎫ ⎝⎛⨯+=⋅=--,所以R =(3+1)r .故选A.答案:A2.解析:设△ABC 的边长为a ,则S △ABC =12a ·a ·sin60°=93,解得a =6(负值舍去).△ABC 的外接圆半径r 满足2r =6sin60°,得r =23,球心到平面ABC 的距离为42-(23)2=2.所以点D 到平面ABC 的最大距离为2+4=6,所以三棱锥D -ABC 体积的最大值为13×93×6=183,故选B.答案:B。
高考数学二轮复习专题十二空间几何体的三视图、表面积及体积练习理
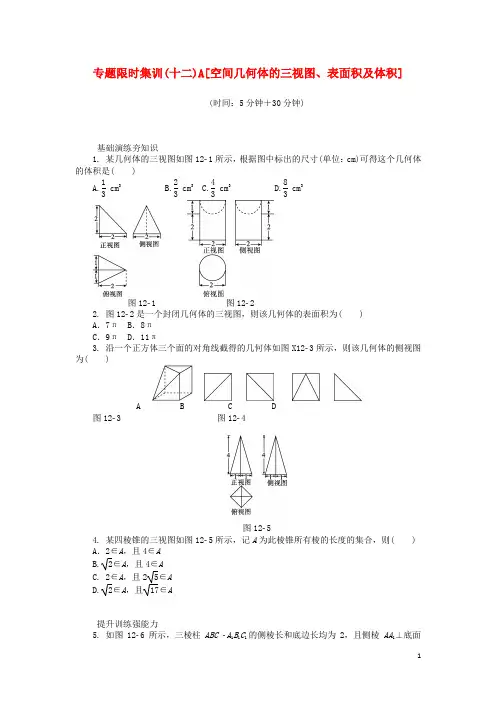
专题限时集训(十二)A[空间几何体的三视图、表面积及体积](时间:5分钟+30分钟)基础演练夯知识1. 某几何体的三视图如图121所示,根据图中标出的尺寸(单位:cm)可得这个几何体的体积是( )A.13cm3 B.23cm3 C.43cm3 D.83cm3图121图1222. 图122是一个封闭几何体的三视图,则该几何体的表面积为( )A.7π B.8πC.9π D.11π3. 沿一个正方体三个面的对角线截得的几何体如图X123所示,则该几何体的侧视图为( )A B C D图123图124图1254. 某四棱锥的三视图如图125所示,记A为此棱锥所有棱的长度的集合,则( )A.2∈A,且4∈AB.2∈A,且4∈AC. 2∈A,且25∈AD.2∈A,且17∈A提升训练强能力5. 如图126所示,三棱柱ABCA1B1C1的侧棱长和底边长均为2,且侧棱AA1⊥底面A 1B 1C 1,正视图是边长为2的正方形,俯视图为一个等边三角形,则该三棱柱的侧视图的面积为( )A.3 B .2 3 C .4 D. 4 3 6. 一个机器零件的三视图如图127所示,其中俯视图是一个半圆内切于边长为2的正方形,则该机器零件的体积为( )A .8+π3B .8+2π3C.8+8π3 D .8+16π3图126 图1277.若某棱锥的三视图(单位:cm)如图128所示,则该棱锥的体积等于( )A .10 cm 3B .20 cm 3C .30 cm 3D .40 cm 3图128 图1298. 一个简单组合体的三视图及尺寸如图129所示,则该组合体的体积为( )A .42B .48C .56D .449. 某由圆柱切割获得的几何体的三视图如图1210所示,其中俯视图是中心角为60°的扇形, 则该几何体的侧面积为( )A .12+103πB .6+103πC. 12+2π D .6+4π图1210 图121110. 如图1211,一个几何体的三视图为两个等腰直角三角形和一个边长为1的正方形,则其外接球的表面积为( )A .πB .2πC .3πD .4π11. 设扇形的圆心角为2π3,面积为3π,若将它围成一个圆锥,则此圆锥的体积是________.专题限时集训(十二)B[空间几何体的三视图、表面积及体积](时间:5分钟+30分钟)基础演练夯知识1. 某空间几何体的三视图如图1212所示,则该几何体的体积为( ) A.83 B .8 C.323D .16图1212 图12132. 一个几何体的三视图如图1213所示,则该几何体的体积为( ) A.13 B.23 C .2 D .1图12143. 如图1214所示是棱长为2的正方体的表面展开图,则多面体ABCDE 的体积为( )A .2 B.23C.43D.834. 一个四面体的四个顶点在空间直角坐标系O xyz 中的坐标分别是(0,0,0),(1,2,0),(0,2,2),(3,0,1),则该四面体以yOz 平面为投影面的正视图的面积为( )A .3 B.52C. 2D.72提升训练强能力5. 一个几何体的三视图如图1215所示,其中正视图是边长为2的正三角形,俯视图为正六边形,则该几何体的侧视图的面积为( )A.32 B .1 C.52 D.12图1215 图12166. 一个几何体的三视图如图1216所示,则它的体积为( ) A.203 B.403C .20D .40 7. 一个几何体的三视图如图1217所示,则这个几何体的体积为( )A .64-16π3B .64-32π3C .64-16πD .64-64π3图1217 图12188. 图1218是一个几何体的三视图,则该几何体的体积是( ) A .54 B .27 C. 18 D .9图12199. 如图1219所示,在三棱锥P ABC 中,PA ,PB ,PC 两两互相垂直,且PA =3,PB =2,PC =1,设M 是底面三角形ABC 内一动点,定义:f (M )=(m ,n ,p ),其中m ,n ,p 分别表示三棱锥M PAB ,M PBC ,M PAC 的体积,若f (M )=⎝ ⎛⎭⎪⎫12,2x ,y ,且1x +a y ≥8恒成立,则正实数a 的最小值是( )A .2+ 2B .2- 2C .3-2 2D .6-4 210. 直三棱柱ABC A 1B 1C 1的各顶点都在同一个球面上.若AB =AC =AA 1=2,∠BAC =120°,则此球的表面积为________.图122011. 如图1220所示,已知球O是棱长为1的正方体ABCDA1B1C1D1的内切球,则平面ACD1截球O的截面面积为________.专题限时集训(十二)A【基础演练】1.C [解析] 该几何体的直观图如图所示,所以V =13×⎝ ⎛⎭⎪⎫12×2×2×2=43(cm 3).2.C[解析] 易知该几何体是一个直径为2,高为3的圆柱上部挖去一个直径为2的半球后剩下的部分,故该几何体的表面积为π·12+2π·3+12(4π·12)=9π.3.B [解析] 由直观图知,侧视图是正方形,且从左上到右下有实对角线,选B.4.D [解析] 该空间几何体是底面边长为2,高为4的正四棱锥,则其侧棱长为42+12=17,故A ={2,17},所以2∈A ,且17∈A .【提升训练】5.B [解析] 由题知,三棱柱的侧视图是边长分别为3,2的矩形,其面积为2 3. 6.A [解析] 由三视图知,几何体是下部为正方体、上部是四分之一球体组成的组合体,其体积V =23+14×43×π×13=8+π3.7.B [解析] 由三视图知,该几何体为在一个直三棱柱上面截去一个三棱锥后剩下的部分,且直三棱柱的底面是直角边分别为3,4的直角三角形,高为5,所以该几何体的体积V =12×3×4×5-13×12×3×4×5=20(cm 3).8.D [解析] 由三视图可知该几何体是一个长、宽、高分别为6,4,1的长方体和一个底面积为12×4×5=10,高为2的三棱柱组合而成的,其体积V =1×4×6+10×2=44.9.C [解析] 该几何体为底面半径为2,母线长为3的圆柱的六分之一,故所求侧面积为16×2π×2×3+2×2×3=2π+12.10.C [解析] 由三视图知几何体是底面是正方形,顶点在底面的射影是正方形的一个顶点的四棱锥,其最长的侧棱是外接球的直径,因此r =32,外接球的表面积S =4πr 2=3π .11.22π3 [解析] 设扇形的半径为R ,由S =12×2π3R 2=3π得R =3.扇形的弧长为2π,因此圆锥的底面半径为r =1,从而圆锥的高为32-12=22,圆锥的体积为V =13×π×12×22=22π3.专题限时集训(十二)B【基础演练】1.B [解析] 由三视图可知,该几何体的体积为12×2×2×4=8.2.B [解析] 由三视图知该几何体是一个四棱锥,四棱锥的底面是一个边长为2的正方形,四棱锥的高为1,所以该几何体的体积V =13×2×2×1=23.3.D [解析] 多面体ABCDE 为四棱锥,利用割补法可得其体积V =4-43=83,选D.4.A [解析] 1,下底边为2,高为2的梯形,所以该梯形的面积为12(1+2)×2=3.【提升训练】5.A [解析] 该几何体为正六棱锥,其侧视图是底边长为3,高为3的等腰三角形,其面积为12×3×3=32.6.B [解析] 此几何体的直观图如图所示,易知其体积V =13×12()1+4×4×4=403.7.A [解析] 由三视图知该几何体是正方体内挖去两个底面在上、下底,且共顶点的圆锥,因此其体积V =43-13π×22×(1+3)=64-16π3.8.C [解析] 由题可知,该几何体是一个四棱锥,其直观图如图所示,该四棱锥的高为3,底面是边长分别为3,6的矩形,故其体积为13×3×6×3=18.9.D [解析] 由三棱锥P ABC 的体积为V =13×12×3×2×1=1,得12+2x +y =1,从而4x +2y =1,所以1x +a y =⎝ ⎛⎭⎪⎫1x +a y (4x +2y )=4+2a +2y x +4axy≥4+2a +28a ,依题意得4+2a+42a ≥8,又a >0得a ≥2-2⇒a ≥6-4 2.10.20π [解析] 设半径为R 的球的内接直三棱柱ABC A 1B 1C 1的上、下底面外接圆的圆心分别为O 1,O 2,则球心O 在线段O 1O 2的中点处.连接OO 1,OA ,O 1A ,则R 2=OA 2=OO 21+O 1A2=1+O 1A 2.在△ABC 中,AB =AC =2,∠BAC =120°,∴ BC =2 3.又BC sin ∠BAC=2O 1A ,∴ O 1A=232sin ∠BAC=2,∴ R =5,∴此球的表面积为4πR 2=20π. 11.π6[解析] 根据题意知,平面ACD 1是边长为2的正三角形,球O 与以点D 为公共点的三个面的切点恰为三角形ACD 1三边的中点,故所求截面的面积是该正三角形的内切圆的面积.易知△ACD 1内切圆的半径是2×32×13=66,则所求的截面圆的面积是π×⎝ ⎛⎭⎪⎫662=π6.。
专题15 空间几何体的三视图、表面积与体积( 理科)原卷版
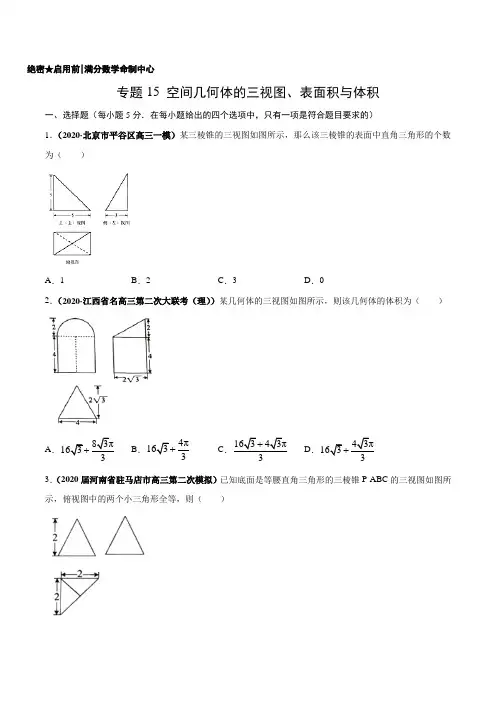
绝密★启用前|满分数学命制中心专题15 空间几何体的三视图、表面积与体积一、选择题(每小题5分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(2020·北京市平谷区高三一模)某三棱锥的三视图如图所示,那么该三棱锥的表面中直角三角形的个数为()A.1 B.2 C.3 D.02.(2020·江西省名高三第二次大联考(理))某几何体的三视图如图所示,则该几何体的体积为()A.83π163+B.4π1633+C.16343π+D.43π163+3.(2020届河南省驻马店市高三第二次模拟)已知底面是等腰直角三角形的三棱锥P-ABC的三视图如图所示,俯视图中的两个小三角形全等,则()A .PA ,PB ,PC 两两垂直 B .三棱锥P-ABC 的体积为83C .||||||6PA PB PC ===D .三棱锥P-ABC 的侧面积为354. (河南省周口一中2019届期末)一个几何体的三视图如图所示,在该几何体的各个面中,面积最小的面的面积为( )A.8B.4C.4 3D.4 25.(吉林东北师大附中2019届高三模拟)某三棱锥的三视图如图所示,则该三棱锥的最长棱的长度为( )A. 5 B .2 2 C .3D .2 36. (南京师大附中2019届高三调研)某几何体的三视图如图所示,则该几何体的侧视图中的虚线部分是( )A.圆弧B.抛物线的一部分C.椭圆的一部分D.双曲线的一部分7.(2020届湖北省黄冈中学高三高考模拟)木匠师傅对一个圆锥形木件进行加工后得到一个三视图如图所示的新木件,则该木件的体积( )A .2493π+B .4893π+C .48183π+D .144183π+8.(2020·湖南省长沙市明达中学高三二模(理)魏晋时期数学家刘徽在他的著作《九章算术注》中,称一个正方体内两个互相垂直的内切圆柱所围成的几何体为“牟合方盖”,刘徽通过计算得知正方体的内切球的体积与“牟合方盖”的体积之比应为π:4.若正方体的棱长为2,则“牟合方盖”的体积为( ) A .16B .163C .163D .12839.(2020届湖南省长沙市长郡中学高三第三次适应性考试)一个几何体的三视图及尺寸如下图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的表面积是 ( )A .16216π+B .1628π+C .8216πD .828π10.(2020届河南省濮阳市高三模拟)在四面体P ABC -中,ABC 为正三角形,边长为6,6PA =,8PB =,10PC =,则四面体P ABC -的体积为( )A.811B.810C.24 D.16311.(2020届河南省天一大联考“顶尖计划”高三二联)已知三棱锥D ABC-的外接球半径为2,且球心为线段BC的中点,则三棱锥D ABC-的体积的最大值为()A.23B.43C.83D.16312.(2020·北京市西城区高三一模)某四棱锥的三视图如图所示,记S为此棱锥所有棱的长度的集合,则()A.2223S S∉∉,且B.2223S S∉∈,且C.2223S S∈∉,且D.2223S S∈∈,且13.(2020届安徽省“江南十校”高三综合素质检测)如图,在平面四边形ABCD中,满足,AB BC CD AD==,且10,8AB AD BD+==,沿着BD把ABD折起,使点A到达点P的位置,且使2PC=,则三棱锥P BCD-体积的最大值为()A.12 B.2C.23D.16314.(2020届河南省六市高三第一次模拟)已知圆锥的高为33圆周都在同一个球面上,则这个球的体积与圆锥的体积的比值为( )5 3B.329C.43D.259A.二、填空题(每小题5分)16.(2020届黑龙江省齐齐哈尔高三二模)如图是某几何体的三视图,俯视图中圆的两条半径长为2且互相垂直,则该几何体的体积为________.17.(2020届陕西省西安中学高三第一次模拟)我国古代数学名著《九章算术》对立体几何有深入的研究,从其中一些数学用语可见,譬如“憋臑”意指四个面都是直角三角形的三棱锥.某“憋臑”的三视图(图中网格纸上每个小正方形的边长为1)如图所示,已知几何体高为22,则该几何体外接球的表面积为__________.18.(2020届四川省成都市高三第二次诊断)已知各棱长都相等的直三棱柱(侧棱与底面垂直的棱柱称为直棱柱)所有顶点都在球O 的表面上.若球O 的表面积为28,π则该三棱柱的侧面积为___________. 19.(2020届河南省驻马店市高三第二次模拟)在矩形ABCD 中,4BC =,M 为BC 的中点,将ABM 和DCM △分别沿AM ,DM 翻折,使点B 与C 重合于点P .若150APD ∠︒=,则三棱锥M PAD ﹣的外接球的表面积为_____.20.(2020届黑龙江省哈尔滨市第三中学高三第一次调研)四面体A BCD -中,AB ⊥底面BCD ,2AB BD ==1CB CD ==,则四面体A BCD -的外接球的表面积为______21.(2020届湖南省岳阳市高三第二次教学质量检测)农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称“粽子”,古称“角黍”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.如图,平行四边形形状的纸片是由六个边长为1的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为____;若该六面体内有一球,则该球体积的最大值为____.22.(2020·陕西省西安中学高三三模(理))已知三棱锥S ABC -中,SA ⊥面ABC ,且6SA =,4AB =,23BC =,30ABC ∠=︒,则该三棱锥的外接球的表面积为__________.23. (江西省九江一中2019届质检)如图是一个几何体的三视图,其中正视图和侧视图均是高为2,底边长为22的等腰三角形,俯视图是边长为2的正方形,则该几何体的外接球的体积是________.24.(黑龙江哈尔滨师大附中2019届高三模拟)已知圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为78,SA 与圆锥底面所成角为45°.若△SAB 的面积为515,则该圆锥的侧面积为________.25、(江苏省南通市、泰州市2019-2020学年高三上学期期末)在正三棱柱ABC - A 1B 1C 1 中,AA 1=AB =2 ,则三枝锥A 1 - BB 1C 1 的体积为______.。
空间几何体与三视图、体积表面积(含答案)
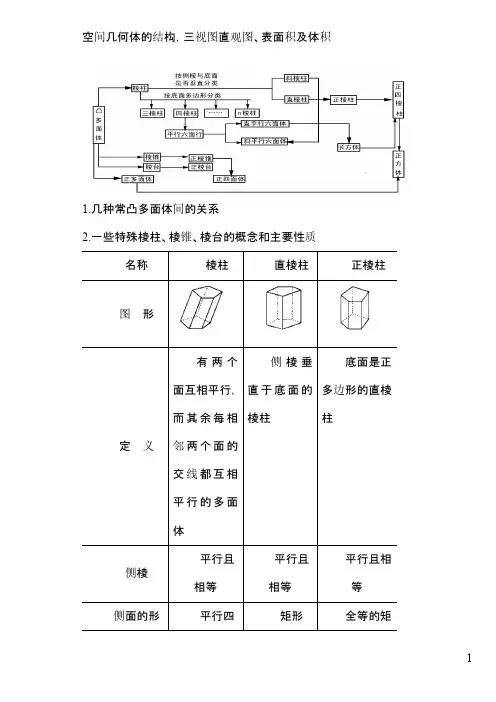
1.几种常凸多面体间的关系2.一些特殊棱柱、棱锥、棱台的概念和主要性质名称棱柱直棱柱正棱柱图形定义有两个面互相平行,而其余每相邻两个面的侧棱垂直于底面的棱柱底面是正多边形的直棱柱有一个底面是用一个由正棱的高要保持平齐相等长度变为原来的一半;④擦去辅助线,图画好后,要擦去X 轴、Y 轴及为画图添加的辅助线(虚线)。
(2)平行投影与中心投影平行投影的投影线是互相平行的,中心投影的投影线相交于一点投影线垂直于投影面产生的投影叫做正投影,投影线不垂直于投影面产生的投影叫做斜投影。
物体投影的形状、大小与它相对于投影面的位置和角度有关。
三视图指正投影(3)射影:所谓射影,就是正投影其中,从一点到一条直线所作垂线的垂足,叫做这点在这条直线上的正投影。
一条线段的两个端点在一条直线上的正投影之间的线段,叫做这条线段在这直线上的正投影题型1.空间几何体的结构例题1正方体ABCD—1A 1B 1C 1D 的棱上到异面直线AB ,C 1C 的距离相等的点的个数为(c )A .2B .3 C. 4 D. 5【答案】:C【解析】解析如图示,则BC 中点,1B 点,D 点,A1D1的中点分别到两异面直线的距离相等。
即满足条件的点有四个,故选C 项变式练习:到两互相垂直的异面直线的距离相等的点(A )只有1个 (B )恰有3个(C )恰有4个(D )有无穷多个①②:当截面与正方体的某一面平行时,可得①,将截面旋转可得点时可得③,即正方体的对角面,不可能得④.答案:( )【答案】2、一个几何体的三视图如图积为10A. 28+65B. 30+6 D.读出的长度,黑色数字【答案】D的体。
2020版高考数学 立体几何第1讲空间几何体的三视图、表面积及体积练习(文)(含解析)

第1讲 空间几何体的三视图、表面积及体积A 级 基础通关一、选择题1.半径为R 的半圆卷成一个圆锥,则它的体积为( ) A.525πR 3B.324πR 3C.58πR 3D.38πR 3 解析:设圆锥的底面圆的半径为r ,高为h , 由2πr =πR ,得r =R2,因此h =R 2-r 2=32R . 所以V 圆锥=13πr 2·h =13π·⎝ ⎛⎭⎪⎫R 22·32R =324πR 3.答案:B2.(2018·北京卷)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为( )A .1B .2C .3D .4解析:由三视图得到空间几何体,如图所示,则PA ⊥平面ABCD ,平面ABCD 为直角梯形,PA =AB =AD =2,BC =1,所以PA ⊥AD ,PA ⊥AB ,PA ⊥BC .又BC ⊥AB ,AB ∩PA =A ,所以BC ⊥平面PAB ,所以BC ⊥PB .在△PCD 中,PD =22,PC =3,CD =5,所以△PCD 为锐角三角形.所以侧面中的直角三角形为△PAB ,△PAD ,△PBC ,共3个.答案:C3.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为( )A .8+3πB .8+4πC .8+5πD .8+6π解析:由题图可知,几何体为半圆柱挖去半球体,几何体的表面积为2×π2×4+π+2×4-π+4π2=8+6π.答案:D4.中国古代数学名著《九章算术》中,将底面是直角三角形的直棱柱称为“堑堵”.已知“堑堵”的正视图和俯视图如图所示,则该“堑堵”的侧视图的面积为( )A .18 6B .18 3C .18 2D.2722解析:在俯视图Rt △ABC 中,作AH ⊥BC 交于点H .由三视图的意义,则BH =6,HC =3,根据射影定理,AH 2=BH ·HC ,所以AH =3 2.易知该“堑堵”的侧视图是矩形,长为6,宽为AH =32,故侧视图的面积S =6×32=18 2.答案:C5.(2019·青岛二中检测)某几何体的三视图如图所示,则该几何体的体积为( )A .6B .4C.223D.203解析:由三视图知该几何体是边长为2的正方体挖去一个三棱柱(如图),且挖去的三棱柱的高为1,底面是等腰直角三角形,等腰直角三角形的直角边长为2,故几何体体积V =23-12×2×2×1=6.答案:A6.(2017·全国卷Ⅲ)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A .πB.3π4C.π2D.π4解析:设圆柱的底面半径为r ,球的半径为R ,且R =1, 由圆柱两个底面的圆周在同一个球的球面上可知,r ,R 及圆柱的高的一半构成直角三角形.所以r =12-⎝ ⎛⎭⎪⎫122=32.所以圆柱的体积为V =πr 2h =34π×1=3π4.故选B.答案:B 二、填空题7.(2019·江苏卷)如图,长方体ABCD-A 1B 1C 1D 1的体积是120,E 为CC 1的中点,则三棱锥E-BCD 的体积是________.解析:设长方体中BC =a ,CD =b ,CC 1=c ,则abc =120,所以V EBCD =13×12ab ×12c =112abc =10.答案:108.(2018·浙江卷改编)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm 3)为________.解析:由三视图可知,该几何体是一个底面为直角梯形的直四棱柱,所以该几何体的体积V =12×(1+2)×2×2=6.答案:69.(2017·北京卷改编)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为________.解析:根据三视图可得该四棱锥的直观图(四棱锥P-ABCD)如图所示,将该四棱锥放入棱长为2的正方体中.由图可知该四棱锥的最长棱为PD,PD=22+22+22=2 3.答案:2 310.(2019·惠州调研)已知一张矩形白纸ABCD,AB=10,AD=102,E,F分别为AD,BC的中点,现分别将△ABE,△CDF沿BE,DF折起,使A,C重合于点P,则三棱锥PDEF的外接球的表面积为________.解析:三棱锥P-DEF中,PD2+PF2=CD2+CF2=DF2,所以∠DPF=90°,且DF2=102+(52)2=150.又∠DEF=90°,所以DF的中点为三棱锥PDEF的外接球的球心,则2R=DF,故球的表面积S=4πR2=150π.答案:150πB级能力提升11.(2019·雅礼中学质检)一个几何体的三视图如图所示,则该几何体的体积为( )A.5π3B .5C.2π3D .π解析:由三视图可知,该几何体是一个组合体,它由半个圆锥与四分之一球体组成,其中圆锥的底面半径为1,高为2,体积为12×13×π×12×2=π3;球的半径为1,体积为14×43π×13=π3.所以该几何体的体积V =π3+π3=2π3.答案:C12.我国齐梁时代的数学家祖暅提出了一条原理:“幂势既同,则积不容异”.意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.椭球体是椭圆绕其轴旋转所成的旋转体.如图,将底面直径都为2b ,高皆为a 的椭半球体和已被挖去了圆锥体的圆柱放置于同一平面β上,用平行于平面β且与平面β任意距离d 处的平面截这两个几何体,可横截得到S 圆及S 环两截面.可以证明S 圆=S 环总成立.据此,半短轴长为1,半长轴长为3的椭球体的体积是________.解析:因为S 圆=S 环总成立,则半椭球体的体积为πb 2a -13πb 2a =23πb 2a .所以椭球体的体积V =43πb 2a .因为椭球体半短轴长为1,半长轴长为3即b =1,a =3. 故椭球体的体积V =43πb 2a =4π.答案:4π13.在《九章算术》中,将底面为矩形且有一条侧棱与底面垂直的四棱锥称之为阳马.如图,若四棱锥P-ABCD 为阳马,侧棱PA ⊥底面ABCD ,且PA =3,BC =AB =4,设该阳马的外接球半径为R ,内切球半径为r ,则R =________,内切球的体积V =________.解析:在四棱锥P-ABCD 中,侧棱PA ⊥底面ABCD ,且底面为矩形,将该“阳马”补成长方体,则(2R )2=AB 2+AD 2+AP 2=16+16+9=41. 因此R =412. 依题意Rt △PAB ≌Rt △PAD ,则内切球O 在侧面PAD 内的正视图是△PAD 的内切圆,且该内切圆与△PAB 的内切圆全等.故内切球的半径r =12(3+4-5)=1,则V =43πr 3=43π.答案:412 43π 14.(2017·全国卷Ⅰ)已知三棱锥S ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA =AC ,SB =BC ,三棱锥S ABC 的体积为9,则球O 的表面积为________.解析:如图,连接OA ,OB .由SA =AC ,SB =BC ,SC 为球O 的直径,知OA ⊥SC ,OB ⊥SC . 由平面SCA ⊥平面SCB , 平面SCA ∩平面SCB =SC , 所以OA ⊥平面SCB . 设球O 的半径为r ,则OA =OB =r ,SC =2r ,所以三棱锥S ABC 的体积V =13×⎝ ⎛⎭⎪⎫12SC ·OB ·OA =r 33, 即r 33=9,所以r =3,所以S 球表=4πr 2=36π. 答案:36π。
空间几何体结构三视图表面积体积练习
空间几何体结构三视图表面积体积练习21.若一个几何体的主视图和左视图都是等腰三角形,俯视图是圆,则这个几何体可能是( A )A .圆锥 B. 圆柱 C . 三棱柱 D. 球体 2.ABC 的斜二侧直观图如图所示,则ABC 的面积为(C ) A 、22B 、C 、2D 、4 3.正三棱锥底面三角形的边长为3,侧棱长为2,则其体积为 ( C )A .41 B .21 C .43 D .49 4.右图是一个实物图形,则它的左视图大致为( D )5.已知正四棱台的上、下底面边长分别为3和6,其侧面积等于两底面积之和,则该正四棱台的高是( A )A .2B .25 C .3 D .27 6.正六棱柱ABCDEF -A 1B 1C 1D 1E 1F 1的侧面是正方形,若底面的边长为a ,则该正六棱柱的外接球的表面积是 ( B )A .4πa 2 B.5 πa 2 C. 8πa 2 D.10πa 27.已知一几何体的三视图如上图,主视图和左视图都是矩形,俯视图为正方形,在该几何体上任意选择4个顶点,以这4个点为顶点的几何形体可能是( )①矩形;②有三个面为直角三角形,有一个面为等腰三角形的四面体; ③每个面都是直角三角形的四面体.A .①②③B .②③C .①③D .①②Oxy 12()C AB8. 如图,将一正方体沿着相邻三个面的对角线截出一个棱锥, 则棱锥的体积与剩下的几何体的体积之比为( B ) A .1∶6 B .1∶5 C .1∶2 D .1∶39.如左上图是由单位立方体构成的积木垛的三视图,据此三视图可知,构成这堆积木垛的单位正方体共有( B )A .6块B .7块C .8块D .9块10.如右下图,在ABC ∆中,2AB =,BC=1.5,120ABC ∠=,如图所示。
若将ABC∆绕BC 旋转一周,则所形成的旋转体的体积是( D )A .92πB .72πC .52πD .32π11.如图,平面四边形ABCD 中,1===CD AD AB ,CD BD BD ⊥=,2,将其沿对角线BD 折成四面体BCD A -',使平面⊥BD A '平面BCD ,若四面体BCD A -'顶点在同一个球面上,则该球的体积为( A )A . π23B . π3C . π32D . π212. 如图所示,三棱锥P -ABC 的高PO =8,AC =BC =3,∠ACB =30°,M 、N 分别在BC 和PO 上,且CM =x ,PN =2x (x ∈[0,3]),下列四个图象大致描绘了三棱锥N -AMC 的体积V 与x 的变化关系,其中正确的是( A )二、选择题12.一个正四棱柱的各个顶点在一个直径为2cm 的球面上.如果正四棱柱的底面边长为1cm ,那么该棱柱的表面积为 cm 2.13.如右图.M 是棱长为2cm 的正方体ABCD-A 1B 1C 1D 1的棱CC 1的中点,沿正方体表面从点A 到点M 的最短路程是 cm .答: 12.224+. 13.13.14.一根细金属丝下端挂着一个半径为1 cm 的金属球,将它浸没在底面半径为2 cm 的圆柱形容器内的水中,现将金属丝向上提升,当金属球全部被提出水面时,容器内的水面下降的高度是________cm.解析:由题意知,金属球的体积等于下降的水的体积,设水面下降h cm ,则有4π3=π×22×h ,解得h =13.15.一个正四棱锥底面一边的长为1,侧棱长也都是1, 求它的表面积是__________,体积是_________。
专题 由三视图求表面积和体积
由三视图求表面积和体积一、方法与技巧二、常见几何体1.(2016•益阳模拟)若某空间几何体的三视图如图所示,则该几何体的表面积是()A.60 B.54 C.48 D.24【解答】解:由三视图知:几何体是一个侧面向下放置的直三棱柱,侧棱长为4,底面三角形为直角三角形,直角边长分别为3,4,斜边长为5.∴几何体的表面积S=S棱柱侧+S底面=(3+4+5)×4+2××3×4=48+12=60.故选:A.2.(2016•凉山州模拟)一个棱锥的三视图如图所示,则这个棱锥的体积是()A.6 B.12 C.24 D.36【解答】解:由已知的三视图可得该棱锥是以俯视图为底面的四棱锥其底面长和宽分别为3,4,棱锥的高是3故棱锥的体积V=Sh=×3×4×3=12故选B3.(2016•衡水校级一模)已知一个几何体的三视图如图所示,则该几何体的体积为()A.B.C.27﹣3πD.18﹣3π【解答】解:由三视图可知,该几何体为放到的直四棱柱,且中间挖去半个圆柱,由三视图中的数据可得:四棱柱的高为3,底面为等腰梯形,梯形的上、下底边分别为2、4,高为2,圆柱的高为3,圆柱底面的半径都是1,∴几何体的体积V==,故选:B.4.(2016•广元二模)一个多面体的三视图分别是正方形、等腰三角形和矩形,其尺寸如图,则该多面体的体积为()A.48cm3B.24cm3C.32cm3D.28cm3【解答】解:由三视图可知该几何体是平放的直三棱柱,高为4,底面三角形一边长为6,此边上的高为4 体积V=Sh==48cm3故选A5.(2016•江门模拟)一个几何体的三视图及其尺寸如下,则该几何体的表面积为()A.12πB.15πC.24πD.36π【解答】解:由三视图可知该几何体为一个圆锥,底面直径为6,母线长为5,底面圆的面积S1=π×()2=9π.侧面积S2=π×3×5=15π,表面积为S1+S2=24π.故选C.6.(2016•安康二模)一空间几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.【解答】解:三视图复原的几何体是三棱锥,底面是底边长为2,高为2的等腰三角形,三棱锥的一条侧棱垂直底面,高为2.三棱锥的体积为:==.故选D.7.(2016•杭州模拟)某几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.【解答】解:该几何体为三棱柱与三棱锥的组合体,如右图,三棱柱的底面是等腰直角三角形,其面积S=×1×2=1,高为1;故其体积V1=1×1=1;三棱锥的底面是等腰直角三角形,其面积S=×1×2=1,高为1;故其体积V2=×1×1=;故该几何体的体积V=V1+V2=;故选:A.8.(2016•呼伦贝尔一模)一个几何体的三视图如图所示,其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形.若该几何体的体积为V,并且可以用n个这样的几何体拼成一个棱长为4的正方体,则V,n的值是()A.V=32,n=2 B.C.D.V=16,n=4【解答】解:由三视图可知,几何体为底面是正方形的四棱锥,所以V=,边长为4的正方体V=64,所以n=3.故选B9.(2016•广东模拟)一空间几何体的三视图如图所示,则该几何体的体积为()A.12 B.6 C.4 D.2【解答】解:由三视图知,几何体是一个四棱锥,四棱锥的底面是一个直角梯形,直角梯形的上底是1,下底是2,垂直于底边的腰是2,一条侧棱与底面垂直,这条侧棱长是2,∴四棱锥的体积是=2,故选D.10.(2016•延边州模拟)如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱AA1⊥面A1B1C1,正视图是正方形,俯视图是正三角形,该三棱柱的侧视图面积为()A.B.C. D.4【解答】解:由题意知三棱柱的侧视图是一个矩形,矩形的长是三棱柱的侧棱长,宽是底面三角形的一条边上的高,在边长是2的等边三角形中,底边上的高是2×=,∴侧视图的面积是2.故选A.11.(2016•江西校级一模)如图是一个无盖器皿的三视图,正视图、侧视图和俯视图中的正方形边长为2,正视图、侧视图中的虚线都是半圆,则该器皿的表面积是()A.π+24 B.π+20 C.2π+24 D.2π+20【解答】解:该器皿的表面积可分为两部分:去掉一个圆的正方体的表面积s1和半球的表面积s2,s1=6×2×2﹣π×12=24﹣π,s2==2π,故s=s1+s2=π+24故选:A.12.(2016•太原二模)某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,两条虚线互相垂直,则该几何体的体积是()A.B.C.D.【解答】解:由三视图知原几何体是一个棱长为2的正方体挖去一四棱锥得到的,该四棱锥的底为正方体的上底,高为1,如图所示:所以该几何体的体积为23﹣×22×1=.故选A.13.(2016•太原校级二模)某几何体的三视图如图所示,则该几何体中,面积最大的侧面的面积为()A.B.C.D.3【解答】解:由三视图可知,几何体的直观图如图所示,平面AED⊥平面BCDE,四棱锥A﹣BCDE的高为1,四边形BCDE是边长为1的正方形,则S△AED==,S△ABC=S△ADE==,S△ACD==,故选:B.14.(2016•河西区模拟)如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是()A.B. C.D.【解答】解:由三视图知几何体的直观图是半个圆锥,又∵正视图是腰长为2的等腰三角形∴r=1,h=∴故选:D.15.(2016•岳阳二模)一个几何体的三视图如图所示,已知这个几何体的体积为,则h=()A.B.C. D.【解答】解:三视图复原的几何体是底面为边长5,6的矩形,一条侧棱垂直底面高为h,所以四棱锥的体积为:,所以h=.故选B.16.(2016•汉中二模)一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积是()A.1 B.2 C.3 D.4【解答】解:由题设及图知,此几何体为一个四棱锥,其底面为一个对角线长为2的正方形,故其底面积为=2由三视图知其中一个侧棱为棱锥的高,其相对的侧棱与高及底面正方形的对角线组成一个直角三角形由于此侧棱长为,对角线长为2,故棱锥的高为=3此棱锥的体积为=2故选B.17.(2016•榆林一模)某三棱锥的三视图如图所示,该三棱锥的体积为()A.80 B.40 C.D.【解答】解:由三视图可知该几何体是如图所示的三棱锥:PO⊥平面ABC,PO=4,AO=2,CO=3,BC⊥AC,BC=4.从图中可知,三棱锥的底是两直角边分别为4和5的直角三角形,高为4,体积为V=.故选D.18.(2016•揭阳一模)已知某空间几何体的三视图如图所示,则该几何体的体积是48.【解答】解:由三视图可知原几何体如图所示,可看作以直角梯形ABDE为底面,BC为高的四棱锥,由三棱锥的体积公式可得V=××(2+6)×6×6=48,故答案为:48.三、常见几何体的组合体19.(2016•佛山模拟)已知某几何体的三视图如图所示,其中,正(主)视图,侧(左)视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为()A.B.C. D.【解答】解:由三视图可得该几何体的上部分是一个三棱锥,下部分是半球,所以根据三视图中的数据可得:V=××=,故选C.20.(2016•乐山模拟)一个几何体的三视图如图所示,则此几何体的体积是()A.112 B.80 C.72 D.64【解答】解:由三视图可知,此几何体是由一个棱柱和一个棱锥构成的组合体,棱柱的体积为4×4×4=64;棱锥的体积为×4×4×3=16;则此几何体的体积为80;故选B.四、常见几何体的切割体21.(2016•茂名一模)若某几何体的三视图(单位:cm)如图所示,则该几何体的体积等于()A.10cm3B.20cm3C.30cm3D.40cm3【解答】解:由三视图知几何体为三棱柱削去一个三棱锥如图:棱柱的高为5;底面为直角三角形,直角三角形的直角边长分别为3、4,∴几何体的体积V=×3×4×5﹣××3×4×5=20(cm3).故选B.22.(2016•威海一模)一个棱长为2的正方体沿其棱的中点截去部分后所得几何体的三视图如图示,则该几何体的体积为()A.7 B.C.D.【解答】解:依题意可知该几何体的直观图如图示,其体积为正方体的体积去掉两个三棱锥的体积.即:,故选D.23.(2016•张掖校级模拟)某几何体的三视图如图所示,则该几何体的体积为26【解答】解:由三视图知几何体为为三棱柱,去掉一个三棱锥的几何体,如图:三棱柱的高为5,底面是直角边为4,3,去掉的三棱锥,是底面是直角三角形直角边为4,3,高为2的三棱锥.∴几何体的体积V==26.故答案为:26.24.(2016•商洛模拟)已知一个几何体的三视图是三个全等的边长为l的正方形,如图所示,则该几何体的体积为()A.B.C.D.【解答】解:该几何体是正方体削去一个角,体积为1﹣=1﹣=.故选:D.25.(2016•银川校级一模)如图,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则被截去部分的几何体的表面积为54+18.【解答】解:由三视图可知正方体边长为6,截去部分为三棱锥,作出几何体的直观图如图所示:∴被截去的几何体的表面积S=+×(6)2=54+18.故答案为54+18.26.(2016•哈尔滨校级二模)一个空间几何体的三视图如图所示,则这个几何体的体积为.【解答】解:根据已知中的三视图,可得几何体的直观图如下图所示:该几何是由一个以俯视图为底面的四棱锥,切去两个棱锥所得的组合体,四棱柱的体积为:×(2+4)×4×4=48,四棱锥F﹣EHIJ的体积为:×(2+4)×4×2=8,中棱锥F﹣HGJ的体积为:=,故组合体的体积V=,故答案为:4.(2011•北京模拟)已知一个几何体的三视图如所示,则该几何体的体积为()A.6 B.5.5 C.5 D.4.5【考点】由三视图求面积、体积.【分析】由三视图知几何体是一个长方体割去两个三棱锥,三棱锥的底面是一个底面面积可以做出,高是3,做出截去得到三棱锥的体积,长方体的体积也可以做出.【解答】解:由三视图知几何体是一个长方体割去两个三棱锥,三棱锥的底面是一个底面面积是×1×1=,高是3,∴截去得到三棱锥的体积是2××=1,长方体的体积是3×2×1=6∴几何体的体积是6﹣1=5故选C.。
高考数学空间几何体三视图表面积与体积专题测试(含答案解析)
高考数学空间几何体三视图表面积与体积专题测试(含答案解析)试题可以协助考生停止查缺补漏,为此查字典数学网整理了空间几何体三视图、外表积与体积专题测试,请考生停止练习。
一、选择题1.(2021武汉调研)一个几何体的三视图如下图,那么该几何体的直观图可以是()解析 A、B、C与仰望图不符.答案 D2.将长方体截去一个四棱锥,失掉的几何体如下图,那么该几何体的侧(左)视图为()解析抓住其一条对角线被遮住应为虚线,可知正确答案在C,D中,又结合直观图知,D正确.答案 D3.(2021安徽卷)一个多面体的三视图如下图,那么该多面体的外表积为()A.21+3B.18+3C.21D.18解析由三视图知,该多面体是由正方体割去两个角所成的图形,如下图,那么S=S正方体-2S三棱锥侧+2S三棱锥底=24-231211+234(2)2=21+3.答案 A4.S,A,B,C是球O外表上的点,SA平面ABCD,ABBC,SA=AB=1,BC=2,那么球O的外表积等于()A.4B.3C.2解析如下图,由ABBC知,AC为过A,B,C,D四点小圆直径,所以ADDC.又SA平面ABCD,设SB1C1D1-ABCD为SA,AB,BC为棱长结构的长方体,得体对角线长为12+12+22=2R,所以R=1,球O的外表积S=4.故选A.答案 A5.(2021湖南卷)一块石材表示的几何体的三视图如下图.将该石材切削、打磨,加工成球,那么能失掉的最大球的半径等于()A.1B.2C.3D.4解析由三视图可得原石材为如下图的直三棱柱A1B1C1-ABC,且AB=8,BC=6,BB1=12.假定要失掉半径最大的球,那么此球与平面A1B1BA,BCC1B1,ACC1A1相切,故此时球的半径与△ABC内切圆的半径相等,故半径r=6+8-102=2.应选B.答案 B6.点A,B,C,D均在同一球面上,其中△ABC是正三角形,AD平面ABC,AD=2AB=6,那么该球的体积为()A.323B.48C.643D.163解析如下图,O1为三角形ABC的外心,过O做OEAD,OO1面ABC,AO1=33AB=3.∵OD=O A,E为DA的中点.∵AD面ABC,AD∥OO1,EO=AO1=3.DO=DE2+OE2=23.R=DO= 23.V=43(23)3=323.答案 A二、填空题7.某四棱锥的三视图如下图,该四棱锥的体积是________. 解析由三视图可知,四棱锥的高为2,底面为直角梯形ABCD.其中DC=2,AB=3,BC=3,所以四棱锥的体积为132+3322=533. 答案 5338.如图,在三棱柱A1B1C1-ABC中,D,E,F区分是AB,AC,AA1的中点,设三棱锥F-ADE的体积为V1,三棱柱A1B1C1-ABC 的体积为V2,那么V1V2=________.解析设三棱柱A1B1C1-ABC的高为h,底面三角形ABC的面积为S,那么V1=1314S12h=124Sh=124V2,即V1V2=124. 答案 1249.在四面体ABCD中,AB=CD=6,AC=BD=4,AD=BC=5,那么四面体ABCD的外接球的外表积为________.解析结构一个长方体,使得它的三条面对角线区分为4、5、6,设长方体的三条边区分为x,y,z,那么x2+y2+z2=772,而长方体的外接球就是四面体的外接球,所以S=4R2=772. 答案 772三、解答题10.以下三个图中,左边是一个正方体截去一个角后所得多面体的直观图.左边两个是其正(主)视图和侧(左)视图. (1)请在正(主)视图的下方,依照画三视图的要求画出该多面体的仰望图(不要求表达作图进程).(2)求该多面体的体积(尺寸如图).解 (1)作出仰望图如下图.(2)依题意,该多面体是由一个正方体(ABCD-A1B1C1D1)截去一个三棱锥(E-A1B1D1)失掉的,所以截去的三棱锥体积VE-A1B1D1=13S△A1B1D1A1E=1312221=23,正方体体积V正方体AC1=23=8,所以所求多面体的体积V=8-23=223.11.(2021安徽卷)如图,四棱柱ABCD-A1B1C1D1中,A1A底面ABCD.四边形ABCD为梯形,AD∥BC,且AD=2BC.过 A1,C,D三点的平面记为,BB1与的交点为Q.(1)证明:Q为BB1的中点;(2)求此四棱柱被平面所分红上下两局部的体积之比.解 (1)证明:由于BQ∥AA1,BC∥AD,BCBQ=B,ADAA1=A,所以平面QBC∥平面A1AD.从而平面A1CD与这两个平面的交线相互平行,即QC∥A1D.故△QBC与△A1AD的对应边相互平行,于是△QBC∽△A1AD.所以BQBB1=BQAA1=BCAD=12,即Q为BB1的中点.(2)如图,衔接QA,QD.设AA1=h,梯形ABCD的高为d,四棱柱被平面所分红上下两局部的体积区分为V上和V下,BC=a,那么AD=2a.VQ-A1AD=13122ahd=13ahd,VQ-ABCD=13a+2a2d12h=14ahd,所以V下=VQ-A1AD+VQ-ABCD=712ahd,又V四棱柱A1B1C1D1-ABCD=32ahd,所以V上=V四棱柱A1B1C1D1-ABCD-V下=32ahd-712ahd=1112ahd.故V上V下=117.B级才干提高组1.(2021北京卷)在空间直角坐标系Oxyz中,A(2,0,0),B(2,2,0),C(0,2,0),D(1,1,2).假定S1,S2,S3区分是三棱锥D-ABC在xOy,yOz,zOx坐标平面上的正投影图形的面积,那么()A.S1=S2=S3B.S2=S1且S2S3C.S3=S1且S3 S2D.S3=S2且S3S1解析作出三棱锥在三个坐标平面上的正投影,计算三角形的面积.如下图,△ABC为三棱锥在坐标平面xOy上的正投影,所以S1=1222=2.三棱锥在坐标平面yOz上的正投影与△DE F(E,F 区分为OA,BC的中点)全等,所以S2=1222=2.三棱锥在坐标平面xOz上的正投影与△DGH(G,H区分为AB,OC 的中点)全等,所以S3=1222=2.所以S2=S3且S1S3.应选D. 答案 D2.(2021山东卷)三棱锥P-ABC中,D,E区分为PB,PC的中点,记三棱锥D-ABE的体积为V1,P-ABC的体积为V2,那么V1V2=________.解析由于VP-ABE=VC-ABE,所以VP-ABE=12VP-ABC,又因VD-ABE=12VP-ABE,所以VD-ABE=14VP-ABC,V1V2=14.答案 143.(理)(2021课标全国卷Ⅱ)如图,四棱锥P-ABCD中,底面ABCD 为矩形,PA平面ABCD,E为PD的中点.(1)证明:PB∥平面AEC;(2)设二面角D-AE-C为60,AP=1,AD=3,求三棱锥E-ACD的体积.解 (1)衔接BD交AC于点O,衔接EO.由于ABCD为矩形,所以O为BD的中点.又E为PD的中点,所以EO∥PB.EO平面AEC,PB平面AEC,所以PB∥平面AEC.(2)由于PA平面ABCD,ABCD为矩形,所以AB,AD,AP两两垂直.如图,以A为坐标原点,AB的方向为x轴的正方向,|PA|为单位长,树立空间直角坐标系A-xyz.那么D(0,3,0),E0,32,12, AE=0,32,12.设B(m,0,0)(m0),那么C(m,3,0),AC=(m,3,0),设n1=(x,y,z)为平面ACE的法向量,那么n1AC=0,n1AE=0,即mx+3y=0,32y+12z=0,可取n1=3m,-1,3.又n2=(1,0,0)为平面DAE的法向量,由题设|cos〈n1,n2〉|=12,即 33+4m2=12,解得m=32.由于E为PD的中点,所以三棱锥E-ACD的高为12.三棱锥E-ACD的体积V=131233212=38.3.(文)如图,在Rt△ABC中,AB=BC=4,点E在线段AB上.过点E作EF∥BC交AC于点F,将△AEF沿EF折起到△PEF 的位置(点A与P重合),使得PEB=30.(1)求证:EF(2)试问:当点E在何处时,四棱锥P-EFCB的正面PEB的面积最大?并求此时四棱锥P-EFCB的体积.解 (1)证明:∵AB=BC,BCAB,又∵EF∥BC,EFAB,即EFBE,EFPE.又BEPE=E,EF平面PBE,EFPB.(2)设BE=x,PE=y,那么x+y=4.S△PEB=12BEPEsinPEB=14xy14x+y22=1.当且仅当x=y=2时,S△PEB的面积最大.此时,BE=PE=2.由(1)知EF平面PBE,平面PBE平面EFCB,在平面PBE中,作POBE于O,那么PO平面EFCB.即PO为四棱锥P-EFCB的高.又PO=PEsin30=212=1.S梯形EFCB =12(2+4)2=6.VP-BCFE=1361=2.空间几何体三视图、外表积与体积专题测试的答案和解析希望考生好好应用,提高效果。
高考数学(文科)-空间几何体的三视图、表面积与体积-专题练习 (含答案与解析)
高考数学(文科)专题练习空间几何体的三视图、表面积与体积一、选择题.B...2.如图,一个棱柱的正视图和侧视图分别是矩形和正三角形,则这个三棱柱的俯视图为A....(2016·河南郑州一测如图是一个四面体的三视图,这三个视图均是腰长为和俯视图的虚线是三角形的中线,则该四面体的体积为(C.8 3及其三视图中的正视图和侧视图如图所示,则棱C.38D.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该B.54185+D.81某几何体的三视图如图所示,则该几何体的体积等于C.5 2如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是C.8π《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺。
问:积及为米几何?”其意思为“在屋内墙角处堆放米尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已立方尺,圆周率约为3,估算出堆放的米约有C.36斛如图,网格纸上正方形小格的边长为1(表示,高为6cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯C.10 27均在球O的球面上,AB)的正三角形的三个顶点都在球的表面积为____________.已知一个三棱柱,其底面是正三角形,且侧棱与底面垂直,一个体积为高考数学(文科)专题练习空间几何体的三视图、表面积与体积答案一、选择题1~5.CDABB 6~10.CBBCC二、填空题11;12.40π;13..14.13高考数学(文科)专题练习空间几何体的三视图、表面积与体积解析一、选择题1.解析:该几何体的侧视图即为其在面BCC1B1上的射影,又A点射影为点B,E点射影为线段CC1的中点,故选C.2.解析:由正视图和侧视图可知,这是一个横放的正三棱柱,一个侧面水平放置,则俯视图应为D.3.解析:四面体的直观图如图A-BCD,所以V=×(×1×2)×2=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间几何体的三视图、表面积、体积专题练习
1、若一个几何体的正视图与侧视图均为边长是1的正方形,且体积为
1
2
,则该几何体的俯视图是
2.
3.已知某几何体的俯视图是如图所示的边长为2的正方形,主视图与左视图 是边长为2的正三角形,则其全面积是 A .8
B .12
C
.4(1
D
.
4. 一个几何体的三视图如图所示,则该几何体的体积为
A .14+π
B .
13
4+π
C .83
4+π
D .84+π
5. 如右图,已知一个锥体的正(主)视图,侧(左)视图和俯视图均为直角三角形,且面积分别为3,4,6,则该锥体的体积为
A .24
B .8
C .12
D .4
6. 如右图,一个简单空间几何体的三视图其主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形,则其体积是( ) A.
423 B.433 C.36 D.8
3
7.用大小相同的且体积为1的小立方块搭一个几何体,使它的主视图和俯视图如右图所示,则它的体积的最小值与最大值分别为(
)
俯视图
A .9与13
B .7与10
C .10与16
D .10与15
8.下列几何体各自的三视图中,有且仅有两个视图相同的是( ) A .①② B .①③ C .①④ D .②④
9.一个几何体的三视图如图所示,其中正视图中
ABC 是边长为2的正三角形,俯视图为正六边
形,那么该几何体的侧视图的面积为 A.12 B.32
C.2
3 D.6
10. 如右图所示是某一容器的三视图,现向容器中匀速注水,容器中水面的高度h 随时间t 变化的
图象可能是( )
11.某几何体的一条棱长为7,在该几何体的正视图中,这条棱的投影是长为6的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a 和b 的线段,则a +b 的最大值为( ) A. 22 B. 23 C. 4 D. 2 5
12.如图,一个封闭的立方体,它的六个表面各标有A,B,C,D,E,F 这六个字母之一,现放置成如图的三种不同的位置,则字母A,B,C 对面的字母分别为 ( )
(A) D ,E ,F ( B) F ,D ,E ( C) E, F ,D ( D) E, D,F
13.一个正三棱柱的三视图如下所示,则这个正三棱柱的高 和底面边长分别为( ).
A. 2,
B.
,2 C. 4,2 D. 2,4
14如右图为一个几何体的三视图,尺寸如图所示,则该几何体的表面积为( ).
(不考虑接触点)
主
视
正视图侧视图
俯视图
俯视图
左视图
正视
俯视
侧视
C
A
A.
π
4π
π D. 32+π
15.下列图形不能够成正方体的展开图的是( )
A B C D
16.正方体ABCD-A ’B ’C ’D 中,E 、F 分别为AA ’,C ’D ’的中点,G 为正方形BCC ’B ’中心,则四边形AEFG 在该正方体各个面的投影可能是( ) (本题为多选题)
17.已知正三棱柱(侧棱与底面垂直,底面是正三角形)的高与底面边长均为2,其直观图和正(主)视图如下,则它的左(侧)视图的面积是
.
18.设某几何体的三视图如下左图所示(尺寸的长度单位为m )。
则该几 何体的体积为 3
m
19.一个几何体的三视图及其尺寸(单位:cm)如上右图,则该几何体的 侧面积为________cm 2.
20.如图是一个几何体的三视图,若它的体积是
33,则
a =________.
21.如图E 、F 分别是正方体的面ADD 1A 1、面
BCC
1B
1
的中心,则四边形
BFD
1E 在该正方体的面上的射影可能是下图中的_________(要求把可能的序号都填上).
直观正视
22.如下的三个图中,左边的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm )。
(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;(2)按照给出的尺寸,求该多面体的体积;
23.已知一个圆锥的底面半径为R ,高为H 。
在其中有一个高为x 的内接圆柱。
(1)求圆柱的侧面积。
(2)x 为何值时,圆柱的侧面积最大?
24、如图所示,一个倒圆锥形的容器,它的截面是一个正三角形,在容器内放一个半径为r 的铁球,并向容器内注水,使水面与铁球相切,将球取出后,容器内的水深是多少?
正视图。
