主体间效应的检验
主体间效应的检验
(I-J)
标准误差
Sig.
95%置信区间
下限
上限
初一
初二
11.8000*
3.91052
.021
1.3494
22.2506
高一
13.8000*
3.60211
.002
4.1737
23.4263
高二
5.4818
3.99050
.522
-5.1825
16.1461
初二
初一
-11.8000*
3.91052
.021
-22.2506
-1.3494
高一
2.0000
3.40367
.935
-7.0960
11.0960
高二
-6.3182
3.81233
.358
-16.5063
3.8700
高一
初一
-13.8000*
3.60211
.002
-23.4263
-4.1737
初二
-2.0000
3.40367
.935
-11.0960
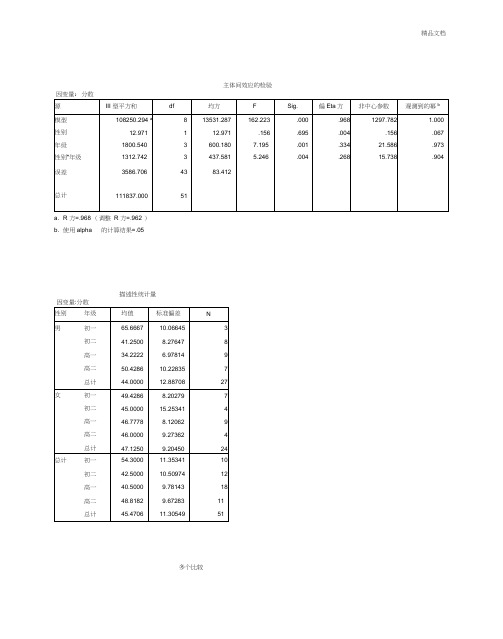
主体间效应的检验
因变量：分数
源
III型平方和ห้องสมุดไป่ตู้
df
均方
F
Sig.
偏Eta方
非中心参数
观测到的幂b
模型
108250.294a
8
13531.287
162.223
.000
.968
1297.782
1.000
性别
12.971
1
12.971
.156
.695
.004
.156
主体间效应的检验
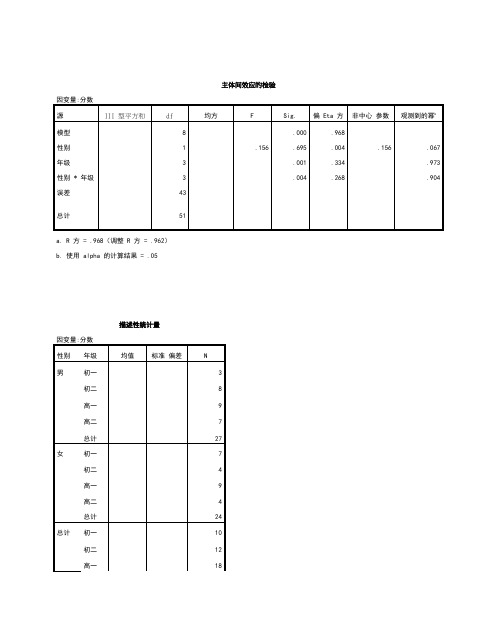
描述性统计量
因变量:分数
性别
年级
均值
标准 偏差
N
男
初一
3
初二
8
高一
9
高二
7
总计
27
女
初一
7
初二
4
高一
9
高二
4
总计
24
总计
初一
10
初二
12
高一
18
高二
11
总计
51
多个比较
分数ቤተ መጻሕፍቲ ባይዱ
Tukey HSD
(I) 年级
(J) 年级
均值差值 (I-J)
标准 误差
Sig.
95% 置信区间
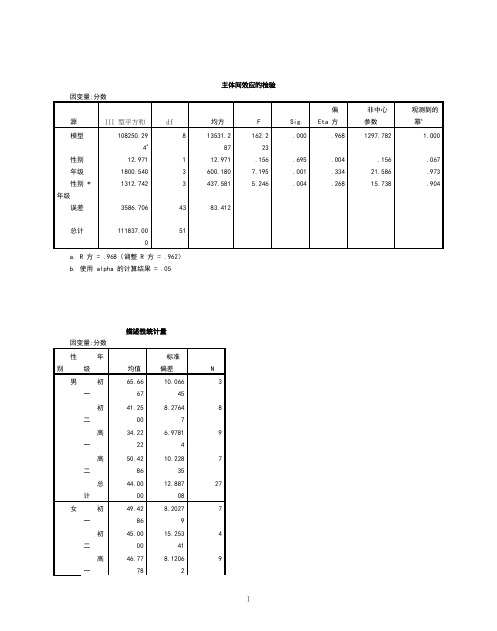
主体间效应的检验
因变量:分数
源
III 型平方和
df
均方
F
Sig.
偏 Eta 方
非中心 参数
观测到的幂b
模型
8
.000
.968
性别
1
.156
.695
.004
.156
.067
年级
3
.001
.334
.973
性别 * 年级
3
.004
.268
.904
误差
43
总计
51
a. R 方 = .968（调整 R 方 = .962）
下限
上限
初一
初二
*
.021
高一
*
.002
高二
.522
初二
初一
*
.021
高一
.935
高二
主体间效应的检验
初二
初一
-11.8000*
3.91052
.021
-22.2506
-1.3494
高一
2.0000
3.40367
.935
-7.0960
11.0960
高二
-6.3182
3.81233
.358
-16.5063
3.8700
高一
初一
-13.8000*
3.60211
.002
-23.4263
-4.1737
.096
-1.0226
17.6590
基于观测到的均值。
误差项为均值方 (错误) = 83.412。
*. 均值差值在 .05 级别上较显著。
初二
-2.0000
3.40367
.935
-11.0960
7.0960
高二
-8.3182
3.49526
.096
-17.6590
1.0226
高二
初一
-5.4818
3.99050
.522
-16.1461
5.1825
初二
6.3182
3.81233
.358
-3.8700
16.5063
高一
8.3182
3.49526
分数
Tukey HSD
(I) 年级
(J) 年级
均值差值 (I-J)
标准 误差
Sig.
95% 置信区间
下限
上限
初一
初二
11.8000*
3.91052
.021
1.3494
22.2506
高一
13.8000*
主体间效应检验python -回复
主体间效应检验python -回复"主体间效应检验python"是指利用Python编程语言进行主体间效应的检验。
主体间效应指的是不同主体（受试者、实验组等）之间的差异，可以用于评估某种处理或干预对不同主体产生的影响的大小。
在进行主体间效应检验时，我们希望能够确定这种差异是否是由于处理造成的，还是由于随机因素引起的。
在进行主体间效应检验之前，需要先收集相关数据。
数据应包括处理组和对照组的观测值或测量结果。
接下来，我们将使用Python进行主体间效应检验的步骤如下：步骤一：导入所需库首先，我们需要导入Python中的一些库，例如pandas、numpy和scipy。
pandas库用于处理数据，numpy库用于数值计算，scipy库用于统计分析。
pythonimport pandas as pdimport numpy as npfrom scipy import stats步骤二：读取数据和数据预处理接下来，我们需要读取数据并进行必要的数据预处理。
首先将数据转换为pandas的DataFrame格式。
pythondata = pd.read_csv('data.csv')确保数据包含处理组和对照组的信息，并进行数据清洗，处理缺失值或异常值等。
步骤三：计算统计量接下来，我们将计算主体间差异的统计量。
常用的统计量有均值、方差、标准差和相关系数等。
pythonmean_group1 = data['group1'].mean()mean_group2 = data['group2'].mean()var_group1 = data['group1'].var()var_group2 = data['group2'].var()std_group1 = data['group1'].std()std_group2 = data['group2'].std()corr = data['group1'].corr(data['group2'])步骤四：可视化数据分布我们可以使用Python中的matplotlib库来可视化处理组和对照组的数据分布情况。
主体间效应的检验
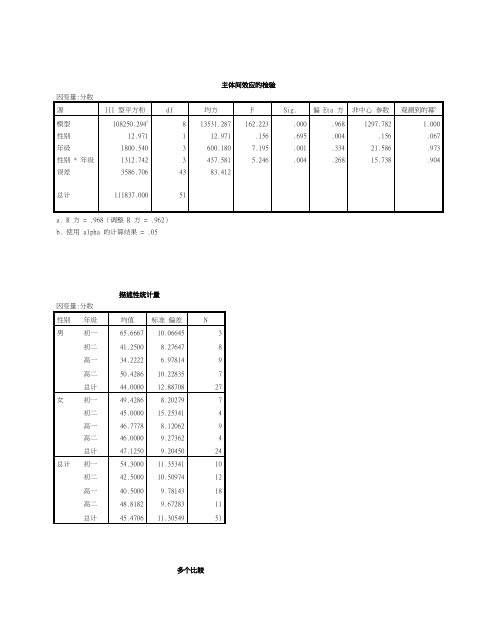
主体间效应的检验因变量:分数源III 型平方和df 均方 F Sig. 偏 Eta 方非中心参数观测到的幂b 模型108250.294a8 13531.287 162.223 .000 .968 1297.782 1.000 性别12.971 1 12.971 .156 .695 .004 .156 .067 年级1800.540 3 600.180 7.195 .001 .334 21.586 .973 性别 * 年级1312.742 3 437.581 5.246 .004 .268 15.738 .904 误差3586.706 43 83.412总计111837.000 51a. R 方 = .968（调整 R 方 = .962）b. 使用 alpha 的计算结果 = .05描述性统计量因变量:分数性别年级均值标准偏差N男初一65.6667 10.06645 3初二41.2500 8.27647 8高一34.2222 6.97814 9高二50.4286 10.22835 7总计44.0000 12.88708 27女初一49.4286 8.20279 7初二45.0000 15.25341 4高一46.7778 8.12062 9高二46.0000 9.27362 4总计47.1250 9.20450 24总计初一54.3000 11.35341 10初二42.5000 10.50974 12高一40.5000 9.78143 18高二48.8182 9.67283 11总计45.4706 11.30549 51多个比较分数Tukey HSD(I) 年级(J) 年级均值差值(I-J) 标准误差Sig.95% 置信区间下限上限初一初二11.8000* 3.91052 .021 1.3494 22.2506 高一13.8000* 3.60211 .002 4.1737 23.4263高二 5.4818 3.99050 .522 -5.1825 16.1461 初二初一-11.8000* 3.91052 .021 -22.2506 -1.3494 高一 2.0000 3.40367 .935 -7.0960 11.0960高二-6.3182 3.81233 .358 -16.5063 3.8700 高一初一-13.8000* 3.60211 .002 -23.4263 -4.1737 初二-2.0000 3.40367 .935 -11.0960 7.0960高二-8.3182 3.49526 .096 -17.6590 1.0226 高二初一-5.4818 3.99050 .522 -16.1461 5.1825 初二 6.3182 3.81233 .358 -3.8700 16.5063高一8.3182 3.49526 .096 -1.0226 17.6590 基于观测到的均值。
主体间效应检验 主体内效应检验
主体间效应检验主体内效应检验主体间效应检验是实验设计中常见的一种统计分析方法，它用于检验不同实验条件（即不同的处理组）对实验结果是否有显著影响。
主体内效应检验则是用于检验同一主体在不同条件下的实验结果是否存在显著差异。
这两种检验方法在实验设计和统计分析中扮演着重要的角色，对于科研工作者来说，理解和掌握这两种方法是至关重要的。
首先，我们来看主体间效应检验。
主体间效应检验通常用于完全随机化实验设计中，比如单因素实验或双因素实验。
它的基本思想是通过对不同处理组的实验结果进行方差分析，来判断实验处理对实验结果的影响是否显著。
在进行主体间效应检验时，需要计算不同处理组的均值和方差，并进行方差分析。
如果方差分析的结果显示实验处理对实验结果有显著影响，那么就可以得出结论认为不同处理组产生的实验结果是有显著差异的。
而主体内效应检验则是针对重复测量实验设计中的统计分析问题。
在重复测量实验设计中，同一主体会在不同条件下进行多次实验，并在不同条件下产生多个实验结果。
主体内效应检验的目的是检验同一主体在不同条件下的实验结果是否存在显著差异。
通常，我们会使用方差分析或t检验来进行主体内效应检验。
如果检验结果显示在不同条件下主体产生的实验结果存在显著差异，那么就说明实验处理对实验结果有显著影响。
主体间效应检验和主体内效应检验都是用于检验实验处理对实验结果的影响是否显著的方法，但它们的应用场景和方法略有不同。
在实际应用中，研究者需要根据具体的实验设计和实验目的来选择合适的检验方法，以确保对实验结果的分析和解释是准确有效的。
总的来说，主体间效应检验和主体内效应检验都是实验设计和统计分析中的重要内容，它们为研究者提供了强有力的工具，帮助他们对实验结果进行分析和解释。
通过对这两种方法的理解和掌握，研究者可以更好地进行科学研究，并取得更准确有效的研究成果。
主体间效应检验 主体内效应检验
主体间效应检验主体内效应检验主体间效应检验和主体内效应检验是心理学和社会科学研究中常用的两种统计分析方法。
主体间效应检验用于检验不同个体（主体）之间的差异，而主体内效应检验则用于检验同一组个体在不同条件下的差异。
本文将分别介绍这两种方法的基本原理、应用场景和步骤，并举例说明如何进行相应的统计分析。
一、主体间效应检验主体间效应检验是用来检验不同个体之间的差异是否显著的统计方法。
它通常用于比较不同群体、不同条件下的个体，以及不同个体在某一因素下的变化情况。
常用的统计方法包括t检验、方差分析（ANOVA）、卡方检验等。
1.基本原理主体间效应检验的基本原理是比较不同个体或群体之间的平均值或比例是否存在显著差异。
它通过计算统计指标（如t值、F值、卡方值）来判断样本之间的差异是否显著，从而推断总体之间的差异是否存在。
2.应用场景主体间效应检验适用于比较不同群体或条件下的个体之间的差异，如男女在数学成绩上的差异、不同年龄组在健康指标上的差异、不同教育水平之间的收入差异等。
3.步骤主体间效应检验的一般步骤包括：（1）建立假设：提出原假设（两个或多个群体没有显著差异）和备择假设（两个或多个群体存在显著差异）；（2）选择合适的统计方法：根据研究设计和变量类型选择合适的统计方法，如t检验、ANOVA、卡方检验等；（3）收集数据并计算统计指标：对样本数据进行收集和整理，计算相应的统计指标（如t值、F值、卡方值）；（4）判断显著性：根据计算得到的统计指标和显著性水平（通常设定为0.05），判断样本之间的差异是否显著；（5）做出推断：对显著性结果进行解释，判断总体之间的差异是否存在。
例子：某研究者对两个不同教育水平的群体进行了数学成绩测试，想要比较它们之间的成绩是否存在显著差异。
他分别收集了高中和大学两个群体的成绩数据，并使用t检验进行了数据分析。
最终结果显示t值为3.21，显著水平为0.01，因此拒绝原假设，认为两个群体在数学成绩上存在显著差异。
主体间效应检验 主体内效应检验
主体间效应检验主体内效应检验主体间效应检验和主体内效应检验是统计学中常用的两种检验方法，用于评估不同主体或同一主体在不同条件下的变化情况。
本文将从定义、原理、应用、实例等方面进行详细阐述。
1.定义主体间效应检验和主体内效应检验是统计学中用于分析实验数据的方法。
主体间效应检验用于比较不同主体（或组）之间的变化情况，主体内效应检验用于比较同一主体在不同条件下的变化情况。
2.原理主体间效应检验是通过比较不同主体（或组）之间的平均值来评估它们之间的变化情况，主要包括方差分析和t检验。
方差分析适用于多个水平的分析，t检验适用于两个水平的分析。
主体内效应检验是通过比较同一主体在不同条件下的平均值来评估它们之间的变化情况，主要包括重复测量t检验和方差分析。
3.应用主体间效应检验和主体内效应检验广泛应用于社会科学、医学、工程等领域的实验研究中。
通过这两种检验方法，研究人员可以更准确地评估实验结果的可靠性和有效性，从而做出科学的结论。
4.实例假设一项实验研究中，研究人员想要比较不同疗法对高血压患者的疗效。
为了评估这一效应，研究人员对不同疗法的患者进行了实验观察。
首先，研究人员使用方差分析方法比较了不同疗法组之间的平均血压变化情况，结果显示不同疗法组之间存在显著差异。
其次，研究人员对每个患者在不同疗法下的平均血压进行了重复测量t检验，结果显示同一患者在不同疗法下的平均血压也存在显著差异。
通过这两种效应检验方法，研究人员得出了科学的结论。
总结而言，主体间效应检验和主体内效应检验是统计学中常用的两种检验方法，用于评估不同主体或同一主体在不同条件下的变化情况。
通过合理的使用这两种方法，可以更准确地评估实验结果，为科学研究提供可靠的数据支持。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
主体间效应的检验
因变量:分数
源III 型平方和df 均方 F Sig. 偏 Eta 方非中心参数观测到的幂b 模型108250.294a8 13531.287 162.223 .000 .968 1297.782 1.000 性别12.971 1 12.971 .156 .695 .004 .156 .067 年级1800.540 3 600.180 7.195 .001 .334 21.586 .973 性别 * 年级1312.742 3 437.581 5.246 .004 .268 15.738 .904 误差3586.706 43 83.412
总计111837.000 51
a. R 方 = .968（调整 R 方 = .962）
b. 使用 alpha 的计算结果 = .05
描述性统计量
因变量:分数
性别年级均值标准偏差N
男初一65.6667 10.06645 3
初二41.2500 8.27647 8
高一34.2222 6.97814 9
高二50.4286 10.22835 7
总计44.0000 12.88708 27
女初一49.4286 8.20279 7
初二45.0000 15.25341 4
高一46.7778 8.12062 9
高二46.0000 9.27362 4
总计47.1250 9.20450 24
总计初一54.3000 11.35341 10
初二42.5000 10.50974 12
高一40.5000 9.78143 18
高二48.8182 9.67283 11
总计45.4706 11.30549 51
多个比较
分数Tukey HSD
(I) 年级(J) 年级均值差值
(I-J) 标准误差Sig.
95% 置信区间
下限上限
初一初二11.8000* 3.91052 .021 1.3494 22.2506
高一13.8000* 3.60211 .002 4.1737 23.4263
高二 5.4818 3.99050 .522 -5.1825 16.1461
初二初一-11.8000* 3.91052 .021 -22.2506 -1.3494
高一 2.0000 3.40367 .935 -7.0960 11.0960
高二-6.3182 3.81233 .358 -16.5063 3.8700
高一初一-13.8000* 3.60211 .002 -23.4263 -4.1737
初二-2.0000 3.40367 .935 -11.0960 7.0960
高二-8.3182 3.49526 .096 -17.6590 1.0226
高二初一-5.4818 3.99050 .522 -16.1461 5.1825
初二 6.3182 3.81233 .358 -3.8700 16.5063
高一8.3182 3.49526 .096 -1.0226 17.6590
基于观测到的均值。
误差项为均值方 (错误) = 83.412。
*. 均值差值在 .05 级别上较显著。
【下载本文档，可以自由复制内容或自由编辑修改内容，更多精彩文章，期待你的好评和关注，我将一如既往为您服务】。