假设检验spss操作例题
SPSS假设检验作业
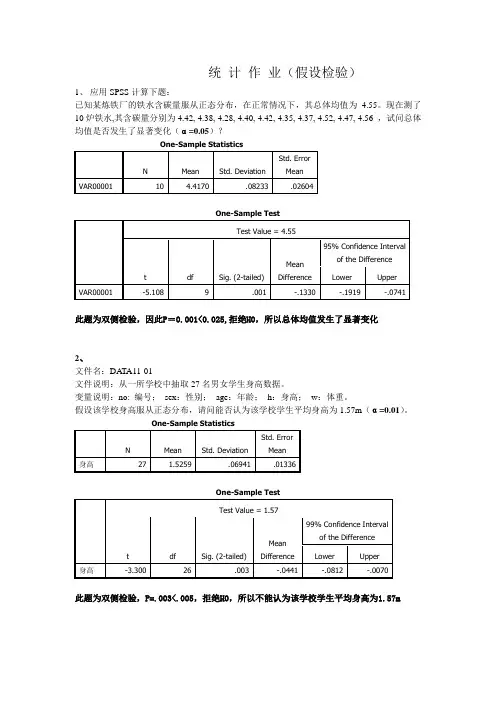
统计作业（假设检验）1、应用SPSS计算下题：已知某炼铁厂的铁水含碳量服从正态分布，在正常情况下，其总体均值为 4.55。
现在测了10炉铁水,其含碳量分别为4.42, 4.38, 4.28, 4.40, 4.42, 4.35, 4.37, 4.52, 4.47, 4.56 ，试问总体均值是否发生了显著变化（α=0.05）？One-Sample Test此题为双侧检验，因此P＝0.001<0.025,拒绝H0，所以总体均值发生了显著变化2、文件名：DATA11-01文件说明：从一所学校中抽取27名男女学生身高数据。
变量说明：no: 编号；sex：性别；age：年龄；h：身高；w：体重。
假设该学校身高服从正态分布，请问能否认为该学校学生平均身高为1.57m（α=0.01）。
One-Sample Test此题为双侧检验，P=.003<.005，拒绝H0，所以不能认为该学校学生平均身高为1.57m3、文件名：DATA11-02文件说明：1973年某市测量120名12岁男孩身高资料。
变量说明：height: 12岁男孩身高当显著性水平分别为α=0.05与0.01时，该市12岁男孩平均身高与该地区男孩平均身高（142.3cm）有无显著差异，并说明所得结论的理由。
当α=0.05时One-Sample Statistics此题为双侧检验，因此P=.162>.025，所以该市12岁男孩平均身高与该地区男孩平均身高（142.3cm）无显著差异当α=0.01时One-Sample StatisticsOne-Sample Test此题为双侧检验，因此P=.162>.005，所以该市12岁男孩平均身高与该地区男孩平均身高（142.3cm）无显著差异4、文件名：DATA09-03文件说明：1969-1971年美国一家银行的474名雇员情况的调查数据，其中包括工资、受教育水平、工作经验、种族等数据。
spss 假设检验
H0: µ = 0⋅ 081mm
___
H1: µ ≠ 0⋅ 081mm
Z=
x − µ0 n
σ
=
0.076 − 0.081 0.025 200
= −2.83
拒绝域
接受域
拒绝域
α = 0.025 2
1−α = 0.95
α = 0.025 2
− 2.83
−1.96
0
1.96
方差已知的均值检验
某批发商欲从厂家购进一批灯泡，根据合同规定，灯泡的使用寿命平均不能低于1000小时。 已知灯泡使用寿命服从正态分布，标准差为20小时。在总体中随机抽取了100个灯泡，得其均值为 960小时，批发商是否应该购进这批灯泡。
H0: µ ≤ 40000km
___
H1: µ f 40000km
t=
x − µ0 41000 − 40000 = ≈ 2.91 s n 5000 120
接受域
拒绝域
1−α = 0.95
α = 0.05
0
t0.05(119) ≈1.658
2.91
一个正态总体的参数检验
一个正态总体均值检验的统计量与拒绝域列表 总体 方差 检 验 统计量
H0: µ ≤1200
H1: µ f1200
接受域
拒绝域
1−α = 0.95
α = 0.05
Z0.05
0
右侧检验
假设检验中的P值
拒绝域
接受域
拒绝域
α = 0.025 2
α = 0.025 2
− Zα = −1.96
2
P = 0.015
0
Zα =1.96 Z = 2.17
2
假设检验spss操作例题
单样本T检验按规定苗木平均高达1.60m以上可以出圃，今在苗圃中随机抽取10株苗木，测定的苗木高度如下：1.75 1.58 1.71 1.64 1.55 1.72 1.62 1.83 1.63 1.65假设苗高服从正态分布，试问苗木平均高是否达到出圃要求？(要求α=0.05)解：1）根据题意，提出：虚无假设H0：苗木的平均苗高为H0=1.6m;备择假设H1：苗木的平均苗高H1>1.6m；2）定义变量：在spss软件中的“变量视图”中定义苗木苗高, 之后在“数据视图”中输入苗高数据；3)分析过程在spss软件上操作分析，输出如下：表1.1:单个样本统计量N 均值标准差均值的标准误苗高10 1.6680 .08430 .02666表1.2:单个样本检验检验值 = 1.6t df Sig.(双侧) 均值差值差分的 95% 置信区间下限上限苗高 2.551 9 .031 .06800 .0077 .1283 4）输出结果分析由图1.1和表1.1数据分析可知，变量苗木苗高成正态分布，平均值为1.6680m，标准差为0.0843，说明样本的离散程度较小，标准误为0.0267，说明抽样误差较小。
由表1.3数据分析可知，T检验值为2.55，样本自由度为9，t检验的p值为0.031<0.05,说明差异性显著，因此，否定无效假设H0，取备择假设H1。
由以上分析知：在显著水平为0.05的水平上检验，苗木的平均苗高大于1.6m，符合出圃的要求。
独立样本T检验从两个不同抚育措施育苗的苗圃中各以重复抽样的方式抽得样本如下：样本1苗高（CM）：52 58 71 48 57 62 73 68 65 56样本2苗高（CM）：56 75 69 82 74 63 58 64 78 77 66 73设苗高服从正态分布且两个总体苗高方差相等（齐性），试以显著水平α=0.05检验两种抚育措施对苗高生长有无显著性影响。
解：1）根据题意提出：虚无假设H0：两种抚育措施对苗木生长没有显著的影响；备择假设H1：两种抚育措施对苗高生长影响显著；2）在spss中的“变量视图”中定义变量“苗高1”，“抚育措施”，之后在“数据视图”中输入题中的苗高数据，及抚育措施，其中措施一定义为“1”措施二定义为“2”；3）分析过程在spss软件上操作分析输出分析数据如下;表2.1:组统计量抚育措施N 均值标准差均值的标准误苗高1 1 10 61.00 8.233 2.6032 12 69.58 8.240 2.379表2.2:独立样本检验方差方程的Levene 检验均值方程的 t 检验F Sig. t df Sig.(双侧)均值差值标准误差值差分的 95% 置信区间下限上限苗高1 假设方差相等.005 .946 -2.434 20 .024 -8.583 3.527 -15.940 -1.227 假设方差不相等-2.434 19.296 .025 -8.583 3.527 -15.957 -1.2104)输出结果分析由上述输出表格分析知：在两种抚育措施下的苗木高度的平均值分别为61.00cm；69.58cm。
spss第二版习题及答案
spss第二版习题及答案SPSS第二版习题及答案SPSS（Statistical Package for the Social Sciences）是一种统计分析软件，广泛应用于社会科学领域的数据分析和研究中。
对于学习SPSS的人来说，掌握习题并查看答案是提高技能的重要途径之一。
本文将为大家介绍一些SPSS第二版习题及其答案，希望能够帮助读者更好地理解和应用SPSS。
一、描述统计学习题1. 对于以下数据集，请计算平均数、中位数、众数、标准差和极差。
数据集：12，15，18，20，22，25，25，27，30，30答案：平均数：23.4，中位数：24，众数：25和30，标准差：6.89，极差：18 2. 对于以下数据集，请计算四分位数和箱线图。
数据集：10，12，15，18，20，22，25，25，27，30，30，32，35，40，45答案：第一四分位数（Q1）：18.5，第二四分位数（Q2）：25，第三四分位数（Q3）：32.5，箱线图：参考附图1。
二、假设检验学习题1. 一个研究人员想要确定一种新的药物是否对治疗抑郁症有效。
他随机选择了100名患有抑郁症的患者，并将他们分为两组：实验组和对照组。
实验组接受新药物治疗，对照组接受安慰剂。
请使用SPSS进行假设检验，判断新药物是否显著改善了患者的抑郁症状。
答案：使用t检验进行假设检验。
设定零假设（H0）：新药物对抑郁症状无显著改善；备择假设（H1）：新药物对抑郁症状有显著改善。
根据样本数据计算得到t值和p值，如果p值小于设定的显著性水平（通常为0.05），则拒绝零假设，认为新药物对抑郁症状有显著改善。
三、相关性分析学习题1. 一个市场研究人员想要确定广告投入和销售额之间的相关性。
他收集了10个不同广告投入和销售额的数据。
请使用SPSS进行相关性分析，并解释结果。
答案：使用Pearson相关系数进行相关性分析。
根据样本数据计算得到相关系数r，r的取值范围为-1到1，如果r接近1，则表示广告投入和销售额之间存在正相关关系；如果r接近-1，则表示存在负相关关系；如果r接近0，则表示不存在线性相关关系。
统计分析实验3 假设检验 (2)
实验三假设检验
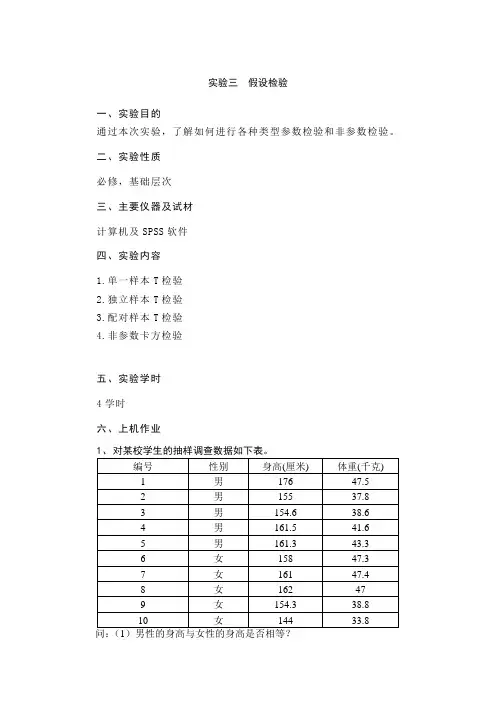
一、实验目的
通过本次实验，了解如何进行各种类型参数检验和非参数检验。
二、实验性质
必修，基础层次
三、主要仪器及试材
计算机及SPSS软件
四、实验内容
1.单一样本T检验
2.独立样本T检验
3.配对样本T检验
4.非参数卡方检验
五、实验学时
4学时
六、上机作业
（2）学生的体重是否等于45公斤？
2.双样本T 检验（Independent-Samples T Test 过程）
分别测得14例老年性慢性支气管炎病人及11例健康人的尿中17酮类固醇
某单位研究饲料中缺乏维生素E 与肝中维生素A 含量的关系，将大白鼠按性别、体重等配为8对，每对中两只大白鼠分别喂给正常饲料和维生素E 缺乏饲料，一段时期后将之宰杀，测定其肝中维生素A 含量（μmol/L ）如下，问饲料
4.如下表
5.某工厂生产一批产品,质量检查规定:其次品率05.00≤p ,则这批产品可以出厂,否则不能出厂. 现从这批产品中抽查50件产品,发现有4件次品,试问这批产品能否出厂?(提示:用非参数的二项分布检验05.00≤p 是否可接受)。
假设检验的SPSS实现
17
试问两种轮胎的耐磨性有没显著差异（a=0.05）？假定甲乙的耐磨性分别符合正太分布，且两个样本独立。
解：首先是输入数据是：
进行配对样本T检验
输出的结果是：
结论：由于显著性概率sig.(2-tailed)=0.025=P-Value<0.05,所以拒绝H0，认为两种轮胎的耐磨性有显著差异。
18
设总体X服从正态分布，总体Y服从正态分布，两个分布相互独立，从两总体分别抽取样本
（1）能否认为是u1=u2，（2）能否认为是两者的方差相等
首先是输入数据：
检验两总体的数学期望是否一致
得到输出的数据：
因为显著性概率sig.(2-tailed)=0.500=P-Value>0.05,所以接受H0，即有两总体分布的数学期望是一致。
spss整理（大题目）
spss整理（大题目）Spass整理第三章统计假设检验二、两样本平均数统计假设检验例3-11.随机抽取 2 个品种的苹果果实的果肉硬度（磅/cm 2），试比较2 品种苹果的果肉硬度是否存在显著差异？SPSS 操作：菜单Analyze —Independent-Samples T Test在独立样本T检验（成组T检验）比较中，结果会分2种情况输出，对应着结果表的数据是2行，第一行是假设方差相等的数据，第二行是假设方差不相等的数据。
最终的结果是看第一行还是第二行，需要看Levene's Test for Equality of Variances（方差齐性检验）的结果。
如果Levene's Test for Equality of Variances 结果是方差相齐的，则看第一行数据，否则看第二行数据。
分析过程：首先，Levene's Test for Equality of Variances H0：2组数据方差相等（相齐），检验结果显著值（Sig.）为0.947 > 0.05，接受H0，2组数据方差相等，看第一行数据. 其次，T检验的显著值（Sig.）是0.458 > 0.05，说明接受T检验的H0：2组数据对应总体的均值无显著差异，即2个品种的苹果果实的果肉硬度无显著差异。
例3-12. 选用10个品种的草莓进行电渗处理和传统方法对草莓果实中钙离子含量的影响，结果如下，请问电渗处理和传统处理方法对草莓果实中钙离子含量是否有显著的差异？SPSS 操作：因为该试验是对10 个品种的每个品种进行2种方法测试，因此需要使用成对样本均值的T 检验，而不能用成组样本的T检验在成对样本T 检验结果表中，需要看T检验的显著值。
分析过程：成对样本T 检验（Paired-Samples T T est）结果，显著值（Sig.）为0 < 0.05 ( 0.01 )，否定H0：2种处理方法对应的总体均值相等，说明传统方法和电渗处理2种方法测试的草莓果实中钙离子含量之间有显著（极显著）差异，根据分析结果，对照—电渗处理的均值小于0，说明电渗处理法测试的草莓果实中钙离子含量显著提高。
SPSS简明操作图示 教学用题
SPSS简明操作图示例1：某医院测得110名男性肾虚病人的Hb值(g/L)为：118148108103138110134140102132140 149138106148133145146123145165148 120135127134141121143100134146132 143135120143140119120148108155128 122130140174160138137134147125141 147137120133123138137147100130112 111120142139142140128141104121132 155131119131142126140146123114142 139102120151122135140147135131138 107149139140125147129142114149151（1）计算均数、中位数、标准差、并比较均数和中位数的差别。
（2）该资料用哪个指标表示集中趋势较好？为什么？（3）编制频数表，绘出频数图。
（4）估计总体参数95%可信区间。
SPSS操作过程：此例分四个步骤进行一、计算描述指标1、建立数据文件如下图左侧HB例所示2、打开分析菜单，选择描述统计，探索，弹出探索对话框，如下图，将需要分析的变量HB 移到因变量列表框内，（当因变量列表框内有变量进入后，“确定”按钮被激活），如下图箭头所示探索对话框的其它内容不用设置，按默认即可，最后单击确定按钮，即可得到分析结果，如下图所示二、进行正态性检验：1、在分析菜单下，选择非参数检验，旧对话框，1－样本K－S，如下图所示2、在弹出对话框中，将待检验变量HB移入检验变量列表框内，如图所示上图中默认钩选了“常规”复选框，这就是作正态性检验的设置，最后单击“确定”，即可得到正态性检验结果，如下图所示从上述结果可知，数据文件HB服从正态分布。
三、编制频数分布表1、在转换菜单里选择“重新编码为不同变量”，弹出如下对话框：2、将HB从左侧移入右侧“数字变量-输出变量框内，在输出变量名称项内输入变量名称X1，然后单击”更改主“按钮，再单击“旧值和新值”按钮，弹出如下对话框：在左侧“旧值”项中，选择“范围”，然后依次填入第一个组段的上下限（100，106.99），在新值项中填入100，再单击“添加”按钮，其它各个组段按此方式填入，总共填入11个组段，最后的组段是（170，176.99），如上图所示，然后单击“继续”按钮。
假设检验-例题讲解
假设检验一、单样本总体均值的假设检验 .................................................... 1 二、独立样本两总体均值差的检验 ................................................ 2 三、两匹配样本均值差的检验 ........................................................ 4 四、单一总体比率的检验 ................................................................ 5 五、两总体比率差的假设检验 .. (7)一、单样本总体均值的假设检验例题：某公司生产化妆品，需要严格控制装瓶重量。
标准规格为每瓶250 克，标准差为1 克，企业的质检部门每日对此进行抽样检验。
某日从生产线上随机抽取16 瓶测重，以95%的保证程度进行总体均值的假设检验。
x t μ-=data6_01 样本化妆品重量 SPSS 操作：（1）打开数据文件，依次选择Analyze （分析）→Compare Means （比较均值）→One Sample T Test （单样本t 检验），将要检验的变量置入Test Variable(s)（检验变量）；（2）在Test Value （检验值）框中输入250；点击Options （选项）按钮，在Confidence Interval（置信区间百分比）后面的框中，输入置信度（系统默认为95%，对应的显著性水平设定为5%，即0.05，若需要改变显著性水平如改为0.01，则在框中输入99 即可）；（3）点击Continue（继续）→OK（确定），即可得到如图所示的输出结果。
图中的第2~5 列分别为：计算的检验统计量t 、自由度、双尾检验p-值和样本均值与待检验总体均值的差值。
使用SPSS 软件做假设检验的判断规则是：p-值小于设定的显著性水平Ɑ时，要拒绝原假设（与教材不同，教材的判断标准是p<Ɑ/2）。
SPSS案例练习一步一步教你操作
字段
设置
可选择： 1.自动选择检验 2.2组以上样本用-Kruskal Wallis
5.答案
Sig值0.001 < 0.05 拒绝原假设 四种病人痰液中嗜酸性白细胞数有差别。
练习题-7
1.题目为两组独立样本 输入资料
2.先检验是否正态 Sig值 0.014,0.292 < 0.05 有数值为非正态
7.答案
检验结果： 方差Sig值 0.759 > 0.05 方差齐 两药降压效果无差异。
练习题-4
1.题目为多组独立样本 输入资料
2.设定变量视图内容
P.S.两组的话：独立样本T检验
3. 因“随机”分配 故选-单因素ANOVA
4. 导入 因子（分组） 因变量（量）
5.检验不同组的方差齐
6.单因素方差分析 显著性（P）0.000 < 0.05 有显著差异，故进一步两两分析
练习题-3
1.题目为2组独立样本 输入资料
2.设定变量视图内容
3.判断差值非正态或正态-探索
4.Sig值0.978，0.533 > 0.05
因正态分布，故选择独立样本T检验 P.S.如果不是正态，用非参-独立样本
左：>100组样本 右：<100组样本
5. 正态分布， 故选择独立样本T检验
6.导入先，后-确定
2.加权个案
计数资料 无论是列联表 或四格表 都要先加权个案
行
4.交叉表设定
列
5.结果-- Pearson卡方统计量
n>=40 且 n'>=5
合计（计数） 所有（期望计数）
6.答案 n’= 26.84 >5 必须使用Pearson卡方 卡方值4.13 Sig值0.042<0.05 有差异 愈合率有差异
实验三 假设检验的SPSS实现
实验三假设检验的SPSS实现一、实验目的与要求1.掌握单样本t检验的基本原理和spss实现方法。
2.掌握两样本t检验的基本原理和spss实现方法。
3.熟悉配对样本t检验的基本原理和spss实现方法。
二、实验内容提要1.从一批木头里抽取5根，测得直径如下（单位：cm）：12.3 12.8 12.4 12.1 12.7(1) 求总体直径95%的置信区间。
（2）是否能认为这批木头的平均直径是12.3cm ?2.比较两批电子器材的电阻，随机抽取的样本测量电阻如题表2所示，试比较两批电子器材的电阻是否相同？A批0.140 0.138 0.143 0.142 0.144 0.148 0.137 B批0.135 0.140 0.142 0.136 0.138 0.140 0.1413. 配对t检验的实质就是对差值进行单样本t检验，要求按此思路对上题进行重新分析，比较其结果和配对t检验的结果有什么异同。
三、实验步骤为完成实验提要1.可进行如下步骤1.在变量视图中新建一个数据，在数据视图中录入数据，在分析中选择比较均值，单样本t检验，将直径添加到检验变量，点击确定。
單一樣本統計資料N 平均數標準偏差標準錯誤平均值直径 5 12.4600 .28810 .12884單一樣本檢定檢定值= 12.3T df 顯著性（雙尾）平均差異95% 差異數的信賴區間下限上限直径 1.242 4 .282 .16000 -.1977 .5177为完成实验提要2.可进行如下步骤2.1 新建一个数据，在变量视图中输入电阻和批次，然后再数据视图中录入数据，分析——比较均值——独立样本T检验（分组选批次，输入1,2）确定群組統計資料批次 N平均數 標準偏差 標準錯誤平均值电阻1 7 .14171 .003773 .001426 27.13886.002610.000986会根据方差齐性检验结果选择T 检验中结果中有用的信息。
为完成内容提要3.需进行如下步骤：3.1. 方法一：在变量视图中添加差值，选择转换的计算变量，在目标变量智能光添加差值，数字表达式为A 组 – B 组，点击确定。
0904-非参数假设检验例题SPSS实现-05信管信计
非参数假设检验SPSS辅助案例六、非参数假设检验：正态分布假设检验
SPSS求解过程：
注：K-S方法的主要思想是通过抽样建立来自总体的经验分布，把经验分布与假设的理论分布相比较，以误差最大建立统计量，求实际最大误差出现时的
P-Value，如果是小概率事件，拒绝
H，否则接受0H。
判别：由于显著性概率sig.(2-tailed)=0.333=P-V alue>0.05,所以接受
H
和用已知分布计算书本题解：计算在各小区间的观察值个数（即实际频数）i
np：
的理论频数i
np计算检验统计量的值，判断总体分布是否为正态分布：由i 、i
在已知观察值出现的频数时，可以用2
分布检验，过程如下：
需要设置频数为权重以识别。
判别：由于显著性概率sig. =0.999=P-V alue>0.05,所以接受
H
七、均匀分布假设检验
判别：由于显著性概率sig.(2-tailed)=1=P-V alue>0.05,所以接受
H
独立性假设检验：
如果应用2 （chi-Square）检验两个总体的独立性，可采用列联表形式，过程如下：
仍需要对频数进行设置为权重以识别。
判别：由于皮尔逊2 检验的显著性概率
sig.(2-tailed)=0.530=P-V alue>0.05, 所以接受
H。
书本题解过程：
应是n。
201204-假设检验例题SPSS实现-05信管信计
一、假设检验例题SPSS实现
（题目描述、SPSS求解、书解过程）
一、正态总体均值（一个总体）、均值差（两个独立总体）的假设检验
1)、一个总体的T检验SPSS求解过程
判别：由于显著性概率sig.(2-tailed)=0.589=P-Value>0.05,所以接受
0H ，其中，均值标准误差定义为: Std. Error Mean=
n
S ,S 是样
本标准差，n 是样本容量 。
2)、两个总体的T 检验SPSS 求解过程
判别：由题意，两总体方差相等，即显著性概率sig.(2-tailed)=0.048=P-Value<0.05,所以否定0H。
书本题解：
二、配对与不配对情况下两个正态总体均值差的假设检验
1）不配对假设检验
判别：由于显著性概率sig.(2-tailed)=0.614=P-Value>0.05,所以接受H。
书本题解：
2）数据配对试验：
判别：由于显著性概率sig.(2-tailed)=0.025=P-Value<0.05,所以拒绝H。
书本题解：
三、二项分布（两点分布）未知参数检验
例：设某市订阅K 杂志的家庭占20%，为了判断是否有比例减少的迹象，抽取100个家庭调查，有16户订阅K 杂志，问是否可判断订阅率有显著下降？
设总体X 是订阅户数，K 杂志的订阅率为P ，每户订阅独立 提出假设：0H ：P=0.2 ，1H ：P 0.2
SPSS 过程如下：
判别：由于显著性概率sig.(1-tailed)=0.36=P-Value>0.05,所以接受
H
0即订阅率没有显著下降。
用SPSS来来验证假设检验是否合理
《数理统计学》上机试验报告格式试验名称：成绩：姓名班级点名号试验日期2011-12-8 试验地点试验目的与要求用SPSS来来验证假设检验是否合理。
试验原理6（2）分析→比较均值→单样本t检验→检验变量选“内径”、a=95、检验值取100 →确定。
12.分析→比较均值→独立样本t检验→检验变量选“型号”、a=99 、分组变量选分组并分别赋值1和2→确定。
14. 分析→比较均值→独立样本t检验→检验变量选“温度”、a=95 、分组变量选组2并分别赋值3和4→确定。
试验内容6（2）. 1. 从一批钢管抽取10根，测得其内径（单位：mm）为：100.36 100.31 99.99 100.11 100.64100.85 99.42 99.91 99.35 100.10.设这批钢管内直径服从正态分布N（μ，σ2），试在下列条件下检验假设（α =0.05）. σ未知。
12.下面给出两种型号的计算器充电以后所能使用的时间（H）的观测值型号A 5.5 5.6 6.3 4.6 5.3 5.0 6.2 5.8 5.1 5.2 5.9 ；型号B 3.8 4.3 4.2 4.0 4.9 4.5 5.2 4.8 4.5 3.9 3.7 4.6设两样本独立且数据所属的两总体的密度函数至多差一个平移量，试问能否认为型号A的计算器平均使用时间比型号B来的长（取a=0.001）?14.在针织品漂白工艺过程中，要考察温度对针织品的断裂强力（主要质量指标）的影响。
为了比较70摄氏度与80摄氏度的影响有无差别，在这两个温度下分别重复做了8次试验，得数据如下（单位：N）：70摄氏度：20.5 18.8 19.8 20.9 21.5 19.5 21.0 21.2；80摄氏度：17.7 20.3 20.0 18.8 19.0 20.1 20.0 19.1根据经验，温度对针织品断裂强度的波动没有影响。
问在70摄氏度的平均断裂强力与80摄氏度断裂强力见是否有显著差别？（假定断裂强力服从正态分布，σ=0.05）试验结论6（2）单个样本统计量N 均值标准差均值的标准误内径10 100.1040 .47596 .15051单个样本检验检验值 = 100t df Sig.(双侧) 均值差值差分的 95% 置信区间下限上限内径.691 9 .507 .10400 -.2365 .4445Sig﹥a 接受所以取μ=10012.组统计量分组N 均值标准差均值的标准误型号甲11 5.5000 .52345 .15783乙12 4.3667 .46775 .13503独立样本检验方差方程的 Levene 检验均值方程的F Sig. t df Sig.(双侧) 均值差标型号假设方差相等.100 .755 5.484 21 .000 1.1假设方差不相等 5.456 20.172 .000 1.1型号甲即型号A的均值为5.5 型号乙即型号B的均值为4.3667,所以A的平均使用时间比乙的长。
SPSS-假设检验
题目：抽样40名学生，教学方案实施后他们的体育成绩是否有显著变化？原始数据：假设检验原始数据.xls解析如下：1、首先分析原始数据是否符合正态分布。
分析步骤1）2）选择选择教学方案实施前后体育成绩变量进入变量框中。
3）在统计量栏中选择相关的标准差、方差等。
4）在图表栏中选择直方图，并在带正态曲线前得复选框中打勾。
5）单击OK。
6）得到正态分布表。
如图所示：我2、进行假设检验分析如图所示：我们可以判定原始数据基本符合正态分布，所以可以对原始数据进行假设检验分析。
注意：组1为前侧，组2为后侧。
分析步骤1）输入数据，依次单击分析—比较均值—独立样本T检验，打开独立样本T检验对话框。
2）选择选择教学方案实施前后体育成绩变量进入检验变量框中。
3）选择选择分组变量进入分组变量框中。
4）在选定分组后点击定义组，在组1，组2后面的方框内输入1,2（分别代表前侧和后侧成绩）然后点击确定。
5）在独立样本T检验对话框中单击选项，置信区间选为95%，缺失值选择按分析顺序排除个案。
6）单击确定。
得到如下结果：分析结果如下：由于F=3.535，P=0.064﹥0.05,所以这40名学生的前后侧成绩方差齐性，前侧的平均成绩为65.28, 后侧的平均成绩为68.13，两个样本的平均水平不等,它们之间的差异是否有显著不同?在两个总体有共同方差的前提下,检验统计量t=-1.055.自由度为df=78,两个样本平均数之差=-2.850，两样本数据之差的标准误=2.703,双尾P=0.295﹥0.10,应接受原假设,即可以认为实施教学方案后学生的体育成绩不存在显著差异。
熟练使用SPSS进行假设检验
熟练使用SPSS进行假设检验试验内容:[试验][例］某克山病区测得11例克山病患者与13名健康人的血磷值mmol/L如下,问该地急性克山病患者与健康人的血磷值是否不同。
表1 克山病区调查数据结果患者0。
84 1.05 1。
20 1.20 1.39 1。
53 1.67 1.80 1。
87 2.07 2。
11健康0.54 0.64 0.64 0。
75 0.76 0。
81 1。
16 1.20 1。
34 1.35 1。
48 1。
56 1.87人1。
录入数据。
将组别设为g，可将患者组设为1 ,健康人设为2，血磷值设为x ，如患者组中第一个测量到的血磷值为0。
84，则g为1,x为0.84,其他数据均仿此录入，如下图所示。
图1 数据输入界面2.统计分析。
依次选择“Analyze"、“Compare means"、“Independent Samples T Test”。
图2 选择分析工具3。
弹出对话框如下图所示，将x选入Test Variables、g选入Grouping Variable,并单击下方的Define Groups按钮，弹出定义组对话框，默认选项为Use Specified Value，在Group1和Group2框中分别填入1和2，即要对组别变量值为1和2的两个组做t检验,另外Options对话框中可选择置信度和处理缺失值的方法.图3 选择变量进入右侧的分析列表SPSS输出的结果和结果说明：图4 输出结果表2 统计量描述列表G N Mean Std.DeviationStd. Error MeanVAR00001 1 11 1.5209 。
4218 .12722 13 1.0846 .4221 .1171表3 假设检验结果表F Sig.t df Sig。
MeanDifference Std. ErrorDifference95% Confidence Interval of theDifferenceLower UpperEqual variances assumed .032。
【SPSS初级教程】6-1(假设检验概念和方法)
假设检验中的两类错误 （决策结果）
H0: 无罪 假设检验就好像一场审判过程
统计检验过程
陪审团审判
裁决
实际情况
之所以用零来修饰原假设，其原因是原假设 的内容总是没有差异或没有改变，或变量间 没有关系等等 零假设总是一个与总体参数有关的问题，所 以总是用希腊字母表示。关于样本统计量如 样本均值或样本均值之差的零假设是没有意 义的，因为样本统计量是已知的，当然能说 出它们等于几或是否相等
提出原假设和备择假设
什么是备择假设？(alternative hypothesis) 与原假设对立的假设，也称“研究假设” 研究者想收集证据予以支持的假设总是有不等号:
5. 建立的原假设与备择假设应为
6.
H0: = 10 H1:
10
双侧检验 (显著性水平与拒绝域 )
抽样分布
拒绝域
置信水平 拒绝域
a/2
1-
a/2
临界值
H0值
样本统计量 临界值
双侧检验 (显著性水平与拒绝域)
抽样分布
置信水平
拒绝域
拒绝域
a/2
1-
a/2
临界值
H0值 临界值 样本统计量
双侧检验 (显著性水平与拒绝域)
1. 总体参数的真值 随着假设的总体参数的减少而增大 2. 显著性水平 当 减少时增大 3. 总体标准差 当 增大时增大 4. 样本容量 n 当 n 减少时增大
什么是P 值? (P-value)
1. 是一个概率值 2. 如果原假设为真，P-值是抽样分布中大于或小于样本统计量的
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
单样本T检验
按规定苗木平均高达1.60m以上可以出圃，今在苗圃中随机抽取10株苗木，测定的苗木高度如下：
1.75 1.58 1.71 1.64 1.55 1.72 1.62 1.83 1.63 1.65
假设苗高服从正态分布，试问苗木平均高是否达到出圃要求？(要求α=0.05)
解：1）根据题意，提出：
虚无假设H0：苗木的平均苗高为H0=1.6m;
备择假设H1：苗木的平均苗高H1>1.6m；
2）定义变量：在spss软件中的“变量视图”中定义苗木苗高, 之后在“数据视图”中输入苗高数据；
3)分析过程
在spss软件上操作分析，输出如下：
表1.1:单个样本统计量
N 均值标准差均值的标准误
苗高10 1.6680 .08430 .02666
表1.2:单个样本检验
检验值 = 1.6
t df Sig.(双侧) 均值差值差分的 95% 置信区间下限上限
苗高 2.551 9 .031 .06800 .0077 .1283 4）输出结果分析
由图1.1和表1.1数据分析可知，变量苗木苗高成正态分布，平均值为1.6680m，标准差为0.0843，说明样本的离散程度较小，标准误为0.0267，说明抽样误差较小。
由表1.3数据分析可知，T检验值为2.55，样本自由度为9，t检
验的p值为0.031<0.05,说明差异性显著，因此，否定无效假设H0，取备择假设H1。
由以上分析知：在显著水平为0.05的水平上检验，苗木的平均苗高大于1.6m，符合出圃的要求。
独立样本T检验
从两个不同抚育措施育苗的苗圃中各以重复抽样的方式抽得样本如下：
样本1苗高（CM）：52 58 71 48 57 62 73 68 65 56
样本2苗高（CM）：56 75 69 82 74 63 58 64 78 77 66 73
设苗高服从正态分布且两个总体苗高方差相等（齐性），试以显著水平α=0.05检验两种抚育措施对苗高生长有无显著性影响。
解：1）根据题意提出：
虚无假设H0：两种抚育措施对苗木生长没有显著的影响；
备择假设H1：两种抚育措施对苗高生长影响显著；
2）在spss中的“变量视图”中定义变量“苗高1”，“抚育措施”，之后在“数据视图”中输入题中的苗高数据，及抚育措施，其中措施一定义为“1”措施二定义为“2”；
3）分析过程
在spss软件上操作分析输出分析数据如下;
表2.1:组统计量
抚育措施N 均值标准差均值的标准误
苗高1 1 10 61.00 8.233 2.603
2 12 69.58 8.240 2.379
表2.2:独立样本检验
方差方程的
Levene 检验均值方程的 t 检验
F Sig. t df Sig.(双
侧)
均值差
值
标准误
差值
差分的 95% 置信
区间
下限上限
苗高1 假设方
差相等
.005 .946 -2.434 20 .024 -8.583 3.527 -15.940 -1.227 假设方
差不相
等
-2.434 19.296 .025 -8.583 3.527 -15.957 -1.210
4)输出结果分析
由上述输出表格分析知：在两种抚育措施下的苗木高度的平均值分别为61.00cm；69.58cm。
苗高均值差异性分析的F值为0.946，说明通过方差方程的检验其两总体的苗高均值齐性，标准差分别为8.233、8.240。
由表2.2知通过均值方程的t检验的t值为-2.434，样本的p值为0.024<0.05，说明差异性显著，因此，拒绝虚无假设H0，肯定备择假设H1。
由分析知，在显著水平为0.05水平时检验，两种抚育措施对于苗高的影响显著。
配对样本T检验
为比较两种方法对乳酸饮料中脂肪含量测定结果是否不同，某人随机抽取了10份乳酸饮料制品，分别用脂肪酸水解法和哥特里－罗紫法测定其结果如下表第(1)～(3)栏。
问两法测定结果是否不同？
两种方法对乳酸饮料中脂肪含量的测定结果(%)
解：1）根据题意提出：
虚无假设H0：两种方法的测定结果是相同的的
备择假设H1：两种方法的测定结果是不同的；
2）在spss中的“变量视图”中定义变量“方法1”，“方法2”，之后在“数据视图”中分别输入题中的方法1和方法2的检测结果。
3）分析过程
在spss软件上操作分析输出分析数据如下：
4)输出结果分析
由上述输出表格分析知：在表3.1中，两种测量方法下的脂肪含量的平均值分别为0.79520%；0.52280%。
标准差分别为0.184362、0.185981。
说明方法1的测定结果均值较高，标准差较小。
采用配对样本t检验进行验证，由表3.2表示配对样本的相关分析。
由表3.3可知，配对t 检验结果, t = 7.926,自由度=9，双侧检验P=0.000＜0.05，说明差异性显著，因此，拒绝虚无假设H0，肯定备择假设H1。
由分析知，在显著水平为0.05水平时检验，可认为两种方法对脂肪含量的测定结果不同，哥特里－罗紫法测定结果较高。
单因素方差分析
某化肥生产商需要检验三种新产品的效果，在同一地区选取3块同样大小的农田进行试验，甲农田中使用甲化肥，在乙农田使用乙化肥，在丙地使用丙化肥，得到6次试验的结果如表所示，试在0.05的显著性水平下分析甲乙丙化肥的肥效是否存在差异。
三块农田的产量
解：1）根据题意提出：
虚无假设H0：三块农田的产量均值是相同的的
备择假设H1：三块农田的产量均值是不同的；
2）在spss中的“变量视图”中定义变量“产量”，“化肥”，之后在“数据视图”中分别输入题中的产量和化肥的数据。
3）分析过程
在spss软件上操作分析输出分析数据如下：
4)输出结果分析
由上述输出表格分析知：在表4.1中，施用三种化肥的产量的平均值分别为48.83 ，41.33，49.31。
标准差分别为2.041 ，4.367 ，1.751。
在图4.1中可以看出三种化肥使用后的产量均值是不相等的，图4.2表明产量是成正态分布的。
对于影响产量的因素仅化肥种类一项，因此可以采用单因素方差分析进行多总体样本均值检验。
由表4.2可知单因素方差组间检验结果 F =13.745,自由度=2，双侧检验P=0.00＜0.05，说明差异性显著，因此，拒绝虚无假设H0，接受备择假设H1。
由分析知，在显著水平为0.05水平时检验，可认为三种化肥对施用后的产量均值不同，其中丙种化肥产量最高，肥效最好。
多因素方差分析
研究目的：超市中某商品的销量与摆放位置和超市规模关系
研究方法：按照超市规模选择大、中、小三家超市，在每家超市中随机选A货架1（货架阳面第一位）、B端架、C堆头、D货架2（货架阳面第二位）各两个位置，记录其统一周期商品的销
售量，然后对其做单变量多因素方差分析。
解：1）根据题意提出：
虚无假设H0：同种商品在不同规模超市和不同摆放位置的情况下，销售量不存在显著差异。
备择假设H1：同种商品在不同规模超市和不同摆放位置的情况下，销售量存在显著差异。
2）在spss中的“变量视图”中定义变量“规模”，“位置”，“销售量”之后在“数据视图”中分别输入题中的规模和位置，销售量的数据。
3）分析过程
在spss软件上操作分析输出分析数据如下：
4)输出结果分析
由表5.1可知，变量“超市规模”有三个水平，即大型、中型和小型，每个水平有8个个案；变量“摆放位置”有4个水平，即A、B、C和D，每个水平有6个个案。
从表5.2可知，从表中可以看出，同种商品不同规模和不同摆放位置的“销售量”的检验统计量F的观测值为30.409，检验的概率值为0，小于0.05，拒绝虚无假设，接受备择假设，可以认为同种商品在不同规模超市和不同摆放位置的情况下，销售量存在显著差异。
由表5.3可知，从表中可以看出，超市规模越大，相应的销量也就越高。
由表5.4可知，C位置销量＞B位置销量＞A位置销量＞B位置销量，也就是说堆头位置销量＞端架位置销量＞货架阳面第一位＞货架阳面第二位，这也就是为什么超市里的堆头、端架向来都是各供应商争抢阵地。
总结：
同种商品在不同规模超市和不同摆放位置的情况下，销售量存在显著差异，并且堆头位置销量＞端架位置销量＞货架阳面第一位＞货架阳面第二位。