用SPSS作假设检验
假设检验及SPSS实现
问两矿所采煤的平均含灰率有无显著差异?(α=0.05)
操作步骤:
(1)定义变量 x，g，输入数据;
(2)正态检验，先分组再检验，方差齐性检验；
(3)选择Analyze
Compare Means
Independent –Sample T Test ;
(4)将变量X放置Test栏中,将g放入分组变量，定 义g的取值;
例3
某单位研究饮食中缺乏维生素E 与肝中维生 素A 含量的关系，将同种属的大白鼠按性别 相同，年龄、体重相近者配成对子。共8对， 并将每对中的两头动物随机分到正常饲料组 和维生素E缺乏组。过一定时期后将大白鼠 杀死，测得其肝中维生素A的含量。
不同饲料组大白鼠维生素A 含量数据表
大白鼠对号 1 2 3 4 5 6 7 8 正常饲料组 3550 2000 3000 3950 3800 3750 3450 3050 维生素E缺乏组2450 2400 1800 3200 3250 2700 2500 1750
(5)单击OK按钮执行.
注：两总体的均值检验要考虑方差相等还是不等，因此事 先要进行方差的检验。
T- Test基本描述统计
甲矿煤的平均含灰率为21.6%，乙矿的平均含灰率为 20.9%，两个样本的平均水平不等,它们之间的差异是 否有显著不同?
T- Test结果
Independent Samples Test
第1章 假设检验
对总体提出一假设，然后借助样本对该 假设进行检验。
基本概念
原假设 H0: 在统计学中,把需要通过样本去推断正 确与否的命题,称为原假设,又称零假设.它常常是 根据已有资料或经过周密考虑后确定的.
备择假设H1: 与原假设对立的假设. 显著性水平(significant level ) α: 确定一
假设检验spss操作例题
单样本T检验按规定苗木平均高达1.60m以上可以出圃，今在苗圃中随机抽取10株苗木，测定的苗木高度如下：1.75 1.58 1.71 1.64 1.55 1.72 1.62 1.83 1.63 1.65假设苗高服从正态分布，试问苗木平均高是否达到出圃要求？(要求α=0.05)解：1）根据题意，提出：虚无假设H0：苗木的平均苗高为H0=1.6m;备择假设H1：苗木的平均苗高H1>1.6m；2）定义变量：在spss软件中的“变量视图”中定义苗木苗高, 之后在“数据视图”中输入苗高数据；3)分析过程在spss软件上操作分析，输出如下：表1.1:单个样本统计量N 均值标准差均值的标准误苗高10 1.6680 .08430 .02666表1.2:单个样本检验检验值 = 1.6t df Sig.(双侧) 均值差值差分的 95% 置信区间下限上限苗高 2.551 9 .031 .06800 .0077 .1283 4）输出结果分析由图1.1和表1.1数据分析可知，变量苗木苗高成正态分布，平均值为1.6680m，标准差为0.0843，说明样本的离散程度较小，标准误为0.0267，说明抽样误差较小。
由表1.3数据分析可知，T检验值为2.55，样本自由度为9，t检验的p值为0.031<0.05,说明差异性显著，因此，否定无效假设H0，取备择假设H1。
由以上分析知：在显著水平为0.05的水平上检验，苗木的平均苗高大于1.6m，符合出圃的要求。
独立样本T检验从两个不同抚育措施育苗的苗圃中各以重复抽样的方式抽得样本如下：样本1苗高（CM）：52 58 71 48 57 62 73 68 65 56样本2苗高（CM）：56 75 69 82 74 63 58 64 78 77 66 73设苗高服从正态分布且两个总体苗高方差相等（齐性），试以显著水平α=0.05检验两种抚育措施对苗高生长有无显著性影响。
解：1）根据题意提出：虚无假设H0：两种抚育措施对苗木生长没有显著的影响；备择假设H1：两种抚育措施对苗高生长影响显著；2）在spss中的“变量视图”中定义变量“苗高1”，“抚育措施”，之后在“数据视图”中输入题中的苗高数据，及抚育措施，其中措施一定义为“1”措施二定义为“2”；3）分析过程在spss软件上操作分析输出分析数据如下;表2.1:组统计量抚育措施N 均值标准差均值的标准误苗高1 1 10 61.00 8.233 2.6032 12 69.58 8.240 2.379表2.2:独立样本检验方差方程的Levene 检验均值方程的 t 检验F Sig. t df Sig.(双侧)均值差值标准误差值差分的 95% 置信区间下限上限苗高1 假设方差相等.005 .946 -2.434 20 .024 -8.583 3.527 -15.940 -1.227 假设方差不相等-2.434 19.296 .025 -8.583 3.527 -15.957 -1.2104)输出结果分析由上述输出表格分析知：在两种抚育措施下的苗木高度的平均值分别为61.00cm；69.58cm。
实验3 假设检验
实验报告课程名称试验设计与数据分析姓名邵建智学号3110100122专业生物系统工程实验名称假设检验浙江大学生物系统工程与食品科学学院二O一三年八月制实验三：假设检验实验类型：上机操作实验地点：农生环D-414指导老师：傅霞萍实验日期：2013 年10 月8 日一、实验目的和要求（1）熟练使用SPSS进行假设检验（工具/Analyze/Compare means）二、实验内容和原理2.1实验原理假设检验是一种由样本的差异去推断样本所在总体是否存在差异的统计方法。
常用于解决两种工艺方法的比较、一种新添加剂与对照两处理的比较、两种食品内含物测定方法的比较、检验某产品是否达到某项质量标准、检验某项有害物指标是否超标等问题。
根据涉及的统计量不同，选择进行u检验、t检验、F检验等显著性检验。
2.2 实验内容（显著性水平α＝5%）（1）单样本t检验问题1：某公司经理宣称他的雇员英语水平很高，如果按照英语六级考试，一般平均得分为75分，现从雇员中随机选出11人参加考试，得分如下：80，81，72，60，78，65，56，79，77，87，76问：该经理的宣称是否可信？（2）两独立样本t检验问题2：分别在10个食品厂各自测定了大米饴糖和玉米饴糖的还原糖含量，结果见下表，试比较两种饴糖的还原糖含量有无显著差异？（3）成对样本（两配对样本）t检验目的：利用来自两个总体的配对样本数据，推断两个总体的均值是否存在显著差异。
问题3：以下是对促销人员进行培训前后的促销数据，试问该培训是否产生了显著效果。
三、主要仪器设备/实验环境（使用的软件等）IBM SPSS 19.0等四、操作方法与实验步骤（必填，上机操作过程，可以插图）a)提出原假设H0b)选择检验统计量c)计算检验统计量观测值和概率P值d)给定显著性水平α并作出决策（1）单样本t检验选择“分析”-“比较均值”-“单样本T检验”检验变量选择“成绩”，检验值设为75，单击“确定”（2）两独立样本t检验选择“分析”-“比较均值”-“独立样本T检验”使用指定值，组1为：1，组2为：2，单击“继续”检验变量选择“含糖量”，分组变量选择“品种”，单击“确定”（3）成对样本（两配对样本）t检验选择“分析”-“比较均值”-“配对样本T检验”成对变量选择“培训前”和“培训后”为一对，单击“确定”五、实验数据记录和处理（必填，图表数据、计算结果、对图表的处理）（1）单样本t检验（3）成对样本（两配对样本）t检验六、实验结果与分析（必填）（1）单样本t检验1）11个样本的均值，标准差，均值的标准误分别为73.73,9,51,2,880。
如何在spss上进行假设检验
当两样本的方差齐时，看第一行。不齐，看第二行。Sig与0.1?
四、完全随机设计方差分析
1、检验是否满足正正态性、方差齐性
Analyze------desctiptive statistic -------explore-------plots-------none normality plots with tests (正态性）、untransformed(组间方差齐性检验)(选择相应的dependent list、factor list)----ok
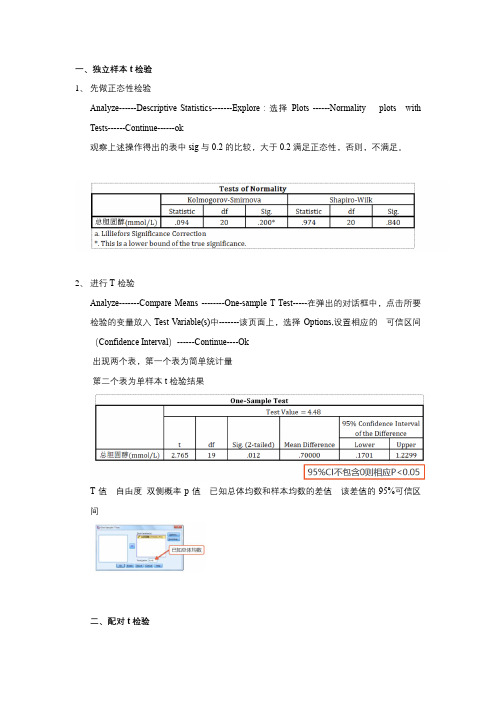
一、独立样本t检验
1、先做正态性检验
Analyze------DescriptiveStatistics-------Explore：选择Plots------Normality plots with Tests------Continue------ok
观察上述操作得出的表中sig与0.2的比较，大于0.2满足正态性，否则，不满足。
3、两组间多重比较
Analyze-----Nonparametric Tests----Legacy Dialogs----2 Independent Samples----选入相应的Test Variable List（应变量）和Grouping Variable选好要比较的两组放在前后相应的位置，两两依次比较---- Mann-Whitney U检验----OK
4、多重比较
Analyze----General Linear Model---- Univariate----Post Hoc----block(区组)----group（处理）------ Bonferroni---- Continue------OK
使用SPSS进行市场调查数据分析的步骤
使用SPSS进行市场调查数据分析的步骤第一章：准备调查数据市场调查数据的准备是进行数据分析的首要步骤。
在这一章节中，我们将讨论如何准备和收集市场调查数据，以便能够进行后续的分析。
1.1 确定调查目的和设计在进行市场调查之前，我们需要明确调查的目的和设计。
这包括确定调查的研究问题、调查对象、调查方式以及样本规模等。
只有明确了调查目的和设计，我们才能有针对性地收集和准备数据。
1.2 收集数据市场调查数据可以通过不同的方式收集，例如问卷调查、个人访谈、焦点小组讨论等。
在收集数据时，我们需要注意确保数据的可靠性和有效性。
因此，在设计问卷或进行访谈时，要保证问题的清晰明确，避免引导性问题和双重否定等。
1.3 数据录入和清洗收集到的市场调查数据需要进行录入和清洗。
数据录入可以通过手动输入或扫描问卷等方式进行。
在录入过程中，要检查数据的准确性，确保没有错误的输入。
清洗数据是指检查和处理数据中的不一致、缺失或异常值等问题，以便后续的分析能够得到可靠的结果。
第二章：数据探索与描述在进行数据分析之前，我们需要对数据进行探索和描述，以了解数据的特征和分布情况。
这有助于为后续的分析提供参考和依据。
2.1 描述性统计描述性统计是对数据进行总体和特征描述的统计方法。
我们可以计算数据的均值、中位数、方差、标准差等指标，来描述数据的集中趋势和离散程度。
此外，还可通过绘制直方图、箱线图等图表来展示数据的分布情况。
2.2 数据相关性分析在市场调查中，数据之间可能存在相关性。
为了了解变量之间的关系，我们可以使用相关系数进行分析。
通过计算相关系数，我们可以判断两个变量之间的线性相关程度，并绘制散点图来展示其关系。
2.3 分组分析市场调查数据通常包含多个变量，我们可以通过分组分析来探究变量之间的差异性。
比如，我们可以将样本分为不同的年龄组或性别组，分析不同群体在某个变量上的差异。
第三章：假设检验在市场调查数据分析中，经常需要进行假设检验来验证研究假设的成立。
spss 假设检验
H0: µ = 0⋅ 081mm
___
H1: µ ≠ 0⋅ 081mm
Z=
x − µ0 n
σ
=
0.076 − 0.081 0.025 200
= −2.83
拒绝域
接受域
拒绝域
α = 0.025 2
1−α = 0.95
α = 0.025 2
− 2.83
−1.96
0
1.96
方差已知的均值检验
某批发商欲从厂家购进一批灯泡，根据合同规定，灯泡的使用寿命平均不能低于1000小时。 已知灯泡使用寿命服从正态分布，标准差为20小时。在总体中随机抽取了100个灯泡，得其均值为 960小时，批发商是否应该购进这批灯泡。
H0: µ ≤ 40000km
___
H1: µ f 40000km
t=
x − µ0 41000 − 40000 = ≈ 2.91 s n 5000 120
接受域
拒绝域
1−α = 0.95
α = 0.05
0
t0.05(119) ≈1.658
2.91
一个正态总体的参数检验
一个正态总体均值检验的统计量与拒绝域列表 总体 方差 检 验 统计量
H0: µ ≤1200
H1: µ f1200
接受域
拒绝域
1−α = 0.95
α = 0.05
Z0.05
0
右侧检验
假设检验中的P值
拒绝域
接受域
拒绝域
α = 0.025 2
α = 0.025 2
− Zα = −1.96
2
P = 0.015
0
Zα =1.96 Z = 2.17
2
spss假设检验
独立样本的T检验 2.2 独立样本的 检验
独立样本的T检验目的是推断两个独立总体的均值是否 独立样本的T检验目的是推断两个独立总体的均值是否 两个独立总体 存在显著差异。 存在显著差异。 例2-2: 科技文教人员与公司职员的平均假日支出是否存在显著差异？ 科技文教人员与公司职员的平均假日支出是否存在显著差异？ 两个独立总体:科技文教人员与公司职员 两个独立总体: 均值:平均假日支出 均值: H 0 : 科技文教人员与公司职员的平均假日支出无显著差异； 科技文教人员与公司职员的平均假日支出无显著差异 无显著差异； 有显著差异。 科技文教人员与公司职员的平均假日支出有显著差异 H1 : 科技文教人员与公司职员的平均假日支出有显著差异。
接受零假设只是表明在给定的显著性水平下， 接受零假设只是表明在给定的显著性水平下， 样本数据不足以拒绝它，并不意味着它肯定是正确的； 样本数据不足以拒绝它，并不意味着它肯定是正确的； 同理，拒绝零假设也只是表明在给定的显著性水平下， 同理，拒绝零假设也只是表明在给定的显著性水平下， 样本数据不足以接受它，并不意味着它肯定是错误的。 样本数据不足以接受它，并不意味着它肯定是错误的。
H 0 : µ = 500
H 1 : µ ≠ 500
其重量的平均值为 X ≈ 505.3,
标准差为 S ≈ 2.9
Sig.<0.05时，拒绝零假设，即认为“有显著差异”。 Sig.<0.05时 拒绝零假设，即认为“有显著差异” Sig.=0.001<0.05, 拒绝零假设，即认为该包装不合格 拒绝零假设，
表2-1 接受教育的平均年限的T检验结果（一） 接受教育的平均年限的T检验结果（
Test Value = 16 95% Confidence Interval of the Difference Lower -2.00 Upper -.28
SPSS假设检验
SPSS假设检验实验⽬的：：实验⽬的1、学会使⽤SPSS的简单操作。
2、掌握假设检验。
：实验内容：实验内容1.⼀个总体均值的检验（⼩样本）；2.两个总体均值之差的检验；3.绘制正态概率图；4.S—W检验。
实验步骤： 1.⼀个总体均值的检验（⼩样本）：单总体的Z检验和t检验。
设是取⾃正态总体的⼀个样本，要检验。
其中为已知的常数。
为了说明如何构造检验统计量和拒绝域，先看⼀个简单的情形。
设总体⽅差是已知的，记为，设为样本均值，则。
设为真，即，对作标准化，得到上述的Z就是要构造的检验统计量。
设定显著性⽔平为0.05，因为，的概率为0.05，所以检验的拒绝域是。
如果由样本计算得到，与⼩概率原理⽭盾，从⽽拒绝原假设。
在实际应⽤中，总体的⽅差是未知的。
因⽽需要样本⽅差代替总体⽅差，相应地，检验统计量编程了t统计量。
设与分别为样本的均值和样本⽅差，当为真时，可知统计量对于给定的显著性⽔平，检验的拒绝域是。
其中临界值满⾜条件。
它就是⾃由度为(N-1)的t分布的双侧分为点。
如果由样本观测值代⼊，计算得到的t值满⾜，则拒绝原假设。
SPSS检验结果不给出临界值，⽽是在给出t值的同时给出它的显著性概率（也成为p值或相伴概率，记为p或Sig）。
计算⼀个双侧检验问题，SPSS操作如下：“分析”→“⽐较均值”→“单样本T检验”，在打开的对话框中填好“检验变量”列表框和“检验值”⽂本框。
单击“确定”。
输出结果中的Sig.(双侧)就是p值。
⽐较p值与检验⽔准。
1 T-TEST2 /TESTVAL=803 /MISSING=ANALYSIS4 /VARIABLES=score5 /CRITERIA=CI(.95).⼀个总体的均值检验 差齐性检验：Sig=0.397>0.05,⽅差不显著，可以认为两个独⽴样本的⽅差⼀致。
均值之差t检验：在⽅差相等的条件下，Sig=0.004<0.05，均值之差显著，可以认为两个独⽴样本均值有显著差异。
直线相关假设检验SPSS步骤
直线相关假设检验SPSS步骤直线相关假设检验是统计学中常用的一种假设检验方法，用于确定两个变量之间是否存在线性相关关系。
SPSS是一种常用的统计分析软件，可以方便地进行直线相关假设检验。
本文将介绍直线相关假设检验的步骤，并以实例说明如何在SPSS中进行相关性分析。
进行直线相关假设检验前，我们需要明确两个变量之间的关系是线性的。
线性关系是指两个变量之间的关系可以用一条直线来描述。
为了验证这个假设，我们可以绘制散点图来观察变量之间的关系。
如果散点图呈现出明显的直线趋势，那么我们可以认为变量之间存在线性关系。
接下来，我们需要进行直线相关系数的计算。
直线相关系数是衡量两个变量之间线性关系强度的指标，常用的直线相关系数有皮尔逊相关系数和斯皮尔曼相关系数。
皮尔逊相关系数适用于连续变量之间的线性关系检验，而斯皮尔曼相关系数适用于有序变量之间的线性关系检验。
在SPSS中进行直线相关假设检验，我们需要进行以下步骤：第一步，导入数据。
打开SPSS软件，选择“文件”菜单下的“导入”选项，选择需要进行直线相关假设检验的数据文件进行导入。
第二步，选择变量。
在导入数据后，我们需要选择需要进行直线相关假设检验的两个变量。
在SPSS的数据视图中，可以通过选中变量名称来选择变量。
第三步，进行相关性分析。
选择“分析”菜单下的“相关”选项，然后在弹出的对话框中选择需要进行直线相关假设检验的两个变量，并点击“确定”按钮。
SPSS会自动计算出皮尔逊相关系数和斯皮尔曼相关系数，并给出显著性水平。
第四步，解读结果。
在进行直线相关假设检验后，SPSS会给出相关系数的大小和显著性水平。
相关系数的取值范围在-1到1之间，绝对值越接近1表示相关性越强。
显著性水平则用来判断相关系数是否具有统计学意义，通常取0.05作为显著性水平的标准。
如果相关系数的显著性水平小于0.05，则可以认为变量之间存在线性相关关系。
以一个具体的例子来说明。
假设我们有一组数据，包括两个变量X 和Y，我们想要检验X和Y之间是否存在线性相关关系。
spss学习第4章-假设检验
（1）假设检验含义
利用统计方法检验一个事先所作出的假设的真伪， 这一假设称为统计假设，对这一假设所作出的检验就 是假设检验
（2）假设检验基本思路
ⅰ. 对总体参数作出某种假设，并假定它是成立的。 ⅱ.根据样本得到的信息（统计量），考虑接受这个 假设后是否会导致不合理的结果，如果合理就接受这个 假设，不合理就拒绝这个假设。 所谓合理性，就是看是否在一次的观察中出现了小 概率事件。
[Ⅰ.提出原假设] [Ⅱ.选择检验统计量]
[Ⅲ.计算检验统计量的观测值和概率P-值]
[Ⅳ.给定显著性水平α，并作出决策]
举例2
利用住房状况问卷调查数据，推断家庭人均住房面积的平均 值是否为20平方米。 [Ⅰ.提出原假设]
[Ⅱ.选择检验统计量]
[Ⅲ.计算检验统计量的观测值和概率P-值]
SPSS软件计算结果
课堂体验 调查内容1：学生视力
抽取22名学生调查他们的视力，假设全校学生的视
力服从于正态分布，是否可以认为学生的视力均值 为0.8？（取显著性水平α=0.05）
调查内容2：每月消费支出（分男、女）
抽取22名学生调查他们的每月消费支出，假设全校学生的消费 支出服从正态分布，比较不同性别同学的消费支出平均值和方 差？是否可以认为该校学生的消费支出均值为 500元 （取显著性水平α=0.05） 男、女同学的月消费支出是否存在显著差异？
[Ⅲ.计算检验统计量的观测值和概率P-值] [Ⅳ.给定显著性水平α，并作出决策]
第二问
[Ⅰ.提出原假设] [Ⅱ.选择检验统计量]
[Ⅲ.计算检验统计量的观测值和概率P-值]
[Ⅳ.给定显著性水平α，并作出决策]
课堂习题
知识点：一个总体参数比例检验 检验量：Z检验
如何在SPSS数据分析报告中进行假设检验？
如何在SPSS数据分析报告中进行假设检验？关键信息项：1、假设检验的类型独立样本 t 检验配对样本 t 检验单因素方差分析多因素方差分析卡方检验2、数据准备要求数据的完整性数据的准确性数据的正态性异常值处理3、假设的设定原假设和备择假设的明确表述假设的合理性和基于的理论或经验基础4、检验步骤选择合适的检验方法在 SPSS 中输入数据和执行检验操作解读检验结果5、结果报告内容检验统计量的值自由度p 值效应量（如适用）6、结果的解释和结论根据 p 值做出决策对效应大小的解释结果在研究背景下的意义11 假设检验的类型在 SPSS 数据分析报告中，常见的假设检验类型包括但不限于以下几种：111 独立样本 t 检验用于比较两个独立样本的均值是否存在显著差异。
例如，比较两组不同治疗方法下患者的康复时间。
112 配对样本 t 检验适用于配对数据，即同一组对象在不同条件下或不同时间点的测量值。
比如，比较同一批患者治疗前后的体重变化。
113 单因素方差分析用于检验一个因素的不同水平对因变量的均值是否有显著影响。
例如，研究不同教育程度对收入的影响。
114 多因素方差分析当存在多个因素同时影响因变量时，使用多因素方差分析。
比如，研究教育程度和工作经验对收入的共同影响。
115 卡方检验主要用于检验两个分类变量之间是否存在关联。
例如，分析性别与某种疾病的患病率是否有关。
12 数据准备要求在进行假设检验之前，确保数据满足以下要求：121 数据的完整性数据应包含所需的所有变量和观测值，不允许有缺失值。
若存在缺失值，需要采取适当的方法进行处理，如删除含缺失值的观测、均值插补或多重插补等。
122 数据的准确性对数据进行仔细检查，确保其没有录入错误或异常值。
异常值可能会对假设检验的结果产生较大影响，需要谨慎处理。
123 数据的正态性对于一些基于正态分布假设的检验方法（如 t 检验和方差分析），需要检查数据是否近似服从正态分布。
可以通过绘制直方图、正态概率图或进行正态性检验（如 ShapiroWilk 检验）来判断。
管理统计学 假设检验的SPSS实现 实验报告
假设检验的S P S S实现一、实验目的与要求1.掌握单样本t检验的基本原理和spss实现方法。
2.掌握两样本t检验的基本原理和spss实现方法。
3.熟悉配对样本t检验的基本原理和spss实现方法。
二、实验内容提要1.从一批木头里抽取5根，测得直径如下（单位：cm），是否能认为这批木头的平均直径是12.3cm12.3 12.8 12.4 12.1 12.72.比较两批电子器材的电阻，随机抽取的样本测量电阻如题表2所示，试比较两批电子器材的电阻是否相同（需考虑方差齐性的问题）A批0.140 0.138 0.143 0.142 0.144 0.148 0.137B批0.135 0.140 0.142 0.136 0.138 0.140 0.1413. 配对t检验的实质就是对差值进行单样本t检验，要求按此思路对例课本13.4进行重新分析，比较其结果和配对t检验的结果有什么异同。
4．一家汽车厂设计出3种型号的手刹，现欲比较它们与传统手刹的寿命。
分别在传统手刹，型号I、II、和型号III中随机选取了5只样品，在相同的试验条件下，测量其使用寿命（单位：月），结果如下：传统手刹： 21.2 13.4 17.0 15.2 12.0型号 I ： 21.4 12.0 15.0 18.9 24.5型号 II ： 15.2 19.1 14.2 16.5 24.5型号 III ： 38.7 35.8 39.3 32.2 29.6（1）各种型号间寿命有无差别?（2）厂家的研究人员在研究设计阶段，便关心型号III与传统手刹寿命的比较结果。
此时应当考虑什么样的分析方法？如何使用SPSS实现？三、实验步骤为完成实验提要1.可进行如下步骤1.在变量视图中新建一个数据，在数据视图中录入数据，在分析中选择比较均值，单样本t检验，将直径添加到检验变量，点击确定。
单个样本统计量N 均值标准差均值的标准误zhijing5 12.460 .2881 .1288单个样本检验检验值 = 0t df Sig.(双侧) 均值差值差分的 95% 置信区间下限上限zhijing96.708 4 .000 12.4600 12.102 12.818为完成实验提要2.可进行如下步骤2.1 新建一个数据，在变量视图中输入dianzu和pici，然后再数据视图中录入数据，选择分析，描述统计，探索，在勾选带检验的正态图，以及未转换，点击确定方差齐性检验Levene 统计量df1 df2 Sig.dianzu 基于均值.653 1 12 .435 基于中值.607 1 12 .451 基于中值和带有调整后的 df.607 1 11.786 .451 基于修整均值.691 1 12 .422为完成内容提要3.需进行如下步骤：3.1.打开pairedt.sav，在变量视图中添加差值，选择转换的计算变量，在目标变量智能光添加chazhi，数字表达式为after – before，点击确定。
统计学spss上机实验
三、用SPSS Statistics软件进行参数估计、假设检验和回归分析。
使用第二题中抽出的样本作为原始数据。
以下假设检验中显著性水平为5%。
1、计算总体中上月平均工资95%的置信区间。
2、检验能否认为总体中上月平均工资等于2000元。
3、检验能否认为男生的平均工资大于女生。
4、一些学者认为，由于经济不景气，学生的平均工资今年和去年相比没有显著提高。
检验这一假说。
5、回归分析。
（1）计算上月工资与平均学分绩点的相关系数并作假设检验。
（2）以上月工资为因变量，平均学分绩点为自变量做回归分析，分析模型的拟合效果和假设检验的结果。
上月工资频率百分比有效百分比累积百分比有效800 1 .6 .6 .61000 2 1.2 1.2 1.81100 1 .6 .6 2.41300 1 .6 .6 2.91400 5 2.9 2.9 5.91500 2 1.2 1.2 7.11600 8 4.7 4.7 11.81700 4 2.4 2.4 14.11800 16 9.4 9.4 23.51900 15 8.8 8.8 32.42000 11 6.5 6.5 38.82100 14 8.2 8.2 47.12200 18 10.6 10.6 57.62300 7 4.1 4.1 61.82400 20 11.8 11.8 73.52500 13 7.6 7.6 81.22600 8 4.7 4.7 85.92700 4 2.4 2.4 88.22800 8 4.7 4.7 92.92900 1 .6 .6 93.53000 3 1.8 1.8 95.33100 3 1.8 1.8 97.13200 2 1.2 1.2 98.23300 2 1.2 1.2 99.44100 1 .6 .6 100.0合计170 100.0 100.0描述统计量标准误上月工资均值2188.24 37.059 均值的 95% 置信区间下限2115.08上限2261.395% 修整均值2183.01中值2200.00方差233470.240标准差483.188极小值800极大值4100范围3300四分位距600偏度.264 .186峰度 1.187 .370统计量上月工资N 有效170缺失0。
熟练使用spss17.0进行假设检验的方法
熟练使用SPSS 进行假设检验[例] 某克山病区测得11例克山病患者与13名健康人的血磷值mmol/L如下,问该地急性克山病患者与健康人的血磷值是否不同。
表1 克山病区调查数据结果患者健康人1.录入数据。
将组别设为g，可将患者组设为1，健康人设为2，血磷值设为x，如患者组中第一个测量到的血磷值为，则g为1，x为，其他数据均仿此录入，如下图所示。
图1 数据输入界面2.统计分析。
依次选择“Analyze”、“ Compare means”、“ Independent Samples T Test”。
图2 选择分析工具3.弹出对话框如下图所示，将x选入Test Variables、g选入Grouping Variable，并单击下方的Define Groups按钮，弹出定义组对话框，默认选项为Use Specified Value，在Group1和Group2框中分别填入1和2，即要对组别变量值为1和2的两个组做t检验，另外Options对话框中可选择置信度和处理缺失值的方法。
图3 选择变量进入右侧的分析列表SPSS输出的结果和结果说明:图4 输出结果表2 统计量描述列表组统计量g N均值标准差均值的标准误x111.42179.12718 213.42215.11708表3 假设检验结果表独立样本检验方差方程的Levene 检验均值方程的 t 检验差分的 95% 置信区间FSig.dfSig.(双侧)均值差值标准误差值下限上限假设方差相等.032.86022.019.43629.17288.07777.79482假设方差不相等.020.43629.17286.07716.79542第一个表格是统计描述,给出了两个组的样本数N、均值Mean、标准偏差、标准误差Std. Error Mean。
第二个表格分两部分(1)方差齐次检验（Levene 检验）。
F＝、 P（ Sig）＝。
(2)t 检验。
因方差齐次与不齐方法不同，（Equal variances assumed 方差齐次和Equal variances not assumed 方差不齐），结果分两行给出。
SPSS中的相关分析及假设检验
相关分析及假设检验 spss1.概念变量之间相关，但是又不能由一个或几个变量值去完全和唯一确定另一个变量值的这种关系称为相关关系。
相关关系是普遍存在的，函数关系仅仅是相关关系的特例。
事物之间有相关关系，不肯定是因果关系，也可能仅是伴随关系，但是事物之间有因果关系，则两者必定相关。
相关分析用于分析两个随机变量的关系，可以检验两个变量之间的相关度或多个变量两两之间的相关程度，也可以检验两组变量之间的相关程度偏相关分析是指在操纵了其他变量的效应以后，对两个变量相关程度的分析。
、2.皮尔逊积差相关系数pearson product－moment correlation coefficient变量之间的相关程度由相关系数来度量，pearson相关系数是应用最广的一种。
它用于检验连续型变量之间的线性相关程度2.1前提假设1〕正态分布皮尔逊积差相关只适用于双元正态分布的变量，即两个变量都是正态分布，注意只有pearson要求正态分布如果正态分布的前提不满足，两变量间的关系可能属于非线性相关2〕样本独立样本必须来自总体的随机样本，而且样本必须相互独立3〕替换极值变量中的极端值如极值、离群值对相关系数的影响较大，最好加以删除或代之以均值或中数2.2相关分析的前提假设检验一般情况下是对是否满足正态分布进行检验，对于正态分布的检验有好几种方法，总的可分为非参数检验和图形检验法1〕非参数检验法spss中的1－sample K－S检验，检验样本数据是否服从某种特定的分布，方法有三种a. Asymptotic only 是一种基于渐进分布的显著性水平的检验指标，通常显著性水平小于0.05则认为显著，适用于大样本。
如果样本过小或分布不好，该指标的适用性会降低b.Monte Carlo 精确显著性水平的无偏估量，适用于样本过大无法使用渐进方法估量显著性水平的情况，可以不必依赖渐近方法的假设前提c.Exact 精确计算观测结果的概率值，通常小于0.05即被认为显著，说明横变量和列变量之间存在相关，同时同意用户键入每次检验的最长时间显著，可以键入1到9999999999之间的数字，但只要一次检验超过指定时间的30分钟，就应该用monte carlo假设是服从某种分布所以如果计算出的值比方Asymp. Sig 小于0.05，那么拒绝原假设，说明样本为非正态分布，否则值越大越服从某种分布单样本K－S首先计算每一阶段实际值与观察值的差异值，再计算每一阶段差异值的绝对值Z，即K－S的Z值，Z值越大，样本服从理论分布的可能性越小还有一个是2 －sample Kolmogorov—Smirnov用于检验2个样本的分布是相同的假设2〕图形法spss中grapha.Q－Q正态检验图图中横坐标为实际观测值，纵坐标为正态分布下的期望值，如果实际观测值取自正态分布的整体，那么图中所示的落点应该分布在趋势线的附近，并且应该表现出肯定的集中趋势，即平均数附近应该聚集较多的落点，越靠近两个极端落点越少。
直线相关假设检验SPSS步骤
直线相关假设检验SPSS步骤一、引言在统计学中，相关分析是用来研究两个或多个变量之间关系的重要方法之一。
直线相关假设检验是判断两个变量之间是否存在线性关系的统计检验方法。
SPSS （Statistical Package for the Social Sciences）是一个常用的统计分析软件，拥有强大的数据处理和分析功能。
本文将详细介绍直线相关假设检验的步骤，以及如何在SPSS中进行相关分析。
二、直线相关假设检验的基本原理直线相关假设检验是基于样本数据对总体相关系数进行推断的方法。
在进行直线相关假设检验时，需要先提出原假设和备择假设。
原假设（H0）通常假定两个变量之间不存在线性关系，备择假设（H1）则假定两个变量之间存在线性关系。
直线相关假设检验的基本原理是通过计算样本数据的相关系数，然后根据统计学原理对总体相关系数进行推断。
常用的相关系数有皮尔逊相关系数（Pearson correlation coefficient）和斯皮尔曼相关系数（Spearman correlation coefficient）。
皮尔逊相关系数适用于两个变量都是连续变量的情况，而斯皮尔曼相关系数适用于至少一个变量是有序变量的情况。
三、直线相关假设检验的步骤进行直线相关假设检验的步骤可以分为以下几个部分：1. 数据准备在进行直线相关假设检验之前，需要先收集相关的数据并进行整理。
确保数据没有缺失值或异常值，并将数据导入SPSS软件中。
2. 建立假设在进行直线相关假设检验之前，需要明确原假设和备择假设。
原假设通常假定两个变量之间不存在线性关系，备择假设则假定两个变量之间存在线性关系。
3. 进行相关分析在SPSS软件中，可以通过选择“分析”菜单下的“相关”选项来进行相关分析。
在相关分析对话框中，选择需要进行相关分析的变量，并选择相关系数类型（如皮尔逊相关系数或斯皮尔曼相关系数）。
4. 查看相关系数及显著性水平相关分析完成后，SPSS会输出相关系数矩阵和显著性水平。
巧用SPSS进行均值的假设检验
Cheng Ying, Chen Xizhen
College of Mathematics and Information science of Wenzhou University (325035) Abstract
Multivariate Testsb
Effect Intercept Pillai's Trace
Wilks' Lambda
Hotelling's Trace
Roy's Largest Root
性别
Pillai's Trace
Wilks' Lambda
Hotelling's Trace
Roy's Largest Root
相应检验规则来判定量均指向量有无显著性差异。问题是能否不通过编程，直接运用 SPSS
输出 S1, S2 , S p ？
2. SPSS 对计算过程的实现
2.1 用 “判别分析”得到男、女的各个指标均值及其协方差阵 S1, S2
将表 1 中数据输入 SPSS 文件中，打开数据文件，选择菜单“Analyze Discriminant”弹出判别分析对话框（文献[2]），
关键词：霍特林统计量；判别分析；多变量方差分析；SPSS13.0
中图分类号：O212.1
文献标识码：A
1. 引言
在对多元正态总体进行假设检验时，由于数据量很大，因此必须借助于计算机进行处理。 常见的统计软件有 SAS，S-PLUS 和 SPSS 等。由于 SPSS 操作方便，学起来上手快，因而 受到很多用户的喜欢，适用范围很广。可它也有不足之处，对于很多计算，我们经常只能得 到最后结果，而不能知道每一步的计算过程，这对学生学习理解这方面的知识是不利的。因 此如何巧用 SPSS，不但得出结果，而且知道每一步的计算过程，就是教师应该研究的一个 问题。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2
0
2
H 0 : 0 假
2
0
2
正确决策的 概率为1-β。
采伪错误的 概率为β。
1
我们希望犯两类错误的概率越小越好。
与的关系
但两类错误并不是互相独立的。减小 β ，
将引起α的增大；减小 α ，又将引起β 的 增大。要同时减少犯两类错误的概率，
唯一的途径是增大样本容量。
H 0: 0 081mm
___
H 1: 0 081mm
拒绝域
Z
x 0 n
0.076 0.081 0.025 200
2.83
接受域
拒绝域
1 0.95
0.025 2 0.025 2
2.83
1.96
0
1.96
某批发商欲从厂家购进一批灯泡，根据合同规定，灯泡的使用寿命平均不能 低于1000小时。已知灯泡使用寿命服从正态分布，标准差为20小时。在总体 中随机抽取了100个灯泡，得其均值为960小时，批发商是否应该购进这批灯 泡。
假设检验基本原理
单样本均值检验 两个独立样本均值检验 两个匹配样本均值检验 总体方差假设检验
总体比率假设检验
小概率原理 假设检验的基本思想
假设检验的基本步骤
双侧检验与单侧检验 假设检验的两类错误 假设检验中的P值
小概率事件在一次试验中几乎不会发生。 （10%，5%，1%）
f X
假设总体服从均
H 0: 1200
___
H 1: 1200
接受域
Z
x 0 1245 1200 1.5 n 300 100
拒绝域
1 0.95
0
0.05
1.5 1.645
电视机显像管批量生产的质量标准为平均使用寿命1200小时，标准差为300 小时。某电视机厂宣称其生产的显像管质量大大超过规定标准。为了进行验 证，随机抽取100件为样本，测得平均使用寿命为1245小时。能否说该厂的
__
Z 2 Z 0.05 2 Z 0.025 1.96
0.95
0.025
0.025
-1.96
0 Z服从标准正态分布
1.96
Z
-3.54
拒绝域
接受域
拒绝域
x Z n
Z统计量
__
1
2 2
显著性水平
2
2
2
Z 2
0
Z
临界值
临界值
假设检验是对我们所关心的却又是未知的总体参数先作出假设，然后抽取样 本，利用样本提供的信息，根据小概率原理对假设的正确性进行判断的一种 统计推断方法。
解二： 显像管质量显著地高于规定标准。
解二：
H 0: 1200
H 1: 1200
拒绝域
___
Z
x 0 1245 1200 1.5 n 300 100
接受域
0.05
1 0.95
1.645
0
1.5
某机器制造出的肥皂的标准厚度为5cm，今欲了解机器性能是否良好，随机 抽取10块肥皂为样本，测得平均厚度为5.3cm，标准差为0.3cm，试以0.01 的显著性水平检验机器性能良好的假设。
250
250.42x来自结论：今日生产线上所生产的全部化妆品重量不符合250克的 规格要求。做出这一推断的把握程度为95%。
令Z
x , 则Z服从标准正态分布即 : Z ~ N 0 1 n
__
x 249.25 250 1.5 n 50 3.54 1.96 Z
2
2
2
0
2
假设检验实践中， 在执行这样的原 则：把最关心的 问题作为原假设
1
提出，从而将后 果较严重的错误 放在 α上，事先加 以控制。
某公司设计出一种充气包，这种充气包在发生交通事故时对司机可起到缓冲
保护作用。该公司宣称其设计的充气包在发生交通事故瞬间只需不超过0.2
秒的时间即可充好气而起到缓冲作用。实践证明，如果其充气时间超过0.2 秒，则来不及对司机起到缓冲保护作用而造成伤亡。试对此问题提出合理的
H 0: 1000小时
拒绝域
H 1: 1000小时
接受域
0.05
1 0.95
0
左侧检验
临界值
电视机显像管批量生产的质量标准为平均使用寿命1200小时，标准差为300 小时。某电视机厂宣称其生产的显像管质量大大超过规定标准。为了进行验 证，随机抽取100件为样本，测得平均使用寿命为1245小时。能否说该厂的 显像管质量显著地高于规定标准
0.05
P 0.0038
0 Z 1.645
Z 2.67
拒绝域 接受域 P 值可用于与规定的显
0.05
著性水平α比较，进行
检验决策，而且提供了
P 0.0038
1.645
样本值统计量的值在一
2.76
0
定范围内出现的概率。
方差已知的均值检验
方差未知的均值检验
某厂加工一种零件，根据经验知道，该厂加工的零件的椭圆度渐近服从正态 分布，其总体均值为0.081mm，总体标准差为0.025mm。今另换一种新机 床进行加工，取200个零件进行检验，得到椭圆度均值为0.076mm。问新 机床加工零件的椭圆度总体均值与以前有无显著差别。
原假设 。
表述方法1 H0：μ≤0.2秒 H1： μ＞0.2秒 表述方法2（可行） H0 ：μ≥0.2秒 H1： μ＜0.2秒
拒 平均充气时间不超过0.2，但却拒绝了 平均充气时间超过0.2秒，但却拒绝了 真 H 认为不合格。这使厂商失去业务机 H0。认为合格。 这可能导致人身伤亡。 错 0 误 会。 采 平均充气时间超过0.2秒，但却认为低 平均充气时间不超过0.2秒，但却接受 伪 于0.2秒，而接受H0。这可能导致人 了H0认为不合格。这使厂商失去业务 错 误 身伤亡。 机会。
值为250克，标 准差为1.5克的
正态分布
250
__ f x
X
依据抽样分析原理，样
本均值应服从以250为
数学期望，以0.21克为 标准差的正态分布 250
x
x
n 1.5 50 0.21
__ f x
0.95
0.025
0.025
249.58
249.25
H 0: 5cm
___
H 1: 5cm
拒绝域 接受域
t
x 0 5.3 5 3.16 s n 0.3 10
拒绝域
0.005 2
1 0.90
0.005 2
3.2498
0
3.16 t0.005 9 3.2498
一个汽车轮胎制造商声称，某一等级轮胎的平均寿命在一定的汽车重量和正
50瓶化妆品重量样本数据（克） 248.7 248.6 248.1 247.5 249.0 248.0 248.8 250.1 248.9 249.5 248.8 248.7 248.3 248.3 250.0 250.8 251.6 250.6 249.2 249.1 249.5 250.9 249.9 249.7 249.2 250.5 248.9 250.7 249.5 250.4 249.6 249.6 249.0 249.5 249.9 248.8 249.0 248.9 248.8 248.7
原假设为假
假设检验中四种可能的决策结果
H0为真 H0为假 正确决策 第二类错误 （采伪错误） 第一类错误 （拒真错误）
0
第二类错误：接受了一个本来是 不真实的原假设。又称采伪错误。
拒绝H0
接受H0
正确决策
H 0 : 0 真
正确决策的 概率为1-α
1
拒真错误的概率为 α/2 + α/2 =α
提出原假设和备择假设
H 0 : 250
作出统计决策
H1 : 250
确定检验统计量
高级营养化妆品需要严格控制瓶装重量。
标准规格为每瓶250克，标准差为1.5克。 质检人员今从生产线上随机抽取50瓶测其 重量，获样本数据。质检验人员现在需要 确认：今日所生产的化妆品瓶装重量是否 附合标准规格。按照上级要求，质检结论 应达到至少95%的把握程度。
248.8 248.8 248.7 248.6 250.0 248.5 249.5 248.7 248.7 248.8
设总体标准差为1.5克，经计算得样本均值249.25克，依据参数估计原理， 瓶装化妆品重量总体均值的95%估计区间为：（248.83，249.67）。
x Z 2
1.5 249.25 1.96 249.25 0.42 n 50
拒绝域 接受域
H 1: 0 081mm
拒绝域
0.025 2
1 0.95
0
双侧检验
0.025 2
Z 1.96
2
Z 1.96
2
某批发商欲从厂家购进一批灯泡，根据合同规定，灯泡的使用寿命平均不能低 于1000小时。已知灯泡使用寿命服从正态分布，标准差为20小时。在总体中 随机抽取了100个灯泡，得其均值为960小时，批发商是否应该购进这批灯泡。
H 0: 1000小时
H 1: 1000小时
___
Z
x 0 960 1000 2 n 20 100
接受域
拒绝域
1 0.95
2