双筋矩形梁正截面承载力计算讲解
第三章(5)双筋矩形截面梁
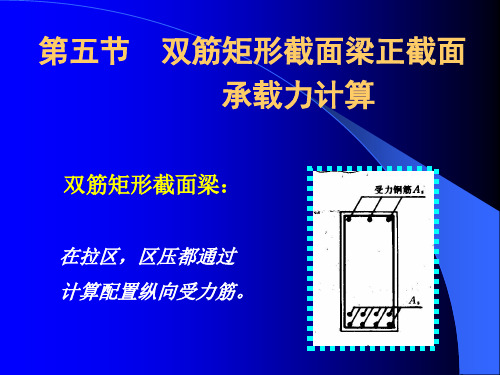
' s
M —— 外荷载所产生的弯矩设计值
M u —— 截面自身的抗弯承载力
T
—— 钢筋所受拉力
f y —— 钢筋抗拉强度设计值(屈服强度)
As —— 受拉钢筋截面面积
fc —— 砼的轴心抗压强度设计值。
b —— 梁截面宽
x
' s
—— 砼受压区高度
f y' —— 钢筋抗压强度设计值(屈服强度)
A —— 受压钢筋截面面积
3 22
2
25 250
例5、同上例,但事先给定压筋2 25 (As´ =982mm2), 求As。
x h0 h0
2
M f y´As (h´ a´ ) 0 s 2 f cm b
解:一、求x
219 106 310 982 (440 35) 440 4402 2 11 200 b h0 0.544 440 239(mm) 440 326 114(m m) 2as´ 2 35 70(mm)
2
11 200 440 0.544 (1 0.5 0.544) 168.7(kN m) M 219(kN m)
2
故应用双筋截面
二、求As´和As
M ´ s max bh0 f cm ´ As f y (h0 a s )
´
2
219 10 6 0.396 200 440 2 11 310 (440 35) 401(mm 2 )
' y ' s
1 fc b
2、求 若
' s
Mu
x ' ' ' f y As h0 as 2
双筋矩形截面正截面承载力计算公式及适用条件

表3.2.5 T形、I形及倒L形截面受弯构件翼缘计算宽度bf'
项次
考虑情况
1
按计算跨度l0考虑
2
按梁(纵肋)净距sn考虑
按翼缘 3 高度hf'
考虑
hf'/h0 ≥0.1 0.1 > hf'/h0 ≥0.05
hf'/h0 <0.05
T形截面、I形截面
肋形梁 肋形板
独立梁
l0/3
l0/3
b + sn
—
倒L形截面 肋形梁 肋形板
l0/6
b + sn/2
—
b + 12hf'
—
b + 12hf' b + 6hf' b + 5hf'
b + 12hf'
b
b + 5hf'
注:表中b为梁的腹板宽度。
2. T形截面的分类
第一类T形截面:中性轴通过翼缘,即x hf 第二类T形截面:中性轴通过肋部,即 x>hf
【解】查表得 fc=11.9N/mm2,ft=1.27N/mm2, fy=360N/mm2,α1=1.0,ξb=0.518
假定纵向钢筋排一层,则h0 = h-35 =400 -35 = 365mm, 1. 确定翼缘计算宽度
根据表3.2.5有: 按梁的计算跨度考虑: bf′ =l / 3=4800/3=1600mm 按梁净距sn 考虑:bf′=b+sn =3000mm 按翼缘厚度hf′考虑:hf′/h0 =80/365=0.219>0.1, 故不受此项限制。
【例3.2.6】某独立T形梁,截面尺寸如图3.2.13◆所示, 计算跨度7m,承受弯矩设计值695kN·m,采用C25级混凝 土和HRB400级钢筋,试确定纵向钢筋截面面积。
双筋矩形梁正截承载力计算

双筋矩形梁正截承载力计算————————————————————————————————作者:————————————————————————————————日期:双筋矩形梁正截面承载力计算一、双筋矩形梁正截面承载力计算图式二、基本计算公式和适用条件1.根据双筋矩形梁正截面受弯承载力的计算图式,由平衡条件可写出以下两个基本计算公式:由∑=0X 得:s y s y c A f A f bx f =''+1α由∑=0M 得:)(2001a h A f x h bx f M M sy c u '-''+⎪⎭⎫ ⎝⎛-=≤α 式中'y f —— 钢筋的抗压强度设计值; 's A —— 受压钢筋截面面积;'a —— 受压钢筋合力点到截面受压边缘的距离。
A s2(c )A s 'xA s1h 0-a 'M u2b a 'ah 0M u1(b )xA s (a )A s 'a 'h ba h 0M u a 'h 0-f y A s2h 0-x 2f y A s1f y 'A s 'f y A sf y 'A s 'a 1f c a 1f c bx a 1f ca 1f c bx题1图 双筋矩形梁正截面承载力计算图式其它符号意义同前。
2.适用条件 应用式以上公式时必须满足下列适用条件:(1)0h x b ξ≤ (2)'2a x ≥如果不能满足(2)的要求,即'2a x <时,可近似取'2a x =,这时受压钢筋的合力将与受压区混凝土压应力的合力相重合,如对受压钢筋合力点取矩,即可得到正截面受弯承载力的计算公式为:)(0a h A f M M s y u '-=≤当b ξξ≤的条件未能满足时,原则上仍以增大截面尺寸或提高混凝土强度等级为好。
双筋矩形截面承载力计算

4.3.3 双筋矩形截面承载力计算如前所述,不但在截面的受拉区,而且在截面的受压区同时配有纵向受力钢筋的矩形截面,称为双筋矩形截面。
双筋矩形截面适用于下面几种情况:※结构或构件承受某种交变的作用(如地震),使截面上的弯矩改变方向;※截面承受的弯矩设计值大于单筋截面所能承受的最大弯矩,而截面尺寸和材料品种等由于某些原因又不能改变;※结构或构件的截面由于某种原因,在截面的受压区预先已经布置了一定数量的受力钢筋(如连续梁的某些支座截面)。
应该说明,双筋截面的用钢量比单筋截面的多,因此,为了节约钢材,应尽可能地不要将截面设计成双筋截面。
◆计算公式及适用条件双筋矩形截面受弯构件正截面承载力计算中,除了引入单筋矩形截面受弯构件承载力计算中的各项假定以外,还假定当x≤2a's时受压钢筋的应力等于其抗压强度设计值f'y(图4-18)。
图4-18 双筋矩形截面计算简图对于图4-18的受力情况,可以像单筋矩形截面一样列出下面两个静力平衡方程式:(4-28)(4-29)式中:A's——受压区纵向受力钢筋的截面面积;a's——从受压区边缘到受拉区纵向受力钢筋合力作用之间的距离。
对于梁,当受压钢筋按一排布置时,可取a's=35mm;当受拉钢筋按两排布置时,可取a's=60mm。
对于板,可取a's=20mm。
式(4-28)和式(4-29)是双筋矩形截面受弯构件的计算公式。
它们的适用条件是:(4-30)(4-31)满足条件式(4-30),可防止受压区混凝土在受拉区纵向受力钢筋屈服前压碎。
满足条件式(4-31),可防止受压区纵向受力钢筋在构件破坏时达不到抗压强度设计值。
因为当x<2a's时,由图4-18可知,受压钢筋的应变ε'y很小,受压钢筋不可能屈服。
当不满足条件式(4-31)时,受压钢筋的应力达不到f'y而成为未知数,这时可近似地取x=2a's,并将各力对受压钢筋的合力作用点取矩得(4-32)用式(4-32)可以直接确定纵向受拉钢筋的截面面积A s。
双筋矩形截面梁正截面承载力计算基本公式

双筋矩形截面梁正截面承载力计算基本公式1.混凝土的承载力:混凝土的抗压强度是计算承载力的重要参数,通常使用标准试验方法得到的混凝土抗压强度值作为设计参数。
2.受拉钢筋的承载能力:由于混凝土的抗拉强度很低,需要通过加设受拉钢筋来增强混凝土的抗拉能力,受拉钢筋的承载能力是计算承载力中的一个关键要素。
3.受压钢筋的承载能力:混凝土承受受压力时,会发生徐变效应,这会导致混凝土的体积增大,从而引起应力的降低。
加设受压钢筋可以减小徐变效应,提高混凝土承载能力。
根据以上几个因素,可以得到双筋矩形截面梁的正截面承载力计算基本公式:1.计算受拉区域的承载能力:$N_{uT}=A_{sc}f_{yd}+A_{st}f_{yd}$2.计算受压区域的承载能力:$N_{uC}=A_{cc}f_{cd}+A_{ct}f_{ct}$3.计算混凝土的承载能力:$N_{uC}=0.85f_{cd}A_{c}$其中,$A_{sc}$表示受拉钢筋的截面积,$f_{yd}$表示受拉钢筋的屈服强度;$A_{st}$表示受拉钢筋的截面积,$f_{yd}$表示受拉钢筋的屈服强度;$A_{cc}$表示受压混凝土的截面积,$f_{cd}$表示受压混凝土的抗压强度;$A_{ct}$表示受压钢筋的截面积,$f_{ct}$表示受压钢筋的屈服强度;$A_{c}$表示混凝土的截面积。
公式中的0.85是修正系数,用于考虑混凝土的不均匀应力分布。
通过计算上述公式,可以得到双筋矩形截面梁的正截面承载能力$N_{u}$,然后与设计荷载进行比较,以确定结构的安全性。
需要注意的是,以上公式仅适用于正截面的双筋矩形截面梁,对于倒置截面和非双筋截面梁,需要进行修正和适当的调整。
总结一下,双筋矩形截面梁的承载力计算基本公式包括计算受拉区域的承载能力、计算受压区域的承载能力和计算混凝土的承载能力。
通过比较计算得到的承载能力和设计荷载,可以判断结构的安全性和可靠性。
双筋矩形截面正截面承载力计算公式及适用条件课件

目录
• 双筋矩形截面简介 • 双筋矩形截面正截面承载力计算公式 • 双筋矩形截面正截面承载力计算公式的适
用条件 • 双筋矩形截面正截面承载力计算公式在工
程实践中的应用 • 结论
01
双筋矩形截面简介
双筋矩形截面的定义
01
双筋矩形截面是指在矩形截面的 混凝土结构中,配置有两层钢筋 的截面形式。
工程实践中的应用案例
大跨度桥梁设计
轨道交通轨道结构
双筋矩形截面正截面承载力计算公式 在大型桥梁设计中广泛应用,如斜拉 桥、悬索桥等,用于计算主梁和桥面 板的承载能力。
在城市轨道交通中,双筋矩形截面正 截面承载力计算公式用于评估轨道钢 轨和轨枕的承载能力,确保列车运行 的安全。
高层建筑结构分析
在高层建筑的结构设计中,双筋矩形 截面正截面承载力计算公式用于分析 梁、柱等关键构件的承载能力,确保 建筑的安全性和稳定性。
相关规范要求。
03
双筋矩形截面正截面 承载力计算公式的适 用条件
适用条件概述
双筋矩形截面正截面承载力计算公式适用于计算双筋矩形截面的承载能力,适用 于梁、柱等结构形式。
该公式基于材料力学、结构力学等理论,通过简化计算过程,适用于工程实践中 的快速估算。
具体适用条件解析
适用条件一
双筋矩形截面的材料应符合相关 规定,如混凝土强度等级、钢材
结构的可靠性和安全性。
THANK YOU
推导过程中采用了数学建模的方法,通过建立数学模型来描述双筋矩形截面的受力 状态。
计算公式中的参数解释
01
02
03
04
钢筋的面积和强度
指用于承受拉力的钢筋的面积 和抗拉强度,是影响承载力的
4受弯构件正截面承载力计算(2)

εmax=0.0033 ε′s=0.002
a′ s M x
α 1 fc
A′s f′y h0 As fy
b x
A′s
εs
as
As
(a)
(b) 图3-12
(c)
(d)
第 三
混凝土
章
由计算图式平衡条件可建立基本计算公式:
∑X =0
′ ′ As f y = As f y + α1 f cbx
有效翼缘宽度 实际应力图块
b′f
等效应力图块
实际中和轴
第 三
图3-15
混凝土
章
b′f的取值与梁的跨度l0, 梁的净距sn, 翼缘高度hf′及 受力情况有关, 《规范》规定按表4-5中的最小值取用。
T型及倒 形截面受弯构件翼缘计算宽度b′f 型及倒L形截面受弯构件翼缘计算宽度 ′ 型及倒 形截面受弯构件翼缘计算宽度
§4.4 双筋矩形截面承载力计算 1. 应用条件: 1.荷载效应较大, 而提高材料强度和截面尺寸受 到限制; 2. 存在反号弯矩的作用(地震作用); 3. 由于某种原因, 已配置了一定数量的受压钢筋。
第 三
混凝土
章
2. 基本公式及适用条件: 基本假定及破坏形态与单筋相类似, 以IIIa作为 承载力计算模式。 (如图)
第 三 章
混凝土
(2)截面复核: 已知:b×h, fc, fy, fy′, As, As′ 求: Mu 解:求 x =
f y As − f
/ y
A/s
α 1 f cb
当2as ′ ≤x≤ξbh0 截面处于适筋状态,
x ′ ′ ′ M u = α1 f cbx (h0 − ) + As f y (h0 − as ) 2
3 双筋矩形截面受弯构件正截面承载力计算

,
若B不满足,说明As' 太小,应按情形 1 重新设计计算; 若C不满足,说明受压钢筋未屈服,可按公式(3) M 直接计算As f y h0 as'
双筋矩形截面受弯构件承载力计算
计算As,一般满足适用条件A,可不验算 由公式(1)得 As
1 f cbx f y' As'
解:
(1)设计参数
f y As 1 1 fcbx f yAs
查表得, fc =14.3N mm2 , f y f y' 300 N mm2 , 1 =1.0, b 0.550
x M 1 f cbx(h0 ) f y As (h0 as ) 2 2
否则设计为双筋截面。
已知:b h、fc、f y、M,求As' 及As。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
双筋矩形梁正截面承载力计算
一、双筋矩形梁正截面承载力计算图式
二、基本计算公式和适用条件
1.根据双筋矩形梁正截面受弯承载力的计算图式,由平衡条件可写出以下两个基本计算公式:
由
∑=0X 得:
s y s
y c A f A f bx f =''+1α 由
∑=0M 得:
)(2001a h A f x h bx f M M s
y c u '-''+⎪⎭⎫ ⎝
⎛
-=≤α 式中'
y f —— 钢筋的抗压强度设计值; 's A —— 受压钢筋截面面积;
'a —— 受压钢筋合力点到截面受压边缘的距离。
其它符号意义同前。
2.适用条件 应用式以上公式时必须满足下列适用条件:
(1)0h x b ξ≤ (2)'
2a x ≥
如果不能满足(2)的要求,即'
2a x <时,可近似取'
2a x =,这时受压钢筋的合力将与受压区混凝土压应力的合力相重合,如对受压钢筋合力点取矩,即可得到正截面受弯承载力的计算公式为:
)(0a h A f M M s y u '-=≤
当b ξξ≤的条件未能满足时,原则上仍以增大截面尺寸或提高混凝土强度等级为好。
只有在这两种措施都受到限制时,才可考虑用增大受压钢筋用量的办法来减小ξ。
三、计算步骤
(一)截面选择(设计题)
设计双筋矩形梁截面时,s A 总是未知量,而's A 则可能有未知或已知这两种不同情况。
1.已知M 、b 、h 和材料强度等级,计算所需s A 和's A (1)基本数据:c f ,y f 及'y f ,1α, 1β,b ξ
(2)验算是否需用双筋截面
由于梁承担的弯矩相对较大,截面相对较小,估计受拉钢筋较多,需布置两排,故取mm a 60=,a h h -=0。
单筋矩形截面所能承担的最大弯矩为:
M bh f M b b c u <-=)5.01(2
01max 1ξξα,说明需用双筋截面。
(3)取0h x b ξ=,则
)5.01(2
01max 1b b c u bh f M ξξα-=
(4)计算受压钢筋
12u u M M M -=
)
(02
a h f M A y u s
'-'=' 从构造角度来说,'s A 的最小用量一般不宜小于2φ12,即2'
min 226
mm A s =。
(5)求受拉钢筋总面积为
y
s y b c s f A f h b f A '
'+=
01ξα
(6)实际选用钢筋,画截面配筋图
2.已知M 、b 、h 和材料强度以及's A ,计算所需s A (1)基本数据:c f ,y f 及'
y f ,1α, 1β,b ξ
(2)利用's A 求2s A 和2u M
y
y s
s f f A A ''=2
)(02s s y u a h A f M '-''=
(3)求1u M ,并由1u M 按单筋矩形截面求1s A
2
011s 2
1bh f M M M M c u u u αα=
-=
(4)根据s α求基本系数
)211(5.0s s αγ-+=,
s αξ211--=
(5)求x 并验算适用条件
'02a h x ≥=ξ 0
1
1h f M A s y u s γ=
(6)求受拉钢筋总面积为
21s s s A A A +=
(7)实际选用钢筋,画截面配筋图 (二)承载力复核
已知截面尺寸b 、h 和材料强度等级以及s A 和's A ,需复核构件正截面的受弯承载力,即求截面所能承担的弯矩。
(1)基本数据:c f ,y f 及'
y f ,1α, 1β,b ξ (2)求x
s y s
y c A f A f bx f =''+1α
(3)当0'2h x a b ξ≤≤时
)(2001a h A f x h bx f M M s
y c u '-''+⎪⎭⎫ ⎝
⎛
-=≤α
(4)当'
2a x <时
)(0a h A f M M s y u '-=≤
(5)当0h x b ξ>时,则说明已为超筋截面。
对于已建成的结构构件,其承载力只能按
0h x b ξ=计算,此时,将0h x b ξ=代入下式
)(2001a h A f x h bx f M M s
y c u '-''+⎪⎭⎫ ⎝
⎛
-=≤α 所得u M 即为此梁的极限承载力。
如果所复核的梁尚处于设计阶段,则应重新设计使之不成为超筋梁。
