三次样条插值在风机叶片外形设计中应用及应力分析

合集下载

matlab三次样条插值例题解析

文章标题：深度解析Matlab三次样条插值1. 前言在数学和工程领域中，插值是一种常见的数值分析技术，它可以用来估计不连续数据点之间的值。

而三次样条插值作为一种常用的插值方法，在Matlab中有着广泛的应用。

本文将从简单到复杂，由浅入深地解析Matlab中的三次样条插值方法，以便读者更深入地理解这一技术。

2. 三次样条插值概述三次样条插值是一种利用分段三次多项式对数据点进行插值的方法。

在Matlab中，可以使用spline函数来进行三次样条插值。

该函数需要输入数据点的x和y坐标，然后可以根据需要进行插值操作。

3. 三次样条插值的基本原理在进行三次样条插值时，首先需要对数据点进行分段处理，然后在每个分段上构造出一个三次多项式函数。

这些多项式函数需要满足一定的插值条件，如在数据点处函数值相等、一阶导数相等等。

通过这些条件，可以得到一个关于数据点的插值函数。

4. Matlab中的三次样条插值实现在Matlab中，可以使用spline函数来进行三次样条插值。

通过传入数据点的x和y坐标，可以得到一个关于x的插值函数。

spline函数也支持在已知插值函数上进行插值点的求值，这为用户提供了极大的灵活性。

5. 三次样条插值的适用范围和局限性虽然三次样条插值在许多情况下都能够得到较好的插值效果，但也存在一些局限性。

在数据点分布不均匀或有较大噪音的情况下，三次样条插值可能会出现较大的误差。

在实际应用中，需要根据具体情况选择合适的插值方法。

6. 个人观点和总结通过对Matlab中三次样条插值的深度解析，我深刻地理解了这一插值方法的原理和实现方式。

在实际工程应用中，我会根据数据点的情况选择合适的插值方法，以确保得到准确且可靠的结果。

我也意识到插值方法的局限性，这为我在实际工作中的决策提供了重要的参考。

通过以上深度解析，相信读者已经对Matlab中的三次样条插值有了更加全面、深刻和灵活的理解。

在实际应用中，希望读者能够根据具体情况选择合适的插值方法，以提高工作效率和准确性。

三次NURBS曲线的插值与应用_陈绍平

a自从1975年美国锡拉丘兹syracuse大学的弗斯普尔versprille在他的博士论文中首先提出有理b样条方法以来经过皮格尔piegl和蒂勒tiller等人的工作该理论得到了很大的发展目前非均匀有理b样条nonuniformrationalbspline简称nurbs方法已成为曲线曲面设计系统中最重要的几何造型方法之一
第 20 卷第 5 期 2001 年 9 月
机械科学与技术 M ECHA N ICA L SCIEN CE A ND T ECHNO L OG Y
文章编号: 1003-8728( 2001) 05-0692-02
SVeop lt.e2m0b erNo2.0501
陈绍平
三次 NU RBS 曲线的插值与应用
陈绍平
( 武汉理工大学, 武汉 430063)
摘要: N U RBS 方法已经被广泛地使用在 CA D 中。本文将通过三次 N U RBS 曲线的矩阵表示给出三次 N U R BS 曲线插值方法, 即反求三次 NU RBS 曲线控制顶点的算法, 并给出数字算例和三次 N U RBS 曲线插值方法在船舶型线设计中的一个应用。
2
,
2
n32 = - ( 3n11 + n33) , n34 = 0
n41 = -
n11, n43 = -
(
1 3
n33
+
n44 +
( ¨i+ 3 ) 2 ¨i2+ 3 ¨3i+ 2
)
,
n42 =
n11 -
n43 -
n44, n44 =
( ¨i+ 3) 2 ¨i3+ 3 ¨2i+ 3

详细讲解三次样条插值法及其实现方法

1
样条函数的定义定义4.1 设区间[a,b]上给定一个节点划分
a=x0<x1<……<xn-1<xn=b 如果存在正整数k使得[a,b]上的分段函数s(x)满足如下两条： (1)在[a,b]上有直到k-1阶连续导数。 (2)在每个小区间[xi,xi+1]上是次数不大于k的多项式。则称分段函数s(x)是以(2.6)为节点集的k次样条函数。
x xi i i 1 hi
) mi1hi
( ) xi1x
1 hi
x [xi , xi1], hi xi1 xi , i 0,1,, n 1
(x) (2x 1)( x 1)2,1(x) x(x 1)2 13
对Si (x)求二阶导数 ,并整理后得
Si( x)
6( xi
xi 1 hi3
2x)
因为分段三次Hermite插值多项式已经至少是一阶连续可导了，为了让它成为三次样条函数只需确定节点处的一阶导数使这些节点处的二阶导数连续即可！
S(xi 0) S(xi 0), i 1,, n 1
S(x)
y ( xxi i 0 hi
)
y ( ) m h ( xi1x i1 0 hi
( yn
yn 1 )
2 hn1
(mn1
2mn )
立即可得下式：
21
其中：
nm1 nmn1 2mn gn
n
h0
h0 hn1
, n
hn1 h0 hn1
1 n
gn
3 n
y1 y0 h0
n
yn
yn1 hn1
联合基本方程得一个广义三对角或周期三对角方程组：
2 1
1
1
2

第八节三次样条插值-PPT精品文档

S(xi 0) S(xi 0) (i 1 ,2 , ,n1 ) S(xi 0) S(xi 0) (i 1 ,2 , ,n1 ) (xi 0) S (xi 0) (i 1 S ,2 , , n1 ) S(xi ) yi (i 0 ,1 ,2 , ,n)
则有
f [ xi 1 , xi ] ( 1 ) m 2 mm i i 1 i i i 1 i ,m m y y 并注意到 , x i 1 ]
差商
内江师范学院数学与信息科学学院吴开腾制作
因而有三对角方程组（基本方程组）
2m 1 1m 2 1 (11) y0 (1 )m 2m m 2 1 2 2 3 2 (1 )m 2m m n2 n3 n2 n2 n1 n2 (1n1)mn2 2mn1 n1 n1 yn
内江师范学院数学与信息科学学院吴开腾制作
边界条件的类型
(1) 已知一阶导数值： (2) 已知二阶导数值：
S ( x ) yS , ( x ) y 0 0 n n
Sx (0 ) ySx , (n ) y 0 n
(3)被逼近函数是周
期函数：
其系数行列式是一个三对角行列式，在后面将用追赶方法求其解，于是得到分段插值多项式，即三次样条函数。
内江师范学院数学与信息科学学院吴开腾制作
基本步骤：
•构造已知条件（由三次样条函数的特征）；
•积分（反推）；
•确定系数：
•确定： •求出：
•利用边界条件，例如：
,i； Si ( x) m i
i
为了保证二阶导数的连续性，要求成立
s (0 x )(0 s x ) ,( 3 8 ) ( i 1 , 2 , , n 1 ) 3 i 3 i

三次样条插值方法的应用

CENTRAL SOUTH UNIVERSITY数值分析实验报告三次样条插值方法的应用一、问题背景分段低次插值函数往往具有很好的收敛性，计算过程简单，稳定性好，并且易于在在电子计算机上实现，但其光滑性较差，对于像高速飞机的机翼形线船体放样等型值线往往要求具有二阶光滑度，即有二阶连续导数，早期工程师制图时，把富有弹性的细长木条（即所谓的样条）用压铁固定在样点上，在其他地方让他自由弯曲，然后沿木条画下曲线，称为样条曲线。

样条曲线实际上是由分段三次曲线并接而成，在连接点即样点上要求二阶导数连续，从数学上加以概括就得到数学样条这一概念。

下面我们讨论最常用的三次样条函数及其应用。

二、数学模型样条函数可以给出光滑的插值曲线（面），因此在数值逼近、常微分方程和偏微分方程的数值解及科学和工程的计算中起着重要的作用。

设区间[]b ,a 上给定有关划分b x x n =<<<=Λ10x a ，S 为[]b ,a 上满足下面条件的函数。

● )(b a C S ,2∈；● S 在每个子区间[]1,+i i x x 上是三次多项式。

则称S 为关于划分的三次样条函数。

常用的三次样条函数的边界条件有三种类型：● Ⅰ型 ()()n n n f x S f x S ''0'',==。

● Ⅱ型 ()()n n n f x S f x S ''''0'''',==，其特殊情况为()()0''''==n n x S x S 。

● Ⅲ型 ()()Λ3,2,1,0,0==j x S x S n j j ，此条件称为周期样条函数。

鉴于Ⅱ型三次样条插值函数在实际应用中的重要地位，在此主要对它进行详细介绍。

三、算法及流程按照传统的编程方法，可将公式直接转换为MATLAB可是别的语言即可；另一种是运用矩阵运算，发挥MATLAB在矩阵运算上的优势。

二次样条与三次样条的研究

二次样条与三次样条插值研究作者：季哲指导老师：陈素根摘要样条插值是使用一种名为样条的特殊分段多项式进行插值的形式。

本文主要讨论在几种不同边值条件下二次样条插值与三次样条插值的求解方法和分析在某特殊边值条件下二次样条插值与三次样条插值的变分性质，并分别对两种插值的余项进行较精确地估算。

另外介绍二次B 样条函数于三次B 样条函数，并对二者的有关性质进行说明和证明。

最后给出三次样条插值在实际中的应有。

关键词二次样条函数三次样条函数变分性质余项1 引言自上世纪60年代以来，由于航空造船等工程设计的需要，人们发展了样条插值技术。

现在样条函数越来越流行，它不仅是现代函数逼近的一个活跃的分支，而且也是现代数值计算中一个十分重要的数学工具。

本文主要研究在几种某特殊边值条件下二次样条插值与三次样条插值求解方法；分析在某特殊边值条件下二次样条插值与三次样条插值的变分性质，并分别对两种插值的余项进行较精确地估算。

本文还主要介绍二次样条与三次样条的基本概念，常见的二、三次B 样条及Berzier 样条等。

最后研究二次样条与三次样条在数据插值中的应用，并举例说明。

2 二次样条与三次样条的计算方法2．1 二次样条的计算方法定义：给定区间[ a,b ]一个分割△01,,...,n x a x x b ==,二次样条函数()S x 满足以下条件：1） ()S x 在每个区间1[,]i i x x -上是一个二次多项式；2） S （x ）在所有节点满足i x (i=1,2,…,n-1)上具有一阶连续导数； 3）S （x ）在所有节点满足S （i x ）= i y (i=0,1,…,n)。

在每个小区间1[,]i i x x -上是一个二次多项式，有3个系数，因此要确定S(x)就要确定3n 个待定参数，而由S （i x ）= i y (i=0,1,…,n),得到n+1个方程；由()()i i S x S x +=-(i=1,2,…，n-1)得到n-1个方程；由/S (i x -)=/S ( i x +)(i=1,2,…,n-1)得到n-1个方程,总共3n-1个方程,为了确定一个待定的样条插值函数,还需增加1个条件,这个条件通常是在区间[,]a b 的两端处给出，即边界条件，边界条件根据实际问题的需求来确定，其类型很多，常见的边界条件类型有：1）给定初始断点的一阶导数值：/S (0x )= 0y 2）给定终端点的一阶导数值：/S (n x )= n y 3）给定初始端点的二阶导数值：//S (0x )= 0y / 4）给定终端点的二阶导数值: //S (n x )= n y /5）若插值函数为周期函数时，此时0y =n y ,给定：/S (0x )=/S (n x )下面针对上面5种情况分别讨论二次样条插值问题。

三次非均匀B样条在矿井通风机叶片类曲面上的应用

ｇ：１
其中，ｄｉ为控制定点，．（ｕ）为ｋ次规范Ｂ样条
基函数，它是由一个节点矢量的非递减参数的序列，也就是ｋ次多项式样条。Ｂ样条的定义有很多中，
，因此，运用该方法
得到非均匀Ｂ样条的节点矢量的公式如下所示：
１６
８．５６６
１５．４９２
２８．３４２
ｌ
ｐ（ｕ）＝∑ Ｊ７、Ｉ．ｕ）＝ｇ汹
收稿日期：２０１３ — ０７ — ０８
作者简介：聂凯，晋城煤炭规划设计院。
２７４
《装备制造技术）２０１３年第１０期
来的计算弊端，相应的能够减少其计算量，提供计算效率，同时这种算法相对比较稳定，数值较安全可靠，能够做为矿井通风机叶片类曲线上的数值。三次非均匀Ｂ样条曲线的反算，可以将曲线定义为ＵＥ［，。］Ｕ［，】内的节点值，将求得的值依次带人到方程中，来满足其差值条件，也就是如下
中图分类号：ＴＨ２１３．４
文献标识码：Ｂ
文章编号：１６７２ — ５４５Ｘ（２０１３）１０机叶片类曲面的从上式中能够看出，如果需要确定第ｉ个Ｋ次Ｂ造型直接决定了通风机的使用效率。这主要是因为通样条的基本函数，就需要， …，。等ｋ个节点。如果曲线方程中的ｎ＋１个控制定点为，因此就风机造型质量的高低就会对后续的加工精度有一定＋１个次Ｂ样条基础函数。的影响，继而就会影响到通风机的使用效率，不仅延需要ｎ长了完工时间，而且还增加了机器维修成本。因此，针三次非均匀Ｂ样条在矿井通风机叶片类对此种情况，就提出了一种三次非均匀Ｂ样条的方２曲面上的应用法，来对通风机叶片类曲面的各截面线进行拟合。

科学计算实习题二三次样条插值

} 4、最后，按照公式（4.39）计算 S（x）的估计值，这一阶段的程序代码为
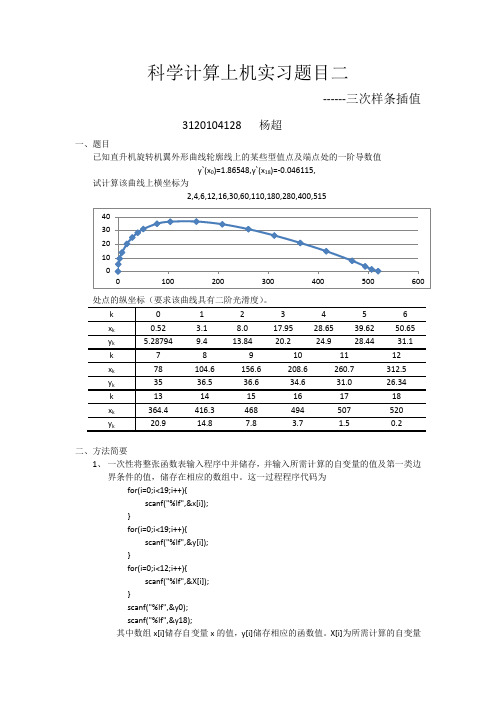
for(i=0;i<12;i++){ for(k=1;k<19;k++){
if((X[i]>x[k-1])&&(X[i]<x[k]))
S[i]=M[k-1]/(6*h[k])*pow(x[k]-X[i],3)+M[k]/(6*h[k])*pow(X[i]-x[k-1],3)+(y[k-1]-M[k-1]/ 6*pow(h[k],2))*(x[k]-X[i])/h[k]+(y[k]-M[k]/6*pow(h[k],2))*(X[i]-x[k-1])/h[k];
} 3、利用解三对角线方程组的追赶法解出在结处的二阶导数值，这一过程程序代码如
下 bt[0]=1.0/2; for(i=1;i<=17;i++){ bt[i]=v[i]/(2-u[i]*bt[i-1]); } f[0]=g[0]*1.0/2; for(i=1;i<=18;i++){ f[i]=(g[i]-u[i]*f[i-1])/(2-u[i]*bt[i-1]); } M[18]=f[18]; for(i=17;i>=0;i--){ M[i]=f[i]-bt[i]*M[i+1];
的值。 2、按照课本第 92 页的公式（4.44）计算确定 M 的线性方程组的系数数组 u、v、g，
并储存在相应的数组中。这一过程程序代码为 for(i=1;i<19;i++){ h[i]=x[i]-x[i-1]; } for(i=1;i<18;i++){ u[i]=h[i]/(h[i]+h[i+1]); v[i]=1-u[i]; } g[0]=6/h[1]*((y[1]-y[0])/h[1]-y0); g[18]=6/h[18]*(y18-(y[18]-y[17])); for(i=1;i<18;i++){ g[i]=6/(h[i]+h[i+1])*((y[i+1]-y[i])/h[i+1]-(y[i]-y[i-1])/h[i]);

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第１３卷第１期２０１４年２月
江南大学学报（自然科学版）ＪｏｕｒｎａｌｏｆＪｉａｎｇｎａｎＵｎｉｖｅｒｓｉｔｙ（ＮａｔｕｒａｌＳｃｉｅｎｃｅＥｄｉｔｉｏｎ）
风能作为可再生能源的重要类别，因其具有巨大蕴藏量，可再生、分布广、无污染等优势，成为全
目的。
关键词：风力发电机；叶片参数；三次样条插值；应力分析中图分类号：ＴＫ８０文献标志码：Ａ文章编号：１６７１—７１４７（２０１４）０１—００８０—０４
ＡｐｐｌｉｃａｔｉｏｎｏｆＣｕｂｉｃＳｐｌｉｎｅＩｎｔｅｒｐｏｌａｔｉｏｎｉｎＣｏｒｒｅｃｔｉｎｇＷｉｎｄ
ｓａｍｅ．Ｔｈｉｓｒｅｓｕｌｔｎｏｔｏｎｌｙｃｏｎｉｆｒｍｔｈｅｆｅａｓｉｂｉｌｉｔｙｏｆｃｕｂｉｃｓｐｌｉｎｅｆｕｎｃｔｉｏｎａｐｐｌｉｅｄｔｏｔｈｅｂｌａｄｅｄｅｓｉｇｎ，ｂｕｔａｌｓｏａｃｈｉｅｖｅ
ＴｕｒｂｉｎｅＢｌａｄｅＡｉｒｆｏｉｌＰａｒａｍｅｔｅｒｓａｎｄＳｔｒｅｓｓＡｎａｌｙｓｉｓｇ
（ＳｃｈｏｏｌｏｆＭｅｃｈａｎｉｃａｌＥｎｇｉｎｅｅｒｉｎｇ，ＪｉａｎｇｎａｎＵｎｉｖｅｒｓｉｔｙ，Ｗｕｘｉ２１４１２２，Ｃｈｉｎａ）
的问题，采用三次样条插值函数对这两个参数进行拟合，使原本离散分布的风机叶片外形转变为呈连续分布的光滑曲线。通过应用于风机叶片设计实例，对插值前后的翼型参数进行比较，插值前后结果基本一致，说明了三次样条函数应用到叶片设计中的可行性，同时达到了减小叶片应力的
Ａｂｓｔｒａｃｔ：Ｆｏｒｔｈｅａｉｒｆｏｉｌｐａｒａｍｅｔｅｒｓｏｂｅｙｉｎｇａｄｉｓｃｒｅｔｅｄｉｓｔｒｉｂｕｔｉｏｎａｌｏｎｇｔｈｅｓｐａｎｗｉｓｅｄｉｒｅｃｔｉｏｎｉｎｔｈｅｔｒａｄｉｔｉｏｎａｌｂｌａｄｅｄｅｓｉｇｎｐｒｏｃｅｓｓ，ａｃｕｂｉｃｓｐｌｉｎｅｉｎｔｅｒｐｏｌａｔｉｏｎｉｓｔａｋｅｎｔｏｉｆｔｔｈｅｃｏｒｒｅｃｔｉｎｇｃｈｏｒｄｌｅｎｇｔｈａｎｄｔｗｉｓｔａｎｇｌｅｏｆｔｈｅｂｌａｄｅｓｃｒｏｓｓｓｅｃｔｉｏｎｓａｉｒｆｏｉｌ，ａｎｄａｓｍｏｏｔｈａｎｄｃｏｎｔｉｎｕｏｕｓｂｌａｄｅｐｒｏｉｆｌｅｃｕｒｖｅｉｓｏｂｔａｉｎｅｄ．Ｂｙｔｈｅｄｅｓｉｇｎｅｘａｍｐｌｅｏｆｔｈｅｆａｎｂｌａｄｅ，ｔｈｅａｉｒｆｏｉｌｐａｒａｍｅｔｅｒｓａｒｅｃｏｍｐａｒｅｄｂｅｆｏｒｅａｎｄａｆｔｅｒｉｎｔｅｒｐｏｌａｔｉｏｎ，ｔｈｅａｎａｌｙｓｉｓｓｈｏｗｓｔｈａｔｔｈｅｒｅｓｕｌｔｓａｒｅｂａｓｉｃａｌｌｙｔｈｅ
ｔｈｅｐｕｒｐｏｓｅｏｆｒｅｄｕｃｉｎｇｔｈｅｂｌａｄｅｓｔｒｅｓｓ．
Ｋｅｙｗｏｒｄｓ：ｗｉｎｄｔｕｒｂｉｎｅ，ｂｌａｄｅｐａｒａｍｅｔｅｒｓ，ｃｕｂｉｃｓｐｌｉｎｅｉｎｔｅｒｐｏｌａｔｉｏｎ，ｓｔｒｅｓｓａｎａｌｙｓｉｓ
Ｖｏ１．１３Ｎｏ．１Ｆｅｂ．２０１４
三次样条插值在风机叶片外形设计中应用及应力分析
喜超，武美萍
（江南大学机械工程学院，江苏无锡２１４１２２）摘要：针对传统叶片设计过程中由理论计算得出的弦长Ｃ和扭转角均沿翼展方向呈离散性分布