临沂中考试题分类

合集下载

临沂市中考试题分类汇编(几何)

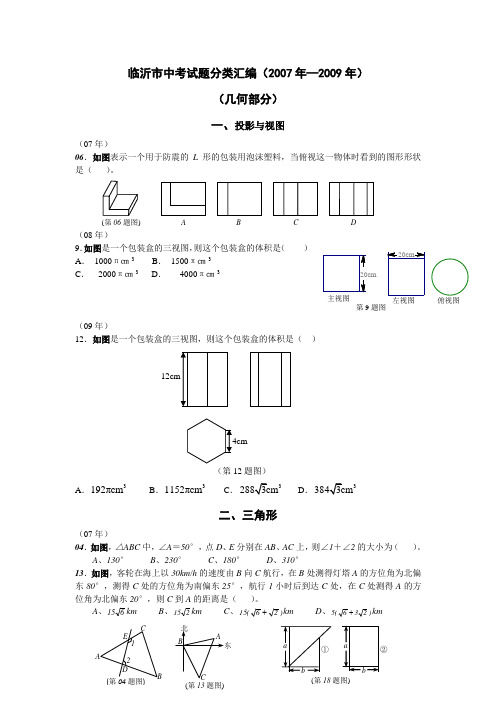
临沂市中考试题分类汇编（2007年—2009年）

（几何部分）一、投影与视图

（07年）

06．如图表示一个用于防震的L 形的包装用泡沫塑料，当俯视这一物体时看到的图形形状是（）。

（08年） 9．如图是一个包装盒的三视图，则这个包装盒的体积是（）

A ． 1000π㎝3

B ． 1500π㎝3

C ． 2000π㎝3

D ． 4000π㎝3

（09年）

12．如图是一个包装盒的三视图，则这个包装盒的体积是（）

A ．3

192πcm

B ．31152πcm C

．3 D

．3

二、三角形

（07年） 04．如图，△ABC 中，∠A ＝50°，点D 、E 分别在AB 、AC 上，则∠1＋∠2的大小为（）。

A 、130°

B 、230°

C 、180°

D 、310°

13．如图，客轮在海上以30km /h 的速度由B 向C 航行，在B 处测得灯塔A 的方位角为北偏东80°，测得C 处的方位角为南偏东25°，航行1小时后到达C 处，在C 处测得A 的方位角为北偏东20°，则C 到A 的距离是（）。

A 、615km

B 、215km

C 、)26(15+km

D 、)236(5+km

C E

A B C D (第06题图)

第9题图

主视图

左视图

俯视图

（第12题图）

18．有如图所示的两种广告牌，其中图①是由两个等腰直角三角形构成的，图②是一个矩形，

从图形上确定这两个广告牌面积的大小关系，并将这种大小关系用含字母a 、b 的不等式表示为。（08年）

4．下列各图中，∠1大于∠2的结果是（）

14.如图已知正三角形ABC 的边长为1，E 、F 、G 分别是AB 、BC 、CA 上的点，且AE ＝BF ＝CG ，设△EFG 的面积为y ，AE 的长为x ，则y 关于x 的函数的图象大致是（）

山东省临沂市兰山区2021-2023年三年中考一模英语试题分类汇编：书面表达(含答案)

山东省临沂市兰山区2021-2023年三年中考一模英语试题分类汇编

书面表达

2023年山东省临沂市兰山区中考一模英语试题

六、书面表达（计15分）

假定你是陈飞, 一个外国游学团要来你校, 学校需要一批志愿者, 你很乐意参加。请阅读下面的招募启事, 并根据邮件内容用英语写一封应征邮件。可以适当发挥。

要求: 1. 词数80左右, 开头和结尾已经写好, 不计入总词数;

2. 语言通顺, 条理清楚, 书写规范;

3. 文中不要出现任何真实人名、校名及其它相关信息, 否则不予评分。

2022年山东省临沂市兰山区中考一模英语试题

八、书面表达（计15分）

61．初中三年，你不仅学到了知识，也具备了一定的能力。当你克服困难第一次成功地完成某件事情时，这份与众不同的经历一定在你的脑海里留下了深刻的印象。请以“My first time to ______”为题，写一篇英语作文，分享你的经历并谈谈你的感受。不少于80词。

要求：

1.补全标题；

2.短文中不得出现任何真实人名、校名及其它相关信息，否则不予评分。

提示：

1.What is your experience?

2.How did you feel?

3.What have you learned from the experience?

My first time to _________

_______________________________________________________________________________ _______________________________________________________________________________ _______________________________________________________________________________

山东省临沂市2017-2019年三年中考英语试题分类汇编：动词应用含答案

According to the police report, a 45-year-old female passenger, surnamed Liu, argued with the driver, surnamed Ran. Liu was angry because Ran refused 70 (stop) the bus after she missed her station. She then hit the driver, causing the accident. The video shows that Liu hit Ran with her mobile phone twice while

71 (drive) the bus. Rather than stop in the middle of the road,. Ran kept driving. But in protecting himself, he lost control of the bus and a tragedy (悲剧) happened.

The police said that both Liu and Ran had broken criminal law by seriously endangering (危及) public safety. And the police 72 (announce), "Liu hit the driver with her phone and prevented the driver from driving the bus safely. The driver, too, didn't do his best to make sure that his driving was safe."

山东省临沂市蒙阴县2020-2022年三年中考一模英语试题分类汇编：阅读表达(含答案)

山东省临沂市蒙阴县2020-2022年三年中考一模英语试题分类汇编

阅读表达

2022年山东省临沂市蒙阴县中考一模英语试题

六、阅读表达（共5小题，计10分）

根据短文内容，回答下列问题。

As a young child, I was pretty lazy when it came to doing chores. If my parents asked me to do something, I would do it — not a problem. But I always needed to be told to do things that I could easily see. That undoubtedly annoyed (惹恼) my parents.

Every Saturday afternoon, my mother drove me to another town for a piano lesson. During my half-hour lesson, she’d rush to the nearby market and buy a week’s food. Considering my mom drove me twelve miles there, twelve miles back, paid for my lesson, and bought me a candy, I should be thankful enough to help her bring the food into the house without being asked. But I didn’t.

山东省临沂市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-03解答题(较难题)

山东省临沂市2023年各地区中考考数学模拟（一模）试题按题型难易度分层分类汇编-03解答题（较难题）

一．二次函数的应用（共2小题）

1．（2023•莒南县一模）如图1，一灌溉车正为绿化带浇水，喷水口H离地竖直高度为h＝

1.5米．如图2，可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线

的部分图象；把绿化带横截面抽象为矩形DEFG，其水平宽度DE＝3米，竖直高度EF＝

0.5米，下边缘抛物线是由上边缘抛物线向左平移得到，上边缘抛物线最高点A离喷水口

的水平距离为2米，高出喷水口0.5米，灌溉车到绿化带的距离OD为d米．

（1）求上边缘抛物线的函数解析式，并求喷出水的最大射程OC；

（2）求下边缘抛物线与x轴交点B的坐标；

（3）要使灌溉车行驶时喷出的水能浇灌到整个绿化带，求d的取值范围．2．（2023•临沭县一模）2021年东京奥运会，中国跳水队赢得8个项目中的7块金牌，优异成绩的取得离不开艰辛的训练．某跳水运动员在进行跳水训练时，身体（看成一点）在空中的运动路线是如图所示的一条抛物线，已知跳板AB长为2米，跳板距水面CD的高BC为3米，训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度k米，现以CD为横轴，CB为纵轴建立直角坐标系．

（1）当k＝4时，求这条抛物线的解析式．

（2）当k＝4时，求运动员落水点与点C的距离．

（3）图中CE＝米，CF＝5米，若跳水运动员在区域EF内（含点E，F）入水时才能达到训练要求，求k的取值范围．

二．全等三角形的判定与性质（共1小题）

3．（2023•蒙阴县一模）【问题情境】如图，在平面直角坐标系中，点A（0，m），B（n，0），且（m﹣n）2+n2﹣4n+4＝0，连接AB，点P、点Q是x轴上的动点，且OP＝BQ．连接AQ，过O点作OD⊥AQ于点E，交直线AB于点D，连接DP，试问在运动过程中，∠BPD与∠AQO是否存在某种特定的数量关系．

山东省临沂市蒙阴县2021-2023年中考英语一模试题分类汇编语法填空

山东省临沂市蒙阴县

2021-2023年中考英语一模试题分类汇编

语法填空

2023年山东省临沂市蒙阴县中考一模英语试题

阅读下面短文, 在空白处填入一个适当的单词或括号内单词的正确形式, 必要时可加助动词或情态动词。

A well-known poem by Tang dynasty（朝代）poet Du Mu tells of a scene in early April：“Rains fall heavily as Qingming comes, and passersby with lowered spirits go. ”

This scene often 46 （take）place on Tomb（坟墓）Sweeping Day, and it is also known as Qingming Festival. Tomb Sweeping Day is a_ 47 (tradition)Chinese festival. It began in the Zhou dynasty, over 2, 500 years 48 . Tomb-sweeping Day falls on either April 4th or 5th of the calendar. In 2023, it falls on April 5th. Tomb Sweeping Day 49 (be) a public holiday in the Chinese mainland since 2008.

山东省临沂市临沭县2021-2023年中考英语二模试题分类汇编：语法填空(含解析)

山东省临沂市临沭县

2021-2023年中考英语二模试题分类汇编

语法填空

2023年山东省临沂市临沭县中考二模英语试题

三、语法填空

阅读下面短文, 在空白处填入一个适当的单词或括号内单词的正确形式。

There is a special coffee shop in Shanghai. It is the 46 (one) coffee shop run by blind people in China. Twin brothers Yin Tianbao and Yin Tianyou serve as baristas ( 咖啡师) there. Tianbao is also the 47______ (manage ) of the shop. The brothers were born blind, but it has never stopped them from ___________(enjoy) their life. They like playing football and they are skilled marathon runners. Their latest effort to challenge 49_______ (they) is running the coffee shop.

Tianbao 50________ (begin )to learn to make coffee in late 2021. It was no easy task for him. He practiced making over 100 cups of coffee every day. "There is no other way but to practice over and over again, "Tianbao said. Latte art (拿铁艺术)was the most challenging part for him. “The milk foam ( 奶泡) is 51_______ light that it' s hard for me to know whether the coffee cup is almost full by the sound. What I can do is to try 52_______ feeling slowly. " he said.

山东省临沂市费县2021-2023年中考英语一模试题分类汇编阅读表达

山东省临沂市费县

2021-2023年中考英语一模试题分类汇编

阅读表达

2023年山东省临沂市费县中考一模英语试题

四、阅读表达（共5小题，计10分）

阅读下面短文，完成短文后的问题。

A Teenager with Autism (自闭症) Swims toward Victory

Chen Xingrong won five medals, including a gold, at the 11th National Games for Persons with

disabilities and the 8th National Special Olympic Games.

Born in Hainan Province, Chen Xingrong could not say a word until he was 2 years old.

When Chen Xingrong was found autistic (自闭的), his parents were worried. In 2012, his father learned that swimming could help people with autism, so he spent months learning how to swim by watching videos and reading books. When Chen Xingrong was 5 years old, he began to teach him how to swim. At the very beginning, he spent three months teaching his son, but all his efforts failed. To his surprise, after another three months, he discovered that his son had developed the ability to control his breath under water, and it greatly increased his confidence.

山东省临沂市费县2021-2023年中考英语一模试题分类汇编语法填空(1)

山东省临沂市费县

2021-2023年中考英语一模试题分类汇编

语法填空

2023年山东省临沂市费县中考一模英语试题

四、语法填空

阅读下面短文，在空白处填入一个适当的单词或用括号内单词的正确形式，必要时可加助动词或情态动词。（共10小题，计10分）

The Old Man and the Sea

The book I recommend (推荐) is The Old Man and the Sea. It is fascinating and worth 46 (read) for young people.

It is a great work written by the US writer Ernest Hemingway, and it is just over 100 pages in length. It is also the last major work of fiction produced in his lifetime. What’s more, it was awarded the Pulitzer Prize for fiction in 1953 and 47 (play) an important part in winning the Nobel Prize for literature in 1954.

The book is about a story of 48 old Cuban fisherman, Santiago. It tells us that he 49(not catch) any fish for 84 days. But 50 the 85th day, we see him go out and catch a huge marlin (枪鱼). That is when the real trouble begins. Santiago is a confident and hard-working fisherman. 51 he ends up with nothing, he never gives up along the way. Many people 52 ( move) by his strong spirit. That spirit is just what we need. Life itself is an endless pursuit (追求). It’s a long road and full of difficulties, but if we have the courage to face the challenge, we 53 (be) a real winner.

2018-2020年山东中考复习数学各地区模拟试题分类(临沂专版)(5)——三角形与四边形

2018-2020年山东中考复习数学各地区模拟试题分类（临沂专版）（5）——

三角形与四边形

一．选择题

1．（2019•平邑县一模）如图，在Rt△ABC中，∠B＝90°，AB＝6，BC＝8，点D在BC上，以AC为对角线的所有平行四边形ADCE中，DE的最小值是（）

A．10 B．8 C．6 D．5

2．（2018•沂水县二模）如图，OA＝OB，∠A＝∠B，有下列3个结论：①△AOD≌△BOC，②△ACE≌△BDE，③点E在∠O的平分线上，其中正确的结论个数是（）

A．0 B．1 C．2 D．3

3．（2020•郯城县一模）如图所示，在四边形ABCD中，AD∥BC，要使四边形ABCD成为平行四边形还需要条件（）

A．AB＝DC B．∠1＝∠2 C．AB＝AD D．∠D＝∠B

4．（2019•兰陵县一模）如图，在平行四边形ABCD中，对角线AC、BD相交于点O，BD＝2AD，E、F、G 分别是OC、OD、AB的中点，下列结论：①BE⊥AC；②四边形BEFG是平行四边形；③△EFG≌△GBE；

④EG＝EF，其中正确的个数是（）

A．1 B．2 C．3 D．4

5．（2019•郯城县一模）如图，用平行四边形纸条沿对边AB、CD上的点E、F所在的直线折成V字形图案，已知图中∠1＝56°，则∠2的度数为（）

A．56°B．66°C．68°D．112°

6．（2019•兰山区二模）如图，O是平行四边形ABCD的对角线交点，E为AB中点，DE交AC于点F，若平行四边形ABCD的面积为16．则△DOE面积是（）

A．1 B．C．2 D．

2023年山东临沂中考化学试题及答案推荐

试卷类型：A

第Ⅰ卷(选择题共36分)

可能用到的相对原子质量：

一、选择题(本题包括18小题，每小题2分，共36分。每小题只有一个正确答案)

1. 下列变化属于化学变化的是（）

A. 干冰升华

B. 石蜡熔化

C. 食物腐败

D. 衣服晾干

2. 分类是化学学习中常用的思维方法。下列物质中，属于纯净物的是

A. 空气

B. 液氧

C. 生铁

D. 石油

3. 学校兴趣小组在“探究土壤酸碱性对植物生长的影响”的实践活动中，测得土壤样品呈酸性，其测得结果可能是

A. B. C. D.

4. 下列图示实验操作中，错误的是

A. 取用固体粉末

B. 倾倒液体

C. 滴加液体

D. 加热液体

5. 下列有关化学用语书写正确的是

A. 汞元素：

B. 酒精：

C. 2个镁离子：

D. 60个碳原子：

6. 学化学，用化学。下列做法中错误的是

A. 实验时碰倒酒精灯着火，立即用湿抹布盖灭

B. 加油站、面粉厂等场所严禁烟火

C. 用甲醛浸泡海产品延长保质期

D. 冬天用煤炉取暖时注意室内通风

7. 端午节插艾草是我国一些地区的习俗。艾草含有丰富的黄酮素，具有较高的药用价值。下列关于黄酮素的说法中错误的是

A. 黄酮素中含有氧分子

B. 黄酮素由三种元素组成

C. 黄酮素完全燃烧生成和

D. 黄酮素中氢、氧元素质量比为

8. 下列有关实验现象的描述，错误的是

A. 硫在氧气中燃烧，产生明亮的蓝紫色火焰

B. 用木炭还原氧化铜时，黑色粉末逐渐变为红色

C. 打开盛有浓盐酸的试剂瓶的瓶盖，瓶口出现白烟

D. 向生锈的铁钉中加入稀盐酸，溶液逐渐变为黄色

2007—2009临沂市中考数学试题分类(代数)

临沂市中考试题分类汇编（2007年—2009年）

（代数部分）一、实数

（07年）

1．－5的绝对值是（）A 、－5 B 、5 C 、5

1 D 、51

2．据了解，我市每年用于校舍维护维修的资金约需7300万元，用科学记数法表示这一数据为（） A 、7.3×106元 B 、73×106元 C 、7.3×107元 D 、73×107元（08年）

1．－

31的倒数是（）A ．－3 B ． 3 C ． 31 D ．－3

1 2．在今年四川汶川地震抗震救灾过程中，国内外社会各界纷纷伸出援助之手，截止5月30日12时，共收到各类捐赠款物折合人民币约399亿元，这个数据用科学记数法表示为（）

A ． 3.99×109元

B ． 3.99×1010元

C ． 3.99×1011元

D ． 399×102元（09年）

1．9-的相反数是（）A ．

B ．19

C ．9-

D ．9

2．某种流感病毒的直径是0.00000008m ，这个数据用科学记数法表示为（） A ．6

810m -⨯

B ．5

810m -⨯

C ．8

810m -⨯

D ．4

810m -⨯

二、代数式

（07年）

3．下列运算正确的是（）

A 、x 3＋x 5＝x 8

B 、(x 3)2＝x 9

C 、x 4·x 3＝x 7

D 、(x ＋3)2＝x 2＋9 5．计算)483

75(12-+的结果是（） A 、6 B 、34 C 、632+ D 、12

15．计算：)3

a a 3a a 3(+--·

a 9

a 2-＝ . 19．如果一个数等于它的不包括自身的所有因数之和，那么这个数就叫完全数.例如，6的不包括自身

山东省临沂市2023年各地区中考考数学模拟(一模)试题按题型难易度分层分类汇编-01选择题(容易题)

山东省临沂市2023年各地区中考考数学模拟（一模）试题按题型难易度分层分类汇编-01选择题（容易题）

一．正数和负数（共1小题）

1．（2023•费县一模）中国是最早采用正负数表示相反意义的量，并进行负数运算的国家．若零上10℃记作+10℃，则零下6℃可记作（）

A．6℃B．0℃C．﹣6℃D．﹣20℃

二．相反数（共1小题）

2．（2023•平邑县一模）﹣的相反数是（）

A．﹣B．4C．﹣4D．

三．绝对值（共1小题）

3．（2023•郯城县一模）2023的绝对值是（）

A．B．C．2023D．﹣2023

四．科学记数法—表示较大的数（共2小题）

4．（2023•郯城县一模）第19届亚运会将于2023年9月23日至10月8日在中国浙江省杭州市举行，杭州奥体博览城游泳馆区建筑总面积272000平方米，将数272000用科学记数法表示为（）

A．0.272×107B．2.72×106C．2.72×105D．272×104 5．（2023•平邑县一模）近年来，我国5G发展取得明显成效，截至2020年底，全国建设开通5G基站达71.8万个，将数据71.8万用科学记数法表示为（）

A．0.718×106B．7.18×105C．71.8×104D．718×103

五．科学记数法—表示较小的数（共1小题）

6．（2023•河东区一模）2022年12月21日，长电科技已经实现4nm工艺制程手机芯片的封装，其中1nm等于0.000000001m，将0.000000001用科学记数法表示为（）

A．1×109B．1×10﹣9C．1×10﹣8D．1×10﹣10

临沂中考试题及答案汇总.doc

首发：2015年临沂中考试题及答案汇总-中

考

总结：话题作文与学期梳理

课程特色:

以写作问题为纲，以解决中高考语文写作问题和讲授踩分词为主，每节课仍会讲解2—3篇阅读题，作为对应练习和提高。学习时，要求学生熟记理解每一讲的”地图内容”，以便考试时融会运用。

适合学员

想扎实写作基础，稳固提高作文水平的初中生

赠送

《中学语文知识地图—中学必考文学常识一本通》

第十五章：学期课程融汇与升华

课程特色:

以解决阅读问题为纲，融会踩分词和阅读答题要求，进行专题训练，侧重点分为两个方面，一是结合《中学语文知识地图踩分词》进行阅读答题运用，二是答题结构与题型

，每节课中以阅读概括能力、理解表述能力、判定分析能力和鉴赏能力题为引导进行学习。

适合学员

现代文阅读答题技巧掌握不够全面，想稳固提高的初中生

赠送

《中学语文知识地图—中学文言文必考140字》

课程特色:

全面地检测与分析学生考试丢分的问题，

让学生清楚自己问题在哪，并且怎样改，通过思维训练，加以解决，重点教会学生如何凭借一张知识地图，去解决所有的语文阅读写作问题。

适合学员

想夯实语文基础知识，成绩稳步提高的初中生

赠送

《学生优秀作品及点评指导（2.0版）》

第八章：以小见大与虚实相应

课程特色:

对考场三大作文类型悉数讲解，针对考场作文，黄保余老师现场充精彩点评得失。

适合学员

作文写作水平寻求短期突破的初中生

赠送

《中学考场作文训练营》（图书）

第八章：以小见大与虚实相应

课程特色:

对考场三大作文类型悉数讲解，针对考场作文，黄保余老师现场充精彩点评得失。

适合学员

作文写作水平寻求短期突破的初中生

2018-2020年山东中考生物各地区模拟试题分类(临沂专版)(1)——生命的结构层次(含解析)

2018-2020年山东中考生物各地区模拟试题分类（临沂专版）（1）——生命

的结构层次

一．选择题（共41小题）

1．（2020•沂水县二模）如图是用显微镜观察气孔时的两个视野，要把视野中的物像从甲图转为乙图，下列实验操作的选择和排序，正确的是（）

①转动细准焦螺旋

②转动粗准焦螺旋

③转动遮光器，换大光圈

④转动遮光器，换小光圈

⑤向下方移动装片

⑥向上方移动装片

⑦转动转换器，换高倍物镜

⑧转动转换器，换低倍物镜

A．⑤→⑦→③→②→①B．⑦→⑤→③→②→①C．⑥→⑦→③→①D．⑤→⑦→③→①

2．（2020•临沂模拟）用光学显微镜的一个目镜分别与物镜甲、乙进行组合，来观察口腔上皮细胞装片（如图2）。下列相关说法中，错误的是（）

A．与甲组合相比，乙组合的视野中看到的细胞数目少

B．图1中物镜由甲转换成乙的过程中不能先将镜筒升高

C．若将图2的细胞移到视野正中央，应先将装片向右下方移动

D．制作口腔上皮细胞装片时，为防止产生气泡，首先在载玻片上滴加1滴清水，然后再盖上盖玻片3．（2020•临沂模拟）如图是细胞构成动物体的流程图，其中1，2表示生理过程，a﹣d表示结构层次，下列叙述中错误的是（）

A．1过程中遗传物质发生复制

B．2过程使细胞种类增多

C．c是由不同的b按照一定次序结合而成

D．人体的皮肤对应的是d

4．（2020•兰陵县二模）图二是某同学利用显微镜观察而绘制的动植物细胞模式图，图三是该同学绘制的某生物细胞发生的一系列变化过程模式图。据图叙述正确的是（）

A．利用图一中的显微镜观察细胞时，若向左移动玻片标本，视野中的细胞会向左移动

山东省临沂市2017-2019年三年中考英语考试试题分类汇编：阅读表达

Many governments are now encouraging people to have larger families. In France, women now receive nearly $1,000 a month for a year if they have a third child. Austrian women receive
for a long time, you may find that its owner has changed.
- Besides China, Britain and Japan also use 11 digit mobile phone numbers. But their numbers
always start with 0. So they cannot create as many numbers as we can. Countries like the United
people, usually aged between 20 and 30,are leaving the country to work abroad 可知，在波兰，许多人，通常年龄在 20 到 30 岁之间，正离开这个国家到国外工作。
80. In France, women will receive nearly $1,000 a month for a year if they have a third child 根