人教B版必修2同步练习1.1.3圆柱、圆锥、圆台和球(含答案)

合集下载

2024-2025年北师大版数学必修第二册6.1.1.3简单旋转体——球、圆柱、圆锥和圆台(带答案)

1．3 简单旋转体——球、圆柱、圆锥和圆台必备知识基础练知识点一球的结构特征1．截一个几何体，所得各截面都是圆面，则这个几何体一定是( )A．圆柱 B．圆锥C．球 D．圆台2．给出以下说法：①球的半径是球面上任意一点与球心所连线段的长；②球的直径是球面上任意两点间所连线段的长；③用一个平面截一个球，得到的截面可以是一个正方形；④球常用表示球心的字母表示．其中正确说法的序号是________．知识点二圆柱的结构特征3．下列关于圆柱的说法中，不正确的是( )A．分别以矩形(非正方形)的长和宽所在的直线为旋转轴旋转一周而得到的两个圆柱是两个不同的圆柱B．用平行于圆柱底面的平面截圆柱，截面是与底面全等的圆面C．用一个不平行于圆柱底面的平面截圆柱，截面是一个圆面D．以一个矩形对边中点的连线所在的直线为旋转轴，其余各边旋转180°而形成的曲面所围成的几何体是圆柱4．将边长为1的正方形以其一边所在的直线为旋转轴旋转一周，所得几何体的底面周长是( )A．4π B．8πC．2π D．π知识点三圆锥、圆台的结构特征5．下列叙述中正确的个数是( )①以直角三角形的一边所在直线为轴旋转所得的旋转体是圆锥；②以直角梯形的一腰所在直线为轴旋转所得的旋转体是圆台；③圆柱、圆锥、圆台的底面都是圆面；④用一个平面去截圆锥，得到一个圆锥和一个圆台．A．0 B．1C．2 D．36．圆台的两底面半径分别为2 cm和5 cm，母线长是310 cm，则它的轴截面面积为________．7．用一个平行于圆锥底面的平面截这个圆锥，截得圆台上、下底面的面积之比为1∶16，截去的圆锥的母线长是3 cm，求圆台的母线长．关键能力综合练一、选择题1.如图，某工厂生产的一种机器零件原胚的直观图是一个中空的圆台，中空部分呈圆柱形状，且圆柱底面圆心与圆台底面圆心重合，该零件原胚可由下面图形绕对称轴(直线l)旋转而成，这个图形是( )2．给出下列命题：①圆柱的母线与它的轴可以不平行；②圆锥的顶点、圆锥底面圆周上任意一点及底面圆的圆心三点的连线都可以构成直角三角形；③在圆台的上、下两底面圆周上各取一点，则这两点的连线是圆台的母线；④圆柱的任意两条母线所在的直线是互相平行的．其中正确的是( )A．①③ B．②④C．①④ D．②③3．下列命题中，正确的个数是( )①圆柱的轴截面是过母线的截面中最大的一个；②用任意一个平面去截球体得到的截面一定是一个圆面；③用任意一个平面去截圆锥得到的截面一定是一个圆面．A．0 B．1C．2 D．34．若圆锥的轴截面是正三角形，则它的侧面积是底面积的( )A．4倍 B．3倍C．2倍 D．2倍5．(探究题)将一个等腰梯形绕着它的较长的底边所在的直线旋转一周，所得的几何体由( )A ．一个圆台、两个圆锥构成B ．两个圆台、一个圆锥构成C ．两个圆柱、一个圆锥构成D ．一个圆柱、两个圆锥构成二、填空题 6．下列说法：①在圆柱的上、下两底面的圆周上各取一点，则这两点的连线是圆柱的母线； ②圆锥的顶点与底面圆周上任意一点的连线是圆锥的母线；③在圆台上、下两底面的圆周上各取一点，则这两点的连线是圆台的母线．其中正确说法的序号为________．7．给出下列说法：(1)以直角三角形的一条边所在直线为轴，其余两边旋转形成的曲面围成的几何体是圆锥；(2)以等腰三角形底边上的中线所在直线为轴，将三角形旋转形成的曲面围成的几何体是圆锥；(3)经过圆锥任意两条母线的截面是等腰三角形；(4)圆锥侧面的母线长有可能大于圆锥底面圆的直径．其中正确说法的序号是________．8．两相邻边长分别为3 cm 和4 cm 的矩形，以一边所在的直线为轴旋转所成的圆柱中，母线长和底面半径分别为________．三、解答题 9.如图所示是一个正三角形和它的内切圆，将阴影部分绕直线l 旋转180°，请说出所得几何体的结构特征．学科素养升级练1.(多选题)某圆锥的底面半径为3，母线长为4，则下列关于此圆锥的说法正确的是( )A ．圆锥的侧面展开图的圆心角为3π2B ．圆锥的高为7C ．过圆锥的两条母线作截面，截面面积的最大值为8D ．圆锥轴截面的面积为3722．(学科素养——数学运算)圆台的上、下底面半径分别为5 cm ，10 cm ，母线长AB ＝20 cm ，从圆台母线AB 的中点M 拉一条绳子绕圆台侧面转到点A (A 在下底面上)，求：(1)绳子的最短长度；(2)在绳子最短时，上底圆周上的点到绳子的最短距离．1．3 简单旋转体——球、圆柱、圆锥和圆台必备知识基础练1．答案：C解析：由球的结构特征知该几何体是球．故选C. 2．答案：①④解析：根据球的定义知，①正确；②不正确，因为球的直径必过球心；③不正确，因为球的任何截面都是圆；④正确．3．答案：C解析：用一个不平行于圆柱底面的平面截圆柱，截面不是圆面，如用垂直于圆柱底面的平面截圆柱，截面是矩形．故选C.4．答案：C 解析：将边长为1的正方形以其一边所在的直线为旋转轴旋转一周，得到的几何体是圆柱，它的底面是半径为1的圆，其周长为2π·1＝2π.故选C.5．答案：B 解析：①中应以直角三角形的直角边所在直线为轴，②中应以直角梯形的直角腰所在直线为轴，④中应用平行于底面的平面去截，③正确．故选B.6．答案：63 cm 2解析：圆台的高为h ＝（310）2－（5－2）2＝9(cm)，∴S ＝（4＋10）×92＝63(cm 2).7．解析：如图所示，设圆台的母线长为l cm ，截得圆台的上、下底面半径分别为r cm ，4r cm.根据相似三角形的性质得33＋l ＝r4r，解得l ＝9.所以圆台的母线长为9 cm.关键能力综合练1．答案：B 解析：根据零件原胚的直观图可知，中空部分呈圆柱形状，而圆柱形状由矩形旋转形成，圆台由梯形旋转形成，分析四个选项，A 项，旋转后圆台；C 项，旋转后圆台；D 项，球体中挖去一个小球．故选B.2．答案：B解析：对于①，圆柱的母线与它的轴是平行的，所以①错误；对于②，圆锥的顶点、圆锥底面圆周上任意一点及底面圆的圆心三点的连线都可以构成直角三角形，所以②正确；对于③，在圆台的上、下两底面圆周上各取一点，这两点的连线不一定是圆台的母线，所以③错误；对于④，圆柱的任意两条母线所在的直线是互相平行的，所以④正确．综上可知，正确命题的序号是②④.故选B.3．答案：C解析：由圆柱与球的结构特征可知①②正确．由圆锥的结构特征可知③错误．故选C. 4．答案：D解析：由题知圆锥的轴截面是正三角形，设底面半径为r ，则圆锥的底面积为πr 2，圆锥的侧面积为12×2πr ×2r ＝2πr 2，所以它的底面积与侧面积之比为1∶2.故选D.5．答案：D解析：旋转体如图，可知选D.6．答案：②解析：①所取的两点与圆柱的轴的连线所构成的四边形不一定是矩形，若不是矩形，则与圆柱母线定义不符．③所取两点连线的延长线不一定与轴交于一点，不符合圆台母线的定义．②符合圆锥母线的定义及性质．7．答案：(2)(3)(4)解析：(1)不正确，因为当直角三角形绕斜边所在直线旋转得到的旋转体不是圆锥；(2)正确，以等腰三角形底边上的中线所在直线为轴，将三角形旋转形成的曲面围成的几何体是圆锥；(3)正确，因为圆锥的母线长都相等，所以经过圆锥任意两条母线的截面是等腰三角形； (4)正确，如图所示，圆锥侧面的母线长l 有可能大于圆锥底面圆半径r 的2倍(即直径). 8．答案：3 cm ，4 cm 或4 cm ，3 cm解析：当以3 cm 长的一边所在直线为轴旋转时，母线长为3 cm ，底面半径为4 cm ；当以4 cm 长的一边所在直线为轴旋转时，母线长为4 cm ，底面半径为3 cm. 9．解析：正三角形绕直线l 旋转180°得到圆锥，圆绕直线l 旋转180°得到的是球体，所以得到的几何体是圆锥挖去一个与圆锥底面和侧面均相切的球．学科素养升级练1．答案：ABC解析：因为圆锥的底面半径为3，所以圆锥的底面周长为2π·3＝6π，又因为圆锥的母线长为4，所以圆锥的侧面展开图的圆心角为6π4 ＝3π2 ，所以A 选项说法正确；因为圆锥的底面半径为3，母线长为4，所以圆锥的高h ＝42－32＝7 ，所以B 选项说法正确；设圆锥的两条母线的夹角为θ，过这两条母线作截面所得截面的面积为12×4×4·sin θ＝8sin θ，当θ＝π2时，面积有最大值，最大值为8，此时，截面与底面交线长为42 ，小于底面直径6，所以C 选项说法正确；圆锥轴截面的面积为12×6×7 ＝37 ，所以D选项说法不正确．故选ABC.2．解析：(1)如图所示，将侧面展开，绳子的最短长度为侧面展开图中AM 的长度，设OB ＝l ，圆心角为θ，则⎩⎪⎨⎪⎧θ·l ＝2π×5，θ·（l ＋20）＝2π×10，解得⎩⎪⎨⎪⎧θ＝π2，l ＝20.所以OA ＝40(cm)，OM ＝30(cm)，所以AM ＝OA 2＋OM 2＝50(cm)，即绳子最短长度为50 cm.(2)作OQ ⊥AM 于点Q ，交弧BB ′于点P ，则PQ 为所求的最短距离．因为OA ·OM ＝AM ·OQ ，所以OQ ＝OA ·OM AM ＝40×3050＝24(cm)，故PQ ＝OQ －OP ＝24－20＝4(cm)，即上底圆周上的点到绳子的最短距离为4 cm.。

高一数学必修2同步训练 1.1.2 圆柱、圆锥、圆台和球

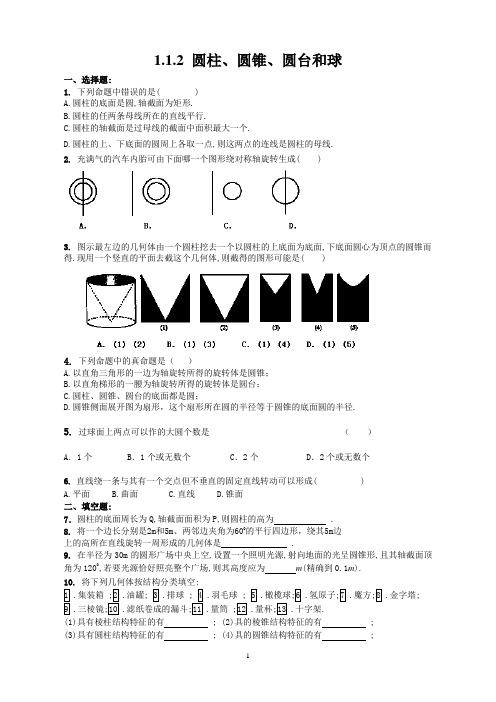
1.1.2 圆柱、圆锥、圆台和球一、选择题:1.下列命题中错误的是( )A.圆柱的底面是圆,轴截面为矩形.B.圆柱的任两条母线所在的直线平行.C.圆柱的轴截面是过母线的截面中面积最大一个.D.圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线.2.充满气的汽车内胎可由下面哪一个图形绕对称轴旋转生成( )3.图示最左边的几何体由一个圆柱挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得.现用一个竖直的平面去截这个几何体,则截得的图形可能是( )4.下列命题中的真命题是（）A.以直角三角形的一边为轴旋转所得的旋转体是圆锥；B.以直角梯形的一腰为轴旋转所得的旋转体是圆台；C.圆柱、圆锥、圆台的底面都是圆；D.圆锥侧面展开图为扇形，这个扇形所在圆的半径等于圆锥的底面圆的半径.5.过球面上两点可以作的大圆个数是（）A．1个 B．1个或无数个 C．2个 D．2个或无数个6.直线绕一条与其有一个交点但不垂直的固定直线转动可以形成( )A.平面B.曲面C.直线D.锥面二、填空题:7．圆柱的底面周长为Q,轴截面面积为P,则圆柱的高为 .8.将一个边长分别是2m和5m、两邻边夹角为60O的平行四边形，绕其5m边上的高所在直线旋转一周形成的几何体是 .9.在半径为30m的圆形广场中央上空,设置一个照明光源,射向地面的光呈圆锥形,且其轴截面顶角为1200,若要光源恰好照亮整个广场,则其高度应为m(精确到0.1m).10.将下列几何体按结构分类填空:集装箱油罐排球羽毛球橄榄球氢原子魔方金字塔;三棱镜滤纸卷成的漏斗量筒量杯十字架.(1)具有棱柱结构特征的有 ; (2)具的棱锥结构特征的有 ;(3)具有圆柱结构特征的有 ; (4)具的圆锥结构特征的有 ;(5)具有棱台结构特征的有 ; (6)具的圆台结构特征的有 ;(7)具有棱台结构特征的有 ; (8)具的圆台结构特征的有 ;(9)其它的有 .二、解答题:11．一个圆锥的母线长为10,底面半径为6,求圆锥的轴截面面积.12.一个圆台的母线长为10,上、下底面的面积分别为4π，64π,求圆台的高.13.如图所示,将阴影部分图形,绕图示直线旋转一周,请说出所得几何体的结构.14.已知圆锥的底面半径为r,高为h,正方体ABCD-A1B I C l D1内接于圆锥,求这个正方体的棱长.15.把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1:4,母线长10cm , 求圆锥的母线长.拓展创新——练能力16.一个圆台的上底面半径、母线长、下底面半径的比为1：2:2,求母线与下底面的夹角.17.已知圆台上、下底面半径的比是1:4,母线长为9cm,母线与轴的夹角为30O,求圆台中截面(过高的中点且平行底面的截面)的面积.18.用一个平行于圆锥底面的平面截这个圆锥,截得圆台上、下底面半径的比是λ,截去圆锥的母线长是l O,求圆台的母线长.参考答案:1. 若上、下底面上的两点，不是同一母线上的两点，则两点的连线就不是母线.故选D.2. 由内胎的结构知，选C3. 截面(2)(3)的外轮廓是整个的矩形，所以是错的.故排除（A ）(B);截面（4）圆锥的轮廓是抛物线而不是三角形，所以是错的.故选D. 4.C 5. 过球面上两点可以作的大圆个数是1个或无数个,故应选B. 6. 锥面，故选D.7. 设底面半径为r,高为h,则2πr=Q,2r ·h=p.∴h=Q p π. 8. 由旋转体的定义得几何体是圆台. 9.∴O ≈17.3.10. ⑴11.l r 高h =22610-=8. ∴S 轴截面=21×12×8＝48 ∴圆锥轴截面面积为48 .12. ∵上、下底面的面积分别为4π，64π,∴上、下底面的半径分别为2，8.∵圆台的母线长为10, ∴圆台的高为22)28(10--=6 . 13. 所得几何体是圆锥挖去一个球的简单几何体.14. 如图所示, 过内接正方体的一组对棱作圆锥的轴截面，如图所示，设圆锥内接正方体的棱长为x ,则在轴截面中,正方体的对角面A 1ACC 1的一组邻边的长分别为x 和2x .∵11VAC ∆∽VMN ∆ , ∴12h x x r h h-==-, 22rh rx =-, ∴x = . 15. 设圆锥的母线长为l ,圆台上、下底半径为,r R ,∵10l l l R -=, ∴1014l l -=, ∴40()3l cm =,即圆锥的母线长为40()3cm . 16. ∵圆台的上底面半径、母线长、下底面半径的比为1：2:2∴设圆台的上底面半径、母线长、下底面半径分别为x,2x,2x. 母线与下底面的夹角为θ. ∴cos θ=2122=-x x x , ∴θ=3π 17. 如图所示,设圆台上、下底面半径分别为,4x x ,则半径差为3x ,∵母线与轴的夹角为300, 圆台的母线长为9cm ,∴932x = , 即32x =. ∴圆台的中截面的半径为45531522224x x r x +===⨯=. ∴22225225()1616S r cm πππ==⨯=中 18. 如图所示,设圆台的母线长为l,截得圆锥底面与原圆锥底面半径分别是x ,λx ,根据相似三角形的性质得:λλ1==+x x l l l O O .∴l =l 0(λ-1).。

【成才之路】人教B版数学必修2练习：1.1.3圆柱、圆锥、圆台和球(含答案解析)

第一章 1.1.3一、选择题1．下列说法中正确的个数是导学号03310104()①半圆弧以其直径为轴旋转所成的曲面叫球；②空间中到定点的距离等于定长的所有点的集合叫球面；③球面和球是同一个概念；④经过球面上不同的两点只能作一个最大的圆．A．1B．2C．3 D．4[答案] A[解析]半圆弧以其直径为轴旋转所成的曲面叫球面，球面围成的几何体叫球，①不正确；②正确；球面和球是两个不同的概念，③错误；若球面上不同的两点恰好为最大的圆的直径的端点，则过此两点的大圆有无数个，故④错误．2．上、下底面面积分别为36π和49π，母线长为5的圆台，两底面间的距离为导学号03310105()A．4 B．3 2C．2 3 D．2 6[答案] D[解析]由题意，得圆台上、下底面半径分别为6和7，在圆台的轴截面等腰梯形中，易求得两底面距离d＝52－－2＝26．3．用一个平面去截一个几何体，得到的截面是四边形，则这个几何体可能是导学号03310106()A．圆锥B．圆柱C．球体D．以上都可能[答案] B[解析]球体被任何平面所截得的截面均为圆面；对圆锥，截面不能为四边形；对于圆柱，当截面过两条母线时，得到四边形．4．一个正方体内接于一个球，过球心作一截面，则截面的不可能图形是导学号03310107()[答案] D[解析] 过球心与正方体的对角面时为B ，过球心与正方体一组平行棱的中点时为C ，过球心及一组平行棱的位于顶点和中点之间的某种分点时为A ，∴不可能为D ．5．在地球北纬60°圈上有A 、B 两点，它们的经度相差180°，A 、B 两地沿纬线圈的弧长与A 、B 两点的球面距离之比为导学号 03310108( )A ．B ．C ．D ．[答案] A[解析] 本题主要考查球面距离的求法，求球心角是求球面距离的关键．由题知∠OAB ＝60°，∴∠AOB ＝60°，O 1A ＝R 2．∴AB 两地的球面距离是l 1＝60180πR ＝13πR ．而AB 两地纬线圈的弧长为小圆的半个圆周， ∴l 2＝π·R 2＝12πR.∴l 21＝1213πR ＝．6．将一个等腰梯形绕着它的较长的底边所在的直线旋转一周，所得的几何体包括导学号 03310109( )A ．一个圆台、两个圆锥B ．两个圆台、一个圆柱C ．两个圆台、一个圆锥D ．一个圆柱、两个圆锥[答案] D[解析] 如图，等腰梯形ABCD ，绕梯形较长的底边AB 所在的直线旋转一周，所得的几何体是如图所示的一个圆柱、两个圆锥．二、填空题7．给出下列说法：①球面上四个不同的点一定不在同一平面内；②球的半径是球面上任意一点和球心的连线段；③球面上任意三点可能在一条直线上；④用一个平面去截球，得到的截面是一个圆面．其中正确说法的序号是________.导学号 03310110[答案] ②④[解析] 作球的一个大圆，在大圆上任取四点，则这四点就在球面上，且共面，故①错误；根据球的半径的定义可知②正确；球面上任意三点一定不共线，故③错误；用一个平面去截球，一定截得一个圆面，故④正确．8．已知圆柱的底面半径是20 cm ，高是15 cm ，则平行于圆柱的轴且与此轴相距12 cm 的截面面积是________.导学号 03310111[答案] 480 cm 2[解析] 设所求截面的底边长为x ，则⎝⎛⎭⎫x 22＝202－122，解得x ＝32，∴S 截＝32×15＝480 cm 2．三、解答题9．一个圆台的母线长为12 cm ，两底面的面积分别为4π cm 2和25π cm 2，求：导学号 03310112(1)圆台的高；(2)截得此圆台的圆锥的母线长．[解析] (1)如图所示，设圆台的轴截面是等腰梯形ABCD ，由已知可得上底的一半O 1A ＝2 cm ，下底的一半OB ＝5 cm.∵腰长为12 cm ，∴高为AM ＝122－－2＝315(cm)．(2)设截得此圆台的圆锥的母线长为l ，则由△SAO 1∽△SBO ，可得l －12l ＝25，∴l ＝20(cm)．即截得此圆台的圆锥的母线长为20 cm.一、选择题1．下列命题中，错误的是导学号 03310113( ) A ．圆柱的轴截面是过母线的截面中面积最大的 B ．圆锥的轴截面是所有过顶点的截面中面积最大的 C ．圆台的轴截面一定是等腰梯形 D ．圆锥的轴截面是全等的等腰三角形 [答案] B[解析] 当圆锥的轴截面的顶角是锐角或直角时，轴截面是所有过顶点的截面中面积最大的，当轴截面的顶角是钝角时，轴截面的面积小于过顶点且顶角为直角的截面面积，故选B ．2．两平行平面截半径为5的球，若截面面积分别为9π和16π，则这两个平面间的距离是导学号 03310114( )A ．1B ．7C ．3或4D ．1或7[答案] D[解析] 如图(1)所示，若两个平行平面在球心同侧，则CD ＝52－32－52－42＝1．如图(2)所示，若两个平行截面在球心两侧，则CD ＝52－32＋52－42＝7．3．以钝角三角形的最小边所在的直线为轴，其他两边旋转一周所得到的几何体是导学号 03310115( )A ．两个圆锥拼接而成的组合体B ．一个圆台C ．一个圆锥D ．一个圆锥挖去一个同底的小圆锥 [答案] D[解析] 如图，以AB 为轴，所得的几何体是一个大圆锥挖去一个同底的小圆锥．4．半径为5的球被一平面所截，若截面圆的面积为16π，则球心到截面的距离为导学号 03310116( )A ．4B ．3C ．2.5D ．2[答案] B[解析] 设截面圆半径为r ，则πr 2＝16π，∴r ＝4.球心到截面的距离为d ＝52－r 2＝52－42＝3．二、填空题5．过球半径的中点，作一垂直于这个半径的截面，截面面积为48π cm 2，则球的半径为________.导学号 03310117[答案] 8 cm[解析] 如图，过球心作垂直于截面的平面，由截面面积为48π cm 2，可得AC ＝4 3 cm ，设OA ＝R ，则OC ＝12R ，∴R 2－⎝⎛⎭⎫12R 2＝(43)2，解得R ＝8(cm)．6．图中最左边的几何体由一个圆柱挖去一个以圆柱的上底面为底面，下底面圆心为顶点的圆锥而得．现用一个竖直的平面去截这个几何体，则所截得的图形可能是________(填序号).导学号03310118[答案]①⑤[解析]组合体的上底面已经挖去，故②错．当截面不过轴时，与圆锥的截线不可能是直线，故③④错．三、解答题7．轴截面为正方形的圆柱叫做等边圆柱．已知某等边圆柱的截面面积为16 cm2，求其底面周长和高.导学号03310119[解析]如图所示，作出等边圆柱的轴截面ABCD.由题意知，四边形ABCD为正方形．设圆柱的底面半径为r，则AB＝AD＝2r．其面积S＝AB×AD＝2r×2r＝4r2＝16(cm2)，解得r＝2 cm．所以其底面周长C＝2πr＝2π×2＝4π(cm)，高2r＝4 cm．8．圆台的一个底面周长是另一个底面周长的3倍，轴截面的面积等于392 cm2，母线与轴的夹角是45°，求这个圆台的高、母线长和两底面半径.导学号03310120 [解析]圆台的轴截面如图所示，设圆台上、下底面半径分别为x cm、3x cm，延长AA1交OO1的延长线于S．在Rt△SOA中，∠ASO＝45°，则∠SAO＝45°，∴SO ＝AO ＝3x ，∴OO 1＝2x ．S 轴截面＝12(6x ＋2x)·2x ＝392，解得x ＝7．故圆台的高OO 1＝14 cm ，母线长A 1A ＝2OO 1＝14 2 cm ，两底面半径分别为7 cm 、21 cm ．。

《圆柱、圆锥、圆台和球》同步练习2(人教B版必修2)

【目标要求】1.理解球的概念，理解球面距离的概念，弄清地球的经度与纬度的概念。

2.理解圆柱、圆锥、圆台的概念【巩固教材——稳扎马步】1. 过球面上两点可以作的大圆个数是 ( )A ．1个B ．1个或无数个C ．2个D ．2个或无数个2. 下列四个命题中正确的是( )A ．当平面到球心的距离小于球半径时，球面与平面的交线总是一个圆．B ．过球面上两点只能作一个球的大圆．C ．过空间四个点总能做一个球．D ．球面上两点间的最短球面距离等于过这两点作一个平面与球面的交线圆上两点间的劣孤长．3.下列命题正确的是 ( )A.以直角三角形的一边所在的直线为旋转轴、旋转所得的几何体是圆锥B.在圆柱的上、下底面的圆周上各取一点，则这两点的连线是圆柱的母线C.圆锥的轴截面是所有过母线的截面中面积最大的D.圆台的所有平行于底面的截面都是圆4.圆柱的高为5cm ，底面半径为6cm,则这个圆柱的截面的对角线长位（）A.12B. 13C. 14D. 16【重难突破——重拳出击】5.在北纬60°处有A 、B 两点，它们的经度相差180°，若地球的半径为R ，则它们的球面距离是( ) A.3Rπ B. R π C. R 22 D. R 26.已知球的两个平行截面的面积分别是5π和8π，且距离为1，那么这个球的半径是( )A.2B.3C.4D.无解7、圆柱的轴截面ABCD 是边长为2的正方形，从A 绕柱面到另一端C 最矩距离是 ( ) A.42+π B.4 C.122+π D.228.正三棱台的上、下底面边长及高，分别为1、2、2，则它的斜高是（） A.339 B.313 C.67 D.637 9.圆锥的轴截面是正三角形，则它的底面积与侧面积之比为( )A ．1∶1B ．1∶2C ．1∶4D ．1∶310.设圆台的上下底面半径分别为10和15，母线长为30，则它的侧面展开图扇环中，两个相对顶点间的距离是( )A ．60B ．90C ．D ．11.设圆柱和圆锥的底面半径都是r,?高是h,?若要使圆柱侧面积小于圆锥侧面积,则有( )A.不存在这种可能?B.h＜h?D.h r12. ?把地球看成球体,它上面有两个城市位于同一经度圈上,它们的纬度分别是北纬22°和40°,?则它们的地面距离等于地球半径的( )A. 12B.13C.12πD.10π【巩固提高——登峰揽月】13.高为8cm，底面半径为5cm的圆柱内，一个平行于圆柱的轴的截面是正方形，求截面到轴的距离.14.半径为5的球内有一个截面，它与球心的距离为3，求这个截面圆周的长.【课外拓展——超越自我】15.若地球半径为6370km，求1）地球经线的长。

人教B版数学必修二讲义：第1章 1.1 1.1.3 圆柱、圆锥、圆台和球 Word版含答案

1.1.3圆柱、圆锥、圆台和球1．圆柱的结构特征由简单几何体组合而成的几何体叫做简单组合体． 6．简单组合体的构成形式有两种基本形式：一种是由简单几何体拼接而成的；另一种是由简单几何体截去或挖去一部分而成的．思考：等边三角形绕其一边的中线所在直线旋转半周形成的面所围成的几何体是什么几何体？[提示] 圆锥1.如图所示的组合体的结构特征是( )A ．一个棱柱中截去一个棱柱B ．一个棱柱中截去一个圆柱C ．一个棱柱中截去一个棱锥D．一个棱柱中截去一个棱台C[由简单组合体的基本形式可知，该组合体是一个棱柱中截去一个棱锥．] 2．圆锥的母线长为10，底面半径为6，则其高等于()A．6B．8C．10D．不确定B[由圆锥的轴截面可知，圆锥的母线、底面半径与高构成直角三角形，所以其高为102－62＝8.]3．有下列说法：①球的半径是球面上任意一点与球心的连线；②球的直径是球面上任意两点间的连线；③用一个平面截一个球，得到的是一个圆．其中正确说法的序号是________．①[利用球的结构特征判断：①正确；②不正确，因为直径必过球心；③不正确，因为得到的是一个圆面．](1)圆柱上底面圆上任一点与下底面圆上任一点的连线都是圆柱的母线；(2)一直角梯形绕下底所在直线旋转一周，所形成的曲面围成的几何体是圆台；(3)圆锥、圆台中过轴的截面是轴截面，圆锥的轴截面是等腰三角形，圆台的轴截面是等腰梯形；(4)到定点的距离等于定长的点的集合是球．[解](1)错．由圆柱母线的定义知，圆柱的母线应平行于轴．(2)错．直角梯形绕下底所在直线旋转一周所形成的几何体是由一个圆柱与一个圆锥组成的简单组合体，如图所示．(3)正确．(4)错．应为球面．1．圆柱、圆锥、圆台和球都是一个平面图形绕其特定边(弦)旋转而成的几何体，必须准确认识各旋转体对旋转轴的具体要求．2．只有理解了各旋转体的生成过程，才能明确由此产生的母线、轴、底面等概念，进而判断与这些概念有关的命题的正误．1．下列命题中正确的是()A．直角三角形绕一条边所在直线旋转得到的旋转体是圆锥B．夹在圆柱的两个平行截面间的几何体还是一个旋转体C．圆锥截去一个小圆锥后剩余部分是圆台D．通过圆台侧面上一点，有无数条母线C[A错误，应为直角三角形绕其一条直角边所在直线旋转得到的旋转体是圆锥；若绕其斜边所在直线旋转得到的是两个圆锥构成的一个组合体．B错误，没有说明这两个平行截面与底面的位置关系，当这两个平行截面与底面平行时正确，其他情况则是错误的．D错误，通过圆台侧面上一点，只有一条母线．故选C.]【例2】如图所示，已知梯形ABCD中，AD∥BC，且AD<BC.当梯形ABCD 绕AD所在直线旋转一周时，其他各边旋转围成一个几何体，试描述该几何体的结构特征．[思路探究]关键是弄清简单组合体是由哪几部分组成．[解]如图所示，旋转所得的几何体是由一个圆柱挖去两个圆锥后剩余部分而成的组合体．本题是不规则图形的旋转问题．对于不规则平面图形绕轴旋转问题，首先要对原平面图形作适当的分割，一般分割成矩形、梯形、三角形或圆(半圆或四分之一圆)等基本图形，然后结合圆柱、圆锥、圆台、球的形成过程进行分析．2．描述下列几何体的结构特征．[解]图①所示的几何体是由两个圆台拼接而成的组合体；图②所示的几何体是由一个圆台挖去一个圆锥得到的组合体；图③所示的几何体是在一个圆柱中间挖去一个三棱柱后得到的组合体．1．圆柱、圆锥、圆台平行于底面的截面是什么样的图形？[提示]圆面．2．圆柱、圆锥、圆台过轴的截面是什么样的图形？[提示]分别为矩形、等腰三角形、等腰梯形．3．经过圆台的任意两条母线作截面，截面是什么图形？[提示]因为圆台可以看成是圆锥被平行于底面的平面所截得到的几何体，所以任意两条母线长度均相等，且延长后相交，故经过这两条母线的截面是以这两条母线为腰的等腰梯形．4．球的截面是什么？[提示]球的截面均是圆面，球面被经过球心的平面截得的圆叫做大圆，被不经过球心的平面截得的圆叫做球的小圆．【例3】一个圆台的母线长为12 cm，两底面面积分别为4π cm2和25π cm2，求圆台的高．[思路探究]作出圆台的轴截面，是一个等腰梯形．[解]圆台的轴截面是等腰梯形ABCD(如图所示)．由已知可得O1A＝2 cm，OB＝5 cm.又由题意知，腰长为12 cm，所以高AM＝122－(5－2)2＝315(cm)．1．将圆台还原为圆锥后，求圆锥的母线长．[解] 如图所示，延长BA ，OO 1，CD ，交于点S ，设截得此圆台的圆锥的母线长为l ，则由△SAO 1∽△SBO ，可得l －12l ＝25，解得l ＝20 cm. 即截得此圆台的圆锥的母线长为20 cm.2．如图，在底面半径为2，母线长为4的圆锥中内接一个高为3的圆柱，求圆柱的底面半径．[解] 设圆锥的底面半径为R ，圆柱的底面半径为r ，则由三角形相似，得R －r R ＝342－22，即1－r 2＝12，解得r ＝1. 即圆柱的底面半径为1.与圆锥有关的截面问题的解决策略求解有关圆锥的基本量的问题时，一般先画出圆锥的轴截面，得到一等腰三角形，进而可得到直角三角形，将问题转化为有关直角三角形的问题进行求解．通常在求圆锥的高、母线长、底面圆的半径长等问题时，都是通过取其轴截面，化归求解．巧妙之处就是将空间问题转化为平面问题来解决．1．本节课的重点是了解圆柱、圆锥、圆台、球的定义及结构特征，难点是能根据结构特征识别和区分这些几何体．2．本节课要重点掌握的规律方法(1)判断旋转体结构特征的方法及旋转体轴截面的应用．(2)简单组合体的构成形式及识别方法．3．本节课的易错点是对概念理解不到位而致错．1．判断(正确的打“√”，错误的打“×”)(1)矩形绕其一边所在直线旋转一周而形成的曲面所围成的几何体是圆柱．()(2)以直角梯形的一腰为轴旋转所得的旋转体是圆台．()(3)用一个平面去截圆锥，得到一个圆锥和一个圆台．()[答案](1)√(2)×(3)×[提示](1)正确；(2)错误，应以直角梯形的垂直于底边的腰为轴；(3)错误，应是平面与圆锥底面平行．2．正方形绕其一条对角线所在直线旋转一周，所得几何体是()A．圆柱B．圆锥C．圆台D．两个圆锥D[连接正方形的两条对角线知对角线互相垂直，故绕对角线旋转一周形成两个圆锥．]3．如图所示的几何体是由简单几何体________构成的．[答案]四棱台和球4．已知一个圆柱的轴截面是一个正方形且其面积是Q，求此圆柱的底面半径．[解] 设圆柱底面半径为r ，母线为l ，则由题意得 ⎩⎪⎨⎪⎧2r ＝l ，2r ·l ＝Q ，解得r ＝Q 2. 所以此圆柱的底面半径为Q 2.。

高中数学人教B版必修2练习：1.1.3 圆柱、圆锥、圆台和球课下检测

一、选择题1．以钝角三角形的较小边所在的直线为轴，其他两边旋转一周所得到的几何体是( )A ．两个圆锥拼接而成的组合体B ．一个圆台C ．一个圆锥D ．一个圆锥挖去一个同底的小圆锥解析：如图以AB 为轴所得的几何体是一个大圆锥挖去一个同底的小圆锥．答案：D2．用一个平面去截一个几何体，得到的截面是四边形，这个几何体可能是( )A ．圆锥B ．圆柱C ．球体D ．以上都可能解析：球体被任何平面所截得的截面均为圆面；对圆锥，截面不能为四边形．而圆柱，当截面过两条母线时，得到四边形．答案：B3．(2012·福鼎高一检测)一个圆锥的母线长为2，圆锥的轴截面的面积为3，则母线与轴的夹角为 ( )A ．30°B ．60°C ．30°或60°D ．60°或75° 解析：设圆锥的高为h ，则底面圆的半径为4－h 2，由题意，得S ＝12h ×24－h 2＝3，平方整理得h 4－4h 2＋3＝0，解得h 2＝1或h 2＝3，∴h ＝1或h ＝ 3.母线与轴的夹角为30°或60°.答案：C4．如图，在半径为3的球面上有A 、B 、C 三点，∠ABC ＝90°，BA ＝BC ，球心O 到平面ABC 的距离是322，则B 、C 两点的球面距离是 ( ) A.π3B ．π C.43π D ．2π 解析：∵∠ABC ＝90°，AB ＝BC .设△ABC 外接圆圆心为O 1，则O 1在AC 中点处．OO 1＝322，OA ＝3， ∴AO 1＝322，BC ＝3，∴∠BOC ＝π3. ∴B 、C 两点的球面距离d ＝π3×3＝π. 答案：B二、填空题5．一个等边圆柱(底面直径等于高)的轴截面面积是S ，则它的底面面积是________．解析：设底面半径为r ，则4r 2＝S ，故底面面积为πr 2＝π·S 4＝π4S . 答案：π4S 6．将一个边长为a 的正方形卷成圆柱侧面，则此圆柱的轴截面的面积为________．解析：令圆柱的底面半径为r ，则2πr ＝a ，∴2r ＝a π，轴截面是长为a ，宽为a π的矩形， ∴面积S ＝a ×a π＝a 2π. 答案：a 2π7．等边圆柱(底面直径等于母线长)的轴截面ABCD 是边长为4的正方形，绕圆柱侧面从A 到C 的最短距离是__________．解析：如图，沿母线DC 把圆柱的侧面展开(矩形A ′B ′CD 是半个圆柱的侧面展开图)，那么曲线上从A 到C 的最短距离就是平面上从A ′到C 的线段长度．∵AB ＝BC ＝A ′B ′＝4，∴B ′C ＝12×2π×42＝2π， ∴A ′C ＝B ′C 2＋A ′B ′2＝(2π)2＋16＝24＋π2.答案：24＋π28．(2012·临沂高一检测)一个正方体内接于一个球，过球心作一截面，如图所示，则截面圆可能是________．解析：①是过球心且与正方体的一组对面斜交的截面；②是过正方体对角面的截面；③是过球心与正方体四条互相平行棱中点的截面．答案：①②③三、解答题9．一个圆台的母线长为12 cm ，两底面积分别为4π cm 2和25π cm 2.求：(1)圆台的高；(2)截得此圆台的圆锥的母线长．解：(1)圆台的轴截面是等腰梯形ABCD ，如图所示，由已知可得上底半径O 1A ＝2 cm ，下底半径OB ＝5 cm ，又腰长为12 cm ，所以高为：AM ＝ 122－(5－2)2＝315(cm)．(2)设截得此圆台的圆锥的母线长为l ，则由△SAO 1∽△SBO 可得l －12l ＝25， ∴l ＝20(cm)．即截得此圆台的圆锥的母线长为20 cm.10．一个圆锥的底面半径为2，高为6，在其中有一个高为x 的内接圆柱．(1)用x 表示圆柱的轴截面面积S ；(2)当x 为何值时，S 最大？解：画出圆柱和圆锥的轴截面．如图，设圆柱的底面半径为r ，则由三角形相似可得x 6＝2－r 2，解得r ＝2－x 3. (1)圆柱的轴截面面积S ＝2r ×x ＝2×(2－x 3)×x ＝－23x 2＋4x ，x ∈(0,6)； (2)∵S ＝－23x 2＋4x ＝－23(x 2－6x ) ＝－23(x －3)2＋6 ∴当x ＝3时，S 有最大值6.。

2017-2018学年高中数学人教B版必修2练习：1-1-3 圆柱、圆锥、圆台和球课堂强化含解析精品

1．矩形ABCD (不是正方形)绕边所在直线旋转得圆柱，则得不同形状的圆柱个数为( )A ．1个B ．2个C ．3个D ．4个解析：根据圆柱的形成，分别以矩形的对边所在直线旋转所得的圆柱是相同的．故只有2个．答案：B2．自行车的轮胎可由下面哪一个图形绕直线l 旋转生成 ( )解析：D 旋转形成球，A 旋转形成的是一个大球里有一个小球，B 旋转形成的是两个游泳圈的组合体．答案：C3．下列说法中正确的是 ( )A ．连接圆柱上、下底面圆周上两点的线段是圆柱的母线B ．夹在圆柱的两个平行截面间的几何体还是一个圆柱体C ．圆锥截去一个小圆锥后剩余部分是圆台D ．通过圆台侧面上一点，有无数条母线解析：A 错误．连接圆柱上、下底面圆周上两点的线段不一定与圆柱的轴平行，所以A 不正确．B 错误，没有说明这两个平行截面的位置关系，当这两个平行截面与底面平行时，正确，其他情况则结论就是错误的．D 错误，通过圆台侧面上一点，只有一条母线．故选C.答案：C4．若母线长是4的圆锥的轴截面的面积是8，则圆锥的高是________．解析：如图设圆锥的底面半径为r ，则圆锥的高是16－r 2.∵12·2r ·16－r 2＝8， ∴r ＝22，∴高为16－(22)2＝2 2.答案：2 25．下列说法：①球面上四个不同的点一定不在同一平面内；②球的半径是球面上任意一点和球心的连线段；③球面上任意三点可能在一条直线上；④用一个平面去截球，得到的截面是一个圆面，其中正确的序号是________．解析：作球的一个大圆，在大圆上任取四点，则这四点就在球面上，且共面，故①错误；根据球的半径的定义可知②正确；球面上任意三点一定不共线，故③错误；用一个平面去截球，一定截得一个圆面，故④正确．答案：②④6．圆台的上底面半径和下底面半径及高的比为1∶4∶4，母线长为10 cm，求截得这个圆台的圆锥的底面积和高．解：由题意可设圆台的上、下底面半径和高分别为x、4x、4x，截得圆台的圆锥的高度为h cm，则(4x)2＋(4x－x)2＝102，∵x>0，解得x＝2.∵hh－4x＝4xx，∴h＝163x＝323(cm)．∴原圆锥的底面积为S′＝πr′2＝π(4×2)2＝64π(cm2)，高为323cm.。

数学人教B必修2学案：1.1.3 圆柱、圆锥、圆台和球 Word版含解析

数学人教B必修2第一章1.1.3 圆柱、圆锥、圆台和球1．理解圆柱、圆锥、圆台和球的有关概念，并能从运动的观点来认识这四种几何体的形成过程．2．掌握圆柱、圆锥、圆台和球的轴截面的特征．3．能运用圆柱、圆锥、圆台和球及简单组合体的结构特征来描述现实生活中简单物体的结构．1．圆柱、圆锥、圆台(1)概念：分别以矩形的________、直角三角形的一________、直角梯形中__________的腰所在的直线为旋转轴，将矩形、直角三角形、直角梯形分别旋转一周而形成的曲面所围成的几何体分别叫做圆柱、圆锥、圆台．其中圆台还可以看成是用________圆锥底面的平面截这个圆锥，截面与底面之间的部分．旋转轴叫做所围成的几何体的______；在轴上的__________叫做几何体的高；垂直于轴的边旋转而成的圆面叫做几何体的________；不垂直于轴的边旋转而成的曲面叫做几何体的________，无论旋转到什么位置，这条边都叫做侧面的________；我们常将圆柱的侧面称为圆柱面，圆锥的侧面称为圆锥面．(2)规定：圆柱和棱柱统称为________，圆锥和棱锥统称为________，圆台和棱台统称为________．【做一做1－1】下列图形为圆柱体的是()．【做一做1－2】下列命题中正确的是()．A．以直角三角形的一直角边为轴旋转所得的旋转体是圆锥B．以直角梯形的一腰为轴旋转所得的旋转体是圆台C．圆柱、圆锥、圆台都有两个底面D．圆锥的侧面展开图为扇形，这个扇形所在圆的半径等于圆锥底面圆的半径2．球(1)概念：一个半圆绕着它的________所在的直线旋转一周所形成的曲面叫做________，球面围成的几何体叫做________．形成球的半圆的圆心叫________；连接球面上一点和球心的线段叫球的________；连接球面上两点且通过球心的线段叫球的________．(2)表示：用表示球心的字母表示．(3)球面也可以看作空间中到一个定点的距离等于________的点的集合．球面被经过球心的平面截得的圆叫做球的________，被不经过球心的平面截得的圆叫做球的________．在球面上，两点之间的最短距离，就是经过这两点的________在这两点间的一段劣弧的长度．事实上，人们把这个弧长叫做两点的__________．(4)圆柱、圆锥、圆台、球等几何体，都是由一个平面图形绕着一条直线旋转产生的曲面所围成的几何体，这类几何体叫做________，这条直线叫做__________．【做一做2－1】下列说法中正确的是()．A．圆台是直角梯形绕其一边旋转而成的B．圆锥是直角三角形绕其一边旋转而成的C．圆柱不是旋转体D．圆台可以看作是由平行于底面的平面截一个圆锥而得到的【做一做2－2】有下列说法：①球的半径是连接球心和球面上任意一点的线段；②球的直径是连接球面上两点的线段；③不过球心的截面截得的圆叫做小圆．其中正确说法的序号是__________．3．组合体(1)概念：由__________等基本几何体组合而成的几何体叫做组合体．(2)基本形式：有两种，一种是由简单几何体拼接而成的简单组合体；另一种是由简单几何体截去或挖去一部分而成的简单组合体．三种简单的组合体：多面体与多面体的组合；多面体与旋转体的组合；旋转体与旋转体的组合．常见的简单组合体及其结构特征：①正方体的八个顶点在同一个球面上，此时正方体称为球的内接正方体，球是正方体的外接球，并且正方体的对角线是球的直径；②一球与正方体的所有棱相切，则正方体每个面上的对角线长等于球的直径；③一球与正方体的所有面相切，则正方体的棱长等于球的直径．【做一做3－1】一个直角三角形绕斜边旋转360°形成的空间几何体为()．A．一个圆锥B．一个圆锥和一个圆柱C．两个圆锥D．一个圆锥和一个圆台【做一做3－2】一个正方体内接于一个球，过球心作一截面，则截面不可能是()．1．圆柱、圆锥、圆台的性质剖析：(1)对于圆柱的性质，要注意以下两点：一是轴线垂直于圆柱的底面；二是三类截面的性质——平行于底面的截面是与底面全等的圆，轴截面是一个由上、下底面圆的直径和母线组成的矩形，平行于轴线的截面是一个由上、下底面圆的弦和母线组成的矩形．(2)对于圆锥的性质，要注意以下两点：一是两类截面——平行于底面的截面是与底面相似的圆，过圆锥的顶点且与底面相交的截面是一个由两条母线和底面圆的弦组成的等腰三角形；二是圆锥的母线l、高h和底面圆的半径R组成一个直角三角形．有关圆锥的计算，一般归结为解这个直角三角形，往往会用到关系式l2＝h2＋R2.(3)对于圆台的性质，要注意以下两点：一是圆台的母线共点，所以由任意两条母线确定的截面为一等腰梯形，但是与上、下底面都相交的截面不一定是梯形；二是圆台的母线l、高h和上底面圆的半径r、下底面圆的半径R组成一个直角梯形，且有l2＝h2＋(R－r)2成立，有关圆台的计算问题，常归结为解这个直角梯形．2．地球的经纬线和经纬度(1)经线和经度．剖析：经线是地球表面上从北极到南极的半个大圆，在同一条经线上的点的经度都相等，如图所示，圆O是赤道面，圆O′是纬线圈，P点的经度与A点的经度相等，如果经过点B 的经线是本初子午线(即0°经线)，则P点的经度等于∠AOB的度数，也等于∠PO′C的度数．(2)纬线和纬度．剖析：赤道是一个大圆，它是0°纬线，其他的纬线都是小圆，它们是由与赤道面平行的平面截球所得到的．某地的纬度就是经过这点的球半径与该半径在赤道面上的正投影所成的角的度数．如图所示，圆O是赤道面，圆O′是纬线圈，P点的纬度等于∠POA的度数，也等于∠OPO′的度数．3．教材中的“探索与研究”对圆柱、圆锥、圆台：(1)平行于底面的截面是什么样的图形？(2)过轴的截面(简称轴截面)分别是什么样的图形？(3)研究圆柱、圆台和圆锥之间的关系．剖析：(1)平行于底面的截面，图形都是圆．(2)过轴的截面，对于圆柱是矩形，对于圆锥是等腰三角形，对于圆台是等腰梯形．(3)圆柱的上底面变小，就变为圆台，当上底面变为一个点时，它就变成了圆锥．圆台是由圆锥截得的，“还台为锥”不失为解决圆台问题的好办法．4．教材中的“思考与讨论”在平面几何中，你学习了直线与圆的位置关系，那么平面与球的位置关系如何？剖析：类比平面上直线与圆的位置关系，平面与球有以下几种位置关系：相离、相切、相交，其中相离是平面与球无公共点，相切是平面与球有且只有一个公共点，相交则是平面与球有无数多个公共点．题型一概念辨析题【例1】下列给出的图形中，绕虚线旋转一周，能形成圆台的是()．反思：通过解决本题，我们应注意旋转图形的形状及所选的轴，即便是同一图形，轴选取的不同，得到的旋转体也可能不相同．题型二简单旋转体中的计算问题【例2】圆台侧面的母线长为2a，母线与轴的夹角为30°，一个底面的半径是另一个底面半径的2倍．求两底面的半径及两底面面积之和．分析：由题目可获取以下主要信息：①已知圆台的母线长及母线与轴的夹角；②上下底面圆的半径关系．解答本题利用圆台的轴截面不难求出．反思：有关圆台的基本量计算问题的流程可归结为：①作轴截面；②构造直角三角形；③解直角三角形．题型三有关组合问题【例3】若圆锥的轴截面是一个面积为93cm2的正三角形，那么其内切球的半径为()．A．4πcm B．6cmC．3cmD．3πcm反思：通过本题可以看到轴截面是旋转体中一类重要的截面，它是立体几何问题向平面几何问题转化的桥梁．【例4】圆锥底面半径为r，高为h，正方体ABCD－A1B1C1D1内接于圆锥，求这个正方体的棱长．分析：研究圆锥主要通过轴截面来讨论，而正方体只有唯一基本量——棱长，而圆锥的轴截面在任何位置都相同，故过正方体的顶点作轴截面便于建立棱长与r、h之间的联系．反思：本题画出轴截面图形是解决问题的关键，从圆锥与正方体的结合入手，过正方体一组对棱的平面截圆锥得到轴截面，从而将空间问题转化为平面问题．题型五易错辨析【例5】设地球半径为R ，在北纬45°圈上有A ，B 两地，它们的纬线圈上的弧长等于24πR ，求A ，B 两地间的球面距离．错解：如图所示，A ，B 是北纬45°圈上两点，O ′为此纬线圈的圆心，易知∠AO ′B 所对的劣弧AB 长为所求球面距离．∴A ，B 两地间球面距离为24πR . 错因分析：没有理解球面距离是过A ，B 两点的大圆所对的劣弧长度．反思：(1)根据球面上两点间距离的定义，A ，B 两点的球面距离是过A ，B 的大圆在A ，B 间的劣弧长度．(2)球面上两点间的距离是指过这两点的球的大圆上两点间的劣弧长．求球面距离的关键是求所对应的球心角的大小，要求球心角，关键是求两点间的直线距离(即弦长)．在纬线圈中求弦长，在大圆中求球心角及球面距离．1下列几何体中是旋转体的是( )．①圆柱；②六棱锥；③正方体；④球体；⑤四面体．A ．①和⑤B ．①和②C ．③和④D ．①和④2下列命题中错误的是( )．A ．圆柱的轴截面是过母线的截面中面积最大的一个B ．圆锥的轴截面是所有过顶点的截面中面积最大的一个C ．圆台的所有平行于底面的截面都是圆D ．圆锥的所有轴截面都是全等的等腰三角形3顶点在同一球面上的正四棱柱ABCD －A ′B ′C ′D ′中，AB ＝1，AA ′＝2，则A ，C 两点间的球面距离为( )．A ．π4B ．π2C ．24πD ．22π 4已知半径为5的球的两个平行截面的周长分别是6π和8π，那么这两个平行截面间的距离是__________．5如图所示，圆锥底面圆的半径OA 是6，轴截面的顶角∠ASB 是直角，过两条母线的截面SCB 截去底面圆周的16，求截面面积．答案：基础知识·梳理1．(1)一边直角边垂直于底边平行于轴这条边(或它的长度) 底面侧面母线 (2)柱体锥体台体【做一做1－1】C 圆柱的上下两个底面是相互平行并且完全相等的．【做一做1－2】A 以直角梯形垂直于底的腰为轴旋转所得的旋转体才是圆台，所以选项B 不正确；圆锥仅有一个底面，所以选项C 不正确；圆锥的侧面展开图为扇形，这个扇形所在圆的半径等于圆锥的母线长，所以选项D 不正确；很明显选项A 正确．2．(1)直径球面球球心半径直径 (3)定长大圆小圆大圆球面距离 (4)旋转体旋转体的轴【做一做2－1】D 直角梯形必须绕其垂直于底边的腰旋转才形成圆台；直角三角形必须绕直角边旋转才形成圆锥；圆柱是由矩形绕其一边旋转而形成的几何体，因而它是旋转体，易知圆锥、圆台也是旋转体，类比棱台的定义，圆台也可以看成是一个圆锥被一个平行于底面的平面所截得的．故选D.【做一做2－2】①③利用球的结构特征判断：①正确；②不正确，因为直径必过球心；③正确．3．(1)柱、锥、台、球【做一做3－1】C 这里要注意旋转轴，可以自己先动手画一下，再结合旋转体的概念可知．【做一做3－2】D 过球心的任何截面都不可能是圆的内接正方形．典型例题·领悟【例1】A 利用旋转体的定义判断．【例2】解：设圆台上底面半径为r ，则下底面半径为2r ，如图，∠ASO ＝30°.在Rt △SA ′O ′中，r SA ′＝sin30°， ∴SA ′＝2r ，在Rt △SAO 中，2r SA＝sin30°， ∴SA ＝4r ，∴SA －SA ′＝AA ′，即4r －2r ＝2a ，r ＝a ，∴S ＝S 1＋S 2＝πr 2＋π(2r )2＝5πr 2＝5πa 2，∴圆台上底面半径为a ，下底面半径为2a ，两底面面积之和为5πa 2.【例3】C 轴截面如图所示，设正△SAB 的边长为a ，则12×32a ×a ＝34a 2＝93，∴a ＝6(cm)．又S △SO ′B ＋S △SO ′A ＋S △AO ′B ＝93，∴3×12×6×R ＝9 3. ∴R ＝3(cm)．故选C.【例4】解：过内接正方体的一组对棱作圆锥的轴截面，如图．设圆锥内接正方体的棱长为x ，则在轴截面中，正方体的对角面A 1ACC 1的一组邻边A 1A 和A 1C 1的长分别为x ，2x .因为△VA 1C 1∽△VMN ，所以2x 2r ＝h －x h. 所以2hx ＝2rh －2rx .所以x ＝2rh 2r ＋2h，即圆锥内接正方体的棱长为2rh 2r ＋2h. 【例5】正解：如图所示，A ，B 是北纬45°圈上的两点，AO ′为此纬线圈的半径， ∴OO ′⊥AO ′，OO ′⊥BO ′.∵∠OAO ′＝∠OBO ′＝45°，∴AO ′＝BO ′＝OA ·cos45°＝22R . 设∠AO ′B 为α，则απ180·AO ′＝απ180·22R ＝24πR ，∴α＝90°.连接AB ，则AB ＝AO ′2＋BO ′2＝⎝⎛⎭⎫22R 2＋⎝⎛⎭⎫22R 2＝R . 在△AOB 中，AO ＝BO ＝AB ＝R ，则△AOB 为正三角形，∴∠AOB ＝60°.∴A ，B 两点间的球面距离为60πR 180＝π3R . 随堂练习·巩固1．D2．B 当圆锥过顶点的轴截面顶角大于90°时，其面积不是最大的．3．B 如图所示，设球的半径为R ，则有R ＝(2)2＋12＋122＝1，连接AC ，连接AC ′与A ′C 交于点O ，则O 为外接球的球心．在△AOC 中，AO ＝OC ＝1，AC ＝2，所以∠AOC ＝90°.所以A ，C 两点间的球面距离为90×π×1180＝π2. 4．1或7分情况讨论：①若这两个平行截面位于球心的同侧，则可求得平行截面间的距离等于1；②若这两个平行截面位于球心异侧，则可解得平行截面间的距离等于7.5．解：由题知，轴截面顶角∠ASB ＝90°，OA ＝6，∴SA ＝SB ＝SC ＝6 2.如图，连接OB ，OC ，作SD ⊥BC 于D .∵弧BC 的长为底面圆周长的16， ∴∠BOC ＝16×360°＝60°.∴OB ＝OC ＝BC ＝6.∴SD ＝SB 2－⎝⎛⎭⎫12BC 2＝72－9＝37.∴S △SCB ＝12×6×37＝97. ∴截面面积为97.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1．下列命题中，错误的是()．
A．圆柱的轴截面是过母线的截面中面积最大的一个
B．圆锥的轴截面是所有过顶点的截面中面积最大的一个
C．圆台的所有平行于底面的截面都是圆
D．圆锥所有的轴截面是全等的等腰三角形
2．圆柱的轴截面是边长为5 cm的正方形ABCD，则圆柱侧面上从A到C的最短距离为()．
A．10 cm B cm
C．D．
3．一个圆台的上、下底面面积分别是1 cm2和49 cm2，一个平行于底面的截面面积为25 cm2，则这个截面与上、下底面的距离之比是()．
A．2∶1B．3∶1C∶1D 1
4．如图是由等腰梯形、矩形、半圆、圆、倒三角形对接形成的轴对称平面图形，若将它绕轴l旋转180°后形成一个组合体，下面说法不正确的是()．
A．该组合体可以分割成圆台、圆柱、圆锥和两个球体
B．该组合体仍然关于轴l对称
C．该组合体中的圆锥和球只有一个公共点
D．该组合体中的球和半球只有一个公共点
5．一件工艺品是将一个彩色半透明的正四面体镶嵌于一个水晶球体内制作而成的．已知正四面体的顶点都在球面上，球的直径为12 cm，则正四面体的棱长为______ cm，球心到正四面体各面的距离为______ cm.
6．长方体ABCD－A1B1C1D1的顶点均在同一个球面上，AB＝AA1＝1，BC=则A，B两点间的球面距离为______．
7．设地球的半径为R ，地球上的两点A 、B 的纬度都是北纬45°，A 、B 两点的球面距离为π3
R ，已知A 在东经20°处，试确定B 点的位置． 8．如图，正方形ABB 1A 1的边长为15，其内有两点P 、Q ，P 到AA 1、A 1B 1的距离均为3，Q 到AB 、BB 1的距离分别为2和4，将正方形卷成一个圆柱，使AB 和A 1B 1相连，求此时P 、Q 两点之间最短的距离(沿圆柱侧面)．
9.棱长为2 cm 的正方体容器中盛满水，把半径为1 cm 的铜球放入水中，铜球刚好被淹没，现向正方体容器内再放入一个铁球，使它也淹没在水中，要使流出来的水量最多，这个铁球的半径应该是多大？
参考答案
1. 答案：B
解析：当圆锥过顶点的轴截面顶角大于90°时，面积不是最大．设圆锥轴截面顶角为α，母线长为l ，则轴截面面积21sin 2
S l α=
，显然α≤90°时，轴截面面积最大；α＞90°时，轴截面面积不最大．
2. 答案：B
3. 答案：A
解析：作圆台的轴截面如图，则有Rt △A 1BE ∽Rt △BAF ，
∴A 1E ∶BF ＝BE ∶AF ，
又A 1O 1＝1 cm ，AO ＝7 cm ，BO′＝5 cm ，
∴A 1E ∶BF ＝2∶1．
4. 答案：A
5. 答案： 2
解析：设正四面体的棱长为a ，球的半径为正四面体的高的34
，∴364=，
∴a =14，即1243⨯⨯=. 6. 答案：π3
解析：1=，设球心为O ，则△AOB 为正三角形， π3
AOB ∠=， ∴A ，B 间的球面距离为
π3.
7. 解：如图所示，∵A 、B 的球面距离是指过A 、B 的大圆的劣弧长，
∴π3
AOB ∠=，因此AB ＝R .
又∵·cos45O'A OA =︒=，
在△AO ′B 中，2AO'BO'==
，AB ＝R ， ∴AB 2＝AO ′2＋BO ′2，∠AO ′B ＝90°，
∵A 在东经20°处，∴B 点的位置为20°±90°处，即B 点位于北纬45°，东经110°或西经70°处．
8. 解：将此正方形卷成圆柱如①所示，若沿CP 所在直线重新展开，所得图形如②所示．
则PQ ===，
即P 、Q 9. 解：过正方体对角线的截面图如图所示．
1AC =AO =
1AS AO OS =-=，
设小球的半径为r.
在△AO 1D 中，1AO =，AS ＝AO 1+O 1S ，
1r -=+，。