新版Matlab中神经网络训练函数Newff的使用方法
MATLAB神经网络工具箱的详细使用步奏
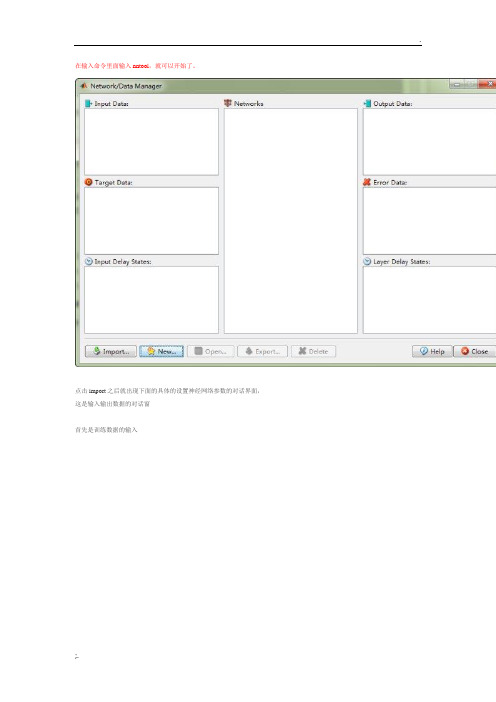
在输入命令里面输入nntool,就可以开始了。
点击import之后就出现下面的具体的设置神经网络参数的对话界面,这是输入输出数据的对话窗
首先是训练数据的输入
然后点击new,创建一个新的神经网络network1,并设置其输入输出数据,包括名称,神经网络的类型以及隐含层的层数和节点数,还有隐含层及输出层的训练函数等
点击view,可以看到这是神经网络的可视化直观表达
创建好了一个network之后,点击open,可以看到一个神经网络训练,优化等的对话框,选择了输入输出数据后,点击train,神经网络开始训练,如右下方的图,可以显示动态结果
下面三个图形则是点击performance,training state以及regression而出现的
下面就是simulate,输入的数据是用来检验这个网络的数据,output改一个名字,这样就把输出数据和误差都存放起来了
在主界面上点击export就能将得到的out结果输入到matlab中并查看
下图就是输出的两个outputs结果。
用神经网训练一个网络函数

学号:姓名:班级:用神经网络训练一个非线性函数一、MATLAB 神经网络工具箱的简单介绍MATLAB 神经网络工具箱以人工神经网络为基础,根据自己的需要调用相关函数,就可以完成网络设计、权值初始化、网络训练等。
本设计中使用了工具箱中BP 神经网络,BP 神经网络工具箱主要包括newff,sim 和train 三个神经网络函数。
newff函数的功能是构建一个BP 神经网络。
其函数形式:net = newff(P,T,S,TF,BTF,BLF,PF,IPF,OPF,DDF)。
sim函数的功能是用训练数据训练BP 神经网络。
其函数形式:[net,tr] =train(NET,X,T,Pi,Ai)。
train函数的功能是用训练好的BP 神经网络预测函数输出,其函数形式:y=sim(net,x)。
二、设要逼近的非线性函数为:y=2*cos(2*pi*x),-0.4<X<3.6。
(1)网络建立:使用net=newff(x,y,20,{'tansig','purelin'},'trainlm','learngdm');语句建立一个前馈BP 神经网络。
该BP神经网络只含有一个隐含层,神经元的个数为20,隐层传递函数tansig,输出层传递函数purelin,训练函数为Leven-berg_Marquardt 的BP 算法训练函数trainlm,网络学习函数是带动量项的BP 学习规则learngdm。
(2)网络训练:使用net=train(net,x,y);语句训练建立喊的BP 神经网络。
在训练网络之前设置好训练参数。
用“net.trainParam.epochs=50;net.trainParam.goal=0.01;net.train-Param.lr=0.01;net.trainParam.show=10;”语句实现。
(3)网络仿真:使用“y1=sim(net,x);y2=sim(net,x);”语句仿真训练前后的BP 神经网络。
matlab神经网络工具箱简介和函数及示例

目前,神经网络工具箱中提供的神经网络模型主 要应用于:
函数逼近和模型拟合 信息处理和预测 神经网络控制 故障诊断
神经网络实现的具体操作过程:
• 确定信息表达方式; • 网络模型的确定; • 网络参数的选择; • 训练模式的确定; • 网络测试
• 确定信息表达方式:
将领域问题抽象为适合于网络求解所能接受的 某种数据形式。
函数类型 输入函数
其它
函数名 称
netsum netprcd concur dotprod
函数用途
输入求和函数 输入求积函数 使权值向量和阈值向量的结构一致 权值求积函数
BP网络的神经网络工具箱函数
函数类型
函数名称 函数用途
前向网络创建 函数
传递函数
学习函数
函数类型 性能函数 显示函数
函数名 函数用途 称
三、BP网络学习函数
learngd 该函数为梯度下降权值/阈值学习函数,通过神经 元的输入和误差,以及权值和阈值的学习速率, 来计算权值或阈值的变化率。
调用格式; [dW,ls]=learngd(W,P,Z,N,A,T,E,gW,gA,D,LP,LS)
二、神经元上的传递函数
传递函数是BP网络的重要组成部分,必须是连续可 微的,BP网络常采用S型的对数或正切函数和线性函数。
• Logsig 传递函数为S型的对数函数。 调用格式为: • A=logsig(N)
N:Q个S维的输入列向量; A:函数返回值,位于区间(0,1) 中
② info=logsig(code)
问题形式的种类:
数据样本已知; 数据样本之间相互关系不明确; 输入/输出模式为连续的或者离散的; 输入数据按照模式进行分类,模式可能会 具有平移、旋转或者伸缩等变化形式; 数据样本的预处理; 将数据样本分为训练样本和测试样本
Matlab中的神经网络实现方法

Matlab中的神经网络实现方法近年来,神经网络技术在各个领域中得到了广泛的应用。
通过对大量的数据进行学习和训练,神经网络可以用于解决诸如图像识别、语音识别、自然语言处理等复杂的问题。
而Matlab作为一种强大的科学计算工具,提供了丰富的神经网络实现方法,帮助研究人员和工程师更好地应用神经网络技术。
在Matlab中,实现神经网络有多种方法,包括使用神经网络工具箱、编写自定义的函数和使用深度学习工具箱等。
下面将分别介绍这些方法的特点和应用。
一、神经网络工具箱Matlab的神经网络工具箱是一个功能强大的工具,可以帮助用户在短时间内搭建和训练神经网络模型。
通过在Matlab中调用神经网络工具箱中的函数,用户可以实现包括前馈神经网络、递归神经网络、自动编码器等各种类型的神经网络模型。
使用神经网络工具箱,用户只需要简单地定义网络的拓扑结构、选择合适的激活函数和学习算法,然后通过输入训练数据进行网络的训练。
训练完成后,用户可以使用训练好的神经网络模型对新的数据进行预测和分类。
神经网络工具箱提供了丰富的函数和工具,帮助用户实现各种复杂的操作,例如特征选择、模型评估和可视化等。
此外,神经网络工具箱还支持并行计算和分布式计算,提高了神经网络模型的训练效率。
二、自定义函数除了使用神经网络工具箱,用户还可以编写自定义的函数来实现神经网络。
这种方式可以更加灵活地控制网络的结构和参数。
在Matlab中,用户可以通过编写自定义的函数来定义网络的拓扑结构、激活函数、学习算法等。
同时,用户还可以使用Matlab提供的矩阵运算和优化工具,对神经网络的参数进行更新和优化。
使用自定义函数实现神经网络需要较高的编程能力和数学知识,但是可以满足对网络结构和参数精细控制的需求。
此外,用户还可以在自定义函数中加入其他自己的算法和操作,提升神经网络的性能和应用效果。
三、深度学习工具箱随着深度学习技术的兴起,Matlab还引入了深度学习工具箱,帮助用户实现包括卷积神经网络、循环神经网络等深度学习模型。
matlab newff函数新版用法

matlab newff函数新版用法Matlab是一种强大的数值计算软件,用于工程、物理、化学、金融等领域的科学计算,尤其是在神经网络相关的计算上得到了广泛应用,其newff函数也是神经网络中的一个核心函数。
在matlab神经网络工具箱中,newff 函数是一个用于构建前向传播神经网络的函数,其可以自动帮助用户建立完整的神经网络模型。
在这篇文档中,我们将研究newff函数的新版用法,包括如何使用newff函数构建前向传播神经网络模型、如何设置网络结构参数、如何训练神经网络模型以及如何进行预测。
一、使用newff函数构建前向传播神经网络模型在matlab神经网络工具箱中使用newff函数,只需执行以下命令:net = newff(inputs, targest, hiddenSizes)其中,inputs表示输入训练样本参数的矩阵,targets表示训练结果的矩阵,hiddenSizes表示隐藏层神经元的个数和层数。
执行这个命令后,我们将得到一个前向传播神经网络变量net。
二、设置网络结构参数在构建神经网络模型之前,我们需要设置一些网络结构参数。
具体而言,我们需要设置输入和输出层的神经元数、隐藏层数和神经元数、学习率、训练算法、误差函数等参数。
我们可以使用set函数轻松地设置这些参数。
例如,下面的命令可以设置前向传播神经网络的输入和输出层神经元数:net.inputs{1}.size=5;net.outputs{2}.size=1;其中“net.inputs{1}.size”表示第一层输入神经元数,本例中设置为5,“net.outputs{2}.size”表示第二层输出神经元数,本例中设置为1。
我们还可以使用下面的命令确定隐藏层神经元数和层数,learning rate(学习率)以及 transfer function(激活函数)等:yers{1}.size=10;yers{2}.size=5;net.trainFcn = 'trainscg';net.learningRate=0.1;net.divideFcn = '';net.performFcn = 'mse';其中“yers{1}.size”表示第一层隐藏神经元数,本例中设置为10,“yers{2}.size”表示第二层隐藏神经元数,本例中设置为5。
Matlab的神经网络工具箱实用指南(3)

静态网络中的批处理方式批处理方式可以用adapt或train函数来实现,虽然由于由于采用了更高效的学习算法,train通常是最好的选择。
增加方式只能用adapt来实现,train函数只能用于批处理方式。
让我们用前面用过的静态网络的例子开始,学习速率设置为0.1。
net = newlin([-1 1;-1 1],1,0,0.1);net.IW{1,1} = [0 0];net.b{1} = 0;用adapt函数实现静态网络的批处理方式,输入向量必须用同步向量矩阵的方式放置:P = [1 2 2 3; 2 1 3 1];T = [4 5 7 7];当我们调用adapt时将触发adaptwb函数,这是缺省的线性网络调整函数。
learnwh是缺省的权重和偏置学习函数。
因此,Widrow-Hoff学习法将会被使用:[net,a,e,pf] = adapt(net,P,T);a = 0 0 0 0e = 4 5 7 7注意网络的输出全部为0,因为在所有要训练的数据提交前权重没有被更新,如果我们显示权重,我们就会发现:>>net.IW{1,1}ans = 4.9000 4.1000>>net.b{1}ans =2.3000经过了用adapt函数的批处理方式调整,这就和原来不一样了。
现在用train函数来实现批处理方式。
由于Widrow-Hoff规则能够在增加方式和批处理方式中应用,它可以通过adapt和train触发。
我们有好几种算法只能用于批处理方式(特别是Levenberg-Marquardt算法),所以这些算法只能用train触发。
网络用相同的方法建立:net = newlin([-1 1;-1 1],1,0,0.1);net.IW{1,1} = [0 0];net.b{1} = 0;在这种情况下输入向量即能用同步向量矩阵表示也能用异步向量细胞数组表示。
用train函数,任何异步向量细胞数组都会转换成同步向量矩阵。
matlab神经网络newff函数的使用

matlab神经网络newff函数的使用设[P,T]是训练样本,[X,Y]是测试样本;net=newrb(P,T,err_goal,spread); %建立网络q=sim(net,p);e=q-T;plot(p,q); %画训练误差曲线q=sim(net,X);e=q-Y;plot(X,q); %画测试误差曲线训练前馈网络的第一步是建立网络对象。
函数newff建立一个可训练的前馈网络。
这需要4个输入参数。
第一个参数是一个Rx2的矩阵以定义R个输入向量的最小值和最大值。
第二个参数是一个设定每层神经元个数的数组。
第三个参数是包含每层用到的传递函数名称的细胞数组。
最后一个参数是用到的训练函数的名称。
举个例子,下面命令将创建一个二层网络。
它的输入是两个元素的向量,第一层有三个神经元(3),第二层有一个神经元(1)。
第一层的传递函数是tan-sigmoid,输出层的传递函数是linear。
输入向量的第一个元素的范围是-1到2[-1 2],输入向量的第二个元素的范围是0到5[0 5],训练函数是traingd。
net=newff([-1 2; 0 5],[3,1],{'tansig','purelin'},'traingd');这个命令建立了网络对象并且初始化了网络权重和偏置,因此网络就可以进行训练了。
我们可能要多次重新初始化权重或者进行自定义的初始化。
下面就是初始化的详细步骤。
在训练前馈网络之前,权重和偏置必须被初始化。
初始化权重和偏置的工作用命令init 来实现。
这个函数接收网络对象并初始化权重和偏置后返回网络对象。
下面就是网络如何初始化的:net = init(net);我们可以通过设定网络参数net.initFcn和yer{i}.initFcn这一技巧来初始化一个给定的网络。
net.initFcn用来决定整个网络的初始化函数。
前馈网络的缺省值为initlay,它允许每一层用单独的初始化函数。
newff函数的使用(含一个新的函数)

matlab神经网络newff函数的使用设[P,T]是训练样本,[X,Y]是测试样本;net=newrb(P,T,err_goal,spread); %建立网络q=sim(net,p);e=q-T;plot(p,q); %画训练误差曲线q=sim(net,X);e=q-Y;plot(X,q); %画测试误差曲线训练前馈网络的第一步是建立网络对象。
函数newff建立一个可训练的前馈网络。
这需要4个输入参数。
第一个参数是一个Rx2的矩阵以定义R个输入向量的最小值和最大值。
第二个参数是一个设定每层神经元个数的数组。
第三个参数是包含每层用到的传递函数名称的细胞数组。
最后一个参数是用到的训练函数的名称。
举个例子,下面命令将创建一个二层网络。
它的输入是两个元素的向量,第一层有三个神经元(3),第二层有一个神经元(1)。
第一层的传递函数是tan-sigmoid,输出层的传递函数是linear。
输入向量的第一个元素的范围是-1到2[-1 2],输入向量的第二个元素的范围是0到5[0 5],训练函数是traingd。
net=newff([-1 2; 0 5],[3,1],{'tansig','purelin'},'traingd');这个命令建立了网络对象并且初始化了网络权重和偏置,因此网络就可以进行训练了。
我们可能要多次重新初始化权重或者进行自定义的初始化。
下面就是初始化的详细步骤。
在训练前馈网络之前,权重和偏置必须被初始化。
初始化权重和偏置的工作用命令init来实现。
这个函数接收网络对象并初始化权重和偏置后返回网络对象。
下面就是网络如何初始化的:net = init(net);我们可以通过设定网络参数net.initFcn和yer{i}.initFcn这一技巧来初始化一个给定的网络。
net.initFcn用来决定整个网络的初始化函数。
前馈网络的缺省值为initlay,它允许每一层用单独的初始化函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新版Matlab中神经网络训练函数Newff的使用方法
一、介绍新版newff
Syntax
•net = newff(P,T,[S1 S2...S(N-l)],{TF1 TF2...TFNl}, BTF,BLF,PF,IPF,OPF,DDF) Description
newff(P,T,[S1 S2...S(N-l)],{TF1 TF2...TFNl}, BTF,BLF,PF,IPF,OPF,DDF) takes several arguments
Examples
Here is a problem consisting of inputs P and targets T to be solved with a network.
•P = [0 1 2 3 4 5 6 7 8 9 10];T = [0 1 2 3 4 3 2 1 2 3 4];
Here a network is created with one hidden layer of five neurons.
•net = newff(P,T,5);
The network is simulated and its output plotted against the targets.
•Y = sim(net,P);plot(P,T,P,Y,'o')
The network is trained for 50 epochs. Again the network's output is plotted.
•net.trainParam.epochs = 50;net = train(net,P,T);Y = sim(net,P);plot(P,T,P,Y,'o') 二、新版newff与旧版newff调用语法对比
Example1
比如输入input(6*1000),输出output为(4*1000),那么
旧版定义:net=newff(minmax(input),[7,1],{'tansig','purelin'},'trainlm');
新版定义:net=newff(input,output,7,{'tansig','purelin'},'trainlm'); Example2
比如输入input(6*1000),输出output为(4*1000),那么
旧版定义:net=newff(minmax(input),[49,10,1],{'tansig','tansig','tansig'},'traingdx');新版定义:net=newff(input,output, [49,10], {'tansig','tansig','tansig'},'traingdx');
三、旧版newff使用方法在新版本中使用
提示:旧版本定义的newff虽也能在新版本中使用,但会有警告,警告如下:
Warning: NEWFF used in an obsolete way.
> In obs_use at 18
In newff>create_network at 127
In newff at 102
See help for NEWFF to update calls to the new argument list.
四、新版newff与旧版newff使用的训练效果对比
旧版本:旧用法训练次数多,但精度高
新版本:新用法训练次数少,但精度可能达不到要求
造成上述原因是:
程序里面的权值、阈值的初始值是随机赋值的,所以每次运行的结果都会不一样,有好有坏。
你可以把预测效果不错的网络的权值和阈值作为初始值。
具体可以查看net.iw{1,1}、net.lw{2,1}、net.b{1}、net.b{2}的值。
现在给一个完整的例子
%% 清空环境变量
clc
clear
%% 训练数据预测数据
data=importdata('test.txt');
%从1到768间随机排序
k=rand(1,768);
[m,n]=sort(k);
%输入输出数据
input=data(:,1:8);
output =data(:,9);
%随机提取500个样本为训练样本,268个样本为预测样本input_train=input(n(1:500),:)';
output_train=output(n(1:500),:)';
input_test=input(n(501:768),:)';
output_test=output(n(501:768),:)';
%输入数据归一化
[inputn,inputps]=mapminmax(input_train);
%% BP网络训练
% %初始化网络结构
net=newff(inputn,output_train,10);
net.trainParam.epochs=1000;
net.trainParam.lr=0.1;
net.trainParam.goal=0.0000004;
%% 网络训练
net=train(net,inputn,output_train);
%% BP网络预测
%预测数据归一化
inputn_test=mapminmax('apply',input_test,inputps);
%网络预测输出
BPoutput=sim(net,inputn_test);
%% 结果分析
%根据网络输出找出数据属于哪类
BPoutput(find(BPoutput<0.5))=0;
BPoutput(find(BPoutput>=0.5))=1;
%% 结果分析
%画出预测种类和实际种类的分类图
figure(1)
plot(BPoutput,'og')
hold on
plot(output_test,'r*');
legend('预测类别','输出类别')
title('BP网络预测分类与实际类别比对','fontsize',12) ylabel('类别标签','fontsize',12)
xlabel('样本数目','fontsize',12)
ylim([-0.5 1.5])
%预测正确率
rightnumber=0;
for i=1:size(output_test,2)
if BPoutput(i)==output_test(i)
rightnumber=rightnumber+1;
end
end
rightratio=rightnumber/size(output_test,2)*100; sprintf('测试准确率=%0.2f',rightratio)。
