格兰杰因果检验(正式版)
格兰杰因果关系检验

• 格兰杰因果关系检验概述 • 格兰杰因果关系检验的步骤 • 格兰杰因果关系检验的应用 • 格兰杰因果关系检验的局限性
• 格兰杰因果关系检验与其他方法的 比较
• 格兰杰因果关系检验的未来发展
01
格兰杰因果关系检验概述
定义与特点
定义
格兰杰因果关系检验是一种用于检验 两个时间序列变量之间是否存在一种 因果关系的统计方法。
自然科学领域的应用
1 2
气候变化与环境因素
研究气候变化与环境因素之间的因果关系,为环 境保护和可持续发展提供科学依据。
生物种群动态与环境因素
分析生物种群数量变化与环境因素之间的因果关 系,揭示生物种群动态的机制。
3
地之间的因果关系,为地 质灾害防治提供科学依据。
检验方法的改进与优化
非参数检验方法
针对参数检验方法的局限性,可以考虑使用非参数检验方法,如基于秩的检验或核密度 估计方法。
考虑非平稳性
对于非平稳时间序列数据,可以使用差分或协整技术来处理,以更准确地检测格兰杰因 果关系。
考虑其他相关因素
在解释格兰杰因果关系时,应综合考虑其他相关因素,如经济理论、市场环境等,以更 全面地理解因果关系的实际意义。
VS
相同点
格兰杰因果关系检验和其他因果关系检验 方法都是为了确定两个变量之间的因果关 系,为进一步的研究或决策提供依据。
与其他时间序列分析方法的比较
不同点
相同点
格兰杰因果关系检验专注于分析时间序列数 据中的因果关系,而其他时间序列分析方法, 如平稳性检验、季节性分解、趋势分析等, 则是针对时间序列数据的不同特征进行描述 和分析。
国际贸易与汇率
分析国际贸易流量和汇率变动之间的因果关系,揭示国际贸易对汇 率的影响机制。
实验八 格兰杰因果关系检验

实验八格兰杰因果关系检验一、因果关系等同于相关关系吗?从一个回归关系式我们并不能确定变量之间是否具有因果关系。
二、Granger因果检验X是Y的原因,必须满足两个条件(1)X应该有助于预测Y(2)Y不应当有助于预测X【实验目的】掌握格兰杰因果检验的基本思想【实验数据】序号SZ SH序号SZ SH序号SZ SH序号SZ SH1 336.56 1125.82 201 430.46 1465.23 401 604.01 1950.66 601 638.7 2161.342 334.89 1119.97 202 434.75 1471.38 402 607.58 1959.31 602 635.83 2146.243 338.3 1132.59 203 432.44 1464.03 403 612.17 1972.04 603 637.37 2140.984 339.18 1137.73 204 428.28 1450.15 404 615.67 1979.1 604 636.78 2146.545 349.84 1168.81 205 426.02 1443.91 405 613.2 1988.94 605 644.91 2150.276 351.11 1172.81 206 426.97 1450.33 406 612.99 1979.51 606 643.8 2179.627 346.44 1158.87 207 426.65 1451.54 407 603.26 1978.43 607 633.43 2169.018 344.1 1148.15 208 422.05 1431.32 408 588.98 1946.75 608 626.48 2136.459 342.69 1148.66 209 429.92 1462.79 409 594.84 1903.15 609 619.54 2112.2610 339.64 1137.31 210 436.87 1482.45 410 590.08 1922.29 610 611.51 2094.0111 344.87 1153.12 211 432.85 1468.47 411 584.44 1907.31 611 577.88 2065.7312 346.93 1158.55 212 431.06 1464.59 412 578.93 1891.98 612 566.51 1956.8213 345.06 1151.37 213 431.51 1462.99 413 583.16 1875.91 613 587.29 1920.3214 347.83 1158.5 214 429.5 1454.58 414 590.71 1887.83 614 578.44 1986.9315 348.77 1162.35 215 426.35 1444.24 415 583.1 1914.09 615 579.37 1957.0316 343.95 1148.12 216 427.21 1444.51 416 590.37 1889.29 616 557.51 1958.717 340.75 1138.21 217 423.82 1435.47 417 592.91 1910.16 617 564.14 1882.1318 343.85 1146.49 218 423.94 1434.97 418 600.14 1915.35 618 562.03 1903.9319 340.78 1140.98 219 428.42 1447.12 419 598.11 1942.15 619 572.81 1895.1720 340.69 1134.67 220 424.36 1435.84 420 595.18 1933.73 620 580.95 1924.5921 337.68 1120.53 221 424.67 1437.23 421 593.63 1926.32 621 581.39 1955.0422 338.81 1125.01 222 422.26 1427 422 589.51 1917.92 622 575.42 1955.123 335.59 1116.87 223 422.7 1428.26 423 591.25 1902.81 623 578.36 1939.5424 330.09 1103.5 224 421.04 1424.85 424 597.07 1909.49 624 570.53 1947.3625 322.76 1081.44 225 418.81 1416.73 425 592.62 1922.85 625 570.62 1919.6426 316.56 1065.82 226 423.3 1428.94 426 602.25 1913.42 626 575.34 192427 324.22 1090.09 227 419.42 1417.11 427 606.6 1947.46 627 578.48 1934.4928 327.84 1097.98 228 422.25 1422.26 428 607.21 1958.94 628 569.93 1938.8829 328.79 1100.92 229 429.84 1451.06 429 611.4 1956.34 629 571.36 1903.4530 336.12 1128.74 230 424.28 1434.87 430 606.29 1977.25 630 566.13 1902.9931 336.54 1128.95 231 419.38 1419.55 431 607.89 1967.67 631 547.27 1886.832 339.76 1132.36 232 412.35 1395.5 432 609.51 1967.41 632 552.45 1827.2533 342.75 1142.11 233 409.75 1387.51 433 605.02 1973.58 633 553.88 1843.3934 341.35 1136.94 234 403.8 1369.46 434 609.49 1961.29 634 549.69 1847.5435 340.46 1132.74 235 399.35 1355.37 435 611.77 1977.36 635 548.48 1839.6436 346.64 1149.93 236 395.69 1345.35 436 611.37 1984.26 636 543.39 1834.1437 349.13 1158.7 237 396.33 1348.82 437 614.03 1981.63 637 557.57 1817.1938 350.59 1164.64 238 399.22 1356.93 438 614.87 1991.17 638 558.62 1862.3639 350.26 1166.93 239 402.18 1366.58 439 618.67 1997.08 639 556.46 1868.2740 347.89 1159.1 240 414.69 1406.37 440 625.71 2012.91 640 538.97 1861.5641 344.67 1151.99 241 415.96 1409.68 441 629.56 2032.48 641 552.28 1808.8542 351.03 1172.93 242 433.06 1463.94 442 636.59 2047.46 642 552.98 1856.5343 351.47 1172.74 243 449.16 1516.6 443 640.37 2070.79 643 545.77 1863.7844 351.5 1170.95 244 458.73 1545.11 444 640.18 2085.12 644 542.91 1852.6145 350.72 1169.03 245 439.99 1479.78 445 645.28 2081.91 645 534.8 1839.9146 346.39 1156.85 246 427.94 1438.02 446 643.98 2095.98 646 521.57 1818.3947 347.58 1161.12 247 425.15 1424.44 447 645.82 2093.24 647 525.95 1784.6148 350.89 1169.49 248 420.47 1408.85 448 644.73 2101.39 648 532.93 1798.6349 346.35 1157.51 249 427.46 1433.33 449 652.58 2097.98 649 531.04 1822.750 348.24 1158.05 250 427.82 1426.62 450 654.37 2113.3 650 526.29 1818.4251 350.38 1168.5 251 434.06 1440.72 451 633.4 2119.44 651 522.48 1807.0252 353.39 1184.4 252 441.42 1466.86 452 633.33 2053.37 652 521.43 1794.9653 356.29 1194.47 253 443.72 1465.09 453 642.33 2049.67 653 514.44 1793.8954 356.76 1199.6 254 451.78 1477.34 454 638.17 2079.4 654 512.96 1767.8255 357.19 1201.63 255 451.85 1476.51 455 639.22 2067.5 655 512.98 1764.9456 356.14 1202.47 256 453.58 1481.12 456 642.75 2070.61 656 501 1764.8857 355.08 1205.14 257 460.74 1506.77 457 647.41 2081.84 657 506.74 1726.5458 351.44 1195.34 258 469.65 1535 458 645.98 2092.14 658 488.71 1744.6459 347.77 1178.19 259 512.24 1673.94 459 638.93 2091.67 659 475.35 1686.6260 349.55 1181.52 260 514.89 1670.67 460 635.89 2075.63 660 488.66 1638.3361 344.78 1170.62 261 527.11 1693.11 461 637.24 2075.04 661 484.45 1691.3362 342.71 1166.24 262 509.79 1640.65 462 627.63 2073.1663 342.06 1159.47 263 518.96 1668.09 463 632.69 2046.0864 345.08 1171.6 264 521.71 1677.14 464 632.55 2059.0565 339.14 1144.07 265 504.62 1632.29 465 631.64 2056.1266 337.77 1137.16 266 490.95 1594.93 466 628.82 2051.0867 342.37 1140 267 504.82 1634.31 467 630.28 2039.3668 337.01 1112.79 268 503.97 1631.58 468 630.91 2044.5569 329.59 1091.7 269 526.18 1704.86 469 637.07 2049.0370 327.51 1091.09 270 524.64 1714.58 470 637.57 2071.2771 333.76 1116.41 271 523.83 1697.74 471 634.92 2076.8972 336.3 1120.93 272 532.14 1738.02 472 632.91 2069.7773 334.28 1111.76 273 511.43 1681.09 473 635.08 2068.1774 335.02 1116.93 274 517.99 1694.8 474 628.51 2076.2775 338.43 1128.22 275 526.79 1726.03 475 629.9 2058.2476 335.05 1120.74 276 526.57 1732.35 476 635.73 2053.777 319.53 1071.93 277 519.34 1705.05 477 644.66 2073.4878 326.01 1095.4 278 528.34 1728.88 478 649.75 2103.4779 325.8 1100 279 517.18 1685.35 479 647.36 2123.980 322.17 1088.86 280 520.03 1681.47 480 648.67 2117.4181 313.27 1063.28 281 495.32 1607.53 481 640.19 2125.382 311.97 1065.56 282 512.42 1658.6 482 638.75 2102.0683 310.65 1059.87 283 527.35 1699.25 483 645.53 2101.1484 325.71 1109.09 284 531.53 1710.32 484 643.32 2125.6185 335.39 1147.71 285 536.25 1720.45 485 638.64 2119.1486 338.95 1168.72 286 545.11 1747.24 486 617.39 2104.7587 352.9 1213.65 287 540.71 1730.5 487 620.33 2032.4488 349.31 1202.89 288 557.4 1775.91 488 617.19 2045.8989 358.77 1236.05 289 561.24 1791.44 489 618.46 2034.5890 372.16 1283.02 290 558.63 1788.81 490 626.18 2043.1191 370.49 1277.15 291 565.36 1810.98 491 609.62 2065.6192 370.87 1279.33 292 560.99 1800.23 492 604.77 2008.0393 380 1311.59 293 557.93 1801 493 599.51 1995.3294 374.68 1287.93 294 545.43 1760.69 494 582.43 1979.9495 370.14 1268.32 295 549.83 1771.2 495 590.34 1930.1496 378.04 1285.58 296 561.67 1809.14 496 589.86 1956.9797 389.32 1326.52 297 566.02 1819.9 497 591.36 1961.2298 392.21 1333.64 298 569.97 1826.06 498 591.85 1963.5399 397.35 1348.61 299 568.87 1821.17 499 586.78 1963.2 100 402.36 1364.34 300 563.85 1807.33 500 585.68 1946.48 101 407.01 1370.39 301 569.56 1831.55 501 591.31 1941.96 102 422.7 1427.71 302 569.1 1833.67 502 587.29 1967.55 103 406.27 1387.59 303 556.39 1795.06 503 570.96 1953.22 104 428.56 1460.17 304 562.07 1813.5 504 568.26 1909.33 105 440.84 1501.01 305 565.46 1828.71 505 575.81 1907.26 106 443.88 1498.92 306 569.22 1847.03 506 583.44 1936.35 107 460.18 1546.41 307 565.27 1841.06 507 586.25 1954.69 108 467.9 1564.44 308 562.36 1837.4 508 585.41 1962.04 109 481.05 1606.5 309 562.72 1833.47 509 589.22 1959.18 110 498 1654.11 310 562.68 1832.78 510 595.52 1965.12 111 479.85 1593.86 311 555.45 1806.83 511 595.12 1985.11 112 512.75 1693.16 312 566.93 1836.32 512 596.29 1984.2 113 525.14 1739.2 313 567.48 1836.64 513 597.3 1990.06114 507.59 1689.43 314 559.41 1806.64 514 601.62 1991.18 115 466.63 1560.79 315 540.75 1752.69 515 606.75 2000.9 116 485.59 1613.53 316 529.32 1724.05 516 608.86 2011.66 117 475.94 1581.82 317 529.26 1720.61 517 604.36 2012.55 118 455.2 1517.25 318 522.22 1704.59 518 610.5 1998.7 119 470.64 1568.65 319 529.91 1724.54 519 612.54 2018.62 120 476.1 1577.99 320 530.03 1725.4 520 613.34 2022.6 121 478.83 1584.75 321 542.42 1758.54 521 619.65 2020.24 122 471.52 1559.73 322 550.84 1777.83 522 624.63 2036.62 123 456.11 1524.82 323 565.57 1824.74 523 629.72 2045.79 124 468.93 1559.52 324 566 1832.08 524 635.24 2066.39 125 465.38 1549.34 325 572.18 1855.49 525 623.55 2087.53 126 454.15 1519.74 326 579.72 1880.7 526 634.18 2053.54 127 438.27 1479.08 327 580.33 1879.62 527 641.94 2089.88 128 469.07 1574.6 328 586.5 1898.75 528 642.05 2107.26 129 477.14 1609.81 329 579.7 1877.47 529 638.2 2106.87 130 457.92 1550.73 330 584.21 1894.55 530 642.12 2101.66 131 467.23 1585.98 331 587.31 1903.49 531 645.03 2112.78 132 472.3 1602.03 332 591.4 1916.25 532 642.16 2125.08 133 469.58 1590.71 333 584.96 1899.09 533 631.9 2123.05 134 472.87 1597.2 334 594.59 1925.54 534 640.05 2090.72 135 472.44 1595.86 335 596.89 1935.03 535 638.66 2112.6 136 473.19 1601.46 336 591.36 1925.21 536 641.7 2108.61 137 479.09 1616.28 337 584.16 1900.79 537 645.32 2117.37 138 480.26 1626.84 338 586.61 1912.56 538 645.96 2128.48 139 485.27 1649.13 339 594 1938.67 539 646.52 2131.4 140 484.8 1653.54 340 592.03 1932.29 540 648.66 2134.8 141 483.18 1646.59 341 594.19 1942.29 541 655.24 2145.4 142 479.15 1628.84 342 590.42 1926.94 542 656.51 2168.06 143 471.8 1602.15 343 589.01 1915.21 543 654.3 2176.68 144 465.18 1583.4 344 584.87 1895.35 544 653.35 2172.56 145 463.28 1575.64 345 592.47 1913.13 545 647.58 2172.87 146 461.55 1571.9 346 593.11 1913.9 546 645.35 2152.34 147 456.46 1560.07 347 600.58 1939.63 547 649.03 2150.43 148 460.81 1576.41 348 606.55 1948.64 548 636.05 2166.17 149 460.8 1581.93 349 606.91 1942.9 549 631.94 2119.18 150 477.74 1637.74 350 607.63 1947.48 550 635.05 2105.06 151 474.98 1628.93 351 606.14 1937.26 551 636.32 2115.11 152 477.86 1645 352 602.06 1928.11 552 641.86 2119.18 153 479.97 1648.47 353 591.04 1895.64 553 641.27 2137.99 154 473.25 1625.77 354 596.71 1907.93 554 644.12 2132.89 155 475.71 1638.23 355 596.2 1909.19 555 645.82 2147.28 156 476.19 1633.9 356 594.15 1902.55 556 650.6 2155.41 157 471.78 1619.04 357 601.67 1932.79 557 653.33 2178.47158 474.43 1627.12 358 605.69 1948.02 558 656.11 2191.06 159 466.07 1599.55 359 609.56 1960.54 559 653.54 2199.51 160 469.94 1611.96 360 612.35 1973.37 560 656.88 2194.65 161 464.33 1587.89 361 613.32 1979.2 561 660 2203.37 162 458.3 1560.68 362 615.14 1987.19 562 659.56 2213.6 163 459.39 1562.79 363 610.26 1982.48 563 655.82 2210.34 164 462.57 1571.6 364 614.32 1993.99 564 656.14 2197.6 165 490.46 1675.12 365 615.01 1998.43 565 655.22 2198.3 166 486.08 1659.93 366 614.24 1991.56 566 650.64 2193.58 167 489.93 1670.14 367 615.39 1996.34 567 649.91 2179.7 168 490.58 1672.89 368 613.02 1989.24 568 658.48 2180.28 169 486.19 1662.8 369 614.99 1996.58 569 659.36 2211.2 170 482.5 1645.51 370 619.24 2012.32 570 659.64 2214.26 171 483 1648.56 371 619.63 2012.35 571 658.64 2219.59 172 477.74 1633.84 372 621.52 2012.79 572 660.09 2226.78 173 476.7 1625.59 373 624.9 2023.54 573 663.78 2234.99 174 475.74 1617.06 374 625.75 2028.15 574 660.28 2238.5 175 471.91 1604.2 375 627.02 2030.68 575 658.29 2229.81 176 476.33 1619.33 376 630.16 2036.3 576 656.3 2223.07 177 472.05 1602.16 377 625.48 2026.36 577 659.3 2214.62 178 468.77 1591.43 378 629.23 2039.42 578 664.85 2222.96 179 467.09 1584.95 379 633.51 2049.92 579 653.64 2242.42 180 464.74 1570.7 380 635.03 2061.18 580 657.46 2202.4 181 455.75 1534.52 381 634.5 2065.94 581 645.23 2210.97 182 452.33 1522.48 382 634.14 2062.67 582 646.75 2167.65 183 455.94 1537.8 383 637.96 2076.3 583 643.96 2170.45 184 447.29 1507.42 384 638.43 2076.82 584 650.7 2163.12 185 445.02 1508.73 385 638.72 2083.47 585 656.36 2189.15 186 455.46 1543.8 386 639.37 2091.59 586 662.47 2206.07 187 443.51 1501.67 387 643.85 2090.18 587 663.11 2230.2 188 432.71 1470.9 388 632.99 2108.69 588 662.04 2233.59 189 436 1485.83 389 627.16 2074.7 589 658.34 2229.83 190 425.82 1458.53 390 631.01 2057.92 590 658.27 2219.25 191 438.26 1497.46 391 636.46 2071.16 591 654.17 2218.03 192 430.75 1468.27 392 639.92 2086.7 592 655.51 2205.99 193 435.96 1482.67 393 642.55 2100.59 593 653.42 2211.83 194 451.58 1536.82 394 635.14 2105.48 594 646.71 2202.06 195 444.94 1514.53 395 617.42 2076.14 595 643.03 2181.66 196 442.07 1504.56 396 611.53 2021.2 596 643.41 2170.52 197 437.46 1493.1 397 616.55 1999.86 597 650.35 2169.66 198 436.58 1487.47 398 604.52 2010.6 598 643.68 2189.79 199 434.25 1475.68 399 593.73 1963.79 599 643.6 2168.74 200 430.1 1464.83 400 601.74 1925.91 600 642.69 2165.49【实验步骤】(1)创建一个1-661的截面序列工作文件,创建变量,并输入数据。
格兰杰因果关系检验

格兰杰因果关系检验因果关系的判断:因果关系的判断分成两类:一类是没有介入因素的情况,另一类是有介入因素的判断。
1. 没干预因素的推论步骤(1)第一步——判断因果关系的前提:行为人的行为给法益制造、升高了法所不允许风险。
(2)第二步——危害结果就是表明出现的结果。
刑法中因果关系中的实害结果,就是指现实出现的结果,不包含假设的结果。
假设的结果与犯罪行为之间的因果关系被称作假设(假设)的因果关系,这种因果关系不是表明的因果关系,不被接纳。
(3)第三步——危害结果是规范保护范围内的结果。
每一个罪名、罪状规范都在保护一种法益,防止一种实害结果。
(4)第四步——危害结果就是行为人统辖范围内的结果。
因果关系探讨的就是还结果,就是行为人统辖内的结果,即为行为人自己存有责任和义务避免出现的结果。
如果避免结果的出现就是他人的统辖范围,则该结果无法免责于行为人。
2. 有介入因素的判断步骤:两步走不异常:引起关系先前犯罪行为与结果存有因果关系介入因素导致(阻断关系)干预因素与否异常先前行为导致异常:单一制关系谁的危害引致结果二者共同导致(叠加关系)3. 干预因素的种类(1)自然时间(2)被害人的特定体质先前行为引发被害人疾病发作,死亡结果与先前行为有因果关系。
先前犯罪行为没引起被害人疾病发作,丧生结果与先前犯罪行为没因果关系。
(3)被害人自身的行为(4)第三人的犯罪行为(5)阻断救助的行为在救助犯罪行为具备救活的可能性时,丧生结果归属于切断救助的犯罪行为,而不归属于先前犯罪行为。
无法查明的案件一、行为人就是一个人(一)一个人实施一个行为这一犯罪行为可能将形成重罪,可能将形成刑事犯罪,可能将不构成犯罪,无法查明到底就是哪种事实。
对此根据难以确定时有助于被告原则,挑选有助于被告的事实予以判定。
(二)一个人实施两个行为二、行为人就是两个人(一)两个人构成共同犯罪根据“部分实行,全部负责管理”原则,无法查明,二人均与结果存有因果关系。
格兰杰因果关系检验
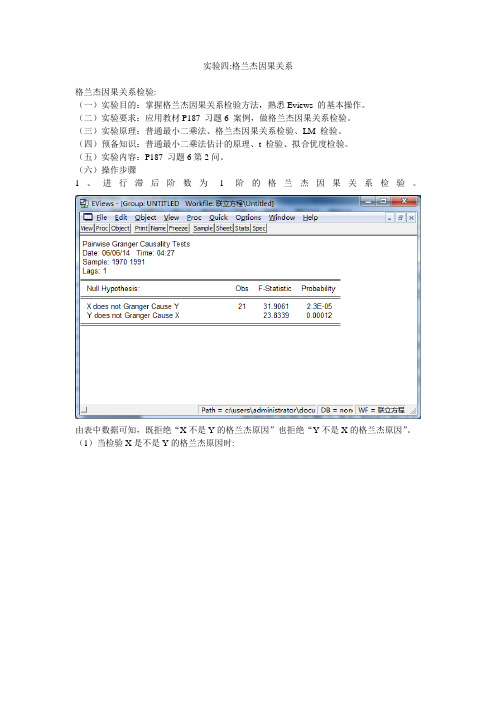
实验四:格兰杰因果关系格兰杰因果关系检验:(一)实验目的:掌握格兰杰因果关系检验方法,熟悉Eviews 的基本操作。
(二)实验要求:应用教材P187 习题6 案例,做格兰杰因果关系检验。
(三)实验原理:普通最小二乘法、格兰杰因果关系检验、LM 检验。
(四)预备知识:普通最小二乘法估计的原理、t 检验、拟合优度检验。
(五)实验内容:P187 习题6第2问。
(六)操作步骤1、进行滞后阶数为1阶的格兰杰因果关系检验。
由表中数据可知,既拒绝“X不是Y的格兰杰原因”也拒绝“Y不是X的格兰杰原因”。
(1)当检验X是不是Y的格兰杰原因时:X(-1)的P值为0.0000小于0.05则拒绝原假设。
此时X是Y的格兰杰原因。
AIC值为6.839780下面检验方程的序列相关性:拉格朗日检验如下:拉格朗日检验的LM=0.426186,P值为0.513866大于0.05,则存在严重的序列相关性。
(2)当检验Y是不是X的格兰杰原因时:Y(-1)的P值为0.0001小于0.05则拒绝原假设。
此时Y是X的格兰杰原因AIC值为:5.990657下面检验序列相关性:拉格朗日检验如下:拉格朗日检验的LM=04.504551,P值为0.033805小于0.05,则不存在严重的序列相关性。
2、进行滞后阶数为2阶的格兰杰因果关系检验。
由表中数据可知,既拒绝“X不是Y的格兰杰原因”也拒绝“Y不是X的格兰杰原因”。
(1)当检验X是不是Y的格兰杰原因时:X(-1)的P值为0.0281小于0.05,X(-2)的P值为0.4565小于0.05 则拒绝原假设。
此时X是Y的格兰杰原因。
AIC值为6.804851下面检验方程的序列相关性:拉格朗日检验如下:拉格朗日检验的LM=3.232597,P值为0.1986小于0.05,则不存在序列相关性。
(2)当检验Y是不是X的格兰杰原因时:Y(-1)的P值为0.0003小于0.05, Y(-1)的P值为0.1996小于0.05 则拒绝原假设。
格兰杰因果检验步骤

格兰杰因果检验步骤引言:格兰杰因果检验是一种常用的统计方法,用于确定两个变量之间是否存在因果关系。
本文将介绍格兰杰因果检验的步骤和应用。
一、确定研究模型在进行格兰杰因果检验之前,首先需要确定研究模型。
研究模型是描述研究变量之间关系的理论框架,可以基于已有理论或实证研究构建。
二、收集数据收集数据是进行格兰杰因果检验的重要步骤。
数据可以通过实地调查、问卷调查、实验等方式获得。
收集的数据应涵盖研究模型中的所有变量,并确保数据的可靠性和有效性。
三、数据预处理在进行格兰杰因果检验之前,需要对收集到的数据进行预处理。
数据预处理包括数据清洗、缺失值处理、异常值处理等。
通过数据预处理,可以提高数据的质量和可靠性,减少误差的影响。
四、计算格兰杰因果检验统计量格兰杰因果检验的核心是计算格兰杰因果检验统计量。
格兰杰因果检验统计量可以通过计算变量之间的相关系数得到。
相关系数衡量了两个变量之间的线性关系强度,可以用来判断是否存在因果关系。
五、设定显著性水平在进行格兰杰因果检验之前,需要设定显著性水平。
显著性水平是判断研究结果是否具有统计学意义的标准。
通常,显著性水平设定为0.05或0.01。
六、进行格兰杰因果检验在设定显著性水平之后,可以进行格兰杰因果检验。
格兰杰因果检验以零假设和备择假设为基础。
零假设认为两个变量之间不存在因果关系,备择假设认为存在因果关系。
七、计算P值进行格兰杰因果检验后,可以得到一个P值。
P值是判断研究结果是否显著的指标。
如果P值小于设定的显著性水平,就可以拒绝零假设,认为存在因果关系;如果P值大于设定的显著性水平,就接受零假设,认为不存在因果关系。
八、解释研究结果根据计算得到的P值,可以解释研究结果。
如果P值小于设定的显著性水平,可以得出结论:存在因果关系。
如果P值大于设定的显著性水平,可以得出结论:不存在因果关系。
九、结果的解释和讨论在解释研究结果时,需要结合研究背景和理论知识进行综合分析。
分析结果时应注意避免歧义和错误信息的产生,确保结果的准确性和严谨性。
格兰杰因果关系检验的步骤

格兰杰因果关系检验的步骤1.收集数据:首先需要收集两个时间序列的数据,分别记为X和Y。
这两个时间序列可以是连续的,也可以是离散的,但要求它们均为平稳的时间序列。
2. 拟合模型:接下来,需要为X和Y拟合合适的模型。
常用的模型包括自回归模型(Autoregressive model, AR)、移动平均模型(Moving Average model, MA)和自回归移动平均模型(Autoregressive Moving Average model, ARMA)。
根据数据的特性进行模型的选择。
3. 确定滞后阶数:通过计算自相关函数(Autocorrelation Function, ACF)和偏自相关函数(Partial Autocorrelation Function, PACF),可以确定X和Y的滞后阶数。
滞后阶数表示因果关系所涉及的时间间隔。
4. 拟合向量自回归模型:通过将X和Y的滞后值作为自变量,建立一个向量自回归模型(Vector Autoregressive model, VAR)。
公式形式为:Y = c + A1*Y(lag1) + ... + An*Y(lagN) + B1*X(lag1) + ... +Bn*X(lagN) + ε,其中c为常数项,Ai和Bi为系数矩阵,N为滞后阶数。
5.检验格兰杰因果关系:对于VAR模型,可以通过计算向量自回归残差的协方差矩阵来检验X对Y的格兰杰因果关系。
设VAR模型的残差为e,如果存在一个时间滞后,称之为k,使得滞后残差e(k)与Y的现值Y(t)相关显著,那么就可以认为X对Y具有格兰杰因果关系。
6.计算p值:通过计算格兰杰因果关系检验的统计量,可以得到一个p值。
如果p值小于设定的显著性水平(通常为0.05),则可以拒绝原假设,认为X对Y具有格兰杰因果关系。
7.解释结果:根据检验结果,可以解释变量X对Y的因果关系的方向和强度。
如果X对Y具有正向影响且显著,可以认为X的变动可以导致Y的变动。
r语言格兰杰因果关系检验

r语言格兰杰因果关系检验格兰杰因果关系检验(Granger causality test)是由Nobel经济学奖得主格兰杰(Clive W. J. Granger)提出的一种时间序列分析方法,用于检验一个时间序列是否因果影响另一个时间序列的变化。
格兰杰因果关系检验在经济学、金融学、计量经济学等领域得到广泛应用。
格兰杰因果关系检验的基本思想是:如果一个时间序列的过去值能够提供关于另一个时间序列未来值的额外信息,那么可以认为前者对后者存在因果关系。
因此,格兰杰因果关系检验的核心问题是,在控制了其他可能的因素之后,一个时间序列的延迟值是否能够预测另一个时间序列的当前值。
具体来说,格兰杰因果关系检验的步骤如下:1. 确定研究的两个时间序列。
假设我们有两个时间序列X和Y。
2. 建立一个基准模型。
基准模型仅包括Y的当前值的自回归模型,没有包含X序列。
基准模型的目的是为了提供对比。
3. 添加X序列到基准模型。
将X序列的延迟值添加到基准模型中,形成一个扩展模型。
4. 使用统计方法对基准模型和扩展模型进行比较。
常用的统计方法有F统计量、卡方统计量等。
如果扩展模型的统计显著性水平小于某个给定的阈值(通常取0.05),则可以认为X序列对Y序列存在因果关系。
需要注意的是,格兰杰因果关系检验的结果并不能确定因果关系的方向,即无法确定X序列是引起Y序列变化的原因,还是Y序列是引起X序列变化的原因。
为了确定因果关系的方向,通常需要进行额外的分析和判断。
此外,格兰杰因果关系检验要求序列之间是平稳的,否则结果可能出现错误。
格兰杰因果关系检验的优点是简单易行、易于解释和使用,对于两个时间序列之间的因果关系提供了一种经验检验的方法。
然而,它也存在一些限制。
首先,格兰杰检验忽略了可能存在的其他潜在因素,可能导致结果的偏误。
其次,格兰杰检验只能检验两个时间序列之间的因果关系,而不能检验多个时间序列之间的复杂关系。
综上所述,格兰杰因果关系检验是一种重要的时间序列分析方法,通过比较基准模型和扩展模型,判断一个时间序列是否对另一个时间序列存在因果影响。
格兰杰因果关系检验

例二
经过Eviews进行格兰杰检验结果如下
可以看出在滞后期为2的情况下,两者互为原因,不 符合格兰杰因果检验。
例三
经过Eviews进行格兰杰检验结果如下 可以看出在滞后期为2的情况下,两者互不为原因。
四、格兰杰因果检验的评价
• 格兰杰的统计学本质上是对平稳时间序列数据一种预测,格兰杰 因果关系检验的结论只是一种预测,是统计意义上的格兰杰因果 性,而不是真正意义上的因果关系,不能作为肯定或否定因果关 系的根据。
二、Granger因果关系检验
变量X是否为变量Y的Granger原因,是可以检验的。
检验X是否为引起Y变化的Granger原因的过程如下:
第一步,检验原假设“H0:X不是引起Y变化的
Granger原因”。首先,估计下列两个回
t 0 i1 i t i i1 i t i t
降水量 20 5 5 15 8 15 41 23 39 5 47 30 28 81 137 35 41 31 57 18 93 67 1 15 10 9
解:(1)建立工作文件。
由于本例数据的时间间隔为旬,Eviews没有提供相应的时 期度量,故应利用鼠标左键单击主菜单选项File,在打开 的下拉菜单中选择New/Workfile,并在工作文件定义对话 框(Workfile Range)的Workfile frequency一栏选择 Undated or irregular项。在起止项中分别输入1和78,表 示每个序列的观测值个数为78个。
有约束回归模型(r): Y
p
Y
t 0 i 1 i t i t
式中,0表示常数项;p和q分别为变量Y和X的最大滞后期 数,通常可以取的稍大一些;t为白噪声。
• 然后,用这两个回归模型的残差平方和RSSu和RSSr 构造F统计量:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.北京的存款增长对北京的人均GDP增长的格兰杰因果检验(一)单根检验1.A1(北京的存款增长)的单根检验Null Hypothesis: A1 has a unit rootExogenous: ConstantLag Length: 0 (Automatic based on SIC, MAXLAG=6)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -4.218621 0.0029 Test critical values: 1% level -3.6998715% level -2.97626310% level -2.627420*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test EquationDependent Variable: D(A1)Method: Least SquaresDate: 10/25/11 Time: 10:04Sample (adjusted): 1983 2009Included observations: 27 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.A1(-1) -0.835841 0.198131 -4.218621 0.0003C 19.33463 5.072943 3.811324 0.0008R-squared 0.415844 Mean dependent var 0.105185 Adjusted R-squared 0.392477 S.D. dependent var 14.84304 S.E. of regression 11.56922 Akaike info criterion 7.805761 Sum squared resid 3346.172 Schwarz criterion 7.901749 Log likelihood -103.3778 F-statistic 17.79676 Durbin-Watson stat 2.021836 Prob(F-statistic) 0.0002822.A2(北京人均GDP增长)的单根检验(1)未滞后Null Hypothesis: A2 has a unit rootExogenous: ConstantLag Length: 0 (Automatic based on SIC, MAXLAG=6)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -2.648793 0.0960 Test critical values: 1% level -3.6998715% level -2.97626310% level -2.627420*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test EquationDependent Variable: D(A2)Method: Least SquaresDate: 10/25/11 Time: 10:08Sample (adjusted): 1983 2009Included observations: 27 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.A2(-1) -0.479685 0.181096 -2.648793 0.0138C 6.910332 2.804785 2.463765 0.0210R-squared 0.219143 Mean dependent var -0.148148 Adjusted R-squared 0.187909 S.D. dependent var 5.045590 S.E. of regression 4.546889 Akaike info criterion 5.937951 Sum squared resid 516.8550 Schwarz criterion 6.033939 Log likelihood -78.16234 F-statistic 7.016106 Durbin-Watson stat 1.735513 Prob(F-statistic) 0.013795(2).A2(-1)单根检验Null Hypothesis: A2(-1) has a unit rootExogenous: ConstantLag Length: 0 (Automatic based on SIC, MAXLAG=6)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -2.962731 0.0519 Test critical values: 1% level -3.7114575% level -2.98103810% level -2.629906*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test EquationDependent Variable: D(A2(-1))Method: Least SquaresDate: 10/25/11 Time: 10:11Sample (adjusted): 1984 2009Included observations: 26 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.A2(-2) -0.540309 0.182368 -2.962731 0.0068C 8.050071 2.860246 2.814468 0.0096R-squared 0.267797 Mean dependent var -0.019231 Adjusted R-squared 0.237288 S.D. dependent var 5.099962 S.E. of regression 4.453969 Akaike info criterion 5.899272 Sum squared resid 476.1083 Schwarz criterion 5.996049 Log likelihood -74.69054 F-statistic 8.777775 Durbin-Watson stat 1.776754 Prob(F-statistic) 0.006779(3).A2(-2)单根检验(效果不好)Null Hypothesis: A2(-2) has a unit rootExogenous: ConstantLag Length: 0 (Automatic based on SIC, MAXLAG=5)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -2.862298 0.0642 Test critical values: 1% level -3.7240705% level -2.98622510% level -2.632604*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test EquationDependent Variable: D(A2(-2))Method: Least SquaresDate: 10/25/11 Time: 10:13Sample (adjusted): 1985 2009Included observations: 25 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.A2(-3) -0.505189 0.176498 -2.862298 0.0088C 7.816925 2.752981 2.839440 0.0093R-squared 0.262649 Mean dependent var 0.328000 Adjusted R-squared 0.230590 S.D. dependent var 4.881386 S.E. of regression 4.281757 Akaike info criterion 5.823222 Sum squared resid 421.6692 Schwarz criterion 5.920732 Log likelihood -70.79028 F-statistic 8.192747 Durbin-Watson stat 1.790508 Prob(F-statistic) 0.0088093.A3(A2的对数化)单根检验(1)未滞后Null Hypothesis: A3 has a unit rootExogenous: ConstantLag Length: 0 (Automatic based on SIC, MAXLAG=6)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -2.611346 0.1031 Test critical values: 1% level -3.6998715% level -2.97626310% level -2.627420*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test EquationDependent Variable: D(A3)Method: Least SquaresDate: 10/25/11 Time: 10:16Sample (adjusted): 1983 2009Included observations: 27 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.A3(-1) -0.533566 0.204326 -2.611346 0.0150C 1.387300 0.542896 2.555371 0.0171R-squared 0.214309 Mean dependent var -0.020242 Adjusted R-squared 0.182882 S.D. dependent var 0.372695 S.E. of regression 0.336896 Akaike info criterion 0.733104 Sum squared resid 2.837478 Schwarz criterion 0.829092 Log likelihood -7.896903 F-statistic 6.819130 Durbin-Watson stat 1.623005 Prob(F-statistic) 0.015031(2)A3(-1)单根检验Null Hypothesis: A3(-1) has a unit rootExogenous: ConstantLag Length: 0 (Automatic based on SIC, MAXLAG=6)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -3.411417 0.0198 Test critical values: 1% level -3.7114575% level -2.98103810% level -2.629906*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test EquationDependent Variable: D(A3(-1))Method: Least SquaresDate: 10/25/11 Time: 10:17Sample (adjusted): 1984 2009Included observations: 26 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.A3(-2) -0.662217 0.194118 -3.411417 0.0023C 1.756069 0.518899 3.384223 0.0025R-squared 0.326557 Mean dependent var -0.002080 Adjusted R-squared 0.298497 S.D. dependent var 0.367688 S.E. of regression 0.307960 Akaike info criterion 0.556109 Sum squared resid 2.276143 Schwarz criterion 0.652886 Log likelihood -5.229419 F-statistic 11.63777 Durbin-Watson stat 1.773706 Prob(F-statistic) 0.002292(二)格兰杰因果检验。
