人教版八年级下数学19.1.2函数的图像优质课件
合集下载
19.1.2函数的图像课件人教版数学八年级下册
巩固新知
(1)在所给的平面直角坐标系中画出函数 y 1 x的图象.
2
（先填写下表，再描点、连线）
x … -3 -2 -1 0 1 2 3 …
y
…
3 2
-1 1
2
0
1 2
13
2
…
(2)点P(5，2)
不在 该函数的图
y 3
象上(填“在”或“不在”).
2 1
-4 -3 -2 -1O-1 -2 -3
12345 x
y/km 0.8 0.6
O8
25 28
58 68 x/min
（2）小明在食堂吃早餐用了多少时间？
解：25-8=17(min)，小明在食堂吃早餐用了17min.
第十七页，编辑于星期日：二十二点 四十五分 。
y/km 0.8 0.6
O8
25 28
58 68 x/min
（3）食堂离图书馆多远？小明从食堂到图书馆用了多少时间？
解：0.8-0.6=0.2(km)，食堂离图书馆0.2km； 28-25=3(min)，小明从食堂到图书馆用了3min.
第十八页，编辑于星期日：二十二点 四十五分 。
y/km 0.8 0.6
O8
25 28
58 68 x/min
（4）小明读报用了多长时间？ 解：58-28=30(min)，小明读报用了30min.
写出正方形的面积S与边长x的函数解析式，并确定自 变量x的取值范围.
S=x2 （x＞0） x 0 0.5 1 1.5 2 2.5 3 3.5 4 S 0 0.25 1 2.25 4 6.25 9 12.25 16
第五页，编辑于星期日：二十二点 四十五分。
在直角坐标系中，描出这些点，然后连接这些点.
人教版八年级下册 19.1.2《函数的图像(2)》 课件(共24张PPT)
2
C
D
1.1
AB
O
0
15 25 37
55
E
80 x/分
人教版数学八年级 下册 第十九章 函数
19.1.2 函数的图象(2)
应用举例
问题4：小明给玉米地锄草用了多少时间？
y/千米
解：由横坐标看出，55-37=18（分钟），小明给玉米地锄草 用了18分钟。
2
C
D
1.1
A
B
O0
15 25 37
55
E
80 x/分
函数图象的画法：
1、列表 列出自变量与函数的对应值表。
注意：自变量的值（满足取值范围）， 并取适当.
2、描点 建立直角坐标系，以自变量的值为横坐标，
相应的函数值为纵坐标，描出表格中数值 对应的各点
3、连线 按照横坐标从小到大的顺序把描出的点用
平滑曲线依次连接起来
y 请画出函数y= x+0.5的图象
A 90
中巴车
小轿车
B
O
1
t(时) 3
人教版数学八年级 下册 第十九章 函数
19.1.2 函数的图象(2)
应用举例
1、下面的图象反映的过程是:小明从家里出发去菜 地浇水，又去玉米地锄草，然后回家，其中x表示时间， y表示小明离他家的距离。小明家、玉米地、菜地在同 一条直线上。请根据图象回答下列问题：
1.1
O0
15 25 37
55
E
80 x/分
小结：解答图象信息题主要运用数形结合思想,化图像信息为数 字信息. 主要步骤如下:
(1)了解横、纵轴的意义
(2)从 图象形状 上判定函数与自变量的关系，
(3)抓住特殊点的实际意义 .
人教版八年级下册数学第十九章《19.1.2函数的图像》公开课课件课件1(16张幻灯片)
s/km 55
乙 甲
t/min O 10 20 30 40 50 60 70
给出下列说法：①学校到景点的路程为55 km；②
甲组在途中停留了5 min；③甲、乙两组同时到达景点； ④相遇后，乙组的速度小于甲组的速度．根据图象信 息，以上说法正确的有 ①② ．
s/km 55
拓展 从图象中 还能获得哪些信息？
• 17、儿童是中心，教育的措施便围绕他们而组织起来。2021/7/272021/7/272021/7/272021/7/27
• 2、Our destiny offers not only the cup of despair, but the chalice of opportunity. (Richard Nixon, American President )命运给予我们的不是失望之酒，而是机会之杯。二〇二一年六月十七日2021年6月17日星期四 • 3、Patience is bitter, but its fruit is sweet. (Jean Jacques Rousseau , French thinker)忍耐是痛苦的，但它的果实是甜蜜的。10:516.17.202110:516.17.202110:5110:51:196.17.202110:516.17.2021 • 4、All that you do, do with your might; things done by halves are never done right. ----R.H. Stoddard, American poet做一切事都应尽力而为，半途而废永远不行6.17.20216.17.202110:5110:5110:51:1910:51:19 • 5、You have to believe in yourself. That's the secret of success. ----Charles Chaplin人必须相信自己，这是成功的秘诀。-Thursday, June 17, 2021June 21Thursday, June 17, 20216/17/2021
乙 甲
t/min O 10 20 30 40 50 60 70
给出下列说法：①学校到景点的路程为55 km；②
甲组在途中停留了5 min；③甲、乙两组同时到达景点； ④相遇后，乙组的速度小于甲组的速度．根据图象信 息，以上说法正确的有 ①② ．
s/km 55
拓展 从图象中 还能获得哪些信息？
• 17、儿童是中心，教育的措施便围绕他们而组织起来。2021/7/272021/7/272021/7/272021/7/27
• 2、Our destiny offers not only the cup of despair, but the chalice of opportunity. (Richard Nixon, American President )命运给予我们的不是失望之酒，而是机会之杯。二〇二一年六月十七日2021年6月17日星期四 • 3、Patience is bitter, but its fruit is sweet. (Jean Jacques Rousseau , French thinker)忍耐是痛苦的，但它的果实是甜蜜的。10:516.17.202110:516.17.202110:5110:51:196.17.202110:516.17.2021 • 4、All that you do, do with your might; things done by halves are never done right. ----R.H. Stoddard, American poet做一切事都应尽力而为，半途而废永远不行6.17.20216.17.202110:5110:5110:51:1910:51:19 • 5、You have to believe in yourself. That's the secret of success. ----Charles Chaplin人必须相信自己，这是成功的秘诀。-Thursday, June 17, 2021June 21Thursday, June 17, 20216/17/2021
(人教版)八年级数学下册：(课件)19.1.2 函数的图像(2)
y
a…1 2 3 4…
l … 3 6 9 12 … 12
10
描点、连线：
8
6
4
2
O 12 345x
3 ．李华和弟弟进行百米赛跑，李华比弟弟跑得快， 如果两人同时起跑，李华肯定赢．现在李华让弟弟先 跑若干米，图中，分别表示两人的路程与李华追赶弟 弟的时间的关系，由图中信息可知，下列结论中正确 的是（ B ） ． Ａ．李华先到达终点 Ｂ．弟弟的速度是8米／秒 Ｃ．弟弟先跑了10米 Ｄ．弟弟的速度是10米／秒
y 5.1
4.5
3 y=0.3t+3
可以近似地表示水位的
变化规律。
0
57
t
（3）据估计这种上涨规律还会持续2 h，预测再过2 h水位高度将达到多少米．
如果水位变化规律不变，可用上述函数预 测，再过2小时，即t=5+2=7时，水位高度 Y=0.3×7+3=5.1(m)
1.函数有哪几种表示方法？这些表示方法分别有哪些 优势和不足？
n 3 4 5 6… m 180 360 540 720 …
所以m=（n-2）·180°（n≥3，且n为自然数）.
2. 用解析式法与图象法表示等边三角形的周长
l是边长a的函数.
解：因为等边三角形的周长l是边长a的3倍，所 以周长l与边长a的函数关系可表示为：l=3a（a＞0）
. 用描点法画函数l=3a的图象.
1、解析法：准确地反映了函数与自变量之间的数 量关系。
2、列表法：具体地反映了函数与自变量的数值对 应关系。
3、图象法：直观地反映了函数随自变量的变化而 变化的规律。
探究一、
例4 一水库的水位在最近5 h 内持续上涨，下表记录 了这5 h 内6 个时间点的水位高度，其中 t 表示时间， y表示水位高度．
a…1 2 3 4…
l … 3 6 9 12 … 12
10
描点、连线：
8
6
4
2
O 12 345x
3 ．李华和弟弟进行百米赛跑，李华比弟弟跑得快， 如果两人同时起跑，李华肯定赢．现在李华让弟弟先 跑若干米，图中，分别表示两人的路程与李华追赶弟 弟的时间的关系，由图中信息可知，下列结论中正确 的是（ B ） ． Ａ．李华先到达终点 Ｂ．弟弟的速度是8米／秒 Ｃ．弟弟先跑了10米 Ｄ．弟弟的速度是10米／秒
y 5.1
4.5
3 y=0.3t+3
可以近似地表示水位的
变化规律。
0
57
t
（3）据估计这种上涨规律还会持续2 h，预测再过2 h水位高度将达到多少米．
如果水位变化规律不变，可用上述函数预 测，再过2小时，即t=5+2=7时，水位高度 Y=0.3×7+3=5.1(m)
1.函数有哪几种表示方法？这些表示方法分别有哪些 优势和不足？
n 3 4 5 6… m 180 360 540 720 …
所以m=（n-2）·180°（n≥3，且n为自然数）.
2. 用解析式法与图象法表示等边三角形的周长
l是边长a的函数.
解：因为等边三角形的周长l是边长a的3倍，所 以周长l与边长a的函数关系可表示为：l=3a（a＞0）
. 用描点法画函数l=3a的图象.
1、解析法：准确地反映了函数与自变量之间的数 量关系。
2、列表法：具体地反映了函数与自变量的数值对 应关系。
3、图象法：直观地反映了函数随自变量的变化而 变化的规律。
探究一、
例4 一水库的水位在最近5 h 内持续上涨，下表记录 了这5 h 内6 个时间点的水位高度，其中 t 表示时间， y表示水位高度．
最新人教版初中八年级下册数学【第十九章一次函数 19.1.2 函数的图像(1)】教学课件
小明家、食堂、图书馆在同一直线上．
根据图象回答下列问题：
（1）食堂离小明家多远？小明
从家到食堂用了多少时间？
（2）小明在食堂吃早餐用了多
少时间？
（3）食堂离图书馆多远？小明
从食堂到图书馆用了多少时间？
（4）小明读报用了多长时间？
（5）图书馆离小明家多远？小
明从图书馆回家的平均速度是
多少？
分析：图象表示小明离家的距离y与时间x
探究新知
对于x的每一个确定的值，S都有唯一确定的值与其对应
活动一
问题1.正方形的边长x与面积S的函数关系_______，
x与S一一对应
平面直角坐标系
有序数对表示点
（x ,S)
探究新知
活动一
• 填写下表：
用平滑曲线
连接各点
S S
= ( > )
当x 2.5时，y 2 x 1 2 2.5 1 4，
点B在函数y 2 x 1的图象上。
解答疑问
疑问二：函数图象千变万化，是否平面直角坐标系里的所有曲
线都是函数图象呢？
解答疑问
例2、下列曲线是否y关于x的函数图象呢？
对于x的每一个确定的值，y都有唯一确定的值与其对应。
解答图象信息题主要运用数形结合思想，化图象信息为数字信息
.
主要方法如下:
(1)了解横、纵轴的意义;
(2)关注特殊点和取值范围;
(3)分析升降趋势、计算相关信息。
巩固练习
小明同学骑自行车去郊外春游,如图表示他离家的距离
y(km)与所用的时间x(h)之间关系的函数图象.
3
(1)根据图象回答:小明到达离家最远的地方需
A
A不是y与x的函数图象
根据图象回答下列问题：
（1）食堂离小明家多远？小明
从家到食堂用了多少时间？
（2）小明在食堂吃早餐用了多
少时间？
（3）食堂离图书馆多远？小明
从食堂到图书馆用了多少时间？
（4）小明读报用了多长时间？
（5）图书馆离小明家多远？小
明从图书馆回家的平均速度是
多少？
分析：图象表示小明离家的距离y与时间x
探究新知
对于x的每一个确定的值，S都有唯一确定的值与其对应
活动一
问题1.正方形的边长x与面积S的函数关系_______，
x与S一一对应
平面直角坐标系
有序数对表示点
（x ,S)
探究新知
活动一
• 填写下表：
用平滑曲线
连接各点
S S
= ( > )
当x 2.5时，y 2 x 1 2 2.5 1 4，
点B在函数y 2 x 1的图象上。
解答疑问
疑问二：函数图象千变万化，是否平面直角坐标系里的所有曲
线都是函数图象呢？
解答疑问
例2、下列曲线是否y关于x的函数图象呢？
对于x的每一个确定的值，y都有唯一确定的值与其对应。
解答图象信息题主要运用数形结合思想，化图象信息为数字信息
.
主要方法如下:
(1)了解横、纵轴的意义;
(2)关注特殊点和取值范围;
(3)分析升降趋势、计算相关信息。
巩固练习
小明同学骑自行车去郊外春游,如图表示他离家的距离
y(km)与所用的时间x(h)之间关系的函数图象.
3
(1)根据图象回答:小明到达离家最远的地方需
A
A不是y与x的函数图象
初中数学 人教版八年级下册 19.1.2 函数的图象 课件
19-1-2 函数的图像
课时1 函数的图像 课时2 画函数图像
函数的图像（课时1）
函数是描述运动和变化过程的重要数学模型，试观察 下面问题中，当自变量的值增大时，函数值如何变化？
某市一天中（1点～12点）气温 T(℃) 随着 时间 t(h)的变化而变化：
t/h 1 2 3 4 5 6 7 8 9 10 11 12 T/℃ -3 -3 -4 -5 -7 -6 -4 0 2 5 6 8
某市一天中气温 T(℃) 随着时间 t(h) 的变化而变化：
t/h 1 2 3 4 5 6 7 8 9 10 11 12 T/℃ -3 -3 -4 -5 -7 -6 -4 0 2 5 6 8
函数的图象：
一般地，对于一个函数，如果把自 t/h变量1 与2函3数的4 每5对对6 应7值8分别9 作1为0 点11的12 T/℃横、-3纵-3坐-标4 ，-5那-么7 坐-6标-4平0面内2 由5这些6 点8
思考
怎样从图象的特征分析中发现函数变化规律和变化 趋势？
图象特征 ——坐标特征 ——变量的变化规律和变化趋势
应用
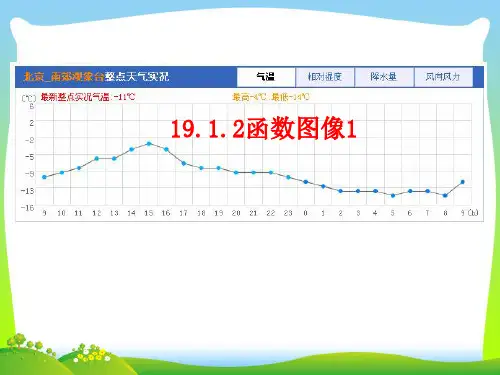
下图是自动测温仪记录的图象，它反映了北京的春 季某天气温 T 如何随时间 t 的变化而变化．你从图象中 得到了哪些信息？
T/℃ 8
O
4
14
-3
24 t/时
第十九章 一次函数
19.1.2 画函数图像（课时2）
组成的图形，就是这个函数的图象．
挑战一下！
上面这个问题只有表格，我们能把自 变量与函数的每对对应值分别作为点 的横、纵坐标，这些点组成这个函数 的图象．你能想办法画出反映下面函 数直观变化规律的图象吗？
正方形面积 S 与边长 x 之间的
函数解析式为 S x2．
课时1 函数的图像 课时2 画函数图像
函数的图像（课时1）
函数是描述运动和变化过程的重要数学模型，试观察 下面问题中，当自变量的值增大时，函数值如何变化？
某市一天中（1点～12点）气温 T(℃) 随着 时间 t(h)的变化而变化：
t/h 1 2 3 4 5 6 7 8 9 10 11 12 T/℃ -3 -3 -4 -5 -7 -6 -4 0 2 5 6 8
某市一天中气温 T(℃) 随着时间 t(h) 的变化而变化：
t/h 1 2 3 4 5 6 7 8 9 10 11 12 T/℃ -3 -3 -4 -5 -7 -6 -4 0 2 5 6 8
函数的图象：
一般地，对于一个函数，如果把自 t/h变量1 与2函3数的4 每5对对6 应7值8分别9 作1为0 点11的12 T/℃横、-3纵-3坐-标4 ，-5那-么7 坐-6标-4平0面内2 由5这些6 点8
思考
怎样从图象的特征分析中发现函数变化规律和变化 趋势？
图象特征 ——坐标特征 ——变量的变化规律和变化趋势
应用
下图是自动测温仪记录的图象，它反映了北京的春 季某天气温 T 如何随时间 t 的变化而变化．你从图象中 得到了哪些信息？
T/℃ 8
O
4
14
-3
24 t/时
第十九章 一次函数
19.1.2 画函数图像（课时2）
组成的图形，就是这个函数的图象．
挑战一下！
上面这个问题只有表格，我们能把自 变量与函数的每对对应值分别作为点 的横、纵坐标，这些点组成这个函数 的图象．你能想办法画出反映下面函 数直观变化规律的图象吗？
正方形面积 S 与边长 x 之间的
函数解析式为 S x2．
人教版八年级数学下册课件：19.1.2函数的图像(2)(共16张PPT)
画出的图象是什么？图象上的点从左向右运动 时，这个点是越来越高还是越来越低？能否用坐标 解释这一图形特点？
y
2.5
y=x+0.5
1.5
0.5 -1 -0.5O
12x
当自变量的值越来越大时，对应的函数值怎样变化？
直线从左向右上升，即当x由小变大时， y=x+0.5随之增大 y
2.5
y=x+0.5
1.5
y6 x
…
6
3
2 1.5 1.2 1 …
从函数图象可以 看出，曲线从左 向右下降，即当 x由小变大时，y 的值随之减小。
练习2
（1）画出函数y=X2的图象。 （2）从图象中观察，当x＜0时， y随x的增大而增大，还是y随x的 增大而减小？当x ＞0时呢？
1、函数图象的画法： 画函数图象的方法为列表、描点、
(2) 货车的速度是 t;0)
标平面上以自变量
的值为横坐标、以
对应的函数值为纵
坐标的点组成的曲
线，函数图象直观
地反映了变量之间
的对应关系和变化 规律．那么，怎样 画一个函数的图象 呢？
用平滑曲线 去连接画出 的点
用空心圈表
示不在曲线
的点
画函数图象一般分为哪几步？
0.5 -1 -0.5O
12x
做一做 练习1
（1）画出函数y=2x-1的图象；
（2）判断点A（-2.5，-4），B（1，3）， C（2.5，4）是否在函数y=2x-1的图象上。
(3).若点P(m,-3)是此函数图象上的一点, 求点P的坐标
例2
画出函数
y
6 x
(x﹥0) 的图象。
x … 1 2 3 4 5 6…
人教版八年级下册数学课件：19.1.2函数的图像
不在曲线的点
2
1
用平滑曲线去 连接画出的点
-5 -4 -3 -2 -1 0 1 2 3 4 5x
-1
这样我们就得到了一幅表示S与x关系的图． 图中每个点都代表x的值与S的值的一种对应关系。
如点(2，4)表示x=2时 S=4。
归纳
函数的图象的意义：
一般地，对于一个函数，如果把自变量 与函数的每对对应值分别作为点的横坐标和 纵坐标，那么坐标平面内由这些点组 成的图形就是这个函数的图象。
解：
小明先走了约3分钟， 到达离家250米处 的一个阅报栏前看 了5分钟报，又向前 走了2分钟，到达离 家450米处返回， 走了6分钟到家。
四、中考实战
甲，乙两同学骑自行车从Ａ地沿同一条路到Ｂ地，已知
乙比甲先出发．他们离出发地的距离s／km和骑行时间
t/h之间的函数关系如图所示，给出下列说法：
a.他们都骑了２０km；
5．一枝蜡烛长20厘米，点燃后每小时燃烧掉5厘 米，则下列3幅图象中能大致刻画出这枝蜡烛点燃 后剩下的长度h（厘米）与点燃时间t之间的函数关
系的是（ C ）.
（二）.小明从家里出发，外出散步，到一个公共阅 报栏前看了一会报后，继续散步了一段时间，然后 回家.下面的图描述了小明在散步过程中离家的距 离s（米）与散步所用时间t（分）之间的函数关系. 请你由图具体说明小明散步的情况.
B 1 (0, 0.5)
-5 -4 -3 -2 A -1 0 1 2 3 4 5x
(y= 6 (x>0) 的图象。
x
解(1)列表:
X ┅ 0.5 1 1. 2 2. 3 3. 4 5 6 ┅
(2)描点:
5
5
5
y ┅ 12 6 4 3 2. 2 1. 1. 1. 1 ┅
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
探究新知 素养考点 1 函数表示方法的相互转化
例1 一水库的水位在最近5 h内持续上涨，下表记录了这5 h内6 个时间点的水位高度，其中 t 表示时间，y表示水位高度．
t/h 0 1 2 3 4 5 y/m 3 3.3 3.6 3.9 4.2 4.5
（2）体育场离文具店多远？ 答：2.5-1.5=1（千米）
（3）张强在文具店停留了多少时间？ 答：65-45=20（分）
（4）张强从文具店回家的平均速度是多少？
解:依题意可得 1.5÷[（100－65）÷60]
1.5 7 12
18（千米/时） 7
课堂检测
能力提升题
给出下列说法：①学校到景点的路程为55 km；②甲组在
2. 会观察函数图象获取信息，根据图象初 步分析函数的对应关系和变化规律.
1. 了解函数图象的意义.
探究新知
知识点 1 函数的图象
写出正方形的面积S与边长x的函数解析式，并确
定自变量x的取值范围. S=x2 （x＞0）
x 0 0.5 1 1.5 2 2.5 3 3.5 4
S 0 0.25 1 2.25 4 6.25 9 12.25 16
课堂检测
基础巩固题
4.下面的图象反映的过程是：张强从家跑步去体育场，在那里 锻炼了一阵后又走到文具店去买笔,然后散步走回家，图中x表 示时间，y表示张强离家的距离.
（1）体育场离张强家多远？张强从家到体育场用了多少时间？
答：体育场离张强家2.5千米. 张强从家到体育场用15分钟.
课堂检测
基础巩固题
应值分别作为点的横、纵坐标，那么坐标平面内由这些点组 成的图形，就是这个函数的图象.
通过图象，我们可以数形结合地研究函数.
探究新知
素养考点 1 画出已知函数的图象
例1 画出下列函数的图象：
（1）y 2x 1 ；
（2）y
6 x
.
解：(1)从函数解析式可以看出，x的取值范围是 全体实数.
第一步：从x的取值范围中选取一些简洁的数值，算出y的
受力后弹簧的长度l是所挂重物m的函数吗？ 答：是, y=0.5x+10
表示弹簧的 长度l与所挂 重物x之间的 函数关系的？
列表格来表示的
探究新知
问题2：有一辆出租车，前3公里内的起步价为8元，每超过1 公里收2元，有一位乘客坐了x（x＞3）公里，他付费y元.用 含x的式子表示y，y是x的函数吗？
答：是, y=8+2（x-3） =2x+2
-3
对应的函数值 越来越大 .
-4
探究新知
解：(2)①列表 ：取一些自变量的值，并求出对应的函数 值，填入表中.
x … -5 -4 -3 -2 -1 1 2 3 4 5 … y … 1.2 1.5 2 3 6 -6 -3 -2 -1.5 -1.2 …
为什么没有 “0”？
探究新知
y
②描点：分别以表中对应的x、
用函数解析 式来表示．
这里是怎样表 示所付费用y与 所走路程x的 函数关系的？
探究新知
问题3：如图是某地某一天的气温变化图.
这里是怎样表示气温T与 时间t之间的函数关系的？
（1）指出其中的两个变量是 气温T ， 时间t .
用平面直 角坐标系 中的一个 图象来表 示的．
（2）其中 气温T 是 时间t 的函数，自变量是 时间t .
巩固练习
1.(1)在所给的平面直角坐标系中画出函数 y 1 x的图象.
2
（先填写下表，再描点、连线）
x … -3 -2 -1 0 1 2
y
…
3 2
-1 1
2
0
1 2
1
(2)点P(5，2)
不在
该函数的
y 3
图象上(填“在”或“不在”).
2 1
3…
3
2…
-4 -3 -2 -1O-1 -2 -3
12345 x
探究新知
请从全面性、直观性、准确性及形象性四个方面来总结归 纳函数三种表示方法的优缺点，填写下表：
表示方法 全面性 准确性 直观性 形象性
列表法
×
√
√×
解析式法 √
√
×
×
图象法
×
×
√√
提示：从所填表中可以清楚看到三种表示方法各有优缺点. 在遇到实际问题时，就要根据具体情况选择适当的方法， 有时为全面地认识问题，需要几种方法同时使用.
课堂检测
拓广探索题
(2)谁在哪一段时间内的生产速度最快？求该段时间内，他每 小时生产零件的个数.
解： 甲在4至7h的生产速度最快， ∵ 40-10 10 7-4 ∴他在这段时间内每小时生产零件10个.
课堂小结
函数的图象
图象的画法
列表 描点 连线
图象表达的实际意义
第二课时
函数的表示方法
返回
导入新知 在计算器上按照下面的程序进行操作：
课堂检测 基础巩固题
1.最近中旗连降雨雪，德岭山水库水位上涨．如图表示某一天 水位变化情况，0时的水位为警戒水位．结合图象判断下列叙 述不正确的是（ C ） A．8时水位最高 B．P点表示12时水位为0.6米 C．8时到16时水位都在下降 D．这一天水位均高于警戒水位
课堂检测
基础巩固题
2.柿子熟了，从树上落下来.下面的哪一幅图可以大致刻画出 柿子下落过程中的速度变化情况?（ C ）
途中停留了5 min；③甲、乙两组同时到达景点；④相遇后，乙
组的速度小于甲组的速度．根据图象信息，以上说法正确的
有 ①②
．
s/km
55
乙 甲
t/min O 10 20 30 40 50 60 70
课堂检测 拓广探索题
某车间的甲、乙两名工人分别同时生产同种零件，他们一 天生产零件y(个)与生产时间t(h)的函数关系如图所示. (1)根据图象填空：①___甲__先完成一 天的生产任务；在生产过程中，__甲__因 机器故障停止生产__2__h； ②当t＝ __3_或__5_.5__ 时，甲、乙生产的零件个数相等.
探究新知 知识点 2 实际问题中的函数图象
下图是自动测温仪记录的图象，它反映了北京的春季某天 气温 T如何随时间 t 的变化而变化．你从图象中得到了哪些信 息？
t/时
探究新知
（1）从这个函数图象可知：这一天中 4
时气温最低
（ -3°C ）, 14时 气温最高（ 8°C ）;
（2）从_ 0时 __至 4时
(1)这一天内，上海与北京何时气温相同？ 答：7时 和 12时.
(2)这一天内，上海在哪段时间比北京气温高？在哪段时间 比北京气温低？ 答：在0时— 7时和12时— 24时比北京气温高； 在7时—12时比北京气温低.
巩固练习
连接中考 （2018•天门）甲、乙两车从A地出发，匀速驶向B地．甲车以 80km/h的速度行驶1h后，乙车才沿相同路线行驶．乙车先到达 B地并停留1h后，再以原速按原路返回，直至与甲车相遇．在此 过程中，两车之间的距离y（km）与乙车行驶时间x（h）之间 的函数关系如图所示．下列说法：①乙车的速度是120km/h； ②m=160；③点H的坐标是（7，80）；④n=7.5．其中说法正确 的是（ A ） A．①②③ B．①②④ C．①③④ D．①②③④
探究新知 函数的三种表示法：图象法、列表法、 解析式法． y = 2.88x
1 4 9 16 25 36 49
探究新知
归纳总结 函数的三种表示方法: (1)列表法：用_表__格____列出自变量与函数的对应值，表 示函数两个变量之间的关系，这种表示函数的方法叫做 列表法. (2)图象法：用__图__象___表示两个变量之间的函数关系， 这种表示函数的方法叫做图象法. (3)解析式法：用___数__学__式___表示函数的方法叫做解析 式法.
探究新知
y/km 0.8 0.6
O8
25 28
58 68 x/min
（3）食堂离图书馆多远？小明从食堂到图书馆用了多少时间？
解：（3）0.8-0.6=0.2，食堂离图书馆0.2km；28-25=3，小明 从食堂到图书馆用了3min.
探究新知
y/km 0.8 0.6
O8
25 28
58 68 x/min
探究新知 在直角坐标系中，描出这些点，然后连接这些点.
用空心 圈表示 不在曲 线的点
用平滑 的曲线 连接
表示x与 S的对应关系 的点有无数 个.但是实际 上我们只能 描出其中有 限个点，同 时想象出其 他点的位置.
探究新知 上图的曲线即函数S=x2 （x＞0）的图象. 一般地，对于一个函数，如果把自变量与函数的每对对
探究新知
方法点拨 解答图象信息题主要运用数形结合思想,化图象信 息为数字信息. 主要步骤如下: (1)了解横、纵轴的意义； (2)从 图象形状 上判定函数与自变量的关系； (3)抓住图象中端点，拐点等特殊点的实际意义.
巩固练习 2.如图是某一天北京与上海的气温随时间变化的图象. 根据图像回答下列问题.
对应值，填写在表格里：
x … -3 -2 -1 0 1 2 3 … y … -5 -3 -1 1 3 5 7 …
探究新知
第二步：根据表中数值描点（x，y）；
第三步：用平滑曲线连接这些点.
y
5 4 3
2 1
y=2x+1
画出的图象是一条
-4
直线 ，
-3
-2
-1
O -1
-2
12345
x
当自变量的值越来越大时，
气温呈下降状态，从4时至 14时
气温呈上升状态，从 14时 至
24时 气温又呈下降
状态.
t/时
探究新知 素养考点 1 从实际问题的图象中读取信息