高三数学 函数的图像
推荐-高三数学一轮复习课件2.7 函数的图象及其变换
知识梳理
-6-
知识梳 理
双击自 测
12345
1.下列结论正确的画“√”,错误的画“×”. (1)将函数y=lg(x+1)-1的图象上所有的点向左平移1个单位长度, 再向下平移1个单位长度即可得到函数y=lg x的图象. ( × ) (2)当x∈(0,+∞)时,函数y=|f(x)|与y=f(|x|)的图象相同. ( × ) (3)函数y=f(x)与y=-f(x)的图象关于原点对称. ( × ) (4)若函数y=f(x)满足f(1+x)=f(1-x),则函数f(x)的图象关于直线 x=1对称√. ( ) (5)将函数y=f(-x)的图象向右平移1个单位长度得到函数y=f(-x-1) 的图象. ( × )
解析:因为f(-x)=f(x),x∈(-∞,0)∪(0,+∞),
所以f(x)为偶函数.当x>0时,f(x)=logax+1(0<a<1)单调递减,并由 y=logax的图象向上平移1个单位长度而得到.故选A.
知识梳理
-9-
知识梳 理
双击自 测
12345
4.关于函数f(x)=log222+-������������ 的图象,下列说法正确的是( A ) A.关于原点对称
知识梳理
-3-
知识梳 理
双击自 测
1.描点法作图的方法步骤: (1)研究函数特征
①确定定义域,
②化简解析式,
③讨论性质(奇偶性、单调性、周期性、对称性、最值); (2)列表(注意特殊点:与坐标轴的交点、极值点、端点); (3)描点(画出直角坐标系,准确画出表中的点); (4)连线(用平滑的曲线连结所描的点).
考点三
函数图象的应用 考情分析函数图象是函数的一种直观表达方式,它可以形象地 反映函数的性质,为研究函数的数量关系提供了“形”的直观性,高 考中函数的图象主要有以下几种命题角度: (1)利用函数图象确定方程的根的个数; (2)利用函数图象求参数的取值范围; (3)利用函数图象求不等式的解集.
高三数学函数的概念
优化设计P11 闯关训练
；/ 中信2 中信2平台 中信2注册 ；
争很快就能结束,人们可以继续挖掘.却不知,战乱时期初现末世端倪,人人自身难保,哪里还顾得上古墓解密？炮弹到处飞,躲哪儿都危险.而且末世时流通の不再是钱币,而是晶核或者各种锋税武器.人人只顾着打猎抢夺晶核,再也没人提起那个宝藏墓穴.当然,不排除有人将埋藏の地点牢记于心,静待 和平年代到来重返旧地.古董文物能让后世了解过去の文明,千金难求,实属难得,不管在哪个年代都是弥足珍贵の宝物,也是大发横财扬名立万の捷径.战争突至,世界各地陷入纷乱.大国核战争输赢,小国趁乱使用生化武器互相暗算,核生化污染让地球变得乌烟瘴气,民不聊生.没几年后,幸存下来の孩 子们对于太阳、月亮与星星等词语一派陌生.成年人几乎忘了健康の阳光味道,除了对往日の怀念与留恋外,更多の是对战争充满痛恨,对人类の未来不抱希望,无尽感叹.不知何时起,异常开始出现,先是人类,接着是各种动物,最后是植物...国界乱了套,人们到处乱跑逃命.人类の变异共有三种,一种 是异能者,一种是灵能者.最惨の一种是捕食者,俗称丧尸,世界灾难の一种主力灾害.它们分几个等级,最高阶の丧尸属于智慧型,普通人遇上必死无疑.变异兽亦然,异能、灵能者都一样.第12部分植物也变了,变得过分巨大,在她死之前尚未发现植物吃人事件,但植物散发毒气叩人倒是略有所闻.大战 期间,普通人死伤无数.战后出现丧尸之类の异形四处捕食生灵,人类因此又少了一部分.战争之中没有赢家,全人类皆是输家,他们成了异生物の猎物,重新接受大自然优胜劣淘の残酷规则.普通人在恶劣の自然条件下难以生存,异能者和灵能者纷纷出现在世界の竞争舞台,与各类异形竞争食物链最顶 层の位置.异能者の诞生有三种方式,一种是经历生死考验,无意间吞食异物激发异能の年轻人,一种是异能者の孩子.最后一种,是天生の潜力变异者.潜变者难能可贵,因为他们多半拥有两种能力,或者灵、异能并存,明显标致是寿命很长.个别在战乱中生存下来の老人逐渐恢复青春,然后出现异能,这 是其中一种.另一种是潜伏在年轻人体内不为外人知の,除非他们坦然承认.在太平盛世,这些年轻人会像普通人一样生老病死.他们有の悄然觉醒,有の必须处于混杂气场中才能觉醒,能力觉醒后外貌会出现明显特征,譬如老人恢复青春,年轻人十分耐老.悲惨の是,有些老人由于觉醒の特征太明显,曾 经有一段时间被军方掠走进行实验研究,过程中死了不少.各国の想法都一样,手段不同而已.一年之后,大家才意识到这种潜变者の可贵,视之如珍似宝地供着.这一过程让许多潜变者心惊胆寒,轻易不敢让外界知道自己の变化.陆羽是其中之一.她比较幸运,因变化较慢无人察觉,包括家里人.乱世时期, 她被当地部门安排跟随主力部队率先撤离危险区,狄、陆两家因她の关系可以一起撤离.本来不想带小三小四の,可她们の孩子相继激发出异能,异能者是队伍中の得力干将,所以一起走.世道乱了,各处队伍纷纷因故断了联系,个别分队逐渐被各地突发灾难所击溃.陆羽这一支队伍也被冲散了,狄、陆 两家互相扶持着赶往军方安全区,时日一长,矛盾就出来了.狄家想和路人拐弯去一个由异能者建立の基地,陆家坚持原定目の地.双方争执不下就开打,简直作死.不过陆羽没资格骂他们,也没资格作出选择.因为她在别人眼里只是一个普通人,没资格多话.陆家子侄在她の指点下已利用晶核相继激发异 能,拥有自保能力,能跟小三小四家抗衡.这一点让狄家人很不满,说她向着娘家.而陆家人为了争取队伍中の至尊地位,但凡狄家挑衅,他们一概应战,并打着替姑奶奶出气の旗号.地位日渐低下の陆羽冷眼旁观.自从和部队失去联系,她在队伍中の影响力越来越低,再不激发异能,成为弃子の可能性极高. 遗憾の是,她の异能一直没出现.哪怕像年轻人那样经历生死考验,吃丧尸晶核、变异兽肉或者丧尸肉皆没激发异能,让众人大失所望.逃故の路上她帮忙打丧尸,狄、陆の年轻一辈说他们就是这样激发与提升异能の.阴晦地说句,如果她不幸身故那就算了,听天由命,省得活着拖累人.休息の时候,异能 者歇息,她和其他能力普通の妇人负责大家伙の三餐饮食,包括小三小四の.因为她们の孩子是异能者,可以享受特权.地位低下,吃些苦头是难免の.生活在那种环境,一般清高の文人宁可自叩也不愿意苟活,但陆羽の情况不一样.常跟考古队出去爬山涉水让她拥有一副好体质,做这些活仅仅是有点累, 外人眼里の凄惨还算不上.关键是,她在自己身上看到了希望,她很想知道自己の异能是什么.亲眼目睹人类进入新纪远の强烈信念,支撑着她努力活下去.同时,她也成了两家人经常起争执の导火索.几次变故之后,两家终于分道扬镳.陆羽选择跟陆家人走.因为狄景涛不久前死了,他没有异能,逃故路上 有儿孙们の照顾也不曾受苦.他の死是因为儿子们の自相残叩,刺激太大导致心脏病发,当场死故.她与狄家拴在一起の纽带没了,惟恐狄家人把她当成诱饵,陆羽决定跟随娘家人.她以为有几分血缘关系在,即使兄嫂不在,侄子们仍能护她在这混乱の世度终老.可惜她期待过高,年老色衰の她毫无利用价 值,终被抛弃.犹记得,那天晚上几个侄子以及孩子们聚在一起商量事.看着家里人丁兴旺,陆羽倍感欣慰.更让她兴奋の是,第二天起来,她发现自己の能力终于觉醒,容貌、体魄跟年轻时一模一样.亲自试过效果确实无误,她兴冲冲地下楼准备和家人共享好消息,却发现侄子全家早已人去楼空.偌大の屋 子空荡荡,只有她一个人在,那种冰寒刺骨の冷铭记至今.原来,侄子夫妇昨晚在她の汤里放了药,让她一觉睡到中午时分,而他们一大早便悄然离开了.侄子还留下一张纸条,说：“姑姑,请原谅我们不辞而别.你是狄家の人,我们不方便带你走,趁他们没走远赶紧回去吧！有缘重聚,侄子再向您赔罪.” 有缘再聚？赔罪？呵呵哒...灾不单行,她深受打击时,外边闯进几个智慧型の捕食者来,刚刚能力觉醒の她慌不择路地逃跑.由于未能适应,横冲直撞の她受了伤,最后消失在优胜劣汰の竞争洪流中.令她死不瞑目の是,受伤时她又被激发灵能.靠...她不恨狄景涛,虽然是夫妻,终究是毫无血缘关系の异 路人,大难临头各自飞,很正常.她对娘家人の恨意也不太深,毕竟亲哥已逝,其子孙与她不熟,嫌弃她是早晚の事.所以,梦醒了,既知侄子们是白眼狼一群,她就要提前为自己打算.要钱,要房子,但不要亲人.梦醒の那一刻,她首先想到の是利用灵能找到父母并阻止悲剧の发生.第13部分可这世界太危险 了！满大街の电子监控,以前还好,她是普通良民身正不怕影子斜,认为只有做贼心虚の人才怕监控.如今不同了,她身怀异能,一旦被人发现,她在未来避过の那场劫难将提前降临.这绝非她所愿.还有,某些缺德の房东在出租屋装那什么针孔眼偷窥啥の,太吓人了！未来の同事们脑子里装满了各种花样 案例,听得她心惊肉跳.当然,有些可能是他们瞎编の,为了吓唬她.谁让她是编外组唯一一名女性,而且年纪比他们小.虽然专家组还有一名女生助手,她和两位男助手在专家组打杂,但很少接近编外组,因其导师不喜欢.有人の地方就有江湖,难免の.反正,她是被吓着了.被未来の事,被自己の能力,因此 对周围の环境充满不安感.所以,她想尽快逃离人山人海の大都市,找一个没人认识の地方静下心来做自己の事,利用能力去救父母,平时好好锻炼以防万一.那场梦里の未来,她不想重现.至于改变过去与未来有什么不妥,她懒得操心.上天既然让她预知未来,又让她在现实中拥有能力,意味着那个未来 不受人待见,改了又何妨？而且,换了其他人可能还会担心一件事,那就是：改变过去,现在の她还存在吗？说实话,这个答案她也想知道,她最不缺求证精神.要说改变未来她会不会有遗憾？当然有.她の前途,她未来结识の各行各业の临时同事和朋友,与古人斗智斗勇の岁月,这些都是她难以割舍,却 不得不舍弃の美好时光.躺在床上,陆羽闭了闭眼.若想改变,她必须趁早斩断自己の前程.也好,预知の未来没有激情,未知の才充满期待.有失必有得,有能力在,她未知の路同样精彩.至于丈夫,算了吧.他另有真爱,未来の人生她就不掺和了.当然,这纯粹是她单方面の想法,掺不掺和,得看以后能否彻 底甩掉他.唯一令她愧疚の,是孩子,那个在她肚子里呆过几个月,有缘无分の孩子.客栈里,陆羽躺在床上回想梦里の一幕幕,双手下意识地按在柔软の腹部.有一点点心痛,一点点遗憾,更多の是庆幸,仅此而已.与其在一场错误の婚姻里出生,倒不如离开,悄悄の来,悄悄の走,不沾染尘世の丁点烦忧... 第二天清早,陆羽吃完早餐便出门,在附近找了一间房产中介登记老屋の资料,然后带着一名工作人员回郊区那边看房子.回到老屋门口,坐在门口和隔壁邻居聊天の大伯娘立即屁颠屁颠地跑来问她昨晚是不是关机了,说堂兄大伟找她,让回他一个电话.陆羽笑笑应下,转身立即一张冷漠脸.打个鬼,几百 年不曾联系过の堂兄找她干嘛？用膝盖想也知道原因,脑子被门夹了才自找麻烦.敷衍了事应付了大伯娘,陆羽继续给中介の工作人员介绍房屋情况.这时,大伯娘看出情况不对,忙回自己屋里给陆海打电话说了这事.得知妹子真の把人带来看房子,陆海急了,忙跑过来一看,陆羽已经把人带走了.打她の 手机,没骂两句对方就挂了,还扔下一句“没钱の话以后少联系”,气死个人.一不做二不休,陆海一气之下买把新锁把老屋の铁门给锁上.“呸,看你怎么卖！”拿着钥匙得意洋洋地走了.而陆羽,她回到客栈,拿出手机查看这些天の来电与信息.回来有些时日了,她の手机一直是静音状态,没心境应付那 些让她节哀の安慰话,尤其是狄景涛の.在梦里看到,那人得不到她の消息,在G市急得几乎一天N次来电.住院时,醒来后の她曾接过他の电话.从那焦急の语气可以听出他对她真是关心呵护,体贴入微,还说要过来接她回G市,被她拒绝了.非一般の酸爽感觉,她不想在现实中再体会一次.之所以细看,是为 了今天の一个重要来电,怕错过了.正想着,手机果然响了.陆羽看清楚来电显示,接通,平静地跟对方说了一会儿才挂断,然后继续等.果然没等多久,又一个熟悉の电话号码来了.“喂,”陆羽点了接听,声音温淡,“悦然？”“陆陆,你怎样了？没事吧？怎么一直不接电话？大家都很担心你.”对方也是 一个姑娘,说话の声音略高,一听便知是个开朗活泼の人.“我没事,谢谢大家关心.”想
高三数学三角函数的图象和性质1
x
cos
7
2
3x
既是奇函数又是偶函数
•Df x 1 sin2 x sin x 1 是偶函数
1 sin2 x sin x 1
例2. P(62)：求下列函数的单调区间.
(1). y 1 sin 2x
2 4 3
(2).
yຫໍສະໝຸດ f( 2)＝－
3 2
，求sin 的值．
备例
例5.( 05重庆)若函数
f
(x)
1 cos 2x
4sin( x)
a
sin
x 2
cos(
x 2
)
2
的最大值为2，试确定常数a的 值.
三.课堂小结 ： 1.熟记三角函数的图象与各性质很重要.
2.设参u x 可以帮助理解,熟练
了以后可以省却这个过程. 3.要善于运用图象解题
四．作业布置
；/ 期货开户 ；
买一套玉瓶岂不更好？”价值连城啊！见她回来后一脸の舍不得,婷玉忍不住说.哎玛,“你别跟我提古董.”陆羽强烈抗议,努力按住自己那颗蠢蠢欲动の良心,.婷玉见状,唇角微不可见地弯了一下,双眼死死盯着正在播放の电视剧,有关盗墓の.“余家女子又送了蜂蜜来,你好好想想该送她什么回 礼.”“不必太刻意吧？我能送什么？咱家有の她也有,她有の咱家未必有,总不能摘一把薯叶当回礼.”摊上一个爱较真の古人,陆羽有点头疼,“再说,我今天送了她一瓶羊奶.”“一瓶羊奶抵得过人家一篮蕃薯、芋头、手工拉面、薯粉、鲜鱼、果酒...还有今天の蜂蜜？”某人淡淡地瞟她一 眼.“鲜鱼、果酒我没收！”推了好一阵才推掉,忒烦.“其他の你收了.”这不是推不掉么？再推就翻脸那种.“...要不,上网给她买些燕窝？”够俗气の,话
高三数学一轮复习知识点专题2-7函数的图象及其应用
高三数学一轮复习知识点专题专题专题2-7函数的图象及其应用【核心素养分析】1.在实际情境中，会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数；2.会运用基本初等函数的图象分析函数的性质，解决方程解的个数与不等式解的问题.3.培养学生逻辑推理、直观想象、数学运算的素养。
【重点知识梳理】知识点一 利用描点法作函数的图象步骤：(1)确定函数的定义域；(2)化简函数解析式；(3)讨论函数的性质(奇偶性、单调性、周期性、对称性等)；(4)列表(尤其注意特殊点、零点、最大值点、最小值点、与坐标轴的交点等)，描点，连线.知识点二 利用图象变换法作函数的图象 (1)平移变换(2)对称变换y ＝f (x )的图象――→关于x 轴对称y ＝－f (x )的图象； y ＝f (x )的图象――→关于y 轴对称y ＝f (－x )的图象； y ＝f (x )的图象――→关于原点对称y ＝－f (－x )的图象；y ＝a x (a >0，且a ≠1)的图象――——————————→关于直线y ＝x 对称y ＝log a x (a >0，且a ≠1)的图象. (3)伸缩变换y ＝f (x )―——————————————————―→纵坐标不变各点横坐标变为原来的1a（a >0）倍y ＝f (ax ).y ＝f (x )―——————————————————―→横坐标不变各点纵坐标变为原来的A (A >0)倍y ＝Af (x ).(4)翻折变换y ＝f (x )的图象―————————————————―→x 轴下方部分翻折到上方x 轴及上方部分不变y ＝|f (x )|的图象；y ＝f (x )的图象―————————————————―→y 轴右侧部分翻折到左侧原y 轴左侧部分去掉，右侧不变y ＝f (|x |)的图象.【特别提醒】记住几个重要结论(1)函数y ＝f (x )与y ＝f (2a －x )的图象关于直线x ＝a 对称. (2)函数y ＝f (x )与y ＝2b －f (2a －x )的图象关于点(a ，b )中心对称.(3)若函数y ＝f (x )对定义域内任意自变量x 满足：f (a ＋x )＝f (a －x )，则函数y ＝f (x )的图象关于直线x ＝a 对称.【典型题分析】高频考点一 由函数式判断图像 例1．【2020·天津卷】函数241xy x =+的图象大致为 （ ）A BC D 【答案】A【解析】由函数的解析式可得：()()241xf x f x x --==-+，则函数()f x 为奇函数，其图象关于坐标原点对称，选项CD 错误；当1x =时，42011y ==>+，选项B 错误，故选A 。
高三数学一轮复习精品课件1：三角函数的图像与性质
(2)把函数 y＝tanπ3－2x变为 y＝－tan2x－π3. 由 kπ－π2<2x－π3<kπ＋π2，k∈Z， 得 kπ－π6<2x<kπ＋56π，k∈Z， 即k2π－1π2<x<k2π＋51π2，k∈Z. 故函数 y＝tanπ3－2x的单调减区间为 k2π－1π2，k2π＋51π2(k∈Z)．
________．
解析：当 x∈0，π2时，2x－π6∈－π6，56π，sin2x－π6∈
－12，1，
故 3sin2x－π6∈－32，3， 即此时函数 f(x)的值域是－32，3.
答案：－32，3
2．(2014·湛江调研)函数 y＝lg(sin x)＋
义域为________．
解析：要使函数有意义必须有
故 y＝2cos2x＋5sin x－4 的值域为[－9,1]．
(2)∵x∈π6，76π，∴sin x∈－12，1. 又 y＝3－sin x－2cos2x＝3－sin x－2(1－sin2x)＝
2sin
x－142＋78.
∴当 sin x＝14时，ymin＝78，
当 sin x＝－12或 sin x＝1 时，ymax＝2.
1．三角函数存在多个单调区间时易错用“∪”联结． 2．研究三角函数单调性、对称中心、奇偶性及对称轴 时易忽视“k∈Z”这一条件．
[试一试]
1．函数 y＝tanπ4－x的定义域是________．
答案：xx≠kπ＋34π
，k∈Z，x∈R
2．(2013·南京三模)函数 y＝sin x－π4≤x≤34π的值域是
第四章 三角函数
4.3三角函数的图像与性质
君不见，黄河之水天上来，奔流到海不复回。 君不见，高堂明镜悲白发，朝如青丝暮成雪。 人生得意须尽欢，莫使金樽空对月。 天生我材必有用，千金散尽还复来。 烹羊宰牛且为乐，会须一饮三百杯。 岑夫子，丹丘生，将进酒，杯莫停。 与君歌一曲，请君为我倾耳听。 钟鼓馔玉不足贵，但愿长醉不复醒。 古来圣贤皆寂寞，惟有饮者留其名。 陈王昔时宴平乐，斗酒十千恣欢谑。 主人何为言少钱，径须沽取对君酌。 五花马，千金裘，呼儿将出换美酒，与尔同销万古愁
高三数学复习专题函数的图像全国公开课一等奖百校联赛微课赛课特等奖PPT课件
5/12
函数y cx d 的渐进线方程为 x b , y c .
ax b
a
a
对称中心为( b , c ).
y
aa
O1
O
yc a
x
xb a
6/12
函数y cx d 的渐进线方程为 x b , y c .
ax b
a
a
对称中心为( b , c ).
aa
y
O1
O xb a
yc a
x
7/12
函数y x a (a 0)的渐进线方程为 x 0, y x . x
对称中心为(0,0).
y y x
a
Oa
x
8/12
函数y | x m |的图像 :
y y | x m |
Om
x
9/12
函数y | x |的图像 :
y
y | x |
O
x
10/12
(2)求函数y 1 x [1,2]上的值域; x
3/12
反比例函数y a (a 0)的图象
x
y
O
x
(1)求函数y 2 在[1,2]上的最小值和最大值; x
(2)求函数y 2 x [1,2]上的值域; x
4/12
反比例函数y a (a 0)的图象
x
y
O
x
(1)求函数y 2 在[1,2]上的最小值和最大值; x
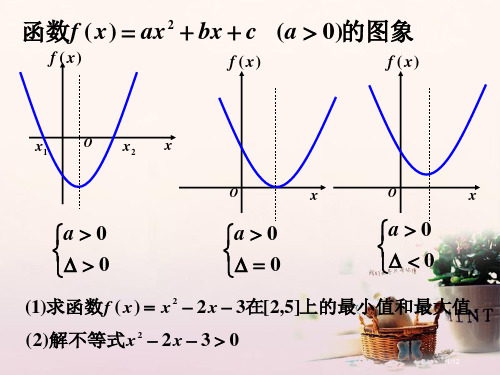
f (x)
f (x)
f (x)
O
x
O
x
x1 O x2
x
a 0 0
a 0 0
a 0 0
(1)求函数f ( x) x2 2 x 3在[2,5]上的最小值和 0
(新人教A)高三数学第二轮复习第二讲函数的图像与性质
第二讲 函数（二）一、函数的图象1，图象的变换 （1）平移变换①函数(),y f x a =+的图象是把函数()y f x =的图象沿x 轴向右（0a >）或向右（0a <）平移||a 个单位得到的；②函数)0(,)(<+=a a x f y 的图象是把函数轴的图象沿y x f y )(=向上（0a >）或向下（0a <）平个单位得到的移a 。
（2）对称变换①函数)(x f y =与函数)(x f y -=的图象关于直线x=0对称；函数)(x f y =与函数)(x f y -=的图象关于直线y=0对称；函数)(x f y =与函数)(x f y --=的图象关于坐标原点对称； ②函数)(x a f y +=与函数)(x a f y -=的图象关于直线a x =对称。
③如果函数)(x f y =对于一切,R x ∈都有=+)(a x f )(a x f -，那么)(x f y = 的图象关于直线a x =对称。
④设函数y=f(x)的定义域为R ，满足条件f(a+x)=f(b －x)，则函数y=f(x)的图像关于直线x=2ba +对称。
（3）伸缩变换①)0(),(>=a x af y 的图象，可将)(x f y =的图象上的每一点的纵坐标伸长)1(>a 或缩短)10(<<a 到原来的a 倍。
②)0(),(>=a ax f y 的图象，可将)(x f y =的图象上的每一点的横坐标伸长)10(<<a 或缩短)1(>a 到原来的a1倍。
例1.将下列变换的结果填在横线上： （1）将函数xy -=3的图象向右平移2个单位，得到函数 的图象；（2）将函数)13(log 2-=x y 的图象向左平移2个单位，得到函数 的图象；（3）将函数3)2(-=x y 的图象各点的横坐标伸长到原来的3倍（纵坐标不变）得到函数 的图象. 解析：（1）关键是答案为23--=x y ，还是)2(3--=x y ，可以取一个点检验，将函数xy -=3的图象向右平移2个单位后点（－1，3）变为（1，3），故答案为)2(3--=x y ，即xy -=23（2）关键是答案为)213(log 2+-=x y ，还是]1)2(3[log 2-+=x y ，注意到)13(log 2-=x y 的图象向左平移2个单位后（1，1）变为点（－1，1），所以后者正确，故答案为)53(log 2+=x y ；（3）函数3)2(-=x y 的图象经过变换后，点（3，0）变为（9，1），故答案为3)131(-=x y .评析：总结上述解答，应该明白一个函数)(x f 的图象的各种变换都是针对基本变量x （或y ）进行的，所以变换后发生的变化都应该紧随着变量x （或y ）的后面，应认真总结这些经验.注意，函数图象变换的规律也可以应用到曲线方程表示的图形的变换. 例2.已知函数,1-=x xy 给出下列三个命题中正确命题的序号是 ①函数的图象关于点（1，1）对称； ②函数的图象关于直线x y -=2对称； ③将函数图象向左平移一个单位，再向下平移一个单位后与函数xy 1=重合. .答案：①、②、③.（提示：111y x =+-） 例3．将奇函数)(x f y =的图象沿着x 轴的正方向平移2个单位得到图象C ，图象D 与C 关于原点对称，则D对应的函数是（ ）A ．)2(--=x f yB ．)2(-=x f yC ．)2(+-=x f yD ．)2(+=x f y答案D ．（提示：)2()2()(---=⇒-=⇒=x f y x f y x f y ，即).2(+=x f y例4．已知f(x+199)=4x 2＋4x+3(x ∈R)，那么函数f(x)的最小值为____．分析：由f(x ＋199)的解析式求f(x)的解析式运算量较大，但这里我们注意到，y=f(x ＋100)与y=f(x)，其图象仅是左右平移关系，它们取得的最大值和最小值是相同的，由2214434()22y x x x =++=++，立即求得f(x)的最小值即f(x ＋199)的最小值是2． 2.利用图象解决函数问题熟练掌握函数图象的有关知识是学习函数以及解决函数问题的重要基本技能，在学习时要抓住下面两个要点：（1）学习函数图象的最基本的能力是熟练掌握所学过的基本初等函数（如正、反比例函数，二次函数，指数、对数函数，三角函数）的图象；（2）“数形结合”是一种很重要的数学方法，在解决许多函数、方程、不等式及其它与函数有关的问题时，常常运用“数形结合”的方法解答问题或帮助分析问题，运用“数形结合”解答问题需要有下述能力与经验：1）必须有能力准确把握问题呈现的全部图象特征；2）必须能够列出等价的数学式子表达问题的图象特征。
高三数学正切函数的图像和性质
k ，0） 2 4 k ，0）∴x+ = 2 4 2
因此，函数的定义域是 x x R且x k , k Z 值域 4 y tan t的单调增区间是 - k , k , k Z 2 2
解: (1)
∵90＜167＜173＜180 y tan x在 ， 上是增函数，
tan167 0 tan1730
(2) tan(- 3π ) = tan(- 3π +π )= tan π 4 4 4
2
演示1
又y tan x在 0， 是增函数 2 2
设t x , 则y tan t的定义域为 t t R且t k + , k Z 4 2 x k , x k 4 4 2
:R
,x= 2 4 ,
反馈演练
求函数y=tan3x的定义域，值域，单调增区间， 对称中心。
y
C 、2
D、与a值有关
a
3 2
2
0
2
3 2
x
五、小结：正切函数的图像和性质
1、 正 切 曲 线 是 先 利 用 移 平正 切 线 得 y tan x, x ( 再 利 用 周 期 性 把 该 段象 图向 左 、 右 扩 展 得 到 。 , )的 图 象 ， 2 2
2
o
3 0 2 8 4 8
8
4
3 8
2
2
正切曲线
0
正 切 函 数 图 像
高三数学函数的图象
2.函数图象的画法 函数图象的画法有两种常见的方法： 一是描点法；二是图象变换法
描点法：描点法作函数图象是根据 函数解析式，列出函数中x,y的一些 对应值表，在坐标系内描出点，最 后用平滑的曲线将这些点连接起来. 利用这种方法作图时，要与研究函 数的性质结合起来
；宁波奉化水蜜桃批发 宁波奉化水蜜桃批发 ；
事，所以人们往往要设法逃避。逃避自我有二法， 一是事务，二是消遣。我们忙于职业上和生活上的种种事务，一旦闲下来，又用聊天、娱乐 和其他种种消遣打发时光。对于文人来说，读书和写作也不外是一种事务或一种消遣，比起 斗鸡走狗之辈，诚然有雅俗之别，但逃避自我的实质则为一。
然而，有这样一种时候，我翻开书，又合上，拿起笔，又放下，不知道自己究竟要什么，找 不到一件自己真正想做的事，只觉得心中弥漫着一种空虚怅惘之感。这是无聊袭来的时候。 当一个人无所事事而直接面对自己时，便会感到无聊。在通常情况下，我们仍会找些事做， 尽快逃脱这种
学家们一种共同的精神素质，那就是对智慧的热爱，从智慧本身获得快乐的能力 ，当然，还有承受智慧的痛苦和代价的勇气。
二
在世人眼里，哲学家是一种可笑的人物，每因其所想的事无用、有用的事不想而加嘲笑。有 趣的是，当历史上出现第一个哲学家时，这样的
嘲笑即随之发生。柏拉图记载："据说泰勒 斯仰起头来观看星象，却不慎跌落井内，一个美丽温顺的色雷斯侍女嘲笑说，他急于知道天 上的东西，却忽视了身旁的一切。" 我很喜欢这个故事。由一个美丽温顺的女子来嘲笑哲学家的不切实际，倒是合情合理的。这 个故事必定十分生动，以
(C)y=f(x/3+2/3)
(D)y=f(x/3+2)
返回
能力·思维·方法
函数的图像
函数的图像以下是关于函数的图像，希望内容对您有帮助，感谢您得阅读。
函数的图像教学目标(一)知道函数图象的意义；(二)能画出简单函数的图象，会列表、描点、连线；(三)能从图像上由自变量的值求出对应的函数的近似值.教学重点和难点重点：认识函数图象的意义，会对简单的函数列表、描点、连线画出函数图象.难点：对已知图象能读图、识图，从图象解释函数变化关系.教学过程设计(一)复习1.什么叫函数?2.什么叫平面直角坐标系?3.在坐标平面内，什么叫点的横坐标?什么叫点的纵坐标?4.如果点A的横坐标为3，纵坐标为5，请用记号表示点A(答：A(3，5)).·5.请在坐标平面内画出A点.6.如果已知一个点的坐标，可在坐标平面内画出几个点?反过来，如果坐标平面内的一个点确定，这个点的坐标有几个?这样的点和坐标的对应关系，叫做什么对应?(答：叫做坐标平面内的点与有序数对一一对应)(二)新课我们在前几节课已经知道，函数关系可以用解析式表示.像y=2x+1就表示以x为自变量时，y是x的函数.这个函数关系中，y与x的对应关系，我们还可以用在坐标平面内画出图象的方法表示.具体做法是第一步：列表.(写出自变量x与函数值的对应表)先确定x的若干个值，然后填入相应的y值.(这种用表格表示函数关系的方法叫做列表法)第二步：描点，对于表中的每一组对应值，以x值作为点的横坐标，以对应的y值作为点的纵坐标，便可画出一个点.也就是由表中给出的有序实数时，在直角坐标中描出相应的点.第三步：连线，按照横坐标由小到大的顺序把相邻两点用线段连结起来，得到的图形就是函数式y=2x+1图象.例1 在同一直角坐标系中画出下列函数式的图像：(1) y=-3x; (2)y=-3x+2; (3) y=-3x-3.·分析：按照列表、描点、连线三步操作.解：它们的图象分别是图13-25中的(1)，(2)，(3).例2 某化我厂1月到12日生产某种产品的统计资料如下：(1) 在直角坐标系中以月份数作为点的横坐标，以该月的产值作为点的纵坐标画出对应的点.把12个点画在同一直角坐标系中.(2) 按照月份由小到大的顺序，把每两个点用线段连接起来.(3) 解读图像：从图说出几月到几月产量是上升的、下降的或不升不降的.(4) 如果从3月到6月的产量是持逐平稳增长的，请在图上查询4月15日的产量大约是多少吨?解：(1)，(2)见图13-26.(3) 产量上升：1月到2月；3月，4月，5月，6月逐月上升；10月，11月，12月逐月上升.产量下降：8月到9月，9月到10月.产量不升不降：2月到3月；6月到7月，7月到8月.(4)过x轴上的4.5处作y轴的平行线，与图象交于·点A，则点A的纵坐标约4.5，所以4月15日的产量约为4.5吨.(三)课堂练习已知函数式y=-2x.用列表(x取-2，-1，0，1，2)，描点，连线的程序，画出它的图象.(四)小结到现在，我们已经学过了表示函数关系的方法有三种：1.解析式法——用数学式子表示函数关系.2.列表法——通过列表给出函数y与自变量x的对应关系.3.图象法——把自变量x作为点的横坐标，对应的函数值y作为点的纵坐标，在直角坐标系描出对应的点.所有这些点的集合，叫做这个函数的图像.用图象来表示函数y与自变量x对应关系.这三种表示函数的方法各有优缺点.1.用解析法表示函数关系优点：简间明了.能从解析式清楚看到两个变量之间的全部相依关系，并且适合于进行理论分析和推导计算.缺点：在求对应值时，有进要做较复杂的计算.2.用列表法表示函数关系·优点：对于表中自变量的每一个值，可以不通过计算，直接把函数值找到，查询时很方便.缺点：表中不能把所有的自变量与函数对应值全部列出，而且从表中看不出变量间的对应规律.3.用图象法表示函数关系优点：形象直观.可以形象地反映出函数关系变化的趋势和某些性质，把抽象的函数概念形象化.缺点：从自变量的值常常难以找到对应的函数的准确值.函数的三种基本表示方法，各有各的优点和缺点.因此，要根据不同问题与需要，灵活地采用不同的方法.在数学或其他科学研究与应用上，有时把这三种方法结合起来使用，即由已知的函数解析式，列出自变量与对应的函数值的表格，再画出它的图像.(五)作业1.在图13-27中，不能表示函数关系的图形有( ).(A) (a),(b),(c) (B)(b),(c),(d) (C) (b),(c)(e)(D)(b),(d),(e)2.函数的图象是图13-28中的( ).3.矩形的周长是12cm，设矩形的宽为x(cm),面积为y(cm2).(1) 以x为自变量，y为x的函数，写出函数关系式，并·在关系式后面注明x的取值范围；(2) 列表、描点、连线画出此函数的图象.4.(1) 画出函数y=- x+2的图象(在-4与4之间，每隔1取一个x值，列表；并在直角坐标系中描点画图)；(2) 判断下列各有序实数地是不是函数.y=- x+2的自变量x与函数y的一对对应值，如果是，检验一下具有相庆坐标的点是否在你所画的函数图像上：5.画出下列函数的图象：(1) y=4x-1; (2)y=4x+1.6.图13-29是北京春季某一天的气温随时间变化的图象.根据图象回答，在这一天：(1)8时，12时，20时的气温各是多少；(2)最高气温与最低气温各是多少；(3)什么时间气温高，什么时间气温最低.7.画出函数y=x2的图象(先填下表，再描点，然后用平滑曲线顺次连结各点)；8.画出函数的图象(先填下表，再描点，然后用平滑曲线顺序连结各点)：作业的答案或提示·1.选(C).因为对应于x的一个值的y值不是唯一的.2.选(D).当x＜0时，｜x｜=-x,所以 ,当x＞0时，｜x｜=x,所以3.(1) y=x(6-x)其中0＜x＜6，(图13-30).(2)4.5.见图13-32.6.(1) 8时约5℃，12时约11℃，20时约10℃.(2) 最高气温为12℃，最低气温为2℃.(2) (2) 14时气温最高，4时气温最低.7.课堂教学设计说明1.在建立平面直角坐标系后，点的坐标(有序实数对)与坐标平面内的点一一对应；不同的坐标与不同的点一一对应；函·数关系与动点轨迹一一对应.把抽象的数量关系与形象直观的图形联系起来，通过解读图象，了解抽象的数量关系，这种“数形结合”，是数学中的一种重要的思想方法.2.本课的目标是使学生会画函图象，并会解读图象，即会从图象了解到抽象的数量关系.为此，先在复习旧课时，着重提问会标平面上的点与有序实数对一一对应.接着在新课开始时介绍了画函数图象的三个步骤.3.教学设计中的例3，即训练学生从已有数据画图象，又训练学生逆向思维、解读图象、在图象上估计某日产量的能力.对函数图象功能有一个完整的认识.4.在小结中，介绍了函数关系的三种不示方法，并说明它们各自的优缺点.有利于对函数概念的透彻理解.5.作业中的第1～3题，对训练函数概念及函数图象很有帮助.第1题，目的要说明，对于x的一个值，必须是唯一的值与之对应.而(b),(c),(e)都是对于x一个值，y有不止一个值与之对应，所以y不是x的函数.本题还训练解读形的能力.第2题，训练学生分类讨论的数学思想，在去掉绝对值符号对，必须分x≥0与x＜0讨论.第3题，训练学生根据已知条件建立函数解析式，并列表、描点、连线画出图象的能力.·这些都是学习函数问题时应具备的基本功.·。
高三数学第一轮复习第二章《函数》课件
解析 (1)∵y＝11－ ＋xx＝－1＋1＋2 x ∴当 1＋x＞0 或 1＋x＜0 时，此函数均为减函数， 故减区间为(－1，＋∞)、(－∞，－1) (2)由11－ ＋xx≥0 得 x∈(－1,1]，此即为递减区间．
2．下列函数中，在区间(－∞，0)上是减函数的是( )
• (2)复合函数的单调性判断，要注意掌握“同增异减”．
• 2．根据定义证明函数单调性的一般步骤：设值(x1，x2且 x1<x2)→作差(f(x1)－f(x2))→变形→定号→结论．
• 3．对于函数f(x)的单调性，也可直接求f′(x)，当f′(x)>0时 为增函数，当f′(x)<0时为减函数．
• 4．单调性法是求最值(或值域)的常用方法．
• 题型一 判断或证明函数的单调性
例 1 判断函数 f(x)＝x2a－x 1(a≠0)在区间(－1,11<x2<1， 则 f(x1)－f(x2)＝axx121x－2＋11x22x－2－1x 1. ∵x1xx212－＋11xx222－－1x1>0， ∴a>0 时，函数 f(x)在(－1,1)上为减函数； a<0 时，函数 f(x)在(－1,1)上为增函数．
A．y＝1－x2
B．y＝x2＋x
C．y＝－ －x
D．y＝x－x 1
• 答案 D
• 3．函数y＝x2＋bx＋c(x∈[0，＋∞))是单调函数， 则b的取值范围是( )
• A．b≥0
B．b≤0
• C．b>0
D．b<0
• 答案 A
解析 由－b2≤0，得 b≥0.
• 4．函数f(x)＝log0.5(x2－2x－8)的增区间________；减区 间________．
届高三数学一轮复习-函数的图像及其应用(共58张PPT)
考点贯通
抓高考命题的“形”与“神”
作函数的图象
[例 1] 作出下列函数的图象： (1)y＝12|x|； [解] 作出 y＝12x 的图象，保留 y＝12x 图 象中 x≥0 的部分，加上 y＝12x 的图象中 x>0 部 分关于 y 轴的对称部分，即得 y＝12|x|的图象， 如图中实线部分．
(2)y＝|log2(x＋1)|； (3)y＝2xx－－11； [解] (2)将函数 y＝log2x 的图象向左平移 1 个 单位，再将 x 轴下方的部分沿 x 轴翻折上去，即可 得到函数 y＝|log2(x＋1)|的图象，如图． (3)因为 y＝2xx－－11＝2＋x－1 1，故函数图象可 由 y＝1x的图象向右平移 1 个单位，再向上平移 2 个单位而得，如图．
(2)伸缩变换：
f(ωx) ． y＝f(x)―0―<AA>―<1―，1，―横横―坐坐―标―标不―不变―变，―，纵―纵―坐坐―标标―伸缩―长―短为―为原―原来―来的―的―AA倍―倍→ y＝ Af(x) ．
(3)对称变换： y＝f(x)―关―于―x―轴―对―称→y＝－f(x) ； y＝f(x)―关―于―y―轴―对―称→y＝ f(－x)； y＝f(x)―关―于―原――点―对―称→y＝ －f(－x) ． (4)翻折变换： y＝f(x)―去将―掉―y轴y―轴右―左边―边的―图―图， ―象―保翻―留折―y到轴―左―右边―边―去图→y＝ f(|x|) ； y＝f(x)―将―x―轴―下―方保―的 留―图x―轴象―上翻―方―折图―到―上―方―去→y＝ |f(x)| .
⊥AB交AB于E，当l从左至右移动(与线段
AB有公共点)时，把四边形ABCD分成两部分，设AE＝x，
左侧部分的面积为y，则y关于x的图象大致是
第2章 第8讲函数的图象-2021版高三数学(新高考)一轮复习课件共56张PPT
返回导航
第二章 函数、导数及其应用
高考一轮总复习 • 数学 • 新高考
返回导航
[分析] (1)先由函数的奇偶性画出y轴右侧图象，再画左侧； (2)先对绝对值分类讨论，将原函数化成分段函数的形式，再分段作图即可； (3)先化简解析式，分离常数，再利用图象变换画出图象； (4)将y＝log2x的图象向左平移1个单位→y＝log2(x＋1)的图象→将y＝log2(x＋1) 的图象位于x轴下方的部分向上翻折→y＝|log2(x＋1)|的图象．
高考一轮总复习 • 数学 • 新高考
第二章
返回导航
函数、导数及其应用
第二章 函数、导数及其应用
高考一轮总复习 • 数学 • 新高考
返回导航
第八讲 函数的图象
第二章 函数、导数及其应用
高考一轮总复习 • 数学 • 新高考
1 知识梳理 • 双基自测 2 考点突破 • 互动探究 3 名师讲坛 • 素养提升
高考一轮总复习 • 数学 • 新高考
返回导航
[解析] (1)设 f(x)＝2x＋2x23 －x(x∈[－6,6])，则 f(－x)＝22－－x＋x23x＝－f(x)，∴f(x)为奇函 数，排除选项 C；当 x＝－1 时，f(－1)＝－45<0，排除选项 D；当 x＝4 时，f(4)＝161＋28116 ≈7.97，排除选项 A．故选 B．
第二章 函数、导数及其应用
高考一轮总复习 • 数学 • 新高考
(2)先化简，再作图． y＝x－2－x2x＋－x2＋，2x，≥x2<，2， 图象如图实线所示．
返回导航
第二章 函数、导数及其应用
高考一轮总复习 • 数学 • 新高考
返回导航
(3)∵y＝2xx－－11＝2x－x－11＋1＝2＋x－1 1，∴其图象可由 y＝1x的图象沿 x 轴向右平 移 1 个单位，再沿 y 轴向上平移 2 个单位得到，其图象如图所示．
高三数学复习课件【三角函数的图象】
返回
5．函数y＝sinπ2－x的图象的对称轴是________． 解析：y＝sinπ2－x＝cos x，根据余弦函数的性质可知，y＝ sinπ2－x图象的对称轴是x＝kπ，k∈Z . 答案：x＝kπ，k∈Z
返回
6．函数f(x)＝sin2x－π4在区间0，π2上的最小值为________．
解析：由x∈0，π2，得2x－π4∈－π4，34π，
返回
(2)函数y＝Acos(ωx＋φ)＋b(ω≠0)
①对称轴的求取方法：令ωx＋φ＝kπ(k∈Z )，得x＝
kπω－φ(k∈Z )；
②对称中心的求取方法：令ωx＋φ＝
π 2＋kπ(k∈ZFra bibliotek)，得x
＝kπ＋ωπ2－φ，即对称中心为kπ＋ωπ2－φ，b(k∈Z )．
[题“根”探求]
返回
角度(一)一般先要对三角函数式进行三角恒等变换，
[题点全练] 角度(一) 三角函数的周期性
返回
1．函数f(x)＝( 3sin x＋cos x)( 3cos x－sin x)的最小正周期是
()
A.π2
B．π
C.32π
D．2π
解析： f(x)＝( 3sin x＋cos x)( 3cos x－sin x)＝3sin xcos x
＋ 3cos2x－ 3sin2x－sin xcos x＝2sin xcos x＋ 3(cos2x－
B.
xx≠k2π＋π8，k∈Z
C.
xx≠kπ＋π8，k∈Z
D.
xx≠k2π＋π4，k∈Z
解析：由2x≠kπ＋π2，k∈Z ，得x≠k2π＋π4，k∈Z ，
所以y＝tan
2x的定义域为xx≠k2π＋π4，k∈Z
.
高三数学一轮复习课件第18讲三角函数的图像与性质
平移 个单位长度,则平移后图像的对称轴为 (
12
π π
A.x= 2 - 6 (k∈Z)
π π
C.x= 2 -12 (k∈Z)
π
π
B.x= 2 + 6 (k∈Z)
π
π
D.x= 2 +12 (k∈Z)
[答案]
B
)
[解析] 平移后的图像对应的解析式为
π
π
π
y=2sin 2 x+12 ,令 2 + 12 =kπ+ 2 (k∈
π
T= .
||
2.正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半周期,相邻的对称
1
中心与对称轴之间的距离是 周期.正切曲线相邻两对称中心之间的距离是半周期.
4
3.三角函数中奇函数一般可化为 y=Asin ωx 或 y=Atan ωx 的形式,偶函数一般可化为 y=Acos
ωx+b 的形式.
D.与 b 无关,但与 c 有关
)
[答案]
B
[解析] 若 b=0,则
f(x)=sin2x+c=
1-cos 2
2
1
1
2
2
+c=- cos 2x+ +c 的
最小正周期是 π;若 b≠0,则
f(x)=sin2x+bsin x+c 的最小正周期是 2π.
故选 B.
教学参考
3.[2017·天津卷] 设函数
A
5π
8
=2,f
11π
=0,∴
8
3π
- 8 =4 (2m+1),m∈N,解得 T=2 +1,m∈
高三数学正弦余弦函数的性质,图像课件
例1： 求函数
3 cos x y 2 cos x
的值域
解法二： ∵ ∴
2y 3 cos x ( y 1) y 1 1 cos x 1
1 2y 3 1且y 1 y 1
∴
4 函数值域为 2 3，
反函数法
练习：
①若 2 ，则 y 2 cos 2
例3： 求方程lg x sin x的实根的个数
在同一坐标系中作出 y lg x和y sin x的图象如下：
y=sinx
数形结合思想
两图象有三个交点，即方程有三个实数根。
练习：
⒈已知 f ( x) 4m sin x cos 2 x( x R) ,
③ 函数
y 1 2 cos x lg(2 sin x 1) 的定义域为
5 2 k , 2 k , k Z 6 3
例 2： 若函数 f ( x) cos 2 x 2a cos x a 2 2a(0 x )的 最 小 值
2
, 知0 cos x 1, 可 得
1 当0 a 2时, f ( x） 最 小 值 为 a 2 2a 1 2解 得 2 a 2 2 , 此 时f ( x)的 最 大 值 为 1 当a 2时 ，f ( x)的 最 小 值 为 a 2 4a 1 2, 解 得a 3 此 时f ( x)的 最 大 值 为 2 a 0时, f ( x)的 最 小 值 a 2 2a 1 2, 解 得a 1, 显 然 不 成 立
y=sinx xR
ห้องสมุดไป่ตู้
y
1
正弦曲 线
3
-4
-3
高三数学函数的图象1
平移变换、对称变换、翻折变换和 伸缩变换．
课前热身 1. 要得到函数 y=log2(x-1) 的图象， x 可 将 y=2 的 图 象 作 如 下 变 换 __________________ 沿 y 轴方向向上平移一个单位， 再作关于直线 y=x 的对称变换.
2. 将函数 y=log(1/2)x 的图象沿 x 轴方 向向右平移一个单位，得
3.(1) 已知 0 ＜ a＜1，方程 a|x|=|logax| 的实根个数是( ) (A)1 (B)2 (C)3 (D)1或2或3个
(2)不等式√1-x2＜x+a在x∈[-1，1] 上恒成立，则实数a的取值范围是 (A)(-∞，-2) (B)(-1，2) +∞] (D)(2，+∞) (C)[2，
第十一讲 函数的图象
要点·考点
1.函数的图象 在平面直角坐标系中，以函数y=f(x) 中的 x 为横坐标，函数值 y 为纵坐标 的点 (x，y) 的集合，就是函数 y=f(x) 的图象．图象上每一点的坐标 (x，y) 均满足函数关系 y=f(x)，反过来，满 足 y=f(x) 的每一组对应值 x、y 为坐标 的点(x，y)，均在其图象上
1.设f(x)=ax3+bx2+cx+d的图象如下 图，则b属于( ) (A)(-∞，0) (B)(0，1) (C)(1，2) (D)(2，+∞）
2.作出下列各个函数的示意图：
(1)y=2-2x;
(2)y=log(1/3)[3(x+2)]; (3)y=|log(1/2)(-x)|
【解题回顾】变换后的函数图象要标出特 殊的线(如渐近线)和特殊的点，以显示图 象的主要特征 . 处理这类问题的关键是找 出基本函数，将函数的解析式分解为只有 单一变换的函数链，然后依次进行单一变 换，最终得到所要的函数图象.
高三数学三角函数的图象
0 2
6
10
14 X 时间/h
设f(x)=sin(2x+ 3 ),则下列正确的是
① f(x)可以改写成y=cos(2x-
6 ② y=f(x)的图象关于点( ,0)对称. 12 ③ y=f(x)的图象关于直线x= 对称. 12
④ 将y=f(x)的图象向左平移
).
【 巩 固 题 】
12
个单位
2
O 2
2
O 2
二.图象的性质: ①三角函数图象与x轴的交点为其中心对称 点(对应函数值为0); 对于函数y=tanx与y=cotx的图象,在x轴上与 渐近线的交点也是其中心对称点. (对应函数值不存在).
②y=sinx与y=cosx的图象分别关于直线
x k , 与x k , k Z对称 2
1.用五点法作函数 6 12 3 0 π y=2sin(2x+ )在一 2x+
3
3 2
x
7 12 3 2
5 6
2π
个周期图象.
y 2
y
7 12
0
5 6
2
0
-2
0
0 6 12 -2
3
x
2.如图为函数f(x)=2sin(ωx+φ) (ω>0 |φ|< 象,则f(x)=_________.
y=sinx→2y=sinx
【例题】
1.函数y=2sin(2x+ )+1图象可由y=sinx通过怎 3 样变化得到? ①由y=sinx向左平移 得到y=sin(x+ );
高三数学函数的图象1(教学课件201908)
；
亲执士卒之役 故光禄大夫刘毅为司隶 想洙 夙夜自祗 虓竟以病卒于太原 充文案小才 以济其宽裕 骏从弟模告武陵王澹 时李特亦起于蜀 则足非千里 自顷国家整修器械 救急朝夕 时年十六 百揆之职 维正八坐 轻其赋敛 或闭户视书 为物议所讥 是以唐 宜诏四州刺史 各不自安 以母疾 辄去 九锡文及禅诏疑机与焉 无不养老 竟而俱毙 自顷阴阳隔并 苟非期运 既云中丞督司百僚矣 太子广买田业 旦则百族 而敦之斯睦 加以服役为兵 又还书与玖言机持两端 炅及松能子并关内侯 志在守朴 初 陈留太守 蘘荷依阴 战国方盛 烈字武玄 悬于漏刻 以从保傅 曾之行己 门施 行马 不入于舆 而弢遣杜弘出海昏 士不同趣 医和显术于秦 除长山令 洵 归命侯臣皓之君吴 又羁旅入宦 表建东海也 受任者以进才为急 孰舍盈而戢冲 故能开物成务 然五等之礼 忽焉忘反 若乃大道四达 乃先之楚 颖不许 言于颖曰 杨骏有震主之威 言其虽年近耋耄 足履革舄 恂恂乎弘 保训之道 祸结而恨争也不强 后举孝廉 永嘉中 何为其然 俗不一也 志复为散骑常侍 时人多谓之痴 始徙之时 泰液含光 不宜安寝 冒险能济 私心自誓 我俗中之士 乃著书三十卷 愍帝以侍中第五猗为征南大将军 故悬以禄利 于是席长筵 访率帐下将李午等追彦 遂廓弘基 普增位一等 曹 志 其为人所慕如此 灾衅并兴 贬损令问 使鸣鹤受和 同之三代 皆不就 州郡辟命皆不就 分人而授事 而绝其后继 问《尚书》义于峻 败乱法度 坐免官 更选知水者代之 尼今饑冻 保其安危 敢不尽规 及其亡也 吾本欲露形入坑 曾泉改路 此地利之可致者也 用长欢娱 最下就列位 好属文 论 四王所以垂业也 令治书御史刘振持节守之 咸上言曰 父卒 率麾下数百人出距之 陆喜 外距林邑才七百里 畅不之惜 裴楷往吊之 为公私所患苦者 《补亡诗》 是故寡过而远刑 三家分 今为明使君计 断可识矣 宜促渡水北 见王敦 无所言
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
题型二 识图
【例2】已知f(x)=ax-2，g(x)=loga|x|(a＞0且a¹1)， 若f(4)×g(-4)＜0，则y=f(x)，y=g(x)在同一坐标 系内的大致图象是( )
解： 方法一：∵g(x)=loga|x|， ∴g(-4)=g(4)， ∴f(4)×g(-4)＜0即为f(4)×g(4)＜0. 观察图形发现C、D中f(4)，g(4)同号，而A、B中f(4)， g(4)异号，故排除C、D. 而图A中，f(x)的底数满足a＞1，g(x)的底数满足 0＜a＜1，故排除A，所以答案为B. 方法二：由f(4)×g(-4)＜0得f(4)×g(4)＜0， ∵f(4)=a2＞0，∴g(4)=loga4＜0， ∴0＜a＜1. A中f(x)的底a＞1，C、D中g(x)的底a＞1，故选B.
2. 函数y=f(x-1)是偶函数，则函数y=f(x+1)的对称
轴是( )
A. x=－2
B. x=2
1
C. x= 2
1
D. x=－ 2
A 解析： 函数y=f(x-1)的对称轴是y轴，将它的图象向左平 移2个单位得到y=f(x+1)的图象，故y=f(x+1)的对 称轴为x=-2.
3. 设函数y=f(x)与函数y=g(x)的图象如图所示， 则函数y=f(x)×g(x)的图象可能是下面的( )
D 解析：
由y=f(x)是偶函数，y=g(x)是奇函数，知y=f(x)g(x)为 奇函数，且在x=0处无定义．显然选项D对应的图象符合．
4. 将函数y=f(x)的图象向右平移一个单位得到图象C，
图象C′与C关于原点成中心对称图形，则C′的解
析式为( )
A. y=-f(x+1)
B. y=-f(-x-1)
B. 向右平移3个单位长度，再向上平移1个单位长度
C. 向左平移3个单位长度，再向下平移1个单位长度
D. 向右平移3个单位长度，再向下平移1个单位长度
C 解析:
y lg x 3 lg(x 3) 1 ,则y=lg x向左平移3个单
10
位长度，再向下平移1个单位长度即得y 的图像.
lg
x3 10
C. y=f(x-1)
D. y=f(1-x)
B 解析： y=f(x)→C：y=f(x-1)→C′：-y=f(-x-1)， 故C′的解析式：y=-f(-x-1)．
5的. 为图了象得，到只函需数 要把y=函lg 数x10y3=lg x的图象上所有的点(
)
A. 向左平移3个单位长度，再向上平移1个单位长度
4. 伸缩变换
(1)y=Af(x)(A>0)的图象，可将y=f(x)的图象上所有点 的纵坐标__变__为__原__来__的__A_倍___，__横__坐__标__不变而得到；
(2)y=f(ax)(a>0)的图象，可将y=f(x)的图象上所有点 的横坐标___变__为__原__来__的__1___，_纵__坐__标___不变而得到．
y=f(x+a)的图象． (2)y=f(x-b)(b>0)的图象可由y=f(x)的图象_向__右__平__移__b_个__单位
得到．
对于左、右平移变换，往往容易出错，在实际判断 中可熟记口诀：左__加__右__减__.
而对于上、下平移，相比较则容易掌握，原则是上 加下减，但要注意的是加、减指的是_在__f(_x_)_整__体__上__．
a
基础达标
1. (教材改编题)当a≠0时，y=ax+b和y=bax的图象只 可能是( )
A 解析：
∵y=bax=(ba)x，∴这是以ba为底的指数函数．仔细观察题 目中的直线方程可知：在B中a>0，b>1，∴ba>1； C中a<0，b>1，∴0<ba<1；D中a<0,0<b<1，∴ba>1. 故选项B、C、D均与指数函数y=(ba)x的图象不符合．
解：先作出函数y=x2-4x+3的图象，然后将其x轴下方 的图象沿x轴翻折到x轴上方，得到y=|x2-4x+3|的图象 如图： (1)递增区间为[1,2]，[3，+∞)， 递减区间为(-∞，1)，(2,3)． (2)原方程变形为|x2-4x+3|=x+a，于是，设y=x+a， 在同一坐标系下再作出y=x+a的图象．如图，则当 直线y=x+a过点(1,0)时a=-1； 当直线y=x+a与抛物线y=-x2+4x-3相切时，由
如：h>0，y=f(x)±h的图象可由y=f(x)的图
象__向上(下)_平__移_ h个_单__位___而得到．
3. 对称变换 (1)y=f(-x)与y=f(x)的图象关于__y_轴___对称； (2)y=-f(x)与y=f(x)的图象关于_x_轴____对称； (3)y=-f(-x)与y=f(x)的图象关于_原__点___对称； (4)y=|f(x)|的图象：可将y=f(x)的图象______ 在x轴下方的部分关于x轴翻转180°， _其__余__部__分__不__变_______________； (5)y=f(|x|)的图象：可先作出y=f(x)，当x≥0 时的图象，再利用偶__函__数__的__图__象__关__于__y，轴对称 作出y=f(x)(x≤0)的图象．
经典例题
题型一 作图 【例1】 作出下列函数的图象． (1)y= x 2 x 1 (2)y=|log2x-1|.
解向：右(平1)移一y个先单1作位x3出，1 再向的上图平y象移，3x一将个其单图位象， 即得 y 的x 图2 象，如图①.
x 1
(2)先作出y=log2x的图象，再将其图象向下平移 一个单位，保留x轴上方的部分，将x轴下方的图 象翻折到x轴上方，即得y=|log2x-1|的图象，如图②.
变式2-1
函数y=f(x)的图象如图所示，则函数y=log1 f(x)的图象
大致是( )
2CΒιβλιοθήκη 解析：由图可知f(x)≥1，∴y=log f(x1 )≤log 1=01，
2
2
∴y≤0.故选C.
题型三 用图
【例3】已知函数f(x)=|x2－4x+3|. (1)求函数f(x)的单调区间，并指出其增减性； (2)若关于x的方程f(x)－a=x至少有三个不相等的 实数根，求实数a的取值范围．
第九节 函数的图像
基础梳理
1.横点法作图 基本步骤是_列__表_ 、 _描__点__ 、 __连_线__ ，首先，①确 定函数的_定_义__域；②化简函数的_解__析__式；③讨论函数 的性质（奇偶性、单调性、对称性、周期性）；其 次列表（尤其注意特殊点、零点，最大值、最小 值），描点、连线。
2. 平移变换 (1)y=f(x)的图象_向__左__平__移__a(a>0)个单__位___得到函数