2010A试卷AMC-A:澳大利亚数学3-4年级中文历年真题
2013E试卷(澳大利亚数学竞赛AMC-E:11-12年级中英文历年真题)

THURSDAY 1 AUGUST 2013SENIOR DIVISIONAUSTRALIAN S CHOOL YEARS 11 and 12TIME ALLOWED: 75 MINUTES©AMT P ublishing 2013 AMTT liMiTed Acn 083 950 341A ustrAliAn M AtheMAtics c oMpetitionsponsored by the c oMMonweAlth b AnkAn AcTiviTy of The AusTrAliAn MATheMATics TrusTNAMEYEAR TEACHERA u s T r A l i A n M A T h e M A T i c s T r u s T姓 名: 年 级: 监考老师:意事项一般规定1.未获监考老师许可之前不可翻开此测验题本。
2.各种通讯器材一律不得携入考场,不准使用电子计算器、计算尺、对数表、数学公式等计算器具。
作答时可使用直尺与圆规,以及两面全空白的草稿纸。
3.题目所提供之图形只是示意图,不一定精准。
4.最前25题为选择题,每题有五个选项。
最后题要求填入的答案为000至999的正整数。
题目一般而言是依照越来越难的顺序安排,对于错误的答案不会倒扣分数。
5.本活动是数学竞赛而不同于学校测验,别期望每道题目都会作。
考生只与同地区同年级的其它考生评比,因此不同年级的考生作答相同的试卷将不作评比。
6.请依照监考老师指示,谨慎地在答案卡上填写您的基本数据。
若因填写错误或不详所造成之后果由学生自行负责。
7.进入试场后,须等待监考老师宣布开始作答后,才可以打开题本进行答题。
作答须知1.限用B 或2B 铅笔填写答案。
2.请用B 或2B 铅笔在答案卡上(不是在题本上)将您认为正确选项的圆圈涂满。
3.您的答案卡将由计算机阅卷,为避免计算机误判,请不要在答案卡上其它任何地方涂划任何记号。
填写答案卡时,若需要修改,可使用软性橡皮小心擦拭,并确定答案卡上无残留痕迹。
AMC10的真题答案及中文翻译

AMC10的真题答案及中文翻译AMC10的真题及中文翻译1、One ticket to a show costs $20 at full price. Susan buys 4 tickets using a coupon that gives her a 25% discount. Pam buys 5 tickets using a coupon that gives her a 30% discount. How many more dollars does Pam pay than Susan?(A) 2 (B) 5 (C) 10 (D) 15 (E) 20中文:一张展览票全价为20美元。
Susan用优惠券买4张票打七五折。
Pam用优惠券买5张票打七折。
Pam比Susan多花了多少美元?2、An aquarium has a rectangular base that measures 100cm by 40cm and has a height of 50cm. It is filled with water to a height of 40cm. A brick with a rectangular base that measures 40cm by 20cm and a height of 10cm is placed in the aquarium. By how many centimeters does that water rise?(A) 0.5 (B) 1 (C) 1.5 (D) 2 (E)2.5中文:一个养鱼缸有100cm×40cm的底,高为50cm。
它装满水到40cm的高度。
把一个底为40cm×20cm,高为10cm的砖块放在这个养鱼缸里。
鱼缸里的水上升了多少厘米?3、The larger of two consecutive odd integers is three times the smaller. What is their sum?(A) 4 (B) 8 (C) 12 (D) 16 (E) 20中文:2个连续的奇整数中较大的数是较小的数的3倍。
AMC Senior 2008(澳大利亚数学竞赛AMC-E:11-12年级中英文历年真题)

A u s t r A l i A n M At h e M At i c s c o M p e t i t i o na n a c t i v it y o f t h e a u s t r a l i a n m a t h e m a t i c s t r u s tT H U R S D AY 31 J U LY 2008SENIOR DIVISION COMPETITION PAPERINSTRUCTIO NS AND INFO RMATIO NGENERAL1. Do not open the booklet until told to do so by your teacher.2. NO calculators, slide rules, log tables, maths stencils, mobile phones or other calculating aids arepermitted. Scribbling paper, graph paper, ruler and compasses are permitted, but are not essential. 3. Diagrams are NOT drawn to scale. They are intended only as aids.4. There are 25 multiple-choice questions, each with 5 possible answers given and 5 questions thatrequire a whole number between 0 and 999. The questions generally get harder as you work through the paper. There is no penalty for an incorrect response.5. This is a competition not a test; do not expect to answer all questions. You are only competingagainst your own year in your own State or Region so different years doing the same paper are not compared.6. Read the instructions on the Answer Sheet carefully. Ensure your name, school name and schoolyear are filled in. It is your responsibility that the Answer Sheet is correctly coded. 7. When your teacher gives the signal, begin working on the problems.THE ANSWER SHEET 1. Use only lead pencil.2. Record your answers on the reverse of the Answer Sheet (not on the question paper) by FULLYcolouring the circle matching your answer.3. Your Answer Sheet will be read by a machine. The machine will see all markings even if they arein the wrong places, so please be careful not to doodle or write anything extra on the Answer Sheet. If you want to change an answer or remove any marks, use a plastic eraser and be sure to remove all marks and smudges.INTEGRITY OF THE COMPETITIONThe AMC reserves the right to re-examine students before deciding whether to grant official status to their score.A U S T R A L I A N S C H O O L Y E A R S 11 A N D 12T I M E A L L O W E D : 75 M I N U T E SSenior DivisionQuestions 1to 10,3marks each1.The value of 8002−2008is (A)200(B)8(C)6006(D)1060(E)59942.The difference between 120and 210is (A)0(B)110(C)35(D)310(E)3203.In the diagram,x equals................................................................................................................................................................................ (x)◦100◦110◦80◦(A)100(B)110(C)120(D)130(E)1404.The value of 200×8200÷8is(A)1(B)8(C)16(D)64(E)2005.The smallest value that x 2−4x +3can have is (A)−1(B)−3(C)1(D)3(E)26.$3is shared between two people.One gets 50cents more than the other.The ratio of the larger share to the smaller share is (A)6:1(B)7:5(C)4:3(D)5:3(E)7:4S 27.When 10002008is written as a numeral,the number of digits written is (A)2009(B)6024(C)6025(D)8032(E)20128.A semicircle is drawn on one side of an equilateral triangle.The ratio of the area of the semicircle to the area of the triangle is(A)1:1(B)π:2√3(C)π:√3(D)√3:π(E)3:π................................................................................................................................................................................................................................................................................................................................................................................................................................................................9.Given that cos x =0.5and 0◦<x <90◦,which of the following has the greatestvalue?(A)cos 2x(B)cos x(C)0.75(D)sin x(E)tan x10.A fishtank with base 100cm by 200cm and depth 100cm contains water to a depthof 50cm.A solid metal rectangular prism with dimensions 80cm by 100cm by 60cm is then submerged in the tank with an 80cm by 100cm face on the bottom..................................................................................................................6.......................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................100100200501006080The depth of water,in centimetres,above the prism is then (A)12(B)14(C)16(D)18(E)20Questions 11to 20,4marks each11.Which of the following numbers is the largest?(A)2500(B)3400(C)4300(D)5200(E)610012.A normal die is thrown 100times.The sum of the numbers obtained will mostlikely be(A)200(B)250(C)300(D)350(E)400S 313.What is the smallest whole number which gives a square number when multipliedby 2008?(A)2(B)4(C)251(D)502(E)200814.A cross is made up of five squares,each with side length 1unit.Two cuts aremade,the first from X to Y and the second from Z to T ,so that ZT X is a right angle.The three pieces are then arranged to form a rectangle...................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................ZYX T IIIIII.................................................................... (II)IIIIWhat is the ratio of the length to the width of the rectangle?(A)3:1(B)√10:1(C)2:1(D)2√3:1(E)5:215.A function is said to be a toggle function on (p,q,r )if f (p )=q ,f (q )=r andf (r )=p .The function f (x )=ax 2+bx +c is a toggle function on (1,2,3).What is the value of c ?(A)−2(B)0(C)3(D)9(E)1416.Two conical rollers with perpendicu-lar axes touch on a line that is 30◦to the axis of the smaller roller and 60◦to the axis of the larger roller.If the larger roller makes 1revolution per sec-ond and there is no slipping,how many revolutions per second does the smaller roller make?(A)12(B)1(C)√2(D)√3(E)2...................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................60◦30◦S 417.Consider the set X ={1,2,3,4,5,6}.How many subsets of X ,with at least one element,do not contain two consecutive integers?(A)16(B)18(C)20(D)21(E)2418.Farmer Taylor of Burra has two tanks.Water from the roof of his farmhouse iscollected in a 100kL tank and water from the roof of his barn is collected in a 25kL tank.The collecting area of his farmhouse roof is 200square metres while that of his barn is 80square metres.Currently,there are 35kL in the farmhouse tank and 13kL in the barn tank.Rain is forecast and he wants to collect as much water as possible.He should:(A)empty the barn tank into the farmhouse tank (B)fill the barn tank from the farmhouse tank(C)pump 10kL from the farmhouse tank into the barn tank (D)pump 10kL from the barn tank into the farmhouse tank (E)do nothing19.A sequence {u 1,u 2,...,u n }of real numbers is defined byu 1=√2,u 2=π,u n =u n −1−u n −2forn ≥3.What is u 2008?(A)−√2(B)2008(√2−2008π)(C)1003√2−1004π(D)π(E)√220.In the diagram,RU is equal in lengthto ST .What is the ratio of the area of QRU to the area of QST ?(A)√3:1(B)2:1(C)√6:1(D)√3:2(E)√6:2......................................................................................................................................................................................................................... (45)◦30◦UT Q RSQuestions 21to 25,5marks each21.P ,Q ,R ,S and T are consecutive vertices of a regular polygon.When extended,the lines P Q and T S meet at U with QUS =160◦.How many sides has the polygon?(A)36(B)42(C)48(D)52(E)54S522.How many numbers from1,2,3,4,...,2008have a cubic number other than1asa factor?(A)346(B)336(C)347(D)251(E)39323.The numbers828and313are3-digit palindromes where828−313=515,whichis also a palindrome.How many pairs(a,b)of3-digit palindromes are there witha>b and with a−b also a3-digit palindrome?(A)1972(B)1980(C)1988(D)1996(E)200824.The centres of all faces of a cube are joined to form an octahedron.The centresof all faces of this octahedron are now joined to form a smaller cube.What is the ratio of an edge of the smaller cube to an edge of the original cube?(A)1:√2(B)1:√3(C)1:2(D)1:3(E)1:425.In thefigure,all line segments are par-allel to one of the sides of the equi-lateral triangle P QR which has sidelength1unit.How long should P Xbe to maximise the smallest of the tenareas defined?(A)13(B)4−√214(C)14(D)15(E)1√10.......................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................PQ RXFor questions26to30,shade the answer as an integer from0to999inthe space provided on the answer sheet.Question26is6marks,question27is7marks,question28is8marks, question29is9marks and question30is10marks.26.All possible straight lines joining the vertices of a cube with mid-points of its edgesare drawn.At how many points inside the cube do two or more of these lines meet?S 627.Let us call a sum of integers cool if the first and last terms are 1and each termdiffers from its neighbours by at most 1.For example,the sum 1+2+3+4+3+2+3+3+3+2+3+3+2+1is cool.How many terms does it take to write 2008as a cool sum if we use no more terms than necessary?28.The positive integers x and y satisfy3x 2−8y 2+3x 2y 2=2008.What is the value of xy ?29.A point O is inside an equilateral triangleP QR and the perpendiculars OL ,OM and ON are drawn to the sides P Q ,QR and RP respectively.The ratios of lengths of the perpendiculars OL :OM :ON is 1:2:3.If area of LONP area of P QR =a b,where a and b are integers with no common factors,what is the value of a +b ?...............................................................................................................................................................................................................................................................................................................................................................................................................................................RPQLMNO.......................................................................................................................................................................................................................................................................................30.What is the smallest value that49+a 2−7√2a + a 2+b 2−√2ab +√50+b 2−10bcan have for positive real numbers a and b ?***Senior 2008 Answers Question Answer 1E2E3D4D5A6B7C8B9E10B11B12D13D14C15A16D17C18D19A20D21E22B23B24D25C26142789282829473013。
澳大利亚数学竞赛题5-6年级10年题

小学高年级(5—6)(2007年)1.下列哪一个数是由1个一百、4个十、3个一所凑成的?(A)413(B)143(C)341(D)1043(E)1342.在下列等式中,□内的数字是什么?2□6+497=703(A)0(B)1(C)3(D)7(E)93.上星期二,某个班级上数学、音乐、英语及美术课的上课时数比例,如下图的饼图所示:下列哪一个叙述为真?(A)上音乐课的时间比上美术课的时间长。
(B)上音乐课的时间比上英语课的时间长。
(C)上音乐课和英语课的时间超过全部上课时间的一半。
(D)上数学课和美术课的时间超过全部上课时间的一半。
(E)上数学课的时间与上美术课的时间一样长。
4.算式14-8÷2+2×3之值等于(A)16(B)15(C)36(D)9(E)45.下列哪一个数最大?(A)百分之三十(B)百分之十三(C)十分之三(D)百分之三十一(E)百分之三6.有一个角锥共有12条棱边。
请问它的底面是什么形状?(A)三角形(B)四边形(C)五边形(D)六边形(E)八边形7.小安的布袋内装有编号为1~20的二十颗球。
她随意从袋子中抓出一个球。
以下哪一种事件的发生有较大的可能性?(A)她抓出的球的编号是1号。
(B)她抓出的球的编号是奇数。
(C)她抓出的球的编号中有数字2。
(D)她抓出的球的编号是9或10号。
(E)她抓出的球的编号是20号。
8.凯伦驾车由市区开往湖边,她经过如下右图的路标:大约过了一个小时,她看到另一个路标显示再过5km即可抵达湖边。
请问从市区算起她已经行驶了多少路程?(A)50km(B)80km(C)125km(D)30km(E)65km9.某一班学生中有60%是女生。
这一班不可能是下列哪一种组合?(A)6位男孩9位女孩。
(B)10位男孩15位女孩(C)15位男孩10位女孩。
(D)12位男孩18位女孩。
(E)12位女孩8位男孩。
10.现在时刻是3:00pm。
在一个24小时计时的时钟上,100小时后将显示的时刻是什么?(A)7:00am (B)3:00am (C)7:00pm (D)3:00pm (E)11:00pm11.下列哪个图的阴影部分占全部面积的八分之三?12.小珍有一片巧克力,它划分成许多小正方形块,它的长有6个小正方形块,宽有8个小正方形块(如下图)。
澳大利亚数学竞赛题3-4年级10年题

小学中年级(3—4)(2007年)1.下列哪一个数最大?(A)231(B)201(C)321(D)123(E)3022.下列哪一个数是由1个一百、4个十、3个一所凑成的?(A)413(B)143(C)341(D)1043(E)1343.在以下的方格表中,不同的位置用不同的图案标记。
例如位于B4。
请问位于哪个小方格内?(A)A3(B)C3(C)D4(D)B4(E)C24.小欧现在年龄为2岁,她的哥哥小马比她大5岁。
请问小马现在几岁?(A)2(B)3(C)5(D)7(E)105.我购买了一件$25的衬衫和一件$12的T恤衫。
若我支付$50,请问应该找回多少钱?(A)$13(B)$23(C)$25(D)$33(E)$376.一个正立方体有多少条棱边?(A)4(B)6(C)8(D)10(E)127.若小安正好排在一列队伍的正中央,请问下列哪个数是这列队伍可能的总共人数?(A)4(B)6(C)8(D)9(E)128.五只猫跑进一间刚刷过油漆的屋子。
有四只猫的两只前腿沾上了油漆,有一只猫的两只后腿沾上了油漆。
请问这些猫共有多少只腿没有沾上油漆?(A)5(B)6(C)8(D)10(E)129.小杰在4:35pm电视卡通节目开演前必须把家庭作业写完。
他写家庭作业需时17分钟,请问他最迟在什么时刻要开始写作业才能及时观看卡通?(A)4:52pm(B)4:20pm(C)4:18pm(D)4:28pm(E)4:08pm10.上星期二,某个班级上数学、音乐、英语及美术课的上课时数比例如下图的饼图所示:下列哪一个叙述为真?(A)上音乐课的时间比上美术课的时间长。
(B)上音乐课的时间比上英语课的时间长。
(C)上音乐课和英语课的时间超过全部上课时间的一半。
(D)上数学课和美术课的时间超过全部上课时间的一半。
(E)上数学课的时间与上美术课的时间一样长。
11.某个家庭中,每位小孩都至少有一位兄弟且至少有二位姊妹。
请问这个家庭中至少有几位小孩?(A)1(B)2(C)3(D)4(E)512.在章鱼大战游戏中,喷水一次可得5分、钩住一次可得3分、缠住一次可得2分。
2010数学真题卷及答案
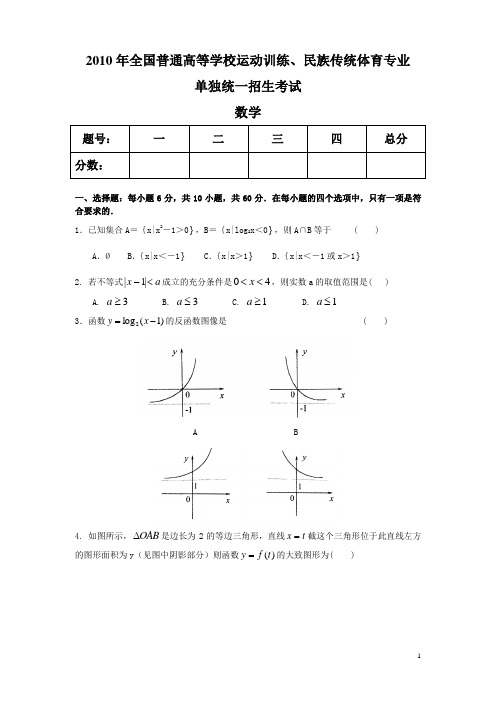
2010年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试数学一、选择题:每小题6分,共10小题,共60分.在每小题的四个选项中,只有一项是符合要求的.1.已知集合A ={x|x 2―1>0},B ={x|log 2x <0},则A ∩B 等于 ( )A .ØB .{x|x <-1}C .{x|x >1}D .{x|x <-1或x >1}2. 若不等式||x a -<1成立的充分条件是04<<x ,则实数a 的取值范围是( ) A. a ≥3B. a ≤3C. a ≥1D. a ≤13.函数)1(log 2-=x y 的反函数图像是 ( )A B4. 如图所示,∆OAB 是边长为2的等边三角形,直线x t =截这个三角形位于此直线左方的图形面积为y (见图中阴影部分)则函数y f t =()的大致图形为( )5.已知a 、b 是非零向量且满足(a -2b )⊥a ,(b -2a )⊥b ,则a 与b 的夹角是( )A .6π B .3π C .32π D .65π6椭圆22143x y +=的右焦点到直线y x =的距离是 ( )A.127. 过圆锥曲线C 的一个焦点F 的直线l 交曲线C 于A 、B 两点,且以AB 为直径的圆与F 相应的准线相交,则曲线C 为A. 双曲线B. 抛物线C. 椭圆D. 以上都有可能 8.若αααααcos sin cos 3sin ,2tan +-=则的值是( )A .31-B .-35C .31 D .35 9.直线052)3(057)3()1(2=-+-=-+-++y x m m y m x m 与直线垂直的充要条件是( )A .2-=mB .3=mC .31=-=m m 或D .23-==m m 或10.已知1(2)2x f x x ++=+,则1(2)f x -+= ( ) A.12x x -+ B.11x -+ C.211x x +-- D.21x x +-+二、填空题:每小题5分,共8小题,共计40分.将答案填在题中的横线上。
实用文档之AMC10美国数学竞赛A卷附中文翻译和答案
实用文档之"2011AMC10美国数学竞赛A卷"1. A cell phone plan costs $20 each month, plus 5¢per text message sent, plus 10¢ for each minute used over 30 hours. In January Michelle sent 100 text messages and talked for 30.5 hours. How much did she have to pay?(A) $24.00 (B) $24.50 (C) $25.50 (D) $28.00 (E) $30.002. A small bottle of shampoo can hold 35 milliliters of shampoo, Whereas a large bottle can hold 500 milliliters of shampoo. Jasmine wants to buy the minimum number of small bottles necessary to completely fill a large bottle. How many bottles must she buy?(A) 11 (B) 12 (C) 13 (D) 14 (E) 153. Suppose [a b] denotes the average of a and b, and {a b c} denotes the average of a, b, and c. What is {{1 1 0} [0 1] 0}?(A) 29(B)518(C)13(D) 718(E) 234. Let X and Y be the following sums of arithmetic sequences:X= 10 + 12 + 14 + …+ 100.Y= 12 + 14 + 16 + …+ 102.What is the value of Y X -?(A) 92(B) 98 (C) 100 (D) 102 (E) 1125. At an elementary school, the students in third grade, fourth grade, and fifth grade run an average of 12, 15, and 10 minutes per day, respectively. There are twice as many third graders as fourth graders, and twice as many fourth graders as fifth graders. What is the average number of minutes run per day by these students?(A) 12 (B) 373 (C) 887 (D) 13 (E) 146. Set A has 20 elements, and set B has 15 elements. What is the smallest possible number of elements in A ∪B, the union ofA and B?(A) 5(B) 15 (C) 20 (D) 35 (E) 3007. Which of the following equations does NOT have a solution?(A) 2(7)0x += (B) -350x += (C) 20=(D) 80x-==(E) -3408. Last summer 30% of the birds living on Town Lake were geese, 25% were swans, 10% were herons, and 35% were ducks. What percent of the birds that were not swans were geese?(A) 20 (B) 30 (C) 40 (D) 50 (E) 609. A rectangular region is bounded by the graphs of the equations y=a, y=-b, x=-c, and x=d, where a, b, c, and d are all positive numbers. Which of the following represents the area of this region?(A) ac + ad + bc + bd (B) ac – ad + bc – bd (C) ac + ad – bc – bd(D) –ac –ad + bc + bd (E) ac – ad – bc + bd10. A majority of the 20 students in Ms. Deameanor’s class bought pencils at the school bookstore. Each of these students bought the same number of pencils, and this number was greater than 1. The cost of a pencil in cents was greater than thenumber of pencils each student bought, and the total cost of all the pencils was $17.71. What was the cost of a pencil in cents?(A) 7(B) 11 (C) 17 (D) 23 (E) 7711. Square EFGH has one vertex on each side of square ABCD. Point E is on AB with AE=7·EB. What is the ratio of the area of EFGH to the area of ABCD?(A)4964 (B) 2532 (C) 78 (D) 8 (E)412. The players on a basketball team made some three-point shots, some two-point shots, some one-point free throws. They scored as many points with two-point shots as with three-point shots. Their number of successful free throws was one more than their number of successful two-point shots. The team’s total score was 61 points. How many free throws did they make?(A) 13(B) 14 (C) 15 (D) 16 (E) 1713. How many even integers are there between 200 and 700 whose digits are all different and come from the set {1, 2, 5, 7, 8, 9}?(A) 12 (B)20 (C)72 (D) 120 (E) 20014. A pair of standard 6-sided fair dice is rolled once. The sum of the numbers rolled determines the diameter of a circle. What is the probability that the numerical value of the area of the circle is less than the numerical value of the circle’s circumference?(A) 136(B)112(C)16(D) 14(E) 51815. Roy bought a new battery-gasoline hybrid car. On a trip the car ran exclusively on its battery for the first 40 miles, then ran exclusively on gasoline for the rest of the trip, using gasoline at a rate of 0.02 gallons per mile. On the whole trip he averaged 55 miles per gallon. How long was the trip in miles?(A) 140 (B) 240 (C) 440 (D) 640 (E) 84016. Which of the following in equal to(A)(B) (C) 2 (D) (E)617. In the eight-term sequence A, B, C, D, E, F, G , H, the value of C is 5 and the sum of any three consecutive terms is 30. What is A + H?(A) 17(B) 18 (C) 25 (D) 26 (E) 4318. Circles A, B, and C each have radius 1. Circles A and B share one point of tangency. Circle C has a point of tangency with the midpoint of AB. What is the area inside Circle C but outside Circle A and Circle B? (A) 32π- (B) 2π (C) 2 (D) 34π (E) 12π+19. In 1991 the population of a town was a perfect square. Ten years later, after an increase of 150 people, the population was 9 more than a perfect square. Now, in 2011, with an increase of another 150 people, the population is once again a perfectsquare. Which of the following is closest to the percent growth of the town’s population during this twenty-year period? (A) 42 (B) 47 (C) 52 (D) 57 (E) 6220. Two points on the circumference of a circle of radius r are selected independently and at random. From each point a chord of length r is drawn in a clockwise direction. What is the probability that the two chords intersect?(A) 16(B) 15(C) 14(D) 13(E) 1221. Two counterfeit coins of equal weight are mixed with 8 identical genuine coins. The weight of each of the counterfeit coins is different from the weight of each of the genuine coins.A pair of coins is selected at random without replacement from the 10 coins. A second pair is selected at random without replacement from the remaining 8 coins. The combined weight of the first pair is equal to the combined weight of the second pair. What is the probability that all 4 selected coins are genuine?(A) 711(B) 913(C) 1115(D) 1519(E) 151622. Each vertex of convex pentagon ABCDE is to be assigned a color. There are 6 colors to choose from, and the ends of each diagonal must have different colors. How many different colorings are possible?(A) 2500 (B) 2880 (C) 3120 (D) 3250 (E) 375023. Seven students count from 1 to 1000 as follows:·Alice says all the numbers, except she skips the middle number in each consecutive group of three numbers. That is Alice says 1, 3, 4, 6, 7, 9, …, 997, 999, 1000.·Barbara says all of the numbers that Alice doesn’t say, except she also skips the middle number in each consecutive grope of three numbers.·Candice says all of the numbers that neither Alice nor Barbara says, except she also skips the middle number in each consecutive group of three numbers.·Debbie, Eliza, and Fatima say all of the numbers that none of the students with the first names beginning before theirs inthe alphabet say, except each also skips the middle number in each of her consecutive groups of three numbers.·Finally, George says the only number that no one else says. What number does George say?(A) 37(B) 242 (C) 365 (D) 728 (E) 99824. Two distinct regular tetrahedra have all their vertices among the vertices of the same unit cube. What is the volume of the region formed by the intersection of the tetrahedra?(A)112 (B) 12 (C) (D) 16 (E)25. Let R be a square region and 4n an integer. A point X in the interior of R is called n-ray partitional if there are n rays emanating from X that divide R into N triangles of equal area. How many points are 100-ray partitional but not 60-ray partitional?(A) 1500(B) 1560 (C) 2320 (D) 2480 (E)25002011AMC10美国数学竞赛A卷1. 某通讯公司手机每个月基本费为20美元, 每传送一则简讯收 5美分(一美元=100 美分)。
澳大利亚数学竞赛小学中年级(3--4年级)(2013年)
澳大利亚数学竞赛小学中年级(3—4)(2013年)1.请问公元 2013 年之后经过十年是公元多少年?()(A)2003 (B)2013 (C)2014 (D)2023 (E)21132.请问一个正立方体共有多少条边?()(A)4 (B)6 (C)8 (D)9 (E)123.小兰学校的操场跑道一圈的长度是 400 m,而小兰一共跑了三圈。
请问她一共跑了多长的距离?()(A)300 m (B)600 m (C)800 m (D)1200 m (E)3000 m4.请问下图中矩形的几分之几被涂上阴影?()(A)五分之一(B)五分之二(C)三分之二(D)三分之一(E)五分之三5.请问 9 和 3 之差的三倍等于多少?()(A)6 (B)9 (C)18 (D)36 (E)816.小珍所戴的帽子上有「COTTON CLUB」的字样。
当小珍向镜子里看去,请问她所看到这顶帽子上的字样是什么?()7.直线棋盘上的格子从左至右的编号为 1, 2, 3, …。
小莎的棋子向右移动 6 格,向左移动 4 格,然后向右移动 3 格。
假如棋子停留在编号为 7 的方格,请问开始时小莎的棋子所在格子上的编号是什么?()(A)1 (B)2 (C)3 (D)4 (E)58.小伊位于一个边长为 10 m 正方形的迷宫之中心。
他知道只要沿着如下图所示螺旋状的路径便可走出这个迷宫。
已知这个迷宫共有A、B、C、D、E 五个出口,请问小伊将会从哪一个出口走出这个迷宫?(A)A (B)B (C)C (D)D (E)E9.用下面 3 张数码卡片拼成三位数,请问在所能拼出的数中,最大的数与最小的数相差多少?()(A)198 (B)200 (C)202 (D)298 (E)30210.小柏在心中想着一个数,他将这个数乘以 2 之后再加 2,所得到的值是 14。
请问他心中原来想的这个数是什么?()(A)6 (B)7 (C)8 (D)12 (E)3011.小艾有两枚 50 元硬币、三枚 20 元硬币与八枚 5 元硬币,小德有四枚 20 元硬币与六枚 10 元硬币。
2009A试卷AMC-A:澳大利亚数学3-4年级中文历年真题
小学中年级卷(3—4年级)考试时间:60分钟──────────────────────────────────小学中年级(3-4年级)卷──────────────────────────────────1-10题,每题3分1.算式1000+200+4等于(A)10204 (B)1204 (C)1000204 (D)10002004 (E)124──────────────────────────────────2.对于以下所显示的数,若将千位数加倍且将十位数减半,请问所得的新数是什么?4224(A)2224 (B)8214 (C)4414 (D)8244 (E)2214──────────────────────────────────3.一个常用的骰子如图所示。
请问没有显露出来的各面上点数的总和是多少?(A)7 (B)11 (C)13 (D)14 (E)15──────────────────────────────────4.请问如下哪一个数加上11后所得到的和为28?(A)39 (B)17 (C)27 (D)7 (E)19──────────────────────────────────5.请问下面哪一项最接近于1000秒?(A)1小时(B)1天(C)45分钟(D)30分钟(E)15分钟──────────────────────────────────6.下图是一个正方体的展开图。
12 3 45 6在这个正方体上,请问与数字6所在的面相对的面上的数字是什么?(A)1 (B)2 (C)3 (D)4 (E)5──────────────────────────────────────────────── MP 2 ───────────── 7. 请问下面哪一个故事情节符合这个算式?14-7+9=16(A )甲有14根棒棒糖,他吃掉其中9根后他的姐姐又给他9根,最后他还有16根棒棒糖。
2013A试卷AMC-A:澳大利亚数学3-4年级中文历年真题
THURSDAY 1 AUGUST 2013MIDDLE PRIMARY DIVISIONAUSTRALIAN S CHOOL YEARS 3 & 4TIME ALLOWED: 60 MINUTESINSTRUCTIONS AND INFORMATION GENERAL 1. Do not open the booklet until told to do so by your teacher. 2. You may use any teaching aids normally available in your classroom, such as MAB blocks, counters, currency, calculators, play money etc. You are allowed to work on scrap paper and teachers may explain the meaning of words in the paper. 3. Diagrams are NOT drawn to scale. They are intended only as aids. 4. There are 25 multiple-choice questions, each with 5 possible answers given and 5 questions that require a whole number answer between 0 and 999. The questions generally get harder as you work through the paper. There is no penalty for an incorrect response. 5. This is a competition not a test; do not expect to answer all questions. You are only competing against your own year in your own State or Region so different years doing the same paper are not compared. 6. Read the instructions on the answer sheet carefully. Ensure your name, school name and school year are entered. It is your responsibility to correctly code your answer sheet. 7. When your teacher gives the signal, begin working on the problems. THE ANSWER SHEET 1. Use only lead pencil.2. Record your answers on the reverse of the answer sheet (not on the question paper) by FULLY colouring the circle matching your answer.3. Your answer sheet will be scanned. The optical scanner will attempt to read all markings even if they are in the wrong places, so please be careful not to doodle or write anything extra on the answer sheet. If you want to change an answer or remove any marks, use a plastic eraser and be sure to remove all marks and smudges.INTEGRITY OF THE COMPETITIONThe AMT reserves the right to re-examine students before deciding whether to grant official status to their score.©AMT P ublishing 2013 AMTT liMiTed Acn 083 950 341A ustrAliAn M AtheMAtics c oMpetitionsponsored by the c oMMonweAlth b AnkAn AcTiviTy of The AusTrAliAn MATheMATics TrusT姓 名: 年 级:监考老师:意事项 一般规定1.未获监考老师许可之前不可翻开此测验题本。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
SATURDAY 7 AUGUST 2010小学中年级卷(3—4年级)考试时间:60分钟注意事项一般规定1.未获监考老师许可之前不可翻开此测验题本。
2.作答时可使用直尺与圆规,以及两面全空白的草稿纸。
对文字不了解时可举手向监考老师发问。
3.题目所提供之图形只是示意图,不一定精准不一定精准。
不一定精准4.最前25题为选择题,每题有五个选项。
最后5题要求填入的答案为0至999的正整数。
题目一般而言是依照越来越难的顺序安排,对于错误的答案不会倒扣分数。
5.本活动是数学竞赛而不同于学校测验,别期望每道题目都会作。
考生只与同地区同年级的其它考生评比,因此不同年级的考生作答相同的试卷将不作评比。
6.请依照监考老师指示,谨慎地在答案卡上填写您的基本数据。
若因填写错误或不详所造成之后果由学生自行负责。
7.进入试场后,须等待监考老师宣布开始作答后,才可以打开题本进行答题。
作答须知1.限用B或2B铅笔填写答案。
2.请用B或2B铅笔在答案卡上(不是在题本上)将您认为正确选项的圆圈涂满。
3.您的答案卡将由计算机阅卷,为避免计算机误判,请不要在答案卡上其它任何地方涂划任何记号。
填写答案卡时,若需要修改,可使用软性橡皮小心擦拭,并确定答案卡上无残留痕迹。
特别约定为确保竞赛之公平性及认证成绩优异学生,AMC主办单位保留要求考生重测之权利。
────────────────────────────────────────────────小学中年级(3-4年级)卷──────────────────────────────────────────────── 1-10题,每题3分1. 请问哪一个数等于1+10+100+1000?(A )1111 (B )11111 (C )1110 (D )1010 (E )10111 ──────────────────────────────────────────────── 2. 请问哪一个数正好介于600和700的正中间?(A )550 (B )645 (C )650 (D )655 (E )700 ──────────────────────────────────────────────── 3. 从有*记号的小方格开始,向上移动两格再向右移动一格。
请问最后停留的小方格上的记号是什么?(A )♡ (B )∞ (C )⊗ (D )△ (E )□──────────────────────────────────────────────── 4. 针对100个人调查他们最喜欢去的景点。
他们最喜欢去的地方为:请问投票给A 地的人比投票给E 地的人多几人?(A )40 (B )20 (C )10 (D )5 (E )7 ──────────────────────────────────────────────── 5. 一个储水桶内储有56公升的水,若再注入28公升的水,请问储水桶内现有多少水?(A )84公升 (B )56公升 (C )28公升 (D )76公升 (E )78公升────────────────────────────────────────────────♡ ∞ ⊗ ◊∞ △ □ ∇∇ * ⊗ ◊ ◊ ♡ △ ♡ △ ∞ ◊ 人数 3025 20 15 10 5 0A 地B 地C 地D 地E 地6. 请问下列哪一个数代表壹仟贰拾柒?(A )100027 (B )10027 (C )1027 (D )127 (E )27 ──────────────────────────────────────────────── 7.(A )饲养的小鸟比金鱼多。
(B )饲养的小狗比小猫多。
(C )全班共饲养30只宠物。
(D )最不受欢迎的宠物是小鸟。
(E )最受欢迎的宠物是小猫。
8. 连接正方形各边的中点,如图所示。
请问涂上阴影部分的面积占原大正方形面积的几分之几?(A )14 (B )16 (C )23(D )13 (E )15──────────────────────────────────────────────── 9. 支付5元购买每张0.55元的邮票三张,请问应找回多少元?(A )1.65元 (B )2.35元 (C )2.45元 (D )3.35元 (E )3.45元 ──────────────────────────────────────────────── 10. 小莲从外观如图所示的一家宠物店内,由它的窗户向外望。
请问她看到窗上的英文字母是什么式样?(A )(B )(C )(D )(E )────────────────────────────────────────────────PET SHOP11-20题,每题4分11. 我从九点三刻开始阅读到十一点半。
请问我读了多久时间?(A )45分钟 (B )1.5小时 (C )1小时45分 (D )2小时15分 (E )2小时45分──────────────────────────────────────────────── 12. 将八块积木依照下图所示方式黏在一起。
请问这些积木共有多少个面黏贴在一起?(A )7 (B )8 (C )10 (D )12 (E )18 ──────────────────────────────────────────────── 13. 王太太打算将16枝花插入两个花瓶内,使得一个花瓶内所插的花是另一个的三倍。
请问插较多花的花瓶内有多少枝花?(A )8 (B )10 (C )12 (D )14 (E )16 ──────────────────────────────────────────────── 14. 下表是某班级每位学生家中拥有的汽车数量之纪录表。
下列哪一项的叙述正确?(A )有两个家庭每家拥有两辆车。
(B )有六个家庭每家至少拥有两辆车。
(C )有四个家庭每家恰好拥有一辆车。
(D )所有的家庭每家都至少有一辆车。
(E )有三个家庭每家恰有两辆车。
────────────────────────────────────────────────家庭数 汽车数量10 86 4 2 0 0 1 2 315.下表是小林在学校平常日的作息时刻表:时刻活动9:00 am -9:10 am 集合9:10 am -11:00 am 上课11:00 am -11:30 am 休息11:30 am -1:00 pm 上课1:00 pm -1:50 pm 午餐1:50 pm -3:00 pm 上课3:00 pm 放学请问小林每天上课的时间共多少分钟?(A)300 (B)250 (C)500 (D)270 (E)240 ────────────────────────────────────────────────16.下列哪一项的三种面额之钞票各五张正好总值是$400?(A)$5、$10、$20 (B)$5、$10、$50 (C)$5、$10、$100 (D)$5、$20、$50 (E)$10、$20、$50────────────────────────────────────────────────17.下图是天平的示意图,请问哪一个箱子最轻?(A)a (B)b (C)c (D)d (E)e────────────────────────────────────────────────18.小文排在小卖部前队伍的正中央,小杰排在小文后面第三位,且在小杰之后面还有4个人。
请问在小卖部前共有多少人排队?(A)8 (B)14 (C)15 (D)16 (E)17────────────────────────────────────────────────19.每一片篱笆组件的宽度是5 m。
将一块三边长为25 m、25 m、30 m的三角地用篱笆围住,请问共需要多少片篱笆组件?(A)13 (B)15 (C)16 (D)17 (E)19────────────────────────────────────────────────20. 小何在笔记本上记载他的四位数密码,但其中有一位数字被墨水涂污,现在他只能看到35●2。
他记得这个密码可以被2整除,但不可被4整除。
请问污损的数字可能是下列哪一个数?(A )1 (B )2 (C )3 (D )5 (E )7 ────────────────────────────────────────────────21-25题,每题5分21. 用下列的图片各许多片不重迭地拼图,请问哪一个图片无法将4×4的方格表填满?(A ) (B ) (C )(D )(E )──────────────────────────────────────────────── 22. 小克从2010开始,每次往后数7,而得到2010、2003、1996、1989、…的数列。
请问下列哪一个数将会被数到?(A )1786 (B )1787 (C )1788 (D )1789 (E )1790 ──────────────────────────────────────────────── 23. 将一个矩形分割为四个较小的矩形,它们以cm 2计的面积如图上标记所示。
请问阴影部分的面积为多少cm 2?(A )21 (B )25 (C )30 (D )31 (E )32 ──────────────────────────────────────────────── 24. 小冬到商场打算购买卫生纸。
请问购买下列哪一项价格最低廉?(A )2卷售价$2.15 (B )1卷售价$2.35 (C )4卷售价$4.20 (D )10卷售价$9.50 (E )12卷售价$11.95────────────────────────────────────────────────6 10 1525. 小安所住的房子在图上标记A 处。
道路每一段的相邻两个交点之间的距离都是1 km 。
小安经常外出作每次6 km 的慢跑,最后回到家,但他喜欢变化他的路径,即每次跑步都不经过任何路段两次或以上。
请问他可以采用多少不同的路径慢跑?(在同一条路径上跑步但方向相反算作是相同)(A )3 (B )4 (C )5 (D )6 (E )8────────────────────────────────────────────────问题26~30的答案为000~999之间的整数之间的整数,,请将答案填在答案卡上对应的位置请将答案填在答案卡上对应的位置。
第26题占6分,第27题占7分,第28题占8分,第29题占9分,第30题占10分。
