高二数学 正态分布练习题
正态分布高中练习题及讲解

正态分布高中练习题及讲解1. 题目一:某工厂生产的零件长度服从正态分布N(50, 16),求长度在48到52之间的零件所占的比例。
2. 题目二:假设某大学新生的数学成绩服从正态分布N(70, 25),求数学成绩超过80分的学生所占的比例。
3. 题目三:某市居民的身高数据服从正态分布N(170, 10),如果随机选择一名居民,求其身高超过180cm的概率。
4. 题目四:某公司员工的工作时间服从正态分布N(8, 2),计算工作时间超过9小时的员工所占的比例。
5. 题目五:某品牌手机的电池寿命服从正态分布N(300, 50),求电池寿命超过350小时的概率。
讲解:正态分布是统计学中最常见的分布之一,其图形呈钟形,对称于均值。
正态分布的数学表达式为N(μ, σ²),其中μ是均值,σ²是方差。
正态分布的特点是:- 均值μ决定了分布的中心位置。
- 方差σ²决定了分布的宽度,方差越大,分布越宽,反之亦然。
- 68%的数据位于距均值一个标准差(σ)的范围内。
- 95%的数据位于距均值两个标准差的范围内。
- 99.7%的数据位于距均值三个标准差的范围内。
要解决上述题目,我们可以使用正态分布的性质和Z分数来计算概率。
解题步骤:1. 将数据转换为Z分数,Z = (X - μ) / σ。
2. 查找Z分数对应的概率,通常可以使用标准正态分布表或计算器。
例如,对于题目一,我们首先计算48和52对应的Z分数:- Z1 = (48 - 50) / 4 = -0.5- Z2 = (52 - 50) / 4 = 0.5然后,查找Z分数表或使用计算器得到Z1和Z2对应的概率,最后计算两者之差。
对于题目二至题目五,解题步骤类似,只需将题目中的数据代入相应的公式中计算即可。
通过这些练习,学生可以更好地理解正态分布的概念,掌握如何使用Z 分数来解决实际问题。
同时,这些练习也有助于提高学生的计算能力和逻辑思维能力。
正态分布练习题

正态分布练习题正态分布是概率论和统计学中非常重要的概率分布之一,广泛应用于各个领域。
为了帮助读者更好地理解和应用正态分布,下面将给出一些正态分布的练习题。
练习题1:某大学的数学成绩呈正态分布,平均分为70,标准差为10。
请计算以下问题的概率:a) 某位学生得分高于85分的概率。
b) 某位学生得分在60分到80分之间的概率。
c) 某位学生得分低于60分的概率。
练习题2:某工厂生产的零件长度呈正态分布,平均长度为100mm,标准差为5mm。
请计算以下问题的概率:a) 从生产线上随机抽取一只零件,其长度在105mm到110mm之间的概率。
b) 从生产线上随机抽取10只零件,其平均长度大于105mm的概率。
c) 从生产线上随机抽取100只零件,其平均长度在98mm到102mm 之间的概率。
练习题3:某城市的日降水量呈正态分布,平均降水量为10mm,标准差为3mm。
请计算以下问题的概率:a) 某天降水量超过14mm的概率。
b) 连续5天的平均降水量低于8mm的概率。
c) 连续10天的总降水量在90mm到110mm之间的概率。
练习题4:某配送中心的送货时间呈正态分布,平均送货时间为30分钟,标准差为5分钟。
请计算以下问题的概率:a) 某次送货时间少于20分钟的概率。
b) 连续10次送货的平均时间在28分钟到32分钟之间的概率。
c) 某天送货总时间超过8小时的概率。
练习题5:某社交平台上用户每日登录次数呈正态分布,平均登录次数为50次,标准差为10次。
请计算以下问题的概率:a) 某用户某天登录次数超过60次的概率。
b) 某用户连续7天的登录次数少于45次的概率。
c) 某用户连续30天的平均登录次数在48次到52次之间的概率。
以上是关于正态分布的一些练习题,通过计算这些概率问题可以更好地理解正态分布的特点和应用。
希望读者能够通过这些练习题提高对正态分布的理解和掌握。
正态分布(习题版)
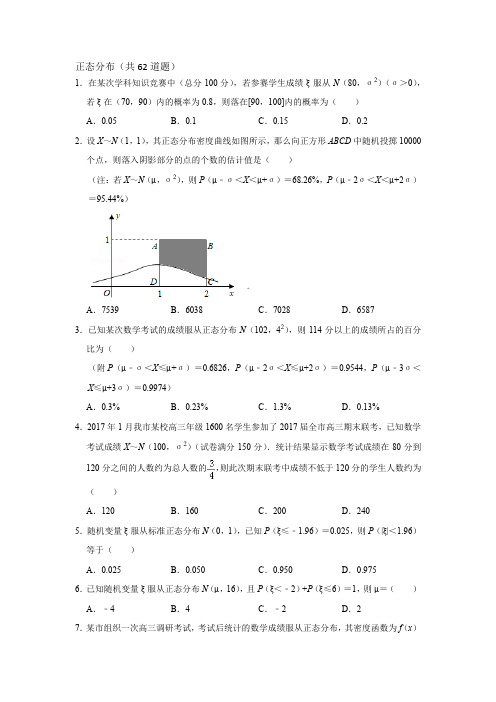
28.某一部件由四个电子元件按如图方式连接而成,元件1或元件2正常工作,且元件3或元件4正常工作,则部件正常工作.设四个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为.
A.0.25B.0.1C.0.125D.0.5
6.随机变量X服从正态分布X~N(10,σ2),P(X>12)=m,P(8≤X≤10)=n,则 的最小值为( )
A. B. C. D.
7.在某项测量中,测得变量ξ﹣N(1,σ2)(σ>0).若ξ在(0,2)内取值的概率为0.8,则ξ在(1,2)内取值的概率为( )
37.某中学为了了解该校高中学生的体重情况,现随机抽取该校150名高中学生,并测量每个人的体重后得到如图5的频率分布直方图.
(1)求这150名高中学生体重的样本平均数 和样本方差s2;(同一组中的数据用该区间的中点值代替)
(2)根据频率分布直方图,我们认为该校高中学生的体重Z服从正态分布N(u,δ2),其中u近似为样本平均数 ,δ2近似为样本方差s2;如果体重Z满足Z<33.4或Z>106.6,则该生的体重有严重问题.
28.2018年元旦期间,某高速公路收费站的三个高速收费口每天通过的小汽车数X(单位:辆)均服从正态分布N(600,σ2),若P(500<X<700)=0.6,假设三个收费口均能正常工作,则这个收费口每天至少有一个超过700辆的概率为( )
A. B. C. D.
29.设随机变量ξ:N(2,2),则D( ξ)=( )
A. ﹣ B.计,某市高三学生期末数学成绩X﹣N(85,σ2),且P(80<X<90)=0.3,则从该市任选一名高三学生,其成绩不低于90分的概率是( )
正态分布课后练习题

正态分布课后练习题正态分布是概率论与统计学中非常重要的一个概念,它在现实生活中的应用非常广泛。
为了更好地掌握正态分布的相关知识,下面我将给大家提供一些正态分布的课后练习题,希望能够帮助大家巩固所学知识。
练习题1:某公司的员工薪资服从正态分布,均值为5000元,标准差为1000元。
请计算以下几个问题:1. 员工薪资在4000元以上的概率是多少?2. 员工薪资在6000元以下的概率是多少?3. 员工薪资在4000元到6000元之间的概率是多少?练习题2:某学校的学生身高服从正态分布,均值为165厘米,标准差为5厘米。
请计算以下几个问题:1. 学生身高在170厘米以上的概率是多少?2. 学生身高在160厘米以下的概率是多少?3. 学生身高在160厘米到170厘米之间的概率是多少?练习题3:某超市的顾客购买的商品金额服从正态分布,均值为50元,标准差为10元。
请计算以下几个问题:1. 顾客购买的商品金额在60元以上的概率是多少?2. 顾客购买的商品金额在40元以下的概率是多少?3. 顾客购买的商品金额在40元到60元之间的概率是多少?练习题4:某地区的降雨量服从正态分布,均值为50毫米,标准差为10毫米。
请计算以下几个问题:1. 降雨量在60毫米以上的概率是多少?2. 降雨量在40毫米以下的概率是多少?3. 降雨量在40毫米到60毫米之间的概率是多少?以上是一些关于正态分布的课后练习题,希望能够帮助大家更好地理解和应用正态分布的知识。
在解答这些问题时,可以利用标准正态分布表或者统计软件进行计算。
同时,在计算过程中要注意将问题转化为标准正态分布的问题,再进行计算,以便得到准确的结果。
正态分布在实际生活中有着广泛的应用,比如在质量控制中,我们可以利用正态分布来判断产品是否合格;在心理学研究中,我们可以利用正态分布来分析人群的智力水平分布;在金融领域,我们可以利用正态分布来分析股票价格的变动情况等等。
因此,掌握正态分布的相关知识对我们的学习和工作都具有重要意义。
高二数学正态分布练习题

xyO正态分布㈠ 知识点回顾:1、正态分布概念:若连续型随机变量ξ的概率密度函数为),(,21)(222)(∞+-∞∈=--x ex f x σμσπ,其中,σμ为常数,且0σ>,则称ξ服从正态分布,简记为ξ~()2,N μσ。
()f x 的图象称为正态曲线。
2、正态分布的期望与方差 若ξ~()2,Nμσ,则2,E D ξμξσ==3、正态曲线的性质:①曲线在x 轴的上方,与x 轴不相交. ②曲线关于直线x=μ对称. ③曲线在x=μ时位于最高点.④当x<μ时,曲线上升;当x>μx 轴为渐进线,向它无限靠近.⑤当μ一定时,曲线的形状由σ确定.σ越大,曲线越“矮胖”,表示总体的分布越分散;σ越小,曲线越“瘦高”,表示总体的分布越集中.4、在标准正态分布表中相应于0x 的值()0x Φ是指总体取值小于0x 的概率即 ()()00x P x x Φ=<00≥x 时,则)(0x Φ的值可在标准正态分布表中查到00<x 时,可利用其图象的对称性获得)(1)(00x x -Φ-=Φ来求出,5、两个重要公式:① ②(6)、()2,Nμσ与()0,1N的关系:()()00P x F x ξ<==Φ①若ξ~()2,N μσ,有()212xP x x x σ⎛<<=Φ ⎝②若ξ~()2,N μσ,则)(0x Φ())()(1221x x x x P Φ-Φ=<<ξ())(100x x -Φ-=Φ(二)习题 一、选择题1.某市组织一次高三调研考试,考试后统计的数学成绩服从正态分布,其密度函数为)(1021)(200)80(2R x ex f x ∈⋅=--π,则下列命题不正确的是 ( B )A .该市这次考试的数学平均成绩为80分;B .分数在120分以上的人数与分数在60分以下的人数相同;C .分数在110分以上的人数与分数在50分以下的人数相同;D .该市这次考试的数学成绩标准差为10. 2.设随机变量ξ服从标准正态分布()0,1N ,若()1P p ξ>=,则()10P ξ-<<=(D )A.2pB. 1p -C. 12p -D. 12p -3.设随机变量),(~2σμξN ,且 )()(c P c P >=≤ξξ,则c 等于( D ) 4. 已知正态分布曲线关于y 轴对称,则μ值为( )A .1B .-1C .0 D.不确定5.正态分布N (0,1)在区间(-2,-1)和(1,2)上的取值的概率分别为12,p p ,则12,p p的大小关系为( ) A .12p p <B .12p p >C .12p p =D.不确定6.设随机变量),(~2σμξN ,且1,3==ξξD E ,则)11(≤<-ξP =( B )7.已知随机变量ξ服从正态分布2(2)N σ,,(4)0.84P ξ=≤,则(0)P ξ=≤( A )A .0.16B .0.32C .0.68D ,0.848.设随机变量ξ服从正态分布(2,9)N ,若(1)(1)P c P c ξξ>+=<-,则c = ( B )A.1B.2C.3D.49.已知随机变量ζ服从正态分布N (3,a 2),则P (3)ζ<=( D )(A)15(B)14(C)13(D)1210.若φ(3)=0.9987,则标准正态总体在区间(-3,3)内取值的概率为 (B) A .0.9987 B .0.9974 C .0.944 D . 0.8413 11、设随机变量服从正态分布N(0,1),p(ξ>1)=P ,则P(-1<ξ<1)=( C ) A .12PB .1-PC .1-2PD .12-P12.(07湖南卷,5)设随机变量ξ服从标准正态分布()0,1N。
【高中】正态分布经典练习题

【高中】正态分布经典练习题-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN正态分布一、选择题1.已知随机变量ξ服从正态分布)9,2(N ,若)1()1(-<=+>c P c P ξξ,则c 等于( )A.1B.2C.3D.42.已知随机变量ξ服从正态分),2(2σN ,且8.0)4(=<ξP ,则)20(<<ξP 等于( )A.0.6B.0.4C.0.3D.0.23.已知随机变量ξ服从正态分布),2(2σN ,(4)0.84P ξ=≤,则(0)P ξ≤等于( )A.0.16B.0.32C.0.68D.0.844.已知随机变量X 服从正态分布),2(2σN ,8.0)40(=<<X P ,则)4(>X P 等于( )A .0.1 B.0.2 C.0.4 D.0.65.已知随机变量ξ服从正态分布),3(2σN ,且3.0)2(=<ξP ,则)42(<<ξP 等于( )A.0.5B.0.2C.0.3D.0.46.已知随机变量ξ服从正态分布),3(2σN ,(4)0.842P ξ=≤,则(2)P ξ≤等于( )A.0.842B.0.158C.0.421D.0.3167.已知随机变量X 服从正态分布)1,3(N ,且6826.0)42(=<<X P ,则)4(>X P 等于( )A.0.1588B.0.158C.0.1586D.0.15858.已知随机变量X 服从正态分布),0(2σN ,若023.0)2(=>X P ,则(22)P X -≤≤等于( )A.0.477B.0.628C.0.954D.0.9779.在某次联考数学测试中,学生成绩ξ服从正态分布2(100,)(0)σσ>,若ξ在(80,120)内的概率为0.8,则落在(0,80)内的概率为( )A.0.05B.0.1C.0.15D.0.210.已知随机变量X 服从正态分布2(,)N μσ,且(22)0.9544P X μσμσ-<<+=, ()0.6826P X μσμσ-<<+=,若4,1μσ==, 则(56)P X <<=( )A.0.1358B.0.1359C.0.2716D.0.271811.某商场经营的一种袋装的大米的质量服从正态分布)1.0,10(2N (单位kg ),任选一袋这种大米,其质量在9.8~10.2kg 的概率为( )A.0.0456B.0.6826C.0.9544D.0.997412.一批电池的使用时间X (单位:小时)服从正态分布)4,36(2N ,在这批灯泡中任取一个“使用时间不小于40小时”的概率是( )A.0.9544B.0.6826C. 0.3174D. 0.1587二、填空题13.某校在本学期期中考试中,理科数学考试成绩),90(~2σξN ,统计结果显示8.0)12060(=≤≤ξP ,该校参加此次考试的理科学生共420人,试估计该校成绩高于120分的理科学生数为__________.14. 某班有50名学生,一次考试的成绩ξ服从正态分布),100(2σN , 已知3.0)10090(=≤≤ξP ,估计该班数学成绩在110分以上的人数为__________.15. 某中学200名考生的高考数学成绩近似服从正态分布)10,120(2N ,则此校数学成绩在140分以上的考生人数约为__________.16. 某市高二理科学生数学考试的成绩x 服从正态分布,其密度曲线如图,已知该市理科学生总数是10000人,则成绩位于]85,65(的人数约__________.17. 在某项测量中,测量结果ξ服从正态分布)0(),1(2>σσN ,若ξ在)1,0(内取值的概率为0.4,则ξ在(0,2)内取值的概率为__________.18. 假设每天从甲地去乙地的旅客人数X 是服从正态分布)50,800(2N 的随机变量.记一天中从甲地去乙地的旅客人数不超过900的概率为__________.19. 一批电阻的阻值X 服从正态分布)5,1000(2N (单位Ω).今从甲乙两箱成品中各随机抽取一个电阻,测得阻值分别为1011Ω和982Ω,可以认为__________. (填写正确序号) ①甲乙两箱电阻均可出厂; ②甲乙两箱电阻均不可出厂;③甲箱电阻可出厂,乙箱电阻不可出厂; ④甲箱电阻不可出厂,乙箱电阻可出厂.20. 某一部件由三个电子元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作.设三个电子元件的使用寿命(单位:小时)均服从正态分布)50,1000(2N ,且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为__________. O x 7515216题图 20题图。
高二数学正态分布试题

高二数学正态分布试题1.在某项测量中,测量结果服从正态分布,若在内取值的概率为,则在内取值的概率为A.B.C.D.【答案】A【解析】因为服从正态分布,所以正态分布曲线关于;又因为在内取值的概率为,所以在内取值的概率为,所以在内取值的概率为. 考点:正态分布曲线的特点及意义.2.已知随机变量服从正态分布,,则()A. B. C. D,【答案】A【解析】由正态曲线的性质可知,答案为A【考点】正态曲线3.在某市组织的一次数学竞赛中全体参赛学生的成绩近似服从正态分布N(60,100),已知成绩在90分以上(含90分)的学生有13人.(1)求此次参加竞赛的学生总数共有多少人?(2)若计划奖励竞赛成绩排在前228名的学生,问受奖学生的分数线是多少?【答案】(1) 10000人 (2) 80分【解析】解:(1)设学生的成绩为X,共有n人参加竞赛,∵X~N(60,100),∴μ=60,σ=10.∴P(X≥90)=[1-P(30<X<90)]=(1-0.9974)=0.0013.又P(X≥90)=,∴=0.0013.∴n=10000.故此次参加竞赛的学生总数共有10000人.(2)设受奖的学生的分数线为x.则P(X≥x)==0.0228.∵0.0228<0.5,∴x0>60.∴P(120-x0<X<x)=1-2P(X≥x)=0.9544,∴x=60+20=80.故受奖学生的分数线是80分.4.随机变量服从正态分布,若,则()A.B.C.D.【答案】C【解析】根据题意,由于随机变量服从正态分布,若,则可知1-0.4=0.6,故可知答案为C.【考点】正态分布点评:主要是考查了正态分布的概率的求解,属于基础题。
5.已知随机变量X服从正态分布N(3,1),且=0.6826,则()A.0.1585B.0.1588C.0.1587D.0.1586【解析】∵=0.6826,∴0.3413,,∴,故选C【考点】本题考查了正态分布列的性质点评:求正态分布中的概率时常常利用图象的对称性,属基础题6.已知随机变量服从正态分布,且,则()A.B.C.D.【答案】C【解析】因为,所以,由正态分布曲线的对称性知:。
正态分布练习题

正态分布练习题一、选择题1. 正态分布的数学表达式为:A. N(μ, σ^2)B. N(σ, μ^2)C. N(μ, σ)D. N(μ^2, σ)2. 正态分布的均值μ和标准差σ分别代表:A. 位置参数和形状参数B. 形状参数和位置参数C. 形状参数和尺度参数D. 尺度参数和形状参数3. 标准正态分布的均值和标准差分别是:A. 0和1B. 1和0C. 1和1D. 0和04. 68-95-99.7规则描述的是:A. 正态分布的对称性B. 正态分布的均值和标准差C. 正态分布的密度函数D. 正态分布数据的分布范围5. 正态分布曲线下,从均值到一个标准差之外的区域所占的面积比例是:A. 68%B. 95%C. 99.7%D. 34%二、填空题6. 正态分布的密度函数为 \(f(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\),其中\(\sigma\)代表______,\(\mu\)代表______。
7. 如果一个正态分布的均值为100,标准差为15,则该分布的3σ原则表示数据落在65到135之间的概率为______。
8. 标准正态分布的密度函数是 \(f(z) = \frac{1}{\sqrt{2\pi}}e^{-\frac{z^2}{2}}\),其中\(z\)代表______。
9. 假设某次考试的成绩服从正态分布,均分为75分,标准差为10分。
如果一个学生的成绩是85分,那么他的Z分数是______。
10. 正态分布的对称性意味着对于任意的正数a,有P(X < a) =______。
三、简答题11. 解释正态分布的三个特征,并给出每个特征在实际应用中的意义。
12. 描述68-95-99.7规则,并解释其在数据分析中的重要性。
13. 如果你有一个正态分布的数据集,如何计算其均值和标准差?14. 为什么标准正态分布是数据分析中的一个重要工具?15. 给出一个实际例子,说明正态分布如何应用于解决实际问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y 正态分布
㈠ 知识点回顾: 1、正态分布概念:若连续型随机变量ξ的概率密度函数为
),(,21
)(22
2)(∞+-∞∈=--x e x f x σμσπ,
其中,σμ为常数,且0σ>,则称ξ服从正态分布,简记为ξ~()2,N μσ。
()f x 的图象称为正态曲线。
2、正态分布的期望与方差
若ξ~()2,N μσ,则2,E D ξμξσ==
3、正态曲线的性质:
①曲线在x 轴的上方,与x 轴不相交.
②曲线关于直线x=μ对称.
③曲线在x=μ时位于最高点.
④当x<μ时,曲线上升;当x>μ时,曲线下降.并且当曲线向左、右两边无限延伸时,以x 轴为渐进线,向它无限靠近.
⑤当μ一定时,曲线的形状由σ确定.σ越大,曲线越“矮胖”,表示总体的分布越分散;σ越小,曲线越“瘦高”,表示总体的分布越集中.
4、在标准正态分布表中相应于0x 的值()0x Φ是指总体取值小于0x 的概率即 ()()00x P x x Φ=<
00≥x 时,则)(0x Φ的值可在标准正态
分布表中查到
00<x 时,可利用其图象的对称性获得
)(1)(00x x -Φ-=Φ来求出,
)()()()()(121221x x x P x P x x P Φ-Φ=<-<=<<ξξξ
5、两个重要公式:① ②
标准正态分布曲线
())()(1221x x x x P Φ-Φ=<<ξ())(100x x -Φ-=Φ)(0x Φ
(6)、()2,N μσ与()0,1N 的关系: ①若ξ~()2,N μσ,有()()000x P x F x μξσ-⎛⎫<==Φ ⎪⎝⎭
②若ξ~()2,N μσ,则()2112x x P x x x μμσσ--⎛⎫⎛⎫<<=Φ-Φ ⎪ ⎪⎝⎭⎝⎭
(二)习题
一、选择题
1.某市组织一次高三调研考试,考试后统计的数学成绩服从正态分布,其密度函数为
)(10
21)(200)80(2R x e x f x ∈⋅=--π,则下列命题不正确的是 ( B ) A .该市这次考试的数学平均成绩为80分;
B .分数在120分以上的人数与分数在60分以下的人数相同;
C .分数在110分以上的人数与分数在50分以下的人数相同;
D .该市这次考试的数学成绩标准差为10.
2.设随机变量ξ服从标准正态分布()0,1N ,若()1P p ξ>=,则()10P ξ-<<=(D )
A.
2
p B. 1p - C. 12p - D. 12p - 3.设随机变量),(~2σμξN ,且 )()(c P c P >=≤ξξ,则c 等于( D )
μμσ...0.D C B A -
4. 已知正态分布曲线关于y 轴对称,则μ值为( ) A .1 B .-1 C .0 D.不确定
5.正态分布N (0,1)在区间(-2,-1)和(1,2)上的取值的概率分别为12,p p ,则12,p p 的大小关系为( )
A .12p p <
B .12p p >
C .12p p = D.不确定
6.设随机变量),(~2σμξN ,且1,3==ξξD E ,则)11(≤<-ξP =( B )
1)2(2.)4()2(.)2()4(.1)1(2.-ΦΦ-ΦΦ-Φ-ΦD C B A
7.已知随机变量ξ服从正态分布2(2)N σ,,(4)0.84P ξ=≤,则(0)P ξ=≤( A )
A .0.16
B .0.32
C .0.68
D ,0.84
8.设随机变量ξ服从正态分布(2,9)N ,若(1)(1)P c P c ξξ>+=<-,则c = ( B )
A.1
B.2
C.3
D.4
9.已知随机变量ζ服从正态分布N (3,a 2),则P (3)ζ<=( D ) (A)15 (B)14 (C)13 (D)12
10.若φ(3)=0.9987,则标准正态总体在区间(-3,3)内取值的概率为 (B)
A .0.9987
B .0.9974
C .0.944
D . 0.8413
1x 2
x
11、设随机变量服从正态分布N(0,1),p(ξ>1)=P ,则P(-1<ξ<1)=
( C )
A .12P
B .1-P
C .1-2P
D .12-P
12.(07湖南卷,5)设随机变量ξ服从标准正态分布()0,1N 。
已知()1.960.025Φ-=,则()1.96P ξ<=( C ) A. 0.025 B. 0.050 C. 0.950 D. 0.975
13.(07浙江卷,5)已知随机变量ξ服从标准正态分布()22,N σ,()40.84P ξ≤= 则()0P ξ≤=( A )
A. 0.16
B. 0.32
C. 0.68
D. 0.84
二、填空题
14.设随机变量),4(~2σζN ,且3.0)84(=<<ζP ,则)0(<ζP =___0.2____
15. 已知机变量X 服从正态分布2(0)N σ,且(20)P X -≤≤0.4=,则(2)P X >= .
16.一项测量中,测量结果ξ服从正态分布2(1)(0)N σσ>,.若ξ在(01),内取值的概率为0.4,则ξ在
(02),内取值的概率为 .
18.(07全国卷Ⅱ,14):在某项测量中,测量结果ξ服从正态分布()()21,0N σσ>.若ξ在()0,1内取值的概率为0.4,则ξ在()0,2内取值的概率为----------。
