专题复习:巧用相似解决一类与圆有关的小压轴题
备战中考数学—圆与相似的综合压轴题专题复习含答案

备战中考数学—圆与相似的综合压轴题专题复习含答案一、相似1.如图,在△ABC中,点N为AC边的任意一点,D为线段AB上一点,若∠MPN的顶点P为线段CD上任一点,其两边分别与边BC,AC交于点M、N,且∠MPN+∠ACB=180°.(1)如图1,若AC=BC,∠ACB=90°,且D为AB的中点时,求,请证明你的结论;(2)如图2,若BC=m,AC=n,∠ACB=90°,且D为AB的中点时,则 =________;(3)如图3,若 =k,BC=m,AC=n,请直接写出的值.(用k,m,n表示)【答案】(1)解:如图1中,作PG⊥AC于G,PH⊥BC于H,∵AC=BC,∠ACB=90°,且D为AB的中点,∴CD平分∠ACB,∵PG⊥AC于G,PH⊥BC于H,∴PG=PH,∵∠PGC=∠PHC=∠GCH=90°,∴∠GPH=∠MPN=90°,∴∠MPH=∠NPG,∵∠PHM=∠PGN=90°,∴△PHM∽△PGN,∴ =1(2)(3)解:如图3中,作PG⊥AC于G,PH⊥BC于H,DT⊥AC于T,DK⊥BC于K,易证△PMH∽△PGN,∴,∵,∴,∵DT∥PG,DK∥PH,∴,∴,∴【解析】【解答】解:(2)如图2中,作PG⊥AC于G,PH⊥BC于H,∵∠PGC=∠PHC=∠GCH=90°,∴∠GPH=∠MPN=90°,∴∠MPH=∠NPG,∵∠PHM=∠PGN=90°,∴△PHM∽△PGN,∴,∵△PHC∽△ACB,PG=HC,∴,故答案为:;【分析】(1)作PG⊥AC于G,PH⊥BC于H,根据已知条件可证△PHM和△PGN的两角对应相等,进而可得△PHM∽△PGN,由相似三角形的对应边成比例即可求出。
(2)作PG⊥AC于G,PH⊥BC于H,由两角对应相等,可得△PHM∽△PGN,由相似三角形的对应边成比例可得 = ,由两角对应相等,可得△PHC∽△ACB,又PG=HC,相似三角形的对应边成比例及等量代换即可求出。
2020-2021中考数学—圆与相似的综合压轴题专题复习

2020-2021中考数学—圆与相似的综合压轴题专题复习一、相似1.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a>0)与x轴相交于点A(﹣1,0)和点B,与y轴交于点C,对称轴为直线x=1.(1)求点C的坐标(用含a的代数式表示);(2)联结AC、BC,若△ABC的面积为6,求此抛物线的表达式;(3)在第(2)小题的条件下,点Q为x轴正半轴上一点,点G与点C,点F与点A关于点Q成中心对称,当△CGF为直角三角形时,求点Q的坐标.【答案】(1)解:∵抛物线y=ax2+bx+c(a>0)的对称轴为直线x=1,而抛物线与x轴的一个交点A的坐标为(﹣1,0)∴抛物线与x轴的另一个交点B的坐标为(3,0)设抛物线解析式为y=a(x+1)(x﹣3),即y=ax2﹣2ax﹣3a,当x=0时,y=﹣3a,∴C(0,﹣3a)(2)解:∵A(﹣1,0),B(3,0),C(0,﹣3a),∴AB=4,OC=3a,∴S△ACB= AB•OC=6,∴6a=6,解得a=1,∴抛物线解析式为y=x2﹣2x﹣3(3)解:设点Q的坐标为(m,0).过点G作GH⊥x轴,垂足为点H,如图,∵点G与点C,点F与点A关于点Q成中心对称,∴QC=QG,QA=QF=m+1,QO=QH=m,OC=GH=3,∴OF=2m+1,HF=1,当∠CGF=90°时,∵∠QGH+∠FGH=90°,∠QGH+∠GQH=90°,∴∠GQH=∠HGF,∴Rt△QGH∽Rt△GFH,∴ = ,即,解得m=9,∴Q的坐标为(9,0);当∠CFG=90°时,∵∠GFH+∠CFO=90°,∠GFH+∠FGH=90°,∴∠CFO=∠FGH,∴Rt△GFH∽Rt△FCO,∴ = ,即 = ,解得m=4,∴Q的坐标为(4,0);∠GCF=90°不存在,综上所述,点Q的坐标为(4,0)或(9,0).【解析】【分析】(1)根据抛物线是轴对称图形和已知条件可求得抛物线与x轴的另一个交点B的坐标,再用交点式可求得抛物线的解析式,然后根据抛物线与y轴交于点C可得x=0,把x=0代入解析式即可求得点C的坐标;(2)由(1)的结论可求得AB=4,OC=3a,根据三角形ABC的面积=AB•OC=6可求得a的值,则解析式可求解;(3)设点Q的坐标为(m,0).过点G作GH⊥x轴,垂足为点H,根据中心对称的性质可得QC=QG,QA=QF=m+1,QO=QH=m,OC=GH=3。
中考数学压轴题专题复习—圆与相似的综合及答案解析

中考数学压轴题专题复习—圆与相似的综合及答案解析一、相似1.如图,在⊙O中,直径AB经过弦CD的中点E,点M在OD上,AM的延长线交⊙O于点G,交过D的直线于F,且∠BDF=∠CDB,BD与CG交于点N.(1)求证:DF是⊙O的切线;(2)连结MN,猜想MN与AB的位置有关系,并给出证明.【答案】(1)证明:∵直径AB经过弦CD的中点E,, = ,即是的切线(2)解:猜想:MN∥AB.证明:连结CB.∵直径AB经过弦CD的中点E,∴ = , = ,∴∵∴∴∵∴∵∵∴∴∴MN∥AB.【解析】【分析】(1)要证DF是⊙O的切线,由切线的判定知,只须证∠ODF=即可。
由垂径定理可得AB⊥CD,则∠BOD+∠ODE=,而∠ODF=∠CDF+∠ODE,由已知易得∠BOD=∠CDF,则结论可得证;(2)猜想:MN∥AB.理由:连结CB,由已知易证△CBN∽△AOM,可得比例式,于是由已知条件可转化为,∠ODB是公共角,所以可得△MDN∽△ODB,则∠DMN=∠DOB,根据平行线的判定可得MN∥AB。
2.在矩形ABCD中,BC=6,点E是AD边上一点,∠ABE=30°,BE=DE,连接BD.动点M 从点E出发沿射线ED运动,过点M作MN∥BD交直线BE于点N.(1)如图1,当点M在线段ED上时,求证:MN= EM;(2)设MN长为x,以M、N、D为顶点的三角形面积为y,求y关于x的函数关系式;(3)当点M运动到线段ED的中点时,连接NC,过点M作MF⊥NC于F,MF交对角线BD于点G(如图2),求线段MG的长.【答案】(1)证明::∵ °, ° ,∴ °∵ ,∴∵∥ ,∴∴ °,∴过点作于点 ,则 .在中,∴∴(2)解:在中,,∴∵a.当点在线段上时,过点作于点 ,在中,由(1)可知:,∴∴∴b.当点在线段延长线上时,过点作于点在中, ,在中, ,∴ ,∴(3)解:连接 ,交于点 .∵为的中点∴ ,∴ .∵ ,∴ ,∴ ,∴ ,∴ .∵∥∴ ,∴ ,,∵ ,∴ ,又∵ ,∴∽ ,∴,即 ,∴【解析】【分析】(1)过点E作EH⊥MN于点H ,由已知条件易得EN=EM,解直角三角形EMH易得MH和EM的关系,由等腰三角形的三线合一可得MN=2MH即可求解;(2)在Rt△ABE中,由直角三角形的性质易得DE=BE=2AE,由题意动点M从点E出发沿射线ED运动可知点M可在线段ED上,也可在线段ED外,所以可分两种情况求解:①当点M在线段ED上时,过点N作NI⊥AD于点I ,结合(1)中的结论MN=EM即可求解;②当点M在线段ED延长线上时,过点N作NI'⊥AD于点I ',解RtΔNI′M 和可求得NI'和NE,则DM=NE−DE,所以以M、N、D为顶点的三角形面积y=MD.NI可求解;(3)连接CM,交BD于点N',由(2)中的计算可得MN、CD、MC的长,解直角三角形CDM可得∠DMC的度数,于是由三角形内角和定理可求得∠NMC=,根据平行线的性质可得DMN'是直角三角形,根据直角三角形的性质可得MN′=MD;则NC的长可求,由已知条件易得ΔNMC∽ΔMN′G根据所得的比例式即可求解.,3.如图,抛物线y= x2+bx+c 与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点.(1)求抛物线的解析式及点D的坐标;(2)如图1,抛物线的对称轴与x轴交于点E,连接BD,点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;(3)如图2,若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P在x轴上,点Q在坐标平面内,以线段MN为对角线作正方形MPNQ,求点Q的坐标.【答案】(1)解:把B(6,0),C(0,6)代入y= x2+bx+c,得解得 ,抛物线的解析式是y= x2+2x+6, 顶点D的坐标是(2,8)(2)解:如图1,过F作FG⊥x轴于点G,设F(x, x2+2x+6),则FG= ,∵∠FBA=∠BDE,∠FGB=∠BED=90°,∴△FBG∽△BDE,∴,∵B(6,0),D(2,8),∴E(2,0),BE=4,DE=8,OB=6,∴BG=6-x,∴当点F在x轴上方时,有,∴x=-1或x=6(舍去),此时F1的坐标为(-1,),当点F在x轴下方时,有,∴x=-3或x=6(舍去),此时F2的坐标为(-3,),综上可知F点的坐标为(-1,)或(-3,)(3)解:如图2,不妨M在对称轴的左侧,N在对称轴的左侧,MN和PQ交于点K,由题意得点M,N关于抛物线的对称轴对称,四边形MPNQ为正方形,且点P在x轴上∴点P为抛物线的对称轴与x轴的交点,点Q在抛物线的对称轴上 ,∴KP=KM=k,则Q(2,2k),M坐标为(2-k,k),∵点M在抛物线y= x2+2x+6的图象上,∴k= (2-k)2+2(2-k)+6解得k1= 或k2=∴满足条件的点Q有两个,Q1(2,)或Q2(2,).【解析】【分析】(1)根据点B、C的坐标,利用待定系数法建立关于b、c的方程组,求解就可得出函数解析式,再求出顶点坐标。
中考数学—圆与相似的综合压轴题专题复习及答案.doc
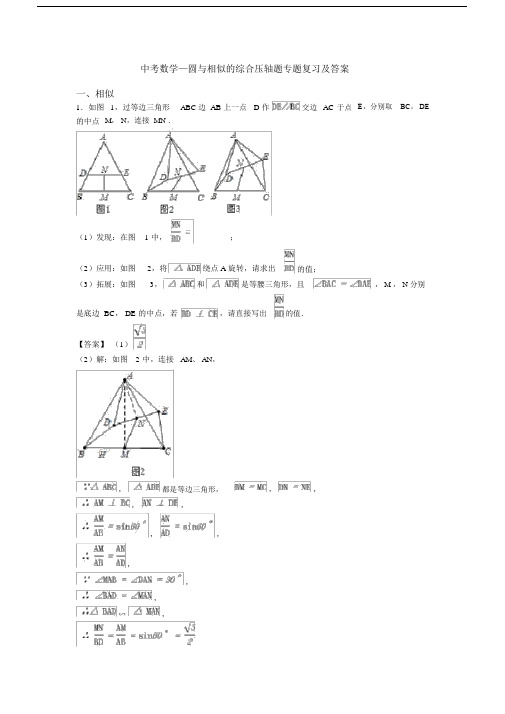
中考数学—圆与相似的综合压轴题专题复习及答案一、相似1.如图的中点1,过等边三角形M, N,连接 MN .ABC 边AB 上一点 D 作交边AC 于点E,分别取BC, DE(1)发现:在图 1 中,________;(2)应用:如图2,将绕点 A 旋转,请求出的值;(3)拓展:如图3,和是等腰三角形,且, M , N 分别是底边 BC, DE 的中点,若,请直接写出的值.【答案】(1)(2)解:如图 2 中,连接AM、 AN,,,都是等边三角形,,,,,,,,,∽,(3)解:如图 3 中,连接AM、 AN,延长 AD 交 CE于 H,交 AC 于 O,,,,,,,,,,,,,,,∽,,,,,,≌,,,,,,,,,,【解析】【解答】解:(1)如图 1 中,作于H,连接AM,,,,时等边三角形,,,,,平分线段DE,,、 N、 M 共线,,四边形 MNDH 时矩形,,,故答案为:;【分析】( 1)作DH ⊥ BC 于 H,连接AM.证四边形MNDH 时矩形,所以MN=DH,则MN : BD=DH:BD=sin60 ,°即可求解;(2)利用△ ABC ,△ ADE 都是等边三角形可得AM : AB=AN: AD,易得∠BAD = ∠MAN ,从而得△ BAD ∽ △ MAN,则 NM: BD=AM:AB=sin60 ,°从而求解;(3)连接 AM、 AN,延长 AD 交 CE 于 H,交 AC 于 O.先证明△BAD∽△ MAN可得NM : BD=AM:AB=sin∠ ABC;再证明△ BAD ≌ △ CAE,则∠ ABD = ∠ ACE ,进而可得∠ABC = 45 ,可求出°答案 .2.如图, Rt△ AOB 在平面直角坐标系中,已知:B(0,),点OA=3,∠BAD=30°,将△ AOB 沿 AB 翻折,点O 到点 C 的位置,连接A 在 x 轴的正半轴上,CB 并延长交 x 轴于点D.(1)求点 D 的坐标;(2)动点 P 从点 D 出发,以每秒 2 个单位的速度沿 x 轴的正方向运动,当△ PAB为直角三角形时,求 t 的值;(3)在( 2)的条件下,当△ PAB为以∠ PBA为直角的直角三角形时,在y 轴上是否存在一点 Q 使△ PBQ 为等腰三角形?如果存在,请直接写出Q 点的坐标;如果不存在,请说明理由 .【答案】( 1)解:∵ B(0,),∴OB=.∵OA=OB,∴OA=3,∴AC=3.∵∠ BAD=30 ,°∴∠ OAC=60 .°∵∠ ACD=90 ,°∴∠ ODB=30 ,°∴=,∴O D=3,∴D(﹣ 3,0);(2)解:∵ OA=3,OD=3,∴ A( 3,0), AD=6,∴A B=2,当∠PBA=90时°.∵P D=2t,∴O P=3﹣2t.∵△ OBA∽ △ OPB,2∴3﹣ 2t==1,解得 t=1,当∠APB=90 时°,则 P 与 O 重合,∴t=;(3)解:存在 .①当 BP 为腰的等腰三角形.∵OP=1,∴BP==2,∴Q1( 0,+2), Q3( 0.﹣2);②当 PQ2=Q2B 时,设 PQ2=Q2 B=a,在 Rt△ OPQ2中, 12+(﹣x)2=x2,解得x=,∴Q2( 0,);③当 PB=PQ 时, Q ( 0,﹣)4 4综上所述:满足条件的点Q 的坐标为Q1( 0,+2), Q2( 0 ,), Q3( 0.﹣2), Q4( 0,﹣) .【解析】【分析】( 1)根据已知得出OA、 OB 的值以及∠ DAC 的度数,进而求得∠ ADC,即可求得 D 的坐标;( 2)根据直角三角形的判定,分两种情况讨论求得;(3)求得 PB 的长,分四种情形讨论即可解决问题.3.(1)问题发现:如图① ,正方形 AEFG的两边分别在正方形ABCD的边 AB 和 AD 上,连接 CF.①写出线段CF与 DG 的数量关系;②写出直线CF与 DG 所夹锐角的度数.(2)拓展探究:如图②,将正方形AEFG绕点用图②进行说明 .(3)问题解决如图③,A 逆时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请利△ABC 和△ ADE 都是等腰直角三角形,D 在直线 BC 上运动,连接OE,则在点∠BAC=∠ DAE=90°, AB=AC=4,O 为 AC 的中点 .若点D 的运动过程中,线段OE 的长的最小值.(直接写出结果)【答案】( 1)①CF=(2)解:如图:DG,②45①连接 AC、 AF,在正方形ABCD中,延长CF交 DG 与 H 点,∠CAD=∠BCD=45,设 AD=CD=a,易得 AC=a=AD,同理在正方形AEFG中,∠FAG=45 ,AF=AG,∠CAD=∠FAG,∠ CAD-∠ 2=∠ FAG-∠ 2,∠1=∠ 3又△CAF∽ DAG,=,CF=DG;②由△ CAF∽ DAG,∠ 4=∠ 5,∠ACD=∠ 4+∠ 6=45 ,∠5+∠ 6=45,∠5+∠ 6+∠ 7=135 ,在△ CHD中,∠CHD=180 -135 =45,(1)中的结论仍然成立(3) OE 的最小值为.【解析】【解答】( 3)如图:由∠ BAC=∠ DAE=90 ,可得∠ BAD=∠ CAE,又AB=AC,AD=AE, 可得△ BAD≌ △ CAE,∠A CE=∠ ABC=45 ,又∠ ACB=45 ,∠ BCE=90 ,即CE⊥ BC,根据点到直线的距离垂线段最短,OE⊥ CE时, OE 最短,此时OE=CE,△ OEC为等腰直角三角形,OC=AC=2,由等腰直角三角形性质易得,OE=,OE 的最小值为.【分析】( 1 )①易得CF=DG;②45;(2)连接AC、 AF,在正方形ABCD 中,可得△CAF∽ DAG,=,CF=DG,在△ CHD 中,∠ CHD=180 -135 =45,(1)中的结论是否仍然成立;(3) OE⊥ CE 时, OE 最短,此时OE=CE,△ OEC 为等腰直角三角形, OC=AC=2,可得 OE 的值 .4.已知菱形的一个角与三角形的一个角重合,然后它的对角顶点在这个重合角的对边上,这个菱形称为这个三角形的亲密菱形,如图,在△ CFE中, CF=6,CE=12,∠ FCE=45°,以点 C 为圆心,以任意长为半径作AD,再分别以点 A 和点 D 为圆心,大于AD 长为半径做弧,交于点 B,AB∥ CD.(1)求证:四边形 ACDB为△ CFE的亲密菱形;(2)求四边形 ACDB的面积 .【答案】( 1)证明:由已知得:AC=CD,AB=DB,由已知尺规作图痕迹得:BC 是∠ FCE 的角平分线 ,∴∠ ACB=∠ DCB,又∵ AB∥ CD,∴∠ ABC=∠ DCB,∴∠ ACB=∠ ABC,∴AC=AB,又∵ AC=CD,AB=DB,∴AC=CD=DB=BA,四边形 ACDB是菱形,又∵∠ ACD与△ FCE中的∠ FCE重合,它的对角∠ABD顶点在EF上,∴四边形 ACDB为△ FEC的亲密菱形 .(2)解:设菱形 ACDB的边长为 x,∵ CF=6,CE=12,∴FA=6-x,又∵ AB∥ CE,∴△ FAB∽ △ FCE,∴,即,解得: x=4,过点 A 作 AH⊥ CD于点 H,在Rt△ ACH中,∠ ACH=45°,∴s in∠ ACH= ,∴AH=4 ×=2,∴四边形 ACDB的面积为:.【解析】【分析】( 1)依题可得: AC=CD,AB=DB,BC是∠ FCE 的角平分线 ,根据角平分线的定义和平行线的性质得∠ ACB=∠ ABC,根据等角对等边得 AC=AB,从而得 AC=CD=DB=BA,根据四边相等得四边形是菱形即可得四边形ACDB是菱形;再根据题中的新定义即可得证. (2)设菱形ACDB 的边长为x,根据已知可得CF=6,CE=12,FA=6-,x根据相似三角形的判定和性质可得,解得: x=4,过点 A 作 AH⊥CD 于点 H,在 Rt△ ACH 中,根据锐角三角形函数正弦的定义即可求得AH ,再由四边形的面积公式即可得答案.5.如果三角形的两个内角α与β满足2α +β =90,那°么我们称这样的三角形为“准互余三角形”.(1)若△ ABC 是“准互余三角形”,∠ C> 90°,∠ A=60°,则∠B=________°;(2)如图①,在 Rt△ ABC中,∠ ACB=90°, AC=4, BC=5.若 AD 是∠BAC 的平分线,不难证明△ ABD 是“准互余三角形”试.问在边 BC上是否存在点 E(异于点 D),使得△ ABE 也是“准互余三角形”?若存在,请求出 BE的长;若不存在,请说明理由 .(3)如图②,在四边形 ABCD 中, AB=7, CD=12, BD⊥ CD,∠ ABD=2∠BCD,且△ABC 是“准互余三角形”,求对角线AC 的长 .【答案】( 1) 15(2)解:如图①中,在Rt△ ABC中,∵ ∠ B+∠ BAC=90°,∠ BAC=2∠ BAD,∴∠ B+2∠BAD=90 ,°∴△ ABD 是“准互余三角形”,∵△ ABE 也是“准互余三角形”,∴只有 2∠ B+∠ BAE=90 ,°∵∠ B+∠BAE+∠ EAC=90 ,°∴∠ CAE=∠ B,∵∠ C=∠ C=90 ,°∴△ CAE∽ △ CBA,可得 CA2=CE?CB,∴C E= ,∴B E=5﹣= .(3)解:如图②中,将△ BCD沿 BC 翻折得到△BCF.∴CF=CD=12,∠BCF=∠ BCD,∠CBF=∠ CBD,∵∠ ABD=2∠ BCD,∠BCD+∠CBD=90 ,°∴∠ ABD+∠ DBC+∠CBF=180 ,°∴A、B、 F 共线,∴∠ A+∠ ACF=90 °∴2∠ ACB+∠ CAB≠ 90,°∴只有 2∠ BAC+∠ ACB=90 ,°∴∠ FCB=∠ FAC,∵ ∠ F=∠ F,∴△ FCB∽ △ FAC,∴CF2=FB?FA,设 FB=x,则有: x( x+7) =122,∴x=9 或﹣ 16(舍去),∴AF=7+9=16,在 Rt△ ACF中, AC=【解析】【解答】( 1)∵ △ ABC是“准互余三角形”,∠ C> 90°,∠ A=60°,∴2∠ B+∠A=90 ,°解得,∠ B=15°;【分析】( 1 )根据“准互余三角形”的定义构建方程即可解决问题;( 2 )只要证明△CAE∽△ CBA,可得 CA2=CE?CB,由此即可解决问题;( 3)如图②中,将△ BCD沿 BC翻折得到△ BCF只.要证明△ FCB∽ △ FAC,可得 CF2=FB?FA,设 FB=x,则有: x( x+7)=122 ,推出 x=9 或﹣ 16(舍弃),再利用勾股定理求出AC即可;6.如图,点O 为矩形 ABCD的对称中心,AB= 5cm, BC= 6cm,点 E.F.G分别从 A.B.C 三点同时出发,沿矩形的边按逆时针方向匀速运动,点 E 的运动速度为1cm/s ,点 F 的运动速度为 3cm/s ,点 G 的运动速度为 1.5cm/s,当点 F 到达点 C(即点 F 与点 C 重合)时,三个点随之停止运动 .在运动过程中,△ EBF 关于直线 EF 的对称图形是△ EB′设F.点 E.F.G运动的时间为 t(单位: s) .(1)当 t 等于多少s 时,四边形EBFB′为正方形;(2)若以点E、 B、 F 为顶点的三角形与以点F, C, G 为顶点的三角形相似,求t 的值;(3)是否存在实数t ,使得点B’与点 O 重合?若存在,求出t 的值;若不存在,请说明理由.【答案】( 1)解:若四边形 EBFB′为正方形,则 BE= BF, BE= 5﹣ t, BF=3t,即: 5﹣ t = 3t,解得 t= 1.25;故答案为: 1.25(2)解:分两种情况,讨论如下:①若△ EBF∽ △ FCG,则有,即,解得: t= 1.4;②若△ EBF∽ △ GCF,则有,即,解得: t=﹣ 7﹣(不合题意,舍去)或∴当 t= 1.4s 或 t =(﹣ 7+)s时,以点点的三角形相似. t =﹣ 7+.E、 B、F 为顶点的三角形与以点F, C, G 为顶(3)解:假设存在实数t,使得点B′与点 O 重合 .如图,过点O 作 OM⊥ BC于点 M,则在 Rt△ OFM 中, OF= BF= 3t ,FM=BC﹣ BF= 3﹣ 3t, OM = 2.5,由勾股定理得: OM 2+FM 2= OF2,即: 2.52+( 3﹣ 3t)2=( 3t )2解得: t=;过点 O 作 ON⊥AB 于点 N,则在Rt△ OEN 中, OE=BE=5 ﹣t , EN= BE﹣ BN=5﹣ t ﹣2.5=2.5﹣t ,ON= 3,由勾股定理得:ON2+EN2= OE2,即: 32+( 2.5﹣ t)2=( 5﹣ t )2解得: t=.∵≠,∴不存在实数t ,使得点B′与点 O 重合【解析】【分析】( 1 )利用正方形的性质,得到BE= BF,列一元一次方程求解即可;( 2)△ EBF 与△ FCG 相似,分两种情况,需要分类讨论,逐一分析计算;(3)本问为存在型问题 .假设存在,则可以分别求出在不同条件下的t 值,它们互相矛盾,所以不存在7.如图,在 Rt△ ABC中,∠ ACB= 90°,AC= 6cm, BC=8cm.动点 M 从点 B 出发,在 BA 边上以每秒 3cm 的速度向定点 A 运动,同时动点 N 从点 C 出发,在 CB 边上以每秒 2cm 的速度向点 B 运动,运动时间为t 秒,连接MN.(1)若△ BMN 与△ABC 相似,求t 的值;(2)连接 AN, CM,若 AN⊥ CM,求 t 的值.【答案】(1)解:∵∠ ACB= 90°, AC= 6cm, BC= 8cm,∴ BA==10(cm).由题意得BM=3tcm ,CN= 2tcm,∴ BN= (8- 2t)cm.当△ BMN∽ △ BAC时,,∴=,解得t=;当△ BMN∽ △ BCA时,=,∴=,解得t=.综上所述,△ BMN 与△ ABC相似时, t 的值为或(2)解:如图,过点M 作 MD ⊥CB 于点 D,∴∠ BDM=∠ACB= 90 °,又∵ ∠B=∠ B,∴ △BDM ∽ △ BCA,∴==. ∵ AC= 6cm, BC= 8cm, BA= 10cm, BM=3tcm ,∴DM =tcm, BD=tcm ,∴CD=cm.∵AN⊥CM,∠ ACB= 90 °,∴∠ CAN+∠ ACM= 90 °,∠ MCD+∠ ACM= 90 °,∴∠ CAN=∠MCD. ∵ MD ⊥CB,∴ ∠ MDC=∠ ACB= 90 °,∴ △ CAN∽ △ DCM,∴=,∴=,解得t=.【解析】【分析】( 1)在直角三角形ABC 中,由已知条件用勾股定理可求得AB 的长,再根据路程 =速度时间可将BM、 CN 用含 t 的代数式表示出来,则BN=BC-CN也可用含t 的代数式表示出来,因为△ BMN与△ABC相似,由题意可分两种情况,①当△BMN ∽△ BAC 时,由相似三角形的性质可得比例式:,将已知的线段代入计算即可求解;②当△ BMN∽ △BCA 时,由相似三角形的性质可得比例式:的线段代入计算即可求解;( 2 )过点M作MD ⊥ CB 于点 D ,根据有两个角对应相等的两个三角形相似可得,将已知△BDM ∽ △ BCA,于是可得比例式数式表示 DM 、 BD 的长,则,将已知的线段代入计算即可用含CD=CB-BD 也可用含t的代数式表示出来,同理易证t 的代△CAN∽ △ DCM,可得比例式,将已表示的线段代入计算即可求得t 的值。
备战中考数学与圆与相似有关的压轴题附详细答案

备战中考数学与圆与相似有关的压轴题附详细答案一、相似1.设C为线段AB的中点,四边形BCDE是以BC为一边的正方形.以B为圆心,BD长为半径的⊙B与AB相交于F点,延长EB交⊙B于G点,连接DG交于AB于Q点,连接AD.求证:(1)AD是⊙B的切线;(2)AD=AQ;(3)BC2=CF•EG.【答案】(1)证明:连接BD,∵四边形BCDE是正方形,∴∠DBA=45°,∠DCB=90°,即DC⊥AB,∵C为AB的中点,∴CD是线段AB的垂直平分线,∴AD=BD,∴∠DAB=∠DBA=45°,∴∠ADB=90°,即BD⊥AD,∵BD为半径,∴AD是⊙B的切线(2)证明:∵BD=BG,∴∠BDG=∠G,∵CD∥BE,∴∠CDG=∠G,∴∠G=∠CDG=∠BDG= ∠BCD=22.5°,∴∠ADQ=90°﹣∠BDG=67.5°,∠AQB=∠BQG=90°﹣∠G=67.5°,∴∠ADQ=∠AQD,∴AD=AQ(3)证明:连接DF,在△BDF中,BD=BF,∴∠BFD=∠BDF,又∵∠DBF=45°,∴∠BFD=∠BDF=67.5°,∵∠GDB=22.5°,在Rt△DEF与Rt△GCD中,∵∠GDE=∠GDB+∠BDE=67.5°=∠DFE,∠DCF=∠E=90°,∴Rt△DCF∽Rt△GED,∴ ,又∵CD=DE=BC,∴BC2=CF•EG.【解析】【分析】(1)连接BD,要证AD是圆B的切线,根据切线的判定可知,只须证明∠ADB=即可。
由正方形的性质易得BC=CD,∠DCB=∠DCA=,∠DBC=∠CDB=,根据点C为AB的中点可得BC=CD=AC,所以可得∠ADC=,则∠∠ADB=,问题得证;(2)要证AQ=AD,需证∠AQD=∠ADQ。
由题意易得∠AQD=-∠G,∠ADQ=-∠BDG,根据等边对等角可得∠G=∠BDG,由等角的余角相等可得∠AQD=∠ADQ,所以AQ=AD;(3)要证乘积式成立,需证这些线段所在的两个三角形相似,而由正方形的性质可得CD=DE=BC,所以可知BC、CF、EG分别在三角形DCF和三角形GED中,连接DF,用有两对角对应相等的两个三角形相似即可得证。
中考数学—圆与相似的综合压轴题专题复习及详细答案

中考数学—圆与相似的综合压轴题专题复习及详细答案一、相似1.如图所示,将二次函数y=x2+2x+1的图象沿x轴翻折,然后向右平移1个单位,再向上平移4个单位,得到二次函数y=ax2+bx+c的图象.函数y=x2+2x+1的图象的顶点为点A.函数y=ax2+bx+c的图象的顶点为点B,和x轴的交点为点C,D(点D位于点C的左侧).(1)求函数y=ax2+bx+c的解析式;(2)从点A,C,D三个点中任取两个点和点B构造三角形,求构造的三角形是等腰三角形的概率;(3)若点M是线段BC上的动点,点N是△ABC三边上的动点,是否存在以AM为斜边的Rt△AMN,使△AMN的面积为△ABC面积的?若存在,求tan∠MAN的值;若不存在,请说明理由.【答案】(1)解:y=x2+2x+1=(x+1)2的图象沿x轴翻折,得y=﹣(x+1)2,把y=﹣(x+1)2向右平移1个单位,再向上平移4个单位,得y=﹣x2+4,∴所求的函数y=ax2+bx+c的解析式为y=﹣x2+4(2)解:∵y=x2+2x+1=(x+1)2,∴A(﹣1,0),当y=0时,﹣x2+4=0,解得x=±2,则D(﹣2,0),C(2,0);当x=0时,y=﹣x2+4=4,则B(0,4),从点A,C,D三个点中任取两个点和点B构造三角形的有:△ACB,△ADB,△CDB,∵AC=3,AD=1,CD=4,AB= ,BC=2 ,BD=2 ,∴△BCD为等腰三角形,∴构造的三角形是等腰三角形的概率=(3)解:存在,易得BC的解析是为y=﹣2x+4,S△ABC= AC•OB= ×3×4=6,M点的坐标为(m,﹣2m+4)(0≤m≤2),①当N点在AC上,如图1,∴△AMN的面积为△ABC面积的,∴(m+1)(﹣2m+4)=2,解得m1=0,m2=1,当m=0时,M点的坐标为(0,4),N(0,0),则AN=1,MN=4,∴tan∠MAC= =4;当m=1时,M点的坐标为(1,2),N(1,0),则AN=2,MN=2,∴tan∠MAC= =1;②当N点在BC上,如图2,BC= =2 ,∵BC•AN= AC•BC,解得AN= ,∵S△AMN= AN•MN=2,∴MN= = ,∴∠MAC= ;③当N点在AB上,如图3,作AH⊥BC于H,设AN=t,则BN= ﹣t,由②得AH= ,则BH= ,∵∠NBG=∠HBA,∴△BNM∽△BHA,∴,即,∴MN= ,∵AN•MN=2,即•(﹣t)• =2,整理得3t2﹣3 t+14=0,△=(﹣3 )2﹣4×3×14=﹣15<0,方程没有实数解,∴点N在AB上不符合条件,综上所述,tan∠MAN的值为1或4或【解析】【分析】(1)将y=x2+2x+1配方成顶点式,根据轴对称的性质,可得出翻折后的函数解析式,再根据函数图像平移的规律:上加下减,左加右减,可得出答案。
中考数学压轴题专题复习—圆与相似的综合含详细答案

中考数学压轴题专题复习—圆与相似的综合含详细答案一、相似1.如图,在四边形ABCD中,AD//BC,,BC=4,DC=3,AD=6.动点P从点D出发,沿射线DA的方向,在射线DA上以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).(1)设的面积为,直接写出与之间的函数关系式是________(不写取值范围).(2)当B,P,Q三点为顶点的三角形是等腰三角形时,求出此时的值.(3)当线段PQ与线段AB相交于点O,且2OA=OB时,直接写出 =________. (4)是否存在时刻,使得若存在,求出的值;若不存在,请说明理由.【答案】(1)(2)解:如图1,过点P作PH⊥BC于点H,∴∠PHB=∠PHQ=90°,∵∠C=90°,AD∥BC,∴∠CDP=90°,∴四边形PHCD是矩形,∴PH=CD=3,HC=PD=2t,∵CQ=t,BC=4,∴HQ=CH-CQ=t,BH=BC-CH=4-2t,BQ=4-t,∴BQ2= ,BP2= ,PQ2= ,由BQ2=BP2可得:,解得:无解;由BQ2=PQ2可得:,解得:;由BP2= PQ2可得:,解得:或,∵当时,BQ=4-4=0,不符合题意,∴综上所述,或;(3)(4)解:如图3,过点D作DM∥PQ交BC的延长线于点M,则当∠BDM=90°时,PQ⊥BD,即当BM2=DM2+BD2时,PQ⊥BD,∵AD∥BC,DM∥PQ,∴四边形PQMD是平行四边形,∴QM=PD=2t,∵QC=t,∴CM=QM-QC=t,∵∠BCD=∠MCD=90°,∴BD2=BC2+DC2=25,DM2=DC2+CM2=9+t2,∵BM2=(BC+CM)2=(4+t)2,∴由BM2=BD2+DM2可得:,解得:,∴当时,∠BDM=90°,即当时,PQ⊥BD.【解析】【解答】解:(1)由题意可得BQ=BC-CQ=4-t,点P到BC的距离=CD=3,∴S△PBQ= BQ×3= ;( 3 )解:如图2,过点P作PM⊥BC交CB的延长线于点M,∴∠PMC=∠C=90°,∵AD∥BC,∴∠D=90°,△OAP∽△OBQ,∴四边形PMCD是矩形,,∴PM=CD=3,CM=PD=2t,∵AD=6,BC=4,CQ=t,∴PA=2t-6,BQ=4-t,MQ=CM-CQ=2t-t=t,∴,解得:,∴MQ= ,又∵PM=3,∠PMQ=90°,∴tan∠BPQ= ;【分析】(1)点P作PM⊥BC,垂足为M,则四边形PDCM为矩形,根据梯形的面积公式就可以利用t表示,就得到s与t之间的函数关系式。
中考数学——圆与相似的综合压轴题专题复习及详细答案

∵
=1 且∠ ABC=∠ AMN,
∴ △ ABC~△ AMN
∴
,
∵ AB=BC,
∴ ∠ BAC= (180°﹣∠ ABC), ∵ AM=MN
∴ ∠ MAN= (180°﹣∠ AMN), ∵ ∠ ABC=∠ AMN, ∴ ∠ BAC=∠ MAN, ∴ ∠ BAM=∠ CAN, ∴ △ ABM~△ ACN, ∴ ∠ ABC=∠ ACN (3)解:如图 3,连接 AB,AN,
∴ BI=
=24,
∵ BI=24<32,
∴ 中位线 IK 的两端点在线段 AB 和 DE 上,
过点 K 作 KL⊥BC 于点 L,
由【探索发现】知矩形的最大面积为 ×BG• BF= ×(40+20)× (32+16)=720, 答:该矩形的面积为 720; (4)解:如图 2,延长 BA、CD 交于点 E,过点 E 作 EH⊥BC 于点 H,
由题意知四边形 ABCH 是矩形, ∵ AB=32,BC=40,AE=20,CD=16, ∴ EH=20、DH=16, ∴ AE=EH、CD=DH, 在△ AEF 和△ HED 中,
∵
,
∴ △ AEF≌ △ HED(ASA),
∴ AF=DH=16,
同理△ CDG≌ △ HDE,
∴ CG=HE=20,
(2)解:∵ 四边形 ABED 内接于⊙O,∴ ∠ CED=∠ CAB,
∵ ∠ C=∠ C,∴ △ CED∽ △ CAB,∴
,
∵ AB=BC=10,CE=2,D 是 AC 的中点,
∴ CD= ;
(3)解:延长 EF 交⊙O 于 M,
在 Rt△ ABD 中,AD= ,AB=10,
∴ BD=3 , ∵ EM⊥AB,AB 是⊙O 的直径,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题复习:巧用“相似”解决与圆有关的小压轴题 【复习目标】 能以“圆.”为背景,寻找(构造)“相似..
”,并能运用相似知识求解. (南通市中考常在第10题呈现,一般属于选择或填空压轴题)
【活动设计】
活动一、错题回顾
1.(2011·大邑模拟)如图,在△ABC 中,∠C=60°,以分别交AC ,BC 于点D ,E ,已知圆O 的半径为23 .则DE 的长为 .
2.(2015·南通)如图,AB 为⊙O 的直径,C 为⊙O 上一点,弦AD 平分∠BAC ,交BC 于
点E ,AB=6,AD=5,则AE 的长为【 】
A .2.5
B .2.8
C .3
D .3.2
3.(2016·海门一模)如图,在△ABC 中,CD ⊥AB 于D .若AD =2,BC =8,
CD =6,则△ABC 的外接圆的半径为【 】 A .3
104 B .102 C .10 D .72
4.(2012·万州模拟)如图,⊙O 的直径AB 长为10,弦AC 的长为6,∠ACB 的角平分线
交⊙O 于D ,则CD 长为 .
A
C B D
·O
(第3题)
活动二、课堂测试 1.(2016·如皋一模)如图,△ABD 内接于⊙O ,点C 在线段AD 上,AC =2CD ,点E 在弧
BD 上,∠ECD =∠ABD ,EC =1,则AE 等于【 】
A .2
B .32
C .3
D .2
2.(2013·南通)如图.Rt △ABC 内接于⊙O ,BC 为直径,AB=4,AC=3,D 是弧AB 的中
点,CD 与AB 的交点为E ,则CE:DE 等于【 】
A .4
B .2.5
C .3
D .2.8
3.(2014·苏州)如图,直线l 与半径为4的⊙O 相切于点A ,P 是⊙O 上的一个动点(不与点A 重合),过点P 作PB ⊥l ,垂足为B ,连接PA .设PA=x ,PB=y ,则(x —y )的最大值 .
4.如图,BC 是半⊙O 的直径,EF ⊥BC 于点F ,
5BF FC =,又AB=8,AE=2,则AD 的长为 【 】
A .13+
B .
132+ C .32 D .12+
(第2题)
· O D A B C
E。
