高考数学大一轮总复习 第二章 第8讲 函数的图象课件 理
【高考数学】一轮总复习:第二章 第8讲 对数函数

【解】 (1)因为 f(1)=1,所以 log4(a+5)=1,因此 a+5=4,即 a=-1, 所以 f(x)=log4(-x2+2x+3). 由-x2+2x+3>0 得-1<x<3,即函数 f(x)的定义域为(-1,3). 令 g(x)=-x2+2x+3. 则 g(x)在(-1,1)上单调递增,在[1,3)上单调递减. 又 y=log4x 在(0,+∞)上单调递增, 所以 f(x)的单调递增区间是(-1,1),单调递减区间是[1,3).
A.a<b<c
B.b<a<c
√C.c<b<a
D.c<a<b
2
2
【解析】 (1)因为 23<32,所以 2<33,所以 log32<log333=23,所以 a<c.因为
2
2
33>52,所以 3>53,所以 log53>log553=23,所以 b>c,所以 a<c<b,故选 A.
(2)因为 f(x)为奇函数,所以 f(-x)=-f(x),
一、思考辨析
判断正误(正确的打“√”,错误的打“×”) (1)函数 y=log2x 及 y=log13x 都是对数函数.( × )
3
(2)对数函数 y=logax(a>0 且 a≠1)在(0,+∞)上是增函数.( × ) (3)函数 y=ln 11+-xx与 y=ln(1+x)-ln(1-x)的定义域相同.( √ )
(2)构造函数 f(x)=4x 和 g(x)=logax, 当 a>1 时不满足条件,
高考数学一轮复习第二章函数导数及其应用第8讲指数与指数函数精选教案理
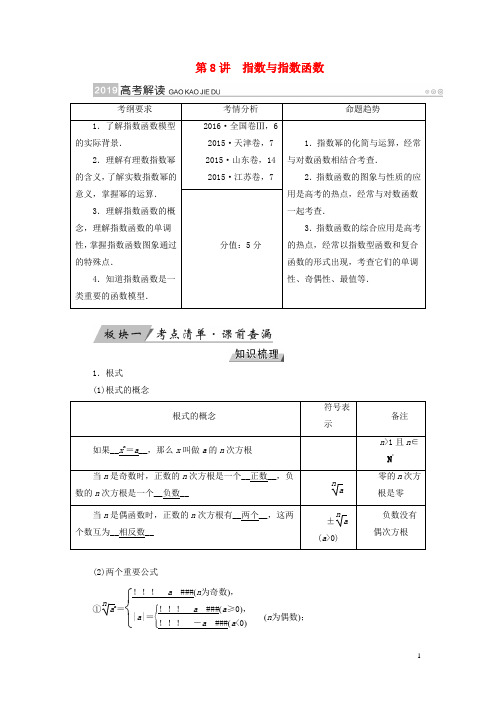
第8讲指数与指数函数1.根式(1)根式的概念(2)两个重要公式①na n=⎩⎨⎧!!!a###(n为奇数),|a|=⎩⎪⎨⎪⎧!!!a###(a≥0),!!!-a###(a<0)(n为偶数);②(na )n=__a __(注意:a 必须使na 有意义). 2.有理数的指数幂 (1)幂的有关概念①正分数指数幂:a mna >0,m ,n ∈N *,且n >1);②负分数指数幂:a -mn =!!! 1a n###=!!! 1 ###(a >0,m ,n ∈N *,且n >1).③0的正分数指数幂等于__0__,0的负分数指数幂__无意义__. (2)有理数指数幂的性质 ①a r a s=__ar +s__(a >0,r ,s ∈Q );②(a r )s =__a rs__(a >0,r ,s ∈Q ); ③(ab )r=__a r b r__(a >0,b >0,r ∈Q ). 3.指数函数的图象与性质1.思维辨析(在括号内打“√”或“×”). (1)na n与(na )n 都等于a (n ∈N *).( × ) (2)2a·2b=2a b .( × )(3)函数y =3·2x与y =2x +1都不是指数函数.( √ )(4)若a m<a n(a >0且a ≠1),则m <n .( × ) (5)函数y =2-x在R 上为单调减函数.( √ ) 解析 (1)错误.当n 为偶数,a <0时,na 不成立.(2)错误.2a ·2b =2a +b≠2ab.(3)正确.两个函数均不符合指数函数的定义. (4)错误.当a >1时,m <n ;而当0<a <1时,m >n .(5)正确.y =2-x=⎝ ⎛⎭⎪⎫12x ,根据指数函数的性质可知函数在R 上为减函数.2.函数f (x )=1-2x的定义域是( A ) A .(-∞,0] B .[0,+∞) C .(-∞,0)D .(-∞,+∞)解析 ∵1-2x≥0,∴2x≤1,∴x ≤0. 3.已知函数f (x )=4+a x -1的图象恒过定点P ,则点P 的坐标是( A )A .(1,5)B .(1,4)C .(0,4)D .(4,0)解析 当x =1时,f (x )=5.4.不等式2x 2-x <4的解集为__{x |-1<x <2}__.解析 不等式2x 2-x <4可化为2x 2-x <22,由指数函数y =2x 的性质可得,x 2-x <2,解得-1<x <2,故所求解集为{x |-1<x <2}.5.若函数y =(a 2-1)x在(-∞,+∞)上为减函数,则实数a解析 由题意知0<a 2-1<1,即1<a 2<2,得-2<a <-1或1<a < 2.一 指数幂的化简与求值指数幂运算的一般原则(1)有括号的先算括号里的,无括号的先做指数运算. (2)先乘除后加减,负指数幂化成正指数幂的倒数.(3)底数是负数,先确定符号;底数是小数,先化成分数;底数是带分数的,先化成假分数.(4)若是根式,应化为分数指数幂,尽可能用幂的形式表示,运用指数幂的运算性质来解答.【例1】 计算:(1)3a 92 a -3÷3a -73a 13;(2)(0.027) -13 -⎝ ⎛⎭⎪⎫17-2+⎝ ⎛⎭⎪⎫27912 -(2-1)0;(3)已知m 12 +m -12=4,求m 32 -m -32m 12 -m -12 .解析 (1)原式=(a 92 a -32 )13 ÷(a -73 a 133 )12 =(a 3)13 ÷(a 2)12 =a ÷a =1.(2)原式=⎝ ⎛⎭⎪⎫271 000-13 -72+⎝ ⎛⎭⎪⎫25912-1=103-49+53-1=-45.(3)∵m 12 +m -12 =4,∴m +m -1+2=16,∴m +m -1=14, ∴m 32 -m -32 m 12 -m -12 =(m 12 -m -12 )(m +m -1+1)m 12 -m -12=m +m -1+1=14+1=15.二 指数函数的图象及应用指数函数图象的画法及应用(1)画指数函数y =a x(a >0,a ≠1)的图象,应抓住三个关键点(1,a ),(0,1),⎝ ⎛⎭⎪⎫-1,1a 和一条渐近线y =0.(2)与指数函数有关的函数的图象的研究,往往利用相应指数函数的图象,通过平移、对称变换,得到其图象.(3)一些指数方程、不等式问题的求解,往往利用相应的指数型函数图象数形结合求解. 【例2】 (1)函数y =a x-1a(a >0,且a ≠1)的图象可能是( D )(2)若曲线|y |=2x+1与直线y =b 没有公共点,则b 的取值范围是__[-1,1]__.解析 (1)函数y =a x-1a(a >0,且a ≠1)的图象必过点(-1,0),故选D .(2)曲线|y |=2x+1与直线y =b 的图象如图所示,由图象可得:如果|y |=2x+1与直线y =b 没有公共点,则b 应满足的条件是b ∈[-1,1].三 指数函数的性质及应用指数函数性质问题的类型及解题思路(1)比较指数幂大小问题.常利用指数函数的单调性及中间值(0或1).(2)简单的指数不等式的求解问题.解决此类问题应利用指数函数的单调性,要特别注意底数a 的取值范围,并在必要时进行分类讨论.(3)求解与指数函数有关的复合函数问题,首先要熟知指数函数的定义域、值域、单调性等相关性质,其次要明确复合函数的构成,涉及值域、单调区间、最值等问题时,都要借助“同增异减”这一性质分析判断,最终将问题归结为内层函数相关的问题加以解决.【例3】 已知函数f (x )=e x -e -x(x ∈R ,且e 为自然对数的底数). (1)判断函数f (x )的单调性与奇偶性;(2)是否存在实数t ,使不等式f (x -t )+f (x 2-t 2)≥0对一切x ∈R 都成立?若存在,求出t ;若不存在,请说明理由.解析 (1)∵f (x )=e x-⎝ ⎛⎭⎪⎫1e x ,∴f ′(x )=e x+⎝ ⎛⎭⎪⎫1e x ,∴f ′(x )>0对任意x ∈R 都成立,∴f (x )在R 上是增函数.∵f (x )的定义域为R ,且f (-x )=e -x-e x=-f (x ),∴f (x )是奇函数.(2)存在,由(1)知f (x )在R 上是增函数和奇函数,则f (x -t )+f (x 2-t 2)≥0对一切x ∈R 都成立⇔f (x 2-t 2)≥f (t -x )对一切x ∈R 都成立⇔x 2-t 2≥t -x 对一切x ∈R 都成立⇔t 2+t ≤x 2+x =⎝ ⎛⎭⎪⎫x +122-14对一切x ∈R 都成立⇔t 2+t ≤(x 2+x )min =-14⇔t 2+t +14=⎝ ⎛⎭⎪⎫t +122≤0,又⎝ ⎛⎭⎪⎫t +122≥0,∴⎝ ⎛⎭⎪⎫t +122=0,∴t =-12,∴存在t =-12,使不等式f (x -t )+f (x 2-t 2)≥0对一切x ∈R 都成立.1.(2018·山东德州一模)已知a =⎝ ⎛⎭⎪⎫3525 ,b =⎝ ⎛⎭⎪⎫2535 ,c =⎝ ⎛⎭⎪⎫2525 ,则( D ) A .a <b <c B .c <b <a C .c <a <bD .b <c <a解析 ∵y =⎝ ⎛⎭⎪⎫25x为减函数,∴b <c ,又∵y =x 25 在(0,+∞)上为增函数,∴a >c ,∴b <c <a ,故选D .2.(2018·北京模拟)已知函数f (x )=a x,其中a >0,且a ≠1,如果以P (x 1,f (x 1)),Q (x 2,f (x 2))为端点的线段的中点在y 轴上,那么f (x 1)·f (x 2)=( A )A .1B .aC .2D .a 2解析 ∵以P (x 1,f (x 1)),Q (x 2,f (x 2))为端点的线段的中点在y 轴上,∴x 1+x 2=0,又∵f (x )=a x,∴f (x 1)·f (x 2)=ax 1·ax 2=ax 1+x 2=a 0=1,故选A .3.函数y =4x+2x +1+1的值域为( B )A .(0,+∞)B .(1,+∞)C .[1,+∞)D .(-∞,+∞)解析 令2x=t (t >0),则函数y =4x+2x +1+1可化为y =t 2+2t +1=(t +1)2(t >0).∵函数y =(t +1)2在(0,+∞)上递增,∴y >1.∴所求值域为(1,+∞),故选B .4.函数f (x )=a x+log a (x +1)(a >0,且a ≠1)在[0,1]上的最大值和最小值之和为a ,则a 的值为( B )A .14 B .12 C .2D .4解析 ∵在[0,1]上y =a x与y =log a (x +1)具有相同的单调性,∴f (x )=a x+log a (x +1)在[0,1]上单调,∴f (0)+f (1)=a ,即a 0+log a 1+a 1+log a 2=a ,化简得1+log a 2=0,解得a =12.易错点 忽视对含参底数的讨论错因分析:对数函数、指数函数的底数含字母参数时,要分底数大于1和大于0小于1讨论.【例1】 已知函数f (x )=|a -1|a 2-9(a x -a -x)(a >0且a ≠1)在R 上为增函数,求a 的取值范围.解析 ①当a >1时,a x 在R 上为增函数,y =a -x =⎝ ⎛⎭⎪⎫1a x 在R 上为减函数,∴y =a x -a-x为增函数.∵f (x )为增函数,∴|a -1|a 2-9>0,解得a >3或a <-3,又∵a >1,∴a >3.②当0<a <1时,y =a x 在R 上为减函数,y =a -x在R 上为增函数, ∴y =a x-a -x在R 上为减函数.∵f (x )为增函数,∴|a -1|a 2-9<0,解得-3<a <1或1<a <3.又∵0<a <1,∴此时0<a <1.综上,a 的取值范围为(0,1)∪(3,+∞).【跟踪训练1】 (2018·东北三校联考)若关于x 的方程|a x-1|=2a (a >0,且a ≠1)有两个不等实根,则a 的取值范围是( D )A .(0,1)∪(1,+∞)B .(0,1)C .(1,+∞)D .⎝ ⎛⎭⎪⎫0,12 解析 方程|a x-1|=2a (a >0,且a ≠1)有两个实数根转化为函数y =|a x-1|与y =2a 有两个交点.①当0<a <1时,如图①,∴0<2a <1,即0<a <12;②当a >1时,如图②, 而y =2a >1不符合要求.∴0<a <12.课时达标 第8讲[解密考纲]本考点主要考查指数的运算、指数函数的图象与性质、简单的复合函数的单调性等,通常以选择题、填空题的形式呈现,题目难度中等或中等偏上.一、选择题1.(2016·全国卷Ⅲ)已知a =243 ,b =425 ,c =2513 ,则( A ) A .b <a <c B .a <b <c C .b <c <aD .c <a <b解析 因为a =243 =1613 ,b =425 =1615 ,c =2513 ,且幂函数y =x 13 在R 上单调递增,指数函数y =16x在R 上单调递增,所以b <a <c .2.(2018·河南洛阳模拟)已知函数f (x )=2x-2,则函数y =|f (x )|的图象可能是( B )解析 |f (x )|=|2x-2|=⎩⎪⎨⎪⎧2x-2,x ≥1,2-2x,x <1,易知函数y =|f (x )|的图象的分段点是x =1, 且过点(1,0),(0,1),⎝ ⎛⎭⎪⎫-1,32,故选B .3.已知f (x )=3x -b(2≤x ≤4,b 为常数)的图象经过点(2,1),则f (x )的值域为( C )A .[9,81]B .[3,9]C .[1,9]D .[1,+∞)解析 由f (x )过定点(2,1)可知b =2,因为f (x )=3x -2在[2,4]上是增函数,f (x )min =f (2)=1,f (x )max =f (4)=9,故选C .4.(2018·山西太原模拟)函数y =2x -2-x是( A ) A .奇函数,在区间(0,+∞)上单调递增 B .奇函数,在区间(0,+∞)上单调递减 C .偶函数,在区间(-∞,0)上单调递增 D .偶函数,在区间(-∞,0)上单调递减解析 令f (x )=2x -2-x ,则f (-x )=2-x -2x=-f (x ),所以函数f (x )是奇函数,排除C 项,D 项.又函数y =-2-x,y =2x 均是R 上的增函数,故y =2x -2-x在R 上为增函数,故选A .5.(2018·浙江丽水模拟)当x ∈(-∞,-1]时,不等式(m 2-m )·4x -2x<0恒成立,则实数m 的取值范围是( C )A .(-2,1)B .(-4,3)C .(-1,2)D .(-3,4)解析 原不等式变形为m 2-m <⎝ ⎛⎭⎪⎫12x .∵函数y =⎝ ⎛⎭⎪⎫12x在(-∞,-1]上是减函数,∴⎝ ⎛⎭⎪⎫12x ≥⎝ ⎛⎭⎪⎫12-1=2, 当x ∈(-∞,-1]时,m 2-m <⎝ ⎛⎭⎪⎫12x 恒成立等价于m 2-m <2,解得-1<m <2,故选C .6.(2018·山东济宁模拟)已知函数f (x )=|2x-1|,a <b <c ,且f (a )>f (c )>f (b ),则下列结论中,一定成立的是( D )A .a <0,b <0,c <0B .a <0,b ≥0,c >0C .2-a<2cD .2a+2c<2解析 作出函数f (x )=|2x-1|的图象,如图,∵a <b <c ,且f (a )>f (c )>f (b ), 结合图象知0<f (a )<1,a <0,c >0, ∴0<2a<1.∴f (a )=|2a -1|=1-2a<1, ∴f (c )<1,∴0<c <1,∴1<2c<2, ∴f (c )=|2c -1|=2c-1, 又∵f (a )>f (c ),∴1-2a >2c-1, ∴2a +2c<2,故选D . 二、填空题7.已知函数f (x )=a -x(a >0,且a ≠1),且f (-2)>f (-3),则a 的取值范围是__(0,1)__.解析 因为f (x )=a -x=⎝ ⎛⎭⎪⎫1ax ,且f (-2)>f (-3),所以函数f (x )在定义域上单调递增,所以1a>1,解得0<a <1.8.已知函数y =a 2x +2a x-1(a >1)在区间[-1,1]上的最大值是14,则a =__3__.解析 y =a 2x +2a x -1(a >1),令a x =t ,则y =t 2+2t -1⎝ ⎛⎭⎪⎫1a≤t ≤a ,此二次函数图象开口向上,对称轴为t =-1,又a >1,所以当t =a ,即x =1时取最大值,所以a 2+2a -1=14, 解得a =3.9.(2018·皖南八校联考)对于给定的函数f (x )=a x-a -x(x ∈R ,a >0,a ≠1),下面给出五个命题,其中真命题是__①③④__(只需写出所有真命题的编号).①函数f (x )的图象关于原点对称; ②函数f (x )在R 上不具有单调性; ③函数f (|x |)的图象关于y 轴对称; ④当0<a <1时,函数f (|x |)的最大值是0; ⑤当a >1时,函数f (|x |)的最大值是0.解析 ∵f (-x )=-f (x ),∴f (x )为奇函数,f (x )的图象关于原点对称,①真;当a >1时,f (x )在R 上为增函数,当0<a <1时,f (x )在R 上为减函数,②假;y =f (|x |)是偶函数,其图象关于y 轴对称,③真;当0<a <1时,y =f (|x |)在(-∞,0)上为增函数,在[0,+∞)上为减函数,∴当x =0时,y =f (|x |)取最大值为0,④真;当a >1时,f (|x |)在(-∞,0)上为减函数,在[0,+∞)上为增函数,∴当x =0时,y =f (|x |)取最小值为0,⑤假.综上,真命题是①③④.三、解答题10.化简:(1)a 3b 23ab 2(a 14 b 12 )4a -13 b 13(a >0,b >0);(2)⎝ ⎛⎭⎪⎫-278 -23+(0.002)-12-10(5-2)-1+(2-3)0. 解析 (1)原式=(a 3b 2a 13b 23 ) 12ab 2a -13 b 13=a 32 +16 +13 -1·b 1+13 -2-13 =ab -1.(2)原式=⎝ ⎛⎭⎪⎫-278-23 +⎝ ⎛⎭⎪⎫1500-12 -105-2+1 =⎝ ⎛⎭⎪⎫-82723 +50012 -10(5+2)+1=49+105-105-20+1=-1679. 11.已知函数f (x )=⎝ ⎛⎭⎪⎫13a x 2-4x +3. (1)若a =-1,求f (x )的单调区间;(2)若f (x )有最大值3,求a 的值.解析 (1)当a =-1时,f (x )=⎝ ⎛⎭⎪⎫13-x 2-4x +3,令g (x )=-x 2-4x +3,由于g (x )在(-∞,-2)上单调递增,在(-2,+∞)上单调递减,而y =⎝ ⎛⎭⎪⎫13t 在R 上单调递减,所以f (x )在(-∞,-2)上单调递减,在(-2,+∞)上单调递增,即函数f (x )的单调递增区间是(-2,+∞),单调递减区间是(-∞,-2).(2)令g (x )=ax 2-4x +3=a ⎝ ⎛⎭⎪⎫x -2a 2+3-4a,∵f (x )有最大值,∴g (x )应有最小值,且g (x )min =3-4a(a >0), ∴f (x )max =⎝ ⎛⎭⎪⎫133-4a =3,∴3-4a =-1,∴a =1. 12.已知定义域为R 的函数f (x )=-2x +b 2x +1+a是奇函数. (1)求a ,b 的值;(2)解关于t 的不等式f (t 2-2t )+f (2t 2-1)<0.解析 (1)因为f (x )是定义在R 上的奇函数,所以f (0)=0,即-1+b 2+a=0,解得b =1,所以f (x )=-2x +12x +1+a. 又由f (1)=-f (-1)知-2+14+a =--12+11+a,解得a =2. (2)由(1)知f (x )=-2x+12x +1+2=-12+12x +1. 由上式易知f (x )在(-∞,+∞)上为减函数.又因为f (x )是奇函数,所以不等式f (t 2-2t )+f (2t 2-1)<0等价于f (t 2-2t )<-f (2t 2-1)=f (-2t 2+1).因为f (x )是减函数,由上式推得t 2-2t >-2t 2+1,即3t 2-2t -1>0,解不等式可得解集为t ⎪⎪⎪⎭⎬⎫t >1或t <-13.精美句子1、善思则能“从无字句处读书”。
高考数学一轮复习第2单元函数、导数及其应用第8讲指数与指数函数课件理

发资金比上一年增长 12%,则该公司全年投入
的研发资金开始超过 200 万元的年份是(参考
数据:lg 1.12≈0.05,lg 1.3≈0.11,lg 2≈0.30)( )
A.2018 年
B.2019 年
C.2020 年
D.2021 年
[答案] B
[解析] 设 x 年后该公司全年投入的研发 资金开始超过 200 万元,由题可 知,130(1+12%)x≥200,解得 x≥log1.12210300=lglg2-1lg.112.3≈3.80,因为 x 为整数, 所以 x 取 4,故开始超过 200 万元的年份是 2019 年.
3x-
1 3
������
=-f(x),所以 f(x)为奇函数.又因为 y=3x
为增函数,y= 1 ������为减函数,所以 f(x)=3x- 1 ������
3
3
为增函数.故选 A.
教学参考
2.[2016·四川卷] 某公司为激励创新,计划逐年
加大研发资金投入.若该公司 2015 年全年投入
研发资金 130 万元,在此基础上,每年投入的研
第8讲 PART 2
指数与指数 函数
教学参考│课前双基巩固│课堂考点探究│教师备用例题
考试说明
1.了解指数函数模型的实际背景. 2.理解有理数指数幂的含义,了解实数指数幂的意义,掌握幂的运算. 3.理解指数函数的概念及其单调性,掌握指数函数图像通过的特殊点. 会画底数为 2,3,10, 的指数函数的图像. 4.体会指数函数是一类重要的函数模型.
1.指数函数 y=ax+b(a>0 且 a≠1)的图像恒过定点(0,1+b). 2. 指数函数 y=ax(a>0 且 a≠1)的图像以 x 轴为渐近线.
《课堂新坐标》高考数学一轮总复习课件:第二章 第八节 函数与方程(共33张PPT)

2+4 确度 ε=0.01,取区间(2,4)的中点 x1= 2 =3,计算
得 f(2)·f(x1)<0,则此时零点 x0 所在的区间为( )
A.(2,4)
B.(3,4)
探究·提知能
C.(2,3)
D.(2.5,3)
课后作
【解析】 由零点存在性定理知x0∈(2,3),故选C.
【答案】 C
菜单
新课标 ·文科数学(广东专用)
菜单
新课标 ·文科数学(广东专用)
Δ=b2-4ac
落实·固基础
Δ>0
二次函数 y=ax2+bx+c
(a>0)的图象
Δ=0
Δ<0
高考体验·明
探究·提知能与x轴的交点 零点个数
_(_x_1,___0_),___(x_2_,__0__) __(_x_1,___0_)_
2
1
无交点 课后作 0
菜单
新课标 ·文科数学(广东专用)
菜单
新课标 ·文科数学(广东专用)
落实·固基础
1.解答本题一要从图表中寻找数量信息,二要注 高考体验·明 意“精确度”的含义,切不可与“精确到”混淆.
2.(1)用二分法求函数零点的近似解必须满足①y
=f(x)的图象在[a,b]内连续不间断,②f(a)·f(b)<0.(2)
在第一步中,尽量使区间长度缩短,以减少计算量及计
落实·固基础
新课标 ·文科数学(广东专用)
第八节 函数与方程
高考体验·明
探究·提知能 菜单
课后作
新课标 ·文科数学(广东专用)
落实·固基础 1.函数零点
高考体验·明
(1)定义:对于函数y=f(x)(x∈D),把使____f_(x_)_=_0___成
2-8 函数的图象 PPT课件 【2021衡水中学高考一轮总复习 理科数学】

高考一轮总复习 · 数学· 理(新课标版)
1.判断下列说法是否正确(打“√”或“×”). (1)若函数 y=f(x)满足 f(1+x)=f(1-x),则函数 y=f(x)的图 象关于直线 x=1 对称. (2)若函数 y=f(x)满足 f(x+1)=f(x-1),则函数 y=f(x)的图 象关于直线 x=1 对称.
【解析】 ①将y=2x的图象向左平移2个单位长度.图象如 图①.
①
②
第19页
高考一轮总复习 · 数学· 理(新课标版)
②因y=1+
3 x-1
,先作出y=
3 x
的图象,将其图象向右平移
ห้องสมุดไป่ตู้
一个单位长度,再向上平移一个单位长度,即得y=
第14页
高考一轮总复习 · 数学· 理(新课标版)
5.若关于 x 的方程|x|=a-x 只有一个解,则实数 a 的取值 范围是________.
第15页
高考一轮总复习 · 数学· 理(新课标版)
答案 (0,+∞) 解析 在同一直角坐标系中,画出函数 y=|x|和函数 y=-x +a 的图象,如图可知当 a>0 时,两函数有且只有一个交点,即|x| =a-x 只有一个解.
第5页
高考一轮总复习 · 数学· 理(新课标版)
(2)对称变换. y=f(-x)与 y=f(x)的图象关于__y_轴__对称; y=-f(x)与 y=f(x)的图象关于__x_轴__对称; y=-f(-x)与 y=f(x)的图象关于_原__点__对称; y = |f(x)| 的 图 象 可 将 y = f(x) 的 图 象 在 x 轴 下 方 的 部 分 _折__到_x_轴__上_方___,其余部分不变而得到; y=f(|x|)的图象可先作出 y=f(x)当 x≥0 时的图象,再作关于 y 轴的对称图象.
第2章 第8讲函数的图象-2021版高三数学(新高考)一轮复习课件共56张PPT

返回导航
第二章 函数、导数及其应用
高考一轮总复习 • 数学 • 新高考
返回导航
[分析] (1)先由函数的奇偶性画出y轴右侧图象,再画左侧; (2)先对绝对值分类讨论,将原函数化成分段函数的形式,再分段作图即可; (3)先化简解析式,分离常数,再利用图象变换画出图象; (4)将y=log2x的图象向左平移1个单位→y=log2(x+1)的图象→将y=log2(x+1) 的图象位于x轴下方的部分向上翻折→y=|log2(x+1)|的图象.
高考一轮总复习 • 数学 • 新高考
第二章
返回导航
函数、导数及其应用
第二章 函数、导数及其应用
高考一轮总复习 • 数学 • 新高考
返回导航
第八讲 函数的图象
第二章 函数、导数及其应用
高考一轮总复习 • 数学 • 新高考
1 知识梳理 • 双基自测 2 考点突破 • 互动探究 3 名师讲坛 • 素养提升
高考一轮总复习 • 数学 • 新高考
返回导航
[解析] (1)设 f(x)=2x+2x23 -x(x∈[-6,6]),则 f(-x)=22--x+x23x=-f(x),∴f(x)为奇函 数,排除选项 C;当 x=-1 时,f(-1)=-45<0,排除选项 D;当 x=4 时,f(4)=161+28116 ≈7.97,排除选项 A.故选 B.
第二章 函数、导数及其应用
高考一轮总复习 • 数学 • 新高考
(2)先化简,再作图. y=x-2-x2x+-x2+,2x,≥x2<,2, 图象如图实线所示.
返回导航
第二章 函数、导数及其应用
高考一轮总复习 • 数学 • 新高考
返回导航
(3)∵y=2xx--11=2x-x-11+1=2+x-1 1,∴其图象可由 y=1x的图象沿 x 轴向右平 移 1 个单位,再沿 y 轴向上平移 2 个单位得到,其图象如图所示.
届高考数学一轮复习讲义第二章函数图象

[难点正本 疑点清源] 1.一个函数的图象关于原点对称与两个函数的图象关于原
点对称 一个函数的图象关于原点对称与两个函数的图象关于原 点对称不是一回事.函数 y=f(x)的图象关于原点对称是 自身对称,说明该函数为奇函数;而函数 y=f(x)与函数 y=-f(-x)图象关于原点对称,是两个函数的图象对称.
5.已知函数 f(x)=x-x 1. (1)画出 f(x)的图象; (2)指出 f(x)的单调区间. 解 (1)∵f(x)=x-x 1=(x-x-1)1+1=1+x-1 1, ∴f(x)的中心在(1,1).如图.
(2)f(x)的单调减区间为(-∞,1)、(1,+∞).
作函数的图象
例 1 分别画出下列函数的图象: (1)y=|lg x|; (2)y=2x+2; (3)y=xx++23; (4)y=x2-2|x|-1.
答案 ④
探究提高
寻找图象与函数解析式之间的对应关系的方法: (1)知图选式: ①从图象的左右、上下分布,观察函数的定义域、值域; ②从图象的变化趋势,观察函数的单调性; ③从图象的对称性方面,观察函数的奇偶性; ④从图象的循环往复,观察函数的周期性. 利用上述方法,排除、筛选错误与正确的选项.
(2)知式选图: ①从函数的定义域,判断图象左右的位置;从函数的值域, 判断图象的上下位置; ②从函数的单调性,判断图象的变化趋势; ③从函数的奇偶性,判断图象的对称性; ④从函数的周期性,判断图象的循环往复. 利用上述方法,排除、筛选错误与正确的选项.
a
答案 ④
函数图象的应用
例 3 已知函数 f(x)=x|m-x| (x∈R),且 f(4)=0. (1)求实数 m 的值; (2)作出函数 f(x)的图象; (3)根据图象指出 f(x)的单调递减区间; (4)根据图象写出不等式 f(x)>0 的解集.
高考数学一轮总复习 第二章 函数、导数及其应用 第8讲 幂函数课件 理

定点
(0,0),(1,1)
(1,1)
1.所有幂函数的图象都经过的定点的坐标是( C )
A.(0,0)
C.(1,1)
1
2.函数 y=x3 的图象是( B )
B.(0,1) D.(-1,-1)
3.已知幂函数 y=f(x)的图象过点(4,2),则 f13=( B )
调性(比较大小).命题
图象,了解它们
形式一般为选择题、填
的变化情况
空题中的一部分
1.幂函数的定义 一般地,形如 y=xα(α∈R)的函数称为幂函数,其中 x 是自 变量,α是常数.
2.幂函数的图象
1
五个常用幂函数 y=x,y=x2,y=x3,y=x 2 ,y=x-1 的图 象,如图 2-8-1.
答案:E C A G B D H F 【规律方法】(1)探讨幂函数图象的分布规律,应先观察图 象是否过原点,过原点时α>0,否则α<0;若α>0,再观察图象 是上凸还是下凸,上凸时 0<α<1,下凸时α>1;最后由 x>1 时, α的值按逆时针方向依次增大得出结论.
(2)幂函数 y=xα(α∈R)的图象如下表:
f(x)=12x-x
1 3
,f(0)=1>0,f13=12
1 3
-13
1 3
,由于
幂函数
y=x
1 3
单调递增,得
f13=12
1 3
-13
1 3
>0;f12=12
1 2
-12
1 3
,ห้องสมุดไป่ตู้
解:由函数 f(x)在(0,+∞)上是增函数,
得
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)作出函数 y=2x-3 的图象关于 y 轴对称的图象,得到
函数 y=2-x-3 的图象;
(3)把函数 y=2-x-3 的图象向上平移 1 个单位,得到函数
y=2-x-3+1 的图象.
A
19
方法二:(1)作出函数 y=2x 的图象关于 y 轴的对称图象, 得到 y=2-x 的图象;
(2)把函数 y=2-x 的图象向左平移 3 个单位,得到 y= 2-x-3 的图象;
以函数 f(x)=ln(x-1x)的定义域为(-1,0)∪(1,+∞).所以选
项 A、C 不正确.
当 x∈(-1,0)时,g(x)=x-1x是增函数,因为 y=lnx 是增
函数,所以函数 f(x)=ln(x-1x)是增函数.
答案:B
A
23
【温馨提示】判断图象问题,一般借助:函数的定义 域、值域、单调性、奇偶性、周期性、以及函数的图象的 变化趋势等.要敏锐地从所给图象中找出诸如对称性、零 点、升降趋势等决定函数走势的因素,进而结合选择填空 题,作出合理取舍.
(3)利用函数 y=log2x 的图象进行平移和翻折变换,图象
如上图(c).
A
16
【温馨提示】画函数图象的一般方法:(1)直接法:当
函数表达式(或变形后的表达式)是熟悉的基本函数时,就可
根据这些函数的特征直接作出;(2)图象变换法:若函数图
象可由某个基本函数的图象经过平移、翻折、对称得到,
可利用图象变换作出,但要注意变换顺序,对不能直接找
A
1
第8讲 函数的图象
A
2
A
3
1.函数 y=5x 与函数 y=-51x的图象关于(C )
A.x 轴对称
B.y 轴对称
C.原点对称
D.直线 y=x 对称
A
4
2. 把函数 f(x)的图象向左、向下分别平移 2 个单位,得
到 y=2x 的图象,则 f(x)=(C )
A.2x+2+2
B.2x+2-2
A
7
解析:因为函数 y=3×(13)x 可化成 y=(31)(x-1),所 以把函数 y=(31)x 的图象向右平移 1 个单位长度得到函 数 y=3×(13)x 的图象.
A
8
4.(2013·福建)函数 f(x)=ln(x2+1)的图象大致是( A )
A.
B.
C.
D.
A
9
5.已知下列曲线:
以下编号为①②③④的四个方程:
A
24
【跟踪训练 2】(2014·福建)若函数 y=logax(a>0,且 a≠1) 的图象如图所示,则下列函数图象正确的是( )
A
B
C
D
A
25
解析:利用幂函数、指数函数、对数函数的图象和性质
解决.由题意 y=logax(a>0,且 a≠1)的图象过(3,1)点,可解 得 a=3.选项 A 中,y=3-x=(31)x,显然图象错误;选项 B 中, y=x3,由幂函数图象可知正确;选项 C 中,y=(-x)3=-x3,
(3)把函数 y=2-x-3 的图象向上平移 1 个单位,得到函数 y=2-x-3+1 的图象.
A
20
二 识图与辨图
【例 2】函数 f(x)=ln(x-1x)的图象是( )
A.
B.
C.
A D.
21
【思路点拨】求出函数的定义域,通过函数的定义域, 判断函数的单调性,推出选项即可.
A
22
【解答过程】因为 x-1x>0,解得 x>1 或-1<x<0,所
C.2x-2+2
D.2x-2-2
A
5
解析:由题意,y=2x 的图象向右、向上分别平移 2 个单 位得 y=2x-2+2 的图象.由题意得 f(x)=2x-2+2.故选 C.
A
6
3.为了得到函数 y=3×(31)x 的图象,可以把函数 y=(13)x
的图象( D )
A.向左平移 3 个单位长度 B.向右平移 3 个单位长度 C.向左平移 1 个单位长度 D.向右平移 1 个单位长度
到熟悉的基本函数的要先变形,并应注意平移变换与伸缩
变换的顺序对变换单位及解析A式的影响.
17
【跟踪训练 1】说明由函数 y=2x 的图象经过怎样的图象 变换得到函数 y=2-x-3+1 的图象.
A
18
解析:方法一:(1)将函数 y=2x 的图象向右平移 3 个单
位,得到函数 y=2x-3 的图象;
A
11
A
12
一 作函数的图形
【例 1】作出下列函数的图象: (1)y=|x-2|·(x+1); (2)y=(21)|x|; (3)y=|log2(x+1)|.
A
13
【思路点拨】(1)先利用对绝对值分类讨论将原函数化
简成分段函数的形式,再分段作图即可;(2)先利用偶函数 的定义判断出此函数为偶函数,再利用 y=(21)x(x≥0)的图
象进行变换,作出关于 y 轴对称的图形即得;(3)利用 y=
log2x 的图象翻折变换→y=|log2x|的图象,再进行向左平移
1 个单位→y=|log2(x+1)|的图象即可.
A
14
【解答过程】(1)先化简,再作图.
y=x-2-x2x+-x2+2
x≥2 x<2
.图象如下图(a).
A
15
(2)此函数为偶函数,利用函数 y=(21)x(x≥0)的图象进行 变换,图象如下图(b).
① x- y=0;②|x|-|y|=0;③x-|y|=0;④|x|-y=0.
请按曲线 A、B、C、D 的顺序,依次写出与之对应的方
程的编号 ④②①③ .
A
10
解析:对于①同解于 x≥0,y≥0,x=y 故其图象 应该为 C;对于②同解于 x2=y2,即 y=±x,故其图象 应该为 B;对于③同解于 y≥0 时 x=y 或 y≤0 时 y= -x,故其图象应该为 D;对于④同解于 x≥0 时 y=x 或 x≤0 时 y=-x,故其图象为 A.
显然与所画图象不符;选项 D 中,y=log3(-x)的图象与 y=
log3x 的图象关于 y 轴对称,显然不符.故选 B.
A
26
【跟踪训练 3】函数 y=f(x)与 y=g(x)的图象如图所示,则 函数 y=f(x)·g(x)的图象可能是( )Βιβλιοθήκη A27A.
B.
C.
D.
A
28
解析:因为 y=f(x)有两个零点,且 x=0 时,y=g(x)的 函数值不存在,所以函数 y=f(x)·g(x)也有两个零点 M,N, 且 x=0 时,函数值不存在,当 x∈(-∞,M)时,y<0;当 x ∈(M,0)时,y>0;当 x∈(0,N)时,y<0;当 x∈(N,+∞) 时,y>0;只有 A 中的图象符合要求.
