时间反演(简介)
4.4 时间反演分立对称性

对j半整数体系,则-|n>=ΘΘ|n>=Θeiδ|n>=|n>,故|n>与 Θ|n>不可能为同一状态,存在简并,这不依赖于E的 复杂程度。因此,具有不同奇偶电子的晶体在外电场 中的行为很不相同。
十、粒子与电和磁场的相互作用:Kramers简并
有外磁场时,H含
S B , p A A p , ( B A ). 由 于 p , S
(k ) q
j T
(k )
j
jkmq
2 j 1
只要考虑q=0的分量即可。
对厄米球张量,其时间反演奇偶性由q=0分量确定:
Tq 0
(k ) 1
T q 0 . 对 A T q 0, 有
(k ) (k )
由于x对应于k=1,且对时间反演是偶的,故对jm的本 征态<x>=0,这对非宇称本征态亦成立
θ是反幺正的
五、时间反演算符Θ
时间反演态(运动反演态):Θ |α>
上面讨论知,动量本征态|p>的时间反演态:
Θ|p>=|-p> 时间反演算符的基本性质:
由态矢时间反演的对称性
得:-iHΘ=ΘiH,Θ应为反幺正算符
HΘ=ΘH
五、时间反演算符Θ
重要等式:
这是因为对
对时间反演,波函数变为复共轭,应有
~ ~ *
: ~ , ~
定义:对变换
*;
,如果
( c1 c 2 ) c1 * c 2 * ),
信号对时间反演电磁波聚焦特性影响的数值仿真研究

摘要*时间反演技术(Time Reversal, TR)是指对时域信号的一种逆序操作,该技术可以克服多径效应这一传统通信中的不利因素,将多径效应充分利用,获得空间复用及自适应聚焦的效果,即时空聚焦特性。
TR技术独特的时空聚焦特性使其在通信、输能以及高分辨率成像领域都具有广泛的应用前景。
但现今TR技术在电磁波领域的研究还处于初始阶段,尤其在信号对TR电磁波聚焦特性影响的研究方面还有所欠缺。
针对上述问题,本文的主要工作内容如下:(1)介绍TR技术的基本理论。
首先引出时间反演镜(Time Reversal Mirror, TRM)和多径效应两个重要概念。
接着从数学理论的角度探讨TR技术的时间聚焦特性和空间聚焦特性及相应性能表征,最后详细阐述TR技术的单天线MIMO效应。
(2)研究信号对TR电磁波聚焦特性的影响并提出改善聚焦性能的方法。
首先利用时域有限差分法算法(Finite-Difference Time-Domain, FDTD)电磁仿真工具以及MATLAB软件建立有限数量TRM阵列单元金属腔仿真模型,接着对三种信号特性(信号波形,信号带宽,信号载频)对TR电磁波时间聚焦和空间聚焦特性的影响进行了仿真实验和结果分析。
最后实验结果表明,信号特性对TR电磁波的时间聚焦和空间聚焦特性有明显的影响,选择合适的信号类型或提高信号带宽,可以增强TR电磁波时空聚焦性能。
(3)研究信号对TR单天线MIMO效应中信道有效多径数量的影响并提出增加有效多径数量的方法。
首先利用仿真实验和物理实测实验,得到空间信道冲激响应,最后对信道有效多径数量的影响进行了统计和分析。
实验结果表明增加信号带宽可以有效增加信道有效多径数量,实现更优的TR单天线MIMO性能。
关键词:时间反演;信号特性;时空聚焦;单天线MIMO效应;数值仿真*本课题得到国家自然科学基金(61871193)、广东省自然科学基金重点项目(2018B030311049)和工信部国家物联网专项(工信部科函[2014]351 号)的资助。
§4.4时间反演分立对称性
a'
a'
a'
a" a" UU a' a' * θ是反幺正的
a' a"
五、时间反演算符Θ
时间反演态(运动反演态): Θ |α> 如由上面讨论知,动量本征态|p>的时间反演态: Θ|p>=|-p> 时间反演算符的基本性质 假设态矢具有时间反演对称性:
得:-iHΘ=ΘiH,Θ应为反幺正算符 HΘ=ΘH
六、时间反演算符Θ的运算
仅考虑Θ从左边作用于右矢,和利用 ~ ~ * 及左右矢的对偶对应关系
重要等式: 这是因为对
,有
故
七、厄米算符的时间反演对称性
对厄米算符A,有
若ΘAΘ-1=±A,称A在时间反演下具有偶(奇)对称
由此,
可得A在时间反演态的期望值:
由
,知 ΘpΘ-1=-p
而 故对任意|α>:
此外,由于
不妨约定 1/2体系,该约定对应于取 i )
(对自旋
一般地可约定: 注:相位约定依处理问题方便而定,但Θ2=±1与相位约定无关。
十一、球张量的时间反演性质
对
若A是
T (k) q
的分量,由于Wigner-Eckart定理
j T (k) j
jm
T (k) q
§4.4 时间反演分立对称性
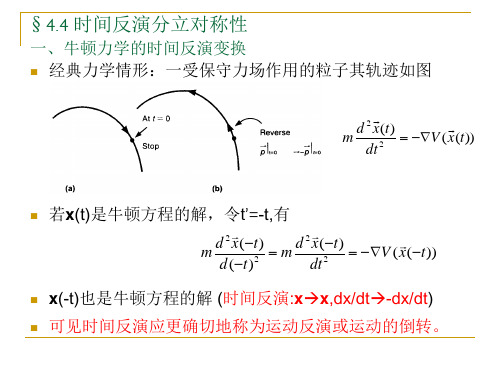
一、牛顿力学的时间反演变换
经典力学情形:一受保守力场作用的粒子其轨迹如图
m
d
2
x(t)
V
(x(t))
dt 2
若x(t)是牛顿方程的解,令t’=-t,有
m
d 2 x(t) d (t)2
m
d 2 x(t) dt 2
4.4 时间反演分立对称性

Xr(t)=x(-t)也是牛顿方程的解 (时间反 演:xx,dx/dt-dx/dt)
时间反演应更确切地称为运动反演或运动的倒转。
二、电动力学的时间反演变换
Maxwell方程:
Lorentz力:
1 F e E (v B) c
对t-t变换,若
对j半整数体系,则-|n>=ΘΘ|n>=Θeiδ|n>=|n>,故|n>与 Θ|n>不可能为同一状态,存在简并,这不依赖于E的 复杂程度。因此,具有不同奇偶电子的晶体在外电场 中的行为很不相同。
十、粒子与电和磁场的相互作用:Kramers简并
有外磁场时,H含
S B, p A A p, (B A). 由于p, S
对
(k ) T 若A是 q 的分量,由于Wigner-Eckart定理
j m T
(k ) q
jm jkm q jkjm
j T ( k ) j
2 j 1
只要考虑q=0的分量即可。
对厄米球张量,其时间反演奇偶性由q=0分量确定:
k ) 1 (k ) (k ) Tq( T . 对 A T 0 q 0 q 0,有
在时间反演下是奇的, [Θ,H]≠0 ,不存在Kramers简 并
一般而言,反幺正算符可写成θ=UK,U为幺正算 符,K为复共轭算符。K对右矢的叠加系数作用, 即 Kc c * K .若 为基矢,则K 若|α>不是基矢,可展开为以|a’>为基矢的矢量:
Ca a ,则K Ca * a
高量15-时间平移和时间反演

ˆ ( H 不显含时间)
i ˆ H
所以:
ˆ D( ) e
d dt
e
6
§21-2 时间反演
一、态函数的时间反演变换
ˆ 1.时间反演算符 T0
ˆ 设系统的 H 为实算符(不含虚数),且不含时,无自
旋。系统的态满足Schrö dinger方程:
ˆ i (r, t ) H (r, t ) t
14
3. 时间反演算符的数学性质
无自旋系统的时间反演算符可以写成
ˆ ˆ T0 KT1
ˆ K (r, t ) * (r, t )
T1 (r, t ) (r,t )
不寻常的数学性质:
ˆ (1)时间反演算符 T0 不是线性算符,它是反线性算符。
它虽然满足 但是
ˆ ˆ ˆ T0 ( 1 2 ) T0 1 T0 2 ˆ ˆ ˆ T0 (a ) a *T0 aT0
ni
i En t
式中
ˆ H ni (r ) En ni (r )
i 1,2, , d n
i Ent
d n 是能级 En 的简并度。
* * ˆ (r, t ) T0 (r, t ) * (r,t ) ani ni (r )e 时间反演态: ni
T 除了符合 T0 所满足的21.10式或21.19式之外,还应满足
TST 1 S
S是粒子的自旋算符。令 T UT0
其中 T0 KT1 , U 是一个 2 2 矩阵,为自旋空间中的算符。
TST 1 UT0ST0 U 1 US*U 1
1
22
在 S z 表象中,
1 0 Sz 0 1 2
基于全电子技术的时间反演镜_从声波到微波_梁木生

的核心部件,因此,TRM 实现一直是研究者们关注 的问题。
按照 应 用 频 率 的 高 低,TRM 可 以 分 为 声 波 TRM、微波 TRM 和光波 TRM。声波 / 超声波频率较 低,其 TRM 实现技术日趋成熟,应用领域最为广泛, 包括水下声波通信、人体超声波碎石等。微波信号 的 TRM 实现鲜有报道,尚处于方案探索阶段,目前 主要借助高端仪器如高端任意波形发生器( AWG) 、 示波器( DSA) 等实现时间反演。光波 TRM 实现已 有部分报道,因涉及激光源等设备,其研究成本较为 高昂。因此,随着频率的增高,TRM 实现的难度和 成本也随之增加。
本文将从声波 TRM 的研究现状出发,简单分析
* 收稿日期:2011-04-17; 修回日期:2011-09-08 基金项目:国家自然科学 基 金 ( 61071031 ) ; 教 育 部 博 士 点 基 金 ( 20100185110021 ) ; 中 央 高 校 基 本 科 研 业 务 费 项 目 ( E022050205)
第 27 卷第 6 期 2011 年 12 月
微波学报
JOURNAL OF MICROWAVES
Vol. 27 No. 6 Dec. 2011
文章编号:1005-6122( 2011) 06-0001-05
基于全电子技术的时间反演镜:从声波到微波*
梁木生 王秉中 丁 帅
( 电子科技大学应用物理研究所,成都 610054)
目前基于全电子技术实现声波trm实现方案分析基于全电子技术实现声波trm的常用方案有时间变换系统框图caputi还利用傅里叶变换理论进行了推导分析并通过简单的实验验证了该方案的可行schwartz等人利用该原理通过全电子技术实现了微波信号在时域上的拉伸15其关键器件是电磁带ebg啁啾色散延迟线161989年kolnernazatathy提出了时域成像和时间透镜概念17
物理量及物理方程的时间反演变换

收稿日期:2019年4月17日;录用日期:2019年5月3日;发布日期:2019年5月10日
文章引用: 李大庆. 物理量及物理方程的时间反演变换[J]. 现代物理, 2019, 9(3): 162-175. DOI: 10.12677/mp.2019.93018
李大庆
Modern Physics 现代物理, 2019, 9(3), 162-175 Published Online May 2019 in Hans. /journal/mp https:///10.12677/mp.2019.93018
Time Inversion of Physical Quantity and Physical Equation
Open Access
1. 引言
当前被人们普遍接受的观点是,时间反演变换是一种将物理量及物理方程中的时刻 t 直接用−t 替换 从而导致时间方向逆转的数学变换[1],是用于研究物理过程与其逆过程之间对称关系的重要方法以及研 究物理过程可逆性的重要数学工具;同时,由于时间反演变换被认为可导致与原物理过程变化方向相反 的物理过程,因此时间和物理过程两者常被认为是同一的,而且人们普遍认为(热力学)过程的不可逆导致 时间的单向性[2],换句话说“时间前进的方向就是气体分子变得越来越均匀,从而达到越来越高的熵的 方向”[3]。据此推论,经典力学、电磁学等所描述的最基本物理过程的可逆性应导致时间的双向(或无向) 性,而且人们在思考相关问题时都会在不知不觉中产生类似的观点[4]。那么这是否意味着时间既是单向 的、(至少在理论上)又是双向的呢?美国物理学家布赖恩·格林在其著作中就提出过类似的问题,但并没 有给出明确的结论[5],由此可见,目前采用的时间反演变换的概念及方法有值得商榷之处。本文的研究 表明,产生这一问题的根源在于,物理过程的时间反演变换虽然是其关于 t = 0 轴(或坐标原点 O(0,0)) 的对称变换,但人们却直接将变换所得物理过程作为原物理过程的逆转变换。而正是在对时间反演变换 定义中物理过程方向性的详细分析基础上,本文获得了在时间保持正向流逝条件下时间反演变换将改变 物理过程的方向的重要结论;同时,在此基础上还推论出在时间反演变换操作中物理过程与其逆过程的 微分、导数以及常用算符之间的对称关系,并对几个重要物理方程的时间反演变换进行了讨论。结果表 明,当前物理学中普遍采用的时间反演变换的操作定义虽然能获得正确结论,但操作方法并不恰当,并 且将时间的单向性归结为热力学过程的不可逆性的观念也有问题。
时间平移和时间反演概述

时间平移和时间反演概述时间平移和时间反演是物理学中常用的两个概念,它们都与时间的变化有关,但有着不同的含义和应用。
时间平移是指在时间上进行整体的移动或平移。
在物理学中,我们通常关注某个系统、现象或过程在不同时间点上的变化。
时间平移是指将这些时间点整体向前或向后移动,以便进行更详细或全面的观察和研究。
通过时间平移,我们可以在不同的时间点上观察和比较物理量的变化,以了解系统的演化规律、发展趋势或特性。
时间反演是指将一个物理现象或过程的时间轴倒置。
即,将时间向前的方向转换为时间向后的方向,以便研究物理现象的对称性、逆向演化或关联性。
时间反演是物理学中的基本操作之一,它常常应用于求解物理问题、理解系统行为和预测未来的发展趋势。
例如,在天体物理学中,通过时间反演可以研究宇宙的起源和演化;在热力学中,时间反演可以揭示系统的热传导规律和热平衡状态等。
时间平移和时间反演在物理学的研究中具有重要的应用价值。
它们不仅可以帮助我们理解物理现象的规律和本质,还可以推动科学技术的发展和应用。
例如,通过时间平移和时间反演的分析,我们可以预测和追溯地震、气候变化、流体动力学和量子力学等领域的发展趋势和演化规律。
同时,时间平移和时间反演还在工程、生物、经济等领域中发挥着重要作用,为我们解决实际问题和改善生活提供理论和方法支持。
总之,时间平移和时间反演是物理学研究中常用的两个概念。
它们通过调整时间轴的位置和方向,帮助我们更好地理解系统的演化和规律,预测未来的发展趋势和态势,以及解决实际问题和改善生活。
它们的应用广泛,是推动科学技术进步和实现可持续发展的重要工具和方法之一。
时间平移和时间反演作为物理学中常用的两个概念,在各个领域都具有广泛的应用。
接下来,我们将进一步探讨这两个概念在各个学科和实践领域中的应用和重要性。
在经典物理学中,时间平移和时间反演的应用非常广泛。
在力学中,时间平移可以帮助我们观察和比较物体的运动情况。
通过比较不同时间点上的位置和速度,我们可以了解到物体在不同时间段内的运动规律和变化趋势。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
附件1
时间反演(简介)
人们常说时间如箭,而箭射出去不会自己飞回来。
这实际上表明了时间的一种特性:方向性。
我们记得昨天发生了什么,但已经没有办法再去改变它们了。
而对于未来,是可以找到办法来影响的。
如果把一部电影倒转过来看,你会看到一栋倒塌的大楼自己又立了起来,一堆灰烬又恢复成为完整的木材,它会显得不真实,甚至于可笑。
在人类的日常经验当中,过去和未来属于不同的区域,有着不同的性质,相互不能交换。
但是在物理学中,对于最基本的物理定律有着不一样的故事。
自从17世纪现代物理学诞生直到20世纪,基本物理规律对于过去和未来都表现不出差别。
尽管一部反着播放的电影看上去是荒谬的,但如果盯着其中的粒子看,却发现它们是高度符合物理定律的。
如果我们对一个近乎于无摩擦环境下的一个盒子里四处乱飞的小球拍摄录像,该录像正着放、反着放都看不出区别。
也就是说,对于基本物理定律,时间是正着走,还是反着走都没有区别。
这被称为时间反演对称性,经常用字母T表示。
与时间对称性紧密相关的是空间的对称性,称为空间反演对称性,常又称为宇称,用字母P来表示。
宇称这种对称性表达的意思是如果你通过一个镜子观察世界的话,所看到的物理规律和镜子外看到的真实世界是一样的。
空间反演是通过一面镜子将左和右进行交换,而时间反演是将一部电影正着放变为反着放。
在1956年之前,所有已知的物理定律都符合空间反演对称性。
但李政道先生和杨振宁先生在1956年从理论上提出,如果弱相互作用不遵守空间反演对称性,那么当时在其理论研究中遇到的一些困难就可以得到解决。
弱相互作用是已知的四种基本相互作用之一,它可以使得一种粒子变成另外一种,比如将中子变为质子。
吴健雄女士及其他的一些人不久就通过精心设计的实验证明了这一想法。
1957年李政道和杨振宁因此获得了诺贝尔物理学奖。
对于宇称不守恒(即空间反演对称性失效)的研究使得理论物理学的研究有了很大的进展,极大加深了人们对于弱相互作用的认识和理解。
受到宇称不守恒的影响,物理学家对于时间反演对称性进行了细致的验证。
他们开展了很多灵敏的实验,寻找是否存在时间反演不变性的破坏。
最终在1964年James Cronin 和 Val Fitch发现在高能加速器上产生的某些不稳定粒子的表现行为中,表现出了时间反演对称性微弱的破坏。
James Cronin 和 Val Fitch因此获得了1980年的诺贝尔奖。
对于时间反演对称性破坏的研究产生了很多成果。
Makoto Kobayashi和Toshihide Maskawa由此提出存在着一系列的新粒子,并且这些新粒子都相继被观察到了。
他们因此获得了2008年的诺贝尔奖。
今天,在物理学的前沿,人们依然在进行着对于时间反演对称性破坏的研究。
为什么时间反演对称性看上去如此的无可厚非?在Roberto Peccei 和Helen Quinn的工作基础上,Frank Wilczek和Steven Weinberg提出一种被称为轴子的新粒子,它可以保持过去和未来之间的平衡。
在预言中,轴子与普通物质之间只有非常微弱的相互作用,因此很难在实验中被发现。
目前轴子依然只是个假设,全世界有很多的实验团队非常努力地在寻找轴子。
天文学家在观测引力场时发现质量有所缺失,他们把缺失的物质称为暗物质,有一个重要的理论认为暗物质就是由轴子组成的。
我们在时间之河中飘荡,河水带着我们不可逆转地向前流动。
但在想象的空间中,我们可以令时间之河倒流。
那种景象是神奇和美丽无比的,可以让我们深入洞察世界之妙。
让艺术家们也拥有这样的机会吧。
作者简介:Frank Wilczek,2004年诺贝尔物理学奖得主、李政道研究所所长
译者简介:李晟,李政道研究所所长助理。
