一般锐角的三角函数值
《一般锐角的三角函数值》PPT课件
知2－讲
【例3】已知下列锐角三角函数值，用计算器求其相应的 锐角：
(1)sin A＝0.516 8(结果精确到0.01°)； (2)cos A＝0.675 3(结果精确到1″)； (3)tan A＝0.189(结果精确到1°)． 导引：已知锐角三角函数值，利用计算器求锐角的度数
时要注意先按 2nd F 键．
一、启发类
1. 集体力量是强大的，你们小组合作了吗?你能将这个原理应用于生活吗?你的探究目标制定好了吗? 2. 自学结束，请带着疑问与同伴交流。 3. 学习要善于观察，你从这道题中获取了哪些信息? 4. 请把你的想法与同伴交流一下，好吗? 5. 你说的办法很好，还有其他办法吗?看谁想出的解法多? 二、赏识类
1 已知三角函数值，用计算器求锐角A和B：（精确到 1′）
（1）sinA=0.708 3,sinB=0.568 8； （2）cosA=0.829 0,cosB=0.993 1； （3）tanA=0.913 1,tanB=31.80.
（来自教材）
知2－练
2 已知β为锐角，且tan β＝3.387，则β约等于
()
A．73°33′
B．73°27′
C．16°27′
D．16°21′
3 在△ABC中，∠C＝90°，BC＝5，AB＝13，用科
学计算器求∠A约等于( )
A．24°38′
B．65°22′
C．67°23′
D．22°37′
知2－练
4 如果∠A为锐角，cos A＝ 1 ，那么( ) 5
A．0°<∠A<30° B．30°<∠A<45° C．45°<∠A<60° D．60°<∠A<90°
知1－练
锐角三角函数值表课件
锐角a
三角函数 sin a cos a tan a
30°
1 2 3 2
3 3
45°
2 2
2 2
1
60°
3 2
1 2
3
对于sinα与tanα，角度越大，函数值也越大； 对于cosα，角度越大，函数值越小。
米．然后他很快就算出旗杆的高度了。
你想知道小明怎样 算出的吗？
?
1.65米
30°
10米
练习：P83-练习
例3、(1)如图，在Rt△ABC中， ∠C=90°，AB= 6 ,BC= 3。求∠A的度数。
(2)如图,已知圆锥的高AO等于圆锥的底面半 径OB的 3 倍,求α.
A
B
(2)
6
3
A
C
(1)
O B
Q sin A CD 1 CD 1 2 3 3
AC 2
2
A
Q cos A AD 3 AD 3 2 3 3
AC 2
2
D
B
Q tan B CD 3 BD 2
BD
3 2 2 3
AB AD BD 3 2 5
练习
1. 求下列各式的值：
例4 如图，在Rt△ABC中，∠ACB=90度，CD⊥AB于D ，已
知∠B=30度，计算 tan ACD sin BCD 的值。
A D
B
C
例5 如图，在△ABC中，∠A=30度， tanB 3 , AC 2 3,
2
求AB。
C
解：过点C作CD⊥AB于点D
∠A=30度， AC 2 3
（1）1－2 sin30°cos30°
23.一般锐角的三角函数值PPT课件(沪科版)
B C = C D 4 .2 5 .9 (千 米 )， sin C BA sin 45
【方法总结】解决问题的关键是作出辅助线，构造直 角三角形，利用三角函数关系求出有关线段的长．
例4：如图，课外数学小组要测量小山坡上塔的高度 DE，DE所在直线与水平线AN垂直．他们在A处测得塔 尖D的仰角为45°，再沿着射线AN方向前进50米到达B 处，此时测得塔尖D的仰角∠DBN＝61.4°，小山坡坡 顶E的仰角∠EBN＝25.6°.现在请你帮助课外活动小组 算一算塔高DE大约是多少米 (结果精确到个位)．
解：延长DE交AB延长线于点F，则∠DFA＝90°.
∵∠A＝45°，
∴AF＝DF.
设EF＝x，
∵tan25.6°＝ EF ≈0.5，
BF
∴BF＝2x，则DF＝AF＝50＋2x，
故tan61.4°＝
DF BF
50 2x 2x
＝1.8，
解得x≈31.
故DE＝DF－EF＝50＋31×2－31＝81(米)．
所以，塔高DE大约是81米．
归纳总结
解决此类问题要了解角之间的关系，找到 与已知和未知相关联的直角三角形，当图形中 没有直角三角形时，要通过作高或垂线构造直 角三角形．
巩固练习
1. 已知下列锐角三角函数值，用计算器求其相应 的锐角： （1）sinA=0.627 5，sinB＝0.054 7；
∠A=38°51′57″ ∠B=38°8″
初中正弦余弦正切公式
初中正弦余弦正切公式“初中数学必背三角函数公式、三角函数值”主要包括正弦、余弦、正切函数的定义式和关系式，特殊锐角的正弦、余弦、正切值。
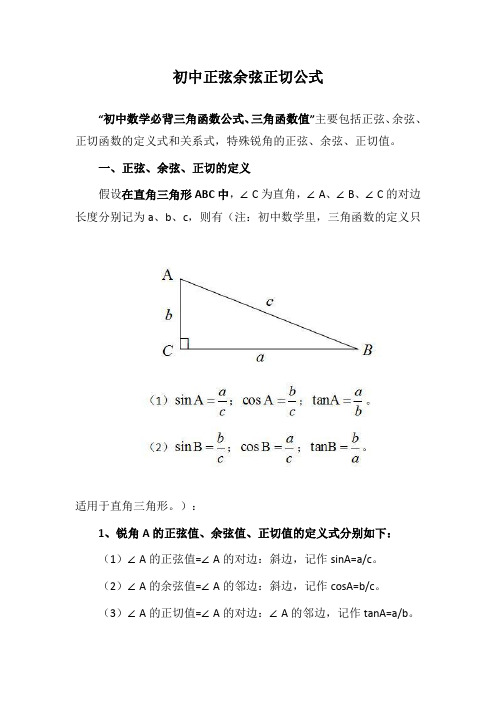
一、正弦、余弦、正切的定义假设在直角三角形ABC中，∠C为直角，∠A、∠B、∠C的对边长度分别记为a、b、c，则有（注：初中数学里，三角函数的定义只适用于直角三角形。
）：1、锐角A的正弦值、余弦值、正切值的定义式分别如下：（1）∠A的正弦值=∠A的对边：斜边，记作sinA=a/c。
（2）∠A的余弦值=∠A的邻边：斜边，记作cosA=b/c。
（3）∠A的正切值=∠A的对边：∠A的邻边，记作tanA=a/b。
2、锐角B的正弦值、余弦值、正切值的定义式分别如下：（1）∠B的正弦值=∠B的对边：斜边，记作sinB=b/c。
（2）∠B的余弦值=∠B的邻边：斜边，记作cosB=a/c。
（3）∠B的正切值=∠B的对边：∠B的邻边，记作tanB=b/a。
【注】正弦=“对比斜”、余弦=“邻比斜”、正切=“对比邻”。
3、互余的两个角间的正弦、余弦、正切值关系假设在直角三角形ABC中，∠C为直角，则∠A与∠B互余。
通过∠A和∠B的正弦、余弦、正切值的定义式的对比，我们不难发现：∠A的正弦值与∠B的余弦值相等，∠A的余弦值与∠B的正弦值相等，∠A的正切值与∠B的正切值互为倒数。
所以，当∠A与∠B互余时我们有以下3个同时成立的等式关系：（1）sinA=cosB；（2）sinB=cosA；（3）tanA·tanB=1。
二、同角的正弦值、余弦值、正切值间的关系式1、商数关系：tanA=sinA/cosA；tanB=sinB/cosB.2、平方关系：同一个锐角的‘正弦的平方’与‘余弦的平方’的和为1，即(sinA)^2+(cosA)^2=1；(sinB)^2+(cosB)^2=1.3、倒数关系：tanA·cotA=1；tanB·cotB=1.【注】“cotA”称为为∠A的余切，它等于∠A的邻边比上∠A的对边。
锐角的三角函数值
锐角的三角函数值（4）——一般锐角的三角函数值导学目标：会使用计算器求锐角三角函数值，会使用计算器根据锐角三角函数值求对应的锐角。
一自主预习：1.在利用计算器求一个锐角的三角函数值时,应先使计算器设置在”“状态.标志是屏幕上显示 .2.sin-1,cos-1,tan-1键是表示由求锐角度数的功能键3.求sin400的值的按键顺序是什么？4.求值(精确到0.0001)⑴cos34035/⑵tan66015/17//二．合作探究：探究点1：求一个锐角的三角函数值。
我们知道sin300=,那么sin3002/是多少呢？说明：⑴用计算器求一个角的三角函数值时，首先要把计算器设置在“角度”状态下，也就是在计算器的显示屏上出现“DEG”的字样。
⑵在角度单位状态为度的情况下，先输入数据，再按sin,cos,tan键可以直接求出一个角的正弦，余弦，正切值了例1：用计算器求下列各三角函数的值（精确到0.001）⑴sin240⑵tan63027/ ⑶cos18059/27//例2.用计算器求：①sin100,sin200,sin300,……sin900的值.②cos100,cos200,cos300,……,cos900的值.③tan100,tan200,tan300,……,tan900的值.⑵根据所求结果总结：①随角度变化函数值的变化规律。
②同角的正余弦函数值间的关系⑵比较大小：①sin72032/ 620 ; ②cosa cosβ (a<β,a,β为锐角)⑶sin12012/ cos78030探究点二：已知三角函数值求锐角。
例.根据下列条件求∠A 的度数（用度，分，秒表示）⑴cosA=o.6753 ⑵tanA=87.54 ⑶sinA=0.4553说明：计算器中sin-1,cos-1,tan-1，这些键的功能是由正弦值，余弦值，正切值求锐角的度数。
在角度状态为“度“的情况下，求锐角时，先输入数据，再按2ndF键，再按sin-1,cos-1,tan-1键，即可得到相应的角度。
特殊角的三角函数值及用计算器求角的三角函数值
（1）我们要用到科学计算器中的 键： sin cos tan
（2）按键顺序
◆如果锐角恰是整数度数时，以 “求sin18°”为例，按键顺序如下：
按键顺序 显示结果
sin18°
sin 18 sin18
0.309 016 994
∴ sin18°= 0.309 016 994≈0.31
1、用科学计算器求一般锐角的三角函数值：
7
4
=
显示结果
17.30150783
如果再按“度分秒健”就换算成度分 秒， °′″
即∠ α＝17o18’5.43”
2.熟练掌握用科学计算器由已知三角函
数值求出相应的锐角.
例如：sin A=0.9816，∠A＝
；
cos A＝0.8607，∠A＝
；
tan A＝56.78，∠A＝
。
小结 :
1.30°、45°、60°角的三角函数值， 并且进行计算；
（1）m的值；（2）∠A与∠B的度数．
活动4
当锐角A是特殊角时，可以求得这些角的正弦、余 弦、正切值；如果锐角A不是这些特殊角，怎样得 到它的三角函数值呢？
我们可以用计算器来求锐角的三角函数值。 sin37°24′ sin37°23′ cos21°28′ cos38°12′
用科学计算器求一般锐角的三角函数值：
两块三角尺中有几个不同的锐 角？分别求出这几个锐角的正 弦值、余弦值和正切值．
60°
30° 45°
45°
设30°所对的直角边长为a，那么斜边长为2a
另一条直角边长＝ 2a2 a2 3a
sin 30o a 1 2a 2
30°
cos 30o 3a 3 2a 2
tan 30o a 3 3a 3
锐角三角函数知识点总结
锐角三角形必背知识点1 定义直角三角形中角A的正弦（sin）,余弦（cos）和正切（tan）叫做角A的三角函数。
正弦（sin）等于对边比斜边；sinA=a/c余弦（cos）等于邻边比斜边；cosA=b/c正切（tan）等于对边比邻边；tanA=a/b锐角三角函数值的定义方法是在直角三角形中定义的，所以求锐角的三角函数值，要通过构造直角三角形来完成的，即把这个角放到某个直角三角形中。
2 特殊角的三角函数值角度30°45°60°正弦(sin) 1/2 √2/2 √3/2余弦(cos) √3/2 √2/2 1/2正切(tan) √3/3 1 √3（注θ是锐角：0<sinθ<1 0<cosθ<1 tanθ>0）3锐角三角函数值的符号及其变化规律1）锐角三角函数值都是正值。
2）当角度在0°~90°间变化时，正弦值随着角度的增大（或减小）而增大（或减小）；余弦值随着角度的增大（或减小）而减小（或增大）；正切值随着角度的增大（或减小）而增大（或减小）；4同角三角函数基本关系式a a a tan cos sin ⋅=5互为余角的三角函数间的关系a a cos )90sin(=-a a sin )90cos(=-6 解直角三角形的基础知识在Rt ABC ∆中， 90=∠C ，A ∠，B ∠，C ∠所对的边分别为a ，b ，c（1） 三边之间的关系：222c b a =+（2） 锐角之间的关系：A ∠+B ∠=C ∠= 90（3） 边角之间的关系：c a A =sin ；c b A =cos ；ba A =tan ； c a B =cos ；c b B =sin ；ab B =tan （4） 面积公式：ch ab S 2121==∆（h 为斜边上的高） 7 解直角三角形的基本类型及其解法如下表：解直角三角形的思路可概括为“有斜（斜边）用弦（正弦、余弦），无斜用切（正切），宁乘勿除，取原避中”。
锐角三角函数。
锐角三角函数。
锐角三角函数是数学中的一个重要概念，它在解决三角函数问题时起着关键作用。
锐角指的是小于90度的角，锐角三角函数包括正弦、余弦和正切三种函数，它们分别表示了锐角三角形中的比例关系。
下面我们将逐一介绍这三种函数的定义和性质。
1. 正弦函数（sine function）正弦函数是锐角三角函数中最常见的一种函数，它表示了锐角三角形中的对边与斜边之间的比例关系。
设锐角为θ，对边长度为a，斜边长度为h，则正弦函数的定义为sinθ = a/h。
正弦函数的取值范围是[-1, 1]，当θ为0度时，正弦函数的值为0；当θ为90度时，正弦函数的值为1。
2. 余弦函数（cosine function）余弦函数也是锐角三角函数中常用的一种函数，它表示了锐角三角形中的邻边与斜边之间的比例关系。
设锐角为θ，邻边长度为b，斜边长度为h，则余弦函数的定义为cosθ = b/h。
余弦函数的取值范围也是[-1, 1]，当θ为0度时，余弦函数的值为1；当θ为90度时，余弦函数的值为0。
3. 正切函数（tangent function）正切函数是锐角三角函数中最特殊的一种函数，它表示了锐角三角形中的对边与邻边之间的比例关系。
设锐角为θ，对边长度为a，邻边长度为b，则正切函数的定义为tanθ = a/b。
正切函数的取值范围是(-∞, +∞)，当θ为0度时，正切函数的值为0；当θ为45度时，正切函数的值为1。
锐角三角函数在数学和物理中有着广泛的应用。
例如，在三角函数的图像中，正弦函数和余弦函数是周期函数，它们的图像呈现出波浪形状，常用于描述周期性的现象；而正切函数则常用于描述角度的变化率，例如在物体运动的分析中。
除了上述三种常见的锐角三角函数外，还有其余的三角函数，如余切函数、正割函数和余割函数，它们的定义和性质与前述三种函数类似，但使用频率相对较低。
在实际问题中，锐角三角函数可以用于解决各种与角度相关的计算和分析问题。
例如，可以利用正弦函数计算在斜面上物体的下滑速度，利用余弦函数计算在斜面上物体的压力分量，利用正切函数计算两个物体之间的相对速度等等。
初三常用三角函数值表
初三常用三角函数值表
在初中数学学习中，三角函数是一个非常重要的概念，而
三角函数值表则是初学者经常需要掌握的内容之一。
三角函数包括正弦、余弦和正切三种函数，它们在不同角度下的取值可以通过表格形式展示，方便学生查找和运用。
在初三阶段，学生通常需要熟记特定角度下的三角函数值，这对于解决三角函数问题和推导公式都有很大帮助。
正弦函数值表
角度0°30°45°60°90°
正弦值00.5√2/2√3/21
余弦函数值表
角度0°30°45°60°90°
余弦值1√3/2√2/20.50
正切函数值表
角度0°30°45°60°90°
正切值0√3/31√3不存在
通过上面的三角函数值表，我们可以看到在常见角度下，
正弦、余弦和正切函数的取值情况。
这些数值是通过三角函数的定义和几何图形推导得到的，对于初三学生来说，熟练掌握这些数值对于解答题目是非常有帮助的。
同时，这些数值也在实际生活和工程领域中有着广泛的应用，比如在建筑、航海、天文学等领域都会用到三角函数的概念和数值。
除了常用的角度下的数值，还有一些其他角度下的三角函
数值也是初中阶段需要记住的，比如120°、150°、210°、240°等。
通过不断练习和记忆，学生可以更加熟练地运用三
角函数值，解决各种数学问题，为未来的学习打下坚实的基础。
希望初三的学生能够认真学习三角函数，掌握相关的数值表，提高数学水平，为未来的学习和发展奠定扎实的基础。
初中常用的三角函数值表
初中常用的三角函数值表
在初中数学学习中，三角函数是一个非常重要的概念。
三角函数在数学中起到了非常关键的作用，它们与角度的关系紧密联系在一起。
我们常用的三角函数包括正弦函数、余弦函数和正切函数，它们在初中阶段被广泛讨论和运用。
了解三角函数值的表格对于解题和理解三角函数的性质非常有帮助。
正弦函数值表
正弦函数是三角函数中的一个重要概念，它表示一个角的正弦值。
正弦函数的值域在-1到1之间变化，下表列出了一些常见角度对应的正弦函数值：
角度0°30°45°60°90°
正弦值01/2√2/2√3/21
余弦函数值表
余弦函数是另一个常用的三角函数，它表示一个角的余弦值。
余弦函数的值域也在-1到1之间，下表列出了一些常见角度对应的余弦函数值：
角度0°30°45°60°90°
余弦值1√3/2√2/21/20
正切函数值表
正切函数是三角函数中的另一个重要概念，它表示一个角的正切值。
正切函数的值可以是任意的实数，下表列出了一些常见角度对应的正切函数值：
角度0°30°45°60°90°
正切值0√3/31√3无穷大
通过上述三角函数的值表，我们可以看到不同角度对应的正弦、余弦和正切函数值的关系。
这些数学概念在几何学、物理学等领域中有着广泛的应用，掌握它们有助于我们更深入地理解数学知识。
在初中阶段，三角函数值表是一个重要的学习工具，帮助我们更好地理解和运用三角函数的性质和特点。
锐角三角函数
锐角三角函数定义锐角角A的正弦（sin）,余弦（cos）和正切（tan）,余切（cot）以及正割（sec），余割（csc）都叫做角A的锐角三角函数。
正弦（sin）等于对边比斜边；sinA=a/c余弦（cos）等于邻边比斜边；cosA=b/c正切（tan）等于对边比邻边；tanA=a/b余切（cot）等于邻边比对边；cotA=b/a 正割（sec)等于斜边比邻边；secA=c/b余割(csc)等于斜边比对边。
cscA=c/a初中学习的锐角三角函数值的定义方法是在直角三角形中定义的，所以在初中阶段求锐角的三角函数值，都是通过构造直角三角形来完成的，即把这个角放到某个直角三角形中。
到了高中三角函数值的求法是通过坐标定义法来完成的，这个时候角也扩充到了任意角。
所谓锐角三角函数是指：我们初中研究的都是锐角的三角函数。
初中研究的锐角的三角函数为：正弦（sin），余弦（cos），正切（tan）。
函数值特殊角特殊角的三角函数值如下：注：非特殊角的三角函数值，请查三角函数表。
变化情况1.锐角三角函数值都是正值2.当角度在0°～90°间变化时，正弦值随着角度的增大（或减小）而增大（或减小），余弦值随着角度的增大（或减小）而减小（或增大）；正切值随着角度的增大（或减小）而增大（或减小），余切值随着角度的增大（或减小）而减小（或增大）；正割值随着角度的增大（或减小）而增大（或减小），余割值随着角度的增大（或减小）而减小（或增大）。
3.当角度在0°≤A≤90°间变化时，0≤sinA≤1, 1≥cosA≥0；当角度在0°<A0, cotA>0。
关系式同角三角函数基本关系式tanαcotα=1sinαcscα=1cosαsecα=1sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα(sinα)^2+(cosα)^2=11+tanα=secα1+cotα=cscα诱导公式sin（－α）=－sinαcos（－α）=cosαtan（－α）=－tanαcot（－α）=－cotαsin（π/2－α）=cosαcos（π/2－α）=sinαtan（π/2－α）=cotαcot（π/2－α）=tanαsin（π/2+α）=cosαcos（π/2+α）=－sinαtan（π/2+α）=－cotαcot（π/2+α）=－tanαsin（π－α）=sinαcos（π－α）=－cosαtan（π－α）=－tanαcot（π－α）=－cotαsin（π+α）=－sinαcos（π+α）=－cosαtan（π+α）=tanαcot（π+α）=cotαsin（3π/2－α）=－cosαcos（3π/2－α）=－sinαtan（3π/2－α）=cotαcot（3π/2－α）=tanαsin（3π/2+α）=－cosαcos（3π/2+α）=sinαtan（3π/2+α）=－cotαcot（3π/2+α）=－tanαsin（2π－α）=－sinαcos（2π－α）=cosαtan（2π－α）=－tanαcot（2π－α）=－cotαsin（2kπ+α）=sinαcos（2kπ+α）=cosαtan（2kπ+α）=tanαcot（2kπ+α）=cotα(其中k∈Z)二倍角、三倍角的正弦、余弦和正切公式Sin(2α)=2sinαcosαCos(2α)=（cosα）^2－(sinα)^2=2(cosα)^2－1=1－2(sinα)^2Tan(2α)=2tanα/(1-tanα)sin(3α)=3sinα-4sin^3α=4sinα·sin(60°+α)sin(60°-α)cos(3α)=4cos^3α-3cosα=4cosα·cos(60°+α)cos(60°-α)tan(3α)=(3tanα-tan^3α)/(1-3tan^2α)=tanαtan(π/3+α)tan(π/3-α) 和差化积、积化和差公式sinα+sinβ=2sin[(α+β)/2]·cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]·sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]·cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]·sin[(α-β)/2] sinαcosβ=-[sin（α+β）+sin（α－β）]sinαsinβ=-[1][cos（α+β）-cos（α-β）]/2 cosαcosβ=[cos（α+β）+cos（α-β）]/2sinαcosβ=[sin（α+β）+sin（α-β）]/2cosαsinβ=[sin（α+β）-sin（α-β）]/2。
锐角三角函数锐角三角函数
03
证明方法
利用正弦定理和余弦定理，将边的关 系转化为角的关系，再利用三角函数 的性质推导得出。
05
锐角三角函数的作图及演 示
利用计算器或计算机软件绘制锐角三角函数图像
总结词
通过使用计算器或计算机软件，我们可以 轻松地绘制出锐角三角函数的图像。
详细描述
首先，我们需要输入锐角的角度值，然后 在计算器或计算机软件中选择对应的三角 函数（正弦、余弦或正切）。这样，我们 就可以得到一个关于角度的函数值。将这 些值在坐标系中表示，就可以形成锐角三 角函数的图像。
证明方法
通过正弦定理将角的关系转化为 边的关系，再利用勾股定理推导 得出。
正切定理的公式及证明
01
02
总结词
详细描述
正切定理是指在一个三角形中，任意 两边长度的比值等于这两边所夹角的 正切值与第三边所对应角的正切值的 比值。
正切定理的公式为 tan(A)/tan(B) = c/b。其中，A、B、C 分别代表与三 边相对应的角度，a、b、c 分别代表 三角形的三边长。
求边长
已知直角三角形的一个锐角和对应的边长，可以应用锐角三 角函数来求解另一条边长。例如，在直角三角形ABC中，已 知角A为30度，对应边a为10单位长度，那么对应边b的长度 可以通过应用三角函数求解。
在实际问题中求解角度或边长
地球定位
在地球上定位一个点，需要知道该点与北极的夹角和该点到北极的距离。这些信息可以通过应用锐角 三角函数来求解。
余弦定理
对于任意三角形ABC，有cosA = (b² + c² - a²) / (2bc)，其中a、b、c分别是三角形的三边长度。这表明一个 角的余弦值等于由该角两边长度和它们夹角所确定的三角形的另一边的平方与两邻边平方和的差与两邻边的积 之比。
锐角三角函数的特殊值。
锐角三角函数的特殊值。
锐角三角函数是数学中常见的一类函数，它们在三角学和解析几何中有着重要的应用。
这些函数的特殊值在计算和解题中起着重要的作用，下面我们将详细介绍锐角三角函数的特殊值。
一、正弦函数的特殊值正弦函数是最基本的三角函数之一，它表示一个角的对边与斜边的比值。
在锐角三角函数中，正弦函数的特殊值主要集中在0°、30°、45°、60°和90°五个角度上。
1. 当角度为0°时，正弦函数的值为0。
这是因为0°角的对边为0，所以正弦函数的值也为0。
2. 当角度为30°时，正弦函数的值为1/2。
这是因为30°角的对边等于斜边的一半，所以正弦函数的值为1/2。
3. 当角度为45°时，正弦函数的值为√2/2。
这是因为45°角的对边等于斜边的一半，所以正弦函数的值为√2/2。
4. 当角度为60°时，正弦函数的值为√3/2。
这是因为60°角的对边等于斜边的一半，所以正弦函数的值为√3/2。
5. 当角度为90°时，正弦函数的值为1。
这是因为90°角的对边等于斜边，所以正弦函数的值为1。
二、余弦函数的特殊值余弦函数是三角函数中的另一个重要函数，它表示一个角的邻边与斜边的比值。
在锐角三角函数中，余弦函数的特殊值也主要集中在0°、30°、45°、60°和90°五个角度上。
1. 当角度为0°时，余弦函数的值为1。
这是因为0°角的邻边等于斜边，所以余弦函数的值为1。
2. 当角度为30°时，余弦函数的值为√3/2。
这是因为30°角的邻边等于斜边的一半，所以余弦函数的值为√3/2。
3. 当角度为45°时，余弦函数的值为√2/2。
这是因为45°角的邻边等于斜边的一半，所以余弦函数的值为√2/2。
人教版锐角三角函数
新知探索:30°角的三角函数值
sin30°= A的对边 1
斜边 2
3
cos30°= A的邻边 3
斜边
2
tan30°= A的对边 3
A的邻边 3
新知探索:45°角的三角函数值
sin45°= A的对边 2
2
斜边
2
cos45°= A的邻边 2
斜边
2
tan45°= A的对边 1 A的邻边
rldmm8989889
新知探索:60°角的三角函数值
sin60°= A的对边 3
斜边
2
2
3 cos60°= A的邻边 1
斜边 2
1
tan60°= A的对边 3
A的邻边
30°、45°、60°角的正弦值、余弦值和正切值 如下表：
锐角a 三角函数
30°
45°
60°
sin a
1
2
3
2
2
2
cos a
3
2
1
2
2
2
tan a
★我们把锐角A的邻边与斜边的比叫做∠A的
余弦（cosine），记作cosA， 即
cos
A
A的邻边 斜边
b c
斜边c
B 对边a
A 邻边b C
★我们把锐角A的对边与邻边的比叫做∠A的 正切（tangent），记作tanA， 即
tan
A
A的对边 A的邻边
a b
注意
▪ cosA，tanA是一个完整的符号，它表示∠A 的余弦、正切，记号里习惯省去角的符号 “∠”；
AC DC tan 42,
D 42°
C
1.6m
AB AC CB 20 tan 42 1.6. 少呢？
第4课时 一般锐角的三角函数值
第4课时一般锐角的三角函数值【学习目标】1．会用计算器求一些锐角的三角函数值．2．运用锐角三角函数解决一些简单解直角三角函数值．【学习重点】会用计算器求一些锐角的三角函数值．【学习难点】会用计算器求一些锐角的三角函数值．一、情景导入生成问题旧知回顾：1.填写下表2.我们学习了特殊锐角(30°、45°、60°)三角函数值，那么你知道15°、55°等一般锐角三角函数值吗？本节课就将学习它们的求法．二、自学互研生成能力知识模块一一般锐角的三角函数值的求法阅读教材P120～121页的内容，回答以下问题：1．任意画一锐角A，并用量角器量出它的角度，再用计算器求出它的正弦，作直角三角形量出并计算BCAB的值，你有什么发现？答：锐角A的度数与它的三角函数值是一一对应的，知道其中一个可求出另两个．2．如何利用计算器求一般锐角三角函数值，举例说明．答：(1)观察手中计算器的各种按键，了解它们的功能．(2)求sin40°的值．(精确到0.0001)∴sin40°≈0.6428.范例：求sin 63°52′41″的值．(精确到0.0001)解：先用如下方法将角度单位状态设定为“度”：MODE MODE 1显示D 再按下列顺序依次按键：sin 63°′″52°′″41°′″＝显示结果为0.897 859 012.所以sin 63°52′41″≈0.8979.知识模块二 利用三角函数值求解实际问题范例1：已知锐角α的三角函数值，求锐角α的值： (1)sin α＝0.6325；(2)cos α＝0.3894；(3)tan α＝3.5492解：(1)依次按键2nd F sin ，然后输入函数值0.6325，得到结果α＝39.23480979°；(2)依次按键2nd F cos ，然后输入函数值0.3894，得到结果α＝67.0828292°；(3)依次按键2nd F tan ，然后输入函数值3.5492，得到结果α＝74.26462479°.范例2：如图，在Rt △ABC 中，∠C ＝90°，∠A ＝35°，AC ＝6，求BC ，AB 的长(精确到0.001)．解：因为BCAC ＝tan A ＝tan 35°，由计算器求得tan 35°≈0.7002，所以BC ＝AC·tan A ≈6×0.7002≈4.201，又AC AB ＝cos A ≈cos 35°，由计算器求得cos 35°＝0.8192，所以AB ＝ACcos A ≈7.324.范例3：如图，工件上有一V 型槽，测得它的上口宽20mm ，深19.2mm .求V 型角(∠ACB)的大小(结果精确到度)．解：∵tan ∠ACD ＝AD CD ＝1019.2≈0.5208，由计算器求得∠ACD ≈27.51°，∴∠ACB ＝2∠ACD ≈2×27.51°≈55°.∴V 型角的大小约为55°.三、交流展示 生成新知1．将阅读教材时“生成的问题”和通过“自学互研”得出的“结论”展示在各小组的小黑板上．并将疑难问题也板演到黑板上，再一次通过小组间就上述疑难问题相互释疑．2．各小组由组长统一分配展示任务，由代表将“问题和结论”展示在黑板上，通过交流“生成新知”．知识模块一一般锐角的三角函数值的求法知识模块二利用三角函数值求解实际问题四、检测反馈达成目标见《名师测控》学生用书．五、课后反思查漏补缺1．收获：________________________________________________________________________ 2．困惑：________________________________________________________________________。
23.1.3一般锐角的三角函数值
解析:由于余弦函数在角为锐角时,函数值随着角度的增大而减小,所以 cos 60° <cos 40° ;正切函数在角为锐角时,函数值随着角度的增大而增大,所 以 tan 44° <tan 88° .
答案:(1)<
(2)<
余弦函数的增减性与正弦函数、 正切函数的增减性不一样,容易将余弦函数 看成和正弦函数一样而出现错误 cos 60° >cos 40° .
<
tan 68° > tan 43° . 6.已知 α,β 为锐角,若 cos α>cos β,则 α
β(填“>”“=”或“<”).
2
课前预习 1 2
课堂合作 课堂合作
当堂检测
1.用计算器求一般锐角的三角函数值 【例 1】 用计算器计算 cos 44° 的结果(精确到 0.01)是( A.0.90 B.0.72 C.0.69 D.0.66
������������ ������ = = ������������ ( 2+1)x
2-1.
答案
12
着角度的增大而 增大 ,余弦函数值随着角度的增大而 减小 . 3.已知一个角的三角函数值,求这个锐角,也可用 计算器 来解决. 4.用计算器求值:sin 23° 5'+cos 66° 55'≈ 0.784 1 . 5.比较大小: sin 36° < cos 54° > sin 72° ; cos 83° ;
解析:不同的计算器的操作方法不同. 答案:B
)
3
课前预习 1 2
课堂合作 课堂合作
当堂检测
针对性训练 见当堂检测· 基础达标栏目第 5 题
4
课前预习 1 2
锐角函数
锐角函数定义锐角角A的正弦（sin）,余弦（cos）和正切（tan）,余切（cot）以及正割（sec），余割（csc）都叫做角A的锐角三角函数。
正弦（sin）等于对边比斜边；sinA=a/c余弦（cos）等于邻边比斜边；cosA=b/c正切（tan）等于对边比邻边；tanA=a/b余切（cot）等于邻边比对边；cotA=b/a初中学习的锐角三角函数值的定义方法是在直角三角形中定义的，所以在初中阶段求锐角的三角函数值，都是通过构造直角三角形来完成的，即把这个角放到某个直角三角形中。
到了高中三角函数值的求法是通过坐标定义法来完成的，这个时候角也扩充到了任意角。
所谓锐角三角函数是指：我们初中研究的都是锐角的三角函数。
初中研究的锐角的三角函数为：正弦（sin），余弦（cos），正切（tan）。
函数值特殊角特殊角的三角函数值如下：注：非特殊角的三角函数值，请查三角函数表。
取值范围θ是锐角：0<sinθ<10<cosθ<1tanθ>0cotθ>0变化情况1.锐角三角函数值都是正值。
2.当角度在0°～90°间变化时，正弦值随着角度的增大（或减小）而增大（或减小），余弦值随着角度的增大（或减小）而减小（或增大）；正切值随着角度的增大（或减小）而增大（或减小），余切值随着角度的增大（或减小）而减小（或增大）；正割值随着角度的增大（或减小）而增大（或减小），余割值随着角度的增大（或减小）而减小（或增大）。
3.当角度在0°≤A≤90°间变化时，0≤sinA≤1, 1≥cosA≥0；当角度在0°<A0, cotA>0。
关系式同角三角函数李善兰三角函数展开式（此公式又称“李善兰三角函数展开式”或”李氏三角恒等式“）tanα·cotα=1希腊三角函数公式sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα1+(tanα)^2=(secα)^21+(cotα)^2=(cscα)^2锐角三角函数诱导公式sin（－α）=－sinαcos（－α）=cosαtan（－α）=－tanαcot（－α）=－cotαsin（π/2－α）=cosαcos（π/2－α）=sinαtan（π/2－α）=cotαcot（π/2－α）=tanαsin（π/2+α）=cosαcos（π/2+α）=－sinαtan（π/2+α）=－cotαcot（π/2+α）=－tanαsin（π－α）=sinαcos（π－α）=－cosαtan（π－α）=－tanαcot（π－α）=－cotαsin（π+α）=－sinαcos（π+α）=－cosαtan（π+α）=tanαcot（π+α）=cotαsin（3π/2－α）=－cosαcos（3π/2－α）=－sinαtan（3π/2－α）=cotαcot（3π/2－α）=tanαsin（3π/2+α）=－cosαcos（3π/2+α）=sinαtan（3π/2+α）=－cotαcot（3π/2+α）=－tanαsin（2π－α）=－sinαcos（2π－α）=cosαtan（2π－α）=－tanαcot（2π－α）=－cotαsin（2kπ+α）=si nαcos（2kπ+α）=cosαtan（2kπ+α）=tanαcot（2kπ+α）=cotα(其中k∈Z)二倍角、三倍角的正弦、余弦和正切公式Sin(2α)=2sinαcosαCos(2α)=（cosα）^2－(sinα)^2=2(cosα)^2－1=1－2(sinα)^2 Tan(2α)=2tanα/(1-tanα)sin(3α)=3sinα-4sin^3α=4sinα·sin(60°+α)sin(60°-α)cos(3α)=4cos^3α-3cosα=4cosα·cos(60°+α)c os(60°-α)tan(3α)=(3tanα-tan^3α)/(1-3tan^2α)=tanαtan(π/3+α)tan(π/3-α)公式和差化积、积化和差公式有如下几个：sinα+sinβ=2sin[(α+β)/2]·cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]·sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]·cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]·sin[(α-β)/2]sinαcosβ=-[sin（α+β）+sin（α－β）]sinαsinβ=-[1][cos（α+β）-cos（α-β）]/2cosαcosβ=[cos（α+β）+cos（α-β）]/2sinαcosβ=[sin（α+β）+sin（α-β）]/2cosαsinβ=[sin（α+β）-sin（α-β）]/2。