哈工大研究生课程-高等结构动力学-第五章解析
合集下载
哈工大研究生课程-高等结构动力学-第五章
④Vb实现
x a pq
1 y (a pp aqq ) 2 x
x2 y 2
x tan 2 y
2
sin 2
sin
2(1 1 )
2
cos 1 sin
第p列 1 S
设系统作j阶主振动 ,则有： 2 {x} j {A}( j ) sin j t 2 j {x} 代入得特征方程： 1
([ ][ M ]
有
11m11
1
2 j
12 m12 22 m22
1
2 j
[ I ]){x} 0
1n m1n 2 n m2 n
1 1 1 1 1 [ ] [ K ] 1 2 2 k 1 2 3
1 1 1 m [ D ] [ ][ M ] 1 2 2 k 1 2 3
1 1 1 1 1 m 3m A1{}1 [ D]{}0 1 2 2 1 1.66 k k 1 2 3 1 2
响应数值分析：
1.中心差分法
2.Wilson-θ法 3.Newmark法
响应求解方法的选择取决的因素有：载荷、结构、精度要求、非线性 影响程度、方法的稳定性等。
对结构过于复杂的情况，宜采用直接积分法，结构较简单的情况可采用 模态迭加法。 对精度要求较低的初步设计阶段，可采用取少数模态的模态迭加法。对 精度要求较高的最后设计阶段，宜采用直接积分法 综合各方面的因素，比较、权衡，才能判定所应采取的方法；有时为了 互相验证，也可以同时采取两种以上的方法来处理动响应分析
哈尔滨工业大学结构动力学第五次课
m cx kx f ( t ) 当 f ( t ) 是一个简单函数时，有解析解。 x
当 f ( t ) 为非函数表达时，应求助于数值解。
一、力插值法
1、分段常数插值 将力作用时间的间隔 T 分成n等分
t t i 1 t i
f i ( f i f i 1 ) 2
上次课程回顾
单位脉冲响应函数
1 ( t ) e n sin ( d ( t )) m d h (t ) 0
t t
单位阶跃响应 冲击响应谱
1 x t 1 k
e
nt 2
1
sin d t
i
i 1
m i cx i kx i f i x
m i 1 cx i 1 kx i 1 f i 1 x
将两式相减 ｝
i i 1 i x x x
x i x i 1 x i
x i x i 1 x i
2
ac 2
1
2
ac ac c a b 2 2
2
—— , 分别称为一阶固有频率和二阶固有频率。 将两阶固有频率分别回代特征方程，得
A1
1 1
b a 1
b a 2
2
A2
2
c 1 c
2
1
1
,
A 1 1 1 A1 1 A2
*
k i xi f i
*
2
2c t
4m t
fi fi [
当 f ( t ) 为非函数表达时，应求助于数值解。
一、力插值法
1、分段常数插值 将力作用时间的间隔 T 分成n等分
t t i 1 t i
f i ( f i f i 1 ) 2
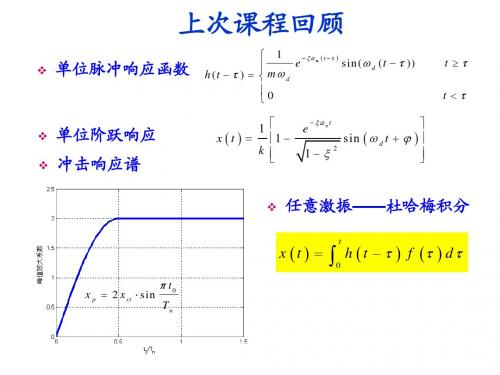
上次课程回顾
单位脉冲响应函数
1 ( t ) e n sin ( d ( t )) m d h (t ) 0
t t
单位阶跃响应 冲击响应谱
1 x t 1 k
e
nt 2
1
sin d t
i
i 1
m i cx i kx i f i x
m i 1 cx i 1 kx i 1 f i 1 x
将两式相减 ｝
i i 1 i x x x
x i x i 1 x i
x i x i 1 x i
2
ac 2
1
2
ac ac c a b 2 2
2
—— , 分别称为一阶固有频率和二阶固有频率。 将两阶固有频率分别回代特征方程，得
A1
1 1
b a 1
b a 2
2
A2
2
c 1 c
2
1
1
,
A 1 1 1 A1 1 A2
*
k i xi f i
*
2
2c t
4m t
fi fi [
哈工大研究生课程-高等结构动力学-第一章
用偏微分方程得到弦线振动的波动方程，并求出行波解。
四、结构动力学的发展史
◇伯努利（D.Bernoulli)： 用无穷多个模态叠加的方法得到了弦线振动的驻波解，1759 年拉格朗日（grange):从驻波解推得行波解 ◇傅里叶（J.B.Fourier): 1811年提出函数的阶数展开理论，完成了严格的数学证明， 欧拉和伯努利分别与1744和1751年研究了梁的横向振动
EI
W=1
三. 自由度的确定
8) 平面上的一个刚体 y2
11) W=1 12)
y1
W=3
9)弹性地面上的平面刚体 W=3 10)
m
EI
W=13
自由度为1的体系称作单自由度体系； 自由度大于1的体系称作多（有限）自由度体系; 自由度无限多的体系为无限自由度体系。 W=2
§1.3 建立结构运动方程的一般方法
静荷载。静荷只与作用位置有关，而动荷是坐标和时间的函数。
简谐荷载 周期 非简谐荷载 确定 冲击荷载 非周期 阶跃荷载 动荷载 其他确定规律的动荷载 风荷载 地震荷载 不确定 其他无法确定变化规律的荷载
四、结构动力学的发展史
▼公元前6世纪 古希腊毕达哥拉斯（Pythagoras):试验 测得：弦线振动的性质； ▼我国战国时期《庄子》明确记载了共振现象； ▼伽利略（G.Galileo）:对动力学进行了开创性研究， 他发现了单摆的等时性，并利用自由落体公式计算 单摆的周期．
§1.4 建立振动微分方程举例
例-1 图示单自由度振动系统 设静平衡位置为坐标原点,则在静平衡位置弹簧的伸长量为
st
mg k
f e k ( x st )
f d c x ; f I m x
结构动力学哈工大结构动力学
m ?y?(t)
P(t )
m?y?(t) ? P(t) 运动方程
m P(t) ? m?y?(t)
P(t) ? [ ? m?y?(t)] ? 0
形式上的平衡方程，实质上的运动方程
惯性力
一、柔度法
P(t) m ? m?y?(t) =1 ?11
y(t )
l EI
? [11 P(t) ? m?y?(t)]
结构动力学
哈尔滨工业大学 土木工程学院 结构力学教研室 张金生 2004年7月
结构动力学
目录
第一章 绪论 第二章 单自由度体系的振动分析 第三章 有限自由度体系的振动分析 第四章 实用计算方法 第五章 无限自由度体系的振动分析 第六章 动力有限元分析 第七章 分析动力学
主要参考书
《结构动力学》克劳夫 王光远等译 科学出版社 《结构动力学》赵光恒主编 水利水电出版社 《建筑结构振动计算》郭长城主编 建工出版社 《建筑结构振动计算续编》郭长城编著 建工出版社 《结构动力学》邹经湘主编 哈工大出版社 《应用分析动力学》王光远编著 科学出版社 《DYNAMICS OF STRUCTURES 》Anil K.Chopra
W
? m?y?(t)
?1
? 11
? st
y(t )
Y (t) ? y(t) ? ? st
加速度为
Y??(t) ? ?y?(t)
y(t) ? ? st ? ?11[P(t) ? W ? m?y?(t)]
? st ? W?11
y(t) ? ?11[P(t) ? m?y?(t)]
? 11
?
l3 48EI
列运动方程时可不考虑重力影响
?
?m1 ?? 0
0 ???y?1? m2?????y?2??
结构动力学-5z
π
T
t
荷载离开后 ( t > t1 ) 令 t = t − t1
ɺ t = 0 时 y 0 = y ( t1 ) = y st (1 − cos ω t1 ) v 0 = y ( t1 ) = y st ω sin ω t1 v0 y ( t ) = y 0 cos ω t + sin ω t = A sin( ω t + ε )
∆τ
t
t
---杜哈美积分 ---杜哈美积分
P(t ) P
τ
∆τ
t
4
t
计阻尼时
P(τ ) −ξω (t −τ ) y(t) = ∫ e sinωD (t −τ )dτ 0m ωD
t
=
∫
t
0
h ( t − τ ) P (τ ) d τ
1 −ξω (t −τ ) h(t −τ ) = e sin ωD (t −τ ) mωD
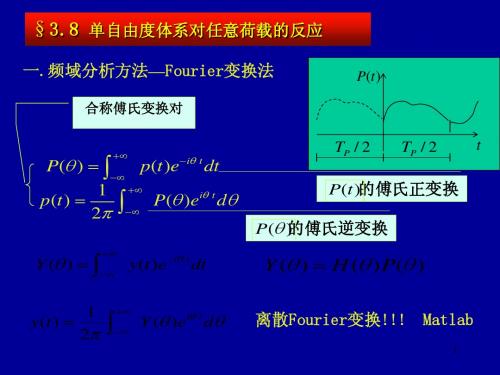
§3.8 单自由度体系对任意荷载的反应
Fourier变换法 一.频域分析方法—Fourier变换法 频域分析方法 Fourier
合称傅氏变换对
+∞
P(t )
P(θ ) = ∫ p(t)e−iθ t dt −∞ 1 +∞ p(t) = P(θ )eiθ t dθ 2π ∫−∞
Y (θ ) =
TP / 2
π
T
t1
t1/T
µ
0 0
0.01 0.063
0.02 0.126
0.05
0.10
1/6 1.0
0.2
0.3
0.4
≥ 0 .5
2
0.313 0.618
1.176 1.618 1.902
结构动力学课件PPT
地震作用
200 0 -200
t(sec)
0 5 10 15 20 25 30 35 40 45 50
结构在确定性荷载作用下的响应分析通 常称为结构振动分析。 结构在随机荷载作用下的响应分析， 被称为结构的随机振动分析。 本课程主要学习确定性荷载作用下的结 构振动分析。
§1-3 动力问题的基本特性
§2-5 广义单自由度体系：刚体集合
刚体的集合（弹性变形局限于局部弹性
元件中） 分布弹性（弹性变形在整个结构或某些 元件上连续形成） 只要可假定只有单一形式的位移，使得 结构按照单自由度体系运动，就可以按 照单自由度体系进行分析。
E2-1
A
x
x p( x,t ) = p a ( t )
1
令：
5l FE (t ) q(t ) 8
y FE (t )
FE(t) 定义为体系的等效动荷载或等效干扰力。其通用表达式
P FE (t )
含义：等效动荷载直接作用在质量自由度上产生的动位移与
实际动荷载产生的位移相等！
已经知道柔度和刚度k 之间的关系为： k 表达式成为：
简支梁： 比较： 刚架： 基本质量弹簧体系：
大型桥梁结构 的有限元模型
§1-5 运动方程的建立
定义
在结构动力分析中，描述体系质量运动规律的数学 方程，称为体系的运动微分方程，简称运动方程。 运动方程的解揭示了体系在各自由度方向的位移 随时间变化的规律。 建立运动方程是求解结构振动问题的重要基础。 常用方法：直接平衡法、虚功法、变分法。
（2-3）
刚度法: 取每一运动质量为隔离体，通过分析所受 的全部外力，建立质量各自由度的瞬时力平衡方 程，得到体系的运动方程。
理论力学第五章
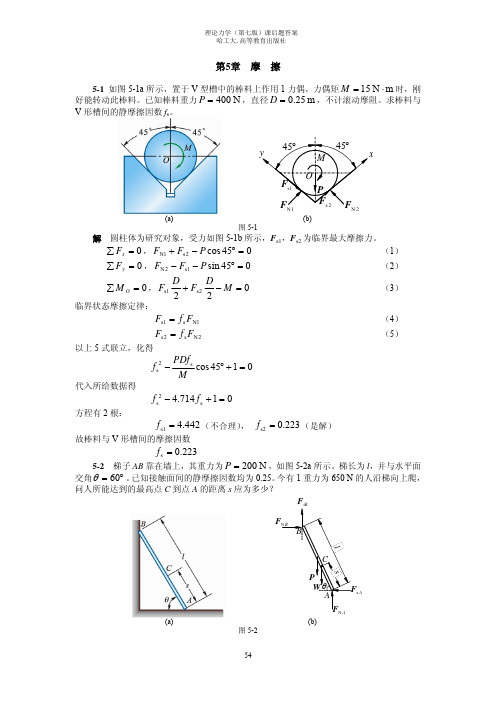
∑ Fx = 0 ， F = FsE + FsA ， FsE = f s FNE ， FsA = f s FNA FsE = FsA ， F = 2 FsA 2h ∑ME = 0，F − FsA h − FNA ⋅ bmin = 0 3
综上化得
b 4h − h − min = 0 3 fs
56
理论力学（第七版）课后题答案 哈工大.高等教育出版社
2 R = O1O2 = KD = CD = O1 A = KL = O2 L = 0.5 m ， O1 B = 0.75 m ，AC = O1 D = 1 m ， ED = 0.25 m ，求作用于鼓轮上的制动力矩。
′ FEK K FN 2 FO2 x
θ
FEK θ ′ FDx FOy FOx
E FDy
5-5 门高为 h 。 若在门上 不计自重的拉门与上下滑道之间的静摩擦因数均为 f s ，
2 h处 3
用水平力 F 拉门而不会卡住，求门宽 b 的最小值。问门的自重对不被卡住的门宽最小值是 否有影 (b)
E
Fs E FN E
解 （1）不计自重时受力如图 5-5b 所示 ∑ Fy = 0 ， FNE = FNA
F 较大时，滑块 B 滑动趋势与图 c 相反，即摩擦力 Fs 与图 c 所示相反，则此时式（1） ， （4） 不变，式（2）变为
' FAB sin θ − F cos β + Fs = 0
式（1） ， （4）代入上式，得
M M sin θ − F cos β + f s + f s F sin β ) = 0 l cosθ l M (tan θ + f s ) = F (cos β − f s sin β ) l M (tan θ + f s ) F= l (cos β − f s sin β ) 同样令 f s = tan ϕ ，则 M sin(θ + ϕ ) F= l cosθ cos( β + ϕ ) M sin(θ − ϕ ) M sin(θ + ϕ ) ≤F≤ l cos θ cos( β − ϕ ) l cos θ cos( β + ϕ ) 5-7 轧压机由两轮构成，两轮的直径均为 d = 500 mm ，轮间的间隙为 a = 5 mm ，两 轮反向转动，如图 5-7a 上箭头所示。已知烧红的铁板与铸铁轮间的摩擦因数 f s = 0.1 ，问
哈工大研究生培养方案
哈工大研究生培养方案一、总体思路土木工程一级学科硕士研究生分学术研究型和应用研究型两类进行分类培养。
学术研究型学生的培养方案适当增加理论性课程比例，基础理论课程学时适度增加，在学位论文阶段应重点培养学生从事本学科基础性科学研究工作的能力。
应用研究型学生的培养方案适当增加应用性课程比例，增加工程实践课程学时，增设实践环节。
在学位论文阶段应重点培养学生的工程实践能力，以及解决实际技术问题的能力。
全日制工程硕士研究生培养方案与应用研究型相同。
二、培养方案、课程体系设置学术研究型：硕士研究生攻读学位期间所修学分总和不少于32学分，其中学位课不少于19学分，选修课不少于7学分，课程学习阶段应完成29学分。
课程体系框架如下：1、学位课（19学分）（1）马克思主义理论课程（3学分）（课程讲授2学分，社会实践1学分）（2）第一外国语（2学分）（3）数学基础课或基础理论课（4学分）（4）学科基础课（不少于6学分）（5）学科专业课（不少于2学分）学科基础课和学科专业课的总学分不少于10学分。
2、选修课（不少于7学分）3、专题课程（2学分）专题课程在研究生学位论文阶段完成，结合学科的前沿和热点研究内容，以若干个教师开设系列专题讲座的方式进行。
4、学术活动（1学分）研究生在攻读学位期间应在土木工程一级学科范围内参加5次以上学术研讨活动，参加学术活动应有书面记录，并交导师签字认可，方得1学分。
应用研究型：硕士研究生攻读学位期间所修学分总和不少于31学分，其中学位课不少于16学分，选修课不少于11学分，课程学习阶段应完成29学分。
课程体系框架如下：1、学位课（16学分）（1）马克思主义理论课程（3学分）（课程讲授2学分，社会实践1学分）（2）第一外国语（2学分）（3）数学基础课或基础理论课（2学分）（4）应用基础课（不少于6学分）（5）应用技术课（不少于2学分）应用基础课和应用技术课的总学分不少于9学分。
2、选修课（不少于11学分）3、实践课程（1学分）实践课程在研究生学位论文阶段完成，结合专业特点，到实习基地学习实践1周。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
m1 m2 m3
11
9l 3 768EI
22
16l 3 768EI
33
9l 3 768EI
1
2 22
9
1
m 22
2l3m 16l
768EI 16l 3m
3m 34l
2 11
1
m 11
3m1 4.752
2 33
768EI 9l 3m
EI
ml 3 1 4.933
EI 精确解 ml 3
12 768EI 768EI 768EI
设质量矩阵 M ，柔度矩阵为
则有 x M x 0
设系统作j阶主振动,则有：
{x} 2j {A}( j) sinjt 2j {x}
代入得特征方程：
([ ][M
有
11m11
1
2 j
12m12
]
1
2 j
[
I
]){ห้องสมุดไป่ตู้} 0
1n m1n
m 21 21
m 22 22
1
2 j
2 n m2 n
0
m n1 n1
n 2 mn 2
nn mnn
1
2 j
假设质量矩阵为对角阵，展开得：
1
2n j
(11m11
22m22
nn
mnn
)
1
2(n j
1)
0
根据多项式的根与系数之间的关系
1
2 j
的n个根
1
12
，122
1 之和为
n2
1
12
1
22
1
n2
11m11 22m22
nnmnn
由于二阶频率往往比基频高得多
sii 1i p,q
[S ] [S ](1)[S ](2) [S ](n)
用雅可比法求n阶对称矩阵[A]的特征值和特征向量的步骤
①设S In 为单位矩阵
②在A中选取非对角线元素中绝对值最大的元素 apq
③ apq
④Vb实现
x apq
x
1 y 2 (app aqq )
x2 y2
tan 2 x
T 1 {x}T [M ]{x} 2
V 1 {x}T [K ]{x} 2
系统作j阶主振动时 {x}( j) {A}( j) sin(jt )
速度及加速度
{x}(
j)
{A}(
j) j
cos(jt
)
{x}( j)
{A}(
j
)
2 j
sin(jt
)
Tmax
1 2
2 j
{
A}(
j
)T
[
M
]{
A}(
j
得 ([K ] 2[M ]){a} 0
问题又归结为矩阵的本征值问题，但与原系统的本征值 比，矩阵的阶数r小于原系统的阶数n.
1
11
忽略 1 22
1得
n2
n2
22 12
1
12
11m11 22m22
n
nnmnn iimii i 1
1
1
n
ii mii
i 1
设
ii
kii mii
1
ii mii
ii表示仅有质量mii单独存在时（原多自由度系统变成单
自由度系统）的固有频率
如例题
1
12
1
2 11
1
2 22
1
2 nn
2.雅可比（Jacobi）法求特征方程 设[A]为对称阵， [A]{x} {x}
[S ]T [ A][S ] [D] diag(d1, d2, dn )
即可断定[D]的n个对角元素就是[A]的n个特征值，而[S]
的第i列就是[D]中第i个对角元素所对应的特征向量，
[S]为坐标变换矩阵。 在[A]中非对角线元素中选取一个绝对值最大的元素，设
综合各方面的因素，比较、权衡，才能判定所应采取的方法；有时为了 互相验证，也可以同时采取两种以上的方法来处理动响应分析
§5.2 求解系统固有频率主振型的近似解法
1.邓克利法：是邓克利首先通过实验方法建立起来的一个计
算公式，后来才得到完整的数学证明。
1894年邓克利：提出一种近似计算多圆盘轴横向振动基频 的实用方法（偏小）
y
sin 2
sin
2(1 1 2 )
cos 1sin2
1
S
第p列
1
cos
1
sin
第q列
sin
1
cos
1
第p行
第q行
1
作业：5-1（2）
3.瑞利（Rayleigh）法和里兹法
已知系统的刚度[K]，质量[M]，并设定系统的j阶主振型为
{A( j)}
对于作简谐运动的多自由度系统，其动能T与势能V
响应数值分析：
1.中心差分法 2.Wilson-θ法 3.Newmark法
响应求解方法的选择取决的因素有：载荷、结构、精度要求、非线性 影响程度、方法的稳定性等。
对结构过于复杂的情况，宜采用直接积分法，结构较简单的情况可采用 模态迭加法。
对精度要求较低的初步设计阶段，可采用取少数模态的模态迭加法。对 精度要求较高的最后设计阶段，宜采用直接积分法
为 apq ，利用平面旋转矩阵[S( p, q, )]
对 A进行正交变换：[ A]i1 [S( p, q, )](i)[ A](i)[S( p, q, )](i)
其中 spp cos sqq cos spq sin
sqp sin sij 0
tg2 2apq
app aqq
i, j p, q
第五章 结构动力学中常用的数值解法
§5.1概述
数值分析技术为结构的动态分析提供了有力的保障，为 工程结构在各种复杂的动力学环境下的模拟和仿真提供 了有效工具。
工程结构的动态分析主要包括两个方面：结构的动态 特性分析和结构动态响应分析
标准特征值问题
1 雅可比方法（Jacobi）、 2.Rayleigh-Ritz 3.子空间迭代法 4. 行列式搜索法
行列式搜索法是求解大型特征值问题的另一种方法。它的特点 是综合运用多项式加速割线迭代，移轴向量逆迭代，Sturm序列的性质 以及Gram－Schmidt正交化过程，直接计算所需要的任意特征对，通 常是计算最小的部分特征值及相应的特征向量。
因此，它是一种计算部分特征对的特殊求解方法。此方法具有
计算速度快，精度高，灵活等优点。
)
Vmax
1 {A}( j)T [K ]{A}( j) 2
2 j
{A}( j)T [K ]{A}( j) {A}( j)T [M ]{A}( j)
2 j
K j T M j T
j j
里兹法：是瑞利法的改进
将瑞利法使用的单个假设模态改进为若干个独立的假设
模态 ( j) ( j 1, 2 r)的线性组合 r {A} aj ( j) [ ]{a}
{a} {a1 a2
a } j1
T
r
R(
a)
{A}T [K]{A} {A}T [M ]{A}
{a}T [K]{a} {a}T [M ]{a}
[K ] [ ]T [K ][ ]
[M ] [ ]T [M ][ ]
瑞利商在真实模态处取驻值 R 0 ( j 1, 2 r)
a j
（参见 刘延柱振动力学 107页和谢官模振动力学244页）