数学北师大版七年级下册专题复习——与轴对称有关的线段最值问题
2024年北师大七年级下册数学知识点总结生活中的轴对称和经典例题对接

第五章ﻩ生活中的轴对称一、轴对称图形1、假如一个图形沿一条直线折叠后,直线两旁的部分能够完全重叠,那么这个图形叫做轴对称图形,这条直线叫做对称轴。
2、了解轴对称图形要抓住如下几点:(1)指一个图形;(2)存在一条直线(对称轴);(3)图形被直线提成的两部分相互重叠;(4)轴对称图形的对称轴有的只有一条,有的则存在多条;(5)线段、角、长方形、正方形、菱形、等腰三角形、圆都是轴对称图形;二、轴对称1、对于两个图形,假如沿一条直线对折后,它们能相互重叠,那么称这两个图形成轴对称,这条直线就是对称轴。
能够说成:这两个图形有关某条直线对称。
2、了解轴对称应注意:(1)有两个图形;(2)沿某一条直线对折后能够完全重叠;(3)轴对称的两个图形一定是全等形,但两个全等的图形不一定是轴对称图形;(4)对称轴是直线而不是线段;轴对称图形轴对称区分是一个图形自身的对称特性是两个图形之间的对称关系对称轴也许不止一条对称轴只有一条共同点沿某条直线对折后都能够相互重叠假如轴对称的两个图形看作一个整体,那么它就是一个轴对称图形;假如把轴对称图形提成两部分(两个图形),那么这两部分有关这条对称轴成轴对称。
三、角平分线的性质1、角平分线所在的直线是该角的对称轴。
2、性质:角平分线上的点到这个角的两边的距离相等。
四、线段的垂直平分线1、垂直于一条线段并且平分这条线段的直线叫做这条线段的垂直平分线,又叫线段的中垂线。
2、性质:线段垂直平分线上的点到这条线段两端点的距离相等。
五、等腰三角形1、有两条边相等的三角形叫做等腰三角形;2、相等的两条边叫做腰;另一边叫做底边;3、两腰的夹角叫做顶角,腰与底边的夹角叫做底角;4、三条边都相等的三角形也是等腰三角形。
5、等腰三角形是轴对称图形,有一条对称轴(等边三角形除外),其底边上的高或顶角的平分线,或底边上的中线所在的直线都是它的对称轴。
6、等腰三角形的三条重要线段不是它的对称轴,它们所在的直线才是等腰三角形的对称轴。
北师大版七年级数学下册第五章:生活中的轴对称 章末复习总结

七年级数学(下)复㊀习㊀课㊀开心预习梳理,轻松搞定基础.㊀重难疑点,一网打尽.1.把一个图形沿一条直线翻折过去,如果㊀㊀㊀㊀㊀㊀,那么这两个图形关于这条直线成轴对称.2.如果一个图形沿一条直线对折,直线㊀㊀㊀㊀的部分能够㊀㊀㊀㊀,那么这个图形叫做轴对称图形.3.线段是㊀㊀㊀㊀图形,它有㊀㊀㊀㊀条对称轴,线段的垂直平分线是它的一条㊀㊀㊀㊀,线段的垂直平分线上的点到㊀㊀㊀㊀的距离相等.4.角是㊀㊀㊀㊀图形,对称轴是㊀㊀㊀㊀,角平分线上的点到㊀㊀㊀㊀的距离相等.5.等腰三角形是㊀㊀㊀㊀图形,有㊀㊀㊀㊀条对称轴,是㊀㊀㊀㊀,其主要性质有(1)㊀㊀㊀㊀;(2)㊀㊀㊀㊀;(3)㊀㊀㊀㊀.6.等边三角形有㊀㊀㊀㊀条对称轴,是㊀㊀㊀㊀.其主要性质有㊀㊀㊀㊀.7.如图,把一个长方形纸片沿E F 折叠后,点D ㊁C 分别落在D ᶄ㊁C ᶄ的位置.若øE F B =65ʎ,则øA E D ᶄ等于(㊀㊀).A.70ʎB .65ʎC .50ʎD.25ʎ(第7题)㊀㊀㊀㊀(第8题)圆是轴对称图形.㊀㊀8.如图,三角形纸片A B C ,A B =10c m ,B C =7c m ,A C =6c m ,沿过点B 的直线折叠三角形,使顶点C 落在边A B 上的点E 处,折痕为B D ,则әA E D 的周长为㊀㊀㊀㊀cm .9.如图,等边әA B C 的边长为1c m ,D ㊁E 分别是A B ㊁A C 上的点,将әA D E 沿直线D E 折叠,点A 落在点A ᶄ处,且点A ᶄ在әA B C 外部,则阴影部分的周长为㊀㊀㊀㊀c m .(第9题)㊀㊀㊀㊀(第10题)10.如图,将矩形A B C D 沿B E 折叠,若øC B A ᶄ=30ʎ,则øB E A ᶄ=㊀㊀㊀㊀.11.如图,әA B C 是等腰三角形,øB A C =90ʎ,B E 是øA B C 的平分线,D E ʅB C ,垂足为D .(1)请写出图中所有的等腰三角形;(2)请你判断A D 与B E 是否垂直,并说明理由;(3)如果B C =10,求A B +A E 的长.(第11题)12.已知P ㊁Q 是әA B C 的边A B ㊁A C 上的点,你能在B C 上确定一点R ,使әP Q R 的周长最短吗?(第12题)13.如图,C D E F 是一个矩形的台球面,有黑白两球分别位于点A ㊁B 两点,试问怎样撞击黑球A ,使A 先碰到台边F C 反弹后再击中白球B ?(第13题)七年级数学(下)㊀源于教材,宽于教材,举一反三显身手.14.如图,一个算式在镜中所成的像构成的算式是正确的,但是在实际中是正确的吗?实际中这个算式是什么?(写出即可)(第14题)15.如图,在等边三角形A B C中,øB㊁øC的平分线相交于点O,作B O㊁C O的垂直平分线分别交B C于点E㊁F.小明说: E㊁F是边B C的三等分点. 你同意他的说法吗?请说明理由.(第15题)16.如图,A D为әA B C的高,øB=2øC,用轴对称图形说明:C D=A B+B D.(第16题)复㊀习㊀课1.和另一个图形完全重合2.两旁㊀互相重合3.轴对称㊀2㊀对称轴㊀线段两端点4.轴对称㊀角平分线所在的直线㊀角两边5.轴对称㊀1㊀顶角平分线所在的直线(或底边上的高线所在的直线,或底边上的中线所在的直线)(1)三线合一㊀(2)两个底角相等(3)如果一个三角形有两个角相等,那么它们所对的边也相等.3㊀三边的垂直平分线㊀三个角都相等且等于60ʎ.C㊀8.9㊀9.3㊀10.60ʎ1.(1)әA B C,әA B D,әA D E,әE D C.(2)A D与B E垂直.理由:因为B E是øA B C的平分线, E AʅB A,D EʅB C,所以E A=E D,所以әA B E和әD B E关于B E对称,从而B A=B D,即әB A D为等腰三角形,所以B EʅA D.(3)因为A E=D E=D C,A B=B D,所以A B+A E=B D+C D=B C=10.2.作点Q关于B C的对称点D,连接P D交B C于R,连接P Q㊁P R㊁Q R,则点R就是B C上的一点使得әP Q R的周长最短.(第12题)3.作点B关于F C的对称点G,连接A G交F C于P,则击打A球至点P就能击中B球.(第13题)4.正确,151+25+12=188.5.同意.理由如下:连接O E㊁O F.由题意可知B E=O E,C F=O F,øO B C=øO C B=30ʎ,ʑ㊀øB O E=øO B C,øC O F=øO C B,øB O C=120ʎ.ʑ㊀øE O F=60ʎ,øO E F=60ʎ,øO F E=60ʎ.是等边三角形ʑ㊀O E=O F=E F=B E=C F.ʑ㊀E㊁F是B C的三等分点.6.在C D上取一点E使D E=B D,连接A E.则A D是әA B E的对称轴,ʑ㊀B D=D E,A B=A E.ȵ㊀øB=2øC,ʑ㊀øB=øA E D=øC+øE A C=2øC.ʑ㊀øE A C=øC.(第16题)ʑ㊀A E=E C.ʑ㊀C D=D E+E C=A B+B D.。
数学北师大版七年级下册专题复习——与轴对称有关的线段最值问题

PADCM A 专题复习 线段最值问题(1)——与轴对称有关的最小值问题成都市人民北路中学 2017级数学组 薛强【学习目标】1、掌握“将军饮马”问题的数学模型。
2、利用“将军饮马”问题的数学模型解决与轴对称有关的最值问题。
3、感受数学建模思想、转化思想的同时,培养层层推衍的学习思维和不断挑战的创造力。
【学习重点】利用“将军饮马”问题的数学模型解决与轴对称有关的最值问题。
【学习难点】根据题意准确作出对称点,构建特殊三角形计算最值。
【学习过程】 一、原生问题 【将军饮马】一位将军从A 地出发到小河MN 边饮马,然后再前往B 地,怎样走才能使PA+PB 最小?二、衍生问题问题1 如图Rt △ABC 中,AB =BC =4,D 为BC 的中点,E 为AC 边上一动点, 连结ED 、EB ,则△BDE 周长的最小值为______.问题2 如图所示,已知点C(1,0),直线7y x =-+与两坐标轴分别交于 A ,B 两点,D ,E 分别是AB ,OA 上的动点,则△CDE 周长的最小值 是______.练习:如图,已知正方形ABCD 边长为3,点E 在AB 边上且BE=1,点P ,Q 分别是边BC ,CD 的动点(均不与顶点重合),则四边形AEPQ 的周长的最小 值为__________.BABA ABF问题3 如图,在Rt △ABC 中,∠ACB=90°,AC=6,BC=8,AD 是∠BAC 的平分线。
若P 、Q 分别是AD 和AC 上的动点,则PC+PQ 的最小值为 ____________.三、探究结果1、学科知识2、学科技能3、思想方法四、分层检测1.如图,在边长为4的正方形ABCD 中,E 是AB 边上的一点,且AE =3, 点Q 为对角线AC 上的动点,则△BEQ 周长的最小值为________.2.如图,AB 是⊙O 的直径,AB=8,点M 在⊙O 上,∠MAB=20°, N 是MB 的中点,P 是直径AB 上的一动点.若MN=1,则△PMN 周长的最小值为___________.★3. 如图,直线y =+x 轴、y 轴分别交于点A 点C 、D 分别为线段AB 、OB 上的动点,点P 坐标为(-2,0)PCD ∆的周长最小值为____________.五、拓展延伸如图,点O 是边长为2的正方形ABCD 的对角线交点,正方形 OEFG 的面积为8 . 正方形ABCD 固定,把正方形OEFG 绕点O 逆时针旋转一周. 点M 为A G 的中点,在旋转过程中,线段 MF 的长度最大值为______________,最小值为___________.A BNT 1.(2014成都第24题)如图,在边长为2的菱形ABCD 中,∠A=60°,M 是AD 边的中点, N 是AB 边上的一动点,将△ AMN 沿MN 所在直线翻折得到△ A′MN , 连接A′C ,则A′C 长度的最小值是 .2.(2011成都第24题)在三角形纸片ABC 中,已知∠ABC=90°,AB=6,BC=8。
数学北师大版七年级下册线段和的最小值

理论依据:两点之间,线段最短 基本解法:利用对称性将“折”拉“直”
B P l
B′
模型2:一定点,两定直线,两动点:
如图,点P是∠MON内的一定点,分别在OM, ON上作点A,B,使△PAB的周长最小。 可以分别作点P关于OM、ON的对称点P1, P2,连接P1P2,P1P2长即为所求△PAB的周 P2 长最小值. M
模型3:两条定直线,两定点,两动点。如图,点
P,Q为∠MON内的两定点,分别在OM、ON上 作点A、B,使四边形PABQ的周长最小,.
先作出点p关于直线OM的对 称点P然后再作 Q关于ON的 对称点Q′连接P′Q′交OM, ON于点A,B,当四点共线时, 四边形PABQ的周长最小。 O
• 理论依据:两点之间,线段最短 • 基本解法:利用对称性将“折”拉“直”
理论依据:两点之间,线段最短 基本解法:利用对称性将“折” 拉“直”
A
P O B P1 N
练习:如图,∠AOB=45°,P是∠AOB内一 点,OP=10,Q、R分别是OB、OA上的动 点,则△PQR周长的最小值(C ) A.10 B. 8 C. 10 2 D. 10 2 10
P1
B
Q
P
O
R
A
P2
A
l
P
A`
P`
• 练习:如图,A、B是半圆O上的两点,MN 是直径,OB⊥MN,AB=4,OB=5,P是 MN上一个动点,则PA+PB的最小值为( D ) 。 A.6 B. 8 C.4 D. 2 21
A
M B
P
O
轴对称最值问题(辨识求解)(北师版)(含答案) (1)

学生做题前请先回答以下问题问题1:解决几何最值问题的理论依据有哪些?问题2:解决几何最值问题的主要方法是______,通过变化过程中_____________的分析,利用_______________________等手段把所求量进行转化,构造出符合几何最值问题理论依据的___________进而解决问题.问题3:轴对称最值问题——线段和最小与线段差最大问题中,它们的理论依据分别是什么?问题4:轴对称最值问题——线段和最小与线段差最大问题中,操作时有什么不同?轴对称最值问题(辨识求解)(北师版)一、单选题(共7道,每道14分)1.如图,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点,则PB+PE的最小值是( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:轴对称最值问题2.如图,在△ABC中,∠ACB=90°,以AC为一边在△ABC外侧作等边三角形ACD,过点D作DE⊥AC,垂足为F,DE与AB相交于点E.AB=10cm,BC=6cm,P是直线DE上的一点,连接PC,PB,则△PBC周长的最小值为( )A.16cmB.cmC.24cmD.26cm答案:A解题思路:试题难度:三颗星知识点:轴对称最值问题3.如图,在平面直角坐标系中,A,B两点的坐标分别为A(2,-3),B(4,-1),若C(a,0),D(a+3,0)是x轴上的两个动点,当四边形ABDC的周长最短时,a的值为( )A. B.1C. D.答案:C解题思路:试题难度:三颗星知识点:轴对称最值问题4.如图,在四边形ABCD中,AD∥BC,AB=AD=CD=1,∠ABC=60°,EF垂直平分AD,分别交AD,BC于点E,F,P是EF上一点,则PA+PB的最小值为( )A. B.C.2D.答案:D解题思路:试题难度:三颗星知识点:轴对称最值问题5.如图,正方形ABCD的边长为a,点M是AB的中点,,P是直线AC上的一点,则的最大值是( )A.aB.C. D.答案:B解题思路:试题难度:三颗星知识点:轴对称最值问题6.如图,∠AOB=45°,角内有一点P,OP=10,在角的两边上有两点Q,R(均不同于点O),则△PQR周长的最小值为( )A.10B.C.5D.答案:B解题思路:试题难度:三颗星知识点:轴对称最值问题7.如图,已知直线是第一、三象限的角平分线,A,B两点的坐标分别为,B(1,2),在直线上找一点P,使的值最大,则此时点P的坐标是( )A.(-1,-1)B.C.(-2,-2)D.答案:A解题思路:试题难度:三颗星知识点:轴对称最值问题。
有关坐标对称及最值问题5种题型

坐标对称及最值问题是数学中的常见问题,常常出现在函数、几何、三角函数等领域。
这类问题需要运用对称思想,以及寻找最值的方法。
下面列举了5种常见的题型及相应的解法。
题型一:函数的最值对于函数f(x),其最值可能出现在最小值(f(x)min)和最大值(f(x)max)上。
对于这类问题,我们通常需要观察函数的对称性,例如,如果函数是关于原点对称的,那么最小值和最大值可能在左右两侧取得。
解法上,我们通常需要利用导数或其他方法来找到函数的极值点,从而确定最值。
题型二:两点之间的距离在两点之间的距离问题中,如果两个点关于某个轴对称,那么它们之间的距离可以通过简单的轴对称距离公式来计算。
解法上,我们通常需要利用轴对称距离公式,以及两点之间的距离公式来求解。
题型三:圆的半径的最值在圆的半径的最值问题中,如果圆关于某条直线对称,那么我们需要找到圆的半径与对称轴的位置关系,从而确定圆的半径的最值。
解法上,我们通常需要利用圆的半径公式,以及对称轴的位置关系来求解。
题型四:三角形的重心坐标在三角形的重心坐标问题中,如果三个顶点关于某条直线对称,那么我们需要找到重心坐标与对称轴的关系,从而确定重心的坐标。
解法上,我们通常需要利用重心的几何性质,以及对称轴的位置关系来求解。
题型五:椭圆的离心率在椭圆的离心率问题中,如果焦点关于某轴对称,那么我们需要找到椭圆的离心率与对称轴的关系,从而确定椭圆的离心率。
解法上,我们通常需要利用椭圆的离心率公式,以及对称轴的位置关系来求解。
总的来说,坐标对称及最值问题的解法主要依赖于对称性和位置关系。
对于不同类型的题目,我们需要灵活运用这些方法来解决问题。
同时,对于不同类型的题目,也需要进行相应的变化和拓展,以适应更复杂的情况。
希望以上信息对您有所帮助。
如果您有任何具体问题或需要进一步的解释,请随时告诉我。
轴对称最值问题(线段和最小或差最大)(北师版)(含答案)
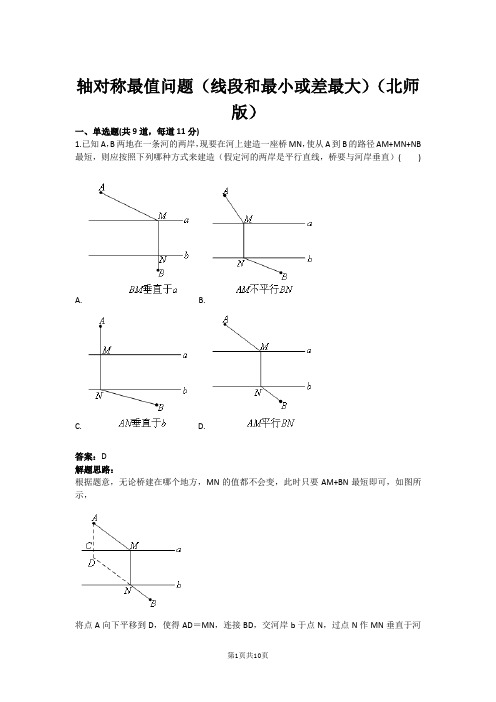
轴对称最值问题(线段和最小或差最大)(北师版)一、单选题(共9道,每道11分)1.已知A,B两地在一条河的两岸,现要在河上建造一座桥MN,使从A到B的路径AM+MN+NB 最短,则应按照下列哪种方式来建造(假定河的两岸是平行直线,桥要与河岸垂直)( )A. B.C. D.答案:D解题思路:根据题意,无论桥建在哪个地方,MN的值都不会变,此时只要AM+BN最短即可,如图所示,将点A向下平移到D,使得AD=MN,连接BD,交河岸b于点N,过点N作MN垂直于河岸b,交河岸a于点M,通过作图可知,最短时,AM∥DN,即AM∥BN.故选D试题难度:三颗星知识点:轴对称最值问题2.如图,已知A(1,3),B(5,1),长度为2的线段PQ在x轴上平行移动,当AP+PQ+QB 的值最小时,点P的坐标为( )A. B.C.(1,0)D.(5,0)答案:B解题思路:通过题意可知,PQ的长固定,所以若要AP+PQ+QB的值最小,则AP+BQ的值最小即可.如图,BQ向左平移两个单位到B′P,此时就转化为要求AP+B′P的最小值.作出点B′关于x轴的对称点B″,此时连接AB″,与x轴的交点即为所求的点P.根据题意可得,点B″的坐标为(3,-1),∴AB″的直线解析式为:y=-2x+5,∴点P的坐标为.故选B试题难度:三颗星知识点:轴对称最值问题3.在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A,B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.若E,F为边OA上的两个动点,且EF=2,则当四边形CDEF的周长最小时,点F的坐标为( )A. B.C.(2,0)D.(3,0)答案:B解题思路:通过题意可知,EF和CD的长固定,所以若要四边形CDEF的周长最小,则DE+CF的值最小即可.如图,CF向左平移两个单位到C′E,此时就转化为要求DE+C′E的最小值.作出点D关于x轴的对称点D′,此时连接C′D′,与x轴的交点即为点E.根据题意可得,点C′的坐标为(1,4),点D′的坐标为(0,-2),∴C′D′的直线解析式为:y=6x-2,∴点E的坐标为,∴点F的坐标为.故选B试题难度:三颗星知识点:轴对称最值问题4.如图,当四边形PABN的周长最小时,a的值为( )A. B.1C.2D.答案:A解题思路:通过题意可知,PN和AB的长固定,且PN=2,所以若要四边形PABN的周长最小,则AP+BN 的值最小即可.如图,BN向左平移两个单位到B′P,此时就转化为要求AP+B′P的最小值.作出点B′关于x轴的对称点B″,此时连接AB″,与x轴的交点即为点P.根据题意可得,点B″的坐标为(2,-1),∴AB″的直线解析式为:y=-4x+7,∴点P的坐标为.故选A试题难度:三颗星知识点:轴对称最值问题5.如图,两点A,B在直线MN的同侧,A到MN的距离AC=8,B到MN的距离BD=6,CD =4,P在直线MN上运动,则的最大值为( )A. B.C. D.答案:C解题思路:根据题意,若要的值最大,连接AB并延长与MN的交点即为点P,此时最大值即为线段AB的长.如图,过点B作BE⊥AC交AC于点E.∵AC=8,BD=6,CD=4,∴AE=2,BE=4,∴AB=.故选C试题难度:三颗星知识点:轴对称最值问题6.如图,已知两点A,B在直线的异侧,A到直线的距离AC=6,B到直线的距离BD=2,CD=3,点P在直线上运动,则的最大值为( )A. B.3C.1D.5答案:D解题思路:如图,作点B关于直线的对称点B′,连接AB′,AB′的长度即为所求.∵AC=6,BD=2,CD=3,∴AE=4,B′E=3,∴AB=5.故选D试题难度:三颗星知识点:轴对称最值问题7.如图,已知两点A,B在直线的异侧,A到直线的距离AC=5,B到直线的距离BD=2,DC=4,点P在直线上运动,则的最大值为( )A.1B.5C.3D.2答案:B解题思路:如图,作点B关于直线的对称点B′,连接AB′,AB′的长度即为所求.∵AC=5,BD=2,DC=4,∴AE=3,B′E=4,∴AB=5.故选B试题难度:三颗星知识点:轴对称最值问题8.如图,在平面直角坐标系中,已知A(0,1),B(3,-4),在x轴上有一点P,当的值最大时,点P的坐标是( )A. B.(-1,0)C.(0,0)D.(3,0)答案:B解题思路:如图,作点A关于x轴的对称点A′,连接BA′并延长与x轴的交点即为点P.∵A(0,1),B(3,-4),∴A′(0,-1),∴A′B的直线解析式为:y=-x-1,∴点P的坐标为(-1,0).故选B试题难度:三颗星知识点:轴对称最值问题9.如图,在平面直角坐标系中,已知A(-2,1),B(1,2),若P是x轴上使得PA+PB的值最小的点,Q是y轴上使得的值最大的点,则的值是( )A. B.-3C. D.3答案:C解题思路:分别作点B关于x轴,y轴的对称点B′,B″,连接AB′与x轴的交点即为点P,连接AB″并延长与y轴的交点即为点Q.∵B(1,2),∴B′(1,-2),B″(-1,2),∴AB′的直线解析式为:y=-x-1,AB″的直线解析式为:y=x+3,∴P点坐标为(-1,0),Q点坐标为(0,3),∴.故选C试题难度:三颗星知识点:轴对称最值问题。
数学北师大版七年级下册轴对称的应用(最短路径问题)课件

练习4
5. 如图,在平面直角坐标系中,已知A(1,4)、 B(2,3) C为x轴正半轴上一动点,D为y轴正半 轴上一动点,则四边形ABCD周长的最小值为____.
练习5
通过本节课的学习,你能谈谈我们都用了哪些数学 知识和数学思想吗? (1)两点之间线段最短 (2)三角形的三边关系 (3)轴对称的性质 (4)线段垂直平分线的性质 “转化”的数学思想.
西安市第十四中学 许亚琦
唐朝诗人李欣的诗《古从军行》开头两句说: “白日登山望烽火,黄昏饮马傍交河”。诗中隐含 着一个有趣的数学问题---将军饮马问题: 例一:如图1,将军在观望烽火之后从山脚下 的A点出发,走到笔直的河岸l去饮马,再去B点宿营, 走什么样的路线最短呢?
归纳:模型一“一线两点”型(将军饮马) 已知一直线及直线同侧两点,在直线上找一点,使 其到已知两点的距离之和最小,通常作其中一点关 于直线的对称点,对称点与另一点的连线与直线的 交点即为所求点. 动画演示一
例三:如图,设点A为马棚,点B为住房.牧马人从 马棚牵出一匹马,先到草地吃草,再到河边饮水, 然后回到住房.问牧马人怎样走才能使路程最短?
归纳:模型三“两线两点”型 已知两直线及两线之间的两点,在两直线上分别找 一点使其与已知两点顺次连接的线段和(四边形周 长)最小,通常分别作两点关于两直线的对称点, 连接两对称点,与两条直线的交点即为满足条件的 点,再根据题意求解. 动画演示三
1. 如图,已知等边△ABC的边长为8,点D为AC的 中点,点E为BC的中点,点P为BD上一动点,则 PE+PC的最小值为( ) A.3 B.4 2 C.2 3 D.4 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P
A
D
C
M A 专题复习 线段最值问题(1)
——与轴对称有关的最小值问题
成都市人民北路中学 2017级数学组 薛强
【学习目标】
1、掌握“将军饮马”问题的数学模型。
2、利用“将军饮马”问题的数学模型解决与轴对称有关的最值问题。
3、感受数学建模思想、转化思想的同时,培养层层推衍的学习思维和不断挑战的创造力。
【学习重点】
利用“将军饮马”问题的数学模型解决与轴对称有关的最值问题。
【学习难点】
根据题意准确作出对称点,构建特殊三角形计算最值。
【学习过程】 一、原生问题 【将军饮马】
一位将军从A 地出发到小河MN 边饮马,然后再前往B 地,怎样走才能使PA+PB 最小?
二、衍生问题
问题1 如图Rt △ABC 中,AB =BC =4,D 为BC 的中点,E 为AC 边上一动点, 连结ED 、EB ,则△BDE 周长的最小值为______.
问题2 如图所示,已知点C(1,0),直线7y x =-+与两坐标轴分别交于 A ,B 两点,D ,E 分别是AB ,OA 上的动点,则△CDE 周长的最小值 是______.
练习:如图,已知正方形ABCD 边长为3,点E 在AB 边上且BE=1,点P ,Q 分别是边BC ,CD 的动点(均不与顶点重合),则四边形AEPQ 的周长的最小 值为__________.
B
A
B
A A
B
F
问题3 如图,在Rt △ABC 中,∠ACB=90°,AC=6,BC=8,AD 是∠BAC 的平分线。
若P 、Q 分别是AD 和AC 上的动点,则PC+PQ 的最小值为 ____________.
三、探究结果
1、学科知识
2、学科技能
3、思想方法
四、分层检测
1.如图,在边长为4的正方形ABCD 中,E 是AB 边上的一点,且AE =3, 点Q 为对角线AC 上的动点,则△BEQ 周长的最小值为________.
2.如图,AB 是⊙O 的直径,AB=8,点M 在⊙O 上,∠MAB=20°, N 是MB 的中点,P 是直径AB 上的一动点.若MN=1,则△
PMN 周长的最小值为___________.
★3. 如图,直线y =
+x 轴、y 轴分别交于点A 点C 、D 分别为线段AB 、OB 上的动点,点P 坐标为(-2,0)PCD ∆的周长最小值为____________.
五、拓展延伸
如图,点O 是边长为2的正方形ABCD 的对角线交点,正方形 OEFG 的面积为8 . 正方形ABCD 固定,把正方形OEFG 绕点O 逆时针旋转一周. 点M 为A G 的中点,在旋转过程中,线段 MF 的长度最大值为______________,最小值为___________.
A B
N
T 1.(2014成都第24题)
如图,在边长为2的菱形ABCD 中,∠A=60°,M 是AD 边的中点, N 是AB 边上的一动点,将△ AMN 沿MN 所在直线翻折得到△ A′MN , 连接A′C ,则A′C 长度的最小值是 .
2.(2011成都第24题)
在三角形纸片ABC 中,已知∠ABC=90°,AB=6,BC=8。
过点A 作直线l 平行于BC ,折叠三角形纸片ABC ,使直角顶点B 落在直线l 上的T 处,折痕 为MN .当点T 在直线l 上移动时,折痕的端点M 、N 也随之移动.若限定 端点M 、N 分别在AB 、BC 边上移动,则线段AT 长度的最大值与最小值之和 为_________ (计算结果不取近似值).
3.(2012成都第25题)
如图,长方形纸片ABCD 中,AB=8cm ,AD=6cm ,按下列步骤进行裁剪和拼图:
第一步:如图①,在线段AD 上任意取一点E ,沿EB 、EC 剪下三角形纸片EBC(余下部分不再使用); 第二步:如图②,沿三角形EBC 的中位线GH 将纸片剪成两部分,并在线段GH 上任意取一点M ,线段BC 上任意取一点N ,沿MN 将梯形纸片GBCH 剪成两部分;
第三步:如图③,将MN 左侧纸片绕G 点按顺时针方向旋转180°,使线段GB 与GE 重合,将MN 右侧纸片绕H 点按逆时针方向旋转180°,使线段HC 与HE 重合,拼成一个与三角形纸片EBC 面积相等的四边形纸片. (注:裁剪和拼图过程均无缝且不重叠)
则拼成的这个四边形纸片的周长的最小值为
________cm ,最大值为________cm .。
