九年级数学《圆》单元测试题襄州教研

合集下载

九年级数学《圆》单元测试(含参考答案与试题解析)

九年级数学《圆》单元测试学校：___________姓名：___________班级：___________考号：___________题号一二三总分得分评卷人得分一．选择题（共10小题）1．圆锥的地面半径为10cm．它的展开图扇形半径为30cm，则这个扇形圆心角的度数是（）A．60°B．90°C．120°D．150°2．已知⊙O的半径为5，点P到圆心O的距离为8，那么点P与⊙O的位置关系是（）A．点P在⊙O上B．点P在⊙O内C．点P在⊙O 外 D．无法确定3．一块等边三角形的木板，边长为1，现将木板沿水平线翻滚（如图），那么B点从开始至结束所走过的路径长度为（）A．B．C．4 D．2+4．⊙O的半径为R，点P到圆心O的距离为d，并且d≥R，则P点（）A．在⊙O内或⊙O上B．在⊙O外C．在⊙O上D．在⊙O外或⊙O上5．已知⊙O和⊙O′的半径分别为5cm和7cm，且⊙O和⊙O′相切，则圆心距OO′为（）A．2 cm B．7 cm C．12 cmD．2 cm或12 cm6．如图，AB是半圆O的直径，AC为弦，OD⊥AC于D，过点O作OE∥AC交半圆O于点E，过点E作EF⊥AB于F．若AC=2，则OF的长为（）A．B．C．1 D．27．如图，AB是⊙O的直径，弦CD与AB相交，且∠ABC=32°，则∠CDB的度数为（）A．58°B．32°C．80°D．64°8．如图，A，B，C是⊙O上的三点，已知∠AOC=110°，则∠ABC的度数是（）A．50°B．55°C．60°D．70°9．如图，A、B、C三点在⊙O上，若∠AOB=80°，则∠ACB等于（）A．160°B．80°C．40°D．20°10．如图，AB是⊙O的直径，弦CD交AB于点E，且E为OB的中点，∠CDB=30°，CD=4，则阴影部分的面积为（）A．πB．4πC．πD．π二．填空题（共4小题）11．如图，四边形ABCD是菱形，⊙O经过点A、C、D，与BC相交于点E，连接AC、AE．若∠D=78°，则∠EAC=°．12．如图，正六边形A1B1C1D1E1F1的边长为1，它的六条对角线又围成一个正六边形A2B2C2D2E2F2，如此继续下去，则正六边形A4B4C4D4E4F4的面积是．13．如图，在Rt△ABC中，∠A=30°，BC=2，以直角边AC为直径作⊙O交AB于点D，则图中阴影部分的面积是．14．如图，PA与⊙O相切于点A，弦AB⊥OP，垂足为C，OP与⊙O相交于点D，已知OA=2，OP=4，则弦AB的长．三．解答题（共6小题）15．如图，直线AB、BC、CD分别与⊙O相切于E、F、G，且AB∥CD，OB=6cm，OC=8cm．求：（1）∠BOC的度数；（2）BE+CG的长；（3）⊙O的半径．16．如图，O为等腰三角形ABC内一点，⊙O与底边BC交于M、N两点，且与AB、AC相切于E、F两点，连接AO，与⊙O交于点G，与BC相交于点D．（1）证明：AD⊥BC；（2）若AG等于⊙O的半径，且AE=MN=2，求扇形OEM的面积．17．如图所示，AB是半圆O的直径，∠ABC=90°，点D是半圆O上一动点（不与点A、B重合），且AD∥CO．（1）求证：CD是⊙O的切线；（2）填空：①当∠BAD=度时，△OBC和△ABD的面积相等；②当∠BAD=度时，四边形OBCD是正方形．18．如图，A、B、C为⊙O上的点，PC过O点，交⊙O于D点，PD=OD，若OB⊥AC于E点．（1）判断A是否是PB的中点，并说明理由；（2）若⊙O半径为8，试求BC的长．19．已知：如图，在平行四边形ABCD中，⊙O是经过A、B、C三点的圆，CD与⊙O相切于点C，点P是上的一个动点（点P不与B、C点重合），连接PA、PB、PC．（1）求证：CA=CB；（2）①点P满足时，△CPA≌△ABC，请说明理由；②当∠ABC的度数为时，四边形ABCD是菱形．20．（1）如图，在△ABC中，AD是中线，分别过点B、C作AD及其延长线的垂线BE、CF，垂足分别为点E、F．求证：BE=CF．（2）如图，△ABC内接于⊙O，AB为⊙O的直径，∠BAC=2∠B，AC=6，过点A作⊙O的切线与OC的延长线交于点P，求PA的长．参考答案与试题解析一．选择题（共10小题）1．圆锥的地面半径为10cm．它的展开图扇形半径为30cm，则这个扇形圆心角的度数是（）A．60°B．90°C．120°D．150°【分析】根据圆锥的侧面展开图为扇形，圆锥的底面圆的周长等于扇形的弧长得到圆锥的展开图扇形的弧长=2π•10，然后根据扇形的弧长公式l=计算即可求出n．【解答】解：设圆锥的展开图扇形的圆心角的度数为n．∵圆锥的底面圆的周长=2π•10=20π，∴圆锥的展开图扇形的弧长=20π，∴20π=，∴n=120．故选C．2．已知⊙O的半径为5，点P到圆心O的距离为8，那么点P与⊙O的位置关系是（）A．点P在⊙O上B．点P在⊙O内C．点P在⊙O 外 D．无法确定【分析】根据点在圆上，则d=r；点在圆外，d＞r；点在圆内，d＜r（d即点到圆心的距离，r即圆的半径）．【解答】解：∵OP=8＞5，∴点P与⊙O的位置关系是点在圆外．故选：C．3．一块等边三角形的木板，边长为1，现将木板沿水平线翻滚（如图），那么B点从开始至结束所走过的路径长度为（）A ．B ．C ．4D ．2+【分析】根据题目的条件和图形可以判断点B 分别以C 和A 为圆心CB 和AB 为半径旋转120°，并且所走过的两路径相等，求出一个乘以2即可得到．【解答】解：如图：BC=AB=AC=1，∠BCB′=120°，∴B 点从开始至结束所走过的路径长度为2×弧BB′=2×=，故选B ．4．⊙O 的半径为R ，点P 到圆心O 的距离为d ，并且d ≥R ，则P 点（）A ．在⊙O 内或⊙O 上B ．在⊙O 外C ．在⊙O 上D ．在⊙O 外或⊙O 上【分析】根据点与圆的位置关系进行判断．【解答】解：∵d ≥R ，∴点P 在⊙O 上或点P 在⊙O 外．故选D ．5．已知⊙O 和⊙O′的半径分别为5cm 和7cm ，且⊙O 和⊙O′相切，则圆心距OO′为（） A ．2 cm B ．7 cm C ．12 cmD ．2 cm 或12 cm【分析】此题考虑两种情况：两圆外切或两圆内切．再进一步根据位置关系得到数量关系．设两圆的半径分别为R 和r ，且R ≥r ，圆心距为d ：外离，则d ＞R +r ；外切，则d=R +r ；相交，则R ﹣r ＜d ＜R +r ；内切，则d=R ﹣r ；内含，则d ＜R ﹣r ．【解答】解：当两圆外切时，则圆心距等于两圆半径之和，即7+5=12；当两圆内切时，则圆心距等于两圆半径之差，即7﹣5=2．故选D ．6．如图，AB 是半圆O 的直径，AC 为弦，OD ⊥AC 于D ，过点O 作OE ∥AC 交半圆O 于点E ，过点E 作EF ⊥AB 于F ．若AC=2，则OF 的长为（）A．B．C．1 D．2【分析】根据垂径定理求出AD，证△ADO≌△OFE，推出OF=AD，即可求出答案．【解答】解：∵OD⊥AC，AC=2，∴AD=CD=1，∵OD⊥AC，EF⊥AB，∴∠ADO=∠OFE=90°，∵OE∥AC，∴∠DOE=∠ADO=90°，∴∠DAO+∠DOA=90°，∠DOA+∠EF=90°，∴∠DAO=∠EOF，在△ADO和△OFE中，，∴△ADO≌△OFE（AAS），∴OF=AD=1，故选C．7．如图，AB是⊙O的直径，弦CD与AB相交，且∠ABC=32°，则∠CDB的度数为（）A．58°B．32°C．80°D．64°【分析】由AB是⊙O的直径，可得知∠ACB=90°，根据三角形内角和为180°可求出∠BAC 的度数，再由同弦的圆周角相等得出结论．【解答】解：∵线段AB为⊙O的直径，∴∠ACB=90°，∴∠BAC=180°﹣∠ACB﹣∠ABC=58°．∵∠CDB与∠BAC均为弦BC的圆周角，∴∠CDB=∠BAC=58°．故选A．8．如图，A，B，C是⊙O上的三点，已知∠AOC=110°，则∠ABC的度数是（）A．50°B．55°C．60°D．70°【分析】由A，B，C是⊙O上的三点，已知∠AOC=110°，根据圆周角定理，即可求得答案．【解答】解：∵A，B，C是⊙O上的三点，∠AOC=110°，∴∠ABC=∠AOC=55°．故B．9．如图，A、B、C三点在⊙O上，若∠AOB=80°，则∠ACB等于（）A．160°B．80°C．40°D．20°【分析】直接根据圆周角定理求解．【解答】解：∠ACB=∠AOB=×80°=40°．故选C．10．如图，AB是⊙O的直径，弦CD交AB于点E，且E为OB的中点，∠CDB=30°，CD=4，则阴影部分的面积为（）A．πB．4πC．πD．π【分析】首先证明OE=OC=OB，则可以证得△OEC≌△BED，则S阴影=半圆﹣S扇形OCB，利用扇形的面积公式即可求解．【解答】解：连结BC．∵∠COB=2∠CDB=60°，又∵OB=OC，∴△OBC是等边三角形．∵E为OB的中点，∴CD⊥AB，∴∠OCE=30°，CE=DE，∴OE=OC=OB=2，OC=4．S阴影==．故选D．二．填空题（共4小题）11．如图，四边形ABCD是菱形，⊙O经过点A、C、D，与BC相交于点E，连接AC、AE．若∠D=78°，则∠EAC=27°．【分析】根据菱形的性质得到∠ACB=∠DCB=（180°﹣∠D）=51°，根据圆内接四边形的性质得到∠AEB=∠D=78°，由三角形的外角的性质即可得到结论．【解答】解：∵四边形ABCD是菱形，∠D=78°，∴∠ACB=∠DCB=（180°﹣∠D）=51°，∵四边形AECD是圆内接四边形，∴∠AEB=∠D=78°，∴∠EAC=∠AEB﹣∠ACE=27°，故答案为：27．12．如图，正六边形A1B1C1D1E1F1的边长为1，它的六条对角线又围成一个正六边形A2B2C2D2E2F2，如此继续下去，则正六边形A4B4C4D4E4F4的面积是．【分析】由正六边形的性质得：∠A1B1B2=90°，∠B1A1B2=30°，A1A2=A2B2，由直角三角形的性质得出B1B2=A1B1=，A2B2=A1B2=B1B2=，由相似多边形的性质得出正六边形A2B2C2D2E2F2的面积：正六边形A1B1C1D1E1F1的面积=，求出正六边形A1B1C1D1E1F1的面积=，得出正六边形A2B2C2D2E2F2的面积，同理得出正六边形A4B4C4D4E4F4的面积．【解答】解：由正六边形的性质得：∠A1B1B2=90°，∠B1A1B2=30°，A1A2=A2B2，∴B1B2=A1B1=，∴A2B2=A1B2=B1B2=，∵正六边形A1B1C1D1E1F1∽正六边形A2B2C2D2E2F2，∴正六边形A2B2C2D2E2F2的面积：正六边形A1B1C1D1E1F1的面积=（）2=，∵正六边形A1B1C1D1E1F1的面积=6××1×=，∴正六边形A2B2C2D2E2F2的面积=×=，同理：正六边形A4B4C4D4E4F4的面积=（）3×=；故答案为：．13．如图，在Rt△ABC中，∠A=30°，BC=2，以直角边AC为直径作⊙O交AB于点D，则图中阴影部分的面积是﹣π．【分析】连接连接OD、CD，根据S阴=S△ABC﹣S△ACD﹣（S扇形OCD﹣S△OCD）计算即可解决问题．【解答】解：如图，连接OD、CD．∵AC是直径，∴∠ADC=90°，∵∠A=30°，∴∠ACD=90°﹣∠A=60°，∵OC=OD，∴△OCD是等边三角形，∵BC是切线．∴∠ACB=90°，∵BC=2，∴AB=4，AC=6，∴S阴=S△ABC﹣S△ACD﹣（S扇形OCD﹣S△OCD）=×6×2﹣×3×3﹣（﹣×32）=﹣π．故答案为：﹣π．14．如图，PA与⊙O相切于点A，弦AB⊥OP，垂足为C，OP与⊙O相交于点D，已知OA=2，OP=4，则弦AB的长2．【分析】由已知条件可知Rt△POA中，OP=2OA，所以可求出∠P=30°，∠O=60°，再在Rt△AOC中，利用勾股定理求解直角三角形即可得到AB的长．【解答】解：∵PA与⊙O相切于点A，∴OA⊥AP，∴三角形△POA是直角三角形，∵OA=2，OP=4，即OP=2OA，∴∠P=30°，∠O=60°，则在Rt△AOC中，OC=OA=1，则AC=，∴AB=2，故答案为2．三．解答题（共6小题）15．如图，直线AB、BC、CD分别与⊙O相切于E、F、G，且AB∥CD，OB=6cm，OC=8cm．求：（1）∠BOC的度数；（2）BE+CG的长；（3）⊙O的半径．【分析】（1）根据切线的性质得到OB平分∠EBF，OC平分∠GCF，OF⊥BC，再根据平行线的性质得∠GCF+∠EBF=180°，则有∠OBC+∠OCB=90°，即∠BOC=90°；（2）由勾股定理可求得BC的长，进而由切线长定理即可得到BE+CG的长；（3）最后由三角形面积公式即可求得OF的长．【解答】解：（1）连接OF；根据切线长定理得：BE=BF，CF=CG，∠OBF=∠OBE，∠OCF=∠OCG；∵AB∥CD，∴∠ABC+∠BCD=180°，∴∠OBE+∠OCF=90°，∴∠BOC=90°；（2）由（1）知，∠BOC=90°．∵OB=6cm，OC=8cm，∴由勾股定理得到：BC==10cm，∴BE+CG=BC=10cm．（3）∵OF⊥BC，∴OF==4.8cm．16．如图，O为等腰三角形ABC内一点，⊙O与底边BC交于M、N两点，且与AB、AC相切于E、F两点，连接AO，与⊙O交于点G，与BC相交于点D．（1）证明：AD⊥BC；（2）若AG等于⊙O的半径，且AE=MN=2，求扇形OEM的面积．【分析】（1）根据切线长定理得到AE=AF，∠EAO=∠FAO，根据等腰三角形的性质得到AD ⊥EF，根据三角形的内角和得到∠B=∠C=（180°﹣∠BAC），∠AEF=（180°﹣∠BAC），等量代换得到∠AEF=∠B，根据平行线的性质即可得到结论．（2）由AG等于⊙O的半径，得到AO=2OE，由AB是⊙O的切线，得到∠AEO=90°，根据直角三角形的性质得到∠EAO=30°，根据三角形的内角和得到∠AOE=60°，由垂径定理得到DM=MN=，根据三角函数的定义得到∠MOD=60°，根据扇形的面积公式即可得到结论．【解答】（1）证明：∵AB、AC相切于E、F两点，∴AE=AF，∠EAO=∠FAO，∴AD⊥EF，∵AB=AC，∴∠B=∠C=（180°﹣∠BAC），∵AE=AF，∴∠AEF=（180°﹣∠BAC），∴∠AEF=∠B，∴EF∥BC，∴AD⊥BC；（2）解：∵AG等于⊙O的半径，∴AO=2OE，∵AB是⊙O的切线，∴∠AEO=90°，∴∠EAO=30°，∴∠AOE=60°，∵AE=2，∴OE=2，∵OD⊥MN，∴DM=MN=，∵OM=2，∴sin∠MOD==，∴∠MOD=60°，∴∠EOM=60°，∴S扇形EOM==π．17．如图所示，AB是半圆O的直径，∠ABC=90°，点D是半圆O上一动点（不与点A、B重合），且AD∥CO．（1）求证：CD是⊙O的切线；（2）填空：①当∠BAD=60度时，△OBC和△ABD的面积相等；②当∠BAD=45度时，四边形OBCD是正方形．【分析】（1）连接OD．只要证明△COD≌△COB，即可推出∠ODC=∠OBC=90°，推出CD是⊙O的切线．（2））①当∠BAD=60度时，△OBC和△ABD的面积相等；②当∠BAD=45度时，四边形OBCD 是正方形．【解答】（1）证明：连接OD．∵AD∥CO，∴∠A=∠BOC，∠ADO=∠DOC，∵OA=OD，∴∠A=∠ADO，∴∠BOC=∠DOC，在△COD和△COB中，，∴△COD≌△COB，∴∠ODC=∠OBC=90°，∴CD是⊙O的切线．（2）①当∠BAD=60度时，△OBC和△ABD的面积相等；理由此时AD=OB，AB=OC，△OBC≌△DAB，所以面积相等．②当∠BAD=45度时，四边形OBCD是正方形．此时∠DOB=90°，∵∠ODC=∠OBC=90°，∴四边形OBCD是矩形，∵OB=OD，∴四边形OBCD是正方形．故答案分别为60，45．18．如图，A、B、C为⊙O上的点，PC过O点，交⊙O于D点，PD=OD，若OB⊥AC于E 点．（1）判断A是否是PB的中点，并说明理由；（2）若⊙O半径为8，试求BC的长．【分析】（1）连接AD，由CD是⊙O的直径，得到AD⊥AC，推出AD∥OB，根据平行线等分线段定理得到PA=AB；（2）根据相似三角形的性质得到OB=8，求得AD=4，根据勾股定理得到AC==4，根据垂径定理得到AE=CE=2，由勾股定理即可得到结论【解答】解：（1）A是PB的中点，理由：连接AD，∵CD是⊙O的直径，∴AD⊥AC，∵OB⊥AC，∴AD∥OB，∵PD=OD，∴PA=AB，∴A是PB的中点；（2）∵AD∥OB，∴△APD∽△BPO，∴，∵⊙O半径为8，∴OB=8，∴AD=4，∴AC==4，∵OB⊥AC，∴AE=CE=2，∵OE=AD=2，∴BE=6，∴BC==4．19．已知：如图，在平行四边形ABCD中，⊙O是经过A、B、C三点的圆，CD与⊙O相切于点C，点P是上的一个动点（点P不与B、C点重合），连接PA、PB、PC．（1）求证：CA=CB；（2）①点P满足当AC=AP时，△CPA≌△ABC，请说明理由；②当∠ABC的度数为60时，四边形ABCD是菱形．【分析】（1）作CE⊥AB于E，由于CA=CB，根据等腰三角形的性质得CE为AB的垂直平分线，则点O在CE上，再根据平行四边形的性质得AB∥CD，（2）当AC=AP时，△CPA≌△ABC．由于AC=BC，AC=AP，则∠ABC=∠BAC，∠APC=∠ACP，根据圆周角定理得∠ABC=∠APC，则∠BAC=∠ACP，加上AC=CA，即可得到△CPA≌△ABC；（3）如图2，连接OC，AC，OB，根据平行线的性质得到∠BCD=120°，根据切线的性质得到∠OCD=90°，推出BO垂直平分AC，即可得到结论．【解答】（1）证明：连接CO并延长交AB于E，如图，∵CD与⊙O相切于点C，∴CE⊥CD，∵四边形ABCD为平行四边形，∴AB∥CD，∴CE⊥AB，∴AE=BE，∴BC=AC；（2）解：当AC=AP时，△CPA≌△ABC．证明如下：∵AC=BC，AC=AP，∴∠ABC=∠BAC，∠APC=∠ACP，∵∠ABC=∠APC，∴∠BAC=∠ACP，在△CPA与△ABC中，，∴△CPA≌△ABC；故答案为：AC=AP；（3）解：当∠ABC的度数为60°时，四边形ABCD是菱形，如图2，连接OC，AC，OB，∵∠ABC=60°，∴∠BCD=120°，∵CD与⊙O相切于点C，∴∠OCD=90°，∴∠BCO=30°，∵OB=OC，∴∠OBC=30°，∴∠ABO=30°，∴BO垂直平分AC，∴AB=BC，∴四边形ABCD是菱形．故答案为：60°．20．（1）如图，在△ABC中，AD是中线，分别过点B、C作AD及其延长线的垂线BE、CF，垂足分别为点E、F．求证：BE=CF．（2）如图，△ABC内接于⊙O，AB为⊙O的直径，∠BAC=2∠B，AC=6，过点A作⊙O的切线与OC的延长线交于点P，求PA的长．【分析】（1）由垂直定义得∠E=∠CFD=90°，根据中线知BD=CD，利用“AAS”证△BED≌△CFD 可得答案；（2）根据AB是圆的直径，则△ABC是直角三角形，根据∠BAC=2∠B即可求得∠BAC的度数，证得△OAC是等边三角形．再根据PA是圆的切线，可以证得∠P=30°，则可求得OP的长，在直角△OAP中，利用勾股定理即可求得PA的长．【解答】解：（1）∵分别过点B、C作AD及其延长线的垂线BE、CF，垂足分别为点E、F，∴∠E=∠CFD=90°，∵AD是中线，∵BD=CD，在△BED和△CFD中，∵，∴△BED≌△CFD（AAS），∴BE=CF；（2）∵AB为⊙O的直径∴∠ACB=90°∴∠B+∠BAC=90°又∵∠BAC=2∠B∴∠B=30°，∠BAC=60°∵OA=OC∴△OAC是等边三角形．∴OA=AC=6，∠AOC=60°∵AP是⊙O的切线．∴∠OAP=90°∴在直角△OAP中，∠P=90°﹣∠AOC=90°﹣60°=30°∴OP=2OA=2×6=12，∴PA===6．。

度湘教版数学九年级下册第二章圆单元检测试卷

度湘教版数学九年级下册第二章圆单元检测试卷班级姓名第2章质量评价试卷一、选择题(每题4分，共40分)1．以下说法错误的选项是()A．圆上的点到圆心的距离相等B．过圆心的线段是直径C．直径是圆中最长的弦D．半径相等的圆是等圆2．[2021·聊城]如图，在⊙O中，弦BC与半径OA相交于点D，衔接AB，OC.假定∠A＝60°，∠ADC＝85°，那么∠C的度数是() A．25°B．27.5°C．30°D．35°3．如图，在△ABC中，AB＝AC＝4 cm，BC＝6 cm，D是BC的中点，以点D为圆心作一个半径为3 cm的圆，那么以下说法正确的选项是()A．点A在⊙D外B．点B在⊙D内C．点C在⊙D上D．无法确定4．如图，四边形ABCD的边AB，BC，CD，DA和⊙O区分相切于点L，M，N，P.假定四边形ABCD的周长为20，那么AB＋CD 等于()A．5 B．8 C．10 D．125．如图，AB为⊙O的直径，弦CD⊥AB点于E.假定CD＝12，BE ＝2，那么⊙O 的直径为( )A ．8B ．10C ．16D ．206．[2021·济宁]如图，点B ，C ，D 在⊙O 上．假定∠BCD ＝130°，那么∠BOD 的度数是( )A ．50°B ．60°C ．80°D ．100°7．[2021·黄石]如图，AB 是⊙O 的直径，点D 为⊙O 上一点，且∠ABD ＝30°，BO ＝4，那么的长为( )A ．83πB ．43πC ．2πD ．.23π8．等边三角形的内切圆半径、外接圆半径和高的比为( )A ．1∶2∶ 3B ．1∶2∶ 3C ．1∶3∶2D ．1∶2∶39．Rt △ABC 中，∠C ＝90°，AC ＝3 cm ，BC ＝4 cm ，以点C 为圆心作圆．假定⊙C 与直线AB 相切，那么⊙C 的半径为( )A ．2 cmB ．2.4 cmC ．3 cmD ．4 cm10．[2021·德州]如图，从一块直径为2 m 的圆形铁皮上剪出一个圆心角为90°的扇形，那么此扇形的面积为( )A ．π2 m 2B ．32π2 m 2C ．π m 2D ．2π m 2二、填空题(每题4分，共24分)11．如图，⊙O 的半径为4 cm ，直线l ⊥OA ，垂足为O ，那么直线l 沿射线OA 方向平移____cm 时与⊙O 相切．12．[2021·泰安]如图，⊙O是△ABC的外接圆，∠A＝45°，BC ＝4，那么⊙O的直径为_______．13．[2021·邵阳]如下图，四边形ABCD为⊙O的内接四边形，∠BCD＝120°，那么∠BOD的大小是_______．14．如图，点I为△ABC的内心，且∠ABC＝40°，∠ACB＝70°，那么∠BIC＝____.15．[2021·通辽]如图，⊙O的半径为10，圆心O到弦AB的距离为5，那么弦AB所对的圆周角的度数是________．16．在Rt△ABC中，∠C＝90°，AC＝6，BC＝8，那么△ABC的内切圆半径r＝____．三、解答题(共86分)17．(10分)如图，AB是⊙O的弦(非直径)，C，D是AB上的两点，并且AC＝BD.求证：OC＝OD.18．(10分)如图，△ABC内接于⊙O，AB＝AC，∠BOC＝120°，延伸BO交⊙O于点D.(1)试求∠BAD的度数；(2)求证：△ABC为等边三角形．19．(11分)[2021·重庆]如图，AB是⊙O的直径，点P在BA的延伸线上，PD与⊙O相切于点D，过点B作PD的垂线交PD的延伸线于点C.假定⊙O的半径为4，BC＝6，求PA的长．20．(12分)如图，AB是⊙O的直径，AC与⊙O相切，切点为A，D为⊙O上一点，AD与OC相交于点E，且∠DAB＝∠C.求证：OC∥BD.21．(14分)如图，点E在△ABC的边AB上，∠C＝90°，以AE 为直径的⊙O切BC于点D.(1)求证：AD平分∠BAC；(2)∠B＝30°，AD＝23，求图中阴影局部的面积．22．(14分)[2021·温州]如图，D是△ABC的BC边上一点，衔接AD，作△ABD的外接圆，将△ADC沿直线AD折叠，点C的对应点E落在上．(1)求证：AE＝AB.(2)假定∠CAB＝90°，cos ∠ADB＝13，BE＝2，求BC的长．23．(15分)[2021·天门]如图，在⊙O中，AB为直径，AC为弦．过BC延伸线上一点G，作GD⊥AO于点D，交AC于点E，交⊙O 于点F，M是GE的中点，衔接CF，CM.(1)判别CM与⊙O的位置关系，并说明理由；(2)假定∠ECF＝2∠A，CM＝6，CF＝4，求MF的长．参考答案一、选择题(每题4分，共40分)1．B2．D【解析】∵∠A＝60°，∠ADC＝85°，∴∠B＝85°－60°＝25°，∠CDO＝95°，∴∠AOC＝2∠B＝50°，∴∠C＝180°－95°－50°＝35°.3．C4．C5．D6．D7．A【解析】衔接OD ，如答图，∵∠ABD ＝30°，∴∠AOD ＝2∠ABD ＝60°，∴∠BOD ＝120°，∴的长＝120π×4180＝8π3.8．D9．B10．A【解析】衔接AC ，如答图．∵从一块直径为2 m 的圆形铁皮上剪出一个圆心角为90°的扇形，即∠ABC ＝90°，∴AC 为直径，即AC ＝2 m ，AB ＝BC .∵AB 2＋BC 2＝22，∴AB ＝BC ＝2m ，∴阴影局部的面积是90π×〔2〕2360＝12π(m 2)．二、填空题(每题4分，共24分)11．412．4 2【解析】如答图，衔接OB ，OC .∵∠A ＝45°，∴∠BOC ＝90°，∴△BOC 是等腰直角三角形．又∵BC ＝4，∴BO ＝CO ＝BC ·cos 45°＝2 2. ∴⊙O 的直径为4 2.13．120°14．125°【解析】 ∵∠IBC ＝12∠ABC ＝20°，∠ICB ＝12∠ACB ＝35°，∴在△BIC 中，∠BIC ＝180°－(∠IBC ＋∠IC B)＝125°.15．60°或120°【解析】由图可知，OA ＝10，OD ＝5. ∴在Rt △OAD 中，AD ＝OA 2－OD 2＝53，∴tan ∠1＝AD OD ＝3，∴∠1＝60°.同理可得∠2＝60°，∴∠AOB ＝∠1＋∠2＝60°＋60°＝120°， ∴圆周角的度数是60°或120°.16．2【解析】由勾股定理得：AB ＝AC 2＋BC 2＝62＋82＝10，由切线长定理可得：r ＝AC ＋BC －AB 2＝6＋8－102＝2.三、解答题(共86分)17．证明：衔接OA ，OB (图略)，∵OA ＝OB ，∴∠OAC ＝∠OBD .又∵AC ＝BD ，∴△AOC ≌△BOD ，∴OC ＝OD .(10分)18． (1)解：∵BD 是⊙O 的直径，∴∠BAD ＝90°.(4分)(2)证明：∵∠BOC ＝120°，∴∠BAC ＝12∠BOC ＝60°.又∵AB ＝AC ，∴△ABC 是等边三角形．(10分)19．解：衔接DO ，如答图．∵PD 与⊙O 相切于点D ，∴∠PDO ＝90°. ∵∠C ＝90°，∴DO ∥BC ，∴△PDO ∽△PCB ， ∴DO BC ＝PO PB ＝46＝23.设PA ＝x ，那么x ＋4x ＋8＝23，解得x ＝4， ∴PA ＝4.(11分)20．证明：∵AC 与⊙O 相切，∴AC ⊥AB ，∴∠DAB ＋∠CAE ＝90°.∵∠DAB ＝∠C ，∴∠C ＋∠CAE ＝90°，∴∠CEA ＝90°，即OC ⊥AD .(8分)又∵AB 是⊙O 的直径，∴BD ⊥AD ，(10分) ∴OC ∥BD .(12分)21．(1)证明：如答图，衔接OD .∵BC 为⊙O 的切线，∴OD ⊥BC .又∵∠C ＝90°，∴OD ∥AC ，∴∠ODA ＝∠DAC .又∵OD ＝OA ，∴∠OAD ＝∠ODA ，∴∠OAD ＝∠DAC ，即AD 平分∠BAC .(6分)(2)解：∵∠B ＝30°，∴∠BAC ＝60°，∴∠BAD ＝∠DAC ＝30°，∴BD ＝AD ＝2 3.(7分)在Rt △OBD 中，tan B ＝OD BD ，即33＝OD 23， ∴OD ＝2，且∠BOD ＝60°，(9分)∴S 阴影＝S △OBD －S 扇形OED＝12×23×2－60π×22360＝23－2π3.(14分)22．(1)证明：由折叠的性质可知，△ADE≌△ADC，∴∠AED＝∠ACD，AE＝AC.∵∠ABD＝∠AED，∴∠ABD＝∠ACD，∴AB＝AC，∴AE＝AB.(6分)(2)解：如答图，过A作AH⊥BE于点H.∵AB＝AE，BE＝2，∴BH＝EH＝1.∵∠ABE＝∠AEB＝∠ADB，cos ∠ADB＝13，∴cos ∠ABE＝cos ∠ADB＝13，∴BH AB ＝13.∴AC＝AB＝3，∵∠BAC＝90°，AC＝AB，∴BC＝3 2.(14分) 23．解：(1)CM与⊙O相切．理由如下：衔接OC，如答图．∵GD⊥AO于点D，∴∠G＋∠GBD＝90°.∵AB为直径，∴∠ACB＝90°.∵M点为GE的中点，∴MC＝MG＝ME，∴∠G＝∠1.∵OB＝OC，∴∠B＝∠2，∴∠1＋∠2＝90°，∴∠OCM＝90°，∴OC⊥CM，∴CM为⊙O的切线．(7分)(2)∵∠1＋∠3＋∠4＝90°，∠5＋∠3＋∠4＝90°， ∴∠1＝∠5，而∠1＝∠G ，∠5＝∠A ， ∴∠G ＝∠A .∵∠4＝2∠A ，∴∠4＝2∠G ，而∠EMC ＝∠G ＋∠1＝2∠G ，∴∠EMC ＝∠4，而∠FEC ＝∠CEM ，∴△EFC ∽△ECM ， ∴EF CE ＝CE ME ＝CF CM ，即EF CE ＝CE 6＝46，∴CE ＝4，EF ＝83，∴MF ＝ME －EF ＝6－83＝103.(15分)。

九年级数学《圆》单元测试卷及答案含有详细解析

九年级数学《圆》单元测试卷一、选择题1、如果⊙O 的半径为6 cm ，OP ＝7cm ，那么点P 与⊙O 的位置关系是( ) A ．点P 在⊙O 内 B ．点P 在⊙O 上 C ．点P 在⊙O 外 D ．不能确定2、如图，在⊙O 中，AB =AC ，∠AOB=40°，则∠ADC 的度数是（）。

A ．40° B ．30° C ．20° D ．15°（第2题图）（第3题图）（第4题图）（第5题图） 3、如图，AB 是⊙O 的直径，弦CD ⊥AB ，垂足为P ．若CD=8，OP=3，则⊙O 的半径为（） A ．10 B ．8 C ．5 D ．34、如图所示，四边形ABCD 内接于⊙O ，F 是弧CD 上一点，且弧DF=弧BC ，连接CF 并延长交AD 的延长线于点E ，连接AC.若∠ABC ＝105°，∠BAC ＝25°，则∠E 的度数为( )A. 45°B. 50°C. 55°D. 60°5、如图，AB 是⊙O 的切线，B 为切点，AO 与⊙O 交于点C.若∠BAO ＝40°，则∠CBA 的度数为( )A. 15°B. 20°C. 25°D. 30°6、如图，菱形ABCD 的对角线AC ，BD 相交于点O ，AC=8，BD=6，以AB 为直径作一个半圆，则图中阴影部分的面积为（）（第6题图）（第7题图）A ．25π-6B ．π-6C ．π-6 D ．π-67、如图，在△ABC 中，AB=CB ，以AB 为直径的⊙O 交AC 于点D ．过点C 作CF ∥AB ，在CF 上取一点E ，使DE=CD ，连接AE ．对于下列结论：①AD=DC ；②△CBA ∽△CDE ；③；④AE 为⊙O 的切线，一定正确的结论全部包含其中的选项是（）A ．①②B ．①②③C ．①④D ．①②④二、填空题8、如图，已知以直角梯形ABCD 的腰CD 为直径的半圆O 与梯形上底AD 、下底BC 以及腰AB 均相切，切点分别是D ，C ，E ．若半圆O 的半径为2，梯形的腰AB 为5，则该梯形的周长是。

人教版数学九年级上册第二十四章圆单元测试含教学反思案例教案学案说课稿.docx

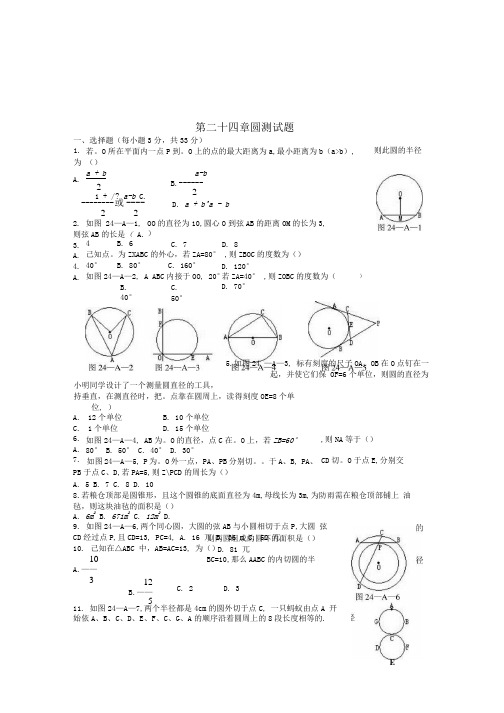
第二十四章圆测试题一、选择题（每小题3分，共33分） 1. 为 A. 若。

O 所在平面内一点P 到。

O 上的点的最大距离为a,最小距离为b （a>b ）, （）a +b 则此圆的半径 2 1 + /? a-b C. --------或 ---- 2 2 2. 如图 24—A —1, 则弦AB 的长是（ A.3. A.4. A. a-b B. ------ 2 D. a + b^a - b OO 的直径为10,圆心O 到弦AB 的距离OM 的长为3,） C. 7 4 B. 6 己知点。

为ZXABC 的外心，若ZA=80° ,则ZBOC 的度数为（）40° B. 80°C. 160° 如图24—A —2, A ABC 内接于OO, 20°D. 8 D. 120° 若ZA=40° ,则ZOBC 的度数为（ D. 70° B. 40° C.50°）小明同学设计了一个测量圆直径的工具，持垂直，在测直径时，把。

点靠在圆周上，读得刻度OE=8个单位, ）12个单位 1个单位 A. C. 6. A. 7. B. 10个单位 D. 15个单位 5.如图24 —A —3, 标有刻度的尺子OA 、OB 在O 点钉在一起，并使它们保 OF=6个单位，则圆的直径为如图24—A —4, AB 为。

O 的直径，点C 在。

O 上，若ZB=60° 80° B. 50° C. 40° D. 30° 如图24—A —5, P 为。

O 外一点，PA 、PB 分别切。

于A 、B, PA 、PB 于点C 、D,若PA=5,则Z\PCD 的周长为（） ,则NA 等于（）CD 切。

O 于点E,分别交 A. 5 B. 7 C. 8 D. 108.若粮仓顶部是圆锥形，且这个圆锥的底面直径为4m,母线长为3m,为防雨需在粮仓顶部铺上油毡，则这块油毡的面积是（） A. 6m 2 B. 671m 2 C. 12m 2 D.9. 如图24—A —6,两个同心圆，大圆的弦AB 与小圆相切于点P,大圆弦CD 经过点P,且CD=13, PC=4, A. 16 兀 B. 36 n C. 52 兀 10. 己知在△ABC 中，AB=AC=13, 为（） 10 A.—— 3 则两圆组成的圆环的面积是（） D. 81 兀 BC=10,那么AABC 的内切圆的半12 B.—— 5 C. 2 D. 3 11. 如图24—A —7,两个半径都是4cm 的圆外切于点C, 一只蚂蚁由点A 开始依A 、B 、C 、D 、E 、F 、C 、G 、A 的顺序沿着圆周上的8段长度相等的.E绕行，蚂蚁在这8段路径上不断爬行，直到行走2006 Ji cm后才停下来，则蚂蚁停的那一个点为（）A. D点B. E点C. F点D. G点二、填空题（每小题3分，共30分）12.如图24—A—8,在（30中，弦AB等于（30的半径，OC_LAB交。

九年级上册数学《圆》单元综合检测卷(带答案)

（3）若⊙O的半径为3，∠B A C=60°，求DE的长．
参考答案
一、选择题（每小题3分，共30分）
1.半径为5的圆的一条弦长不可能是()
A.3B.5C.10D.12
[答案]D
[解析]
∵圆的半径为5，
∴圆的直径为10，
又∵直径是圆中最长的弦，
∴圆中任意一条弦的长度 .
故选D.
2.如图，在⊙O中，＝，∠AOB＝40°，则∠A D C的度数是（）
6.如图，某数学兴趣小组将边长为6的正方形铁丝框A B C D变形为以A为圆心，A B为半径的扇形（忽略铁丝的粗细），则所得的扇形D A B的面积为（）
A.12B.14C.16D.36
[答案]D
[解析]
解：
∵扇形A B D的弧长D B等于正方形两边长的和B C＋D C＝12，
扇形A B D的半径为正方形的边长6；
九年级上册数学《圆》单元测试卷
（满分120分，考试用时120分钟）
一、选择题（每小题3分，共30分）
1.半径为5的圆的一条弦长不可能是( )
A.3B.5C.10D.12
2.如图，在⊙O中，＝，∠AOB＝40°，则∠A D C的度数是（）
A. 40°B. 30°C. 20°D. 15°
3.在公园的O处附近有E、F、G、H四棵树，位置如图所示（图中小正方形为边长均相等），现计划修建一座以O为圆心，OA为半径的圆形水池，要求池中不留树木，则E、F、G、H四棵树中需要被移除的为（）
18.如图所示，本市新建一座圆形人工湖，为测量该湖的半径，小杰和小丽沿湖边选取A，B，C三根木柱，使得A，B之间的距离与A，C之间的距离相等，并测得B C长为120米，A到B C的距离为4米，请你帮他们求出该湖的半径．

第2章圆数学九年级下册-单元测试卷-湘教版(含答案)

第2章圆数学九年级下册-单元测试卷-湘教版(含答案)一、单选题(共15题，共计45分)1、如图，CE是圆O的直径，⊙O的直径，AB为⊙O的弦，EC⊥AB，垂足为D，下面结论正确的有（）①AD=BD；②= ；③= ；④OD=CD．A.1个B.2个C.3个D.4个2、如图，以O为圆心的两个同心圆中，大圆的弦AB与小圆相切于点C，若大圆半径为10cm，小圆半径为6cm，则弦AB的长为（）A.2cmB.4cmC.8cmD.16cm3、如图，已知扇形AOB的半径为10公分，圆心角为54°，则此扇形面积为多少平方公分？（）A.100πB.20πC.15πD.5π4、如图，等边△ABC中，P为三角形内一点，过P作PD⊥BC，PE⊥AB，PF⊥AC，连结AP、BP、CP，如果S△APF+S△BPE+S△PCD=，那么△ABC的内切圆半径为（）A.1B.C.D.25、如图，己知等腰，以为直径的圆交于点，过点的⊙的切线交于点，若，则⊙的半径是（）A. B.5 C.6 D.6、如图，由等边三角形、正方形、圆组成的轴对称图案中，等边三角形与三个正方形的面积和的比值为（）A. B.1 C. D.7、如图，AB是⊙O的直径，弦CD交AB于点E，且AE=CD=8，∠BAC= ∠BOD，则⊙O的半径为（）A.4B.5C.4D.38、在平面直角坐标系中，以O为圆心的圆过点A（0,-4）,则点B（-2，3）与⊙O的位置关系是（）A.在圆内B.在圆外C.在圆上D.无法确定9、下列问题中，错误的个数是（）（ 1 ）三点确定一个圆；（2）平分弦的直径垂直于弦；（3）相等的圆心角所对的弧相等；（4）正五边形是轴对称图形.A.1个B.2个C.3个D.4个10、如图，在△ABC中，BC＝4，以点A为圆心，2为半径的⊙A与BC相切于点D，交AB于点E，交AC于点F.P是⊙A上一点，且∠EPF＝40°，则图中阴影部分的面积是（）A.4－B.4－C.8－D.8－11、如图，四边形ABCD内接于⊙O，若它的一个外角∠DCE＝65°，∠ABC＝68°，则∠A 的度数为（）.A.112°B.68°C.65°D.52°12、如图，已知⊙O的两条弦AC，BD相交于点E，∠A=70°，∠c=50°，那么sin∠AEB的值为（）A. B. C. D.13、如图，点C是以AB为直径的半圆O的三等分点，AC=2，则图中阴影部分的面积是（）A. B. C. D.14、如图，已知四边形ABCD内接于⊙O，直径AC=6，对角线AC、BD交于E点，且AB=BD，EC=1，则AD的长为（）A. B. C. D.315、点G为△ABC的重心（△ABC三条中线的交点），以点G为圆心作⊙G与边AB，AC相切，与边BC相交于点H，K，若AB＝4，BC＝6，则HK的长为（）A. B. C. D.二、填空题(共10题，共计30分)16、如图，PA、PB是⊙0的切线，A、B为切点，AC是⊙O的直径，∠P=40°，则∠BAC=________．17、已知△ABC的外接圆半径为，且BC=2，则∠A=________.18、如图，在正六边形ABCDEF中，分别以C，F为圆心，以边长为半径作弧，图中阴影部分的面积为24π，则正六边形的边长为________．19、如图，已知A、C是半径为2的⊙O上的两动点，以AC为直角边在⊙O内作等腰Rt△ABC，∠C=90°．连接OB．则OB的最小值为________．20、已知：点A、点B在直线的两侧．（点A到直线的距离小于点B到直线的距离）．如图，⑴作点B关于直线的对称点C；⑵以点C为圆心，的长为半径作，交于点E；⑶过点A作的切线，交于点F，交直线于点P；⑷连接、．根据以上作图过程及所作图形，下列四个结论中：①是的切线；②平分；③；④．所有正确结论的序号是________．21、如图，⊙O的直径为5，在⊙O上位于直径AB的异侧有定点C和动点P，已知BC：CA ＝4：3，点P在半圆弧AB上运动（不与A，B重合），过C作CP的垂线CD交PB的延长线于D点.则△PCD的面积最大为________.22、如图，四边形ABCD为的内接四边形，已知，则的度数为________.23、如图，正方形ABCD的面积为36cm2，点E在BC上，点G在AB的延长线上，四边形EFGB是正方形，以点B为圆心，BC的长为半径画，连接AF，CF，则图中阴影部分的面积为________．24、如图，一根6m长的绳子，一端拴在围墙墙角的柱子上，另一端拴着一只小羊A（羊只能在草地上活动）那么小羊A在草地上的最大活动区域面积是________m2.25、如图，PA，PB是⊙O的切线，A，B为切点，点C在⊙O上，且∠ACB=55°，则∠APB 等于________度。

初三圆单元测试题及答案

初三圆单元测试题及答案一、选择题（每题3分，共30分）1. 若圆的半径为r，则圆的面积为（）A. πr²B. 2πrC. πrD. 4πr²2. 圆的周长公式为（）A. 2πrB. πrC. 2πr²D. πr²3. 圆的直径是半径的（）A. 1倍B. 2倍C. 3倍D. 4倍4. 圆的切线垂直于（）A. 半径B. 直径C. 弦D. 切点5. 圆的内接四边形的对角线（）A. 相等B. 互补C. 垂直D. 平行6. 圆的外切四边形的对角线（）A. 相等B. 互补C. 垂直D. 平行7. 圆的切线与半径的关系是（）A. 垂直B. 平行C. 相交D. 重合8. 圆的弦中，最长的弦是（）A. 直径B. 半径C. 切线D. 弦9. 圆的半径增加1倍，面积增加（）A. 1倍B. 2倍C. 3倍D. 4倍10. 圆的半径减少1倍，面积减少（）A. 1倍B. 2倍C. 3倍D. 4倍二、填空题（每题3分，共30分）1. 圆的周长公式为C=2πr，其中C表示______，r表示______。

2. 圆的面积公式为A=πr²，其中A表示______，r表示______。

3. 直径是圆的两个点之间的最长距离，它的计算公式为d=______。

4. 圆的切线与半径的关系是______。

5. 圆的内接四边形的对角线具有______的性质。

6. 圆的外切四边形的对角线具有______的性质。

7. 圆的切线与半径垂直，即切线与半径的夹角为______度。

8. 圆的弦中，直径是______的弦。

9. 圆的半径增加1倍，面积增加到原来的______倍。

10. 圆的半径减少1倍，面积减少到原来的______倍。

三、解答题（每题20分，共40分）1. 已知圆的半径为5cm，求该圆的周长和面积。

2. 已知圆的周长为31.4cm，求该圆的半径，并计算其面积。

答案：一、选择题1-5：A A B A B6-10：A B A A D二、填空题1. 周长，半径2. 面积，半径3. 2r4. 垂直5. 互补6. 垂直7. 908. 最长9. 410. 1/4三、解答题1. 周长：C=2πr=2×3.14×5=31.4cm；面积：A=πr²=3.14×5²=78.5cm²。

湘教版九年级数学下册《第二章圆》单元评估检测试卷(有答案)

湘教版九年级数学下册第二章圆单元评估检测试卷一、单选题（共10题；共30分）1.可以作圆，且只可以作一个圆的条件是（）A.已知圆心B.已知半径C.过三个已知点D.过不在一直线上的三点2.如图，已知AB是⊙O直径，BC是弦，∠ABC=40°，过圆心O作OD⊥BC交弧BC于点D，连接DC，则∠DCB 为（）A.20°B.25°C.30°D.35°3.如图，是⊙的直径，，是圆上两点，∠°，则∠的度数为（）A.°B.°C.°D.°4.如图，AB为⊙O的直径，点C在⊙O上，∠A=40°，则∠B的度数为（）A.20°B.40°C.50°D.60°5.正六边形的外接圆的半径与内切圆的半径之比为（）A.1：B.：2C.2：D.：16.如图，两圆相交于A，B两点，小圆经过大圆的圆心O，点C、D分别在两圆上，若∠ADB=110°，则∠ACB 的度数为（）A.35°B.40°C.50°D.80°7.如图，PA、PB、CD分别切⊙O于A、B、E，CD交PA、PB于C、D两点，若∠P=40°，则∠PAE+∠PBE的度数为（）A.50°B.62°C.66°D.70°8.若正方形的边长为6，则其外接圆半径与内切圆半径的大小分别为（）A.6，B.，3C.6，3D.，9.坐标网格中一段圆弧经过格点A、B、C.其中点B的坐标为(4,3),点C坐标为(6,1),则该圆弧所在圆的圆心坐标为（）A.（0,0）B.（2，-1）C.（0，1）D.（2，1）10.如图，⊙O中，弦AB的长为8cm，圆心O到AB的距离为3cm，则⊙O的半径长为（）A.3cmB.4cmC.5cmD.6cm二、填空题（共10题；共30分）11.如图，在⊙O中，点A，B，C在⊙O上，且∠ACB=110°，则∠α=________．12.如图，AB为⊙O的弦，AB=8，OA=5，OP⊥AB于P，则OP=________．13.如图：四边形ABCD内接于⊙O，E为BC延长线上一点，若∠A=n°，则∠DCE=________°．14.如图，在△Rt ABC中，∠A=60°，AB=1，将△Rt ABC绕点C按顺时针方向旋转到△A1B1C的位置，点A1刚好落在BC的延长线上，则点A从开始到结束所经过的路径长为（结果保留π）________．15.一个圆的直径是10cm，另一个圆的面积比这个圆的面积少16πcm2，则另一个圆的半径长为________m．16.已知扇形的圆心角为120°，弧长为2π，则它的半径为________．17.如图，四边形ABCD内接于⊙O，OC∥AD，∠DAB＝60°，∠ADC＝106°，则∠OCB＝________°．18.圆锥的底面直径为40cm，母线长90cm则它的侧面展开图的圆心角度数为________19.如图，AB=BC=CD，∠BAD=80°，∠AED=________．20.如图，△ABC中，∠BAC=60°，∠ABC=45°，AB=，D是线段BC上的一个动点，以AD为直径画⊙O 分别交AB、AC于E、F，连接EF，则线段EF长度的最小值为________．三、解答题（共8题；共60分）21.如图，已知AB是⊙O的弦，C是的中点，AB=8，AC=，求⊙O半径的长．22.如图，直径是50cm圆柱形油槽装入油后，油深CD为15cm，求油面宽度AB。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

九年级数学《圆》单元测试题
（总分：120）姓名：分数：
一、精心选一选，相信自己的判断！（本题共12小题，每小题3分，共36分）
1.如图，把自行车的两个车轮看成同一平面内的两个圆，则它们的位置关系是（）
A .外离
B .外切
C .相交
D .内切 2.如图，在⊙O 中，∠ABC =50°，则∠AOC 等于（） A ．50° B ．80° C ．90° D ．100°
3.如图，
AB 是⊙O 的直径，∠ABC =30°，则∠BAC =（
） A ．90° B ．60°
C ．45°
D ．30°（）
4.已知⊙O 的直径为12cm ，圆心到直线L 的距离为6cm ，则直线L 与⊙O 的公共点的个数为（） A ．2 B ．1 C ．0 D ．不确定
5.已知⊙O 1与⊙O 2的半径分别为3cm 和7cm ，两圆的圆心距O 1O 2 =10cm ，则两圆的位置关系是（） A ．外切 B ．内切 C ．相交 D ．相离
6.已知在⊙O 中，弦AB 的长为8厘米，圆心O 到AB 的距离为3厘米，则⊙O 的半径是（） A ．3厘米 B ．4厘米 C ．5厘米 D ．8厘米
7.下列命题错误．．的是（） A ．经过三个点一定可以作圆 B ．三角形的外心到三角形各顶点的距离相等 C ．同圆或等圆中，相等的圆心角所对的弧相等 D ．经过切点且垂直于切线的直线必经过圆心
8.在平面直角坐标系中，以点（2，3）为圆心，2为半径的圆必定（） A ．与x 轴相离、与y 轴相切 B ．与x 轴、y 轴都相离 C ．与x 轴相切、与y 轴相离 D ．与x 轴、y 轴都相切
9.同圆的内接正方形和外切正方形的周长之比为（）
A ． 2 ∶1
B ．2∶1
C ．1∶2
D ．1∶ 2 10.在Rt △AB C 中，∠C=90°，AC=12，BC=5，将△ABC 绕边AC 所在直线旋转一周得到圆锥，则该圆锥的侧面积是（）
A ．25π
B ．65π
C ．90π
D ．130π 11.如图，Rt △AB C 中，∠ACB=90°，∠C AB =30°，BC =2，O 、H 分别为边AB 、AC 的中点，将△ABC 绕点B 顺时针旋转120°到△A 1BC 1的位置，则整个旋转过程中线段OH 所扫过部分的面积（即阴影部分面积）为（） A ．73 π－7
8 3
B ．43 π+7
8
3
C ．π
D ．4
3
π+ 3
12.如图，已知圆锥的底面圆半径为r (r >0)，母线长OA 为3r ，C 为母线OB 的中点，在圆锥的侧面上，一只蚂蚁从点A 爬行到点C 的最短路线长为（） A .
3
2
r
B .3 3 2
r
C .
3 3
r
D .3 3 r
二、细心填一填，试自己的身手！（本大题共6小题，每小题3分，共18分）
13.各边相等的
圆内接多边形_____正多边形；各角相等的圆内接多边形_____正多边形.（填“是”
第1题图
A B O C
第2题图第3题图
C
D
A H B
O
C 1O
1H 1A
1C
或“不是”）
14.△ABC 的内切圆半径为r ，△ABC 的周长为l ，则△ABC 的面积为_______________ .
15.已知在⊙O 中，半径r =13，弦AB ∥CD ，且AB=24，CD =10，则AB 与CD 的距离为__________.
16.一个定滑轮起重装置如图所示，滑轮的半径是10cm ，当重物上升10cm 时，滑轮的一条半径OA 绕轴心O 按逆时针方向旋转的角度约为_______ (假设绳索与滑轮之间没有滑动，结果精确到1°)
17.如图，在边长为3cm 的正方形中，⊙P 与⊙Q 相外切，且⊙P 分别与DA 、DC 边相切，⊙Q 分别与BA 、BC 边相切，则圆心距PQ 为______________．
18.如图，⊙O 的半径为3cm ，B 为⊙O 外一点，OB 交⊙O 于点A ，AB =OA ，动点P 从点A 出发，以πcm/s 的速度在⊙O 上按逆时针方向运动一周回到点A 立即停止．当点P 运动的时
19、为_________s 时，BP 与⊙O 相切．
已知⊙O 的半径为2，点P 为⊙O 外一点，OP 长为3，那么以P 为圆心且与⊙O 相切的圆的半径为。

20．一个圆锥的底面半径为3，高为4，则圆锥的侧面积是。

三、用心做一做，显显自己的能力！（本大题共7小题，满分60分）
21.（6分）如图，圆柱形水管内原有积水的水平面宽CD=20cm ，水深GF=2cm.若水面上升2cm （EG=2cm ），则此时水面宽AB 为多少？
22.（6分）如图，P A ，PB 是⊙O 的切线，点A ，B 为切点，AC 是⊙O 的直径，∠ACB =70°．求∠P 的度数．
21.（8分）如图，线段AB 经过圆心O ，交⊙O 于点A 、C ，点D 在⊙O 上，连接AD 、BD ，∠A =∠B =30°，BD 是⊙O 的切线吗？请说明理由．
23.（10分）如图10，P 是⊙O 外的一点，PA 、PB 分别与⊙O 相切于点A 、
B ，
C 是上的任意一点，过点C 的切线分
第18题图
第
16题图第17题图
别交PA 、PB 于点D 、E.
(1)若PA=4,求△PED 的周长； (2)若∠P=40°,求∠DOE 的度数．
24. （12分）已知：如图8，△ABC 中，AC ＝BC ，以BC 为直径的⊙O 交AB 于点D ，过点D 作DE ⊥AC 于点E ，交BC 的延长线于点F ．（8分）
求证：（1）AD ＝BD ；（2）DF 是⊙O 的切线．
25、（6分）如图24—B —17，AB 是⊙O 的弦（非直径），C 、D 是AB 上的两点，并且AC=BD 。

求证：OC=OD 。

26. （12分）已知：如图△ABC 内接于⊙O ，OH ⊥AC 于H ，过A 点的切线与OC 的延长线交于点D ，∠B =30°，OH=5 3 ．请求出：
（1）∠AOC 的度数；
（2）劣弧AC 的长（结果保留π）；（3）线段AD 的长（结果保留根号）.
B 图24—B —17
25.（本题满分12分）如图，在平面直角坐标系中，⊙M与x轴交于A、B两点，Array AC是⊙M的直径，过点C的直线交x轴于点D，连接BC，已知点M的坐标为
（0， 3 ），直线CD的函数解析式为y=－ 3 x＋5 3 ．
⑴求点D的坐标和BC的长；
⑵求点C的坐标和⊙M的半径；
⑶求证：CD是⊙M的切线．
x。