电磁学课件第六章
合集下载
2020高中物理竞赛-电磁学篇(电磁场理论)06电磁波的辐射:辐射场及计算公式(共18张PPT)

V
r
1 r'
r'
,t
r
r' exp
j t
r
r' a
V
r r'
r' a
dV
dV
Ar ,t
0
4π
V
0
4π
V
J r'
,t
r
r r' a
r'
dV
J
r'
exp
j
t
r
r' a
dV
r r'
e jtr
Ar e jt
Er ,t r ,t
Br ,t Ar ,t
t
Ar ,t
影响很小,而相位项的微小变化对结果影响大。 所以在磁矢势中,对于振幅因子取零级的近似, 对相位因子保留一级近似
1
r
r'
1 r
exp jk r r' exp jk r 2 r'2 2r r ' cos expjkrˆ r'kr
得到: A r
0
e jkr
4r
V
J r' e jk rˆ r' dV
j0
Ar
0
4π
V
J r' exp
r r'
jk
r
r'
dV
0
4π
V
J r' dV
r r'
这说明在源区附近,磁矢势蜕变为静态电磁场的 磁矢势。由磁矢势计算得到的磁场必然具有静态 场的特点。因此在源区的附近,源激发的电磁场 可以采取静态电磁场方法进行计算。这也意味着 在源区附近,源直接产生的静态电磁场远大于电 磁场相互激发所产生的电磁场。场量与r2 成反比
2020_2021学年新教材高中物理第六章电磁现象与电磁波第四节电磁波及其应用课件

【问题探究】 如图所示为美国最先进的KH—12光学侦察卫星,采用先进的自适应光学成像技 术,地面分辨率最高可达0.1 m,是美国天基侦查的主力军。那么,你知道它上 面携带的相机在夜间进行红外摄像时工作在什么波段吗?该波段有什么特点?
提示:工作在红外线这一波段。该波段的波长大于可见光而小于无线电波,主要 效应为热效应,常用于加热理疗、红外遥感摄像等。
【素养训练】 1.(多选)关于电磁波的应用,下列说法正确的是 ( ) A.医院里常用X射线对病房和手术室进行消毒 B.工业上利用γ射线检查金属部件内有无砂眼或裂缝 C.刑侦上用紫外线拍摄指纹照片,因为紫外线波长短,分辨率高 D.卫星用红外遥感技术拍摄云图照片,因为红外线穿透能力较强 【解析】选B、C。医院里用紫外线杀菌消毒,A错误;卫星用红外遥感技术拍摄 云图照片是利用了一切温度不同的物体都有频率不同的红外辐射的特点,再说 红外线穿透能力并不强,故D错误,B、C正确。
角度2 不同电磁波的特性及应用 1.电磁波谱图:各电磁波按波长从大到小或频率从低到高可排列成如图电磁波 谱。
2.不同电磁波的应用:
电磁波谱 无线电波 红外线 可见光 紫外线 X射线 γ射线
频率/Hz
由左向右,频率由低到高
真空中波长
由左向右,波长由长到短
特性
波动 性强
热作用强
感光性 强
化学作用, 荧光效应
【易错辨析】
(1)变化的电场一定产生变化的磁场。 ( × )
(2)恒定电流周围产生磁场,磁场又产生电场。 ( × )
(3)电磁波和光在真空中的传播速度都是3.0×108 m/s。 ( √ )
(4)麦克斯韦预言并验证了电磁波的存在。
(×)
(5)电磁波在任何介质中的传播速度均为3×108 m/s。 ( × )
大学物理电磁学第六章教学课件——麦克斯韦电磁理论

两件事情使他重新考虑研究方法
法拉第力线与流体两者不宜简单类比
法拉第的力线有纵向收缩、横向扩张的趋势,力 线越密,应力越大
流体力学中流线越密的地方压力越小,流速越快
电的运动与磁的运动也无法简单类比
从电解质现象中知道电的运动是平移的 从偏振光在透明晶体中旋转动现象看,磁的运动
好像是介质中分子的旋转运动
问题
Weber的公式只涉及动生电动势无法解释感生电动势; Weber的运动电荷相互作用力定律是否与能量守恒原
理协调一致 ?这个问题曾经在Weber和 Helmholtz 之间产生激烈的争论。所以公式建立以后很快遭到了批 评,最终被抛弃了
Maxwell对上述工作的评价
“由Weber和Neumann发展起来的这种 理论是极为精巧的,它令人惊叹地广泛应 用于静电现象、电磁吸引、电流感应及抗 磁现象;并且,由于在电测量中引入自洽 的单位制和实际上迄今尚未知祥的精度确 定了电学量,它适宜于指导人们作出种种 推测,从而在电科学实用方面取得重大进 展,因此它对于我们而言更具有权威性。”
把感应电动势用电动力学势a表示出来
a 只是运算中代替一积分的辅助量,没有明确的 物理意义
理论中,无须考虑线圈周围的情况,把感应电动 势归结为两个电流相互作用时电动力学势变化率 的积分,这样他就把电磁感应定律纳入了超距作 用的电动力学体系。
引入电动力学势是一个重要的贡献,在电磁学理 论中起着重要的作用
他在纪念Maxwell 诞辰100周年的文集 中写道:
“自从牛顿奠定理论物理学的基础以来,物理 学的公理基础的最伟大的变革是由法拉第和 麦克斯韦在电磁现象方面的工作所引起的”。 “这样一次伟大的变革是同法拉第、麦克斯韦 和赫兹的名字永远联在一起的。这次变革的 最大部分出自麦克斯韦。”
大学物理《电磁学》PPT课件
欧姆定律
描述导体中电流、电压和电阻之间关系的 定律。
电场强度
描述电场强弱的物理量,其大小与试探电 荷所受电场力成正比,与试探电荷的电荷 量成反比。
恒定电流
电流大小和方向均不随时间变化的电流。
电势与电势差
电势是描述电场中某点电势能的物理量, 电势差则是两点间电势的差值,反映了电 场在这两点间的做功能力。
电介质的极化现象
1 2
电介质的定义 电介质是指在外电场作用下能发生极化的物质。 极化是指电介质内部正负电荷中心发生相对位移, 形成电偶极子的现象。
极化类型 电介质的极化类型包括电子极化、原子极化和取 向极化等。
3
极化强度
极化强度是描述电介质极化程度的物理量,用矢 量P表示。极化强度与电场强度成正比,比例系 数称为电介质的电极化率。
磁场对载流线圈的作用
对于载流线圈,其受力可分解为沿线圈平面的法向力和切线方 向的力,分别用公式Fn=μ0I²S/2πa和Ft=μ0I²a/2π计算。
05
电磁感应原理及技 术应用
法拉第电磁感应定律
法拉第电磁感应定律的内容
01
变化的磁场会产生感应电动势,感应电动势的大小与磁通量的
变化率成正比。
法拉第电磁感应定律的数学表达式
安培环路定理及其推广形式
安培环路定理
磁场中B沿任何闭合路径L的线积分, 等于穿过这路径所围面积的电流代数 和的μ0倍,即∮B·dl=μ0∑I。
推广形式
对于非稳恒电流产生的磁场,安培环路 定理可推广为 ∮B·dl=μ0∑I+ε0μ0∂/∂t∮E·dl。
磁场对载流导线作用力计算
载流导线在磁场中受力
当载流导线与磁场方向不平行时,会受到安培力的作用,其大 小F=BILsinθ,方向用左手定则判断。
电磁学(梁灿彬)第六章_电磁感应与暂态过程.

楞次定律是判断感应电动势方向电的磁感定应与律暂,态过程 但却是通过感应电流的方向来表达。从定律本 身看来,它只适用于闭合电路。
如果是开路情况,可以把它“配”成闭合 电路,考虑这时会产生什麽方向的感应电流, 从而判断出感应电动势的方向。
“阻碍”的意义:当磁通量沿某方向增加 时,感应电流的磁通量就与原来的磁通量方向 相反(阻碍它的增加);当磁通量沿某方向减 少时,感应电流的磁通量就与原来的磁通量方 向相同(阻碍它的减少)。
拔出时情况可作同样的分析
本例和其它例子都表明:
当导体在磁场中运动时,导体中由于出现感 应电流而受到的磁场力(安培力)必然阻碍此 导体的运动。
这是楞次定律的第二种表述。
感应电动势遵从的规律?
电磁感应与暂态过程
大量精确的实验表明:导体回路中感应电动势 的大小与穿过回路的磁通量的变化率 d 成正 比,这个结论称为法拉第电磁感应定律。dt
用公式表示则
i
d
dt
k是比例常数,其值取决于有关量的单位的选择
如果磁通量Ф的单位用Wb(韦伯),时间单
位用S(秒),ε的单位用V(伏特),则
电磁感应与暂态过程
[实验二] 一个体积较大的线圈A与电流计G接成
闭合回路,另一个体积较小的线圈B与直流电源 和电键K串联起来组成另一回路,并把B插入线圈 A内,可以看到,在接通和断开K的瞬间,电流计 的指针突然偏转,并随即回到零点。若用变阻器 代替电键K,同样会观察到这个现象。从这个实 验可归纳出:相对运动本身不是线圈产生电流的 原因,应归结为线圈A所在处磁场的变化。
电磁学讲义
电磁感应与暂态过程
Electromagnetism Teaching materials
第六章 电磁感应与暂态过程
大学物理《电磁学》PPT课件

电场性质
对放入其中的电荷有力的作用 ,且力的方向与电荷的正负有 关。
磁场性质
对放入其中的磁体或电流有力 的作用,且力的方向与磁极或
电流的方向有关。
库仑定律与高斯定理
库仑定律
描述真空中两个静止点电荷之间的相互作用 力,与电荷量的乘积成正比,与距离的平方 成反比。
高斯定理
通过任意闭合曲面的电通量等于该曲面内所包围的 所有电荷的代数和除以真空中的介电常数。
当导体回路在变化的磁场中或导体回路在恒定的磁场中运动时
,导体回路中就会产生感应电动势。
法拉第电磁感应定律公式
02
E = -n(dΦ)/(dt)。
法拉第电磁感应定律的应用
03
用于解释电磁感应现象,计算感应电动势的大小,判断感应电
动势的方向。
自感和互感现象分析
自感现象
当一个线圈中的电流发生变化时 ,它所产生的磁通量也会随之变 化,从而在线圈自身中产生感应 电动势的现象。
程称为磁化。随着外磁场强度的增大,铁磁物质的磁感应强度也增大。
03
铁磁物质的饱和现象
当铁磁物质被磁化到一定程度后,其内部磁畴的排列达到极限状态,此
时即使再增加外磁场强度,铁磁物质的磁感应强度也不会再增加,这种
现象称为饱和现象。
04
电磁感应与暂态过程
法拉第电磁感应定律及应用
法拉第电磁感应定律内容
01
06
现代电磁技术应用与发展趋势
超导材料在电磁领域应用前景
超导材料的基本特性:零电阻、完全抗磁性
超导磁体在MRI、NMR等医疗设备中的应用
超导电缆在电力传输中的优势及挑战
高温超导材料的研究进展及潜在应用
光纤通信技术发展现状及趋势
电磁学(新概念)第六章麦克斯伟理论电磁波

1
(4) 安培环路定理 H dl I0
还有磁场变化时的规律:
(5) 法拉第电磁感应定律
d
dt
感生电动势现象预示着变化的磁场周围产生涡旋电场,因此, 法拉第电磁感应定律预示,在普遍情形下电场的环路定理应是
E
dl
B t
dS
静电场的环路定理是它的一个特例
麦克斯韦在分析了安培环路定理后, 发现将它应用到非恒定情形时遇到了矛盾
13
三、边界条件
1. 磁介质界面上的边界条件
B dS 0
n
(
B2
B1
)
0或
B2n
B1n
H
dl
I0
n
(
H2
H1
)
0或
H2t
H1t
2.电介质界面上的边界条件
n(
D2
D1
)
0或
D2n
D1n
n ( E2
E1
)
0或
E2t
E1t
2020/9/26
Shandong University 2008.6.4
12
在介质内,还需补充三个描述介质性质得方程,对于各向同性得
介质:
相对介电常数
磁导率
D 0E
V
B
0
H
j0 E
VI
VII
(11)
电导率
方程II-VII全面总结了电磁场的规律,是宏观电动力学的基本方 程组,利用它们原则上可以解决各种宏观电磁场的问题。
作业:6-1
2020/9/26
Shandong University Li Jinyu
8
极化电荷的连续性方程
dq'
大学物理电磁学ppt
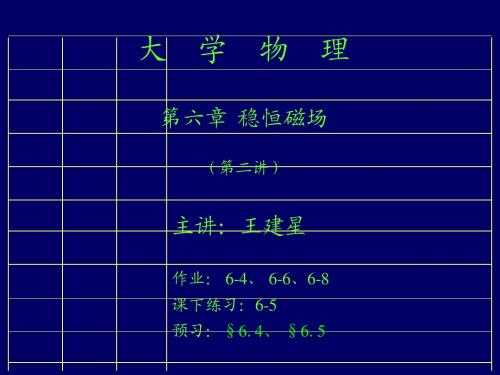
0I B= ——(cos1 cos2) 4a
(6-16')
注意:1 、2是场点至导线两端的连线与导线的夹角2>1 ! 特例:无限长载流直导线 B 0 2 r B 2.圆电流的磁场 dB 0 IR2 B= ————— 2(R2+ x2)3/2 y P 0I 特例: 圆心处(x=0) B0= —— 2R
0 vq sin 2 4 r
B 变化!
3. 适用条件:v << c
名词介绍: 磁偶极子
电流的流向与法向成右手螺旋关系。 I 磁矩(磁偶极矩):
R
n pm
pm NIS n
大小:
(6-15)
pm NIS
方向:与电流流向成右手螺旋关系 注: 磁偶极子并不局限于圆形电流。
B dx
l d2
I
x d1
解:先求 B , 再求d m , 后积分出m 。 0 I B B // d S 2 x 0 I l dx d Φm B dS 2 x
0 Il d2 dx m B dS S 2 d1 x
O x 4a a 2a
0 Il d 2 ln 2 d1
? 通过S1 、 S2 磁通量之比
Φm dΦm B d S
S S
I
(6-17)
I
a O C
(6-18) (6- 19)
1
3.一段圆弧电流 在圆心处的磁场
R
I x O P x
O
0 I B 4R
(6-J1)
记住以上两类典型载流导线的B公式,解题时可直接引用! 注意方向!
解: 可看成两个直线电流的组合。B BL BL
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
q
运动
不做功不 作功
分力 传递
供 能
? 否
矛 盾
总洛不作功 不提供能量
正负功和为零 接受输出能等
V u
两 分 力
e
总 F eV B eu B [e B] FA FL V F V FL (u ) FA (u ) FL u FA 0 总
a b
Bl
框
0
非 匀
d ( B) dl
a
B
l
b
( B) dl
L
讨 ( B) dl 论 b
a
两个 角度
B 0 B dl
0 B0
2、方向
楞次定律
(1) 、两种表述
I应
导体
应
阻碍
原
阻碍
变 化
大 小
应 原
方向反 同
右旋 I应 应 B应) (
方向
I应
安培力
例平动
运动
B
(2) 、一个实质
能量
守恒 转化
体现
I F
例平动
二 、法拉第电磁感应定律 实 N 验
快 慢
I 应 现象
本质
负
正 (
d dt
-------
判定
同楞 供
a
b
电能
B
正
回路 P I Bl I 0
功 F外 F 率
能量?
外界克
功 F Id l B
L
P外 F外 IlB I
发 电 机
机械能
其 它 能
二 、 洛力不作功与动生势的内在联系
洛仑 兹力 明 确
i原
第五六节 1、自感
现象
自感和互感 回路
自身
I
变
23
自
R RL S1
先亮于
S2
IL IS
断开 更亮
1)、自感系数 L
I
BI
自 B I
l、 N 、 S
知
自 LI
L?
N自 自 I 自 LI
I 1
自 L 亨利 自 L
例 求空心长螺管
解 设
通
I
B 0
N I l
2
N2 自 N自 NBS 0 2 lS I 0 n 2VI l
类 C 为正
常数
几何
L 自 I 0n V
与 I 无关
2)、自感电动势
(自 L )
""
I
L
L
d L dI L dt dt
正
实
正向同
维持原 不变
前提
代数
dB 内 E感 2r r 2 dt
""
规 定
与 S L
右旋
dB 非 E dt B 感
右旋
E感 与 dB dt 反号(左旋)
L 绕向 (dl ) 同向正 法向 (ds ) 反向负 S
S
E感
E感 0 反 解出 E感 0 E感 与 L 绕向同 E感 0 逆 若 dB 0 上图设 L 顺有 B 0
机械能
B
l
电能
0 设线框平面 B
t 0
转动 任 t
T
a
d d ( BS cost ) dt dt BS sin t m sin t
I
功 能 关 系
2
B
正弦变化
t 2t T F安
m
R
t
B
sin t I m sin t
dt 0 E感 0 顺
反号
B
正负 相对
L
右旋
d dt
同 左旋
楞
dB 外 B 限内 E感 2r R 2
dt
R 2 dB 1 E感 0 2r dt r
四、电子感应加速器 结 构 柱形
线 圈 外 正弦 电磁铁 两极间
E感
e
枪 逆
设
考 察
6 11 3.
第一 (二) 节 电磁感应 一 、感应电流产生的条件及其方向的判定
1、条件 两类 (1) 方法 一个 (2)条件
方法
回 路
多
归纳两类
B 不变
平 转动 静S上
I应 I应
特点
特点 切割
B线
B变
B(t )
变
(t ) BS cos
磁通量 共性
开关通、断
0
正 负
d 0 0 反 dt
d 0 0 同 dt
产生 实质
非静 电力
运动 B变
洛仑兹力 感生电场力
动 生电动势 感
第三节
动生电动势
一 、动生电动势的表达式
图
e 随棒
B
同步 运动
F E非 B e
( B) dl
I
a
F安
t 0
pm ISn ˆ M pm B
0
2
维持
外力矩
俯视图
作功
机械能 正比 M
电能
断路无功
第四节 感生电动势 感生电场 E感 Ei Ei 一、现象分析 I (t ) B(t ) i Ii 静螺 R 外回路 非静电力 ?
L 镇流器
热膨 辉光放电 停 止
c 启辉器
两 触 点
灯丝 接通
c 氖泡
i
热电子
冷缩
脱瞬
L
L ( E)
电流
灯管两端 击穿
点燃
正 发 常 光
稳 定
保证发光平稳
例 同轴电缆
R1 R2
解 电流反向
B
R1 R2
求长
距轴
l L ( I )
场
环
L0 L l
I 2r
r
间
2
r
B
Il R dr Il R2 d Bldr R r 2 ln R1 2
反映
L
实向
图当 I 0
同向
自感有
反 同
I
特性
图
dI dt
0 L 0 I 应
L
大
小
阻I 变
dI L 常 dt L
回路
dI dt
L 大 I 状
小 大
I
变难
易
m 变
自感
量度
态 难 惯性
I
渐变
dI L L dt
L
dI dt
L 电磁
例 日光灯
E 交流电源
接 通 电压
12 MI1
N1 21 MI 2 21 MI 2
M 12 21
M
例 长螺线管 (R )内垂直轴放圆环 (r R)
环 Br 0 nI管 r
2
2
M 环 I管 0nr
2
2) 互感电动势 3) 耦合系数 两线圈
法
ij MIi
某
t
B
交流电 向上 E感环形真空室 极间Fra bibliotek E感正弦
e
(b)
F
Bt
切向 洛径 环形
e力
B
a
向心力
定轨 回旋
e
Bt T E感 t
方 坐标 B 0 向 变 向上 B 化 (b) 图
E感
加速 减速 减速
向环心 向环心 背环心
加速
背环心
传递 转
牵连 定向 u
机械能
电能
正形成
负迫外供
洛
中介
电流(能)
非静电能
三 、 计算举例
例 菱形线圈
知 ( xc ) B 问线圈平面 // B 时 U ac ? I U ac IRac ac 解 B 顺 c B x ac ( B) dl ( B) 与 dl 夹 a
磁 场 能 量
本章作业
思考 4 3、 、 、 、 . 4 13 14 17
6 2 3
6 4 2、 . 4
6 3 2、 、 . 5 7 6 5 1、 。 3 6 8 5 6 10 2
6 6 1、3.
6 9 1、5、6.
1
l R2 L ln I 2 R1
2 互感 相邻电路 I 变
② ①
在彼此回路
① ②
1) 互感系数 M
12 I1 12 M 12 I1
几何尺寸 正 相对位置
21 I 2 21 M 21 I 2
推 N 212 MI1 广
M 12 M 21 M
I1 I 2 1
B 0
a
b
B
a
b
0
a
B
B
B
无切割
dx d d Bl Bl ( Blx ) dt dt dt
a
运动
不做功不 作功
分力 传递
供 能
? 否
矛 盾
总洛不作功 不提供能量
正负功和为零 接受输出能等
V u
两 分 力
e
总 F eV B eu B [e B] FA FL V F V FL (u ) FA (u ) FL u FA 0 总
a b
Bl
框
0
非 匀
d ( B) dl
a
B
l
b
( B) dl
L
讨 ( B) dl 论 b
a
两个 角度
B 0 B dl
0 B0
2、方向
楞次定律
(1) 、两种表述
I应
导体
应
阻碍
原
阻碍
变 化
大 小
应 原
方向反 同
右旋 I应 应 B应) (
方向
I应
安培力
例平动
运动
B
(2) 、一个实质
能量
守恒 转化
体现
I F
例平动
二 、法拉第电磁感应定律 实 N 验
快 慢
I 应 现象
本质
负
正 (
d dt
-------
判定
同楞 供
a
b
电能
B
正
回路 P I Bl I 0
功 F外 F 率
能量?
外界克
功 F Id l B
L
P外 F外 IlB I
发 电 机
机械能
其 它 能
二 、 洛力不作功与动生势的内在联系
洛仑 兹力 明 确
i原
第五六节 1、自感
现象
自感和互感 回路
自身
I
变
23
自
R RL S1
先亮于
S2
IL IS
断开 更亮
1)、自感系数 L
I
BI
自 B I
l、 N 、 S
知
自 LI
L?
N自 自 I 自 LI
I 1
自 L 亨利 自 L
例 求空心长螺管
解 设
通
I
B 0
N I l
2
N2 自 N自 NBS 0 2 lS I 0 n 2VI l
类 C 为正
常数
几何
L 自 I 0n V
与 I 无关
2)、自感电动势
(自 L )
""
I
L
L
d L dI L dt dt
正
实
正向同
维持原 不变
前提
代数
dB 内 E感 2r r 2 dt
""
规 定
与 S L
右旋
dB 非 E dt B 感
右旋
E感 与 dB dt 反号(左旋)
L 绕向 (dl ) 同向正 法向 (ds ) 反向负 S
S
E感
E感 0 反 解出 E感 0 E感 与 L 绕向同 E感 0 逆 若 dB 0 上图设 L 顺有 B 0
机械能
B
l
电能
0 设线框平面 B
t 0
转动 任 t
T
a
d d ( BS cost ) dt dt BS sin t m sin t
I
功 能 关 系
2
B
正弦变化
t 2t T F安
m
R
t
B
sin t I m sin t
dt 0 E感 0 顺
反号
B
正负 相对
L
右旋
d dt
同 左旋
楞
dB 外 B 限内 E感 2r R 2
dt
R 2 dB 1 E感 0 2r dt r
四、电子感应加速器 结 构 柱形
线 圈 外 正弦 电磁铁 两极间
E感
e
枪 逆
设
考 察
6 11 3.
第一 (二) 节 电磁感应 一 、感应电流产生的条件及其方向的判定
1、条件 两类 (1) 方法 一个 (2)条件
方法
回 路
多
归纳两类
B 不变
平 转动 静S上
I应 I应
特点
特点 切割
B线
B变
B(t )
变
(t ) BS cos
磁通量 共性
开关通、断
0
正 负
d 0 0 反 dt
d 0 0 同 dt
产生 实质
非静 电力
运动 B变
洛仑兹力 感生电场力
动 生电动势 感
第三节
动生电动势
一 、动生电动势的表达式
图
e 随棒
B
同步 运动
F E非 B e
( B) dl
I
a
F安
t 0
pm ISn ˆ M pm B
0
2
维持
外力矩
俯视图
作功
机械能 正比 M
电能
断路无功
第四节 感生电动势 感生电场 E感 Ei Ei 一、现象分析 I (t ) B(t ) i Ii 静螺 R 外回路 非静电力 ?
L 镇流器
热膨 辉光放电 停 止
c 启辉器
两 触 点
灯丝 接通
c 氖泡
i
热电子
冷缩
脱瞬
L
L ( E)
电流
灯管两端 击穿
点燃
正 发 常 光
稳 定
保证发光平稳
例 同轴电缆
R1 R2
解 电流反向
B
R1 R2
求长
距轴
l L ( I )
场
环
L0 L l
I 2r
r
间
2
r
B
Il R dr Il R2 d Bldr R r 2 ln R1 2
反映
L
实向
图当 I 0
同向
自感有
反 同
I
特性
图
dI dt
0 L 0 I 应
L
大
小
阻I 变
dI L 常 dt L
回路
dI dt
L 大 I 状
小 大
I
变难
易
m 变
自感
量度
态 难 惯性
I
渐变
dI L L dt
L
dI dt
L 电磁
例 日光灯
E 交流电源
接 通 电压
12 MI1
N1 21 MI 2 21 MI 2
M 12 21
M
例 长螺线管 (R )内垂直轴放圆环 (r R)
环 Br 0 nI管 r
2
2
M 环 I管 0nr
2
2) 互感电动势 3) 耦合系数 两线圈
法
ij MIi
某
t
B
交流电 向上 E感环形真空室 极间Fra bibliotek E感正弦
e
(b)
F
Bt
切向 洛径 环形
e力
B
a
向心力
定轨 回旋
e
Bt T E感 t
方 坐标 B 0 向 变 向上 B 化 (b) 图
E感
加速 减速 减速
向环心 向环心 背环心
加速
背环心
传递 转
牵连 定向 u
机械能
电能
正形成
负迫外供
洛
中介
电流(能)
非静电能
三 、 计算举例
例 菱形线圈
知 ( xc ) B 问线圈平面 // B 时 U ac ? I U ac IRac ac 解 B 顺 c B x ac ( B) dl ( B) 与 dl 夹 a
磁 场 能 量
本章作业
思考 4 3、 、 、 、 . 4 13 14 17
6 2 3
6 4 2、 . 4
6 3 2、 、 . 5 7 6 5 1、 。 3 6 8 5 6 10 2
6 6 1、3.
6 9 1、5、6.
1
l R2 L ln I 2 R1
2 互感 相邻电路 I 变
② ①
在彼此回路
① ②
1) 互感系数 M
12 I1 12 M 12 I1
几何尺寸 正 相对位置
21 I 2 21 M 21 I 2
推 N 212 MI1 广
M 12 M 21 M
I1 I 2 1
B 0
a
b
B
a
b
0
a
B
B
B
无切割
dx d d Bl Bl ( Blx ) dt dt dt
a
