第六章气体动理论习题课

合集下载

气体动理论习题课

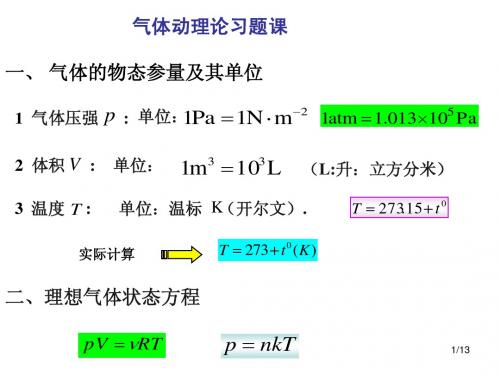
5 E氧 = ν RT 2
2 ε 转动 = ν RT 2
12/13
9 .某理想气体定压摩尔热容为 29.1J ⋅ mol −1 ⋅ K −1 。求它某理想气体定压摩尔热容为在温度为273 K时分子平均转动动能． = 1.38 × 10 −23 J ⋅ K −1 时分子平均转动动能．在温度为时分子平均转动动能 k
2/13
五、理想气体压强、温度的统计意义理想气体压强、
2 P = nε k 3
εk
1 3 2 = m v = kT 2 2
p = nkT
六、三种速率
v =
2
3 kT = m
3 RT M
2kT 2 RT vp = = m M
v ≈ 1 . 60
kT = 1 . 60 m
RT M
3/13
七、理想气体自由度数目
i E = ν RT 2
pV氧 = ν 氧 RT
E氧 = ν 氧
5 RT 2
E氦 = ν 氦
3 RT 2
pV氦 = ν 氦 RT
2. 压强为、体积为的氢气（视为刚性分子理想气体）内能为：压强为p、体积为V的氢气视为刚性分子理想气体）内能为：的氢气（ (A)
5 PV 2 3 (B) PV 2
i C P = CV + R = R + R 2
2(C P − R ) CP i= = 2 − 1 = 5 R R
可见是双原子分子。可见是双原子分子。只有两个转动自由度
2 ε r = kT = kT = 3.77 × 10 − 21 J 2
13/13
气体动理论习题课一、气体的物态参量及其单位
1 气体压强 2 体积 V : 3 温度 T :

气体动理论习题课(新)

∞
7、对分布曲线的进一步讨论
fm(v) 已知平衡态下的N个粒子系统个粒子系统，已知平衡态下的个粒子系统，
f (v)
其速率分布曲线如图。其速率分布曲线如图。求 (１) 速率１间的粒子数。２在V0 →2V0 间的粒子数。 (２) 速率 o 分布函数的极大值为多少? 分布函数的极大值为多少
∫
v2 v 1
v N d
N
速率间隔V 速率间隔 1 →V2内分子的速率之和占总分子的比率。总分子的比率。
5、求标准状态下氧气的、 (1) 单位体积中分子数单位体积中分子数n (2) 分子质量分子质量m (3) 质量密度ρ 质量密度ρ
Mm m= = NA
P n= = K T
ρ = nm
2
(4) 分子间的平均距离。分子间的平均距离l。
1 (t +r +2s) RT —1ｍol气体的内能ｍ气体的内能 2
2、容器中装有理想气体，容器以速率运动，当容、容器中装有理想气体，容器以速率v运动运动，器突然停止，则容器温度将升高。器突然停止，则容器温度将升高。若有两个容器，一个装有，另一装有H 若有两个容器，一个装有He，另一装有 2，如果它们以相同速率运动，当它们突然停止时，们以相同速率运动，当它们突然停止时，哪一个容器的温度上升较高? 的温度上升较高
kT i = (t + r + 2s) ⋅ = kT 2 2
=
理想气体的内能：理想气体的内能： U
1 du η = ρ vλ 黏性 dK = −η ( ) z0 A ⋅ dt 3 dz dT 1 非平衡态下的输运过程热传导 dQ = −k( ) z0 A ⋅ dt k = ρ v λ C V 3 dz dρ 1 自扩散 dM = − D( ) z0 A ⋅ dt D = v λ 3 dz

物理答案第六章气体动理论答案-ZSH

物理答案第六章⽓体动理论答案-ZSH第六章⽓体动理论6-1 处于平衡状态的⼀瓶氦⽓和⼀瓶氮⽓的分⼦数密度相同，分⼦的平均平动动能也相同，则它们（ C ） (A)温度、压强均不相同.(B)温度相同，但氦⽓压强⼤于氮⽓压强. (C)温度、压强都相同.(D)温度相同，但氦⽓压强⼩于氮⽓压强.6-2 三容器A 、B 、C 中装有同种理想⽓体，其分⼦数密度 n 相同，⽽⽅均根速率之⽐为4:2:1)(:)(:)(212212212=CBAv v v ，则其压强之⽐C B A P P P :: 为（ C ）(A) 4:2:1 (B) 8:4:1 (C) 16:4:1 (D) 1:2:46-3 在⼀个体积不变的容器中，储有⼀定量的某种理想⽓体，温度为0T 时，⽓体分⼦的平均速率为0v ，分⼦平均碰撞次数为0Z ，平均⾃由程为0λ，当⽓体温度升⾼为04T 时，⽓体分⼦的平均速率为v ，分⼦平均碰撞次数为Z ，平均⾃由程为λ分别为（ B ） (A) 04v v =，04Z Z =，04λλ= (B) 02v v =，02Z Z =，0λλ= (C) 02v v =，02Z Z =，04= (D) 04v v =，02Z Z =，0=6-4 已知n 为单位体积的分⼦数，)(v f 为麦克斯韦速率分布函数，则dv v nf )(表⽰（）(A) 速率v 附近，d v 区间内的分⼦数(B) 单位体积内速率在v ~ v +d v 区间内的分⼦数 (C) 速率v 附近d v 区间内分⼦数占总分⼦数⽐率(D) 单位时间内碰到单位器壁上速率在v ~ v +d v 区间内的分⼦数6-5 温度为0℃和100℃时理想⽓体分⼦的平均平动动能各为多少？欲使分⼦的平均平动动能等于1eV,⽓体的温度需多⾼？解：=1ε231kT ＝5.65×2110-J=2ε232kT ＝7.72×2110-J 由于1eV=1.6×1910-J , 所以理想⽓体对应的温度为：T=2ε/3k =7.73×310 K6-6 ⼀容器中储有氧⽓，其压强为0.1个标准⼤⽓压，温度为27℃，求：(1)氧⽓分⼦的数密度n ；(2)氧⽓密度ρ；(3)氧⽓分⼦的平均平动动能k ε？解： (1)由⽓体状态⽅程nkT p =得，242351045.23001038.110013.11.0?===-kT p n 3m - (2)由⽓体状态⽅程RT M MpV mol= (M ，mol M 分别为氧⽓质量和摩尔质量) 得氧⽓密度：13.030031.810013.11.0032.05mol ====RT p M V Mρ 3m kg -? (3) 氧⽓分⼦的平均平动动能21231021.63001038.12323--?===kT k ε6-7 在容积为2.0×33m 10-的容器中，有内能为6.75×210J 的刚性双原⼦理想⽓体分⼦，求（1）⽓体的压强；（2）设分⼦总数5.4×2210个，求⽓体温度；（3）⽓体分⼦的平均平动动能？解：（1）由2iRT M m =ε以及RT M mpV =可得⽓体压强 p =iVε2=1.35×510 Pa （2）分⼦数密度V Nn =, 得该⽓体的温度62.3===NkpV nk p T ×210K (3)⽓体分⼦的平均平动动能为=ε23kT =7.49×2110-J6-8 2100.2-?kg 氢⽓装在3100.4-?m 3的容器内，当容器内的压强为51090.3?Pa 时，氢⽓分⼦的平均平动动能为多⼤？解：由RT M m pV =得 mR MpV T = 所以221089.32323-?=?==mRMpVk kT εJ6-9 1mol 刚性双原⼦⽓体分⼦氢⽓，其温度为27℃，求其对应的平动动能、转动动能和内能各是多少?（求内能时可不考虑原⼦间势能）解：理想⽓体分⼦的能量为RT in E 2=，所以氢⽓对应的平动动能为（3=t ） 5.373930031.8231==t J转动动能为（2=r ） 249330031.8221==r εJ内能5=i 5.623230031.8251==i ε J6-10 设有N 个粒⼦的系统，其速率分布如图所⽰，求：(1)分布函数)(v f 的表达式； (2)速度在1.50v 到2.00v 之间的粒⼦数；(3) N 个粒⼦的平均速率；解：(1)从上图所给条件得：≥=≤≤=≤≤=)2(0)()2()()0(/)(00000v v v Nf v v v a v Nf v v v av v Nf 由此可得分布函数表达式为：≥≤≤≤≤=)2(0)2(/)0(/)(00000v v v v v Na v v Nv av v f 类似于概率密度的归⼀化条件，故)(v f 满⾜?+∞∞-1d )(＝v v f ,即=+00020,1d d v v v v a v v av 计算得032v Na =，带⼊上式得分布函数)(v f 为：≥≤≤≤≤=)2(0)2(32)0(3/2)(0000020v v v v v v v v v v v f (2)该区间对应的)(v f 为常数32v N，所以可通过计算矩形⾯积得该区间粒⼦数为： N v v v N N 31)5.12(32000=-=(3) N 个粒⼦平均速率+===∞∞+∞-00020202d 32d 32d )(d )(v v v v v v v v v v v vf v v vf v 0911v = 6-11 设N 个粒⼦系统在各速率区间对应的粒⼦数变化率为：Kdv dN = （为常量K v V ,0>>），0=dN （V v >）（1）画出速率分布函数图；（2）⽤N 和V 表⽰常量K ；（3）⽤V 表⽰出平均速率和⽅均根速率。

普通物理学第五版第6章气体动理论答案(精品课件)

结束目录
解：
μ gh
M gh
P = P0 e kT =P0 e RT
ln
P P0
=
Mg h RT
h=
RT Mg
ln P P0
=
8.31×273 28×10-3×9.8
ln
0.75
= 2.3km
结束目录
6-15 求压强为1.013×105Pa、质量为 2×10-3kg、容积为1.54×10-3m3的氧气的分子的平均平动动能。
结束目录
解：P = ( h1 h2)d =(0.76 0.60)×1.33×105 Pa
V = 0.28×2.0×10-4 =5.6×10-4 m3
T = 273+27=300 K
M = 0.004 kg/mol
PV
=
m M
RT
m
=
M PV RT
=
0.04×0.16×1.33×105×5.6×10-4 8.31×300
提示：
2 p
01e- x2dx =0.847
2 p
0∞e- x2dx =1
结束目录
解：(1)
v=
v0pv dN vp dN
0
=
vp 0
v
3e
vp 0
v
2e
dv v 2
v
2
p
dv v 2
v
2
p
令
x=
v vp
dv= vp dx
v
=
vp
1 0
1 0
x 3e-x
2 dx
x 2e-x 2 dx
结束目录
6-3 一封闭的圆筒，内部被导热的不漏气的可移动活塞隔为两部分。最初，活塞位于筒中央，圆筒两侧的长度 l1= l2。当两侧各充以T1、p1，与T2、p2的相同气体后，问平衡时活塞将在什么位置上（即 l1/l2 是多少）？已知 p1=1.013×105Pa, T2= 680K, p2 = 2.026×105Pa, T2 =280K。

气体分子动理论习题解PPT课件

1 mv2 3 kT,可得
2
2
N 1 mv2 3 NkT
2
2
即
N
1 2
mv2
3 2
RTN
/(Nd m)
3 (M 2
/
M mol )RT
3 2
(RT
/
M mol )V
7.31106
E
1 2
(M
/
M mol )iRT
(V
/
M mol )
1 2
iRT
4.16104
J
(v2 )1/2
(v
2 2
)1/
2
(v21)1/2
(1) 气体分子的平动动能总和． (2) 混合气体的压强． (普适气体常量R＝8.31 J·mol-1·K-1 )
3 kT 8.281021 J
2
Ek
N
( N1
N2)
3 kT 2
4.14105 J
p nkT 2.76 105 Pa
第6页/共10页
17．一瓶氢气和一瓶氧气温度相同．若氢气分子的平均平动动能为 = 6.21×10-21
［B］
8．速率分布函数f(v)的物理意义为：
(A) 具有速率v的分子占总分子数的百分比．
(B) 速率分布在v附近的单位速率间隔中的分子数占总分子数的百分比．
(C) 具有速率v的分子数．
(D) 速率分布在v附近的单位速率间隔中的分子数．
［B ］
9．设某种气体的分子速率分布函数为f(v)，则速率在v 1─v 2区间内的分子的平均速
4．一瓶氦气和一瓶氮气密度相同，分子平均平动动能相同，
而且它们都处于平衡状态，则它们
(A) 温度相同、压强相同．

大学物理热学习题课

dN m 32 4 ( ) e Ndv 2kT
v2
对于刚性分子自由度单原子双原子多原子
i tr
(1)最概然速率
2kT 2 RT RT vp 1.41 m
(2)平均速率
i=t=3 i = t+r = 3+2 = 5 i = t+r = 3+3 =6
6、能均分定理
8kT 8 RT RT v 1.60 m
M V RT ln 2 M mol V1
QA
绝热过程
PV 常量
M E CV T M mol
(2)由两条等温线和两条绝热线组成的循环叫做卡诺循环。 •卡诺热机的效率
Q0
Q2 T2 卡诺 1 1 Q1 T1
M P1V1 P2V2 A CV T M mol 1
E 0
•热机效率
A Q1 Q2
M E CV T M mol M Q C P T M mol
A Q1 Q2 Q2 1 Q1 Q1 Q1
A=P(V2-V1) 等温过程
A
E 0
Q1 Q2 •致冷系数 e W Q1 Q2
热机效率总是小于1的，而致冷系数e可以大于1。
定压摩尔热容
比热容比
CP ( dQ )P dT i2 i
8、平均碰撞次数平均自由程
z
2d v n
2
CV •对于理想气体：

Cp
v z
1.热力学第一定律
1 2 2d n
二、热力学基础
Q ( E2 E1 ) A dQ dE dA
准静态过程的情况下
4. 摩尔数相同的两种理想气体一种是氦气，一种是氢气，都从相同的初态开始经等压膨胀为原来体积的2倍，则两种气体( A ) (A) 对外做功相同，吸收的热量不同. (B) 对外做功不同，吸收的热量相同. (C) 对外做功和吸收的热量都不同. (D) 对外做功和吸收的热量都相同. A=P(V2-V1)

(完整版)《大学物理》习题册题目及答案第6单元气体动理论

第6单元气体动理论序号学号姓名专业、班级一选择题[ C ]1．在标准状态下, 若氧气（视为刚性双原子分子的理想气体）和氦气的体积比2121=V V ，则其内能之比21/E E 为： (A) 1/2 (B) 5/3 (C) 5/6 (D) 3/10[ B ]2．若理想气体的体积为V ，压强为p ，温度为T ，一个分子的质量为m ，k 为玻耳兹曼常量，R 为摩尔气体常量，则该理想气体的分子数为(A) pV/m (B) pV/(kT)(C) pV/(RT) (D) pV/(mT)[ D ]3．若)(v f 为气体分子速率分布函数，N 为分子总数，m 为分子质量，则 )(21221v Nf mv v v ⎰ d v 的物理意义是 (A) 速率为v 2的各分子的总平均动能与速率为v 1的各分子的总平均动能之差。

(B) 速率为v 2的各分子的总平动动能与速率为v 1的各分子的总平动动能之和。

(D) 速率处在速率间隔v 1~ v 2之内的分子平动动能之和。

[ D ]4．在一密闭容器中，储有A 、B 、C 三种理想气体，处于平衡状态，A 种气体的分子数密度为 1n ，它产生的压强为 1p ，B 种气体的分子数密度为 12n ，C 种气体的分子数密度为3n 1，则混合气体的压强p 为(A)31p (B)41p(C)51p (D)61p二填空题1．在定压下加热一定量的理想气体，若使其温度升高1K 时，它的体积增加了0.005倍，则气体原来的温度是_________200k__________。

2．用总分子数N 、气体分子速率v 和速率分布函数f(v)，表示下列各量：(1)速率大于0v 的分子数= ⎰∞0)(v dv v Nf ；(2)速率大于0v 的那些分子的平均速率=⎰⎰∞∞00)()(v v dv v f dv v vf ；(3)多次观察某一分子的速率，发现其速率大于0v 的概率=⎰∞0)(v dv v f 。

华东理工大学《大学物理》第六章气体动理论习题及答案

M2 所以
ΔT = 2ΔE m Ri M
= 2 ×1012 ×1.6 ×10 −19 0.1× 8.31× 3
= 1.28×10 −7 K
6、质量为 50.0g、温度为 180c的氮气装在容积为 10.0 升的密闭绝热容器内，容器以 v=200m/s的速率作匀速直线运动，若容器突然停止运动，其定向运动的动能全部转化为分子热运动的动能，那么，平衡后氮气的温度和压强将各增大多少？
解：（1）Q v = ∴z =
8RT
P = nkT
πM
2πd 2 vn = 4d 2 N 0 P 3πm
M
E
E = m 6 RT M2
（2） v p =
2RT = M
2E 3m
（3） εk
=
3 2
kT
=
ME 2N A m
（其中NA为阿伏伽德罗常数）
12、一真空管的真空度为 1.33×10-3Pa，试求在 270C时单位体积的分子数及分子平均自由程。设分子的有效直径d=3.0×10-10m。解： n = P = 1.33 × 10 −3 = 3.22 × 1017 个 m 3
× 300
= 1.00 ×10 −8 J
3） εk转总 = NkT = 1.61×1012 ×1.38×10−23 × 300 = 6.67 ×10−9 J
4） εk总 = εk平总 + εk转总 = 1.67 ×10−8 J
39
大学物理习题册题解
5、一能量为 1012eV的宇宙射线粒子，射入一氖管中，氖管中含有氖气 0.1mol。如果宇宙射线粒子的能量全部被氖气分子所吸收而变为热运动能量，问氖气温度升高多少度？解：等容吸热 ΔE = m i RΔT

第6章气体动理论习题解答

第6章习题解答6-1 若理想气体的体积为V ，压强为p ,温度为T ，一个分子的质量为m ，k 为玻耳兹曼常量，R 为摩尔气体常量，则该理想气体的分子数为[ B ]A. /pV m .B. /pV kT . C . /pV RT . D. /pV mT .6-2 两容器内分别盛有氢气和氦气，若在平衡态时，它们的温度和质量分别相等，则[ A ] A. 两种气体分子的平均平动动能相等. B. 两种气体分子的平均动能相等. C . 两种气体分子的平均速率相等. D. 两种气体的内能相等.6-3 两瓶不同类别的理想气体，设分子平均平动动能相等，但其分子数密度不相等，则[ B ]A ．压强相等，温度相等．B ．温度相等，压强不相等．C ．压强相等，温度不相等．D ．压强不相等，温度不相等．6-4 温度，压强相同的氦气和氧气，它们的分子平均动能ε和平均平动动能k ε有如下关系 [ A ] A. k ε相等，而ε不相等. B. ε相等，而k ε不相等. C .ε和k ε都相等.D.ε和k ε都不相等.6-5 一定量的理想气体贮于某一容器中，温度为T ，气体分子的质量为m . 根据理想气体的分子模型和统计假设，在x 方向分子速度的分量平方的平均值为[ D ]A. 2x =v B. 2x =v C . 23x kT m =v . D. 2x kT m =v .6-6 若()f v 为气体分子速率分布函数，N 为气体分子总数，m 为分子质量，则2121()d 2m Nf υυ⎰v v v 的物理意义是[ A ] A. 速率处在速率间隔12~v v 之间的分子平动动能之和. B. 速率处在速率间隔12~v v 间的分子平均平动动能.C . 速率为2v 的各分子的总平动动能与速率1v 为的各分子的总平动动能之和. D. 速率为2v 的各分子的总平动动能与速率1v 为的各分子的总平动动能之差.6-7在A 、B 、C 三个容器中装有同种理想气体，其分子数密度n 相同，方均根速率之比为1:2:4=，则其压强之比::A B C p p p 为[ C ]A. 1:2:4B. 4:2:1 C . 1:4:16 D. 1:4:86-8 题6-8图所示的两条曲线，分别表示在相同温度下氧气和氢气分子的速率分布曲线；令()2O p v 和()2H pv 分别表示氧气和氢气的最概然速率，则[ B ]A ．图中ａ表示氧气分子的速率分布曲线，()()22O H/4p p =v v ．B ．图中ａ表示氧气分子的速率分布曲线，()()22O H1/4p p =v v ．题6-8图 C ．图中ｂ表示氧气分子的速率分布曲线，()()22O H1/4pp =v v ． D ．图中ｂ表示氧气分子的速率分布曲线，()()22O H/4pp =v v ．6-9 题6-9图是在一定的温度下，理想气体分子速率分布函数曲线。

06气体动理论习题解答

第六章气体动理论一选择题1. 若理想气体的体积为V ，压强为p ，温度为T ，一个分子的质量为m ，k 为玻耳兹曼常量，R 为摩尔气体常量，则该理想气体的分子总数为( )。

A. pV /mB. pV /(kT )C. pV /(RT )D. pV /(mT )解理想气体的物态方程可写成NkT kT N RT pV ===A νν，式中N =ν N A 为气体的分子总数，由此得到理想气体的分子总数kTpVN =。

故本题答案为B 。

2. 在一密闭容器中，储有A 、B 、C 三种理想气体，处于平衡状态。

A 种气体的分子数密度为n 1，它产生的压强为p 1，B 种气体的分子数密度为2n 1，C 种气体的分子数密度为3 n 1，则混合气体的压强p 为 ( )A. 3p 1B. 4p 1C. 5p 1D. 6p 1 解根据nkT p =，321n n n n ++=，得到故本题答案为D 。

3. 刚性三原子分子理想气体的压强为p ，体积为V ，则它的内能为 ( )A. 2pVB.25pV C. 3pV D.27pV解理想气体的内能RT iU ν2=，物态方程RT pV ν=，刚性三原子分子自由度i =6，因此pV pV RT i U 3262===ν。

因此答案选C 。

4. 一小瓶氮气和一大瓶氦气，它们的压强、温度相同，则正确的说法为：( ) A. 单位体积内的原子数不同 B. 单位体积内的气体质量相同 C. 单位体积内的气体分子数不同 D. 气体的内能相同解：单位体积内的气体质量即为密度，气体密度RTMpV m ==ρ（式中m 是气体分子质量，M 是气体的摩尔质量），故两种气体的密度不等。

单位体积内的气体分子数即为分子数密度kTpn =，故两种气体的分子数密度相等。

氮气是双原子分子，氦气是单原子分子，故两种气体的单位体积内的原子数不同。

根据理想气体的内能公式RT iU 2ν=，两种气体的内能不等。

《大学物理》气体动理论练习题及答案解析

《大学物理》气体动理论练习题及答案解析一、简答题1、你能够从理想气体物态方程出发，得出玻意耳定律、查理定律和盖吕萨克定律吗? 答：方程RT Mm pV '=描述了理想气体在某状态下，p ，V ，T 三个参量所满足的关系式。

对给定量气体（Mm '不变），经历一个过程后，其初态和终态之间有222111T V p T V p =的关系。

当温度不变时，有2211V p V p =，这就是玻意耳定律；当体积不变时，有2211T p T p =，这就是查理定律；当压强不变时，有2211T V T V =，这就是盖吕萨克定律。

由上可知三个定律是理想气体在经历三种特定过程时所表现出来的具体形式。

换句话说，遵从玻意耳定律、查理定律和盖吕萨克定律的气体可作为理想气体。

2、为什么说温度具有统计意义? 讲一个分子具有多少温度，行吗?答：对处于平衡态的理想气体来说，温度是表征大量分子热运动激烈程度的宏观物理量，是对大量气体分子热运动状态的一种统计平均，这一点从公式kT v m 23212=中的2v 计算中就可以看出（∑∑=iii Nv N v22），可见T 本质上是一种统计量，故说温度具有统计意义，说一个分子的T 是毫无意义的。

3、解释下列分子运动论与热力学名词：(1) 状态参量；(2) 微观量；(3) 宏观量。

答：（1）状态参量：在一定的条件下，物质系统都处于一定的状态下，每个状态都需用一组物理量来表征，这些物理量称为状态参量。

（2）微观量：描述个别分子运动状态的物理量。

（3）宏观量：表示大量分子集体特征的物理量。

4、一定量的理想气体处于热动平衡状态时，此热力学系统的不随时间变化的三个宏观量和不随时间变化的微观量分别有哪些？建议：本题“不随时间变化的微观量分别有哪些”不知道通过该设问需要学生掌握什么东西。

其实从微观角度来讲，分子的任何量，如分子速度，动能，动量，严格说来甚至质量也是变化的。

可能会有人回答为平均速度、平均速率、平均自有程等，但那又是一种统计行为，该值对应着某些宏观量，这只能称为统计量，与微观量和宏观量相区别。

《大学物理学》气体的动理论自学练习题

《大学物理学》气体动理论可能用到的数据：8.31/R J mol =； 231.3810/k J K -=⨯； 236.0210/A N mol =⨯。

一、选择题12-1．处于平衡状态的一瓶氮气和一瓶氦气的分子数密度相同，分子的平均平动动能也相同，则它们( C )（A ）温度，压强均不相同；（B ）温度相同，但氦气的压强大于氮气的压强；（C ）温度，压强都相同；（D ）温度相同，但氦气的压强小于氮气的压强。

【分子的平均平动动能3/2ktkT ε=，仅与气体的温度有关，所以两瓶气体温度相同；又由公式P nkT =，n 为气体的分子数密度，知两瓶气体的压强也相同】2．容器中储有一定量的处于平衡状态的理想气体，温度为T ，分子质量为m ，则分子速度在x 方向的分量平均值为：（根据理想气体分子模型和统计假设讨论）( D )（A ）x υB ）x υC ）x υ=m kT 23；（D ）x υ=0。

【大量分子在做无规则的热运动，某一的分子的速度有任一可能的大小和方向，但对于大量分子在某一方向的平均值应为0】3．若理想气体的体积为V ，压强为P ，温度为T ，一个分子的质量为m ，k 为玻耳兹曼常量，R 为摩尔气体常量，则该理想气体的分子数为 ( B )（A ）m PV /；（B ）)/(kT PV ；（C ）)/(RT PV ；（D ）)/(mT PV 。

【由公式P nkT =判断，所以分子数密度为Pnk T=，而气体的分子数为N nV=】4．根据气体动理论，单原子理想气体的温度正比于( D ) （A ）气体的体积；（B ）气体分子的压强；（C ）气体分子的平均动量；（D ）气体分子的平均平动动能。

【见第1题提示】5．有两个容器，一个盛氢气，另一个盛氧气，如果两种气体分子的方均根速率相等，那么由此可以得出下列结论，正确的是( A )（A ）氧气的温度比氢气的高；（B ）氢气的温度比氧气的高；（C ）两种气体的温度相同；（D ）两种气体的压强相同。

《物理学基本教程》课后答案第六章气体动理论

第六章气体动理论6-1 一束分子垂直射向真空室的一平板，设分子束的定向速度为v ，单位体积分子数为n ，分子的质量为m ，求分子与平板碰撞产生的压强．分析器壁单位面积所受的正压力称为气体的压强．由于压强是大量气体分子与器壁碰撞产生的平均效果，所以推导压强公式时，应计算器壁单位面积在单位时间内受到气体分子碰撞的平均冲力．解以面积为S 的平板面为底面，取长度等于分子束定向速度v 的柱体如图6-1所示，单位时间内与平板碰撞的分子都在此柱体内．柱体内的分子数为nSv ．每个分子与平板碰撞时，作用在平板上的冲力为2mv ，单位时间内平板所受到的冲力为v v nS m F ⋅=2根据压强的定义，分子与平板碰撞产生的压强为22v nm SFp ==6-2 一球形容器，直径为2R ，内盛理想气体，分子数密度为n ，每个分子的质量为m ，(1)若某分子速率为v i ，与器壁法向成θ角射向器壁进行完全弹性碰撞，问该分子在连续两次碰撞间运动了多长的距离？(2)该分子每秒钟撞击容器多少次？(3)每一次给予器壁的冲量是多大？(4)由上结果导出气体的压强公式．分析任一时刻容器中气体分子的速率各不相同，运动方向也不相同，由于压强是大量气体分子与器壁碰撞产生的平均效果，气体压强公式的推导过程为：首先任意选取某一速率和运动方向的分子，计算单位时间内它与器壁碰撞给予器壁的冲力，再对容器中所有分子统计求和．v图6-1解 (1)如图6-2所示，速率为v i 的分子以θ角与器壁碰撞，因入射角与反射角都相同，连续两次碰撞间运动的距离都是同样的弦长，为θcos 2R AB =(2)该分子每秒钟撞击容器次数为θcos 2R AB ii v v =(3)每一次撞击给予器壁的冲量为θcos 2i m v(4)该分子每秒钟给予器壁的冲力为Rm R m i i i 2cos 2cos 2v v v =θθ由于结果与该分子的运动方向无关，只与速率有关，因此可得容器中所有分子每秒钟给予器壁的冲量为21212222221v v v v v v v RmN N N R m R m R m R m R m R m N i i N i i N i ===+++++∑∑== 其中n R N 334π=．根据压强的定义，分子与器壁碰撞产生的压强为W n m n nm R R m Np 3221323142222=⎪⎭⎫ ⎝⎛===v v vπ 其中W 为分子的平均平动动能．6-3 容积为10 L 的容器内有1 mol CO 2气体，其方均根速率为1440 km/h ，求CO 2气体的压强（CO 2的摩尔质量为31044-⨯kg/mol ）．分析在常温常压下可以将气体视为理想气体，理想气体压强公式中引入了统计平均量----方均根速率2v 和分子数密度n ，1 mol 的气体中分子数为阿伏图6-2伽德罗常量N A ，根据这些关系可求出压强．解容积为V 的容器中有1 mol CO 2气体，则分子总数为N A ，摩尔质量为M ，则分子数密度为V N A ，分子质量为A N M，因此由气体压强公式得22A A 2313131v v v VM N M V N nm p ===代入数字得Pa 102.35Pa 3600101440101010443131523332⨯=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯⨯⨯==--v V M p 6-4 在实验室中能够获得的最佳真空相当于大约Pa 10013.19-⨯，试问在室温（273K ）下在这样的“真空”中每立方厘米内有多少个分子？分析引入玻尔兹曼常量k 和分子数密度n 后，理想气体状态方程可以表示为nkT p =．解由理想气体状态方程nkT p =得3-113-239m 1069.2m 2731038.110013.1⨯=⨯⨯⨯==--kT p n 6-5 已知气体密度为1 kg/m 3，压强为Pa 10013.15⨯，(1)求气体分子的方均根速率；(2)设气体为氧，求温度．分析气体密度ρ是单位体积中气体的质量，因此与分子数密度n 和分子质量m 的关系为nm =ρ．解压强公式可写为 223131v v ρ==nm p(1)分子的方均根速率m/s 551m/s 110013.13352=⨯⨯==ρpv(2)氧的摩尔质量M =31032-⨯kg/mol ，由定义MRT32=v ，则 K 390K 31.8310325513322=⨯⨯⨯==-R M T v6-6 体积为10-3 m 3，压强为Pa 10013.15⨯的气体，所有分子的平均平动动能的总和是多少？分析气体动理论的能量公式给出了微观量气体分子的平均平动动能和宏观量气体温度之间的关系．分子的平均平动动能是大量分子的统计平均值，是每个分子平均占有的平动动能量值．解由气体动理论的能量公式，分子的平均平动动能为kT m 23212=v 容器中分子数nV N =，又由压强公式nkT p =，可得容器中所有分子的平均平动动能的总和为J152J 1010013.123232321352=⨯⨯⨯===-pV kT nV m Nv6-7 一容器内贮有氧气，其压强为Pa 10013.15⨯=p ，温度T =C 27︒，求(1)单位体积内的分子数；(2)氧气的密度；(3)氧分子的质量；(4)分子间的平均距离；(5)分子的平均平动动能；(6)若容器是边长为0.30 m 的立方体，当一个分子下降的高度等于容壁的边长时，其重力势能改变多少？并将重力势能的改变与其平均平动动能相比较．分析常温和常压下，氧气可视为理想气体．从宏观的角度，可以认为气体是空间均匀分布的，因此分子间的平均距离的立方就是每个分子平均占有的体积．通过本题的计算，可以得到气体动理论中常用到的物理量的量级概念．解 (1) 由理想气体的状态方程nkT p =，可得单位体积内的分子数为3-253-235m 1045.2m 3001038.110013.1⨯=⨯⨯⨯==-kT p n (2) 利用理想气体的状态方程RT MmpV =，氧气的密度为 3335kg/m 3.1kg/m 30031.8103210013.1=⨯⨯⨯⨯===-RT pM V m ρ(3) 氧分子的质量为kg 105.3kg 1045.23.126-25⨯=⨯==nm ρ(4) 分子平均占有的空间开方等于分子间的平均距离m 10443m 1045.21193253.n d -⨯=⨯== (5) 分子的平均平动动能J 10.216J 3001038.123232121-232⨯=⨯⨯⨯==-kT m v(6) 一个氧分子下降的高度等于容壁的边长时，其重力势能改变为J 101.56J 30.08.9103.5-2526⨯=⨯⨯⨯=-mgh与分子平均平动动能相比较，有4252121098.31056.11021.621⨯=⨯⨯=--mgh m v 6-8 在什么温度时，气体分子的平均平动动能等于一个电子由静止通过1 V 电位差的加速作用所得到的动能（即1eV 的能量）．解根据题意，气体分子的平均平动动能J 10260.1eV 12321192-⨯===kT m v 则 K 7739K 1038.1310602.122319=⨯⨯⨯⨯=--T 6-9 1 mol 氢气，在温度C 27︒时，求(1)具有若干平动动能；(2)具有若干转动动能；(3)温度每升高C 1︒时增加的总动能是多少？分析氢气是双原子分子气体，如果作为刚性分子看待，就具有3个平动自由度和2个转动自由度，根据能量按自由度均分原则可以求出平均平动动能和平均转动动能．解 (1) 1 mol 氢气的平动动能为J 10.743J 30031.82323233A⨯=⨯⨯==RT kT N(2) 1 mol 氢气的转动动能为J 10.492J 30031.8223A⨯=⨯==RT kT N(3) 温度每升高C 1︒，1 mol 氢气增加的总动能为J 8.02J 131.8252525A=⨯⨯=∆=∆T R T k N 6-10 1 mol 单原子理想气体和1 mol 双原子理想气体，温度升高C 1︒时，其内能各增加多少？1 g 氧气和1 g 氢气温度升高C 1︒时，其内能各增加多少？分析一定量理想气体的内能T R iM m E ∆=2，对于单原子理想气体3=i ，对于双原子理想气体5=i ，对于1 mol 理想气体1=Mm．氧气和氢气都是双原子气体，氧气的摩尔质量kg/mol 10323-⨯=M ．解 1 mol 单原子理想气体温度升高C 1︒，内能增量为J 5.12J 131.8232=⨯⨯=∆T R i1 mol 双原子理想气体温度升高C 1︒，内能增量为J 8.02J 131.8252=⨯⨯=∆T R i1 g 氧气温度升高C 1︒，内能增量为J 65.0J 131.8251032101233=⨯⨯⨯⨯⨯=∆--T R i M m 1 g 氢气温度升高C 1︒，内能增量为J 4.01J 131.825102101233=⨯⨯⨯⨯⨯=∆⋅--T R i M m 6-11 计算：(1)氧分子在C 0︒时的平均平动动能和平均转动动能；(2)在此温度下，4 g 氧的内能．分析氧气是双原子分子气体，如果作为刚性分子看待，就具有3个平动自由度和2个转动自由度，5=i ．解 (1) 氧分子在C 0︒时的平均平动动能为J 10.655J 2731038.1232321-23⨯=⨯⨯⨯=-kT 平均转动动能为J 10.773J 2731038.12221-23⨯=⨯⨯==-kT kT(2) 4 g 氧在C 0︒时的内能为J 709J 27331.8251032104233=⨯⨯⨯⨯⨯=⋅--RT i M m 6-12 有40个粒子速率分布如下表所示 (其中速率单位为m/s)：速率区间100以下100~200 200~300 300~400 400~500 500~600 600~700 700~800 800~900 900以上粒子数 1 4 6 8 6 5 4 3 2 1若以各区间的中值速率标志处于该区间内的粒子速率值，试求这40个粒子的平均速率v 、方均根速率2v 和最概然速率p v ，并计算出p v 所在区间的粒子数占总粒子数的百分率．分析为了更深入地理解麦克斯韦速率分布律以及气体动理论中引入的平均速率v 、方均根速率2v 和最概然速率p v 的统计意义，有必要通过实际例子，经过计算，体验速率分布规律和统计方法．解这40个粒子分成了10个速率区间，若取1000 m/s 为粒子速率在900 m/s 以上的速率区间的中值速率，则根据定义，其平均速率v 为m/s448.75 m/s )1100028503750465055506450 835062504150150(4011101=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯⨯==∑=i i i N N v v 方均根速率2v 为m/s 499.9 m/s )]1100028503750465055506450 835062504150150(401[121222222222210122=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯⨯==∑=i i i N Nv v 最概然速率m/s 350p =v ．p v 所在区间的粒子数占总粒子数的百分率为%20%100408p =⨯=∆NN 6-13上题所给分布情况，若以200m/s 为间隔作重新统计，列出分布情况表，计算出相应的v 、2v 和p v ，以及p v 所在区间的粒子数占总粒子数的百分率，并与上题结果进行比较．分析通过本题和上题计算结果可以看出，在某一速率区间中的分子数和所计算的三种速率不但与速率区间位置有关，还与速率区间的宽度有关．只有当所统计的分子总数足够大，划分的速率区间足够小时，才可能获得处于平衡状态的气体分子速率的一个确定的分布函数，三种速率也才有确定值．解以200m/s 为间隔对上题粒子速率作重新统计，速率分布情况为(其中速率单位为m/s)：速率区间 200以下 200~400 400~600 600~800 800以上粒子数 5 14 11 7 3这40个粒子分成了5个速率区间，若取900 m/s 为粒子速率在800 m/s 以上的速率区间的中值速率，则根据定义，其平均速率v 为m/s445 m/s)3900770011500143005100(401151=⨯+⨯+⨯+⨯+⨯⨯==∑=i i i N N v v 方均根速率2v 为498m/sm/s )]39007700 11500143005100(401[121222225122=⨯+⨯+⨯+⨯+⨯⨯==∑=i i iN Nvv最概然速率m/s 300p =v ．p v 所在区间的粒子数占总粒子数的百分率为%35%1004014p =⨯=∆NN 6-14 N 个假想的气体分子，速率分布如图6-14所示．(1)用N 和v 0表示出a 的值；(2)求最概然速率p v ；(3)以v 0为间隔等分为三个速率区间求各区间中分子数占总分子数的百分率．分析速率分布函数)(v f 表示气体分子速率在v 值附近单位速率区间内的分子数占总分子数的百分率．本题给出了一个特殊的分布情况，通过计算，理解速率分布函数和最概然速率的物理意义，以及各速率区间中分子数占总分子数的百分率的计算方法．解 (1) 由图6-14可见，分布函数与气体分子总数N 的乘积曲线下的总面积应等于气体分子总数N ，即000302322121d )(0v v v v v v a a a f N =⋅+==⎰则 032v Na =Nf (v )a0 v 0 2 v 0 3 v 0 v图6-14(2) 最概然速率 0p v v =(3) 以v 0为间隔等分为三个速率区间，分子数占总分子数的百分率分别为%3.3331211d )(10010==⋅==⎰v v v v a N f N N N %5021431d )(10220==⋅==⎰v v v v v a N f N N N %7.1661411d )(103230==⋅==⎰v v v v v a N f NN N *6-15在速率区间1v ～2v 内麦克斯韦速率分布曲线下的面积等于分布在此区间内的分子数的百分率．应用(6-17)式和麦克斯韦速率分布函数表示式(6-18)式，求在速率区间v p ～1.01v p 内的气体分子数占总分子数的比率．分析麦克斯韦速率分布律表明，由速率分布函数)(v f 可得气体分子速率在v ～v v ∆+速率区间内的分子数占分子总数的百分率为v v ∆=∆)(f NN．解麦克斯韦速率分布函数22232e24)(v v v kT m kT m f -⎪⎭⎫ ⎝⎛=ππ，因mkT2p =v ，则分布函数可写为1p 2p223p2p22p2e4e4)(----==v v v v v v v v v v ππππf 速率区间v p ～1.01v p 内的气体分子数占总分子数的比率为%83.001.01e 4e4e 4)(1p 2p223p 2p22p2=⨯⨯⨯=∆=∆=∆=∆----πππv v v v v v v v v v v v v f N N *6-16应用平均速率表示式(6-20)*式、麦克斯韦速率分布函数表示式(6-18)式以及积分公式bb 21d e23=-∞⎰v v v 求v 的值．分析这里采用的是数学中加权求某量值的平均值的方法，权重就是麦克斯韦速率分布函数)(v f ．如果要计算方均根速率2v ，可先求速率平方的平均值，只需将积分式中的v 改为2v ，即v v)v v d 022⎰∞=f(，再将积分结果开方．解麦克斯韦速率分布函数表示式(6-18)式和平均速率表示式(6-20)*式给出v v v v)v v v d e24d 0322302⎰⎰∞-∞⎪⎭⎫⎝⎛==kTm kT m f(ππ利用积分公式bb 21d e 23=-∞⎰v v v 得 mkTkT m kT m f(πππ822124d 2230=⎪⎭⎫ ⎝⎛⎪⎭⎫⎝⎛==⎰∞v v)v v *6-17 试由麦克斯韦速率分布律推出相应的平动动能分布律，并求出最概然能量E p ，它是否就等于2p 21v m ．分析要找出分子按平动动能的分布规律，即求出分布在平动动能区间E k ～E k +d E k 中的分子数占总分子数的百分率．解速率为v 的分子的平动动能为E k = 221v m ，则v v d d k m E =，麦克斯韦速率分布律可改写为kk k k 232212232223d )(d e12 d e 2112 d e 24d )(d k 22E E f E E kT m m kT kT m f N N kTE kT m kT m =⎪⎭⎫ ⎝⎛=⋅⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛==---ππππv v v v v v v v v即分子按平动动能分布律，其中分布函数kTE E kT E f k e12)(k 23k -⎪⎭⎫⎝⎛=π参考最概然速率的定义，令0d )(d kk =E E f ，由上式得最概然动能 kT E 21k p =因m kT 2p =v ，则 k p 2p 221E kT m ==v 6-18 飞机起飞前机舱中的压强计指示为Pa 10013.15⨯，温度为C 27︒．起飞后压强计指示为Pa 1010.84⨯，温度仍为C 27︒．试计算飞机此时距地面的高度．解根据玻尔兹曼分子数密度按高度分布公式kT mgh n n /0e -=和压强公式nkT p =，在高度1h 和2h 的压强分别为1p 和2p ，则有kT h h mg p p /)(2121e --=得m 100.2m 1010.810013.1ln 8.9102930031.8 ln ln 3453212112⨯=⨯⨯⨯⨯⨯⨯==+=-p p Mg RTp p mg kT h h6-19 设地球大气是等温的，温度为C 17︒，海平面上的气压为Pa 100.150⨯=p ，已知某地的海拔高度为h = 2000 m ，空气的摩尔质量kg/m ol 10293-⨯=M ，求该地的气压值．解根据玻尔兹曼分子数密度按高度分布公式kT mgh n n /0e -=和理想气体状态方程nkT p =，在高度h 处的压强p 为Pa 107.90Pa e100.1e 429031.820008.910295/03⨯=⨯⨯==⨯⨯⨯⨯---RT Mgh p p6-20 在某一粒子加速器中，质子在Pa 10333.14-⨯的压强和273 K 的温度的真空室内沿圆形轨道运动．(1)估计在此压强下每立方厘米内的气体分子数；(2)如果分子有效直径为2.0×10-8 cm ．则在此条件下气体分子的平均自由程为多大？分析由理想气体状态方程nkT p =可得压强和分子数密度的关系，并由此可计算平均自由程．解 (1) 由理想气体状态方程可得3103163234cm 1054.3m 1054.3m 2731038.110333.1----⨯=⨯=⨯⨯⨯==-kT p n (2) 由定义，平均自由程为cm 101.59m )102(1054.32121428102⨯=⨯⨯⨯⨯⨯==-ππλnd6-21设电子管内温度为300 K ，如果要管内分子的平均自由程大于10 cm时，则应将它抽到多大压强？（分子有效直径约为3.0×10-8 cm ）．分析由平均自由程定义和理想气体状态方程可建立压强与平均自由程以及温度之间的关系．解由平均自由程定义221ndπλ=和理想气体状态方程nkT p =，得Pa 0.1035Pa 1.0)103(23001038.12210232=⨯⨯⨯⨯⨯==--πλπd kT p6-22 计算：(1)在标准状态下，一个氮分子在1 s 内与其它分子的平均碰撞次数；(2)容积为4 L 的容器，贮有标准状况下的氮气，求1 s 内氮分子间的总碰撞次数．（氮分子的有效直径为3.76×10-8 cm ．）解 (1) 因平均速率MRTπ8=v ，标准状态下22.4 L 中的分子数为A N ，则平均碰撞次数1-91-32321033-A 22s 1067.7 s 104.2210023.6)1076.3(102827331.816 1022.4162⨯=⨯⨯⨯⨯⨯⨯⨯⨯=⨯==---πππN d M RT n d Z v(2) 4 L 氮的分子数N =A 4.224N ，分子间的总碰撞次数为1321923s 10125.4s 1067.710023.64.2242121-⨯=⨯⨯⨯⨯⨯=-Z N 6-23 假设氦气分子的有效直径为10-10 m ，压强为Pa 10013.15⨯，温度为300 K ，(1)计算氦气分子的平均自由程λ和飞行一个平均自由程所需要的时间τ；(2)如果有一个带基本电荷的氦离子在垂直于电场的方向上运动，电场强度为104 V/m ，试计算氦离子在电场中飞行τ时间内沿电场方向移动的距离s 及s 与λ的比值；(3)气体分子热运动的平均速率与氦离子在电场方向的平均速率的比值；(4)气体分子热运动的平均平动动能与氦离子在电场中飞行一个λ远的距离所获得的能量和它们的比值．解 (1) 由平均自由程定义221ndπλ=和理想气体状态方程nkT p =，得m 1029m 10013.1)10(23001038.1275210232-.pd kT ⨯=⨯⨯⨯⨯⨯==--ππλ 平均速率 m/s 1260m/s 10430031.8883=⨯⨯⨯⨯==-ππM RT v 则 s 107.3s 1260102.910-7⨯=⨯==-v λτ (2) 氦离子质量为A N M m =，沿电场方向受到的电场力为eE ，加速度meE a =，在τ时间内沿电场方向移动的距离为m 106.4m 1042103.710023.610106.1 2218-310234192A 2⨯=⨯⨯⨯⨯⨯⨯⨯⨯===---M eEN a s ττ 14.4104.6102.987=⨯⨯=--s λ(3) 氦离子沿电场方向的平均速率为m/s 87.7m/s 103.7104.6108E =⨯⨯==--τsv 14.4E==s λv v(4) 氦气分子平均平动动能为J 106.21J 3001038.1232321-23⨯=⨯⨯⨯=-kT 氦离子在电场中飞行一个λ远的距离所获得的能量为J 101.472J 102.910106.1-217419⨯=⨯⨯⨯⨯=--λeE二者之比为 22.410472.11021.62121=⨯⨯-- *6-24用范德瓦耳斯方程计算压强为Pa 10013.18⨯，体积为0.050 L 的1 mol氧气的温度，如果用理想气体状态方程计算，将引起怎样的相对误差？已知氧的范德瓦耳斯常数为：225/mol L Pa 10378.1⋅⨯=a ；L/mol 0318.0=b ．解由范德瓦耳斯方程得K 342.6K 10)0318.0050.0(050.010378.110013.131.81 )(13258020=⨯-⨯⎪⎪⎭⎫ ⎝⎛⨯+⨯⨯=-⎪⎪⎭⎫⎝⎛+=-b V V a p R T由理想气体状态方程得K .5609K 31.810050.010013.138=⨯⨯⨯==-R pV T相对误差为%7878.06.3426.3425.609==-*6-25在C 27︒时，2 mol 氮气的体积为0.1 L ，分别用范德瓦耳斯方程及理想气体状态方程计算其压强，并比较结果．已知氮气224/mol L Pa 1039.8⋅⨯=a ，L/mol 1005.32-⨯=b ．解范德瓦耳斯方程)(222RT M m b V V a M m p =-⎪⎪⎭⎫ ⎝⎛+，得Pa 109.43Pa 101039.82Pa 1005.321030031.82 782254222⨯=⨯⨯-⨯⨯-⨯⨯=--=----V a M m bMm V RTM m p 由理想气体状态方程得Pa 104.99Pa 1030031.8274⨯=⨯⨯==-V RT M m p 结果表明由理想气体状态方程计算出的压强小于由范德瓦耳斯方程的计算值．*6-26实验测知C 0︒时氧的粘滞系数1.92×10-4 s)g/(cm ⋅，试用它来求标准状态下氧分子的平均自由程和分子的有效直径．解粘滞系数 v λρη31= 其中密度Vm=ρ．又由理想气体状态方程 RT Mm pV =平均速率MRTπ8=v ，联立可得m109.49 m 1032827331.810013.11092.138338-355⨯=⨯⨯⨯⨯⨯⨯⨯⨯===--ππηρηλM RT p v 分子的有效直径为m 102.97m 1049.910013.122731038.1 210-8523⨯=⨯⨯⨯⨯⨯⨯⨯==--πλπp kT d*6-27实验测知氮气C 0︒时热传导系数为23.7×10-3 W/(m ·K)，定体摩尔热容为20.9 J/(mol ·K)，试由此计算氮分子的有效直径．解热传导系数 λρκv MC mV,31=其中密度A N nM =ρ，平均速率MRTπ8=v ，平均自由程221nd πλ=，则2Am V,132dM RT N C ππκ=m 102.23m 1102827331.810023.6107.2339.202 13210-4343233434Am V,⨯=⨯⨯⋅⨯⨯⨯⨯⨯=⋅=--ππκM RT N C d。