展开计算方法
钣金展开计算方法

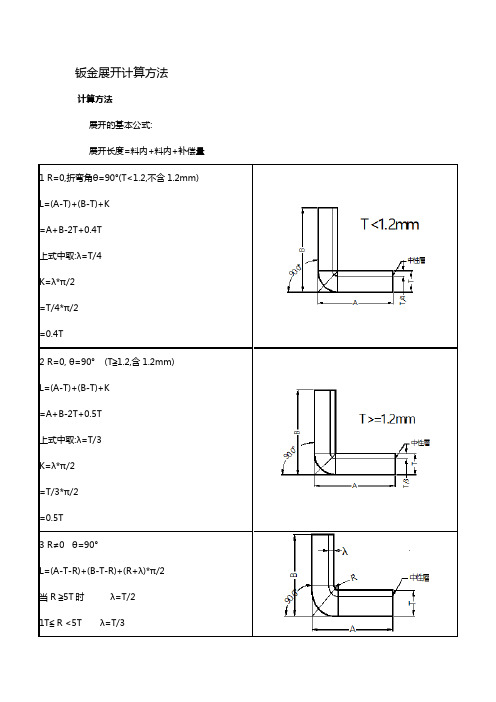
钣金展开计算方法计算方法展开的基本公式:展开长度=料内+料内+补偿量1 R=0,折弯角θ=90°(T<1。
2,不含1。
2mm)L=(A—T)+(B-T)+K=A+B-2T+0。
4T上式中取:λ=T/4K=λ*π/2=T/4*π/2=0。
4T2 R=0, θ=90°(T≧1。
2,含1.2mm)L=(A-T)+(B-T)+K=A+B-2T+0.5T上式中取:λ=T/3K=λ*π/2=T/3*π/2=0.5T3 R≠0 θ=90°L=(A—T—R)+(B-T-R)+(R+λ)*π/2当R ≧5T时λ=T/21T≦ R 〈5T λ=T/30 < R 〈t λ=t 4〈=””p=""〉〈/t λ=t>(实际展开时除使用尺寸计算方法外,也可在确定中性层位置后,通过偏移再实际测量长度的方法.以下相同)4 R=0 θ≠90°λ=T/3L=[A-T*tan(a/2)]+[B-T*tan(a/2)]+T/3*a(a单位为rad,以下相同)5 R≠0 θ≠90°L=[A-(T+R)* tan(a/2)]+[B—(T+R)*tan(a/2)]+(R+λ)*a当R ≧5T时λ=T/21T≦ R 〈5T λ=T/30 〈R 〈t λ=t 4<="" p=""〉〈/t λ=t〉6 Z折1。
计算方法请示上级,以下几点原则仅供参考:(1)当C≧5时,一般分两次成型,按两个90°折弯计算。
(要考虑到折弯冲子的强度)L=A—T+C+B+2K(2)当3T〈c<5时:〈/c<5时L=A—T+C+B+K(3)当C≦3T时〈一次成型〉:L=A—T+C+B+K/27 Z折2。
C≦3T时〈一次成型〉:L=A—T+C+B+D+K8 抽芽抽芽孔尺寸计算原理为体积不变原理,即抽孔前后材料体积不变;ABCD四边形面积=GFEA所围成的面积. 一般抽孔高度不深取H=3P(P为螺纹距离),R=EF 见图∵ T*AB=(H -EF)*EF+π*(EF)2/4∴ AB={H*EF+(π/4—1)*EF2}/T∴预冲孔孔径=D – 2ABT≧0。
产品展开计算方法
一般折弯:(R=0, θ=90°)L=A+B+K1. 当0T0.3时, K=02. 对于铁材:(如GI,SGCC,SECC,CRS,SPTE,SUS等)a.当0.3T 1.5时, K=0.4Tb. 当1.5T 2.5时, K=0.35Tc. 当T 2.5时, K=0.3T3. 对于其它有色金属材料如AL,CU:当T0.3时, K=0.4T注: R 2.0时, 按R=0处理,2<r<=3則R=3.一般折弯(R≠0 θ=90°)L=A+B+KK值取中性层弧长1. 当T 1.5 时λ=0.5T2. 当T 1.5时λ=0.4T一般折弯(R=0 θ≠90°)L=A+B+K’1. 当T0.3 时K’=02. 当T0.3时K’=(/90)*K注: K为90∘时的补偿量一般折弯(R≠0 θ≠90°)L=A+B+K1. 当T 1.5 时λ=0.5T2. 当T 1.5时λ=0.4TK值取中性层弧长注: 当R 2.0, 且用折刀加工时, 则按R=0来计算, A﹑B依倒零角后的直边长度取值当2<R<3时,按R=3计算Z折1(直边段差).1. 当H5T时, 分两次成型时,按两个90°折弯计算2. 当H5T时, 一次成型, L=A+B+KK值依附件中参数取值H与TZ折3(斜边段差).1. 当H2T时当θ≦70∘时,按Z折1(直边段差)的方式计算, 即: 展开长度=展开前总长度+K (此时K=0.2)当θ>70∘时完全按Z折1(直边段差)的方式计算2. 当H2T时, 按两段折弯展开(R=0 θ≠90°).。
产品展开计算方法

产品展开计算方法手工展开计算是一种传统的方法,适用于简单的产品或者需要快速计算的情况。
手工展开计算主要通过图纸上的测量工具(如尺子、量角器等)进行计算。
以纸箱为例,手工展开计算可以通过测量纸箱的各个面的长度、宽度和高度,然后按照一定的规则和比例进行展开、计算,得到纸箱展开平面的尺寸和形状。
计算机辅助设计(CAD)展开计算是一种现代化的方法,可以大大提高计算的准确性和效率。
CAD软件可以将产品的三维模型转化为二维图形,并提供自动展开计算功能。
通过CAD软件,设计师可以快速准确地计算出产品的展开尺寸和形状,并进行相应的优化和调整。
在进行产品展开计算时,需要考虑以下几个方面:1.尺寸测量:正确测量产品各部分的长度、宽度、高度等尺寸。
2.材料消耗:根据产品展开图的面积和形状,计算材料的消耗量。
这对于成本控制和资源利用非常重要。
3.容差和余量:考虑产品的装配、加工和使用过程中的容差和余量,确保展开计算结果的精确性和实用性。
4.形状优化:通过展开计算,可以发现产品的形状缺陷和设计问题,从而进行相应的优化和改进。
产品展开计算方法的应用范围非常广泛。
在家具行业,可以通过展开计算确定家具板材的尺寸和形状,进行材料采购和生产计划;在车辆制造行业,可以通过展开计算确定车身板材的尺寸和形状,进行钣金加工和装配;在建筑行业,可以通过展开计算确定建筑构件(如屋顶、墙体、门窗等)的尺寸和形状,进行施工和材料采购。
总之,产品展开计算是一项重要而复杂的工作,可以帮助设计师和生产者准确计算产品的尺寸和形状,优化产品设计和生产过程,提高生产效率和产品质量。
随着计算机技术的不断发展,产品展开计算方法将会得到更广泛的应用和进一步的发展。
数学代数式的展开

数学代数式的展开数学代数是数学中的一个重要分支,是一门研究代数结构、代数方程、代数式及其计算方法的学科。
其中,代数式的展开是数学代数的基础之一,它通过符号运算将复杂的代数式转化为更简单的形式,使数学问题的求解更加便捷。
本文将介绍数学代数式的展开过程、方法和应用。
一、数学代数式的展开过程数学代数式的展开是指将一个复杂的代数式,根据代数运算的规则,逐步进行符号运算,将其转化为一个或多个简化的代数式。
展开过程通常包括以下几个步骤:1. 去括号:将代数式中的括号按照乘法分配律展开,并合并同类项。
示例:展开(a+b)(c+d)可得ac+ad+bc+bd。
2. 幂运算:根据幂运算的基本法则,将代数式中的乘方进行展开,并合并同类项。
示例:展开(x+y)^2可得x^2+2xy+y^2。
3. 乘法运算:将代数式中具有乘法关系的项进行相应运算,并合并同类项。
示例:展开3(x+2y)可得3x+6y。
4. 除法运算:将代数式中具有除法关系的项进行相应运算,并合并同类项。
示例:展开(a^2+2a)/(a+1)可得a+1。
二、数学代数式的展开方法数学代数式的展开方法根据具体的代数式形式和展开要求,采用不同的策略和运算规则。
常见的展开方法主要包括:1. 多项式展开:对于多项式的展开,可以采用去括号和合并同类项的方法,逐步将复杂的代数式转化为简化的形式。
示例:展开(a+b)(c+d)可得ac+ad+bc+bd。
2. 幂展开:对于含有乘方项的代数式,可以运用幂运算的基本法则,将乘方项展开为一系列的乘法项,并合并同类项。
示例:展开(x+y)^2可得x^2+2xy+y^2。
3. 二项式展开:对于二项式的展开,可以利用二项式定理,根据展开式的次数,将其展开为一系列的项,并合并同类项。
示例:展开(a+b)^3可得a^3+3a^2b+3ab^2+b^3。
4. 泰勒展开:对于复杂的函数关系,可以使用泰勒级数展开,将函数展开为无穷项级数,并近似计算函数的值。
展开的计算法

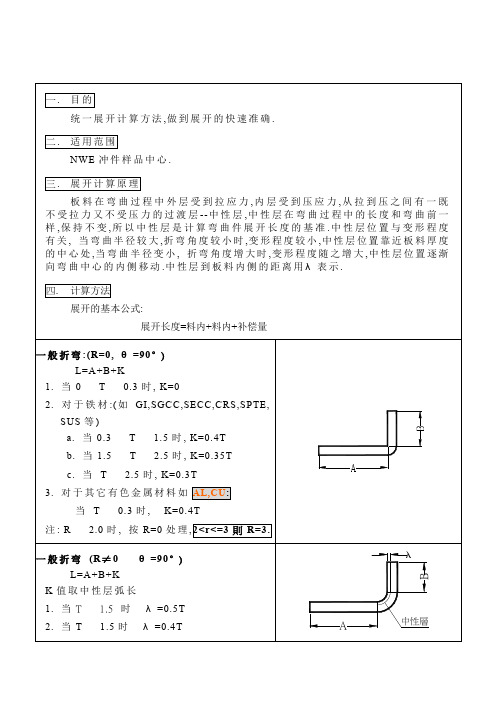
板料在弯曲过程中外层受到拉应力,内层受到压应力,从拉到压之间有一既不受拉力又不受压力的过渡层--中性层,中性层在弯曲过程中的长度和弯曲前一样,保持不变,所以中性层是计算弯曲件展开长度的基准.中性层位置与变形程度有关, 当弯曲半径较大,折弯角度较小时,变形程度较小,中性层位置靠近板料厚度的中心处,当弯曲半径变小, 折弯角度增大时,变形程度随之增大,中性层位置逐渐向弯曲中心的内侧移动.中性层到板料内侧的距离用λ表示. 展开的基本公式: 展开长度=料内+料内+补偿量 一般折弯:(R=0, θ=90°) L=A+B+K 1. 当0 T 0.3时, K=0 2. 对于铁材:(如GI,SGCC,SECC,CRS,SPTE, SUS等) a. 当0.3 T 1.5时, K=0.4T b. 当1.5 T 2.5时, K=0.35T c. 当T 2.5时, K=0.3T 3. 对于其它有色金属材料如AL,CU: 当T 0.3时, K=0.5T 注: R 2.0时, 按R=0处理. 一般折弯(R≠0 θ=90°) L=A+B+K K值取中性层弧长 1. 当T 1.5 时λ=0.5T 2. 当T 1.5时λ=0.4T 一般折弯(R=0 θ≠90°) L=A+B+K’ 1. 当T 0.3 时K’=0 2. 当T 0.3时K’=( /90)*K 注: K为90∘时的补偿量 一般折弯(R≠0 θ≠90°) L=A+B+K 1. 当T 1.5 时λ=0.5T 2. 当T 1.5时λ=0.4T K值取中性层弧长 注: 当R 2.0, 且用折刀加工时, 则按R=0来计算, A、B依倒零角后的直边长度取值 Z折1(直边段差). 1. 当H 5T 时, 分两次成型时,按两个90°折弯计算 2. 当H 5T时, 一次成型, L=A+B+K K值依附件中参数取值 Z折2(非平行直边段差). 展开方法与平行直边Z折方法相同(如上栏),高度H取值见图示 Z折3(斜边段差). 1. 当H 2T时 当θ≤70∘时,按Z折1(直边段差)的方式计算, 即: 展开长度=展开前总长度+K (此时K=0.2) 当θ>70∘时完全按Z折1(直边段差)的方式计算 2. 当H 2T时, 按两段折弯展开(R=0 θ≠90°). Z折4(过渡段为两圆弧相切): 1. H≤2T 段差过渡处为非直线段为两圆弧相切展开时,则取两圆弧相切点处作垂线,以保证固定边尺寸偏移以一个料厚处理,然后按Z折1(直边段差)方式展开 2. H>2T,请示后再行处理 抽孔 抽孔尺寸计算原理为体积不变原理,即抽孔前后材料体积不变;一般抽孔,按下列公式计算, 式中参数见右图(设预冲孔为X, 并加上修正系数–0.1): 1. 若抽孔为抽牙孔(抽孔后攻牙), 则S按下列原则取值: T≤0.5时取S=100%T 0.5<T<0.8时取S=70%T T≥0.8时取S=65%T 一般常见抽牙预冲孔按附件一取值 2. 若抽孔用来铆合, 则取S=50%T, H=T+T’+0.4 (注: T’是与之相铆合的板厚, 抽孔与色拉孔之间隙为单边0.10~0.15) 3. 若原图中抽孔未作任何标识与标注, 则保证抽孔后内外径尺寸; 4. 当预冲孔径计算值小于1.0时, 一律取1.0 反折压平 L= A+B-0.4T 1. 压平的时候,可视实际的情况考虑是否在折弯前压线,压线位置为折弯变形区中部; 2. 反折压平一般分两步进行 V折30° 反折压平 故在作展开图折弯线时, 须按30°折弯线画, 如图所示: N折 1. 当N折加工方式为垫片反折压平, 则按L=A+B+K 计算, K值依附件中参数取值. 2. 当N折以其它方式加工时, 展开算法参见“一般折弯(R≠0 θ≠90°)” 3. 如果折弯处为直边(H段),则按两次折弯成形计算:L=A+B+H+2K (K=90∘展开系数) 备注: a.标注公差的尺寸设计值:取上下极限尺寸的中间值作设计标准值. b.对于方形抽孔和外部包角的展开,其角部的处理方法参照<产品展开工艺处理标准>,其直壁部分按90°折弯展开。
(完整版)钣金展开计算方法
上式中取:λ=T/3
K=λ*π/2
=T/3*π/2
=0.5T
3 R≠0 θ=90°
L=(A-T-R)+(B-T-R)+(R+λ)*π/2
当R ≧5T时 λ=T/2
1T≦ R <5T λ=T/3
0 < R <t λ=t 4<="" p=""></t λ=t>
(实际展开时除使用尺寸计算方法外,也可在确定中性层位置后,通过偏移再实际测量长度的方法.以下相同)
D/2={(r+T/3)2
+2(r+T/3)*(h+T/3)
-0.86*(Rd-2T/3)*[(r+T/3)
+0.16*(Rd-2T/3)]}1/2
12卷圆压平
图(a): 展开长度
L=A+B-0.4T
图(b): 压线位置尺寸 A-0.2T
图(c): 90°折弯处尺寸为A+0.2T
图(d): 卷圆压平后的产品形状
4 R=0 θ≠90°
λ=T/3
L=[A-T*tan(a/2)]+[B
-T*tan(a/2)]+T/3*a
(a单位为rad,以下相同)
5 R≠0 θ≠90°
L=[A-(T+R)* tan(a/2)]+[B
-(T+R)*tan(a/2)]+(R+λ)*a
当R ≧5T时 λ=T/2
1T≦ R <5T λ=T/3
以下Hmax取值原则供参考.
当R≧4MM时:
材料厚度T=1.2~1.4取Hmax =4T
钣金展开计算原理及计算方法!

一、展开计算原理板料在弯曲过程中外层受到拉应力,内层受到压应力,理论上内外层之间有一既不受拉也不受压的过渡层------中性层,中性层为一假想层,在弯曲过程中中性层被假想为与弯曲前状态保持一致,即长度始终不变,所以中性层是计算弯曲件长度的基准。
中性层位置与变形程度有关,当弯曲半径较大,折弯角度较小时,变形程度较小,中性层位置靠近板料厚度的中心处;当弯曲半径变小,折弯角度增大时,变形程度随之增大。
中性层位置逐渐向弯曲中心的内侧移动。
中性层到板料内侧的距离用A表示(图1)。
二、折弯方法的确定折弯方法有单发冲床模具折弯和折弯机模具折弯两种方法。
单发冲床模具折弯的方式及精度是由模具来实现的。
因此只要做出合格的模具,就能够生产出合格的折弯产品。
而采用折弯机折弯不仅需要选用合适的折弯模,还必须调试折弯参数。
因此,如采用折弯机折弯,计算展开尺寸时就必须考虑折弯机的折弯方法。
1.一次一道弯。
此种折弯由普通通用折弯模来完成。
包括折直角,钝角和锐角(图2)。
2. 一次折两道弯——压锻差。
此种折弯由专用特殊模来完成,但折弯难度比普通折弯大(图3)。
3. 压死边。
此种折弯也须用特殊模来完成(图4)。
4.大R圆弧折弯。
些种折弯如R在一定范围内,可用专用R模压成形,如R值过大,则须用小R模多次压制成形(图5)。
这四种折弯的展开计算是不同的。
因此在看图时,要根据零件的折弯尺寸来确定使用何种折弯方法。
其折弯机所配套的普通通用折弯模具V形槽宽度通常为适用该折弯模的板厚的5-6倍。
如采用一次折一道弯的方法,必须考虑到折弯模的V形槽的宽度W1及V形槽一边到模具外侧的宽度L1,如图6所示。
折弯高度H的经验值根据产品形状有如下三种(以90度为例,钝角和锐角与直角相近相似)。
1.简单的90度单边折弯(图7)。
如图7所示,此种折弯只需考虑下模V形槽中心到折弯机定位挡块的距离即可确定。
通常H值为H≥3.5 T + R (R 在1mm 以下)。
数字的展开与合并掌握数字的展开和合并技巧

数字的展开与合并掌握数字的展开和合并技巧数字的展开与合并:掌握数字的展开和合并技巧数字的展开和合并技巧在数学学习中起着重要的作用。
通过展开和合并数字,我们可以更好地理解数的结构和性质。
本文将介绍数字展开和合并的相关概念,并提供一些实用的技巧和例子,帮助读者更好地掌握这一知识点。
一、数字的展开数字的展开是指将一个多位数划分为个位、十位、百位等各个位置上的数,并将其展开、拆分为各个位置上的数字的过程。
这个过程可以帮助我们更好地理解数的组成结构。
以两位数为例,比如数字56。
展开后,可以写为50+6,其中50表示十位上的数字,6表示个位上的数字。
同样,三位数和更多位数的数也可以进行展开。
在展开数字时,我们需要明确每个位置上数字的含义和权重。
比如,对于三位数123,它可以展开为100+20+3,其中100表示百位上的数字,20表示十位上的数字,3表示个位上的数字。
通过这种方式,我们可以更清楚地理解数字的大小和结构。
二、数字的合并数字的合并是指将各个位置上的数字按照一定的规则合并成一个整体的过程。
通过数字的合并,我们可以简化计算,并找到数字的规律和性质。
以两个位数为例,比如数字50+6。
可以合并为56,其中50表示十位上的数字,6表示个位上的数字。
同样,三位数和更多位数的数也可以进行合并。
在合并数字时,我们需要根据每个位置上数字的含义和权重进行合逆运算。
比如,对于三个位数100+20+3,可以合并为123,其中100表示百位上的数字,20表示十位上的数字,3表示个位上的数字。
通过这种方式,我们可以简化计算,并发现数字的规律和性质。
三、数字展开与合并的技巧1. 加减法运算中的数字展开与合并:在进行多位数的加减法运算时,我们可以通过数字展开与合并的方法,将计算过程简化。
例如,计算56+23,我们可以将56展开为50+6,23展开为20+3,然后进行合并得到73。
2. 乘法运算中的数字展开与合并:在进行多位数的乘法运算时,我们可以利用数字展开与合并的方法,找到数字之间的规律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(4)原图档须标注尺寸﹑插入图框,并以DIM识别码另存新档.
(5)必须标注的尺寸:料外折弯尺寸﹑抽孔尺寸﹑抽孔孔位尺寸.
(6)转DXF档时,将除LASER图层以外的图层关闭,输出DXF檔.
展开画法图例
加工类型
图例
注解
一般角度的折弯:
1.折弯线两边为展开前直边部分,折弯线之间为变形区部分,如图a所示.
一.目的:
統一展開計算方法,做到展開的快速准確.
二.適用范圍:
樣品中心工程管制部
三.展開計算原理:
1.板料在彎曲過程中外層受到拉應力,內層受到壓應力,從拉到壓之間有一既不受拉力又不受壓力的過渡層稱為中性層;中性層在彎曲過程中的長度和彎曲前一樣,保持不變,所以中性層是計算彎曲件展開長度的基準.
2.中性層位置與變形程度有關,當彎曲半徑較大,折彎角度較小時,變形程度較小,中性層位置靠近板料厚度的中心處;當彎曲半徑變小,折彎角度增大時,變形程度隨之增大,中性層位置逐漸向彎曲中心的內側移動.中性層到板料內側的距離用λ表示.
注: K值依附件一中參數取值.
Z折2 (非平行直邊段差):
展開方法與平行直邊Z折方法相同(如上欄),高度H取值見圖示.
Z折3 (斜邊段差):
1.當H2T時:
(1)當θ≦70∘時, L = A + B + C + K (此時K=0.2).
(2)當θ>70∘時,按Z折1 (直邊段差)的方式展開.
2.當H2T時,按兩段折彎展開(R=0,θ≠90°).
2.2若客戶圖紙上抽孔沒標抽孔孔徑尺寸,展開時以下列情形處理:
(1)當T'≧0.7T時,取T'=0.7T,並保証抽孔內徑.
(2)當0.5T<T'<0.7T時,按原圖抽孔內﹑外徑取值.
(3)當T'≦0.5T時,取T'=0.5T,並保証抽孔外徑.
注:若計算出的預沖孔孔徑<1.0,則取預沖孔徑為1.0.
反折壓平:
L= A+B-0.4T
1.壓平的時候,可視實際的情況考慮是否在折彎前壓線,壓線位置為折彎變形區中部.
2.反折壓平一般分兩步進行:
(1) V折30°
(2)反折壓平
故在作展開圖折彎線時,須按30°折彎線畫,如圖所示:
N折:
1.1.當N折加工方式為墊片反折壓平,則按L=A+B+K計算, K值依附件一中參數取值.
2.折弯线置于BEND层.
1.若抽孔為抽牙孔(抽孔后攻牙),則S取值原則如下:
(1) T≦0.5時,取S=100%T
(2) 0.5<T<0.8時,取S=70%T
(3) T≧0.8時取S=65%T
注:一般常見抽牙預沖孔按附件一取值.
2.抽孔展開處理:
2.1抽孔與沙拉孔鉚合時,抽孔外徑=沙拉孔底孔孔徑-0.3,壁厚=0.5T (通常情況下)
3.展开时,按照要求作出加工像素并放置于对应图层,画法图例参见附件一;展开长度算法参见《产品展开计算方法》.
4.若无特别指明,则按照"毛刺向内"的原则来判断产品毛刺方向,展开后的图形按毛刺向下的方式放置.
5.图形展开完毕后,必须将所有像素(圆孔除外)串成复线,并清除断点﹑重迭像素,并将外形轮廓作倒圆角处理.
6.所有由短小线段组成的像素,必须重画为规范像素(圆﹑直线);
7.特例情况(传海外图档):
(1)针对传海外图档,若仅要求展开,则除参照1~6条外,必须画出折弯示意图﹑前加工明细表﹑前加工成形示意图(包括抽孔的剖视图)﹑90∘折弯系数,各项具体要求参照《工程图面作业标准》.
(2)尺寸标注参照折床工程图的标注要求;此外,抽孔底孔﹑五金件底孔尺寸也须标注.
1.當T1.5時,λ=0.5T
2.當T1.5時,λ=0.4T
注:當用折刀加工時:
1.當R2.0時,按R=0處理.
2.當2.0<R<3.0時,按R=3.0處理.
3.當R≧3.0時,按原值處理.
Z折1 (直邊段差):
1.當H5T時,分兩次成型時,按兩個90°折彎計算.
2.當H5T時,一次成型, L=A+B+K
2.若变形区宽度小于0.15,则在展开图上仅保留靠近基体的折弯线,如图b所示.
3.折弯线置于BEND层.
段差
1.折弯内转角处倒零角.
2.折弯线两边为展开前两端直边部分.
3.折弯线置于BEND层.
反折压平
1.折弯线按150∘折弯时的画法,即将基体料内边界作为一条折弯线,向外偏5/3K后作为另一条折弯线(K为90∘折弯时系数).
1.展开时,英制单位一律转换为公制单位(乘25.4).
2.图纸标注尺寸与实际量测尺寸不符时,以标注尺寸为准,并按实际情况作下列处理:
(1)以公差要求最高的尺寸中最大的尺寸作为缩放基准,将整个图形缩放至与标识尺寸一致.
(2)若一小部分尺寸与实测尺寸相差0.1mm以上,则必须调整像素位置或大小以使其一致(错误的尺寸标注不在此列).
Z折4 (過渡段為兩圓弧相切):
1. H≦2T段差過渡處為非直線段兩圓弧相切展開時,取基體外側兩圓弧相切點處作垂線,向內側偏移一個料厚按圖示處理,然后按Z折1 (直邊段差)方式展開.
2. H>2T,請示后再按指示處理.
抽孔與抽牙孔:
抽孔尺寸計算原理為體積不變原理,即抽孔前后材料體積不變;一般抽孔,按下列公式計算,式中參數見右圖(設預沖孔徑為X,并加上修正系數–0.1):
四.展開計算Βιβλιοθήκη 法:展開計算的基本公式:展開長度=料內+料內+補償量
一般折彎1 (R=0,θ=90°):
L=A+B+K
1.當0<T≦0.3時, K=0
2.對于鐵材(如SUS﹑SGCC﹑SECC﹑CRS﹑SPTE等):
(1)當0.3<T<1.5時, K=0.4T
(2)當1.5≦T<2.5時, K=0.35T
當2. N折以其它方式加工時,展開算法參見“一般折彎(R 4 (R≠0 ,θ≠90°)”.
3. 3.如果折彎處為直邊(H段),則按兩次折彎成形計算: L= L=A+B+H+2K (K=90∘展開系數)
備註:
1.標注公差的尺寸設計值:取上下極限尺寸的中間值作設計標准值.
2.對於方形抽孔和外部包角的展開,其角部的處理方法參照《產品展開工藝處理標准》,其直壁部分按90°折彎展開.
2.當2.0<R<3.0時,按R=3.0處理.
3.當R≧3.0時,按原值處理.
一般折彎3 (R=0,θ≠90°):
L=A+B+K’
1.當T0.3時, K’=0
2.當T0.3時, K’= (/ 90) * K
注: K為90∘時的補償量.
一般折彎4 (R≠0 ,θ≠90°):
L=A+B+K (K值取中性層弧長)
(3)當T≧2.5時, K=0.3T
3.對于其它有色金屬材料(如Al﹑Cu等):
當T>0.3時, K=0.4T
一般折彎2 (R≠0,θ=90°):
L=A+B+K (K值取中性層弧長)
1.當T<1.5時,λ=0.5T
2.當T≧1.5時,λ=0.4T
注:當用折刀加工時:
1.當R≦2.0時,按R=0處理.
附件一:常見展開標准數據
1.直邊段差展開系數一覽表
2.常見抽牙預沖孔孔徑一覽表
3. N折展開系數一覽表
.目的:
统一展开作业的制作标准,做到展开的快速准确.
二.适用范围:
晟铭钣金部(宁波)
三.程序内容:
展开图是根据展开算法展开后的图,各部分加工像素放置于对应的加工图层,展开图作为工程图的设计基础,不出图.其作业规范如下:
